Introduction

Protein aggregation has become recognized as an important aspect of the protein folding landscape. This process not only interferes with protein expression and recovery assays used in biotechnology, but also impacts the every day live of cells and organisms and is associated with a variety of human diseases (Dobson 2003; Wetzel 2006). Methods to characterize aggregation kinetics comprise predominantly biochemical and biophysical approaches such as gel filtration, sedimentation assays, binding of fluorescent markers, AFM imaging, dynamic light scattering or circular dichroism that report on the oligomerisation state or the overall secondary structure content of the protein (Hurshman et al. 2004; Wetzel 2006).

Real-time solution-state NMR has shown to be useful to follow protein and RNA folding at the level of individual residues (Balbach et al. 1996; Van Nuland et al. 1998; Zeeb and Balbach 2004; Corazza et al. 2010; Lee et al. 2010). In principle, solid-state NMR (ssNMR) offers a complementary spectroscopic means to probe structural and kinetic aspects of protein folding and aggregation, especially as molecular aggregates increase in size. Indeed, ssNMR, has made great progress to structurally study trapped intermediate states of Amyloid (Chimon et al. 2007; Ahmed et al. 2010) and globular (Hu and Tycko 2010) proteins or to examine the effect of protein mutations known to interfere with protein aggregation (Heise et al. 2008; Karpinar et al. 2009; Kim et al. 2009). In principle, kinetic information becomes accessible by repeating ssNMR on cryotrapped intermediates at different time points or by recording NMR data directly during refolding. Indeed, time-resolved 1D ssNMR has been used to detect signal intensity buildup or decay during protein aggregation (Kamihira et al. 2000) and ATP hydrolysis of an ABC transporter (Hellmich et al. 2008) or by combining ssNMR pulse schemes with diffusion measurements using PFGs (Ader et al. 2010). Due to limited spectral resolution 1D ssNMR has to be combined with specific labeling techniques to offer site-specific resolution in proteins. Earlier, we have shown (Etzkorn et al. 2007) that for the Crh protein from B. subtilis, molecular aggregation triggered by a small temperature jump can be followed by two-dimensional ssNMR. Starting from a kinetically destabilized protein precipitate, protein aggregation led to significant increase in β-sheet content, whereas smaller α-helical fragments were retained in the aggregated state. Using Crh as an example, we here demonstrate that 2D ssNMR data sets recording these structural rearrangements in real time offer structural and, in particular, kinetic information about the process of protein aggregation. In general our analysis can offer atom-specific resolution for large segments of the protein and can simultaneously detect and kinetically describe a range of possible intermediate states during protein aggregation under conditions where molecular size or density prohibit the application of other biophysical methods.

Theory, materials and methods

Real-time NMR spectroscopy is sensitive to modulations of the signal induced by a transition between two or more conformational states present in the sample during acquisition. In general these modulations derive from changes in the population profile during the transition. This kinetic profile directly affects the time evolution for each spin and the resulting spectrum can be written (separately for a single spin in different states) as:

$$ \text{Re} (S(\omega )) = \int\limits_{0}^{\infty } {\left( {\sum\limits_{n} {a_{n} P_{n} (k_{i} ,t) \cdot e^{{(2\pi i\omega_{n} - \lambda_{n} )t}} } } \right)} \cdot e^{ - 2\pi i\omega t} dt $$
(1)

While the scaling factors a n account for variations in signal intensity among the different states n, the parameters λn are determined by the transverse spin relaxation rates. The kinetic profile P n (k j , t) reports on the population of state n characterized by resonance frequency ω n at a given time and depends on one or several rate constants k j describing the transition.

Normally, time frame, resolution and sensitivity offered by a single 1D NMR experiment are insufficient for the investigation of protein aggregation. A series of 1D spectra with sufficient repetition steps recorded during the transition (time-resolved NMR spectroscopy) can increase sensitivity and might offer an appropriate observation window. However, site specific resolution for larger fractions of the protein or even the detection of an intermediate species can be difficult to achieve. Instead, multidimensional spectroscopy can be used to follow the transition during the evolution of an indirect dimension (real-time NMR spectroscopy). Under the assumption that the transition during the repetitions of a single time step is negligible small, the spectrum after Fourier transformation (FT) in the direct dimension remains unaffected, whereas the peak shape and amplitude in the indirect dimension is modified. For a 2D spectrum (1) reads as:

$$ \text{Re} (S(\omega_{1} ,\omega_{2} )) = \int\limits_{0}^{\infty } {\left( {\sum\limits_{n} {a_{n} P_{n} (k_{i} ,t)} \cdot e^{{(2\pi i\omega_{1,n} - \lambda_{1,n} )t}} \cdot {L_{n}}(\omega_{2,n} )} \right) \cdot e^{ - 2\pi i\omega t} dt} $$
(2)

Note that (2) already includes the FT in the direct dimension (t 2) leading to the Lorentzian functions L n (ω 2,n ) for the states n. An exponential decay of state A during the evolution period in the indirect dimension is mathematically equivalent to an increased line-width for state A, whereas an exponential increase in the population leads to a base-line distortion and the occurrence of negative ‘shoulders’ of the corresponding peaks. These characteristic features are typically found experimentally in real-time NMR during protein folding in solution (Balbach et al. 1996).

For analysis relevant 1D extracts of real-time 2D spectra are usually fitted to theoretically simulated peak shapes (Balbach et al. 1996; Helgstrand et al. 2000) or a direct analytical solution (Balbach et al. 1999; Zeeb and Balbach 2004). Due to increased spectral overlap in ssNMR, we used (2) to develop a Mathematica (Wolfram scientific) script to calculate the difference of a full theoretical 2D cross peak pattern and the experimental data. Different transition scenarios were examined by varying the mathematical description of the kinetic profile. Amplitude factors a n were set to one, implying the same transfer efficiency for all states. Free theoretical parameters such as λ (1;2),n and ω (1;2),n were chosen according to the line width and position of the peak maxima in the experimental spectrum.

Simulating real-time 2D spectra

Mathematica (Wolfram scientific) version 6.0.1 was used to fit the experimental data to simulated peak patterns by numerically integrating (FT) S(t 1, ω 2) (2) for the population profiles considered. ‘SymbolicProcessing’ was switched off to speed up the integration process. The experimental spectrum was processed using exponential line broadening of 50 Hz. The underlying window function was also implemented in the simulations before FT in the indirect dimension. The effect in the direct dimension was neglected. Resonance frequencies of the occurring states were taken from corresponding cross signals in the experimental spectrum. The line width was measured using the Thr Cβ–Cγ2 cross peaks, which in the real-time 13C–13C 2D spin diffusion spectrum are not symmetric to the Thr Cγ2–Cβ peaks. Here the line width in the direct dimension is resolved and should be largely unaffected by the transition. The line width was comparable for all states, hence justifying in part the assumption a n  = 1 for all n.

Calculating difference plots

Experimental data were taken from Etzkorn et al. (2007). Signal intensity in the simulated spectra was read out at the corresponding data points obtained by processing the whole experimental spectrum with 512 points in ω 1 and 2,048 in ω 2. The spectral extract of the Thr Cγ2–Cβ (Cβ–Cγ2) cross section consists of 31 × 21 (21 × 31) values which were treated individually. Free parameters of the kinetic profile were varied in nested loops.

Conformational analysis

To evaluate the subset of the torsion angle space that is in agreement with the experimentally observed Thr Cβ shift we generated a set of heptapeptides (AATAA) by varying the Thr ψ and ϕ torsion angle in steps of 10°. ShiftX (Neal et al. 2003) was used to predict the expected chemical shift for each peptide. Chemical shift intervals [68.4, 70 ppm], [69.7, 70.8 ppm] and [70.4, 72.5 ppm] were chosen to select a match for the states A, B and C, respectively.

Results

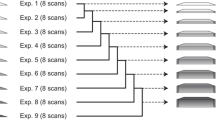
As described in Etzkorn et al. (2007), protein aggregation of the Crh protein induced by a modest temperature increase could be detected in real time during a 2D (13C, 13C) ssNMR experiment. The transition can be readily followed using cross-signal intensities in the Thr Cγ2–Cβ region. As visible in Fig. 1 the transition spectrum reveals resolved peaks for the initial state A (natively folded), an intermediate state B (partially unfolded) and a final state C (aggregated). Hence, application of (2) involves summation over three states (n = A, B, C).

Fig. 1
figure 1

Experimental ssNMR data (as reported in ref Etzkorn et al. (2007) of the Thr Cγ2–Cβ region of Crh recorded before the transition (left), during the transition (middle) and afterwards (right). Refolding was induced by increasing the temperature by 13°C at time t0. The time delay between spectrum 1 (native) and 2 (transition) was about 15 min to allow for system equilibration and readjustment of spectroscopic parameters. Spectra 2 and 3 were recorded without any additional time delay. In each case, data were acquired for about 24 h

Full size image

Conformational analysis

As shown before (Havlin and Tycko 2005; Heise et al. 2005) cross peak positions and line width offer a spectroscopic means to estimate the changes in backbone structure resulting from protein refolding. In the case of the Thr Cγ2–Cβ region, a torsion angle analysis for the involved states is presented in Fig. 2. In Fig. 2a, a subset of torsion angles which agree, according to shiftX (Neal et al. 2003), with the measured Thr Cβ peak position is shown. Note that dihedral angles predicted for the A-state (blue circles) agree well with values predicted from the X-ray structure for involved Threonines (black crosses, see also Etzkorn et al. 2004). An additional refinement of torsion angle space sampled during refolding can be obtained by taking into account allowed regions of the Ramachandran plot (Fig. 2b) and by considering only lowest energies assuming an amino-acid specific torsion angle potential as given in Kuszewski and Clore (2000) (Fig. 2c). Especially for the latter case, we find that the observed changes in the 2D ssNMR spectra can be explained by rather small changes in (Phi, Psi) space, at least in the case of Thr resonances.

Fig. 2
figure 2

Torsion angle analysis for the involved states. a Subset of torsion angles which agree, according to shiftX (Neal et al. 2003), with the measured Thr Cβ peak position (blue circles A-state; empty rectangles B-state; red diamonds C-state; black crosses as found in the X-ray structure for involved Threonines). b Torsion angles that are consistent with the peak position and fall in allowed regions of the classical Ramachandran plot. c Torsion angles that are consistent with the peak position and have most favorable energies assuming an amino-acid specific torsion angle potential as given in Kuszewski and Clore (2000)

Full size image

Crh in a classical three-state folding transition

For the Crh protein, three separate states could be detected in the real-time spectrum. Since the detected folding process is not reversible, we did not consider chemical exchange as a dominant effect to explain our experimental results. Instead, we applied a classical protein folding scenario (Balbach et al. 1996) in which the two underlying transitions are expected to be single exponential, leading to a kinetic profile of the form:

$$ P_{A} (k_{1} ,t) = e^{{ - k_{1} t}} $$
(3a)
$$ P_{B} \left( {k_{1} ,k_{2} ,t} \right) = \left( {1 - e^{{ - k_{1} t}} } \right)e^{{ - k_{2} t}} $$
(3b)
$$ P_{C} \left( {k_{1} ,k_{2} ,t} \right) = \left( {1 - e^{{ - k_{1} t}} } \right)\left( {1 - e^{{ - k_{2} t}} } \right) $$
(3c)

Figure 3a shows the resulting difference plot as a function of the two rate constants k 1 for unfolding and k 2 for aggregation. The resulting kinetic profile and spectral comparison of the best fit are given in Fig. 3d, g, respectively. The timescale of the simulated data and hence the absolute values for the involved rate constants have to be corrected for the difference of the indirect acquisition time and the time of the experiment, according to:

$$ k_{\text{eff}} = {\frac{{t_{\text{NMR}} }}{{t_{\text{real}} }}} \cdot k_{\text{NMR}} \approx 8.1 \times 10^{ - 8} \cdot k_{\text{NMR}} $$
(4)

The global minimum in Fig. 3a is given for the effective rate constants k 1 = 1.36 × 10−4 s−1 and k 2 = 0.58 × 10−4 s−1. Since the best fit (Fig. 3g) still shows some considerable differences to the experimental data, calculation of the error margin is not attempted here. However, the transition predominantly interferes with the acquisition of the indirect dimension rendering the (13C, 13C) spectrum asymmetric and cross peaks on different sides of the diagonal offer an independent set of information.

Fig. 3
figure 3

Results of the kinetic analysis assuming single exponential transitions. a–c Difference plot between normalized experimental data and theoretically calculated Thr Cγ2–Cβ cross signals as a function of both rate constants. For each pair of k1 and k2, the sum of the absolute value of the difference over all considered points in the 2D spectrum is plotted (see “Theory, materials and methods” for more details). Population profile (d–f) and comparison of spectral extract of the resulting best fit (g, h). Positive/negative contours of the experimental spectrum are given in black/blue, whereas theoretical data are given in red/purple. b As in a but for Thr Cβ–Cγ2 cross signal. c Normalized sum of a and b

Full size image

Figure 3b shows the difference plot for the Thr Cβ–Cγ2 cross correlations. The minimum is found for k 1 = 0.77 × 10−4 s−1 and k 2 = 0.52 × 10−4 s−1. Combination of data from both sides of the diagonal leads to the difference plot shown in Fig. 3c. The respective population profiles according to the best fit rate constants allow for an estimation of the accuracy of the method. The rate constants obtained from Fig. 3c are k 1 = 0.91 × 10−4 s−1 and k 2 = 0.65 × 10−4 s−1. Notably, the comparison of the theoretical spectra to the experimental ones (Fig. 3g, h) shows that characteristic features such as line broadening for the initial as well as baseline distortions for the final state are significantly less reproduced by the experimental data than expected for the considered single exponential transition.

Crh in a classical aggregation scenario

The single exponential transition used to describe protein folding (Balbach et al. 1996) is in general not sufficient to kinetically describe an aggregation process since it does not account for a nucleation step. Instead, several mechanisms and their mathematical formalisms have been suggested to describe experimentally determined data of protein aggregation (see, e.g. Thusius et al. 1975; Wegner and Engel 1975; Frieden and Goddette 1983; Eigen 1996; Ferrone 1999; Morris et al. 2008). In general, measurement of a population profile is not sufficient to reveal the underlying mechanism (Ferrone 1999). In the following the “Finke–Watzky” (F–W) model of protein aggregation (Watzky and Finke 1997) was selected to theoretically describe the kinetic profile. The F–W model assumes a 2-step mechanism involving a (slow) continuous nucleation with rate constant k a1, followed by a (fast) autocatalytic surface growth with the rate constant k a2. It was shown that this minimalistic kinetic model is able to account for a broad range of protein aggregation (Morris et al. 2008; Morris et al. 2009). The most convenient form for analyzing the experimental data was suggested (Morris et al. 2008) to be:

$$ \left[ C \right] = \left[ B \right]_{0} - {\frac{{{\frac{{k_{a1} }}{{ka_{2} }}} + \left[ B \right]_{0} }}{{1 + {\frac{{k_{a1} }}{{k_{a2} \left[ B \right]_{0} }}}e^{{\left( {k_{a1} + k_{a2} \left[ B \right]_{0} } \right)t}} }}} $$
(5)

where (5) only describes the aggregation process from the (unfolded) intermediate to the final aggregated state (B → C). The following time dependence of the relative populations was hence used to fit the experimental data:

$$ P_{A} \left( {t} \right) = e^{{ - k_{1} t}} $$
(6a)
$$ P_{B} (k_{a1},k_{a2},t) = \left( {1 - e^{{ - k_{1} t}} } \right){\frac{{{\frac{{k_{a1} }}{{k_{a2} }}} + 1}}{{1 + {\frac{{k_{a1} }}{{k_{a2} }}}e^{{\left( {k_{a1} + k_{a2} } \right)t}} }}} $$
(6b)
$$ P_{C} (k_{a1},k_{a2},t) = \left( {1 - e^{{ - k_{1} t}} } \right)\left( {1 - {\frac{{{\frac{{k_{a1} }}{{k_{a2} }}} + 1}}{{1 + {\frac{{k_{a1} }}{{k_{a2} }}}e^{{\left( {k_{a1} + k_{a2} } \right)t}} }}}} \right) $$
(6c)

Figure 4 summarizes the results obtained with this model. The three-dimensional contour maps shown in Fig. 4a–c, visualize areas which are within 5% (red), 10% (pale yellow) and 15% (white) deviation from the minimum difference between experimental and simulated cross section of Thr Cγ2–Cβ (a), Thr Cβ–Cγ2 (b) and both (c). The resulting population profile of the minimum is shown in Fig. 4d–f, respectively. Figure 4g, h compare the best fit (according to c and f) to the experimental data.

Fig. 4
figure 4

Results of the kinetic analysis using the F–W model. a–c Three-dimensional contour maps of the difference between experimental and simulated data depending on the three parameters k 1, k a1 and k a2. Red, yellow and white contour levels indicate areas within 5, 10 and 15% deviation to the best fit. The results for the Thr Cγ2–Cβ/Thr Cβ–Cγ2 cross section are shown in a/b, whereas c shows the sum of both. The kinetic profiles of the best fit are given in d–f, respectively. g, h Compare the experimental data to the best fit according to c and f. Color code as in Fig. 3 g, h

Full size image

Notably, a comparison to the best fit according to a single exponential three-state transition (Fig. 3a, b, lower part), reveals that the assumption of a nucleation step here did not improve the fitting. Indeed the line broadening of the initial state is predominantly related to the unfolding mechanism and, as evident from Fig. 4g, h, not reproduced even by the best fit of the profiles represented by (6a–6c).

Crh in a stretched exponential unfolding scenario

It has been reported that under specific circumstances a single exponential function is not sufficient to describe protein (un)folding (Sabelko et al. 1999). Phenomenological, these findings were related to a small or absent energy barrier separating the initial and final state (Garcia-Mira et al. 2002; Osváth et al. 2003; Nakamura et al. 2004). The absence of a distinct energy barrier can lead to a variety of possible transitions, each reflected by a different rate constant. Multiple or stretched exponential functions can be used to account for the occurring effects (Nakamura et al. 2004; Ma and Gruebele 2005). Introducing only one additional parameter b є [0, 1] a stretched exponential function was used to describe the protein unfolding as follows:

$$ P_{A} \left( {k_{1} ,b ,t} \right) = e^{{ - \left( {k_{1} t} \right)^{b} }} $$
(7a)
$$ P_{B} (k_{a1} ,k_{a2} ,b ,t) = \left( {1 - e^{{ - \left( {k_{1} t} \right)^{b} }} } \right){\frac{{{\frac{{k_{a1} }}{{k_{a2} }}} + 1}}{{1 + {\frac{{k_{a1} }}{{k_{a2} }}}e^{{\left( {k_{a1} + k_{a2} } \right)t}} }}} $$
(7b)
$$ P_{C} (k_{a1} ,k_{a2} ,b ,t) = \left( {1 - e^{{ - \left( {k_{1} t} \right)^{b}}} } \right) \left( {1 - {\frac{{{\frac{{k_{a1} }}{{k_{a2} }}} + 1}}{{1 + {\frac{{k_{a1} }}{{k_{a2} }}}e^{{\left( {k_{a1} + k_{a2} } \right)t}} }}}} \right) $$
(7c)

Equations 7a–7c contain four free parameters. The results of fitting this model to the experimental spectrum as a series of 3D contour maps depending on the parameter b are shown in Fig. 5. Each 3D plot depends on the same three parameters as described in Fig. 4. Although the high number of free parameters impedes an accurate determination of the rate constants, it is clearly evident that the simulated cross correlation approaches the experimental data for b < 1. Plotting the minimal difference to the experimental data as a function of b (Fig. 5b) reveals that the global minimum is found for b = 0.1. However, also values up to b = 0.4 may reproduce the experimental spectrum within an error of 5%. Figure 5c–e shows the population profile as well as the resulting peak pattern of the best fit (b = 0.1; k 1 = 2.03 × 10−4 s−1; k a1 = 0.78 × 10−4 s−1; k a2 = 0.81 × 10−5 s−1). Indeed the stretched exponential unfolding scenario could explain the missing line broadening in the experimental data of state A.

Fig. 5
figure 5

Kinetic analysis assuming downhill unfolding and the F–W model for aggregation. a 3D contour maps as given in Fig. 4c, but for indicated values of b. The minimal difference found to the experimental data depending on b is plotted in b. c The population profile of the global minimum and (d + e) the corresponding simulated peak pattern

Full size image

Notably, a completely heterogeneous aggregation scenario also involving a stretched exponential aggregation step as suggested for transthyretin aggregation (Hurshman et al. 2004) could also explain the data (see supporting figure SI 1). However, experimental data analyzed here exclusively report on the population profile. Additional studies on the effect of concentration of native Crh and of seeding with preaggregated Crh may help to discriminate between stretched exponential aggregation, i.e. heterogeneous growth of aggregates with the monomer as the critical nucleus size, and the F–W model, i.e. continuous nucleation followed by an autocatalytic surface growth (Ferrone 1999; Hurshman et al. 2004).

Discussion

Several methods exist that allow studying protein aggregation kinetics. Most of these techniques rely on the detection of global factors or indirect mechanisms (e.g. the β-strand content in Thioflavin T binding or CD spectroscopy) and may lack the formation and kinetic properties of intermediate species. Here we have shown that ssNMR can contribute to the kinetic and structural analysis of insoluble protein conformations, in particular of those including intermediate folding states which might be an important target to interfere with the aggregation process (Cohen and Kelly 2003).

While intermediate states might be rapidly frozen for a more detailed structural study (Chimon et al. 2007; Ahmed et al. 2010; Hu and Tycko 2010), real-time ssNMR offers unique possibilities to characterize aggregation kinetics. The range of observable states can be modified by a combination of different sets of polarization transfer mechanisms (e.g. based on dipolar or scalar couplings) (Andronesi et al. 2005) or by simply recording ssNMR spectra after direct excitation (Kamihira et al. 2000). Our analysis was solely based on ssNMR cross-signal intensities from a single kinetic transition to investigate the potential of the method. Changes in backbone conformation were estimated from an analysis of conformation-dependent chemical shifts. Rate constants could be extracted using a single exponential three-state transition as well as a conventional aggregation mechanism. No significant difference between the two approaches could be detected, suggesting that the formation of a nucleus is not a significant step in the aggregation of Crh protein precipitates. Remaining differences to the experimental data additionally suggest that a single exponential transition for the initial unfolding step does not suffice to properly describe the time course of the folding process. Instead, a stretched exponential function, as found in downhill folding (Sabelko et al. 1999; Nakamura et al. 2004), significantly improves the agreement between experimental and theoretical data. The stretched exponential decay would be consistent with a heterogeneous unfolding step involving one or several fast as well as slow decaying components.

While limitations regarding sensitivity and resolution do not allow for a more detailed analysis of the aggregation mechanism from ssNMR at this stage, ssNMR studies using selectively labeled protein variants and the combination with other biophysical methods will provide additional opportunities to refine kinetic and structural profiles. Such studies may not only be relevant in the context of molecular aggregation but their application may also facilitate an atomic description of inter-molecular interactions in the context of molecular gel formation (Ader et al. 2010) or protein insertion into membranes.