Abstract
The 6-dimensional(6D) APSY-seq-HNCOCANH NMR experiment correlates two sequentially neighbor in gamidemoieties in proteins via the C′ and Cα nuclei, with efficient suppression of the back transfer from Cα to the originating amidemoiety. The automatic analysis of two-dimensional(2D) projections of this 6D experiment with the use of GAPRO (Hilleretal., 2005) provides a high-precision 6D peak list, which permits automated sequential assignments of proteins with the assignment software GARANT (Bartels et al., 1997). The procedure was applied to two proteins, the 63-residue 434-repressor(1-3) and the 115-residue TM1290. For both proteins, complete sequential assignments for all NMR-observable backbone resonances were obtained, and the polypeptide segments thus identified could be unambiguously located in the amino acid sequence. These results demonstrate that APSY-NMR spectroscopy in combination with a suitable assignment algorithm can provide fully automated sequence-specific backbone assignments of small proteins.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The 6D APSY-seq-HNCOCANH experiment connects two sequentially neighboring amide moieties in polypeptide chains via the carbonyl and Cα atoms, with the back transfer from Cα to the originating amide moiety suppressed in this sequential (seq) experiment (Figure 1). Thus, each peak from the 6D peak list generated by GAPRO correlates the resonance frequencies of two sequentially adjacent amide moieties. Clearly, this information will be adequate for the sequential assignment of the backbone resonances, provided that there is sufficient dispersion of the amide group chemical shifts. In this paper, we used the 6D peak lists thus obtained as input for the program GARANT (Bartels et al., 1997) in order to obtain NMR assignments for the two proteins 434-repressor(1–63) (Neri et al., 1992) and TM1290 (Etezady-Esfarjani et al., 2004), in an approach which does not involve any further human interaction after starting the APSY-NMR experiments.
Magnetization transfer in the 6D APSY-seq-HNCOCANH experiment. The pathway represented by the dashed arrows a to e (Equation (5)) leads to a single peak in the 6-dimensional frequency space. The dotted arrow indicates an undesired magnetization back transfer, which is suppressed by the experimental scheme shown in Figure 2 (see text).
Materials and methods
NMR measurements
The 6D APSY-seq-HNCOCANH experiment with a 0.9 mM solution of 434-repressor(1–63) was recorded at 30°C on a Bruker DRX 750 MHz spectrometer equipped with a triple-resonance probehead with a z-gradient coil. The spectral widths were 3000 Hz, 1600 Hz, 1900 Hz and 5700 Hz in the 1HN, 15N, 13C′ and 13Cα dimensions, respectively. The interscan delay was 1.0 s, and 32 transients were accumulated for each increment of the combined evolution time. 1024 complex points were recorded in the acquisition dimension, with a sweep width of 11.0 ppm. In the indirect dimension, 64 complex points were measured. The total spectrometer time used for the recording of 25 2D projections (Table 1) was 40 h.
The corresponding experiment with a 3.0 mM solution of TM1290 was recorded at 35°C on a Bruker DRX 500 MHz spectrometer equipped with a triple-resonance cryogenic probehead with a z-gradient coil. The spectral widths were 2000 Hz, 1650 Hz, 1500 Hz, and 3800 Hz in the 1HN, 15N, 13C′ and 13Cα dimensions, respectively. The interscan delay was 1.0 s, and 8 transients were accumulated. 1024 complex points were recorded in the acquisition dimension, with a sweep width of 12.0 ppm. In the indirect dimension, 128 complex points were measured. The total spectrometer time used for the recording of 25 2D projections (Table 1) was 19.6 h.
Recording of projection spectra
For a 2D projection of the 6D APSY-seq-HNCOCANH experiment with the four projection angles α, β, χ and δ, the time domain was sampled along a straight line defined by the unit vector \({{\rm{\vec p}}_1}\),
.
The spectral width, SW, of each 2D projection was calculated from
, where p i1 represents the coordinates of the vector \({{\rm{\vec p}}_1}\) (see Equation (1)), and SW i are the spectral widths of the five indirect dimensions. The dwell time for the recording of discrete data points, Δ, was calculated as
, and the resulting increments for the evolution times t i , Δ i , in the five indirect dimensions are given by
.
Quadrature detection was achieved using hypercomplex Fourier transformation on pure sine and cosine terms of corresponding positive and negative projection angles, which were obtained using the trigonometric addition theorem (Brutscher et al., 1995; Freeman and Kupče, 2004). In the 6D-seq-HNCOCANH experiment (Figure 2), the five evolution time periods t i (i = 1,…,5) were performed as semi-constant time or as constant time periods, depending on the value of the increment Δ i , and on the number of complex points, n, recorded in the indirect dimension. The initial values for t i a, t i b and t i c are given in the caption to Figure 2. For Δ i /2 > t i c/n, semi-constant time evolution periods were applied, with t i c being decremented by Δ i c=t i c/n, and t i a and t i b incremented by Δ i a =Δ i /2 and Δ i b=Δ i a −Δ i c, respectively. In all other situations, constant time evolution periods were used, with t i c decremented by Δ i c =Δ i 2, t i a incremented by Δ i a =Δ i /2, and t i b maintaining its initial value.
6D-APSY-seq-HNCOCANH experimental scheme, which correlates pairs of sequentially adjoining amide protons (Figure 1). The alternative out-and-back magnetization transfer pathway, which ends at the starting amide moiety, is efficiently suppressed (see text). Radio-frequency pulses were applied at 118.0 ppm for 15N, 173.0 ppm for carbonyl carbons (13C′), and 54.0 ppm for 13Cα. At the outset of the pulse sequence (“HN“ on the line 1H), the proton carrier frequency was set in the amide proton region at 8.2 ppm, and at the time point “H2O” the carrier was set to 4.7 ppm. Narrow and wide rectangular bars represent non-selective 90° and 180° pulses, respectively. Thin sine bells are shaped 90° pulses, and fat sine bells are shaped 180° pulses. Individual shaped pulses are identified with the capital letters A to F. The actual shapes depend on the purpose of the pulses, and the durations depend on the shape and the spectrometer frequency (here: 500 MHz): A, Gaussian shape, 150µs; B, Gaussian, 180µs; C, I-burp (Geen and Freeman, 1991), 300µs; D, Gaussian, 120µs; E, E-burp (Geen and Freeman, 1991), 400µs; F, RE-burp (Geen and Freeman, 1991), 525µs. The last six hard pulses on the 1H line represent a 3-9-19 WATERGATE element (Sklenar et al., 1993). The four pulses marked with an asterisk are continuously centered with respect to the time periods t 2 a+t 2 b, t 2 c, t 3 a+t 3 b, and t 3 c, respectively. Grey pulses were applied for compensation of off-resonance effects (Bloch and Siegert, 1948; McCoy and Mueller, 1992). Decoupling using DIPSI-2 on 1H (Shaka et al., 1988) and WALTZ-16 on 15N (Shaka et al., 1983) is indicated by white rectangles. The triangle with t 6 represents the acquisition period. On the line marked PFG, curved shapes indicate sine bell-shaped, pulsed magnetic field gradients applied along the z-axis, with the following durations and strengths: G1, 700µs, 13 G/cm; G2, 1000µs, 35 G/cm; G3, 800µs, 20 G/cm; G4, 800µs, 32 G/cm; G5, 800µs, 13 G/cm; G6, 1000µs, 35 G/cm; G7, 800µs, 18 G/cm. The following phase cycling was used:ϕ 1=y, −y, ϕ 2=x, x, −x, −x, ϕ 3=x, −x, −x, x, ψ 1=x, ψ 2=x, ψ 3=y, ψ 4=x, ψ 5=x, and all pulses without indication of a phase above the pulse symbol were applied with phase x. The time points s, t, u, v, and w are discussed in the text. The following initial delays were used: t 1 a=t 1 c=2.7 ms, t 2 a=t 2 c=14.0 ms, t 3 a=t 3 c=4.75 ms, t 4 a=4.75 ms, t 4 b=20.25 ms, t 4 c=25.0 ms, t 5 a=t 5 c=14.0 ms, and t 1 b=t 2 b=t 3 b=t 5 b=0 ms. The delay τ=2.7 ms was invariant during the experiment, and the delay δ was continuously adjusted to δ=(t 5 a+t 5 b−t 5 c)/2. In the five indirect evolution periods, constant-time or semi-constant-time periods were applied (see text). Quadrature detection for the indirect dimensions was achieved using the trigonometric addition theorem to obtain pure cosine and sine terms for a subsequent hypercomplex Fourier transformation (Brutscher et al., 1995; Kupče andFreeman, 2004). The pulse phases w1 to w5 were used for this purpose for the dimensions ω 1 to ω 5, respectively, and only the pulse phases of the evolution periods which are part of the given projection (Table 1) are phase cycled. For consecutive FIDs, ψ 1, ψ 2, ψ 3, and ψ 4 were simultaneously incremented in 90° steps, and ψ 2 was decremented in 90° steps.
Processing of the 2D projection spectra
All data processing steps were fully automated. Zero-order phase correction for the direct dimension was determined with PROSA (Güntert et al., 1992). The use of constant-time or semiconstant time evolution periods and proper phase settings in the pulse program (Figure 2) provides absorptive in-phase signals for the indirect dimension, without need for phase correction. In both dimensions, the FID was multiplied with a 75°-shifted sine bell prior to Fourier transformation (De Marco and Wüthrich, 1976), and zero-filled to the next power of two complex points. The baseline was corrected using the IFLAT method (Bartels et al., 1995) in the direct dimension, and polynomials in the indirect dimension.
APSY analysis
The 2D projection spectra were automatically peak picked with the peak picking routine of ATNOS (Herrmann et al., 2002), with R min=4.0 for 434-repressor(1–63) and R min=5.0 for TM1290. The resulting peak lists of the projections were analyzed with the algorithm GAPRO (Hiller et al., 2005), which identifies all projected peaks arising from the same 6D peak, and then calculates the final 6D peak list. For 434-repressor(1–63), GAPRO was applied with the parameters j=25, S min,1=S min,2=5, k=50, w=200, r min=50 Hz, Δνmmin=7.5 Hz. The calculation time on a standard LINUX PC with a 2.8 GHz Pentium 4 processor was approximately 10 min. For TM1290, GAPRO was applied with the parameters j=25, S min,1=S min,2=5, k=100, w=400, r min=50 Hz, Δχmin=5.0 Hz. The calculation time was approximately 30 min.
Protocol and parameters used for automated assignment with GARANT
The precise and artifact-free 6D peak lists obtained for the two proteins from the 6D-APSY-seq-HNCOCANH experiment were used as input for the assignment algorithm GARANT (Bartels et al., 1997), which had been modified by increasing the maximally allowed dimension from 4 to 6. GARANT was applied to the 6D peak lists using a standard annealing protocol (Bartels et al., 1997). For each peak list, 30 resonance assignment calculations were performed, using as input the same 6D-APSY-seq-HNCOCANH peak list but different, randomly chosen starting conditions. The 30 resulting sequence-specific resonance assignments were merged into one list. An assignment for a given atom was accepted if the same result, within 0.02 ppm and 0.4 ppm for protons and heavy atoms, respectively, was obtained in at least 50% of the calculations. Otherwise, the backbone atom was considered to remain unassigned.
Results
The 6D APSY-seq-HNCOCANH NMR experiment
This experiment connects sequentially adjacent amide moieties. Previous experimental schemes providing corresponding information include 3D and 4D HN(COCA)NH (Bax and Grzesiek, 1993), which also connect sequential amide moieties via Cα and the carbonyl carbon. With APSY, the full potential of this magnetization transfer pathway is exploited in a six-dimensional experiment (Figure 1). The existing 3D and 4D versions give rise to an intraresidual and a sequential peak (Grzesiek et al., 1993; Matsuo et al., 1996; Panchal et al., 2001). Since the intraresidual peak resulting from the “back transfer” magnetization pathway would not contribute any new information, it is efficiently suppressed in the 6D APSY-seq-HNCOCANH experiment, and only one peak for each pair of sequentially adjacent amide moieties appears in the 6D frequency space. In the coherence transfer scheme of Equation (5), the transfer steps of Figure 1 are represented by Cαrtesian product operators (Sørensen et al., 1983), where chemical shift evolution and transfer efficiencies are not represented, and only relevant magnetization components are retained.
Above the arrows which connect subsequent states, we indicate the active J coupling constants and the evolution periods t i , with the active nucleus in parentheses. Below the arrows, the letters a to e relate the magnetization transfer steps to the corresponding steps in Figure 1. The characters s, t, u, v and w at the end of the individual product operator expressions indicate time points in the experimental scheme shown in Figure 2. The suppression of the back transfer pathway (dotted line in Figure 1) is implemented between the time points u and v, where the one-bond scalar coupling \(^1 J_{NC^\alpha}\) as well as the two-bond coupling \(^2 J_{NC^\alpha}\) are active, leading to the terms Cz α,i−1Nz i−1 and Cz α,i−1Nz i at time v. The term Cz α,i−1Nz i−1 is associated with the sequential pathway and eventually leads to H y/N,i−1x , which is the desired signal measured during the acquisition period. The term Cz α,i−1Nz i leads to back transfer and ends up as undesired magnetization on the amide proton from which the experiment was started, H y/N,i−1x (Panchal et al., 2001). The transfer efficiencies for the terms Cz α,i−1Nz i−1 and Cz α,i−1Nz i, respectively, are proportional to the expressions (6) and (7):
.
The values of \(1/(2 \cdot ^1 J_{NC^\alpha})\) and \(1/(2 \cdot ^2J_{NC^\alpha})\) are similar, and adjusting the time period T=t 4 a +t 4 b+t 4 c between u and v (Figure 2) to the average of these two values results in strong attenuation of the back transfer peak (Equations (5) to (7)). During the period T, the magnetization evolves also due to the scalar coupling between α- and β-carbons, and values of T close to multiples of 27 ms are therefore preferred for optimal sensitivity. Overall, T=50 ms was found to be a good compromise. Considering the variations of \(^1 J_{NC^\alpha}\) and \(^2 J_{NC^\alpha}\) along a polypeptide chain, the back transfer of magnetization (dotted line in Figure 1) can then reach at most 10% of the intensity of the corresponding desired peak (Brutscher, 2002). In the 6D APSY-seq-HNCOCANH experiment the undesired resonance was very well suppressed with T=50 ms, retaining high sensitivity for the observation of the desired sequential signal (Figure 3).
Suppression of the C αi − 1 → 15Ni back transfer (Figure 1) in the 6D-APSY-seq-HNCOCANH spectrum of [13C,15N]-labeled 434-repressor(1–63) (protein concentration = 0.9 mM, 20 mM sodium phosphate at pH 6.5, T=15° C). Shown are 1D cross sections through the projection spectra recorded with the projection angles (α, β, χ, δ)=(0°, 90°, 0°, 0°), which were taken at the Arg 5 15N-frequency of 125.06 ppm and cover the 1HN chemical shift range containing the intraresidual correlation to Arg 5 and the sequential correlation to Ser 4. The time period T=t 4 a+t 4 b+t 4 c (Figure 2) was set to 50 ms (top) and 27 ms (bottom), resulting in experiments with (top) and without (bottom) suppression of back transfer.
APSY-NMR with the proteins 434-repressor(1–63) and TM1290
In the context of this paper, 6D APSY-seq-HNCOCANH experiments (Figure 2) were recorded with the two proteins TM1290 and 434-repressor(1–63). For each protein, 25 projections were measured, using the projection angles given in Table 1. 20 projection angles were chosen such that all possible pairs of evolution dimensions are combined in two projections. In addition, 5 “direct” projections along a single evolution dimension were measured. These projections fully exploit the six-dimensionality of the experiment, even though none of the selected individual projection includes chemical shift information of more than 3 nuclei (Table 1). Combinations of more than two evolution dimensions could readily be recorded and analyzed with the present setup. The price to pay would be that these projection experiments have reduced sensitivity, since the sensitivity is proportional to \({(1/\sqrt 2 )^{n - 1}}\), where n is the number of combined evolution dimensions.
The projection spectra were automatically peak picked, and the 2D peak lists were used as input for the GAPRO algorithm in order to compute the 6D peak positions (Hiller et al., 2005). Since peak picking uses the individual projections, the sensitivity exploited in this step is in principle that of the individual 2D projections. However, GAPRO makes further use of the fact that the NMR peak positions in different projections are correlated, so that noise peaks can be efficiently eliminated. The signal-to-noise ratio can therefore be as low as 3–5 without generating artifacts in the final results from the peak picking (S/N ratio = peak maximum divided by the standard deviation of the noise).
For the two protein samples presented here, sensitivity was not a limiting factor. In both applications, a complete 6D APSY peak list was obtained for the residues with observable 15N-1H signals (see below). Since the 6D APSY-seq-HNCOCANH scheme correlates two sequential amide protons, the N-terminal residue, the Pro residues, and possibly other residues without observable 1HN signal are not contained in this peak list.
For 434-repressor(1–63), the peak list contained 56 out of 57 peaks that would be expected from the chemical structure of the molecule, and there were no artifacts. The connection between residues 2 and 3 was missing, probably because local dynamics lead to a reduction of the signal below the noise level in all projection spectra.
For TM1290, all but three of the peaks expected from the previous, interactively deter mined assignment (Etezady-Esfarjani et al., 2003) were contained in the final 6D peak list. TM1290 contains dynamically disordered regions, which makes the sequential 1HN-1HN connectivities in the regions 46–52 and 72–73 NMR-unobservable (Etezady-Esfarjani et al., 2003). Three additional peaks were missing in the GAPRO peak list, i.e., the connections 19–20, 20–21 and 71–72, because the signal intensities were below the noise level in the 6D APSY-seq-HNCOCANH data set but not in the conventional triple resonance experiments (Etezady-Esfarjani et al., 2003). The final GAPRO peak list thus contained 98 sequential peaks, and there were no artifacts.
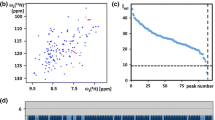
In Figure 4, the 6D peak list obtained from 25 2D projections (Table 1) of the 6D APSY-seq-HNCOCANH experiment with TM1290 is projected onto two experimental 2D projections, visualizing the excellent agreement between the calculated and measured peak positions. The precision of the chemical shifts can be directly measured in the 6D APSY-seq-HNCOCANH data set, since the resonance of each amide moiety is part of two different 6D peaks. In one of these two peaks, the amide proton chemical shift is measured in the direct dimension (ω6) during acquisition, and in the second peak the same 1HN proton shift contributes to the indirect dimension (ω1); the corresponding 15N chemical shift is also measured twice, in ω5 and ω2. There are 93 amide moieties that contribute to two peaks in the 6D peak list of TM1290, and from these the chemical shift differences ω1(1H) − ω6(1H) and ω2(15N) − ω5(15N) were calculated. The resulting standard deviation for the proton chemical shifts was 0.0014 ppm (0.72 Hz), with a maximal deviation of 0.005 ppm (2.5 Hz), and the standard deviation for the nitrogen chemical shifts was 0.0137 ppm (0.69 Hz), with a maximal deviation of 0.048 ppm (2.4 Hz).
Visualization of part of the result of the fully automated sequence-specific backbone resonance assignment of the [13C, 15N]-labeled protein TM1290 (protein concentration 3.0 mM, 20 mM phosphate buffer at pH 6.0, T = 35° C). (a) and (b) are regions of two orthogonal projection spectra from a 6D APSY-seq-HNCACONH experiment with projection angles (α, β, χ, δ)=(0°, 0°, 0°, 0°) and (90°, 0°, 0°, 0°), respectively. The 6D APSY peak list is projected onto the spectra by black dots. The sequence-specific resonance assignment, as found by GARANT, is written next to each peak, using the one-letter amino acid code and the sequence position.
Backbone resonance assignment of 434-repressor (1–63)
The software GARANT had previously been shown to yield reliable automated sequential NMR assignments, provided that an input of precise, artifact-free peak lists was available (Bartels et al., 1997). We therefore chose GARANT to perform sequential assignments based on the presently obtained 6D APSY peak lists.
For the 434-repressor(1–63), 30 GARANT calculations all converged to the correct sequencespecific resonance assignment for all the resonances contained in the 6D peak list. This assignment procedure based on the 6D APSY-seq-HNCOCANH experiment yielded three fragments of length 39, 3 and 17 residues, which could unambiguously be fitted to the sequence of 434-repressor(1–63) in the positions 3–41, 43–45, and 47–63, respectively. These fragments are separated by the two prolines in positions 42 and 46. For the residues 1 and 2, the 15N-1H NMR signals were not observed. A plot corresponding to Figure 5 therefore contains a continuous thick line at the level N=30 for the polypeptide segments 3–41, 43–45, and 47–63 (not shown).
Automated sequence-specific resonance assignment for the protein TM1290 obtained with GARANT (Bartels et al., 1997), using as input the peak lists from a 6D APSY-seq-HNCOCANH experiment calculated with the program GAPRO. GARANT was run 30 times with the same input list of 6D peaks but with different, randomly chosen starting conditions. For each residue the most frequent 1HN assignment was counted and plotted as a square along the vertical N-axis (thick black lines correspond to a sequence of squares). If N ≥ 15 (dashed horizontal line), the sequence-specific assignment was accepted. All other 1HN were considered to remain unassigned. The amide protons of residues 1, 6, 20, 46–52 and 72–73, which include the prolines 6 and 51, are not contained in the 6D APSY-seq-HNCOCANH resonances. With the acceptance criterion used here, all these amide protons remained unassigned.
Backbone resonance assignment for TM1290
30 GARANT calculations made with the 6D APSY-peak list of TM1290 did not all converge to the correct solution, but for all the resonances observed in the 6D experiment the correct sequence-specific assignment was found in at least half of the calculations. Erroneous assignments of residues for which no NMR signals had been observed were obtained only in a small number of the calculations (Figure 5). This result can be rationalized based on previous work with TM1290, which had shown that the proline residue in positions 6, and other residues with NMR-unobservable amide moieties divide the TM1290 sequence into sequentially connected segments of residues 2–5, 7–45, 53–71 and 74–115 (Etezady-Esfarjani et al., 2003). As mentioned above, three signals expected from the results of this earlier work could not be detected by the 6D APSY experiment, so that overall the 6D correlation NMR signals with the residues 1, 6, 20, 46–52 and 72–73 were absent.
Discussion
The results obtained for the 434-repressor(1–63) and for TM1290 (Figures 4 and 5) document that 6D APSY-seq-HNCOCANH data sets can provide the information needed for obtaining de novo backbone resonance assignments for small and medium-size proteins. Here we want to further investigate the robustness of the procedure with respect to deterioration of the 6D data sets, and to replacement of 6D APSY-NMR with lower-dimensional APSY-NMR experiments.
Model calculations on the impact of type and quality of APSY-NMR data on the resonance assignments
Peak lists from 6D APSY-seq-HNCOCANH have outstandingly high information content, with six chemical shifts per peak, high accuracy of the chemical shifts, and no or very few artifacts. The influence of variable quality of the input on the automated assignment procedure was evaluated by computationally generating lower-dimensional peak lists, which in their combinations had, in principle, the same information content as the 6D peak list. We thus generated peak lists for combinations of the two 4D spectra HNCOCA and HNCACO, and the four 3D spectra HNCA, HN(CO)CA, HN(CA)CO and HNCO from the 6D APSY-NMR peak list of TM1290. These peak lists contain overlapping peaks that could not be resolved in the 3D or 4D spectra, but are resolved in the 6D APSYHNCOCANH spectrum. The two 4D and the four 3D peak lists, respectively, were used as input for 30 GARANT calculations (Figure 6, c and d). Although these computationally generated peak lists had the same chemical shift precision as the experimental 6D peak list, 4 and 15 of the previously assigned residues, respectively, were not assigned by GARANT when using the 4D and 3D data sets, and the 4D data sets led to two erroneous assignments.
Extent of the automated backbone assignment of the protein TM1290 achieved with GARANT when using input peak lists of different quality. The height of the diagonally dashed areas along the vertical axis indicates the number of 1HN-15N moieties for which both 1HN and 15N were correctly assigned in the final chemical shift list; gray areas indicate the number of amide group resonances that remained unassigned; vertically dashed areas represent the number of NMR-unobservable amide groups (see text); black areas indicate the number of erroneous assignments, which all occur for residues for which no NMR signals were observed; the white area at the top indicates the residues for which no 1HN signals are expected, i.e., the N-terminal residue and the two prolines. The interpretation of this data can be based on the following properties of TM1290, which are visualized in (a): the protein contains 115 residues with 112 backbone amide groups that should normally be observable by NMR. Of these, 8 were not detected in conventional 2D and 3D NMR experiments, so that sequence-specific assignments were obtained for 104 amide groups (Etezady-Esfarjani et al., 2003). (b) to (g) represent the extent of assignments obtained with GARANT when using the following six different input data sets: (b): final 6D peak list from the 6D APSY-seq-HNCOCANH measurement (same as Figure 5); (c) Two 4D peak lists computed from the original 6D peak list for the experiments 4D APSY-HNCOCA and 4D APSY-HNCACO; (d) Four 3D peak lists computed from the original 6D peak list for the experiments 3D APSY-HNCA, 3D APSY-HN(CO)CA, 3D APSY-HNCO and 3D APSYHN( CA)CO; (e): Ten 6D peak lists generated by randomly varying the peak positions in the experimental 6D peak list (b) along ω 6(1N) and ω 5(15N) within 0.02 and 0.4 ppm, respectively; (f) Ten 6D peak lists generated by adding 10 artifacts at random positions to the experimental 6D peak list (b); (g) Combination of (e) and (f). For each data set, the GARANT analysis was repeated 30 times with different, random starting conditions (Bartels et al., 1997), and the results were analyzed as described in Material and methods. For each of the columns (e) to (g), the average of the results obtained with the 10 deteriorated peak lists is plotted in the figure (see text).
The influence of the accuracy of the chemical shifts, and of the presence of artifacts in the input peak lists on the automated assignment procedure was tested by randomly varying the peak positions in the 6D APSY-NMR peak list of TM1290, and by adding artifacts to it. In one of the “deteriorated” 6D peak lists, the peak positions in the dimensions ω6(1H) and ω5(15N) were randomly changed within ranges of 0.02 ppm and 0.4 ppm, respectively (Figure 6e), ensuring that all connectivities could be found within the tolerance range used by GARANT. In another modification of the 6D peak list, 10 artifacts were added at random positions within the experimental spectral ranges (Figure 6f). Finally, chemical shift variation of individual peaks and the addition of artifacts were combined in a single list (Figure 6g). Each type of deteriorated list was generated 10 times, with different, randomly chosen chemical shift changes and/or additions of artifacts at different random positions. For each of the resulting 30 peak lists, 30 GARANT calculations were performed and analyzed as described above for the experimentally obtained 6D APSY-seq-HNCOCANH peak list. The results for the 10 lists with random chemical shift changes, the 10 lists with artifact peaks, and the 10 lists containing both manipulations, respectively, were then averaged. Figure 6, e to g, shows the average number of correctly assigned residues (diagonally dashed areas), the average number of unassigned residues for which an assignment is expected (gray areas), the average number of “correctly unassigned residues”, i.e., residues for which the 15N-1H NMR signals could not be detected (vertically dashed areas), and the average number of erroneously assigned residues (black areas).
Overall, these model calculations revealed an encouraging robustness of the APSY-NMR-based assignment, since throughout at least 85% of the NMR-observable residues were assigned, with a correctness rate above 97% (Figure 6). Nonetheless, deterioration of the high-quality peak list obtained from the 6D APSY-NMR experiment did lead to fewer residues being assigned, and to introducing some wrong assignments, which however always occur for residues for which no NMR signals were observed. Similar effects resulted from the replacement of 6D APSY-seq-HNCOCANH with, in principle, equivalent combinations of lower-dimensional APSY-NMR experiments, where the combination of four 3D data sets resulted in the lowest yield of correct assignments. The combination of two 4D data sets, in contrast, gave nearly the same extent of correct assignments as the 6D data set, albeit with introduction of erroneous assignments for two NMR-unobservable residues, which we presently attribute to an intrinsic weakness in the GARANT assignment protocol (see below).
Outlook
The use of a single 6D APSY experiment to perform the backbone resonance assignment avoids calibration problems between different spectra, the high dimensionality eliminates resonance overlaps, and the high information content of a 6D peak reduces the number of possible assignment combinations and thus makes the procedure of sequential backbone assignments efficient and robust. Based on the large dispersion of the 15N chemical shifts in polypeptide chains (Braun et al., 1994; Wüthrich, 1986), the 6D-APSY-seq-HNCOCANH experiment should in principle be widely applicable.
For practical applications, it will be of interest to further optimize the sensitivity of APSY-NMR experiments. Obviously, minor but not negligible improvements may result from adding water flipback pulses (Grzesiek and Bax, 1993) and sensitivity enhancement schemes (Palmer et al., 1991; Kay et al., 1992). Furthermore, part of the projections could be measured with individually optimized, shortened pulse sequences, which would improve the sensitivity for these projections (Kupče and Freeman, 2003). For example, direct projection of the ω5(15N)-dimension could be replaced by a standard [15N,1H]-HSQC experiment. In this context, the outcome of the model studies with 3D and 4D APSY-NMR data sets (Figure 6, c and d) is also highly encouraging. For these intrinsically more sensitive APSY experiments, which are based on combining HNCACO and HNCOCA elements, there is a clear promise for use with larger proteins. Current work in our laboratory is focused on generating combinations of lower-dimensional APSY-NMR experiments suitable for use with larger proteins.
The software GARANT used here to derive automated backbone resonance assignments had been developed to work with peak lists obtained from “conventional” heteronuclear correlation and triple resonance NMR spectra. It allows multiple alternative assignments in situations of peak overlap, and it has been laid out to deal with the presence of artifacts. High-dimensional APSYNMR data sets typically contain no or at most few peak overlaps and artifacts. Substituting GARANT with a new assignment algorithm that is tailored specifically for the needs to analyze APSY-NMR data for automated resonance assignment, promises to further enhance the potentialities of APSY-NMR-based automated resonance assignment for proteins.
In conclusion, APSY-NMR combined with a suitable assignment algorithm promises to enable fully automated sequence-specific backbone resonance assignments for small and medium-sized proteins. Eliminating the extensive human interactions typically needed so far for obtaining NMR assignments will further add to making high-resolution NMR with proteins an attractive tool in structural biology and structural genomics. The algorithm GAPRO and the pulse sequence used in this work are available from the authors.
References
BartelsC.,GüntertP.,BilleterM.andWüthrichK.(1997).J.Comput.Chem.18:139–149
BartelsC.,GüntertP.andWüthrichK.(1995).J.Magn.Reson.A117:330–333
BaxA.andGrzesiekS.(1993).Accts.Chem.Res.26:131–138
BlochF.andSiegertA.(1948).Phys.Rev.57:522–527
BraunD.,WiderG.andWüthrichK.(1994).J.Am.Chem.Soc.116:8466–8469
BrutscherB.(2002).J.Magn.Reson.156:155–159
BrutscherB.,MorelleN.,CordierF.andMarionD.(1995).J.Magn.Reson.B109:238–242
WüthrichK.andMarcoA.(1976).J.Magn.Reson.24:201–204
Etezady-EsfarjaniT.,HerrmannT.,PetiW.,KlockH.E.,LesleyS.A.andWüthrichK.(2004).J.Biomol.NMR29:403–406
Etezady-EsfarjaniT.,PetiW.andWüthrichK.(2003).J.Biomol.NMR25:167–168
FreemanR.andKupčeE.(2004).Conc.Magn.Reson.23:63–75
GeenH.andFreemanR.(1991).J.Magn.Reson.93:93–141
GrzesiekS.,AnglisterJ.,RenH.andBaxA.(1993).J.Am.Chem.Soc.115:4369–4370
GrzesiekS.andBaxA.(1993).J.Am.Chem.Soc.115:12593–12594
GüntertP.,DötschV.,WiderG.andWüthrichK.(1992).J.Biomol.NMR2:619–629
HerrmannT.,GüntertP.andWüthrichK.(2002).J.Biomol.NMR24:171–189
HillerS.,FioritoF.,WüthrichK.andWiderG.(2005).Proc.Natl.Acad.Sci.USA.102:10876–10881
KayL.E.,KeiferP.andSaarinenT.(1992).J.Am.Chem.Soc.114:10663–10665
KimS.andSzyperskiT.(2004).J.Biomol.NMR28:117–130
KupčeE.andFreemanR.(2003).J.Am.Chem.Soc.125:13958–13959
KupčeE.andFreemanR.(2004).J.Am.Chem.Soc.126:6429–6440
MatsuoH.,KupčeE.,LiH.J.andWagnerG.(1996).J.Magn.Reson.B111:194–198
McCoyM.A.andMuellerL.(1992).J.Magn.Reson.99:18–36
NeriD.,BilleterM.andWüthrichK.(1992).J.Mol.Biol.223:743–767
PanchalS.C.,BhaveshN.S.andHosurR.V.(2001).J.Biomol.NMR20:135–147
PalmerA.G.,CavanaghJ.,WrightP.E.andRanceM.(1991).J.Magn.Reson.93:151–170
ShakaA.J.,KeelerJ.,FrenkielT.andFreemanR.(1983).J.Magn.Reson.52:335–338
ShakaA.J.,LeeC.J.andPinesA.(1988).J.Magn.Reson.77:274–293
SklenarV.,PiottoM.,LeppikR.andSaudekV.(1993).J.Magn.Reson.A102:241–245
SørensenO.W.,EichG.W.,LevittM.H.,BodenhausenG.andErnstR.R.(1983).Prog.Nucl.Magn.Reson.Spectrosc.16:163–192
SzyperskiT.,YehD.C.,SukumaranD.K.,MoseleyH.N.B.andMontelioneG.T.(2002).Proc.Natl.Acad.Sci.USA.99:8009–8014
WüthrichK.(1986).NMRofProteinsandNucleicAcids.JohnWiley&Sons,NewYork
Acknowledgement
The authors thank Drs. Fred F. Damberger and Touraj Etezady-Esfarjani for gifts of 434-repressor(1–63) and TM1290, respectively. This work was supported by the Schweizerischer Nationalfonds and the ETH Zürich through the National Center for Competence in Research (NCCR) Structural Biology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Francesco Fiorito and Sebastian Hiller-Both authors contributed equally to this work
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Fiorito, F., Hiller, S., Wider, G. et al. Automated Resonance Assignment of Proteins: 6 DAPSY-NMR. J Biomol NMR 35, 27–37 (2006). https://doi.org/10.1007/s10858-006-0030-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10858-006-0030-x