Introduction

Teachers are crucial to student learning (Hattie, 2009, p. 150), and in recent years teachers’ professional development has received increased attention. Traditionally, teacher professional development has consisted of short-term endeavors, such as lectures, where the teachers have consumed knowledge imparted by some external agent. This tradition has not had an expected effect on teaching (e.g., Darling-Hammond et al., 2017) and research suggests that teachers’ professional development should build on teacher collaborations, in which the teachers are challenged to unpack and explore their teaching and to try out, analyze, and evaluate different ways of teaching (e.g., Garet et al., 2001; Garrison, 2016; Slavit et al., 2011; Vescio et al., 2008). However, despite the promises of teacher collaboration, we observe it does not always seem to lead to developing teaching practices (Robutti et al., 2016). Teachers’ joint work may often be reduced to a situation in which only practical issues are discussed (Collinson, 2000; Makopoulou & Armor, 2014; Scherp & Scherp, 2007), such as what new textbook to buy, or to one in which the teachers simply share ideas (Scherp & Scherp, 2007). While we are beginning to amass rather good documentation that teachers’ joint work is not always successful in developing teaching practices, we know less about the basis of such shortcomings. On this account, the present study aims to make a contribution to research on professional learning communities (PLC) in mathematics by distinguishing contradictions that can occur in such activities.

We have adopted the Cultural Historical Activity Theory (CHAT) (Engeström, 1987). This means that we consider PLCs in terms of an activity system and search for contradictions, and manifestations of contradictions, that can occur in such a system. It is important to identify contradictions, as the resolution of a contradiction is crucial in developing an activity system. It is also important to identify contradictions as they may implicitly act as obstacles to the development of an activity system (Engeström, 1987).

Our data consist of two iterations of interviews with four teacher leader coaches with extensive experience in coaching teacher leaders. A teacher leader guides the work in the PLC by planning, structuring, and ensuring a focus the work in the group (Borko et al., 2008; Campbell & Stohl Lee, 2017b; Dobie & Anderson, 2015; Gellert, 2013; Murata et al., 2012; Vangrieken et al., 2017). Hence, by interviewing teacher leader coaches, we can obtain information from a variety of PLCs in mathematics and, consequently, a broad basis for distinguishing and analyzing contradictions in PLCs in mathematics. Our aim is to identify possible contradictions in PLCs in mathematics. We address the research question “What contradictions can be manifested in PLCs in mathematics?”.

Before we go into detail about CHAT and the conceptualization of contradictions, we discuss relevant research on PLCs in mathematics.

Professional learning communities in mathematics

Teacher professional development can be designed in many different ways. Lectures, workshops, coaching, courses over several days, participation in learning communities, and pedagogical development projects are just a few examples of teacher professional development described in the literature (see e.g., Campbell & Griffin, 2017; Vescio et al., 2008; Villegas-Reimers, 2003; Wylie et al., 2008). It can take the form of formal or informal professional development, have different purposes, and include one, several, or a large number of teachers (see e.g., Akiba & Liang, 2016; Levine, 2010; Vangrieken et al., 2017). Research on effective teacher professional development highlights the importance of joint teacher work that contributes to promoting school change beyond individual classrooms (Darling-Hammond et al., 2017; Hord, 1997; Knapp, 2017; Louis et al., 1996; Perez et al., 2007). There are several ways of conceptualizing joint teacher work (Levine, 2010). In this study, we follow Vangrieken et al. (2017), using professional learning communities (PLC) as an overarching term for teachers working together and engaging in continual dialog with the aim to inquire into and develop their teaching. A PLC consists of a “school staff team, which works collaboratively and collegially in order to improve student learning” (Vangrieken et al., 2017, p. 49) by “sharing and critically interrogating their practice in an ongoing, reflective, collaborative, inclusive and learning-oriented, growth-promoting way” (Stoll et al., 2006, p. 223). PLCs can involve both general and subject-specific teaching issues. In this study, we focus on PLCs in mathematics. We have distinguished four structures that research has found to be critical for the productivity of PLCs on both a general and a subject-specific level: allocation of enough time, systematicity in inquiry processes, collaborative engagement of all teachers, and a safe and challenging learning community.

Allocation of enough time

Time is key to teacher learning and school development (Collinson & Fedoruk Cook, 2001). PLCs should be extended over a long duration of time, and teachers need time for engaging in PLCs (Desimone, 2009). There is a need to designate time during which teachers’ learning activities are prioritized and they are not constantly interrupted by other issues (Mason et al., 2019). It takes time to develop norms and attitudes in teacher groups, moving from simply sharing ideas toward a collaborative learning environment where teachers explore and develop their teaching practices (Vangrieken et al., 2017). Moreover, both the teachers and the one who guides the teachers’ work need sufficient time for preparation and work between meetings (Collinson & Fedoruk Cook, 2001; Knapp, 2017; Vangrieken et al., 2017).

Systematicity in inquiry processes

PLCs should take the form of systematically structured inquiry processes. The PLC should follow a cyclic structure in which inquiry into the teachers’ own teaching practice constitutes the basis for the PLC (Kuijpers et al., 2019; Timperley, 2011). In a cyclic process, teachers can be engaged in questioning and reflecting on their teaching and in developing, proving (in practice), evaluating, and adjusting tools or methods for teaching. New insights and understandings lead to new questions in a continuing cycle (Timperley, 2011).

Teaching is a complex enterprise, and research has shown that it is difficult for teachers to inquire into their teaching practice to identify and suggest areas in need of development in PLCs (Campbell & Stohl Lee, 2017b; Slavit et al., 2011). The situation seems to be even more difficult for teachers engaged in subject-specific PLCs, such as PLCs in mathematics, as this requires them to dig into the details of students’ learning of a particular subject matter (Campbell & Stohl Lee, 2017b). PLCs should therefore provide teachers with opportunities to encounter, and learn to use, tools or methods to enhance their ability to examine and scrutinize their teaching (Garrison, 2016; Jaworski, 2006). A teacher leader has been shown to be crucial for organizing and moving a PLC forward. In a traditional initiative on professional development, a teacher leader often takes the role of an educator or expert. In a PLC the teacher leader is supposed to take a guiding role with responsibility for planning, structuring, leading the discussions, distribute the talking space, and ensure the right focus of the work in the group (Borko et al., 2008; Campbell & Stohl Lee, 2017b; Dobie & Anderson, 2015; Gellert, 2013; Murata et al., 2012; Vangrieken et al., 2017).

Collaborative engagement of all teachers

To get the most out of PLCs, there should be active participation among all teachers. All teachers should take on the role of co-producers of knowledge, rather than being passive receivers (consumers) and executors of pre-packaged knowledge provided by a teacher leader or the literature (Desimone, 2009). Having all teachers engaged in the PLC, and making them understand its meaning and potential, can be a major task to accomplish (Makopoulou & Armor, 2014; Vangrieken et al., 2017). Despite the demonstrated effects of PLCs (Hattie, 2009; Swedish National Agency for Education, 2019), teachers are not always positive when it comes to participating in this endeavor. Liljedahl (2014) described a group of mathematics teachers as resistant teachers; i.e., teachers who engage in PLCs with a negative, pessimistic, or defensive attitude. Potari et al. (2010) reported that a defensive attitude in PLCs in mathematics may arise from teachers’ confidence in mathematics; more specifically, what they found was that some teachers, being confident in mathematics, were rather reluctant to scrutinize their teaching. To these teachers, students’ difficulties in learning mathematics were not due to poor teaching but rather to the students’ own shortcomings. These teachers were confident that they were good at explaining mathematics.

Kroksmark (2014) and Liljedahl (2014) stressed that the behavior of resistant teachers is not necessarily permanent. Over time, a teacher initially exhibiting the behavior of a resistant teacher can start to see the value of a PLC and increase his/her contribution. Moreover, pessimistic or defensive utterances like “That will never work” and “I already do that” can also move PLCs in mathematics forward, when evidence and arguments are requested, thus encouraging others to engage in issues of teaching and learning mathematics more critically. However, for this to happen, the teacher leader should strive to move the teachers away from an evaluative to a co-inquiring attitude, “providing more space for the teachers to distance themselves and think critically about their own teaching actions” (Potari et al., 2010, p. 484).

A safe and challenging learning community

PLCs require a safe and tolerant atmosphere (Louis, 2006; Louis et al., 1996). Teachers should dare to question and scrutinize teaching approaches and feel it is worth it to contribute their ideas and test those of others in an open and tolerant climate of discussion. Teachers need to have the right to be engaged and should feel obliged to take responsibility for their engagement. Instead of avoiding disagreements and conflicts, group members should use such occasions to promote creativity and reflection (Garrison, 2016). The group should strive to establish norms of participation, whereby all teachers feel included and their teaching experience is valued and used in exploration and reflection in the collective work (Vangrieken et al., 2017). In PLCs, teachers’ beliefs and implicit teaching assumptions should be challenged and they should be encouraged to explore, examine, and analyze their teaching practices, in order to develop their understanding of teaching and learning in mathematics (Slavit et al., 2011).

Developing PLCs in mathematics is not a straightforward process, and above we have highlighted some key structures that research has shown to be crucial in this process. In this study, we intend to further our understanding of PLCs in mathematics by distinguishing contradictions that can arise in such initiatives for teaching development. We consider contradictions from the perspective of CHAT, where contradictions are a central concept. Contradictions are relevant to PLCs in mathematics since contradictions can affect the work and development in a PLC in different ways, depending on whether they are identified or not. If identified, contradictions can act as a driving force of development, while unidentified contradictions can act as blockers. Identifying contradictions can thus contribute knowledge relevant to the development of PLCs in mathematics. We frame our investigations using CHAT.

Cultural historical activity theory

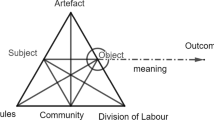
CHAT belongs to the sociocultural family of theories, used to analyze professional work practices and organizations in which people with different roles and perspectives interact and carry out actions aimed to develop their practice. In CHAT analyses, work practices are commonly conceptualized as an activity system, often illustrated through a triangle (Fig. 1) (Engeström, 1987; Foot, 2014).

Fig. 1
figure 1

Reproduced with permission from Engeström

Activity system, as illustrated by Engeström (1987, p. 78).

Full size image

An activity system consists of six nodes and an outcome (Fig. 1). The following description of the six nodes is a synthesis of Engeström (1987) and Engeström (1999), supplemented with examples of a fictitious PLC in mathematics. The object is the true motive of the activity and is always a process of negotiation in the PLC group. In a PLC in mathematics, an object could be to develop new common lesson plans in mathematics. The participants in the system carry out actions aimed to achieve the object (Öhman Sandberg, 2014). The arrows within the activity system represent human actions performed to achieve the object (Hirsh & Segolsson, 2019, p. 3). Subject(s) refer to the participants who share the object, for example, teachers in mathematics and a teacher leader. Mediating artifacts are the tools with which the participants achieve the object of activity. To reach the object of developing common lesson plans, mediating artifacts could be discussions, inquiry-based questions, and video clips of learning situations. Rules describe the explicit or implicit norms and expectations, which are taken as shared by the subjects in the activity. For example, expectations on what should be included in a lesson plan and the teachers’ view on mathematics affect the design of the common lesson plan. Community refers to the context to which the subjects belong, for example, the school where the teachers work. Division of labor describes both the expressed roles of the subjects and the implicit hierarchical structures. In the example of producing common lesson plan, the teachers are expected to be active participants and co-producers of the lesson plan. The teacher leader may introduce the inquiry-based questions and video clips, but do not introduce a ready-made lesson plan. In every activity system, there is also an outcome, which can be defined as the change enacted by and/or the result of the activity. Teachers participating in a PLC in mathematics are simultaneously involved in several neighboring activity systems related to teaching. Wake et al. (2016) give an example of two neighboring activity systems that teachers can be part of—the PLC in mathematics and the classroom where the mathematics teaching takes place—and investigate how these two neighboring activity systems interact in relation to how tools developed in a PLC in mathematics is used in mathematics teaching.

One of the strengths of activity system analyses is the possibility to conduct multidimensional analyses of complex learning situations where both actions, relationships, roles, and artifacts are taken into account (see e.g., Foot, 2014; Gedera & Williams, 2016; Jaworski, 2009; Walshaw & Anthony, 2008; Yamagata-Lynch & Haudenschild, 2008). On this account, CHAT has proven feasible for identifying and making sense of contradictions in educational contexts (Engeström, 2016). In the current study, we focus on contradictions in the educational context of PLCs in mathematics. To CHAT, contradictions are systemic phenomena inherent to all activity systems and necessary for the development of an activity system (Foot & Groleau, 2011). Contradictions are historically and structurally emergent inconsistencies between nodes inside an activity system or between activity systems (Engeström & Sannino, 2011) and possible to identify through subjects’ actions such as dilemmas or conflicts (Engeström & Sannino, 2011; Foot & Groleau, 2011). Contradictions can both promote and obstruct the development of an activity system. An identified contradiction makes inconsistencies visible, and thus also what needs to be changed in the activity to overcome the inconsistency. Identified contradictions can thus work as a driving force of development in an activity system. However, in many activity systems, the subjects are unaware of the contradiction and the inconsistency remains. In such cases, the contradiction can block the development of the activity system. Hence, by conceptualizing PLCs and inherent contradictions within the frame of CHAT, we are provided theoretical tools for giving an account of underlying structures that are crucial for the development of PLCs in mathematic. Such an account can be used both for understanding what might reduce the power of a PLC in mathematics and for developing strategies to move it forward.

Different types of contradictions

Engeström (1987) distinguishes between four types of contradictions. One type of contradiction occurs in single nodes, between different values for participating in the activity (Engeström, 1987). An example of this type of contradiction in teacher professional development is given by Yamagata-Lynch and Haudenschild (2008). In their study, individual teachers, school districts, and universities did not share a common object of professional development. While universities and school districts saw value in general interventions for all teachers in the district to meet certification and accreditation requirements rather than to improve their teaching, teachers saw value in participating in improving their own teaching.

The second type of contradiction occurs between different nodes in an activity system (Engeström, 1987), when new elements are added to and need to be assimilated into an existing activity (Yamagata-Lynch & Haudenschild, 2008). Yamagata-Lynch and Haudenschild (2008) give an example from their study in which the new element “participation in professional development” was not assimilated into the teachers’ ordinary work, resulting in difficulties fulfilling their other daily responsibilities.

The third type of contradiction occurs between nodes when participants have to use new and more advanced methods to achieve the object (Engeström, 1987). In the study by Yamagata-Lynch and Haudenschild (2008), a tertiary contradiction occurred when teachers were required to implement new teaching methods that did not fit with their classroom practice.

The fourth type of contradiction occurs between activity systems (Engeström, 1987) when an activity, due to a change, becomes contradictory to another neighboring activity (Yamagata-Lynch & Haudenschild, 2008). Yamagata-Lynch and Haudenschild (2008) give an example in which the implementation of new teaching methods required teachers to change their overall teaching. Several of the teachers refused to implement the new teaching methods, as they did not fit into the existing teaching style.

Manifestations of contradictions

As contradictions are systemic and historically emergent phenomena, we have no direct access to them in empirical data. Instead, contradictions are identified through their different manifestations in people’s actions and words (Engeström & Sannino, 2011). Engeström and Sannino have identified four types of manifestations of contradictions: dilemmas, conflicts, critical conflicts, and double binds.

Dilemmas are expressions of incompatible evaluations, either by one person or between people. People are torn between judging different alternatives. Dilemmas are commonly expressed in the form of hedges and hesitations, such as “on the one hand[...] on the other hand” and “yes, but” (Engeström & Sannino, 2011).

Conflicts are situations in which participants oppose each other’s opinions and actions and are expressed through resistance, questioning, disagreement, argumentation, and criticism (Engeström & Sannino, 2011).

Critical conflicts are situations in which a person encounters inner doubts on contradictory but mutually dependent motives and meanings that are unsolvable by the person herself. The situation paralyzes her, and she often expresses feelings of violation and guilt (Engeström & Sannino, 2011).

Double binds arise when requirements and conditions are incompatible, often expressed as helplessness or desperate rhetorical questions. People are forced to act in a certain way that they perceive they are not able to (Engeström & Sannino, 2011).

In the next section we describe how we use these manifestations of contradictions to identify contradictions in PLCs in mathematics.

Method

Data collection

Our data was gathered from two iterations of semi-structured interviews with four teacher leader coaches with extensive experience in coaching teacher leaders leading PLCs in mathematics. Coaching teacher leaders entails, for example, developing their understanding of learning theories, training them in leading conversations, and discussing with them the challenges teacher leaders may encounter in leading PLCs. In the interviews with the teacher leader coaches, the focus was on challenges in leading PLCs in mathematics. By focusing on challenges, we approached contradictions in an open way. This open approach was suggested in order to provide us with a rich basis for our investigations of contradictions.

There were three main reasons for interviewing teacher leader coaches. Firstly, they can be expected to have met an extensive number of teacher leaders of PLCs in mathematics. Secondly, previous research on PLCs has shown that it takes time to establish norms of trust whereby teachers dare to reveal their problems (e.g., Slavit et al., 2011). As the same should reasonably apply to teacher leaders, there was a risk that they would have been reluctant to reveal their challenges when talking to a researcher. As a teacher leader coach, you work with teacher leaders for a longer period of time, and thus have the possibility to build norms of trust that allow and encourage teacher leaders to dare to express what they find challenging. Thirdly, the teacher leader coaches meet with the teacher leaders continuously over a long period of time giving them the opportunity to identify different challenges in different parts of the teacher leaders’ work and learning process, which is difficult to capture in a single interview afterward. Consequently, it was expected that the four teacher leader coaches would provide rich information on challenges in the development of PLCs in mathematics, as a basis for an analysis of contradictions and their manifestation in PLCs in mathematics.

Selection of teacher leader coaches

The following criteria were used to find suitable teacher leader coaches:

  1. (1)

    The teacher leader coach should have experience in supporting teacher leaders of PLCs in mathematics.

  2. (2)

    The support must have lasted for a longer time, rather than being conducted only on a few single occasions.

Initially, 17 teacher leader coaches were contacted via e-mail. Ultimately, only four of them (called Kim, Lo, Michelle, and Noa in the article) fulfilled both our criteria. The teacher leader coaches’ experience of PLCs is summarized in Table 1.

Table 1 Summary of the teacher leader coaches’ experience of PLCs
Full size table

Semi-structured interviews

The first author of the article conducted two individual interviews with each of the four teacher leader coaches: one initial in June 2018 (I1) and the second one (I2) in August 2020. The initial interviews were conducted over Skype and lasted 60–90 min. The follow-up interviews were conducted over Skype or telephone and lasted 30–35 min. The themes of the interview guide were jointly discussed by both authors. The interview guide for the initial interview was structured according to three overall themes: (a) design, organization, and outcomes of PLCs, (b) teacher leaders’ challenges and need for support, and (c) outcomes of the support of teacher leaders (see Appendix 1).

In the second interview, we dug more deeply into (b), asking the teacher leader coaches about teacher leaders’ challenges and need for support, with a clear mathematical focus (see Appendix 2). The interview guides were used in a flexible way. For instance, the order of the themes/questions differed between the interviews of the four respondents. All interviews were audio- and video-recorded. All initial interviews were fully transcribed; in the follow-up interviews, only significant segments (see Method of analysis) were transcribed. Both the video recordings and the transcriptions were used in the analysis process.

Method of analysis

The method of analysis was based on the framework for identifying and analyzing manifestations of contradictions presented by Engeström and Sannino (2011). The analysis was conducted in four steps, which resulted in the identification of four types of contradictions, presented in the results section.

In the first step, we reduced our data by identifying segments significant to our research questions (cf., Jordan & Henderson, 1995). We looked for segments in which the respondents mentioned challenges that teacher leaders bring up for discussion in coaching sessions. In the second step, we analyzed each significant segment separately, trying to categorize the section according to the four types of manifestations (Engeström & Sannino, 2011). Table 2 shows an example of how the analysis of manifestations was conducted: each significant segment was noted, summarized based on the author’s understanding of the quote and its context and compared to the descriptions of manifestations, in order to categorize the section as dilemma, conflict, critical conflict, or double bind. Arguments for the categorization of manifestation were also noted, and key words for each manifestation italicized. This resulted in 26 manifestations of contradictions (see Table 3). In the Results section, examples are given of the manifestations, aiming to increase the transparency of the results.

Table 2 Examples of how the analysis of manifestations was conducted
Full size table

In the third step, we inferred which contradictions the manifestations expressed and what the contradiction concerned. For instance, the dilemma described in Table 2 contributed to identifying the contradiction between basing mathematics teaching on the textbook and alternative teaching methods developed through the PLC. All manifestations that concerned the same contradiction were synthesized. This step resulted in four identified contradictions. Finally, we organized the identified contradictions in relation to the four types of contradictions described by Engeström (1987).

The analysis involved both individual and joint work between the two authors of the article. For example, the first author made initial interpretations of each section and what kind of manifestation it was (see Table 2). The interpretations were then discussed and revised jointly by both authors. The first author then returned to the individual work, looking at the data through a sharper lens, developed from the meeting. This iterative process of individual and joint analyses was repeated a number of times.

Results

Our research question concerns what contradictions may occur and how they are manifested in PLCs in mathematics. We identified four different contradictions and 26 manifestations of contradictions, distributed across conflicts and dilemmas (see Table 3).

Before we outline details of the four contradictions, we briefly characterize the PLCs expressed by the teacher leader coaches, in which the contradictions occurred. There were both similarities and differences between these PLCs. There were differences in the number of participating teachers, what experience of teaching mathematics the teachers had, and how much time the teachers were allocated for their participation in a PLC. There were variations in from whom the initiative of a PLC came. In some cases, the initiative came from the board of the school and in other cases from the teachers. There were also variations in which mediating artifacts were used for mapping and exploring teaching. In all the PLCs, covered in the interviews, the subjects included teachers in mathematics and one teacher leader. In every case, the teachers were familiar with each other as colleagues, working at the same school. In some of the PLCs, the teacher leader was recruited from the schools’ own group of teachers in mathematics and, in some PLCs the teacher leader was recruited from outside the schools, and thus unfamiliar to the teacher group. The intended role of the teacher leader was similar across the PLCs and included responsibility for planning, structuring, and leading the discussions by distributing the talking space and ensuring the focus of the work in the group. The teachers were expected to be active participants. The objects in all the PLCs concerned development of mathematics teaching by using inquiry methods. Most of the teachers involved were familiar with collaborative work, but not accustomed to inquiring systematically into their own teaching practice. Instead, they had experience from the implementation of ready-made teaching methods. When PLCs in mathematics are used in the following, we refer to the above-described PLCs in mathematics (Table 3).

Table 3 Summary of the four contradictions and their manifestations found in our study
Full size table

Contradiction between implementing ready-made teaching methods in mathematics and inquiring into teachers’ own teaching in mathematics

We have identified one contradiction inside a single node. This contradiction occurs in the node object; between two different values for developing teaching in mathematics through PLC. These two values can be thought of as two different objects for participating in PLC in mathematics (Fig. 2).

Fig. 2
figure 2

The first type of contradiction. The lightning illustrates where in the activity system the contradiction occurs

Full size image

The first value concerns reforming teaching in mathematics by implementing ready-made teaching methods. New teaching methods are developed by external actors, for example, researchers, who identify general developmental needs in mathematics teaching, and based on this formulate proposals for new teaching methods. Time and money need to be invested in enabling teachers to learn how to master and implement these new methods.

The second value concerns a reformation of teaching by having the teachers themselves identify and analyze developmental needs in their own teaching in mathematics and jointly develop new teaching methods. Time and money need to be invested in enabling teachers to meet in a structured way and jointly discuss and learn how to inquire into their teaching and students’ learning in mathematics.

The teacher leader coaches stress the importance of starting the collaborative teaching development in the teachers’ own teaching practice. Teachers’ knowledge and developmental needs should constitute the driving forces of a PLC. However, in PLCs the teachers’ own knowledge and teaching practices often have low priority, or even become invisible, in favor of implementing ready-made teaching methods:

I sometimes think that in collaborative learning endeavors where teachers or teacher leaders are coached, there’s a view of teachers and teacher leaders as if they don’t… ‘Well, here you have the book, now you should do this.’ ‘Yes, but we’re also knowledgeable?’ ‘No no, this is what you should do’. (Michelle, I1)

This quote exemplifies an endeavor in which an external party has determined a method that the teachers and teacher leaders are required to implement. Trends and research on professional development, rather than the needs identified from the teaching, take priority in the design of the joint work. In such externally driven PLCs, the design and implementation of teaching methods often follow a top-down structure: The PLC and its content are initiated by school reforms or the school board. The object of top-down PLCs concerns the implementation of a ready-made teaching method. Even though teachers implement, analyze, and reflect on the teaching methods presented, there is a risk that they will not fit the needs of the actual teaching and thus not be helpful in increasing the learning of students taught by the participating teachers. Moreover, as the quote above exemplifies, many teachers consider themselves to be knowledgeable. They have extensive experience in teaching and have developed an understanding of teaching and learning that is grounded in practice. They know what works and what needs to be improved in order to further develop their teaching practice.

The contradiction between the two values is manifested in two conflicts. In the first identified conflict, teachers question why their knowledge is not taken into account in the PLC (Michelle, I1). Teachers also show evidence of the conflict between their own needs and knowledge and the teaching methods suggested by the teacher leader, by refusing to participate in the agreed-on activities (Lo, Noa, I1). The second conflict is visible in teachers being reluctant to participate in PLC and questioning the usefulness of PLC and how the suggested teaching methods are helpful in increasing their students’ learning (Michelle, I1).

Contradiction between the given tasks for the teacher leader and the expectations on the teacher leader

We have distinguished one contradiction that occurs as a consequence of the implementation of a new element in the activity system. This contradiction occurs between rules and division of labor, in the process of assimilating a new role for the teacher leader in the PLC. The contradiction occurs when the teacher leader is recruited internally from the school’s own group of teachers (Fig. 3).

Fig. 3
figure 3

The second type of contradiction. A new element, a teacher leader, is added which need to be assimilated. The lightning illustrates where in the activity system the contradiction occurs

Full size image

There are expectations on the teacher leader, which are historically grounded in the teachers’ previous experiences of professional development. Historically, the role of a teacher leader has been to educate and provide teachers with answers and ready-made methods. In the PLCs, to which the four teacher leader coaches refer, the role of the teacher leader is to plan for, guide, and deepen collaborative inquiry processes in the teacher group. A contradiction thus, arises when traditional expectations collide or become incompatible with the inquiry-role of a teacher leader:

Yes, because they come from a professional development project in math where you do tasks to increase your abilities as a teacher. So, then they ask, ‘What tasks should we do?’. […] ‘What should we teach our students?’ I answer: ‘Well, you know that better than I do’. (Michelle, I1)

Another way in which teachers’ expectations can differ from the given role of a teacher leader concerns whether or not the teacher leader should possess more and deeper knowledge in mathematics and mathematics education than the teachers, and based on this ensure that the teachers act mathematically correct ways:

It can be a little bit tricky because as a teacher leader you shouldn’t be the expert when it comes to mathematics education. You won’t be the expert when it comes to what has to be included. If we think theoretically, we should work with the equal sign. What do we need to see? What’s included? What’s important? You shouldn’t be the expert there as the teacher leader, but maybe it’s expected that you’re the expert. But all of us together are the experts, because we’re all knowledgeable in mathematics education. So, we have to be able to explore this jointly. […] Participants expect the teacher leader to master mathematics education as well. That you, as a teacher leader, are a little more of an expert. […] They may want all the answers: ‘How should we think here? Are all the theoretical aspects included in the learning objective? We aren’t missing anything, are we? You know, as someone who’s knowledgeable, don’t you?’. (Kim, I1)

The contradictory expectations may be a dilemma for the teacher leader:

Then it’s very much ‘But am I supposed to know all this now?’ And ‘Now they’re going to ask me questions and I can’t answer that. But I should know all that’ […] Even though they knew they wouldn’t think like that, they got nervous.” (Kim, I1)

And then they also had to think, ‘What role do you want here? Do you want to be the one who gives the right answer? Should you participate in the discussion or not? Is it easier for you to lead the conversation than to contribute your opinions?’. (Lo, I2)

In other words, a dilemma can arise between an effort to act like a conversational leader and meeting expectations that you should be an expert in mathematics/mathematics teaching. The teacher leaders are aware that teachers of PLCs expect them to act as experts, but at the same time they are aware that they should lead the discussion rather than simply transferring knowledge to the teachers.

This contradiction occurs when the role as the teacher leader is assigned by someone from the schools’ group of teachers. An internally recruited teacher leader can struggle between the new role as a teacher leader and the ordinary role of a colleague, and associated expectations of these roles. Changing one’s role from teacher colleague to a teacher leader does not go unnoticed, as it affects the balance of power in the teacher group:

Now they would go from being a participant in the group to leading a group, and that meant that they took on a completely different role toward their colleagues with whom they’re equal and otherwise want to be equal . (Lo, I1)

The contradiction can be manifested as a dilemma, whereby the teacher leader is torn between a will and expectation to be equal to the other teachers and the obligation to lead the group:

What do you do if only three out of eight have read the new article? How do I respond to someone who always comes late and doesn’t want to participate? I can’t reprimand my colleague, can I? (Noa, I1)

Teacher leaders are uncertain how to manage the shift of power that accompanies the transition from colleague to teacher leader. The teacher leaders sometimes need to defend their legitimacy as teacher leaders toward their colleagues. The colleagues sometimes question why this person is better suited for the teacher leader role than anyone else in the group (Lo, I2), which can lead to the teachers refusing to complete tasks or arriving late to meetings (Lo, Noa, I1). According to the teacher leader coaches, these conflicts do not occur very often when a teacher leader comes from outside the school, compared to when the teacher leader is recruited from the teacher group:

When I came from outside, it was easier than… If I say to someone ‘for next time I want you to read these texts’, then it was a little more ‘okay, we should do that’. But when a colleague says that, it’s easier to say, ‘I didn’t have time’ or ‘I haven’t tried the activity’. […] You don’t have the same responsibility or feeling for a colleague. (Lo, I1)

In other words, the tendency to ignore or oppose agreed-on tasks increases when the teacher leader is a colleague, compared to when s/he comes from outside the school, as the teachers do not feel the same responsibility to their colleagues.

Contradiction between inquiry methods used in PLC in mathematics and norms of teacher collaboration

We have identified one contradiction between nodes that occurs as a consequence of the implementation of a more advanced method. The contradiction occurs between the nodes mediating artifacts and rules. When inquiry methods are used in PLCs in mathematics as new and more advanced than previously used methods, they become contradictory to teachers’ established norms of collaboration. The term inquiry methods refer to the node of mediating artifact, i.e., to the tools teachers can use to examine their teaching. What we have found is that learning to use inquiry methods as new and more advanced methods can come to contradict the norms of sharing ideas and of not showing one’s shortcomings in PLC in mathematics (Fig. 4).

Fig. 4
figure 4

The third type of contradiction. A new more advanced method, to inquire into one’s own practice, is added. The lightning illustrates where in the activity system the contradiction occurs

Full size image

Discussing issues of teaching and learning in-depth is stressed as important in PLCs. However, the teacher leader coaches emphasize that all teachers are not initially comfortable talking to colleagues or showing their difficulties or shortcomings:

I think it can be due to a fear of showing that you can’t, you don’t dare show that you don’t know this so well. And it has to do with your role towards your colleagues. It’s a different situation regarding students than towards other adults. (Noa, I2)

A view of mathematics as a subject in which you may be judged as intelligent or unintelligent may be a reason for the fear of disclosing one’s difficulties:

I think it’s so charged. Generally, if you’re smart, you have high grades in math. Mathematics classifies whether you’re smart and intelligent. (Noa, I2)

I think it has to do with the view of mathematics; it’s a bit of a high-status subject, in the sense that you’re smart when you know math. (Lo, I2)

To show one’s difficulties thus means risking being seen as unintelligent or unwise. According to the teacher leader coaches, this fear of sharing sometimes leads to reluctant, non-speaking teachers or someone in the group taking up most of the talking space.

The teacher leader coaches also point out the importance of in-depth reflections on and analyses of one’s teaching and students’ learning in mathematics. Once the PLC participants have passed the initial hurdle of daring to share their teaching difficulties, the next hurdle will thus be to reflect deeply on and analyze these difficulties rather than to continue with surface discussions, which can often be the norm in PLCs in mathematics:

When you [a teacher] have conducted an activity, it becomes easy to tell what my students and I did, but that’s not collaborative learning among teachers. You need to lift it to the next level: ‘Yes, but what did we learn from this? What have we seen?’. (Lo, I1)

Quickly, they [teachers] get good at planning to teach together but evaluating and analyzing completed teaching and then using it to form new teaching is more difficult. (Michelle, I2)

Hence, if teachers do not dare to contribute to the PLC, or if only a few of them are active, it will be difficult to build on the teachers’ own developmental needs and create a PLC in which the teachers’ different experiences of and perspectives on teaching form the basis for the development. More concretely, on the one hand, collaborative inquiry is expected but, on the one hand, it is not always the case that all teachers find the PLC sufficiently safe and tolerant for disclosing their shortcomings in mathematics or mathematics education.

Moreover, according to the teacher leader coaches, digging deeply into analyzing teaching and learning mathematics requires that the teachers jointly take the time to stop, ask in-depth questions, and immerse themselves in the same issue or detail for a longer period of time. However, this practice is incompatible with the practice teachers are more used to; namely, constantly moving forward to new tasks and assignments:

My experience is that throughout a school year, they [teachers] push fast forward all the time. Making in-depth analyses is contrary. Going deeper is not similar to pushing forward. (Noa, I2)

Hence teachers can be torn between taking time to reflect on and discuss something in-depth and the desire to keep moving forward. In other words, the prevailing norm of always closing assignments and moving forward to new ones is incompatible with digging deeply into issues of teaching and learning.

Contradiction between basing mathematics teaching on the textbook and alternative teaching methods developed through PLC

We have identified a contradiction between neighboring activity systems to which teachers belong. This contradiction appears between the activity system of the PLC and the activity system of the teachers’ mathematics teaching practice and can serve as a barrier for implementing the outcome of the PLC in the teachers’ teaching in mathematics (Fig. 5).

Fig. 5
figure 5

The fourth type of contradiction. The lightning illustrates where between the two neighboring activity systems the contradiction occurs

Full size image

Although the work in PLCs results in new teaching methods that are relevant for developing teaching, teachers may hesitate to implement them in their practice:

As soon as a teacher has to make changes in their practice… Well, you can talk about it, but as soon as you have to really make an actual change, it can be hard. ‘Oh, do I have to do this right now?’. So, it’s one thing to discuss it, but here you should really do it in the practice too. And it can create some fear in the teachers who dare to try. (Kim, I1)

According to Lo, this tendency is slightly stronger among mathematics teachers than other teachers:

There was a greater resistance in math groups to leave habitual patterns. […] These math teachers tended to continue just as much as before to teach from the textbook, even though they thought of something else. Or maybe came across testing more manipulatives, but ‘No, it doesn’t work so I did like I usually do instead’. […] There was a resistance to change. (Lo, I2)

Due to the strong tradition of using the textbook in mathematics, it is contradictory when the teaching, as a result of the PLC, is suddenly to be based on other premises. This contradiction between the outcome of the PLC and the existing teaching in the classroom is visible in a double bind for teachers, who are torn between a will to develop teaching based on their identified needs and the perceived obligation to follow established norms implying that teaching should be based on the textbook:

The subject of mathematics carries a lot of traditions. You should have a textbook where you do Page 1 to 200. And it’s such a deeply rooted tradition. Even if we meet teachers who say ‘No, I don’t think you should start from the textbook’, they still have a semester plan where Chapters 1 to 4 have to be done in the autumn. It’s inevitable. […] And the students, I think, see it the same way. Many students carry a feeling that you have to complete all the tasks and do it in the order of the book. (Lo, I2)

Even when a teacher is convinced that the teaching would be improved if it were not guided by the textbook, the textbook tradition is so strong in mathematics that the teacher feels it is almost impossible to break from it. Teachers are hesitant or have difficulty using new methods, as this requires that the textbook will be given a less central place in the teaching. There is a security, and a historically developed norm, in using the textbook as the basis for teaching mathematics, and thus an uncertainty and a risk in trying something else that deviates from this norm. Consequently, some teachers therefore return to their ordinary teaching instead of implementing the teaching methods developed in the PLC, as the implementation requires too-great a change to their teaching practice.

Discussion

In motivating the present study, we claimed that research has provided rather good documentation that teachers’ joint work is not always successful in developing teaching practices but that we know less about the basis of such shortcomings. To make a contribution to such an understanding, we addressed the research question, “What contradictions can be manifested in PLCs in mathematics?” Based on a CHAT analysis of contradictions in two rounds of interviews with four experienced teacher leader coaches, we have distinguished four contradictions and their manifestations.

The results of this study are significant to both research and practice. Research seems to agree that teacher professional development should build on teacher collaborations, in which the teachers engage in processes of unpacking and exploring their teaching and trying out, analyzing, and evaluating different ways of teaching (e.g., Garet et al., 2001; Garrison, 2016; Slavit et al., 2011; Vescio et al., 2008). According to this, the present study shows how a contradiction perspective adds to the understanding of and sheds new light on the underlying structures that are crucial for establishing such processes in PLCs. In relation to practice, we have outlined four empirically grounded contradictions by describing in detail how they can come to be manifested in PLCs in general and in mathematics in particular. These empirically grounded descriptions can be used to take into account, make visible, and increase different stakeholders’ awareness of the contradictions involved in PLCs in mathematics. The contradictions we have outlined and described can also be used as exemplars in extending the search for contradictions that can occur in PLCs in mathematics. We continue discussing the significance of the study by showing how the results can inform on PLCs in mathematics.

Implications for research and practice

Research stresses that PLCs should provide teachers with opportunities to encounter, and learn to use, tools in order to enhance their ability to examine and scrutinize their teaching (Garrison, 2016; Jaworski, 2006). To this end, all teachers should feel included, and their teaching experience should be valued and used in the collective work (Vangrieken et al., 2017). Our study implies that many teachers are open to inquiring into their teaching, whereby their professional knowledge is taken into account and valued. However, what also appears in the interviews is that teachers feel that such inquiry processes can often come to contradict a situation in which they are asked to discuss research findings and implement ready-made methods. In situations of implementing ready-made teaching models, teachers take on the role of executor rather than a role of inquiring into teaching. Teachers’ needs and knowledge become secondary; someone else declares what teachers needs are and what they should do differently. To understand this contradiction, one should also consider the history of teacher professional development. Teachers are used to situations in which some external resource tells them what their needs are and asks them to try its new teaching methods. Hence, in planning for a PLC initiative, our study highlights the importance of considering the tradition and norms of teacher professional development when considering how to foster a norm in which all teachers feel included and dare to show their teaching and difficulties, and in which their teaching experience is valued and used in exploring and reflecting in the collective work.

To get the most out of a PLC, teachers should take on the role of co-producers of knowledge, rather than being passive receivers (consumers) and executors of pre-packaged knowledge provided by a teacher leader or the literature (Desimone, 2009). The teacher leader should not take on the role of an expert who is expected to provide all the answers and tell the teachers how to teach but, take on the role of a guide, with responsibility for planning, structuring, challenging, and focusing the group work (Borko et al., 2008; Campbell & Stohl Lee, 2017a; Dobie & Anderson, 2015; Gellert, 2013; Murata et al., 2012; Vangrieken et al., 2017). We have no reason to question this. However, our study shed new light on the fact that taking on the role of a guide in a PLC in mathematics is not done without friction and, particularly not when the teacher leader is recruited internally from the school’s own group of teachers. On the one hand, our results show that it can be difficult to really guide colleagues and at the same time maintain a good relationship with them. In other words, as a teacher leader, you may not dare to question the teaching of your colleagues as much as needed, because you do not want to risk your personal relationship with them. On the other hand, it can also be difficult to take on a guiding role in a PLC in mathematics since it is subject-specific. According to Campbell and Stohl Lee (2017a), in subject-specific PLCs teachers need to dig into the details of students’ learning of a subject matter. Consequently, if teachers are unfamiliar with such work, or lack the ability and knowledge to perform it, the teacher leader may need to take great responsibility in such processes and thereby reinforce the role of expert in favor of that of a guide. Added to thisis the suggestion that mathematics teachers can be reluctant to reveal their mathematical knowledge, or lack thereof. In such situations, the teacher leader may have to take the lead in the group, which can result in a situation in which the teacher leader starts educating the other teachers instead of using the teachers’ knowledge and experience in teaching mathematics in building the PLC.

Time is crucial for PLCs (Collinson & Fedoruk Cook, 2001). A sufficient length of time is necessary for establishing norms and patterns of interaction productive for PLCs (Vangrieken et al., 2017). Here, we have discussed the contradiction between inquiring into teachers’ own teaching practice and implementing ready-made teaching methods in mathematics, and the contradictions in relation to the role of teacher leader. Fundamental to these contradictions are history and norms in different respects. There is a need for a sufficient amount of time in order to change to an inquiry-oriented PLC in mathematics from a long history of initiatives whereby teachers have been presented with ready-made methods to implement in their teaching. Our study also shows that, when the teacher leader is recruited from the teacher group, it is not always easy to go from being a colleague to being accepted as a leader. Structures are needed to make this work, and in line with Mason et al. (2019), we suggest that time is a critical structure in this endeavor.

Future research

We have identified four contradictions that can occur in PLCs in mathematics. In future research, it is relevant to investigate and provide further evidence for these contradictions by directly observing PLCs in mathematics. We do not claim that the four contradictions provide an exhaustive list of contradictions that can occur in PLCs in general and in mathematics in particular. Thus, future research should also strive to identify more contradictions and their manifestations in PLCs in mathematics.

The hypothesis of the present study is that an increased understanding of contradictions increase the possibility to develop PLCs in mathematics. Foot (2014) points out that different types of contradictions correspond to one another in a cyclic process. While such a correspondence has not been focused on in this study, it is relevant to investigate, in a longitudinal study of PLCs in mathematics, whether and how our identified contradictions interact with each other. The outcomes of such a study could broaden our understanding of how contradictions can act as both obstacles and driving forces in the development of PLCs in mathematics.

Finally, it would be relevant to develop an intervention study to find strategies for promoting organizers’ and teacher leaders’ understanding of contradictions and the use of this understanding in order to develop PLCs in mathematics that contributes to promoting school change beyond individual classrooms. We suggest framing such a study from CHAT and particularly from the construct of contradictions. Contradictions identified in the present study can then be used as starting points in the research process.