The influence of video clubs on teachers’ thinking and practice

Abstract

This article examines a model of professional development called “video clubs” in which teachers watch and discuss excerpts of videos from their classrooms. We investigate how participation in a video club influences teachers’ thinking and practice by exploring three related contexts: (a) teachers’ comments during video-club meetings, (b) teachers’ self-reports of the effects of the video club, and (c) teachers’ instruction across the year. Data analysis revealed changes in all three contexts. In the video-club meetings, teachers paid increased attention to student mathematical thinking over the course of the year. In interviews, teachers reported having learned about students’ mathematical thinking, about the importance of attending to student ideas during instruction, and about their school’s mathematics curriculum. Finally, shifts were also uncovered in the teachers’ instruction. By the end of the year, teachers increasingly made space for student thinking to emerge in the classroom, probed students’ underlying understandings, and learned from their students while teaching.

Introduction

Video clubs are a professional development environment in which groups of teachers watch and discuss excerpts of videos from each other’s classrooms. Video clubs provide teachers with a window into each other’s practices and the opportunity to discuss a variety of issues about teaching and learning. A central goal of video clubs is to help teachers learn to notice and interpret key features of classroom interactions (van Es and Sherin 2008). As classrooms are complex environments with many things happening at once, identifying such events is not a simple matter. This is particularly true in the context of mathematics education reform, where teachers are asked to adopt a responsive approach to teaching, adapting their instruction based on the ideas students raise (Ball and Cohen 1999; Edwards and Protheroe 2003; National Council of Teachers of Mathematics [NCTM] 2000).

To explore what and how teachers learn in video clubs, we studied a group of seven fourth and fifth grade teachers who participated in a video club that met once or twice a month over the course of one school year. The particular research question for this study is: how does participation in a video club focused on examining student mathematical thinking influence teachers’ thinking and practice? To answer this question, we examine data from three related contexts: (a) teachers’ comments during video-club meetings, (b) teachers’ self-reports of the effects of the video club, and (c) teachers’ instruction across the year. Data analysis revealed changes in all three contexts.

We situate this article in research on noticing and summarize the Learning to Notice Framework (van Es and Sherin 2002). Then, we discuss the use of video clubs as a vehicle to help teachers learn to examine classroom interactions. We also discuss prior research on the process through which mathematics teachers make changes in their classroom practice. We then describe our research design and methods, followed by the results. We conclude by discussing the implications of this study for research on teacher cognition and professional development.

Literature review

Learning to notice framework

Several researchers argue that a key component of teaching expertise is the ability to notice and interpret what happens in one’s classroom. Berliner (1994) and Mason (2002) claim that expert teachers have heightened sensitivities to particular aspects of one’s practice, as well as techniques for analyzing, using, and inquiring into these aspects of their work. Ainley and Luntley (2007) refer to this as “attention-dependent knowledge” (p. 3), a range of attentional skills that expert teachers use to attend to the cognitive and affective aspect of classrooms.

We agree with these claims about the importance of noticing in expert teaching. Furthermore, as reported in van Es and Sherin (2002), we propose a framework that identifies three key aspects of teachers’ noticing. One aspect of noticing involves the ability to attend to what is significant in a complex situation, referred to as highlighting (Goodwin 1994) and marking (Mason 2002). In the context of a classroom, there are many things happening at one time. Teachers make choices about where to direct their attention and what events to pursue at any given moment.

Another characteristic of noticing involves using knowledge of one’s context to reason about noteworthy events. Prior research shows that as individuals become familiar with a particular type of situation, they are better able to analyze the same types of situations in the future (Lesgold et al. 1988). Teachers know a great deal about their students, curriculum, and school context, and they use this detailed knowledge to make sense of what they observe.

Noticing also involves the ability to make connections between specific events and the broader principles they represent (Copeland et al. 1994; Hughes et al. 2000). When viewing a class discussion, for example, expert teachers will describe what they see in terms of principles, such as, “This is an assessment issue.” When teachers extrapolate from the specific to the general, they form connections between the specific instances they see and the broader pedagogical issues such events represent.

Despite an increased focus on teacher noticing in recent years, little is known about the development of teachers’ ability to notice and how to effectively support this development. One approach that has received attention in research on teacher education and professional development involves the use of artifacts of practice, such as video or student work, to help teachers learn to observe and make sense of the complex practice of teaching (e.g., Kazemi and Franke 2004). We explore how video artifacts of practice might be productive for helping teachers learn to notice.

Video for teacher learning

Video has been used for decades to support teacher learning, and it appears to be a particularly useful tool for helping teachers learn to notice. Video can capture much of the complexity of classroom interactions, and it can be used in contexts that allow teachers time to reflect on these interactions (Brophy 2004; Tochon 2007). Video has been used to illustrate exemplary teaching practices and to represent the dilemmas teachers encounter in their day-to-day practice (Oonk et al. 2004; Sullivan and Mousley 2001). In either case, using video affords teachers’ opportunities to develop their professional judgment as they reason about the complex nature of teaching (Santagata et al. 2007). Furthermore, because video provides a permanent record of what took place, teachers have opportunities to see noteworthy events that they may not have noticed previously and to view video records several times, adopting different perspectives each time.

The video-club environment seems particularly well suited to helping teachers learn to notice. Teachers have few opportunities to observe their colleagues’ teaching, and video clubs provide teachers with access to each other’s classrooms (Little 2002). Research also suggests that there is value in teachers coming together to examine artifacts from their own classrooms (Lewis et al. 2006). Classroom artifacts become common referents on which teachers can focus their discussions, which can promote deep analyses of teaching and learning issues (Kazemi and Hubbard 2008). Moreover, analyzing video in a group context allows multiple perspectives on the same event to be explored, and this is much less likely to happen if teachers were to analyze video on their own (Tochon 2007).

While video can afford productive discussions of teaching and learning, there are also limitations to its use. First, what is captured on video is only a slice of what occurred in a classroom (Miller and Zhou 2007). Teachers who view records of practice may be quick to draw conclusions from watching a brief segment and not appreciate that it represents a particular moment in time. Second, watching and reflecting on video requires different practices than those teachers typically engage in teaching. Switching between these roles can be quite difficult (Lampert 2003). Finally, video is only a tool for learning. The tasks and structures for learning and the nature of facilitation with video need to be coordinated in such a way to capitalize on what video has to offer (Le Fevre 2004).

A focus on teacher interpretation of student mathematical thinking

When we talk of teachers’ noticing classroom events or interactions, a wide range of issues arise during a typical class session that might capture a teacher’s attention. In the context of mathematics education, a particular class of events is considered important—those relating to students’ thinking about mathematics. Reform efforts encourage teachers to attend to the detailed ideas that students raise, to student confusions and misconceptions, student errors, and the like (e.g., Schleppenbach et al. 2007). In this model, an important skill for teaching is “sizing up students’ ideas” (Ball et al. 2001, p. 453) and learning to carefully listen to what students actually say (Rodgers 2002). Research on effective professional development reveals the importance of focusing on student thinking of content (Kazemi and Hubbard 2008). Sowder (2007) reports that professional development focused on children’s thinking helps teachers design instruction that promotes learning mathematics for understanding and can improve student achievement. Additionally, teachers who attend to student ideas learn about their students and use what they learn while teaching, resulting in a cycle of teacher and student learning (Borko et al. 2008).

In line with these views, we adopt the perspective that teachers need to learn to focus their attention on the particulars of student ideas. Sherin (2007) suggests that this may be particularly important for veteran teachers, who are already skilled at interpreting classroom events. She proposes that they may need to learn to see different kinds of events and see them in different ways, given new views of mathematics teaching.

We also advocate that teachers adopt a particular discourse for analyzing teaching and learning. Nemirovsky et al. (2005) identify two types of discourse that teachers use when discussing case studies of classroom episodes, grounded narrative and evaluative discourse. The former highlights the sequential nature of teachers’ commentary, similar to following the plot of a story, while the latter invokes comments laden with values and judgments, such as what was good or bad. We suggest that a third discourse structure may be useful for teachers, one that is more tentative and interpretive in nature, in which the goal is to make sense of student thinking and use evidence to reason through worthwhile teaching issues (Borko et al. 2008; Seago 2004). The goal is to promote a discourse where teachers seek to ask and answer provocative questions, press on one another’s thinking, and critically analyze events they observe.

Research on changes in teachers’ practice

A key question for this research is the extent to which teacher learning in the video club—in which segments of mathematics lessons are viewed exclusively via video—might influence teachers outside of the video-club context, such as their beliefs about teaching and learning and their instruction. It can be quite difficult for teachers to make changes in their instructional practices (Franke et al. 2007). Teachers may hold well-established beliefs that are not in line with the vision of reform and resistant to revision (Forgasz and Leder 2008). Further, teachers may lack the necessary knowledge and skills to teach in ways envisioned by reform (Ma 1999). Teachers may believe they have adopted new teaching practices, but often their teaching remains relatively unchanged because they lack the knowledge to support students as they work through new types of mathematical problems (Perrin-Glorian et al. 2008). Finally, the school contexts in which teachers work are often resistant to change and may further constrain efforts to adopt new practices. Teachers may need substantial institutional support to change instruction (Correnti and Rowan 2007; Gamoran et al. 2003), including opportunities to participate in extended professional development and access to human and social resources to facilitate learning (Porter et al. 2000).

Thus, we believed it was critical to study not only what teachers learn in the video-club context, but also the extent to which participating in a year-long video club might influence teachers’ thinking and practice beyond the video club itself. On the one hand, the video-club design is based on key principles of effective professional development (Penuel et al. 2007). It is closely tied to teachers’ classroom instruction, is long-term and sustained around a specific focus, and encourages teacher inquiry into the particulars of their practice. Further, the facilitators modeled particular strategies, acting as social and intellectual resources to support teacher growth. At the same time, however, the discussions in the video club were not explicitly focused on changing teachers’ beliefs and the teachers were never asked to try out a new method in their classroom and to report back on their experience at the next meeting. Instead, we attempted to maintain a focus on analyzing student thinking as it appeared in the video excerpts that were viewed together.

Data

Study design

Data for this study come from a year-long set of video-club meetings attended by seven fourth and fifth grade teachers from an urban school (see Table 1). Pseudonyms have been used to protect the teachers’ identities. Two of the teachers were special education specialists and they were assigned to co-teach with two of the classroom teachers as part of the district inclusion program. The school district was in the third year of using a reform-based mathematics curriculum. The teachers had varying levels of experience using the curriculum, with some in their third year using it and others in their first year.

Table 1 Subject information

The video-club group was formed as part of a university–school district partnership. The authors approached a district administrator and offered to facilitate a video club focused on student mathematical thinking. The administrator was enthusiastic about the idea and identified a school and the particular grade level teachers for this project, based on school-level student performance data and on previous mathematics professional development offerings in the school. Prior to the first meeting, the researchers met with the teachers to introduce the idea and to ask if they would be interested in participating in the club and the corresponding research. Teachers were paid a nominal fee for their participation.

We designed the video club to help teachers learn to notice the particulars of student mathematical thinking. Thus, we directed the teachers to examine student mathematical ideas and to use evidence from the video segment and transcript to support their claims about student understanding. To that end, we asked the following types of questions: “What method was Marisa using to solve that problem?”; “Where is that in the transcript?”; and “What does that tell us about her understanding of fractions?”

The teachers came to the meetings with other goals as well. Several of the teachers said they wanted to participate because they had opportunities to collaborate with their colleagues around the new curriculum. Further, the district required the teachers to participate in professional development, and some teachers planned to use the video club to fulfill that requirement. Finally, several teachers had prior experience using video or with other mathematics professional development programs that they believed were valuable. They thought they would benefit from additional opportunities of this sort. Nevertheless, the group agreed that the goal of the video club was to allow them to see images from each other’s classrooms and to learn how video might be a useful tool for reflecting on mathematics teaching and learning.

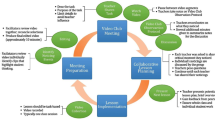
The video-club group met once or twice a month for a total of 10 video-club meetings, each one lasting about one hour. The meetings shared the same format. Two video segments from two teachers’ mathematics lessons were viewed and discussed at each meeting. Before each meeting, a member of the research team videotaped lessons, typically 50–60-min long, from two of the participating teachers’ classrooms. The video camera was placed in the back of the classroom. Three microphones were positioned throughout the classroom, and the teacher wore a lapel microphone. When the students worked together, the researcher used the audio mixer to listen to conversations and determine which discussions to capture on audio and video. These choices were made based on the extent to which students discussed the question or problem posed by the teacher and the substance and length of their conversation. The researcher zoomed the camera on individual or groups of students or moved around the classroom to capture up-close images of student work.

After the classroom observation, the same researcher viewed the tapes and selected a segment that had potential to foster productive discussions of student mathematical thinking. These segments came from whole-class discussions, student-to-student, and teacher-to-student conversations that highlighted student ideas. The clips showed students working through a mathematical problem or explaining how they solved a problem, or they highlighted teachers and students discussing a student’s solution method. The clips were 5–7 min in length. The researcher prepared a corresponding transcript to reference in the meetings. Clips from each of the teacher’s classrooms were viewed two or three times throughout the year.

Data collection

Several sources of data were used in this study. Each video-club meeting was videotaped. The facilitators arranged the desks in a semi-circle and placed a television monitor with a VCR in the center of the group so all members could view the segments clearly. The video camera was located to the side of the monitor, and a microphone was placed on a desk near the group.

Additional data sources include interviews and classroom observations. We conducted an Exit Interview with each teacher at the end of the series of meetings that lasted approximately 30 min. We asked the teachers to comment on what they thought were the most and least valuable aspects of the video club, and how participating in the video club influenced their thinking about mathematics teaching and student learning. We also asked them to discuss how their instructional practices had changed, if at all, as a result of participating in the video club. We constructed a list of questions around these issues to frame the discussion, however, we attempted to establish a conversational tone so the teachers were comfortable sharing additional thoughts and comments.

Finally, classroom observation data were used to study changes in teachers’ instruction from the beginning to the end of the series of meetings. The teachers were observed between three and nine times over the period of the video-club meetings. All of the classroom observations were videotaped, and field notes were collected for each observation. We focus on those observations that took place within 1 month of the first video-club meeting and those that took place within one month of the final video-club meeting. We refer to these as early and late observations.

Analysis

The research reported is largely qualitative in nature. In what follows we describe the specific methods used to analyze teacher learning in each of the three contexts that is a focus of this study. The goal of this analysis is not to make claims that participation in any video club would influence teachers in a particular way. Rather, the primary goal of this study is to investigate how teachers in this video club were influenced in order to explore the potential of video clubs as a context to support the development of teacher thinking and practice.

Analysis of video-club meetings

Fine-grained analysis of videotapes was used to examine teachers’ discussions of classroom interactions in the video-club setting (Erikson 2006). The coding categories were initially created based on prior research (Frederiksen et al. 1998; van Es and Sherin 2002), but they evolved to account for additional issues the teachers raised in the video-club context (see Table 2) (Strauss and Corbin 1998). Following is a description of each category.

Table 2 Coding categories for analysis of discussions in video-club meetings

The first dimension examined whom the teachers commented on in the clip, the Actor of focus, including Student, Teacher, Self, Curriculum Developers, or Other. While the individuals in the clips were the students and teacher, in the meetings, the teachers often referred to their own teaching. Therefore, it seemed important to create a code to clearly note when the actor was not the teacher or students in the clip. They also often commented on the intended goals of the curriculum developers, so we chose to create a new category within the dimension of actor to capture this focus.

The second dimension examined the Topic of the teachers’ comments, which included Mathematical Thinking, Pedagogy, Climate, Management, or Other. Mathematical Thinking refers to mathematical ideas and understandings (e.g., “He was using his fingers to count the groups of ten.”); Pedagogy refers to techniques and strategies for teaching the subject matter (e.g., “What method do you use to teach two-digit addition?”); Climate refers to the social environment of the classroom (e.g., “That was a fun lesson.”); and Management refers to statements about the mechanics of the classroom (e.g., “The teacher handled that disruption really well.”).

The third dimension focused on how the teachers analyzed practice (Describe, Interpret, or Evaluate), or their Stance. Describe refers to statements that recounted events that occurred (e.g., “The students had their hands up. The teacher then called on a girl to come to the board.”); Evaluate refers to statements in which the teachers commented on what was good or bad or should have been done differently (e.g., “I really like how the lesson was set up. That was great.”); and Interpret refers to statements in which the teachers tried to make inferences about what they observed. In other words, they used their observations of what was happening in the video to make hypotheses about why these events were taking place (e.g., “The way he was tapping on the cards and counting the groups means he understands multiplication.”).

The fourth dimension focused on the level of Specificity teachers used to discuss events they noticed, and this category consisted of two codes, General or Specific. General refers to statements that examine a whole class or that are broad generalizations, such as “They all have trouble with fractions.” Specific statements are those that are specific to particular events, ideas, individuals, or issues, such as one student’s idea or a particular teacher move (e.g., “Juan has trouble adding improper fractions.”).

Finally, the fifth dimension refers to the sources of evidence teachers used and examined whether their evidence was based on the video segment they viewed or on events outside of these segments (video-based or non video-based).

To begin, the video-club transcripts were segmented based on when a new topic was raised for discussion in this context (Grant and Kline 2004). Then, each teacher’s participation within each segment was coded along the same five dimensions. Because of the dynamic nature of conversations in the video-club meetings, each teacher may have participated differently within a given segment. To characterize how the individual teachers analyzed video, however, each teacher received one code per dimension for each segment based on his or her primary focus, which was determined by looking at the context in which his or her comments were made. One teacher, Drew, the first-year teacher, was eliminated from this analysis because he made few comments in the second and final meetings, making it difficult to determine the nature of his noticing in this context. Research on quantifying analysis of verbal data (Chi 1997) highlights the value of conceptualizing chunks at different grain sizes, while research on discourse analysis points to the importance of considering the broader context of the conversation in which individual utterances are made (Goffman 1981; Hymes 1974).

One researcher, the first author, coded all 10 of the video-club meetings in this way, while a second researcher coded 5 of the 10 meetings. These five meetings were randomly selected but represented those from the beginning, middle, and end of the series of meetings. Inter-rater reliability was initially 88%. Any differences between the two coders were discussed and resolved through consensus. Once all of the segments were coded, percentages were calculated for each category within the five dimensions. This was done for each teacher, for each of the ten meetings. Based on this analysis, a table was created indicating these percentages.

We then used quantitative methods to investigate significant differences between the ways the teachers analyzed video early and late in the series of meetings. First, to examine whether they talked differently about classroom interactions over time in the video-club context, the percentages for each dimension, per teacher, for the second meeting in which the teachers were present and for the final video-club meeting were compared. We chose not to use the first video club meeting because the discussion focused on introductory and management issues so it was not representative of the kind of discussion that took place in the other meetings. Then, statistical methods were used to test the significance of any changes in teachers’ analyses from the early to the late video-club meeting. Specifically, a two-tailed z-test for dependent samples was conducted to examine the significance of the differences in the percentages of comments the teachers made in the areas of Student, Mathematical Thinking, Interpret, Specific, and Video-Based, from the early to the late meetings. We used a z-test because it is the standard statistical test for analyzing proportions of known populations (Kirk 1990). Z-values greater than 1.99 indicate statistically significant difference in comments between early and late meetings.

Analysis of teacher exit interviews

Analysis of the exit interviews began with a member of the research team transcribing each of the interviews. Next, two researchers, again the first author and another member of the research team, created summaries of each teacher’s comments for each question, following methods similar to Grant et al. (1998). Each summary was then reviewed and any instances in which the teachers indicated they had learned through participating in the video club were highlighted. Following this, the highlighted segments within an individual teacher’s interview were compared in order to identify those areas in which each teacher perceived that he or she had learned. The final phase of analysis involved looking for patterns across the teachers’ perceptions of their learning. This iterative process resulted in the identification of three common areas in which the majority of the teachers reported to have learned: (a) the importance of attending to student thinking, (b) attending to student thinking during instruction, and (c) the school’s mathematics curriculum.

We recognize the limitations of self-report data. However, we also recognize the strong link between teachers’ beliefs and practice (Hoy and Davis 2006). Thus, we wanted to examine whether participation in the video club influenced the teachers’ perceptions of mathematics teaching and learning, particularly around the issue of student thinking. Further, triangulating the data provides additional insight into the ways the teachers may have been influenced by the video-club activities.

Analysis of the classroom observations

Finally, classroom observation data from early and late in the year was used to investigate changes in practice. This analysis provides an existence proof that participation in a video club can have an impact on teachers’ instruction (Eisner 1998). Additionally, we propose that this analysis will provide a useful framework for conducting future investigations into the influence of participation in video-based professional development on teachers’ practice.

Our analysis of the teachers’ classroom practices focused on whole-class and small-group discussions because we thought these would be places where we could see the extent to which teachers focused on student ideas (Hufferd-Ackles et al. 2004). To begin, all portions of the lessons consisting of whole-class or large-group discussion were identified. Two researchers, the first author and another member of the research team, then reviewed these segments of video and the corresponding field notes and created analytic memos (Miles and Huberman 1994) concerning the ways in which the teachers promoted and engaged with student thinking during each lesson observed. This analysis was guided by research that identified teaching practices related to exploring student thinking including the nature of teachers’ questions and explanations and how teachers solicit and respond to student ideas, strategies, and confusions (Cohen 2004; Empson and Jacobs 2008; Hufferd-Ackles et al. 2004; Franke et al. 2007). We used these themes as a starting point for reviewing the data, but we also accounted for additional issues observed in the data set (Strauss and Corbin 1998).

The memos from both researchers were then reviewed, and we identified several common areas in which the teachers appeared to shift from the early to late observations. The memos pointed to six teaching practices that developed over time. Three related to Making Space for Student Thinking: (a) publicly recognizing students have ideas to contribute, (b) providing extended opportunities for student thinking, and (c) eliciting multiple methods or solutions from students. Two additional practices related to Probing Student Thinking: (a) asking for explanations and (b) probing explanations. Finally, review of the memos suggested that the teachers more often took a stance of Teacher as Learner in the later classroom observations.

To systematically investigate these changes, we returned once more to the videotapes of the early and late classroom observations. All portions of the lessons identified as whole-class or large-group discussion were divided into 2-min intervals, similar to the methods employed by Borko et al. (2008). To be clear, both early and late in the year, the length of the lesson across the seven teachers remained the same, 50–60 min-long. Across the classroom observations, there were a total of 125 2-min segments early in the year and 109 late in the year. In the early observations, the teachers spent 22 min on average in whole-class discussions, and they spent 17 min on average in whole-class discussions late in the year. A researcher then coded each interval for evidence of each of the six teaching practices. In addition, a second researcher coded all lessons from three of the teachers’ classroom observations. Inter-rater reliability across each of the six practices was at least 88%. We then created a table that indicated the numbers and percentage of 2-min intervals in which teachers exhibited evidence for each of the six teaching practices that were the focus of analysis.

Next, we used quantitative methods to investigate significant differences between the teachers’ practices early and late in the year. In particular, we compared the percentages of 2-min intervals in which evidence of each of the six practices was identified for all teachers. Again, we used a two-tailed z-test for dependent samples to test the significance of any changes in teachers’ practices from the early to the late classroom observations.

Results

Changes in teachers’ video analyses in the video-club context

Analysis of the teachers’ comments from the early to late meetings reveal that the teachers shifted to notice and interpret student mathematical thinking (see Table 3). They increased in the percentage of comments they made about the students and mathematical thinking. They also came to more frequently interpret the events viewed, and their comments became more specific and more grounded in the events they viewed in the video segments.

Table 3 Teachers’ overall analytic focus in second and final video-club meetings

Using the z-test to examine differences in the percentages of comments made by dependent samples reveals that in all five areas in which we hypothesized there would be an increase, there was a statistically significant difference at the .05 level. The two-tailed z-test statistic for the difference between the teachers’ comments in the early and late meetings on Student was 3.17; on Mathematical Thinking, the two-tailed z-test statistic was 3.0; on Interpret, 6.0; on Specificity, 2.3; and on Video-focus, 5.6. Thus, in the video-club context, the teachers shifted to analyzing students’ mathematical thinking in detailed ways based on the events in the video clips they viewed.

The following examples illustrate this shift. In one of the early meetings, the group viewed a segment from Elena’s class in which students shared solutions at the board for problems related to addition and subtraction of decimals. Upon viewing the segment, the facilitator asked what they found interesting in the clip:

Yvette::

I like that they were using dry erase [boards]. I think that makes it more interesting… It was kind of fun maybe [for kids] to do while the teacher was doing it, maybe more motivational.

Frances::

I noticed they all went from right to left. I know this particular [curriculum] series doesn’t teach them to go from right to left. Do you teach them to go from right to left?

Elena::

Some of them add the hundreds, then the tens, then the ones, and then we have some that just automatically go from right to left.

Frances::

Well it’s the conventional method. I’ve had parents come to me and say, “I don’t want them to learn that way because I can’t help them at all, because I don’t know what they’re doing.” We were over at that meeting at [the middle school] and the [teachers] told us the same thing. They don’t want them learning these other methods.

Yvette::

I think a child has to be strong in at least one of [the methods]. So, I think an introduction is good, but if you’re over frustrating them, I think one strategy is important.

Daniel::

My students are like, “Why are we doing this step if we have to eventually go back and do it the other way?”

Frances::

That was my next question, how do you feel about teaching both ways? Do you teach both then, or do you stick to just the conventional way?

This exchange represents the kind of discussions the teachers had early in the series of meetings. Yvette’s initial response focused on a classroom climate issue, how the use of dry erase boards motivates students. Frances then inquired about what methods the teachers use to teach addition and subtraction, whether they use what the teachers refer to as the conventional method or partial sums. After Elena responded that students use both approaches, Frances, Yvette, and Daniel shared their experiences teaching partial sums, concluding with Frances asking the group again what method they teach. Thus, we see here that they discussed a range of topics, with a primary focus on pedagogy, particularly as it relates to the reform curriculum, and classroom climate. They commented on both the students and themselves as teachers, and their comments were mostly descriptive and evaluative and both general and specific, drawing on some events they viewed in the clip, but with a greater focus on what occurs in their own classrooms.

Later in the series of meetings, though, the teachers initiated and sustained a detailed focus on examining and interpreting students’ mathematical thinking based on the events in the clip. For example, the teachers viewed a clip from Daniel’s classroom in which a student, Maria, solved the problem 0.2 × 8.0 at the board. Her method involved calculating each of the partial products. She sometimes treated 8.0 as 80 and other times as 8.0, yet she consistently recorded each answer with two digits to the right of the decimal point.

While viewing the clip, Daniel asked the facilitator to stop the videotape and then turned to a colleague and said, “You’re nodding, like yes.” The teacher, Wanda, along with several other members of the group, proceeded to interpret the method the student used to solve the problem.

Wanda::

She’s doing it a little early. She’s [recording the decimal point] at each one down, but when you multiply decimals you count the numbers to the right of the decimal and then you count over that amount in your answer. She’s just doing it each time.

Frances::

She doesn’t have to do that until the very end. She’s just doing it each time…

Daniel::

That’s the way [the curriculum designers] are trying to keep them away from counting over for decimals, but I guess, yeah, okay…

Elena::

But it kind of shows that she’s understanding the whole part about decimals and moving over.

Daniel::

I was really trying to figure out, ‘cause I’m like, she’s got the right answer, she knows something here.

Wanda::

It’s partial products.

Facilitator::

…but if she’s doing 8 times 0.2, there’s only one number behind the decimal point, so why is she saying there’s two?

Frances::

…She’s not multiplying 8 times 2.

Daniel::

Eighty…

Facilitator::

She’s doing 80 times 0.2? She can’t say that her answer is both 16 and that she has to have two numbers to the right of the decimal.

This excerpt is rather different from the discussion early in the series of meetings. Here, the teachers seek to understand and explain Maria’s method, using details from the video clip to interpret what they think she understands.

While we were encouraged to observe that the teachers came to interpret particular student mathematical ideas in detailed ways, we were also interested in investigating to what extent this may have influenced them outside of the video-club context.

Teachers’ self-reports of changes in thinking and practice

Analysis of the exit interviews reveals three ways the teachers perceived they were influenced by participating in the video club. Specifically, they claimed to have learned the importance of attending to student thinking, to attend to student thinking during instruction, and about their school’s mathematics curriculum.

Learning about the importance of attending to student thinking

All seven teachers reported learning about the importance of listening to student thinking as a result of participating in the video club. Throughout the exit interviews, teachers made numerous comments indicating that the video club helped them recognize that students can have quite interesting mathematical ideas. For example, Daniel remarked that the video club “made me conscious that there are so many times when [the students]…may be thinking in a way that I’ve never thought of.” Similarly, Linda commented that in the video club she found herself looking closely at students’ ideas and realizing “they really do work through a lot of things.” Along the same lines, Yvette stated that “It was interesting to hear [students’] thoughts…You know,…what was she thinking about, what was he thinking about, where are they coming from…It was thought provoking and interesting.” These comments are reminiscent of what Cohen (2004, p. 46) refers to as teachers coming to understand that students are “havers” of mathematical ideas.

The teachers also indicated that the video club helped them to recognize that it was valuable for them as teachers to pay attention to student ideas. Elena commented, “Listening to the video is kind of like ‘Okay!’ If you listen a couple of times you just hear more…[The student’s idea] makes a lot more sense.” Another teacher, Frances, stated the following:

[In class] a child gives an answer and you’ve got to go onto the next [problem], … you watch the clock… [But in the video club] it’s really focused on the kids [and] if you understood what she was saying. You could really understand if she got this or not …[even if] she didn’t spit it out the way you wanted her to [or] didn’t use the terminology…. But, if you really stop and think, ‘Yeah, she did get it…she was just saying it a different way or she got part of it.’

Frances emphasized the need to think carefully about students’ ideas and the ways in which reflecting on video can support this process. Similarly, Drew explained, “Well again, it goes back to…listening to the children give their remarks… That really hit home on the videos. I know, for myself…I want to do more of that.” Research suggests that there is often a disconnect between teachers’ practices and their beliefs (e.g., Forgasz and Leder 2008). In this case, however, we found that both the teachers’ self-reports and our own analysis of the video-club discussions indicate participants’ increased awareness of student thinking.

Attending to student thinking while teaching

Six teachers commented that they believed that as a result of participating in the video club they paid closer attention to students’ ideas while teaching. For instance, Drew, a first-year teacher, said, “I notice different things that they don’t understand and I have them talk through it.” Drew further explained that he found himself adapting his teaching based on the information students provided about their mathematical understandings and any difficulties that he observed. Elena also remarked that she shifted her instruction. “[I] look to have kids really explain more of how they’re thinking…” Elena also believed that she would often consider how to support learning in her classroom based on what she came to know about students’ understanding from their explanations. Another teacher, Frances, explained, “I think [I’ve come to] slow down and really listen to kids. …[I try to] focus and really listen to kids and find out ‘What exactly do you mean by this?’” Similarly, Linda asserted that she had become “more patient” during class and “probably step[s] back a little bit more” to take in the ideas students are sharing about the mathematics being discussed in class. She also described holding herself back from giving the answer in order to let students work through problems on their own.

Thus, not only did the teachers claim that they learned about the importance of student thinking in the video-club meetings, but these six teachers believed that they also increasingly paid attention to student ideas while teaching. This result is particularly noteworthy given that the video-club discussions were not focused explicitly on helping teachers learn to attend to student thinking during instruction. For the teachers, analyzing student thinking via video seems to have had a strong connection to analyzing student thinking in their classrooms, similar to Schön’s (1983) claims about the potential of reflection-on-action to influence reflection-in-action.

Learning about curriculum

All seven teachers reported that they learned about their school’s mathematics curriculum as they participated in the video club. They explained that having opportunities to view lessons from other teachers’ classrooms and from other grade levels gave them valuable insights into the details of lessons and the broad goals of the curriculum. Recall that the school as a whole was in the third year of using a reform-based mathematics curriculum, though this was a new endeavor for several participants. They expressed concerns about not having been familiar with the overall design and goals of the curriculum, and a few mentioned that they had felt insufficiently prepared to use the materials with their students.

For example, when asked what he thought was the most valuable part of the video club, Daniel, responded:

Just seeing… oh, [the fifth graders are] doing fractions there too! Not that I didn’t know that before, but just to be able to see that and how it’s going on and hear the teachers talking about what their expectations are, what [the students] need to know and how they go about teaching their math. And [seeing] oh, they use this key word, or this phrase, or this vocabulary… We just don’t have enough time in the day to talk about these things. I should know at least all the chapter titles and all the concepts they do in fifth grade, but nobody gives you any time to do that… So, that was valuable.

Being provided the time and space to view their colleagues’ curriculum implementation was a common sentiment across all teachers. Another teacher, Frances, emphasized this point when she said, “Especially, for me, having taught third [grade] and gone to fifth, it was interesting to see how what I taught in third grade really related to fourth and what they’re teaching at fourth, how that has helped me in fifth.” Again, the video club was not designed to support learning about curriculum, but the teachers reported that viewing video of one another’s teaching helped them accomplish this goal.

Changes in teachers’ instruction

The analysis of teachers’ classroom practice identified three changes in teachers’ instruction over time. Specifically, teachers increasingly made space for students’ thinking to become public in the classroom, they more frequently probed students’ thinking, and they took on the stance of learner in the context of teaching.

Making space for student thinking

The first shift we observed is the teachers more often made space for student thinking to emerge in the classroom. They did so in three ways: publicly recognizing students have ideas to contribute, providing extended opportunities for student thinking, and eliciting multiple methods or solutions (see Table 4).

Table 4 Characteristics of making space for student thinking

Publicly recognizing unsolicited student ideas refers to the teacher indicating that a student has a question or idea to contribute to the lesson. For example, late in the year, Yvette led a discussion on converting percents to decimals. She wrote on the overhead several percents and asked the students to represent them in decimal form. She then asked the students to share their answers to each problem. After students provided their answers, Yvette saw that a student had his hand raised, and she turned to him and said, “What’s your question, Steven?” inviting him to participate in the discussion. In another observation late in the year, Yvette noticed a student’s hand raised and she turned to the class and said, “Max has a thought.” The important point here is that she recognized that these students wanted to contribute and that she made space for unsolicited questions to become part of the classroom discourse.

This practice was not a common feature of the teachers’ early classroom observations, occurring in only 24% of the 125 2-min segments coded. Later in the year, the teachers recognized unsolicited ideas in 68% of them 109 2-min segments that were coded. This shift is significant at the .05 level (two-tailed z-test statistic = 4.7).

Teachers also provided extended opportunities for students to work through the mathematics. One way they did this was to encourage students to take more time to work through their ideas, making comments like, “Let’s give some people some time to think” and “I’m not going to tell you. You have to figure it out.” A second approach was to allow students multiple opportunities to express their thinking. For example, when students made an error solving a problem, the teachers allowed them time to rework the problem and then share their revised thinking. This practice indicates that the teachers were creating an environment where students could generate and rework their ideas in order to develop their thinking, both important goals of mathematics education reform (Lampert 2003; National Council of Teachers of Mathematics [NCTM] 2000). In the early observations, we observed this practice in 31% of the total 2-min segments, as compared to 71% of the total coded segments in the late observations. This shift is significant at the .05 level (two-tailed z-test statistic = 5.2).

Finally, the teachers elicited multiple methods or solutions from the students. We observed the teachers posing tasks in ways that prompted students to generate their own solution strategies and then inviting students to the board to share how they solved a problem and explain their solutions. In an observation of Linda, she placed a grid with 100 cubes on the overhead projector and asked the students to come up with a way to divide it into 20 equal parts. She then invited three students to draw on the grid to illustrate their approach. Similarly, when we observed Drew conducting a chapter review, he posed several problems and then invited two or three students to the board to share and explain how they solved each. Across the teachers, we saw evidence of this practice in 20% of the total 2-min segments in the early observations compared to 59% of the total segments in observations late in the year. Again, this shift is significant at the .05 level (two-tailed z-test statistic = 6.3).

Probing student thinking

The second area that we examined concerns teachers’ probing of student thinking. We observed that the teachers probed student thinking in two ways, asking for explanations and probing students’ explanations. The first approach refers to teachers asking follow-up questions when students provide an answer without an explanation. The second concerns teachers probing students’ explanations to gain deeper insight into their thinking.

For example, in Elena’s classroom, she posed the following problem: there are 8 boxes of cupcakes. There are 6 cupcakes per box. How many cupcakes are there in all? One student, Angelina, responded that the answer is 14 and Elena responded, “14? Ok, how did you come up with that number, Angelina?” After she explained her approach, Elena asked Peter for the answer. Following his response, “48”, the teacher said, “Okay, 48. How did you get that?” These two exchanges show Elena asking for an explanation for the students’ answers, with a particular focus on how they arrived at their answers. The teachers also asked for explanations related to students’ reasoning, posing questions like, “Why do you think that?” or “You said something about 20, what do you mean?” In the early observations, the teachers asked students to provide explanations for an answer in 36% of the total number of 2-min segments, compared to 82% of the total number of segments late in the year. This shift is significant at the .05 level (two-tailed z-test statistic = 4.7).

We also observed teachers probing students’ explanations to gain deeper insight into their thinking. Consider the example from Daniel’s classroom when he taught a lesson on multiplying decimals. Maria explained how she solved the problem 8.0 × 2.0. She essentially approached the problem using the partial products method, but her explanation was unclear. Daniel prompted her to explain her solution, and as she talked through her approach the second time, Daniel interrupted her and asked her: “What do you mean, since there’s two things behind the line?”; “You said, ‘Two over’. What do you mean ‘two over’?”; “Where is that coming from? What is our cue to do that?”; “So, are you doing partial products as if there’s no decimal point in there?” These questions further probed the students’ explanation to understand her mathematical reasoning. We observed a shift in teachers’ practice in this dimension as well. Early on, teachers probed student explanations in 5% of the total two-minute segments; whereas, late in the year, they probed explanations in 48% of total number of segments. This shift is significant at the .05 level (two-tailed z-test statistic = 7.2).

Learning while teaching

Finally, the third shift is characterized as learning while teaching. We defined this practice as teachers viewing themselves as mathematics learners in the context of the classroom. We observed teachers adopting a contemplative stance, expressing uncertainty in the act of teaching, pausing in the midst of instruction to consider a student idea, or working through the mathematics during instruction. We also observed the teachers verbalize their confusion during instruction, making comments like, “Hmmm… I’m a little confused. Let me think about this” or “I hadn’t thought of that before.” The teachers also paused during instruction to make sense of an idea about which they appeared confused. In the case of Daniel trying to understand Maria’s strategy, he made statements like: “I’d like to know how that came out but I’m not sure I followed it” and “Now, I’m interested. I’ve never heard of this. Is this just a coincidence that it works?” Furthermore, we observed teachers pausing in the midst of instruction to solve a problem on their own. In one observation of Wanda, for example, the students were working in groups to solve probability problems using factor trees. As they worked together, Wanda solved a problem on the board, checked her answer against her curriculum guide, and then re-solved the problem before pulling the groups back to a whole-class discussion. These teacher moves suggest that the teachers were not always certain about an idea a student raised or about the mathematics and that they were positioning themselves as learners in the classroom. In the early classroom observations, we observed this practice in 6% of the total segments, contrasting that with 41% in the total number of late classroom observations. This shift is significant at the .05 level (two-tailed z-test statistic = 6.2).

Discussion

In this study, we set out to examine how participation in a video club focused on examining student mathematical thinking influenced teachers’ thinking and practice. We investigated data from three related contexts: (a) teachers’ comments in the video club, (b) teachers’ self-reports of the influence of the video club, and (c) observations of teachers’ instruction from early and late in the year.

We found that in the video-club context, the teachers learned to attend to the specifics of student mathematical thinking, and they adopted an interpretive stance to their analyses, using details from events in the clips to support their interpretations. This type of discourse reflects the kind of talk that research suggests teachers need to engage in order to learn to teach mathematics for understanding (Borko 2004). We see that the teachers learned a discourse for analyzing video similar to the teachers who Borko et al. (2008) studied, one that was focused on making sense of what occurs in classrooms and using evidence from classroom events to support their analyses.

In the interview setting, the teachers reported learning about student thinking, that they had come to recognize that students have interesting ideas about mathematics, and that it was valuable for them to carefully consider such ideas. Moreover, they perceived that they adopted several strategies to pay close attention to student ideas in their instruction. Given the strong connection between teachers’ beliefs and practices, and the potential for changes in beliefs to serve as a catalyst for changes in practice (Philipp 2007), we sought to examine teachers’ instruction as well.

Analysis of the classroom observation data confirmed that there were changes in the ways that the teachers attended to student thinking during instruction. They provided more opportunities for students to express their thinking and explore mathematical ideas, and they probed student thinking in substantive ways. Furthermore, it was not the case that the teachers had to dramatically increase the amount of time in class discussion in order to make student thinking visible. In fact, on average, they decreased in the amount of time spent in whole-class discussion but they still managed to introduce these practices in their teaching. This result is noteworthy given that professional development often has little effect on teachers’ thinking and practice (Porter et al. 2000; Wilson 2003), even when teachers are given specific prompts to direct them in their learning (Stephens and Hartmann 2004). In contrast, we observed important shifts in the participants’ practices. Perhaps because the video clips came from the teachers’ own classrooms, they looked similar to what the teachers encounter each day. Thus, there was little distinction between exploring student ideas in the video club to engaging in those same practices in the classroom. Alternatively, it could be the case that because teachers were exploring student thinking in the video club, they had become interested in what students had to say, and therefore looked to create opportunities for students to share their thinking in the classrooms.

We also want to mention two ways that the teachers learned that were not as directly related to examining student mathematical thinking. First, in the exit interviews, the teachers reported learning about curriculum issues, claiming the video club helped them learn about what is taught at different grade levels. Being able to look inside each other’s classrooms appears to have given teachers access to a wealth of information about how related topics were covered across grade levels, and the teachers believed it to be an important benefit of participating in the video club. Using new mathematics curriculum materials has been found to be quite challenging for teachers, and teachers do not always use such materials as intended (Remillard 2005). Perhaps video can become a worthwhile tool for those who educate teachers as they adopt and enact new curricula.

Finally, classroom observation data indicated that the teachers developed a view of themselves as learners of mathematics in the classroom over time. Teachers could be seen, in the midst of instruction, pausing to solve a mathematics problem or thinking out loud about a student solution or explanation. A stance of inquiry on the part of the teacher is an important component of mathematics instruction in the context of reform (Hufferd-Ackles et al. 2004; Sherin 2002). Drake (2006) found, for example, that teachers who viewed themselves as learners of mathematics had more reform-oriented practices than teachers who no longer viewed themselves as mathematics learners. While this was not an explicit goal of the video-club design, perhaps examining their students’ understandings of mathematics helped the teachers become more comfortable considering their own mathematical thinking as well.

Conclusion

We conclude by addressing two important issues. We did not begin this inquiry expecting to see all of the changes we observed. While we are encouraged by these results, we are also cautious about being too optimistic. This study provides evidence that it is possible for teachers who participate in a video club to change their beliefs and instruction in ways that may help them accomplish the vision of mathematics reform pedagogy, however, future research is needed. We recognize that we cannot generalize from this data set to other video-club settings or other video-based professional development. Further, our analysis points to some ways teachers might change but they are likely not the only ways. Additional classroom observations may have provided more or less evidence in support of these changes or we may have identified other influences on teachers’ practice. An important subject of future research is whether or not all teachers who participate in video clubs designed as the one we studied change their practice in these ways across the school year. We also need to investigate if teachers who are not a part of a video club are likely to pay more attention to student thinking in these ways over time as well.

This study raises important questions about how the design of this particular video club helped teachers learn to notice in this setting. Previously, we have explored how the video clips the teachers viewed (Sherin et al. 2009) and participants’ roles (van Es 2009) influenced the group’s discussions. We have also explored how the video-club context enabled the development of teacher community and how that community helped the participants accomplish the goals of the club (van Es 2007). Another important question concerns how the facilitator established norms for analyzing video that helped teachers learn to interpret student mathematical thinking and develop a critical discourse for observing classroom interactions. The results of such research will inform the design of video-based professional development that is both productive and meaningful for teachers.