Novel Mn_0.5Zn_0.5Al_0.1Mg_xLi_xFe_(1.9-x)O₄ nanoferrites: synthesis, theoretical cation distribution, and improving their dielectric properties

Abstract

The effect of Mg²⁺–Li¹⁺ ions in modifying the structural, electrical, and magnetic characteristics of nanocrystalline Mn–Al–Zn ferrites was examined experimentally and theoretically in the current study. The chemical co-precipitation method was used to create the investigated ferrite samples, which have the chemical formula (Mn_0.5Zn_0.5 Al_0.1Mg_x Li_x Fe_(1.9-x)O₄) and concentration range of the substituent (0 ≤ x ≤ 0.2). The cation distribution of the investigated system was assumed and confirmed. Furthermore, the activation energy, AC resistivity, dielectric loss tangent, and dielectric constant were investigated in terms of their compositional dependence. The final results showed that the increasing of Mg²⁺–Li¹⁺ concentration enhanced the physical and dielectric properties of the prepared samples. The experimental findings show also that as temperature rises, ε′, tan δ, and σ all increase but they all decrease as Mg²⁺–Li¹⁺ content increases. With increasing Mg²⁺–Li¹⁺ concentration, the AC resistivity of the prepared samples also continuously increased, resulting in the sample with x = 0.2 having high resistivity, which can be used in specific technical applications such as transformer cores.

1 Introduction

Ferrites are among the most significant dielectrics therefore they are the subject of interest as a result of their practical applications, affordable prices, and excellent properties for solid-state electronics and technological communication. Therefore, a lot of attention has been paid to improve the functional properties of these materials so that they can be employed in additional applications such as the high-frequency transformer cores and high-frequency power supplies. In order to enhance these features for use in technological applications, research is being done on how the ferrite properties rely on the chemical content, manufacturing processes, and size of particles [1,2,3,4,5].

Compared to other ferrites, Mn–Zn ferrites are chosen because of their inexpensive cost and extensive applications such as high-frequency power supply, memory storage devices, TV sets, biomedicines, magnetic resonance, and catalysis. These ferrites are typically utilized for applications where frequency requirements are below 2 MHz and are particularly crucial for stress insensitivity and low noise. Mn–Zn ferrites are of great interest. However, due to their low resistivity and consequently high eddy current losses, these ferrites have certain limitations for magnetic application at higher frequencies above the critical frequency. Properties of these Mn–Zn ferrites and similar ferrites have been investigated extensively by many authors [6,7,8,9,10,11,12,13,14,15,16,17].

The effect of substitution of Fe³⁺ by single ion such as Al³⁺, Y³⁺, In³⁺, and Gd³⁺ ions on the structure and physical properties of Mn–Zn ferrites has been studied by many authors [18,19,20]. Also the effects of various additions of GeO₂ or SnO₂, in a Mn–Zn ferrite on the microstructure and magnetic properties have been studied [21]. The current work investigates the effect of replacing Fe³⁺ ion with two different ions simultaneously, Mg²⁺ and Li¹⁺ ions, on the structural, dielectric, and magnetic properties of Mn–Zn ferrites. Moreover, we tried to obtain more improvement in the electrical properties of Mn–Zn–Al ferrite using the substitution of Fe³⁺ ion by two new ions, Mg²⁺–Li¹⁺ ions.

2 Experimental procedure

Ferrite samples with the general formula Mn_0.5Zn_0.5Al_0.1Mg_x Li_xFe_(1.9-x)O₄ (0.0 ≤ x ≤ 0.2) were synthesized for the current study using the chemical co-precipitation method; the specifics of the production procedure are presented in Fig. 1. High-purity sulfates (99.9% Aldrich) of MnSO₄.H₂o, ZnSO₄.7H₂O, Al₂(SO₄)₃.16H₂O, MgSO₄, Li₂SO₄.H₂o, and Fe₂(SO₄)₃ were mixed together with the proper molecular weight ratio.

Fig. 1

A flowchart outlining the sample preparation process

The used sulpftes of each composition were weighted using a digital electronic sensitive balance with accuracy ± 0.0001 g. The sulfate salts were mixed in stoichiometric ratio, the mixture was put in distilled water to form an aqueous solution, and then sodium hydroxide solution was added. The formation of ferrite nanoparticles takes place in two-step process: (i) conversion of metal salts into hydroxides (co-precipitation step) and (ї) transformation of hydroxides into nanoferrites (ferritization step). In ferritization step, the precipitated hydroxide is heated under continuous stirring to decompose and obtain ferrite structure. The precipitated particles were washed several times with double distilled water to remove the salt residues and other impurities. The precipitated particles were then dried at room temperature to obtain the dried precipitates. The dried precipitates were milled to powered form using mortar and pestle. Table 1 shows the most important information about the used chemical sulfates. A contemporary, automated, and computerized power diffractometer type D8 Advance Bruker with CuK_α radiation (λ = 1.54 Å) was used to acquire X-ray diffraction (XRD) patterns for the prepared samples. At Tanta University’s central lab, the infrared absorption spectra in the range of 200–1000 cm⁻¹ were captured at normal light incidence. Using the LCR Hioki bridge, the ac dielectric properties were evaluated as functions of temperature at various frequencies.

Table 1 The most important information about the used chemical sulfates

3 Results and discussion

3.1 Analysis of structure

3.1.1 X-ray diffraction

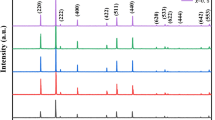
The structure of the generated samples with the general formula (Mn_0.5Zn_0.5 Al_0.1Mg_x Li_x Fe_(1.9-x)O₄) (0 ≤ x ≤ 0.2) was studied Using XRD patterns, and the findings are given in Fig. 2. The single-phase cubic spinel structure of all the produced samples is depicted in Fig. 2. The XRD diffractograms obtained from the different prepared manganese–zinc ferrite spinel stoichiometries (x range from 0 to 0.2) look macroscopically the same but have small differences in the 2θ values, denoting different unit cell sizes. The XRD peaks that correspond to the spinel structure are broad and with low intensities and they can well match to those from a crystalline sample consisting of extremely small crystallites.

Fig. 2

X-ray patterns of the prepared samples formula Mn_0.5Zn_0.5Al_0.1Mg_x Li_xFe_(1.9-x) O₄ (0 ≤ x ≤ 0.2)

The experimental lattice parameter of the prepared samples was calculated and plotted in Fig. 3 as a function of Mg²⁺–Li¹⁺content. The Figure shows that as Mg²⁺–Li¹⁺content increases the lattice parameter increases due to the larger ionic radii of Mg²⁺ (0.80 Å) and Li¹⁺ (0.71 Å) ions than that of Fe³⁺(0.64 Å) ion [20, 22].

Fig. 3

Variation of experimental lattice parameter (a_exp.) with (Mg²⁺–Li¹⁺)—concentration

3.1.2 Analysis of infrared spectra and cation distribution

Studying far-infrared (IR) spectrum is an essential method for learning about position of ions in the crystal through the vibrating modes. The FTIR spectrum for (Mn_0.5Zn_0.5Al_0.1Mg_xLi_xFe_(1.9-x)O₄); (0 ≤ x ≤ 0.2) is shown in Fig. 4. The peak positions with respect to the composition are listed in Table 2.

Fig. 4

Infrared spectra of the prepared samples Mn_0.5 Zn_0.5 Al_0.1 Mg_x Li_x Fe_(1.9-x) O₄ (0 ≤ x ≤ 0.2)

Table 2 The change of wave number of IR transmission bands (cm⁻¹) with content of the prepared samples Mn_0.5 Zn_0.5 Al_0.1 Mg_x Li_x Fe_(1.9-x) O₄ (0 ≤ x ≤ 0.2)

In the IR spectra, chemical bonds will absorb radiation at certain frequencies and these frequencies could be correlated to the interatomic bonds within the compound. It has been reported that the two band frequencies (ν₁,ν₂) are due to the stretching vibration of (F³⁺–O²⁻) groups in the A- and B-sites, respectively. The two band frequencies (ν₁,ν₂) mainly depend on the bond length in A- and B-sites. It is obvious from Table 2 that as (Mg²⁺–Li¹⁺) concentration increases both (µ₁ and µ₂) decreases. This is attributed to the increase in the bond length in A- and B-sites due to the substitution of F³⁺ ion by Mg²⁺–Li¹⁺ ions of larger ionic radii, where the band frequency (µ) is inversely proportional to the bond length [23,24,25,26].

Therefore, in the light of the above discussion of spectrum, one could conclude that (Zn²⁺) ions preferentially occupy tetrahedral A-site, while (Mn²⁺) and (Fe³⁺) ions are distributed between A- and B-sites, and (Al³⁺) ions occupy octahedral B-site [27] and (Li¹⁺) ions occupy only B-site, whereas (Mg²⁺) ions can occupy both A- and B-sites.

For the spinel structure, the theoretical lattice parameter a_th. could be calculated using the following equation: [28]

$$a_{{th}} .{\text{ }} = ~\frac{8}{{\sqrt 3 }}[(r_{A} + R_{o} ){\text{ }} + ~\sqrt 3 (r_{B} + R_{o} )]$$

(1)

where Ro is the ionic radius of the oxygen ion (1.32 Å), r_A and r_B are the ionic radii of tetrahedral (A-site) and octahedral (B-site) sites, respectively.

To calculate r_A and r_B, the following cation distribution is assumed:

$$\left( {{\text{Zn}}_{{0.5}}^{{2 + }} {\text{Mn}}_{{0.3}}^{{2 + }} {\text{Mg}}_{{(2x/3)}}^{{2 + }} {\text{Fe}}_{{(0.2 - 2x/3)}}^{{3 + }} } \right)[{\text{Mn}}_{{0.2}}^{{2 + }} {\text{Al}}_{{0.1}}^{{3 + }} {\text{Mg}}_{{(x/3)}}^{{2 + }} {\text{Li}}_{x}^{{1 + }} {\text{Fe}}_{{(1.7 - 4x/3)}}^{{3 + }} ]{\text{O}}_{4}^{{2 - }}$$

(2)

where the brackets ( ) and [ ] denote A- and B-sites, respectively. The ionic radius for each site is calculated according to the following equation: [29]

$$r_{{\text{A}}} = \left[ {0.5r_{{{\text{Zn}}^{{2 + }} }} + {\text{ }}0.3r_{{{\text{Mn}}^{{2 + }} }} + {\text{ }}\left( {2x/3} \right)r_{{{\text{Mg}}^{{2 + }} }} + {\text{ }}\left( {0.2 - 2x/3} \right)r_{{{\text{Fe}}^{{3 + }} }} } \right]$$

(3)

$$r_{{\text{B}}} = \left[ {0.2r_{{{\text{Mn}}^{{2 + }} }} + {\text{ }}0.1r_{{{\text{Al}}^{{3 + }} }} + {\text{ }}\left( {x/3} \right){\text{ }}r_{{{\text{Mg}}^{{2 + }} }} + {\text{ }}\left( x \right)r_{{{\text{Li}}^{{1 + }} }} + {\text{ }}\left( {1.7 - 4x/3} \right)r_{{{\text{Fe}}^{{3 + }} }} } \right]$$

(4)

where r_Zn²⁺, r_Mn²⁺, _rAl³⁺, r_Mg²⁺, r_Li¹⁺, and r_Fe³⁺ are the ionic radii of Zn²⁺, Mn²⁺, Al³⁺, r_Mg²⁺, r_Li¹⁺, and Fe³⁺ ions, respectively.

As shown in Fig. 5, it was found that the experimental values of the lattice parameter were higher than the theoretical ones. This is due to the formation of Fe²⁺ ions during the sintering process, which have an ionic radius larger than Fe³⁺ ions.

The difference between experimental and theoretical lattice parameter decreases with increasing (Mg²⁺–Li¹⁺) ions concentration which indicates that the concentration of (Fe²⁺) ions decreases as (Mg²⁺–Li¹⁺) ions increases as shown in Fig. 5.

Fig. 5

Variation of the theoretical and experimental lattice parameter (a) with (Mg–Li) – content(x)

3.2 Dielectric properties

3.2.1 Temperature dependence

The conduction in Mn–Zn ferrites results from the jumping of the charge carriers from one ion to another. Mn–Zn ferrites are a particular kind of temperature-activated jumping semiconductor. The AC conductivity of all prepared samples was examined as temperature function at various frequencies from 100 Hz to 5 MHz. The results show that each sample exhibits the same behavior, which is shown in Fig. 6 along with the samples’ behavior. The electrical conductivity is seen to increase with temperature in Figs. 6, 7. The explanation for this behavior is that as temperature rises, charge carriers become more mobile.

Fig. 6

AC conductivity dependence on the temperature for all the studied specimens

Fig. 7

AC conductivity as a function of temperature a for all investigated specimens b for sample x = 0.0

When the temperature increases, the thermal activation occurs causing electrons to jump between Fe²⁺ and Fe³⁺ ions (at the adjacent B-site). The hopping of these electrons at the d-shell results in local displacements in the direction of the applied field. These local displacements of the electronic charge carriers cause the dielectric polarization in the ferrites. So, the mechanism of dielectric polarization in ferrites is similar to that for electric conduction and mainly by the hopping conduction mechanism. Therefore, the dielectric polarization, ε′ (Fig. 8) and tan δ (Fig. 9) increase as temperature increases as well as the electrical conductivity for the present ferrite samples.

Fig. 8

The dielectric constant (ε′) dependence on the temperature (T) at different frequencies for all the prepared specimens

Fig. 9

The dielectric loss tangent (tan $\updelta$) dependence on the temperature (T) at different frequencies for all the prepared specimens

The activation energies of all the specimens were determined utilizing the relationship of lnσ with (1/T) according to the Arrhenius equation:

$$\sigma = \, \sigma_{{\text{o}}} \exp \left( {\frac{ - E\sigma }{{kT}}} \right)$$

(5)

where E_σ is the conduction processs activation energy obtained from the slope of (ln σ) and (1000/T). Figure 7 indicates the two breaks and three distinctive zones (I, II, and III) in the temperature variation of conductivity. The line of each sample was broken at different steps region (I, II, and III). Extrinsic conduction mechanisms (impurities) are responsible for the first zone (I), which includes all samples' ranges from room temperature up to the first transition temperature. The magnetic transition of phase from the ferromagnetic to the paramagnetic state is always owed to the second transition temperature (T_C). According to the previous Eq. (1), the activation energies for the conduction process were estimated from the slopes of each line. Table 3 gives details about the activation energies E_Ferri. for region II, E_Para. For region III, and the transition temperature T_C between ferrimagnetic and paramagnetic region. It should be observed that region II to region III transitions result in a rise in the activation energy value, which is according to the theory presented by Iruin and Turov [30]. The magnetic transition can be described as a second-order transition with a broad temperature range. In the view of thermodynamic theory, the second-order transition is caused by volume expansion, which results due to an increase in jumping length between ions hence an increase in activation energy.

Table 3 The effect of Mg²⁺–Li¹⁺(x) content on the values of activation energies and transition temperature (T_C)

As a function of temperature, the dielectric constant (ε′) of each sample was measured at different frequencies. The obtained results are shown in Fig. 8, where there are two distinct zones. These zones are caused by the presence of two different forms of polarization, as the AC conductivity studies previously showed. From room temperature to about 380 K, in the first temperature range, the dielectric constant (ε′) raised slowly with temperature, showing that electronic polarization was dominant and that the thermal energy applied to the sample was not enough for fully releasing all the localized dipoles to obtain the field’s direction [31]. Above 380 K, in the second temperature range, ε' quickly raised with temperature. This happened due to the fact that the high thermal energy was now enough to liberate a significant number of dipoles, which were then oriented in the direction of the field and increased the polarization plus ε′ but at varying rates depending on the Mg²⁺–Li¹⁺ content. Due to the accumulation of charges on the grain boundaries, interfacial, orientational, and Maxwell–Wagner polarizations are expected to be important in the second temperature range [32,33,34].

Figure 9 shows a perfect curve for the relationship between dielectric loss tangent (tan$\delta$) and temperature at different frequencies. Figure 9 illustrates how the tan δ increases with rising temperature. The high thermal energy, which is enough to disrupt the aligned dipoles and subsequently increase the friction among each other, causes the increase in tan δ. This in turn raises the leakage of energy and dielectric loss. On the contrary, greater energy will be needed to overcome the medium’s inner friction [35].

3.2.2 Compositional dependence

In the present system with increasing (Mg²⁺–Li¹⁺) content, the conductivity decreases continuously as shown in Fig. 10. The same behavior is observed for the dielectric constant (ε′) and dielectric loss tangent (tan $\updelta$) as shown in Fig. 11 and Fig. 12, respectively. The decreasing of conductivity with increasing (Mg²⁺–Li¹⁺) content is attributed to the increasing of (Mg²⁺–Li¹⁺) content which leads to the decrease of (Fe³⁺) ions in B-site so the electron hopping between (Fe²⁺) and (Fe³⁺) decreases leading to decrease in the conductivity as shown in Fig. 10. Moreover, the substitution of Fe³⁺ by Mg^{2 +} and Li¹⁺ ions may induce defect sites due to the dissimilarities between the ions. These defects act as scattering centers of the electrons and hence the conductivity of the samples decreases [26, 36].

Fig. 10

Variation of AC conductivity (σ_ac) of the samples with (Mg²⁺–Li.¹⁺) ions content(x)

Fig. 11

Variation of dielectric constant (ε′) of the samples with (Mg²⁺–Li.¹⁺) ions content(x)

Fig. 12

Variation of dielectric loss (tan $\delta$) of the samples with (Mg²⁺–Li.¹⁺) ions content (x)

As shown in Fig. 11, as Mg²⁺–Li¹⁺ content increases the dielectric constant decreases. Using the assumed cation distribution, this is attributed to Mg²⁺ and Li¹⁺ ions replacing the Fe³⁺ ions on the octahedral site, leading to decreases in the ratio of Fe²⁺/Fe³⁺ ions and limit the valance exchange between Fe²⁺and Fe³⁺ ions in the B-site resulting in a decrease in polarization as well as dielectric constant ε′. Also as Mg²⁺–Li¹⁺content increases the dielectric constant ε′ decreases due to the decreasing of A–B interaction as a result of increasing the nonmagnetic ions in the B-site [20, 22]. Since the hopping conduction mechanism dominates the dielectric polarization process in ferrites, the process is similar to that for electric conduction. Thus, the dielectric constant (ε′) (Fig. 11) and (tan δ) (Fig. 12) exhibit the same behavior.

4 Conclusions

• 1. X-ray diffraction confirmed that the prepared samples possess a cubic single spinel phase without any secondary phases.

• 2. IR measurements were used to confirm the generated samples’ assumed cation distribution, and the theoretical lattice parameter was compared with its experimental value.

• 3. As Mg²⁺ and Li¹⁺ content increases, the lattice parameter increases according to the ionic radii of replacements.

• 4. The obtained results indicate that the analyzed samples exhibit the typical dielectric behavior of ferrites as a function of temperature.

• 5. The obtained results indicate that the dielectric constant (ε′), dielectric loss tangent (tan δ), and the ac conductivity (σ) of the obtained samples all reduced continuously when the Mg²⁺–Li¹⁺ content increases.

• 6. The present work indicates also that the sample Mn_0.5Zn_0.5Al_0.1Mg_0.2Li_0.2 Fe_1.7O₄ shows high ac resistivity and low dielectric loss tangent and most suitable for microwave applications and as transformer cores.