Temperature stability of Co/Pt and Co/Pd synthetic antiferromagnets using an Ir spacer

Abstract

The magnetic properties of Co/Pt and Co/Pd multilayers of perpendicular synthetic antiferromagnets with an Ir spacer were investigated. A strong interlayer exchange coupling of $J_{\mathrm{{ex}}}=2.01$ $\mathrm{{erg/cm}}^2$ was observed in the Co/Pt-based structures and a lower value of $J_{\mathrm{{ex}}}=1.04$ $\mathrm{{erg/cm}}^2$ was found in the Co/Pd multilayers. Only the former revealed a high post-annealing stability at $T_a=330\,^{\circ }$C, as the latter exhibited a ferromagnetic coupling most likely due to the deterioration of the spacer by pinhole coupling. This assumption was confirmed by theoretical calculations of the total energy functional. Moreover, the high temperature stability of Ir-based Co/Pt p-SAF structures was verified by calculating the exchange field $H_{\mathrm{{ex}}}$ from magnetization M(H) loops as a function of temperature, where it reached a temperature of $T_b=370\,^{\circ }$C before losing all interlayer exchange coupling.

Magnetic tunnel junctions (p-MTJs) with perpendicular magnetized layers have shown great potential in spintronics applications such as STT-MRAM [1] and magnetic sensors [2] due to having enhanced temperature stability [3] and lower switching currents [4], whilst also offering compatibility with industrial semiconductor processing [5, 6]. A field-stable in-built magnetic reference is needed for minimal output errors [7].

To improve the field stability of the reference layer, p-MTJs usually rely on perpendicular synthetic antiferromagnetic (p-SAF) structures. Typically, p-SAFs attain high coupling fields that are capable of sustaining the reference system up to several kOe fields. These make use of the antiferromagnetic (AF) interlayer exchange coupling (IEC) effect, which arises when two ferromagnetic (FM) layers are separated by a thin nonmagnetic (NM) spacer. Perpendicular SAF FM layers are often based on Co/Pt and Co/Pd multilayers that exhibit large perpendicular magnetic anisotropy (PMA) energy [8, 9] and high IEC energy. These multilayers have been used in perpendicularly magnetized bit pattern media [10, 11] and in spinvalves using variants such as Co/Tb [12] or Co/Ni [13]. Some novel uses even include Pd-based hydrogen gas sensors [14, 15] and all-optical magnetic switching [16, 17]. When coupled with an Ir spacer, coupling values as large as 2.6 erg/$\hbox {cm}^2$ can be achieved [18], larger than those obtained with a Ru spacer [19]. The tunability of the SAF can be done by changing the spacer of the multilayers (e.g. Ru, Rh or Ir [20]) or combining spacers [21]. The use of bridges between the FM layers can also be used for enhanced thermal endurance [22, 23]. However, insertions of additional materials require more complex processing. Whilst the cost of Ir is considerably higher, Co/Ir-based multilayered structures are also shown to have considerably high tunnel magnetoresistance (TMR) values over 210%, slightly higher than that of Ru [24], and provide better exchange fields [25].

SAF coupling fields dictate the reference stability such that the magnetization of the reference layer withstands high magnetic fields and high temperatures. For a strong IEC to be observed, the spacer layer thickness is typically below 1 nm. Under these dimensions, the two sandwiched FM layers can form direct contacts (i.e. pinholes) due to structure discontinuity and intermixing [19, 26] and lead to a ferromagnetic interlayer coupling. This is further enhanced during annealing at temperatures above 300 $^{\circ }$C [19], which are compatible with typical TMR sensors fabrication processes [27]. Thus, it is of practical interest to ensure temperature stability of the IEC on a wide range of temperatures. In this study, we compare the performance of p-SAFs using an Ir spacer based on Co/Pd multilayers with p-SAFs based on Co/Pt multilayers with the same spacer. In order to understand the influence of each magnetic layer and the effect of the coupling strength between them, a theoretical model of the p-SAF structure was developed and numerically solved. Comparisons between the stability of [Co/Pt]/Ir-based SAF and the stability of a Co/Pt-based p-SAF using a Ru spacer with temperature dependence enhancement via a W bridge layer suitable for STT-RAM devices [22, 23], and a MgO cap [28], were made by performing M(H) measurements as a function of temperature.

The multilayer films were deposited in a 6 target Nordiko 2000 magnetron sputtering system (deposition base pressure equal to $5.5\times 10^{-8}$ Torr) with the following structures: (a) Ta 2.5/Pt 3/[Co $t_1$/Pt 0.2$]_{n_1}$/Co $t_1$/Ir ($t_\text {Ir}$)/[Co $t_2$/Pt 0.2$]_{n_2}$/Ta 2.5 and (b) Ta 2.5/Pd 3/[Co $t_1$/Pd 0.22$]_{n_1}$/Co $t_1$/Ir ($t_\text {Ir}$)/[Co $t_2$/Pd 0.22$]_{n_2}$/Co $t_2$/Ta 2.5 (thicknesses in nm) on $3\times 20$ $\hbox {mm}^2$ glass substrates with varying thicknesses $t_1$ and $t_2$, and number of multilayers $n_1$ and $n_2$. The Pt, Pd, Ta targets were deposited using DC magnetron sputtering, whilst the Ir and Co targets were deposited using RF power. Since a precise control of the Ir deposition rate was needed for the SAF tuning, the deposition conditions were adjusted to achieve a deposition rate of 0.027 nm/s. This was done by optimizing the work pressure (3, 5 and 8 mTorr) and calibrating via Atomic Force Microscopy. The deposition conditions of all targets are detailed in Table 1. The magnetic properties and interlayer couplings were obtained at room temperature via vibrating sample magnetometry (VSM) under out-of-plane magnetic fields, as seen in Fig. 1, before and after annealing at 330 $^{\circ }$C for 2 h under a magnetic field of 5000 Oe. This annealing temperature was defined according to the conditions used in TMR sensor fabrication, where $330\,^{\circ }$C is needed to achieve a crystalline order across the CoFeB/MgO/CoFeB layers, and thus the deposited p-SAFs were also studied for their thermal stability under these conditions.

Fig. 1

Schematic illustration of the a Co/Pt-based p-SAF and b Co/Pd-based p-SAF, using an Ir spacer. The direction of the applied magnetic field for in-plane and out-of-plane measurements is depicted. The annealing was done in the out-of-plane direction

Table 1 Depositions conditions of the targets such as power source (P.S), argon flow rate (F.R), work pressure (W.P), current I, voltage V and power P

Figure 2a shows representative M(H) loops of the deposited p-SAFs. We can see the inversion of the two SAF multilayers with applied magnetic field through the two distinct loops. First, the exchange field $H_\text {ex}$ was measured in order to determine the interlayer exchange energy $J_\text {ex}$ as a function of spacer thickness ($t_\text {Ir}$) from 0.19 to 0.35 nm with the stack: Ta 2.5/Pt 3/[Co 0.25/Pt 0.2$]_{2}$/Co 0.25/Ir ($t_\text {Ir}$)/[Co 0.25/Pt 0.2$]_{3}$/Ta 2.5 (thicknesses in nm) on $3\times 20$ $\hbox {mm}^2$ glass substrates. Both $H_{\mathrm{{ex}}}$ (black) and $J_{\mathrm{{ex}}}$ (red) are plotted as a function of the spacer thickness in Fig. 2b. The former was extracted as the halfway point between the plateaus and saturation—as exemplified in Fig. 3. The latter was calculated through $J_{\mathrm{{ex}}} = H_{\mathrm{{ex}}} M_s t$, where $M_s$ is the saturation magnetization, obtained from the magnetization value at 10 kOe, and t the thickness of all Co layers. There is a discrepancy in the trends of these parameters that can be attributed to slight differences in the extracted $M_s$ from Fig. 2a. The interlayer exchange coupling is clearly ferromagnetic up until a thickness of 0.22 nm, after which it becomes antiferromagnetic. The resulting exchange field $H_\text {ex}$ values reached 9 kOe with wide AF-coupled plateaus. There is a peak around $t_\text {Ir}=0.32$ nm for which $J_\text {ex}$ is highest. Due to a limitation of the applied magnetic field at $\pm 10$ kOe, it is difficult to evaluate if a thickness of $t_\text {Ir}=0.35$ nm presents larger $H_\text {ex}$ than observed. Nevertheless, the M(H) loops distinctly show a sharper transition at zero-field for a thickness of $t_\text {Ir}=0.32$ nm.

Fig. 2

a Magnetization M(H) loops of p-SAF structures and b estimated exchange field $H_{\text{ex}}$ (black) and IEC energy $J_{\text{ex}}$ (red), as a function of Ir spacer thickness $t_\text {Ir}$. The transition between ferromagnetic (FM) and antiferromagnetic (AF) coupling is indicated. The point corresponding to $t_\text {Ir}=0.35$ nm has been highlighted due to the uncertainty of the $H_\text {ex}$ field extraction (Color figure online)

Fig. 3

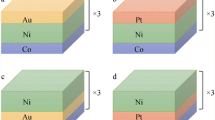
Out-of-plane magnetization M(H) loops of the p-SAF structures obtained for spacer thickness $t_\text {Ir}=0.32$ nm for varying Co thicknesses $t_1$ and $t_2$, and varying multilayer numbers $n_1$ and $n_2$. Firstly, the as-deposited state is shown, with a Co/Pt multilayers and b Co/Pd multilayers. Secondly, the after-annealing state ($T_a=330\,^{\circ }$C for 2 h under a magnetic field of 5000 Oe) is also shown, with c Co/Pt multilayers and d Co/Pd multilayers. For an external magnetic field $\vec {H}$, the orientation of the magnetization of each FM layer is detailed at each state. Additionally, the exchange field $H_\text {ex}$ used in the IEC calculation is specified in the figures (Color figure online)

Afterwards, having chosen the most optimal Ir spacer thickness, we deposited Co/Pt and Co/Pd multilayered films for varying thicknesses and multilayer numbers. Figure 3a and b display the M(H) loops of the p-SAF structures with spacer thickness $t_\text {Ir}=0.32$ nm in the as-deposited state for Co/Pt and Co/Pd-based multilayers, respectively. Once again, the exchange field $H_\text {ex}$ is very high ($\sim 10$ kOe) with a visible sharp inversion of the magnetizations of the FM layers. Through slight tuning, the p-SAF was optimized for a large $H_\text {ex}$ and a small total magnetization at the AF-coupled states. An IEC energy of $J_\text {ex}=2.01$ erg/$\hbox {cm}^2$ was achieved for Co/Pt multilayers and a dramatically lower energy of $J_\text {ex}=1.04$ erg/$\hbox {cm}^2$ was obtained in the case of Co/Pd, an observation that is consistent with previous studies done for these systems [18, 29]. Figure 3c and d show the samples after annealing at $T_a=330\,^{\circ }$C. For the Co/Pt-based films, the M(H) loops exhibit a small decrease of $H_\text {ex}$ and sharper transitions between the AF and FM states of the p-SAF. However, FM interlayer coupling begins to arise and is particularly noticeable by the deterioration of the plateau and the appearance of a FM loop centred at zero-field. This is most likely due to inter-diffusion around the Ir spacer, which creates FM pinholes. As for the Co/Pd, a complete breakdown of the spacer layer has occurred, leading to a pure FM coupling of the multilayers. Once again, this is a degradation that can be attributed to diffusion through the spacer. To confirm these suspicions, transmission electron microscopy (TEM) imaging should be performed.

To better quantify the effects of PMA and IEC on the magnetic behaviour of a FM1/NM/FM2 p-SAF system, a Stoner–Wohlfarth model was used to understand these results. It assumes the ferromagnetic layers can be approximated to magnetic domains and their magnetization orientation is capable of changing due to coherent rotation. This approximation can be done when in the presence of in-plane magnetic fields [30] and when neglecting edge effects [31]. The energy functional $E(\theta _\text {FM1},\theta _\text {FM2},H)$ includes several energy terms, such as the Zeeman, IEC and anisotropy (PMA) energies [31,32,33], and is given by:

$$E(\theta _\text {FM1},\theta _\text {FM2},H) =- M_s^\text {FM1} t_\text {FM1} H \cos {\theta _\text {FM1}} - M_s^\text {FM2} t_\text {FM2} H \cos {\theta _\text {FM2}} + J_\text {ex,1} \cos {(\theta _\text {FM2}-\theta _\text {FM1})} + J_\text {ex,2} \cos ^2{(\theta _\text {FM2}-\theta _\text {FM1})} +K^\text {FM1}_1 t_\text {FM1} \cos ^2{\theta _\text {FM1}} + K^\text {FM1}_2 t_\text {FM1} \cos ^4{\theta _\text {FM1}} +K^\text {FM2}_1 t_\text {FM2} \cos ^2{\theta _\text {FM2}} + K^\text {FM2}_2 t_\text {FM2} \cos ^4{\theta _\text {FM2}},$$

(1)

where $\theta _\text {FM1}$ and $\theta _\text {FM2}$ denote the angle between the magnetization of each FM layer and the in-plane magnetic field H, $J_\text {ex,1}$ and $J_\text {ex,2}$ are the principal and biquadratic IEC energy densities, the latter being responsible for pinhole coupling [34], and $K_1$ and $K_2$ are the first and second order PMA energy densities of each FM layer. The model neglects the magnetostatic coupling urged from the stray fields of each magnetic layer, the self-demagnetizing field and the Néel coupling induced by correlated interface roughness at the spacer interfaces with the FM layers. In addition, it considers the multilayers as one FM layer with the properties of the full system.

The net magnetization M of the structure is the pondered sum of all contributions in the direction of the applied magnetic field:

$$\begin{aligned} M = \frac{M_s^\text {FM1} t_\text {FM1} \cos {\theta _\text {FM1}} + M_s^\text {FM2} t_\text {FM2} \cos {\theta _\text {FM2}}}{t_\text {FM1}+t_\text {FM2}} \end{aligned}$$

(2)

The $M_s$, $K_1$ and $K_2$ values for each FM layer were calculated from fitting in-plane M(H) loop measurements of the [Co($t_\text {Co}$)/Pt]$_{\times n}$ and [Co($t_\text {Co}$)/Pd]$_{\times n}$ multilayers, whilst $J_\text {ex,1}$ and $J_\text {ex,2}$ were fitted according to Eqs. (1) and (2) to the in-plane measurement of the $n_1=n_2=2$, $t_1=0.29$ nm, $t_2=0.39$ nm (green) experimental curve in Fig. 3b. A strong PMA plays an important role in constructing a good p-SAF. As such, for the Co/Pd, the bottom multilayers exhibited a slightly weaker effective PMA energy density, given by $K_\text {eff}=K_1+K_2$, of $6.6\times 10^{5}$ erg/$\hbox {cm}^3$ when compared to the top multilayers, with a $K_\text {eff}$ of $7.6\times 10^{5}$ erg/$\hbox {cm}^3$. It can be seen that the Co/Pd multilayers have a lower PMA energy density than expected for perpendicular multilayers [35], which is reflected by having transitions between the FM and AF coupled states that are not as sharp and, at the same time, a lower $H_\text {ex}$ value at which this transition occurs. This is due to a gradual reversal of the magnetization becoming more unfavourable for the system as the PMA increases. In the case of Co/Pt, the fitted PMA energy density was $1.26\times 10^{6}$ erg/$\hbox {cm}^3$ for the bottom multilayers and $1.36\times 10^{6}$ erg/$\hbox {cm}^3$ for the top multilayers, which is closer to typical PMA values for these structures [19].

By minimizing the energy functional with respect to $\theta _\text {FM1}$ and $\theta _\text {FM2}$, the in-plane theoretical M(H) loop for the as-deposited state is shown in Fig. 4a, alongside the fitted IEC energy densities. The fitted value of $J_{\mathrm{{ex,1}}}=1.16$ $\mathrm{{erg/cm}}^2$ agrees with the one previously obtained through the formula. Moreover, with the introduction of the biquadratic IEC term, both the FM and AF coupled states become unfavourable, which can explain the slope seen in the out-of-plane M(H) loop since a value of $J_\text {ex,2}=0.65$ $\mathrm{{erg/cm}}^2$ is already considered high. If $J_{\mathrm{{ex,2}}}$ becomes large enough, then both collinear states become completely unfavourable. However, since the Zeeman terms are proportional to the magnetic field, FM coupling will eventually overcome the biquadratic IEC term. This term models the impact of pinhole coupling in magnetic structures, which in the case of Fig. 3d led to a degradation of the spacer layer and thus, the FM hysteresis loop observed. In other words, both $J_{\mathrm{{ex,1}}}$ and $J_{\mathrm{{ex,2}}}$ have become zero and the p-SAF behaves as two FM coupled multilayers. Figure 4b shows the out-of-plane M(H) loop using the fitted parameters. It can be seen that the model fails to reproduce the out-of-plane experimental curve, displaying a FM hysteresis loop, thus demonstrating that the application of the Stoner–Wohlfarth model in this direction is not valid.

Fig. 4

a In-plane measured M(H) loop and that calculated by using the total energy functional in the as-deposited state. The exchange terms $J_{\mathrm{{ex,1}}}$ and $J_{\mathrm{{ex,2}}}$ obtained from the fit are denoted in the figures, as well as the saturation magnetization $M_s$, and the effective PMA energy densities of the top and bottom multilayers. b Out-of-plane measured M(H) loop in the as-deposited state and that calculated using the previous fitted parameters

For comparison with the Ir spacer, we deposited a Co/Pt-based p-SAF using a Ru spacer as illustrated in Fig. 5a in a Nordiko 8800 physical vapour deposition system, alongside a Nordiko 3600 ion beam deposition system. It consists of the stack: Si/$\hbox {SiO}_2$/[Ta 5/Ru 10]$_{\times 3}$/Ta 2/Pt 3/[Co 0.34/Pt 0.14]$_{\times 6}$/Co 0.34/Ru $t_\text {Ru}$/Co 0.34/[Pt 0.14/Co 0.34]$_{\times 4}$/W 0.2/CoFeB 1/MgO 1.4/Ta 5/Ru 10 (thicknesses in nm). The Ru spacer layer has a thickness of $t_\text {Ru}=0.8$ nm, which corresponds closely to the second $J_\text {ex}$ peak [36]. The M(H) measurements of this structure in the as-deposited state and after annealing at $T_a=330\,^{\circ }$C are in Fig. 5b. The exchange field was calculated to be $H_\text {ex}=3516$ Oe. Post-annealing, it maintained its $H_\text {ex}$, but there is a noticeable increase of the coercivity of the FM-to-AF loop. The $H_\text {ex}$ values as a function of measurement temperature are shown in Fig. 5c for the $n_1=2$, $n_2=3$, $t_1=0.25$ nm, $t_2=0.33$ nm (green) experimental curve in Fig. 3a and c, and for the previously detailed Ru-based p-SAF. These values were obtained through the same M(H) curves analysis performed previously but measured on the VSM at different temperatures.

Fig. 5

a Schematic illustration of the Co/Pt-based p-SAF using a Ru spacer. The direction of the applied magnetic field is indicated. b Respective measured out-of-plane M(H) loops in the as-deposited state and after annealing at $T_a=330\,^{\circ }$C. c Exchange field $H_{\mathrm{{ex}}}$ as a function of measurement temperature T for the Co/Pt p-SAF using a Ir spacer (blue) and the one using a Ru spacer (red). The experimental curves were fitted with the model described in Eqs. (3) and (4) and the calculated parameters are specified on the figure (Color figure online)

The results were fitted according to a modification of Malozemoff’s model [37]. This model is used to describe exchange bias in AF/FM structures, but can be applied to this situation due to only requiring a temperature-dependent decrease of an interlayer coupling constant $J_\text {int}$. It describes a monotonous decrease of $H_{\mathrm{{ex}}}$ with temperature, by considering a distribution of the temperature $T_b$ at which the exchange field disappears [38]:

$$\begin{aligned} H_{\mathrm{{ex}}}(T)= & {} H_{\mathrm{{ex}}}^0 \sum _i f(T_b^i) {\left\{ \begin{array}{ll} \left( 1-\frac{T}{T_b^i}\right) ^\gamma &{}: T < T_b^i \\ 0 &{}: T > T_b^i \end{array}\right. }\end{aligned}$$

(3)

$$\begin{aligned} f(T_b^i)= & {} \frac{1}{\Delta T_b \sqrt{2\pi }} \exp {\left[ -\frac{(T_b^i-T_b^\text {center})^2}{(2 \Delta T_b)^2}\right] } \end{aligned}$$

(4)

where $H_{\mathrm{{ex}}}^0$ is the exchange field at $0\,^{\circ }$C, $\gamma$ is an exponent related to the material structure, and $f(T_b^i)$ is a Gaussian-like distribution with $T_b^\text {center}$ and $\Delta T_b$ the mean and standard deviation. The Ir-based p-SAF exhibits the largest $T_b$, almost $\sim 70\,^{\circ }$C when compared to the Ru-based p-SAF engineered for that purpose. Due to $\gamma$ being almost unity, the decrease in $H_{\mathrm{{ex}}}$ is also less accentuated on the former, and therefore, alongside the high $H_{\mathrm{{ex}}}^0$, demonstrates a more robust temperature stability overall.

In summary, we studied the magnetic properties of perpendicular SAFs based on Co/Pt and Co/Pd multilayers with an Ir spacer for varying Co thicknesses and varying multilayer number. In the as-deposited state, the Co/Pt multilayers exhibited a very high interlayer exchange energy of $J_{\mathrm{{ex}}}=2.01$ $\mathrm{{erg/cm}}^2$, whilst the Co/Pd multilayers presented a significantly lower energy of $J_{\mathrm{{ex}}}=1.04$ $\mathrm{{erg/cm}}^2$. After annealing at $T_a=330\,^{\circ }$C, the Co/Pt-based p-SAFs mostly retained their high exchange field $H_{\mathrm{{ex}}}$, leading only to a small decrease of the IEC energy. However, the same could not be observed in the Co/Pd-based p-SAFs. Instead, they showed a complete ferromagnetic coupling, which hinted towards the deterioration of the spacer layer. The behaviour of the Co/Pd multilayers was verified through the use of the total energy functional including a biquadratic IEC term. Indeed, there was a large value of $J_{\mathrm{{ex,2}}}=0.65$ $\mathrm{{erg/cm}}^2$ in the as-deposited state, corresponding to the presence of pinhole coupling. Finally, we showed that a Co/Pt-based p-SAF with Ir spacer demonstrates greater temperature stability than the p-SAF using a Ru spacer, even when inserted with a W bridge and MgO cap layers, which are known to improve temperature stability. In the future, it would be of interest to compare the performance of Ir-based p-SAFs with an insertion of W and MgO. In Co/Pd-based multilayers, a W cap has already proven to improve the thermal stability [39]. Moreover, the PMA is highly dependent on the way the Co/Pt and Co/Pd multilayers grow on different substrates and buffers [40]. As a result, it is also an avenue worth investigating if larger values of $J_\text {ex}$ are to be achieved.