1 Introduction

The transducers have a major role in ultrasonic testing because they receive electric signals and transmit ultrasonic echoes. They are composed of a vibrating piezoelectric material that generates mechanical ultrasonic waves. In addition, they contain a matching layer in front of the piezoelectric material and a backing layer in the back. Both the matching and the backing layers may affect the sensitivity and the resolution of the transducer [1, 2].

The choice of matching layers is quite complicated because the matching layer material must have acoustic impedance matching with those of the piezoelectric element and the load material to allow maximum wave transmission and increase transducer sensitivity [3]. If the impedance of the piezoelectric transducer material is \({Z}_{\rm T}\) and the load has an impedance of \({Z}_{\rm L}\), then for maximum sensitivity, the acoustic impedance of the matching layer, \({Z}_{\rm ML}\) will be [4]:

$${Z}_{\rm ML}=\surd ({Z}_{\rm T}{Z}_{\rm L})$$
(1)

The matching layer thickness, \(t\), must equal odd multiples of \(\frac{\lambda }{4}\), thus in phase acoustic waves will be added and out of phase waves will be cancelled.

$$t=(2n-1)\frac{\lambda }{4}$$
(2)
$$\lambda =\frac{C}{f},$$
(3)

where \(n\) is a positive real number of waves, \(\lambda\) is the wavelength, \(C\) the speed of sound waves in the medium, and \(f\) is the transducer’s frequency.

When using a metal–polymer matching layer, the sensitivity of the transducer becomes much higher and its bandwidth wider [5]. As matching layer materials, silver-epoxy and parylene are frequently used [6, 7] for its electric conductivity. Parylene is used as the second matching layer because it is a coverage protective layer [8]. Cannata et al. [9, 10] used Ag-epoxy and parylene C as matching layers. Zhou et al. [11] created matching layer of alumina/polymer nanocomposite films. Tiefensee et al. [12] created matching layer of nanocomposite cerium oxide polymer.

High acoustic wave propagation is performed by adjusting the resonant frequency, \(f\), and equivalent impedance, \({Z}_{\rm eq}\), of the mass-spring system [4]. The resonant frequency, \(f\), and the equivalent impedance, \({Z}_{\rm eq}\) are dependent on the densities and the thicknesses of both the mass and spring layers [8].

$$f=\frac{1}{2\pi }\surd [(\frac{{\rho }_{\rm s}{C}_{\rm s}^{2}}{{t}_{\rm s}})/({\rho }_{\rm m}{t}_{\rm m}+0.4{\rho }_{\rm s}{t}_{\rm s})]$$
(4)
$${Z}_{\rm eq}={\rho }_{\rm s}{C}_{\rm s}^{2}\frac{{\rho }_{\rm m}{t}_{\rm m}+0.4{\rho }_{\rm s}{t}_{\rm s}}{{t}_{\rm s}{Z}_{\rm L}},$$
(5)

where \({\rho }_{\rm s}\) and \({\rho }_{\rm m}\) are the densities of the spring layer and mass layer, respectively; \({t}_{\rm s}\) and \({t}_{\rm m}\) are the thicknesses of the spring layer and mass layer, respectively; \({C}_{\rm S}\) is the ultrasound velocity in the spring layer; and \({Z}_{\rm L}\) is the load impedance.

In this study, a mass-spring system was followed. The matching layers were made from metal–polymer that was added to the transducers’ active element (PZT). To do a comparison study, a transducer with a single matching layer was developed. The study aimed to upgrade the normal beam PZT transducers’ characteristics and increase their usefulness and application in many non-destructive ultrasonic tests, such as increasing their defect detectability.

2 Experimental procedure

2.1 Ultrasonic measurements

Using pulse-echo technique, ultrasonic measurements were done. In this ultrasonic mode of operation, direct contact pulser-receiver transducers were used following the ASTM standard (ASTM E114-15, 2015 [13]). The ultrasonic equipment consisted of a flaw detector (USN60, GE inspection technologies), a vector signal analyzer (89441A-hp), an oscilloscope (LeCroy W, wave Jet 354A), reference standards blocks [VI, VII, and resolution reference block with flat bottom holes (FBH)], and normal beam transducers (2, 4, and 6 MHz, 12 HB-Karl Deutsch).

2.2 Transducers manufacture and matching layers’ choice

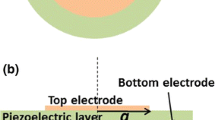
The transducers were manufactured using lead zirconate titanate (PZT) active piezoelectric element of 2, 4 and 6 MHz frequency, epoxy resin/tungsten backing material, the new designed matching materials, and cables [14]. Figure 1 shows the actual transducer’s picture without matching layers and with matching layers. Also, it shows the order of mass-spring matching layers according to the active piezoelectric element and the actual pictures of the transducer’s PZT element and an example of aluminum matching layer.

Fig. 1
figure 1

a Actual transducers’ picture, b Schematic of the order of metal/polymer (mass-spring) matching layers and the active element. c Design of the fabricated transducers with their contents. d  is the diameter and t is the thickness. All the transducers had same diameter (8 mm)

Full size image

Groups of matching layers (ML) were used: parylene single ML, silver/parylene ML, alumina/parylene ML, and copper/parylene ML. Table 1 shows the transducers’ features. Following the system of mass-spring, the matching layers are made from polymer and metal. For performing resonator systems, the mass part must have a higher acoustic impedance than the spring part [7]. Therefore, parylene polymer was chosen as the spring material because of its low acoustic impedance. The metals were chosen to have high acoustic impedances [1]. The metals were silver, nickel silver, and copper, Table 1.

Table 1 Parameters of materials selected for the transducers’ features
Full size table

We tried to choose available materials with a considerably lower cost. In addition, these metals have been investigated previously in the fabrication of ultrasonic transducers [15].

Table 1 shows the parameters of materials selected for the transducers’ features, such as function, velocity, density, and acoustic impedance. Lead zirconate titanate (PZT) was the piezoelectric active element of the used transducers in this study. Parylene acted as a single matching layer and the spring part in the mass-spring matching layer formation. It was also the glue material that adhered the mass (metal) part to the front of the piezoelectric element. Silver, alumina, and copper are the mass parts in the mass-spring matching layer combination. Finally, the resolution reference block with flat bottom holes (FBH) acted as the load material, it was made of steel. Parylene had the lowest longitudinal ultrasonic velocity (2350 m/s), while alumina had the highest one (10,520 m/s). Silver had the highest density (10,600 kg/m3), while parylene had the lowest (1100 kg/m3). The parylene had the lowest acoustic impedance (2.58 MRayls), while the resolution reference block had the highest one (45.63 MRayls).

2.3 The equivalent acoustic impedance

The goal of the matching layers (metal–polymer) was to make the equivalent acoustic impedance, \({Z}_{\rm eq}\), at the surface of the piezoelectric layer be equal to the specific acoustic impedance of the matching layers, \({Z}_{\rm s}\). This insures high wave transmission [7]. The equivalent acoustic impedance, \({Z}_{\rm eq}\) was calculated as follows (Table 2):

$${Z}_{\text{eq}}=\frac{{\rho }_{\text{par}}{C}_{\text{par}}^{2}({\rho }_{\text{m}}{t}_{\text{m}}+0.4{\rho }_{\text{par}}{t}_{\text{par}})}{{t}_{\text{m}}{Z}_{\text{L}}},$$
(6)

where \({\rho }_{\text{par}}\) and \({\rho }_{\text{m}}\) are the density of the parylene and the metal layers, respectively; \({t}_{\text{par}}\) and \({t}_{\text{m}}\) are the thickness of the parylene and the metal layers, respectively; \({C}_{\text{par}}\) is the ultrasound velocity in the parylene; and \({Z}_{\text{L}}\) is the load impedance. The specific acoustic impedance of the matching layers, \({Z}_{\text{s}}\), is calculated as follow:

$${Z}_{\text{s}}=[{\frac{{Z}_{\text{T}}^{2}}{{Z}_{\text{L}}}]}^{1/3},$$
(7)

where the impedance of the piezoelectric transducer material is \({Z}_{\text{T}}\) and the impedance of the load is \({Z}_{\text{L}}\).

Table 2 Equivalent acoustic impedance, \({Z}_{\rm eq}\), matching layers’ thickness, \(t\), and wave transmission, \(T\)
Full size table

After calculation, \({Z}_{\text{s}}\) was about 2.9 MRayls. Table 2 shows the equivalent acoustic impedance, \({Z}_{\text{eq}}\) that is calculated according to formula (13).

From Table 2, the matching layer formed from copper/parylene had equivalent acoustic impedance, \({Z}_{\rm eq}\) of 2.42 MRayls. Thus, it is the most matching layers that meet the specific acoustic impedance \({Z}_{\rm s}\) (2.9 MRayls).

2.4 The thickness of the matching layer

The thickness of the matching layer was optimized by making it equal to odd multiples of \(\frac{\lambda }{4}\) [9]. The matching layers’ thicknesses were calculated according to the relationships (2), Table 2. For 2 MHz transducers, the thicknesses of matching layers ranged from 0.3 to 0.6 mm. For 4 MHz transducers, the thicknesses of matching layers ranged from 0.15 to 0.3 mm. Finally, for 6 MHz transducers, the thicknesses of matching layers ranged from 0.1 to 0.2 mm. We noticed the decrement of matching layers thicknesses as the frequency increased. From formula (2), there is a direct relationship between the thickness of matching layer and the wavelength. Thus, the thickness of matching layer is inversely proportional to the frequency.

2.5 Wave transmission

When the waves travel between three media (as in this study), the wave transmission, \(T\) is determined as follows [4]:

$$T=4/(2+[{((Z}_{3}/{Z}_{1})+({Z}_{1}/{Z}_{3})){\cos}^{2}{k}_{2}d]+[(({Z}_{3}^{2}/{Z}_{1}{Z}_{3})+({Z}_{1}{Z}_{3}/{Z}_{2})){\text{sin}}^{2}{k}_{2}d]),$$
(8)

where \({Z}_{1}\) is the acoustic impedance of first medium (\({Z}_{1}\) is the \(Z\) of PZT), \({Z}_{2}\) is the acoustic impedance of second medium (\({Z}_{2}\) will vary according to the used matching layer), \({Z}_{3}\) is the acoustic impedance of tested specimen (\({Z}_{3}\) is the \(Z\) of steel), \({k}_{2}\) is the wave number in medium, and \(d\) is the matching layer thickness.

From Table 2, there was an increment in \(T\) percentage when using mass-spring ML. The transducer with copper/parylene mass-spring ML had the maximum \(T\) percentage (75, 85, and 89%). The mass-spring ML diminish the echoes loss by reducing the reflections and scattering. The number of the transmitted echoes was increased. While, SML (parylene) had a low \(T\) percentage (42, 64, and 66%), because SML cannot greatly inhibit waves’ reflections and scattering. Also, the 6 MHz transducers exhibited the highest \(T\) percentage (66, 78, 83, and 89%). When the frequency is increased, the number of cycles per second increases and there is a high penetration energy, i.e., the number of echoes transmitted is increased.

3 Results and discussion

3.1 Assessment of new fabricated transducers

To make the assessment of the new fabricated transducers, we must know the parameters that vary with the addition of matching layers. Many transducers’ parameters are affected by the matching layers that are put on the front of the transducers. Among them are the beam diameter (\(BD\)), the beam directivity (\(D\)), the transducer sensitivity (\(S\)), the signal-to-noise ratio (\(S/N\)), the bandwidth (\(BW\)), the echo-height, and the quality factor (\(Q\)).

Generally, the transducer’s parameters must fit the desired application. In ultrasonic imaging, the transducer must have a high center frequency and a broad beam to achieve high imaging resolution. In ultrasonic non-destructive test (NDT), the transducer must have a narrow beam to easily localize tiny defects [11]. In ultrasonic calibration, the transducers must calibrate reference blocks with high accuracy [16].

In this study, the required application is the increment of the transducer’s effectiveness to detect defects in different components. We need to ameliorate the transducer to increase its detectability of defects, so increasing its usage in ultrasonic non-destructive test and in ultrasonic calibration.

3.1.1 Beam diameter analysis

The addition of a matching layer to the transducer front can vary the beam diameter (\(BD\)) of the transducer. Transducers that have got wide beam diameter can scan defects in wide range. Transducers that have got narrow beam diameter can focus more to detect tiny defects. Therefore, we can say that the beam diameter is a good key factor that reflect the suitable application of the transducers.

The beam diameter (\(BD\)) of the transducer is a function of focal length (\(F\)), effective diameter of the transducer, the transducer operating frequency (\({f}_{0}\)), and the load specimen thickness (\(t\)) [17].

$$BD\left(-6dB\right)=1.02Ft/{f}_{0}{D}_{\rm eff}$$
(9)

In this study, the fabricated transducers have operating frequencies (\({f}_{0}\)): 2, 4, and 6 MHz. The load specimen was the resolution reference block with flat bottom holes (FBH). All fabricated transducers have the same effective transducer diameter (\({D}_{\rm eff}\) =12 mm).

Figure 2 shows the beam diameter (\(BD\)) variation with different frequencies and the effect of adding different matching layers (ML) in front of the fabricated transducers

Fig. 2
figure 2

a Beam diameter (BD) and b beam directivity (\(D\)) for the transducers with and without ML. ML matching layer, SML single matching layer

Full size image

From Fig. 2a, the beam diameter decreased with the increase in the transducers’ frequencies. When the frequency increased, the number of waves per time increased, the wavelength also decreased causing a decrement in the beam diameter. The beam could be more concentrated at high frequencies. Moreover, by definition, the focal length of a transducer is the distance from the face of the transducer to the point in the sound field where the signal with the maximum amplitude is located [18]. Thus, we can say that the focal length decreased as the frequency increased because the beam can be broadened and the near-field zone will be diminished, and allowing to increase the capability of the transducer to see defects near to the surface and to scan thinner specimens [2]. Therefore, the added matching layers greatly improved the transducers.

Also, from Fig. 2a we can record the effect of adding different matching layers to the transducers’ front. We observe that at the same frequency the beam diameter increased when adding parylene single matching layer (SML). A further increase took place when using mass-spring matching layers (ML). The highest beam diameter width was when adding the alumina/parylene ML. The matching layers diminish waves’ reflections, inhibit resonance, increase the transmitted waves’ density and increase beam diameter [4]. As the beam diameter increased, the amount of energy reflected by the defects also increased, so the transducer could scan more defects in a wider range [19].

3.1.2 Beam directivity analysis

The direction of the beam and its collimation or scattering are affected by matching layer addition. This may be due to the sensitivity of waves path by any materials, some materials can collimate waves, the others can cause waves scattering or waves absorption. Therefore, it can be said that beam directivity (\(D\)) could be a function of matching layer variation.

For a normal beam transducer, the directivity (\(D\)) depends on the divergence angle (\(\theta\)) [4].

$$D=\frac{2}{(1-\text{cos}\left(\frac{\theta }{2}\right))}$$
(10)

From Fig. 2b, the beam directivity decreased with increasing frequency in transducers of mass-spring matching layers (silver/parylene ML, alumina/parylene ML, and copper/parylene ML). The directivity of an ultrasonic beam depends mainly on the divergence angle, so when increasing the frequency and adding mass-spring matching layers, the divergence surely varied and caused the decrement of the beam directivity. The double matching layers affected the collimation of the beam and may reduce the beam scattering; thus, the beam deflection decreased and the beam directivity decreased. whereas there was no significant variation in beam directivity with frequency in the transducer without ML and in the transducer with SML. This may be referred to the beam that emerged from a transducer without ML, which may suffer from reflections and scattering. In this case, the beam directivity recorded the lowest value. In addition, the transducer with SML will have the same problem of high reflections and scattering, so the beam directivity exhibited a low value.

Also, from Fig. 2b we observed that at the same frequency, the beam directivity values increased with adding ML. The maximum beam directivity values were in transducers of copper/parylene matching layer. This means that the copper/parylene ML produced a uniform response for directivity [15]. In contrast, the lowest values of beam directivity were in transducers without ML. This may be due to the beam cone profile becoming wider when adding ML to the different transducers. This is one of the benefits of adding mass-spring matching layers to the transducers’ front. Finally, we can say that matching layers enhanced the transducers to see more flaws in a wide range [3].

3.1.3 Transducer sensitivity analysis

Transducer sensitivity (S) is an important transducer parameter, it demonstrates the capability of a transducer to detect defects. Transducer of high sensitivity can detect more defects than that of low sensitivity.

Transducer sensitivity (S) is related to the amplitude of the voltage applied to the transducer, V0, and the amplitude of the pulse-echo voltage received from the load specimen, \({V}_{x}\).

$$S\left(\text{dB}\right)=20 \text{log}({V}_{x}/{V}_{0})$$
(11)

The equipment consists of flaw detector, oscilloscope, and transducer. The pulse-echo was initiated then recorded on the oscilloscope. We record the pulse-echo without and with the load specimen. Therefore, we can determine both the voltage applied to the transducer, \({V}_{0}\), and the amplitude of the pulse-echo voltage received from the load specimen, \({V}_{x}\).

Figure 3a shows the transducer sensitivity (\(S\)) variation with different frequencies and the effect of adding different matching layers (ML) in front of the fabricated transducers

Fig. 3
figure 3

a Sensitivity (\(S\)) and b Signal to noise ratio (S/N) for the transducers with and without ML. ML matching layer, SML single matching layer ML matching layer, SML single matching layer

Full size image

In Fig. 3a, we saw the increment of transducers’ sensitivity with the increment of frequency. At 2 MHz, the values of sensitivity ranged from about 1 to 5.8 dB, while at 6 MHz they ranged from about 2.7 to 8.5 dB. When the frequency increased, the received signals increased, so the sensitivity increased. Because increasing a transducer’s sensitivity means increasing the received signal compared to the incident one, this means the increment of the transducer’s ability to receive echoes from the load specimen and its effectiveness to pick different defects in the load specimen [20].

Also, from Fig. 3a, we noted the increment in the sensitivity for the transducers with SML was about 1.5 to 2 times those without the addition of a matching layer, while the increment in the sensitivity for the transducers with silver/parylene ML was about 2 to 3 times that without the addition of a matching layer. The sensitivity increment in the transducers with alumina/parylene ML was about 3 to 4 times greater than that without the addition of a matching layer. Finally, the sensitivity increment in the transducers with copper/parylene ML was from about 3 to 4.8 times that without the addition of the matching layer.

We can argue that the matching layer is a vital component of an ultrasonic transducer since it can reduce internal reflections and suppress resonance, improving the transducer's sensitivity and bandwidth [21]. In recent studies, matching layers were effective in may transducers types such as capacitive micro-machined ultrasound transducers (CMUT). CMUT are mainly used for ultrasound imaging of anatomical features. They can give more images’ details and facilitate the anatomy analysis. They are different to the piezoelectric ultrasonic transducers that can be used for both non-destructive test and ultrasonic imaging [22]. Therefore, the addition of the matching layers enhanced the transducer sensitivity [23]. Copper/parylene ML was more efficient at increasing sensitivity than SML and the other mass-spring matching layers. This may be due to copper/parylene ML having the most compatible acoustic impedance match with the piezoelectric element of the transducer, Table 2.

3.1.4 Signal to noise ratio analysis

Generally, the noisy echoes emerge from many factors, like surface miniature cracks in the specimen, rough specimen surface, non-straight surface, transducer bandwidth, etc. [17]. The noisy echoes can be determined by measuring the signal-to-noise ratio (S/N), which could influence the test measurements of any designed transducer. Note that the noise echo was equal to or below 30% of the CRT screen of the flaw detector.

\(S/N\) is affected by the specimen density (\(\rho\)), the ultrasound velocity in the specimen (C), beam width (\(BW\)), time interval (\(\Delta t\)), echo amplitude (\(A\)) and noise echo (\(N\)) [24].

$$S/N=(\surd \frac{16}{\rho CBW\Delta t})\frac{A}{N}$$
(12)

Figure 3b shows the signal-to-noise ratio (\(S/N\)) for the transducers with and without ML. From Fig. 3b, the \(S/N\) values were high in the transducer without ML compared with the others that had SML or mass-spring ML. The lowest values of \(S/N\) were in the transducer of copper/parylene ML. In addition, the transducers of high-frequency (6 MHz) had low values of \(S/N\), and this is clear in all the transducer cases (without or with ML). From the signal-to-noise ratio (\(S/N\)) values, some fundamental relationships can be noted. The signal-to-noise ratio (\(S/N\)) is related to the detectability of a defect. If it is high, the detectability of a defect becomes low, because echoes from a given defect may be lost within the high noise echoes. Generally, the defect detectability is proportional to both the beam width and the pulse duration of the transducer. A short pulse (in high-frequency transducer) corresponds to a broader bandwidth frequency response and high defect detectability [6]. Therefore, 6 MHz transducers (with low \(S/N\) values) had high defect detectability. Moreover, the transducer without ML had the highest \(S/N\) values and it is the most unsuitable transducer to detect defects. Transducers with mass-spring matching layers had low values of \(S/N\), and they were suitable to detect defects. Transducer with the copper/parylene matching layer had the lowest \(S/N\) values and it is the most effective transducer to detect defects.

3.1.5 Bandwidth analysis

The bandwidth (\(BW\)) of the modified transducers with the matching layers is calculated as follow:

$$BW={f}_{\text{u}}-{f}_{\text{l}},$$
(13)

where \({f}_{\text{l}}\) is the lower frequency and \({f}_{\text{u}}\) is the upper frequency.

Figure 4a shows the transducer bandwidth (\(BW\)) variation with different frequencies and the effect of adding different matching layers (ML) in front of the fabricated transducers

From Fig. 4a, the bandwidth (\(BW\)) increased with increasing frequency and with adding a matching layer. The highest \(BW\) value was for the transducer of copper/parylene ML at 6 MHz (about 4.8 MHz). The lowest \(BW\) value was for the transducer without a matching layer at 2 MHz (about 1.7 MHz). The ML addition caused the broadness of the beam, because ML suppressed resonance, decreased scattering, and increased the bandwidth.

Fig. 4
figure 4

a Bandwidth (\(BW\)). b Wave height from different FBH in the resolution reference block using different transducers. ML matching layer, SML single matching layer

Full size image

3.1.6 Wave height analysis

The wave height recorded from the CRT screen of the flaw detector apparatus. We tested a standard reference block of known defects, to assure the effectiveness of the mass-spring matching layers that ameliorated the transducers’ characteristics and improved their ability to detect defects easily. The resolution reference block of flat bottom holes (FBH) (ASTM E127, ASTM E428) was used to test the efficiency of the modified transducers with SML or mass-spring matching layers. The main calibration functions of this reference block were measurement of straight beam, resolution, sensitivity, and flaw size and depth. Using the pulse-echo technique, the echo-height from FBH was determined for the used transducers (with and without ML) [16]. To assure the stability of measurements, the ultrasonic flaw detector was adjusted to the same conditions (gain, filter coarse, time base, etc.) for all measurements (Fig. 4b).

In Fig. 4b, the recorded wave height percentage increased as per the addition of the ML. It was about 45% to 52% when using transducers without adding ML, then it increased to about 63% to 66% when using transducers with SML, while it reached 89% when adding copper/parylene ML. Therefore, the addition of a matching layer greatly improved the capability of transducers to pick up flaws [12].

3.1.7 Quality factor analysis

The transducers’ quality factor, \(Q\), is the description of the amount of ringing and damping of the transducer. Thus, it can monitor the application of a given transducer. Generally, transducers of high-quality factor have a relatively pure frequency spectrum and a narrow bandwidth with a corresponding short special pulse length (i.e. short ringing). They can be used as good defect detector in a narrow band and in medical application, they can be used to diagnose superficial tissues. In contrast, the transducers of low-quality factor have lower frequency and longer wavelength with higher penetration power. They also have broad-band [25]. \(Q\) depends on the operating frequency, \({f}_{0}\) and the bandwidth, \(BW\) [20] as follow:

$$Q=\frac{{f}_{0}}{BW}$$
(14)

Using the spectrum chart, which was picked from the vector signal analyzer, we recorded the lower frequency (\({f}_{\rm l}\)) and upper frequency (\({f}_{\rm u}\)) at − 6 dB drop. The \(BW\) was calculated according to Eq. (13) and the central (operating) frequency (\({f}_{0}\)) was calculated according to the following [26]:

$${f}_{0}={({f}_{\rm u}{f}_{\rm l})}^{1/2}$$
(15)

After calculating \({f}_{0}\) and \(BW\), the quality factor, \(Q\) was calculated and recorded in Table 3.

Table 3 The quality factor, \(Q\) of the fabricated transducers
Full size table

The quality factor, \(Q\), ranged from 0.8 to 2.2, as shown in Table 3. The obtained \(Q\) values are classified as low \(Q\) values. This indicates that the transducers were manufactured with a broad-band, long ringing, and a relatively long wavelength. As a result, these transducers have high penetration powers in the materials tested. They are good defect detectors and they can scan more defects in a broad range. They can test and calibrate different components and reference blocks, which have different defects (especially sub-surface ones). Furthermore, they have important medical applications because they can be used to diagnose deep tissues. Furthermore, in Table 3, the transducers without matching layers have higher \(Q\) values than the others with matching layers. This indicates that the addition of the matching layer lowered the quality factor. Using matching layers may make ultrasonic wave passage easier. These were consistent with the previously demonstrated results of the increase in the number of transmitted echoes when a matching layer was added.

3.2 Calibration of new fabricated transducers

The new fabricated ultrasonic transducers have been calibrated according to BS EN 12668-2:2001 [16]. Their nominal frequencies are 2, 4 and 6 MHz. To record their beam profiles, we employed an ultrasonic flaw detector (USIP 20, Krautkramer Branson), a vector signal analyzer (IF (89441A, HP) and an oscilloscope (TDS 3052B, Tektronix (USA)). Figure 5 shows some beam profiles that were taken during the calibration of the fabricated transducers.

Fig. 5
figure 5

Beam profiles of some fabricated transducers of different frequencies (these charts were taken from a vector signal analyzer (IF (89441A, HP)

Full size image

After analysis of the beam profiles of the fabricated transducers, some transducers’ parameters were taken from theses beam profiles, such as peak frequency, upper frequency, lower frequency, and so on. The transducers’ parameters are listed in Table 4.

Table 4 The transducers’ parameters after calibration
Full size table

The measurement results were traceable to the SI units, the temperature was 21.4 ± 1 °C and the humidity was 58.6 ± 5%.

According to Table 4, the bandwidth increased with each frequency increment. The maximum bandwidth observed in copper/parylene ML transducers operating at 6 MHz (\(BW=4.6\) MHz). This ensures that copper/parylene ML transducers have broad-band beam, high defect detectability in large range, and high sensitivity.

4 Conclusion

According to the results, the goal of this work was achieved; the modified PZT transducers were improved successfully by adding the designed matching layers that solved the acoustic impedance matching problem between the piezoelectric element and the test specimen. We obtained easy handled transducers with fast and accurate defects detection, due to the enhancement of the sensitivity, the beam width, the beam directivity, the wave height percentage and other factors. These transducers became more able to scan more flaws in a wider range. So, they could be more effective in non-destructive tests using ultrasonic in many industrial applications and in ultrasonic calibration. Finally, the mass-spring ML phenomenon was very useful, especially the copper/parylene ML.