Abstract
In this work, the evolution of the excess conductivity of the YВа2Сu3О7−δ single crystals under electron irradiation is studied. It is shown that irradiation with electrons leads to a significant expansion of the temperature interval that excess conductivity exists. Therefore, the value of the transverse coherence length ξс(0) increases by a factor of 1.4 and the point of the 2D–3D crossover shifts with respect to the temperature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The question of the effect of dimensionality on the formation of the superconducting state in high-temperature superconducting cuprates (HTSC) remains open, despite the intense experimental and theoretical studies carried out in the last 30 years [1,2,3]. As it is established [1, 4], the large penetration depth, the short coherence length and the layered structure contribute to the appearance of an anomalously wide region of excess conductivity (Δσ) in HTSC compounds in the ρab(T) dependences (in the basal plane). Far from the critical temperature (Tc) at Тс ≤ Т < Т* (where T* is the temperature that the deviation from the linear in the ρab(T) dependence commences), Δσ is determined by the so-called pseudogap anomaly (PG) [5,6,7], which was previously studied in detail [8]. Near Тс, Δσ is caused due to the formation of fluctuation superconducting pairs [9, 10]. Therewith, the width and character of the behavior of the fluctuation para-conductivity (FC) section essentially depends on the composition and the structure of the experimental sample [1, 11, 12], such as on the presence or absence of extreme external influences [13, 14].
Presently, it can be reliably considered that near Tc the Δσ(Т) dependence is always well described within the framework of the Aslamazov–Larkin theory [9] for the three-dimensional paraconductivity. During the transition through the 2D–3D crossover point, these curves can be well described in the framework of the Lorentz–Doniach model [15] or Maki–Thompson process [16], depending on the degree of perfection of each particular experimental sample [17]. High pressure [13, 18], high-temperature annealing [19], along with long-term aging processes [20], can substantially shift the 3D crossover point, and also lead to phase separation [14] as a result of the structural relaxation induced by these extreme conditions. The magnetic field, as a rule, leads to a significant blurring of the superconducting transition [21, 22] due to the appearance of specific dynamic transitions in the SC subsystem. Exceptions are the cases of strong pinning of SC fluctuations on a modulated defect superstructure in the form of a developed twinning grid [23], etc.
Notably, despite the large number of investigations of the influence of external impact on the fluctuation conductivity in HTSC, there is practically no regarding the effect of irradiation on FC. The latter, can significantly change both the absolute value of the electrical resistivity ρ and the nature of its temperature dependences ρ(T) [24]. This apart from its fundamental aspect, has a great practical importance, given the very large number of various instruments and devices developed and produced in recent years on the basis of HTSC materials for operation in conditions with high radiation activity.
In the present study, the effect of electron irradiation on the phase transition and the 2D–3D crossover in YBа2Cu3O7−δ superconductor was studied. The choice of the latter as an object of investigation was due to its high critical temperature Тс ≈ 90 K [25] exceeding the boiling point of liquid nitrogen and the greater possibilities for varying its conductive characteristics by doping with substitute elements [26, 27] or by varying the degree of deviation from oxygen stoichiometry [28, 29].
2 Experimental techniques
The YBa2Cu3O7−δ single crystals were grown in a solution-melt procedure in a gold crucible [29]. The technology of obtaining experimental samples and conducting resistive measurements, as well as the analysis of the transport properties of the samples in the normal and superconducting states, were described in detail in previous studies [27, 29]. Irradiation with electrons with energies 0.5–2.5 MeV was carried out at temperatures T < 10 K. Irradiation densities of φ = 1018 1/cm2 by electrons with an energy of 2.5 MeV correspond to an average concentration of defects at all sublattices of 10−4 dpa/аt. displacements per atom [30]. The sequence of measurements was as follows: First, the temperature dependences of the resistivity of the samples before irradiation were measured. Then the temperature was lowered to 5 K and the samples were irradiated. The intensity of the beam was such that the temperature of the sample did not exceed 10 K during the irradiation process. After irradiating the sample it was heated to 300 K and, gradually decreasing the temperature (of the sample), measurements of the temperature dependences of the resistivity at T < 300 K were carried out. The resistivity parameters of the samples are shown in Table 1.
3 Results and discussion
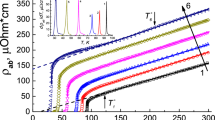
The temperature dependences of the resistivity in the ab-plane ρab(T) of the YBa2Cu3O7−δ single crystal before and after irradiation are shown in Fig. 1. As it can be seen from Fig. 1, the irradiation leads to an anomalously strong suppression of the superconductivity in the YBa2Cu3O7−δ crystal (in comparison with the change in its composition [31]).
Nevertheless, the nature of the changes in the electrical and superconducting properties of HTSCs by varying composition [31] and under irradiation is different. The main difference is as follows: while changing the composition, the decrease in Tc to 86 K is usually accompanied by a change in the shape of the ρ(T) curves from the metallic curve to the so-called “S-shaped curve” with a characteristic thermal activation deflection [31]. In the irradiation, the same absolute decrease in Tc with an appreciable increase of ρ in the temperature interval Tc—300 K is not accompanied by the appearance of the S-shaped ρ(T) dependence. The thermo-activation behavior of the electrical resistance in irradiated samples is manifested only at sufficiently low values of Тс [32]. One of the reasons that lead to a strong decrease in Tc of irradiated samples could be the appearance of dielectric inclusions under the influence of irradiation, due to the redistribution of oxygen between the O(4) and O(5) positions (consistently with the notation of [33]) and the formation of local areas with a tetragonal structure .
It can be seen that the qualitative behavior of the temperature dependence of the conductivity before and after irradiation remains quasimetallic. Moreover, in the ρab(T) dependences in the region of relatively high temperatures, in not irradiated and in irradiated crystals, a rather wide linear region remains, which, according to NAFL theory [34], is a reliable sign of the normal state of the system. After irradiation, the absolute value of the electrical resistivity increases, and the region of existence of the ρab(T) linear dependence decreases substantially at high temperatures.
As can be seen from the table, as well as the inset to Fig. 1, after irradiation, the critical temperature is lowered. Herewith, the narrow initial width of the superconducting transition (ΔTc ≤ 0.3 K) increases substantially, which serves as a sign of the appearance of several phases in the sample [14, 31], having, respectively, different critical temperatures of the transition to the superconducting state.
As the temperature is lowered below a certain characteristic value T*, a deviation of ρab(Т) from the linear dependence occurs, which indicates the appearance of some excess conductivity, which, as noted above, is due to a transition to a pseudogap regime [5,6,7]. The “rounding” of the ρab(T) curves below a certain characteristic temperature T* is due to the appearance of excess conductivity, the temperature dependence of which can be obtained from the formula:
where σ0 = ρ0−1 = (А + ВТ)−1 is the conductivity, determined by interpolating the linear portion of the measurements observed in the high-temperature region to the zero temperature, and σ = ρ−1 is the experimentally measured value of the conductivity at Т < T*.
It is known that near Tc the excess conductivity is probably caused by the fluctuational pairing of current carriers and can be described by the power law dependence obtained in the theoretical Lawrence–Doniach model [15], assuming the presence of a very smooth crossover from the two-dimensional to the three-dimensional fluctuation conductivity regime by decreasing the sample temperature:
where ε = (T − Tmfc)/Tmfc is the reduced temperature; Tmfc is the critical temperature in the mean-field approximation; J = (2ξс(0)/d)2 is the constant of the interplanar pairing; ξс is the coherence length along the c axis and d is the thickness of the two-dimensional layer. In the limiting situations (near Tc, when ξс >> d—the interaction between the fluctuation cooper pairs is realized in the entire volume of the superconductor—the 3D regime or far from Tc, when ξс << d—the interaction is possible only in the planes of the conducting layers—2D-regime) expression (2) is transformed into known relations for three- and two-dimensional cases from the Aslamazov–Larkin theory [9]:
In the case of comparison with the experimental data, it is important to accurately determine the value of Tmfc, which has a significant effect on the slope in the Δσ(ε) dependences. Usually, when compared with the experimental data, the ξс(0), d and Tc in Eqs. (2–4) are adjustable parameters [1]. However, when using such a technique there can be significant quantitative discrepancies between theory and experiment. This, in turn, requires an additional fitting parameter, a scaling factor, the so-called C-factor, which allows to combine the experimental data with the calculated ones and take into account the possible inhomogeneity of the spreading of the transport current for each particular sample [35]. In our case, Tmfc was taken as the Tc, determined, as noted above, at the maximum point on the dρab/dT(T) curves in the region of the superconducting transition [11, 13], as shown in the inset to Fig. 1.
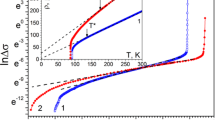
Figure 2 shows the Δσ(Т) dependences in lnΔσ(lnε) coordinates. It is seen that directly near Tc these dependences are satisfactorily approximated by straight lines with an slope angle α1 ≈ − 0.5 corresponding to the exponent − 1/2 in Eq. (4), which indicates the three-dimensional character of the fluctuation superconductivity in this temperature interval. With a further increase in temperature, the rate of decrease Δσ significantly increases (α2 ≈ − 1), which, in turn, can be regarded as an indication of a change in the dimension of the phase transition. As follows from Eqs. (3) and (4), at the 2D–3D crossover point:
Δσ(Т) dependences in Δσ − ε (a) and lnΔσ − lnε (b) coordinates. The numbering of the curves corresponds to the numbering in Fig. 1
In this case, having determined the value ε0 and using the bibliographic on the dependence of Tc and the interplanar distance from δ [36, 37], we can calculate the values of ξс(0). As it can be seen from the table, after irradiation, the value ξс(0) calculated according to Eq. (5) increases from 1.44 to 2.02 Å. This agrees qualitatively with the dependence of ξс(0) from δ obtained on YBa2Cu3O7−δ samples by decreasing Tc [31], but it is significantly smaller from the absolute value of ξс(0) from the values obtained in [31] with a similar decrease in Tc as a result of a decrease in the oxygen content.
As noted above, the electron irradiation is accompanied by a significant expansion of the region of existence of excess conductivity toward high temperatures Т > 1.5Тс, which obviously cannot be explained within the framework of the existing fluctuation theories. According to contemporary concepts (see, for example, [5,6,7]), such a behavior of the ρab(Т) dependences can be caused by the transition to the so-called pseudogap state, characteristic for the “underdoped” compositions of HTSC compounds. A certain role in this is played by the presence of structural and kinematic anisotropy in the system [38,39,40,41,42]. On the other hand, it cannot be completely excluded that this feature can also be partially caused due to the presence of an additive contribution to the conductivity from impurity phases with higher Tc. For example, even in the early work on the study of phase transition in HTSC compounds [43] it was shown that, although superconducting phases with Тс > 140 K are structurally unstable under normal conditions, they can exist as impurity phases in doped and multiphase samples.
4 Conclusions
In the present work it was established that irradiation leads to an anomalously strong (in comparison with the composition change) suppression of superconductivity in the HTSC YBa2Cu3O7−δ. Changing the composition, the decrease in Tc to 86 K is typically by a change in the shape of the ρ(T) curves from metallic curve to curves with a characteristic thermal activation deflection, upon irradiation, the same absolute decrease in Tc, with an appreciable increase of ρ in the interval of temperatures Tc—300 K is not accompanied by the appearance of the “S-shaped” ρ(T) dependence. The electron irradiation leads to a significant expansion of the region of existence of excess conductivity, while the coherence length increases by almost one and a half times and the crossover point shifts substantially with temperature.
References
T.A. Friedmann, J.P. Rice, J. Giapintzakis, D.M. Ginsberg, Phys. Rev. B 39, 4258 (1989)
S.N. Kamchatnaya, I.L. Goulatis, R.V. Vovk, A.I. Chroneos, J. Mater. Sci.: Mater. Electron. 27, 8013 (2016)
R.V. Vovk, N.R. Vovk, G.Y. Khadzhai, O.V. Dobrovolskiy, Z.F. Nazyrov, Curr. Appl. Phys. 14, 1779 (2014)
A.V. Bondarenko, A.A. Prodan, M.A. Obolenskii, R.V. Vovk, T.R. Arouri, Low Temp. Phys. 27, 339 (2001)
M.V. Sadovskii, I.A. Nekrasov, E.Z. Kuchinskii, Th Pruschke, V.I. Anisimov, Phys. Rev. B 72, 155105 (2005)
R.V. Vovk, N.R. Vovk, G.Y. Khadzhai, O.V. Dobrovolskiy, Solid State Commun. 204, 64 (2015)
A.L. Solovjov, L.V. Omelchenko, V.B. Stepanov, R.V. Vovk, H.-U. Habermeier, P. Przyslupski, K. Rogacki, Phys. Rev. B 94, 224505 (2016)
N.A. Azarenkov, V.N. Voevodin, R.V. Vovk, G.Y. Khadzhai, S.V. Lebedev, V.V. Sklyar, S.N. Kamchatnaya, O.V. Dobrovolskiy, J. Mater. Sci.: Mater. Electron. 28, 15886 (2017)
L.G. Aslamazov, A.I. Larkin, Phys. Lett. 26А, 238 (1968)
A.L. Solovjov, L.V. Omelchenko, R.V. Vovk, O.V. Dobrovolskiy, Z.F. Nazyrov, S.N. Kamchatnaya, D.M. Sergeyev, Physica B 493, 58 (2016)
H.A. Borges, M.A. Continentino, Solid State Commun. 80, 197 (1991)
R.V. Vovk, M.A. Obolenskii, A.A. Zavgorodniy, A.V. Bondarenko, I.L. Goulatis, A. Chroneos, J. Mater. Sci: Mater. Electron. 18, 811 (2007)
L. Mendonça Ferreira, P. Pureur, H.A. Borges, P. Lejay, Phys. Rev. B 69, 212505 (2004)
R.V. Vovk, G.Y. Khadzhai, O.V. Dobrovolskiy, S.N. Kamchatna, A. Chroneos, Mod. Phys. Lett. B 30, 1650188 (2016)
W.E. Lawrence, S. Doniach, in Proceedings of the 12th International Conference on Low Temperature Physics, Kyoto, Japan, 1970, ed. by E. Kanda (Keigaku, Tokyo, 1970), p. 361
J.B. Bieri, K. Maki, R.S. Thompson, Phys. Rev. B 44, 4709 (1991)
A.L. Solovjov, M.A. Tkachenko, R.V. Vovk, A. Chroneos, Physica C 501, 24 (2014)
R.V. Vovk, N.R. Vovk, G.Y. Khadzhai, I.L. Goulatis, A. Chroneos, Physica B 422, 33 (2013)
R.V. Vovk, Y.I. Boiko, V.V. Bogdanov, S.N. Kamchatnaya, I.L. Goulatis, A. Chroneos, Physica C 536, 26 (2017)
R.V. Vovk, N.R. Vovk, G.Y. Khadzhai, O.V. Dobrovolskiy, Z.F. Nazyrov, J. Mater. Sci.: Mater. Electron. 25, 5226 (2014)
W.K. Kwok, S. Fleshler, U. Welp, V.M. Vinokur, J. Downey, G.W. Crabtree, M.M. Miller, Phys. Rev. Lett. 69, 3370 (1992)
R.V. Vovk, Z.F. Nazyrov, M.A. Obolenskii, I.L. Goulatis, A. Chroneos, V.M.P. Simoes, J. Alloys Compd. 509, 4553 (2011)
A.V. Bondarenko, V.A. Shklovskij, R.V. Vovk, M.A. Obolenskii, A.A. Prodan, Low Temp. Phys. 23, 962 (1997)
Y.T. Petrusenko, I.M. Neklyudov, A.N. Sleptsov, V.F. Yakovlev, A.V. Bondarenko, M.A. Obolenskii, Physica B 169, 711 (1991)
M.K. Wu, J.R. Ashburn, C.J. Torng, P.H. Hor, R.L. Meng, L. Gao, Z.J. Huang, Y.Q. Wang, C.W. Chu, Phys. Rev. Lett. 58, 908 (1987)
H. Lutgemeier, S. Schmenn, P. Meuffels, O. Storz, R. Schollhorn, Ch Niedermayer, I. Heinmaa, Y. Baikov, Physica C 267, 191 (1996)
R.V. Vovk, M.A. Obolenskiy, A.A. Zavgorodniy, D.A. Lotnyk, K.A. Kotvitskaya, Physica B 404, 3516 (2009)
D.M. Ginsberg ed. Physical Properties High Temperature Superconductors I (Word Scientific, Singapore, 1989)
R.V. Vovk, N.R. Vovk, O.V. Dobrovolskiy, J. Low Temp. Phys. 175, 614 (2014)
A.V. Bondarenko, A.A. Prodan, Y.T. Petrusenko, V.N. Borisenko, F. Dworschak, U. Dedek, Phys. Rev. B 64, 092513 (2001)
M.A. Obolenskii, R.V. Vovk, A.V. Bondarenko, N.N. Chebotaev, Low Temp. Phys. 32, 571 (2006)
J.M. Valles Jr., A.E. White, K.T. Short, R.C. Dynes, J.P. Garno, A.F.J. Levi, M. Anzlowar, K. Baldwin, Phys. Rev. В 39, 11599 (1989)
T. Siegrist, S. Sunshine, D.W. Murphy, R.J. Cava, S.M. Zahurak, Phys. Rev. В 35, 7137 (1987)
B.P. Stojkovic, D. Pines, Phys. Rev. B 55, 8567 (1997)
A.L. Solovjov, H.U. Habermeier, T. Haage, Low Temp. Phys. 28, 144 (2002)
G.D. Chryssikos, E.I. Kamitsos, J.A. Kapoutsis, A.P. Patsis, V. Psycharis, A. Kafoudakis, C. Mitros, G. Kallias, E. Gamari-Seale, D. Niarchos, Physica C 254, 44 (1995)
R.V. Vovk, M.A. Obolenskii, Z.F. Nazyrov, I.L. Goulatis, A. Chroneos, J. Mater. Sci.: Mater. Electron. 23, 1255 (2012)
P.G. Curran, V.V. Khotkevych, S.J. Bending, A.S. Gibbs, S.L. Lee, A.P. Mackenzie, Phys. Rev. B 84, 104507 (2011)
D.H.S. Smith, R.V. Vovk, C.D.H. Williams, A.F.G. Wyatt, Phys. Rev. B 72, 054506 (2005)
V.M. Apalkov, M.E. Portnoi, Phys. Rev. B 65, 125310 (2002)
R.V. Vovk, C.D.H. Williams, A.F.G. Wyatt, Phys. Rev. B 69, 144524 (2004)
I.N. Adamenko, K.E. Nemchenko, V.I. Tsyganok, A.I. Chervanev, Low Temp. Phys. 20, 498 (1994)
N.E. Alekseevskii, A.V. Mitin, V.N. Nizhankovskii et al., Superconductivity 2, 40 (1989)
Acknowledgements
This research has received funding from the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie Grant Agreement No. 644348 (MagIC).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Khadzhai, G.Y., Litvinov, Y.V., Vovk, R.V. et al. Effect of electron irradiation on the fluctuation conductivity in YBa2Cu3O7−δ single crystals. J Mater Sci: Mater Electron 29, 7725–7729 (2018). https://doi.org/10.1007/s10854-018-8768-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10854-018-8768-y