1 Introduction

Germanium (Ge) is an important semiconductor material that is used in nanoelectronic devices, as it has superior materials properties (better carrier mobilities, low dopant activation temperatures and smaller band-gap) as compared to Si [1–5]. Although it was used in the first semiconductor devices, the interest in its use was recently regenerated mainly due to the advent of high-k gate dielectric materials, which have eliminated the requirement of a good quality native oxide in devices [6, 7].

In group IV semiconductors isovalent atoms such as tin (Sn), lead (Pb) and hafnium (Hf) is used in defect engineering strategies and to improve the material properties [8–22]. For example, large isovalent dopants are used to entrap lattice vacanies in Si and thus lead to the reduction in the concentration of oxygen-vacancy pairs. Isovalent atom (i.e. Sn) doping of Ge can be technologically important particularly for the formation of radiation-hard devices. Sn-doped Ge or Sn 1−x Ge x alloys possess advantageous optical properties and may offer a range of strain options so they can be employed as buffer layers to lattice match Si or Ge substrates with III-V and II-VI compounds [8, 9].

Sn diffusion in Ge is mediated by vacancies [10–12]. Friesel et al. [11] determined by means of secondary ion mass spectrometry a diffusion activation enthalpy of 3.26 eV. This activation enthalpy is consistent with the vacancy mechanism and with the available density functional theory results [12].

Forty year ago Varotsos and Alexopoulos [23–29] introduced the cBΩ model which postulated that the defect Gibbs energy g i (where i = defect formation f, diffusion activation act, or migration m) is proportional to the isothermal bulk modulus B and the mean volume per atom Ω. The efficacy of the cBΩ model to describe point defect processes has been demonstrated for numerous materials in previous studies [30–44], but it has not yet been employed to describe Sn diffusion processes in Ge. In the present study we employ the cBΩ model to investigate Sn diffusion in Ge in the temperature range 828–1203 K.

2 Methodology

In the framework of the cBΩ thermodynamic model, the Gibbs free energy for an activation process is described via [26]:

$${g^{act}} = {c^{act}}B\Omega$$
(1)

where B is the isothermal bulk modulus, Ω is the mean volume per atom and \({c}^{act}\) is a dimensionless factor. The latter may be considered to be at a first approximation independent of temperature and pressure.

The self- or dopant-diffusion coefficient of a single mechanism can be described by the Arrhenius equation, \(D = {D_o}\exp ( - {g^{act}}/{k_{\text B}}T)\), which by considering Eq. 1 is expressed as:

$$D = (f{a^2}\nu )\exp \left( { - {c^{act}}B\Omega /{k_B}T} \right)$$
(2)

where kB is Boltzmann's constant, in the pre-exponential term \((D_0= f{a^2}v)\) f is the correlation factor depending upon the structure and the diffusion mechanism, α is the jump distance of the diffusing species (in the order of the lattice parameter), and ν is the jump frequency. The jump frequency is commonly approximated by \({\nu _D}{\left( {{m_m}/{m_d}} \right)^{1/2}}\), with v D to be the Debye frequency and m m , m d are the masses of the host material and the diffusing atom, respectively [28].

Based on Eq. 1, the point defect thermodynamic parameters, i.e., activation entropy, activation enthalpy and activation volume of diffusion are derived through the following relations:

$${s^{act}} = - {\left. {\frac{{\partial {g^{act}}}}{{\partial T}}} \right|_P} = - {c^{act}}\Omega \left\{ {{{\left. {\frac{{\partial B}}{{\partial {\text T}}}} \right|}_P} + \beta B} \right\}$$
(3)
$${h^{act}} = {g^{act}} + T{s^{act}} = {c^{act}}\Omega \left\{ {B - T\beta B - T{{\left. {\frac{{\partial B}}{{\partial {\text T}}}} \right|}_P}} \right\}$$
(4)

and

$${\upsilon ^{act}} = {\left. {\frac{{\partial {g^{act}}}}{{\partial P}}} \right|_T} = {c^{act}}\Omega \left\{ {{{\left. {\frac{{\partial B}}{{\partial P}}} \right|}_T} - 1} \right\}$$
(5)

where β is the volumetric coefficient of thermal expansion.

The key feature of the cBΩ model is the ability to calculate the temperature and/or pressure dependence of diffusion coefficients directly from the bulk properties of the host material through Eq. 2. Different approaches have been proposed to calculate \({c}^{act}\) including the use of a single experimental diffusion coefficient value (mainly for the case where no additional diffusion measurements are available) or the mean value method involving the use of all the available experimental diffusion data [39, 41]. In the single experimental value approach, \({c}^{act}\) can be calculated from Eq. 2 provided that the diffusion coefficient D 1 and the other parameters are known at a temperature T 1:

$$c^{{act}} = \ln \left( {fa^{2} v_{D} \sqrt {\frac{{m_{m} }}{{m_{d} }}} } \right)\frac{{k_{B} T}}{{B_{1} \Omega _{1} }}$$
(6)

After the estimation of \({c}^{act}\), it is possible to calculate the diffusion coefficients at other temperatures, at least to a first approximation. Nevertheless, if diffusivities are known for a range of temperatures, it is preferable to calculate \({c}^{act}\) through the mean value method, as this will limit the uncertainties of the pre-exponential parameters (i.e. the correlation factor and the jump frequency which can be undetermined) [28, 39]. The mean value of \({c}^{act}\) can be derived from Eq. 2:

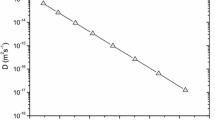
$$\ln D = \ln \left( {fa^{2} v_{D} \sqrt {\frac{{m_{m} }}{{m_{d} }}} } \right) - c^{{act}} \frac{{B\Omega }}{{k_{B} T}}$$
(7)

If a linear correlation of the experimental \(lnD\) versus BΩ/k B T is observed, the cBΩ model is validated. In this plot, c act can be calculated from the slope of the linear fitting. This value of c act can then be employed to reveal the other point defect parameters, as will be discussed in what follows.

3 Results and discussion

3.1 Background

Intrinsic point defects are the main vehicles facilitating self- and dopant-diffusion in materials, whereas in Ge the vacancy mediated mechanism is the prevalent mechanism for most dopants [45–51]. From a technological viewpoint n-type dopant diffusion in Ge is fast and therefore it needs to be controlled to achieve well defined n-type doped regions in Ge-devices [5]. It has been previously established that this is mediated by vacancies via the ring mechanism of diffusion (refer to Fig. 8 of Ref. [5]). A defect strategy that has been considered recently is to codope with Sn as it will attract vacancies and this will reduce the number of vacancies available for the diffusion of the n-type dopants or by increasing the migration energy barriers [52]. In previous experimental and theoretical studies, it was shown that Sn diffuses in Ge via the vacancy diffusion mechanism [11, 12]. Sn diffusion in the temperature range 828–1203 K has been described through the following Arrhenius relation [11]:

$$D_{\exp }^{Sn} = 8.4x{10^{ - 2}}\exp \left( { - \frac{{(3.26 \pm 0.07) eV}}{{{k_B}T}}} \right){m^2}{s^{ - 1}}$$
(8)

3.2 Sn diffusion in Ge

The available data of \(B\left(T\right)\) and Ω(T) for Ge [53] at the temperature range 800–1200 K were approximated by linear relations as follows:

$$B\left( T \right) = {B_o} + \left( {T - {T_o}} \right){(\partial B/\partial T)_P}$$
(9)

and

$$\Omega \left( T \right) = {\Omega _o}\frac{{\left[ {1 + {\beta _o}(T - {T_o})} \right]}}{Z}$$
(10)

where \({B}_{o}\) is the bulk modulus at room temperature (RT) and \({(\partial B/\partial T)_P}\) is its isobaric temperature derivative, Ω 0 is the volume of the unit cell at RT, β 0 is the coefficient of volumetric thermal expansion at RT and Z (=8) is the number of atoms per unit cell. For Ge, \(\Omega _{0} /Z = 2.264 \times 10^{{ - 29}} {\text{m}}^{3} ,\beta _{0} = 1.82 \times 10^{{ - 6}} {\text{K}}^{{ - 1}}\) and \({(\partial B/\partial T)_P} = - 0.0126 {\text{GPa }}{{\text{K}}^{ - 1}}\) [54–56]. The value of B 0 (80.1 GPa) is derived by the linear extrapolation of the reported experimental data [53] using Eq. 9. Subsequently, the temperature dependence of B and Ω can be calculated using these values, in conjunction with Eqs. 9 and 10.

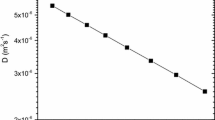
Figure 1 illustrates that a linear correlation describes experimental \(lnD\) and BΩ/k B T for Sn in Ge (correlation factor, \({R}^{2}=0.99\)), supporting the validity of the cBΩ model in this system. The value of \({c^{act}} ( = 0.2712 \pm 0.0026)\) was calculated from the linear fitting of the experimental data. Table 1 reports the calculated values of \({c}^{act}\) for Sn as compared with previous results for Si diffusion and Ge self-diffusion [11, 43, 53, 57, 58]. The Arrhenius plot of the experimental [11] and the calculated via the cBΩ model diffusion coefficients of Sn in Ge is depicted in Fig. 2. A good agreement between the experimental values and the predicted ones is observed, taking into consideration the uncertainties of the model.

Fig. 1
figure 1

Experimental diffusion coefficients of Sn in Ge with respect to the quantity BΩ/k B T. The experimental data were taken from Ref. [11]. The linear behavior indicates the validity of the cBΩ model, according to Eq. 4

Full size image
Table 1 Calculated values of the parameter \({c}^{act}\), activation enthalpy (\({h}_{cB\Omega }^{act}\)), activation entropy (\({s}^{act}\)), activation Gibbs free energy (\({g}^{act}\)) and activation volume (\({\upsilon }^{act}\)), in the framework of the cBΩ model for diffusion in Ge. The calculated values for Sn are compared with previous results for the isovalent Si diffusion and Ge self-diffusion
Full size table
Fig. 2
figure 2

Arrhenius plots of the experimental (points) and calculated (line) diffusion coefficients of Sn in Ge according to the cBΩ model. The shaded region indicates the uncertainties of the model that were calculated by considering the errors propagation of D o, c act, B and Ω to the calculated diffusion coefficients, according to Eq. 2

Full size image

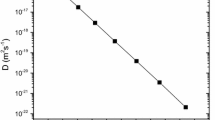
To proceed further with the calculations of the point defect thermodynamic parameters (Eqs. 1 and 3–5), we considered the value \({(\partial B/\partial P)}_{T}=3.0\) and a quadratic relation of the volumetric thermal expansion coefficient [54, 56], i.e., \(\beta \left( {\text{T}} \right) = 1.82 \times 10^{{ - 5}} + 1.03 \times 10^{{ - 7}} \left( {T - 273} \right) - 1.05 \times 10^{{ - 12}} (T - 273)^{2} ~({\text{K}}^{{ - 1}}).\) The Gibbs free energy \({g}^{act}\), the entropy \({s}^{act}\) and the enthalpy \({h}^{act}\) of activation, as well as the energy term \({Ts}^{act}\), are illustrated in Fig. 3. The range of the above point defect parameters along with their calculated uncertainties and other reported values are summarized in Table 1. The calculated values of activation enthalpy (2.94 − 3.11) ± 0.05 eV are in good agreement with the reported experimental value (3.26 ± 0.07) eV for Sn diffusion in Ge, [11], while similar values have been also reported for Si diffusion in Ge and Ge self-diffusion (refer to Table 1).

Fig. 3
figure 3

Point defect thermodynamic parameters (\({g}^{act}\), \({s}^{act}\), \({h}^{act}\) and the energy term \({Ts}^{act}\)) as a function of temperature, for Sn diffusion in Ge, according to the cBΩ model

Full size image

Finally, we observe that the temperature dependence of the activation volume is negligible (∼0.55 ± 0.04 Ωo), over the entire range (828–1203 K). This value is close to activation volumes for self-diffusion in Ge i.e., 0.56 Ωo and (0.52 ± 0.04 Ωo), reported by Werner et al. and by Saltas and Vallianatos, respectively [43, 45].

4 Conclusions

Sn diffusion is Ge was investigated by associating the bulk properties through the cBΩ model. In the present study, it is shown that the cBΩ model describes Sn diffusion in Ge in the temperature range 828–1203 K. The values of activation enthalpy for Sn diffusion in Ge calculated by the cBΩ model are in good agreement with the most recent and reliable experimental results. There is a very small temperature dependence of the activation volume for the temperature range considered. The present study considers the point defect thermodynamic parameters in Sn-doped Ge and can motivate the use of these models in related systems such as Sn 1−x Ge x alloys.