1 Introduction

Sources of renewable energy are intermittent and require efficient energy storage. There are many different energy storage systems amongst which lithium-ion batteries are one of the best candidates. One of the challenges for making high capacity Li-ion batteries is the cathode material with transition metal oxides being one of the attractive candidates [1, 2]. Amongst these oxides, nano-maghemite has received special attention by virtue of its low price and low environmental impact [3–6]. Physical and electrical properties of nanoscale iron oxides are very different to those of micron-size iron oxides [7]; two major differences being: (1) a different Fermi level for nanoscale material as a result of many sub-band-gap states between the conduction band and valence band that arise from surface defects and results in easier electron transfer [8], and (2) reversible lithium insertion into nano-size materials compared to irreversible insertion into bulk or micron-size iron oxides [2, 9].

Maghemite (γ-Fe2O3) has an inverse spinel structure with 2.67 cation vacancies in octahedral sites which are responsible for insertion of lithium ions into the structure [10, 11]. Maghemite can be synthesized by different methods such as: co-precipitation [12–14], hydrothermal [15], microemulsion [16], solution method [17] etc. The co-precipitation method is industrially attractive because of its ability to be scaled up, its reproducibility and its use of eco-friendly reaction conditions.

Different studies have been done to investigate the electrochemical properties of maghemite. Kanzaki et al. [18] synthesized nanoscale γ-Fe2O3, which showed a capacity of 230 mAh g−1 capacity between 1 and 3 V as compared to micron-sized material that had 50 mAh g−1 capacity. Komaba et al. [19] reported that maghemite nanoparticles had a 200 mAh g−1 capacity in the voltage range 1.5–4.5 V. However, the effect of particle size on electrochemical properties of maghemite has not been explicitly studied.

In this research, three different particle sizes of γ-Fe2O3 were studied and it was found that the capacity increased as the particle size of γ-Fe2O3 decreased, with the micron-size γ-Fe2O3 having much lower capacity than nano-sized γ-Fe2O3. We have also used Electrochemical Impedance Spectroscopy (EIS) and Diffuse Reflection Spectroscopy (DRS) investigations to understand the lithium insertion–deinsertion behavior.

2 Experimental procedures

2.1 γ-Fe2O3 synthesis

Different nano-sized maghemite samples were prepared by the co-precipitation method described in references [20, 21]. Magnetite can be synthesized by co-precipitation of Fe2+ and Fe3+ in the presence of NH4OH under an inert atmosphere according to Eq. (1).

$$FeCl_{2} + 2FeCl_{3} + 8NH_{4} OH \to Fe_{3} O_{4} + 4H_{2} O + 8NH_{4} Cl$$
(1)

If the reaction occurs in contact with air or oxygen, the synthesized powder is predominantly maghemite as a result of topotactic oxidation. Ferric chloride (FeCl3·6H2O), ferrous chloride (FeCl2·4H2O), ammonia, and oleic acid (surfactant) were obtained from Sigma-Aldrich. 0.5 M FeCl2·4H2O and 0.5 M FeCl3·6H2O, with a Fe3+:Fe2+ molar ratio of ~2:1, were mixed in air, then, 15 ml of aqueous ammonia solution (25 % v/v) was added to the solution at 60 °C with vigorous stirring until the pH reached 11. Oleic acid (5 % v/v) was also added and the reaction allowed to proceed for different reaction times. The precipitate was separated using a magnet and washed with deionized water. The co-precipitation parameters for the two synthesized nanoscale samples are summarized in Table 1. For size comparison, a commercial micron-size maghemite (sample coded as M in Table 1) was purchased from Sigma-Aldrich.

Table 1 Parameters for maghemite sample preparation
Full size table

2.2 Material characterization

X-ray powder diffraction (XRD) measurements were carried out using a PANalytical X’Pert Pro MPD, with Cu-Kα radiation. Scanning electron microscopy (SEM) was performed using a JEOL JSM-6700F SEM, whilst transmission electron microscopy (TEM) investigations were carried out using a Philips EM201C. Diffuse reflectance spectra (DRS) of the samples were measured using an Avantes (Avaspec-2048-TEC) spectrometer; the incident beam was collimated and reflected light captured by an integrating sphere, a sample reference (BaSO4) was used to provide a nominal 100 % reflectance measurement.

2.3 Electrochemical investigations

Battery assembly was performed using a standard split cell consisting of a Li anode, a liquid electrolyte, a separator and a composite cathode. The anode was battery grade lithium foil (99.9 %, Sigma-Aldrich) and the electrolyte was prepared by dissolving 1 molar bis-(trifluoromethane)-sulfonamide lithium salt (LiTFSI, 99.95 % trace metals basis, Sigma-Aldrich) in a mixture of 1,3-dioxolane (DOL, Sigma-Aldrich) and 1,2-dimethoxyethane (DME, Sigma-Aldrich) (1:1, v/v) in an argon filled glove box. The separator was monolayer polypropylene (Celgard PP2075). The cathode slurry was produced from 80 wt% maghemite, 10 wt% carbon black (Sigma-Aldrich) and 10 wt% Polyvinylidene Fluoride (PVDF, Sigma-Aldrich) dissolved in N-Methyl-2-pyrrolidone (NMP) (>99.5 %, anhydrous, Sigma-Aldrich). This slurry was tape caste onto nickel foil (the current collector) and placed in a vacuum oven at 80 °C for 4 h, until the NMP evaporated. Carbon was added to ensure the conductivity of the cathode.

Charge–discharge tests were carried out using a battery analyzer connected to a PC at different discharge rates and over a voltage range 1.5–4 V versus Li+/Li. EIS investigations were undertaken using an Autolab M101 potentio-galvanostat connected to an Autolab FRA32M impedance analyzer over the frequency range 20 kHz–1 mHz and using a 10 mV ac voltage amplitude.

3 Results and discussion

3.1 Phase and particle size characterization

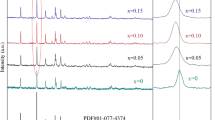
Figure 1 shows the XRD patterns of the maghemite samples which have a good match with JCPDS file (No. 39-1346) of γ-Fe2O3. According to the Bragg’s equation d311 for N1, N2 and M are 2.498, 2.499 and 2.499 Å respectively.

Fig. 1
figure 1

XRD patterns of maghemite samples: N1, N2, and M

Full size image

The crystallite size, d, of the samples was calculated using Scherrer’s equation [22]:

$$d = \frac{0.9\lambda }{\beta \cos \theta }$$
(2)

where λ is the X-ray wavelength (0.154 nm for Cu-Kα), θ is the Bragg angle in degrees and β is the full width at half maximum (FWHM) of the (311), (220) and (440) peaks derived by Gaussian fitting after subtracting the instrumental line broadening in radians. The results are tabulated in Table 2 together with average particle sizes derived from electron microscopy (Fig. 2). The narrow width of the XRD peaks from the micron-sized material (Sample M, Fig. 1c) confirmed the larger crystallite size in this sample. A backscattered SEM image and a particle size distribution of sample M are shown in Fig. 2e, f indicating that the average particle size is 2.2 μm and that the particles are polycrystalline.

Table 2 Average crystallite and particle size of the samples
Full size table
Fig. 2
figure 2

Micrographs and particle size distributions of samples: a, b N1, c, d N2 and e, f M

Full size image

TEM micrographs of samples N1 (Fig. 2a) and N2 (Fig. 2c) samples are shown in Fig. 2. The particle size distribution of samples N1 and N2 derived from the micrographs [23] show an average particle size of 11 and 19 nm, respectively. As expected, with increasing time of co-precipitation method, both the average crystallite and particle sizes were increased which is in good agreement with literature [10, 20]. Higher resolution TEM images (Fig. 3) clearly show that the synthesized nanoparticles are crystalline and predominantly single crystal in nature.

Fig. 3
figure 3

TEM phase contrast images of samples a N1 and b N2

Full size image

3.2 Charge–discharge tests

Figure 4a shows the discharge capacity versus cycle number at different discharge rates. This figure indicates for sample N1, the first cycle capacity at 20 mA g−1 was about 206 mAh g−1 but after 45 cycles, it gave a reversible capacity of 192 mAh g−1 (~93 % of the first cycle capacity). The decrease in capacity with increasing number of cycles may be due to the difference in particle size between the active material (maghemite) and carbon black which has been reported by other researchers [18]. The discharge capacities of the N1 cell were 182, 157 and 114 mAh g−1 at discharge rates of 40, 60 and 100 mA g−1, respectively. For sample N2, the first cycle capacity at 20 mA g−1 was 186 mAh g−1 and after 45 cycles, it decreased to 169 mAh g−1 (~91 %). The discharge capacities of the N2 cell were 157, 129 and 77 mAh g−1 at discharge rates of 40, 60 and 100 mA g−1, respectively.

Fig. 4
figure 4

a Discharge capacity of the N1, N2 and M samples versus Cycle number and b first charge–discharge test of N1, N2 and M samples (1.5–4 V and 20 mA g−1)

Full size image

From these results it can be concluded that the capacity increases as the particle size decreases, presumably due to two main reasons: (1) an increase in the relative surface area for active Li+ diffusion and (2) a change in Fermi level and the emergence of a sub-band-gap as the surface energy is increased [8]. The latter will cause the electron conductivity of the active cathode material to increase resulting in easier electron transfer and the conversion between Fe3+ and Fe2+ inside the maghemite.

At higher discharge rates, diffusion of Li+ into the structure affects the capacity. Figure 4a shows better properties for N1 than N2 due to better Li+ diffusion performance. The shorter diffusion length in sample N1 is evident in the improved discharge capacity. The M sample has a discharge capacity roughly one-eighth of that of the N1 sample, which fades to near zero upon cycling. According to Larcher et al. [4], this is because of irreversible changes in the structure of maghemite during lithium insertion, a lower active reaction surface and the non-conductive nature of micron-sized maghemite compare to nanoscale material. Figure 4b shows, at the first cycle, the about 1.2 Li+ ions were inserted into the maghemite between the open-circuit voltage (3 V) and 1.5 V (vs. Li+/Li).

In summary, the reversible capacities (i.e. 206 mAh g−1 for N1 and 186 mAh g−1 for N2) were better than the theoretical capacity of 170 mAh g−1 for LiFePO4 [24], working capacities of 160 mAh g−1 for LiCoO2 [25], 116 mAh g−1 for LiMn2O4 [26, 27] and 151–173 mAh g−1 for Li(Ni1/3Co1/3Mn1/3)O2 [28–30] at similar discharge rates; in addition, the values are also better than the published results of other researchers for nano-sized γ-Fe2O3 [18, 19].

3.3 Diffuse reflectance spectroscopy

Figure 5 shows diffuse reflectance spectra for the three samples (N1, N2 and M) following Kubelka–Munk transformation [31, 32]. The band-gaps determined by linear extrapolation for samples N1, N2 and M are 1.84, 1.89 and 2.08 eV respectively. As the particle size decreases, the band gap is reduced and low energy gap states become evident arising from the increased relative proportion of surface defects.

Fig. 5
figure 5

Band-gap energies of samples a N1, b N2 and c M obtained from diffuse reflectance measurements following Kubelka–Munk transformation

Full size image

The band-gap decreases to a certain minimum with reduction in particle size from a bulk size value (i.e. 30 nm) to a critical size value (i.e. 10 nm), further decrease in particle size from the critical size caused the band-gap to increase (due to the quantum dots). A possible justification for this reduction in band-gap with reduction of the particle size is that the bulk defects excite the molecular orbitals in the conduction band edge and causes the red-shift of the absorption spectra according to Lin et al. [33]. It is said [34] that for the particle size range of 2–10 nm, quantum dots can cause a reduction in band-gap with increasing the particle size, but for particle sizes more than 10 nm (where there are no quantum dots) the reduction of particle size causes the increasing of the surface and electronic defects; since reduction in energy needed for electron transfer between valance band and conduction band. The effect of particle size on electron transfer resistance is further discussed in EIS investigations below.

3.4 Electrochemical impedance spectroscopy

Figure 6 shows the Nyquist plot for the N1, N2 and M samples at 1.6 V OCV with 10 mV ac amplitude. The shape of these plots can reveal the electrochemical mechanism of the charge–discharge process which consists of physical bonding of Li+ ions and a fast reversible reduction of Fe3+–Fe2+ at the surface of iron oxide particles, followed by slow lithium insertion into the structure. Over the low frequency range, the 45° slope corresponds to lithium insertion to maghemite structure. In contrast, over the high frequency range, lithium does not have enough time to diffuse into the maghemite structure and the capacitive semicircles (Fig. 6a, b) reveal the Fe3+–Fe2+ reduction process. As can be seen in Fig. 6, the semicircle for sample N1 is smaller than that for N2; this is because of the higher surface area presence of more Fe3+ at its surface. For the micron-size cathode, the EIS results indicate a high resistance for the charge–discharge process (Fig. 6c) and explain the lower discharge capacity for this cathode material. These results are in good agreement with the results obtained by DRS and the charge–discharge tests and show the capacitive nature of maghemite for electron storage.

Fig. 6
figure 6

EIS of a N1, b N2 and c M samples at 1.6 V OCV and 10 mV amplitude

Full size image

Figure 8 shows the equivalent circuit of the system over all frequency ranges. The circuit elements consist of RΩ (electrolyte resistance), Rct (charge transfer resistance), ZCPE (constant phase element representing the capacitive nature) and ZW (Warburg or diffusion impedance that represents this lithium diffusion process). ZCPE and Rct represent the reduction process. In the high frequency range, ZW tends to zero (i.e. a lack of diffusion), so that ZW is removed from equivalent circuit as shown in Fig. 7. The values of the circuit elements are given in Table 3 for the N1 and N2 materials over the high frequency range.

Fig. 7
figure 7

Equivalent circuit of EIS spectra at high frequency range. RΩ: electrolyte resistance, Rct: charge transfer resistance and ZCPE: constant phase element

Full size image
Table 3 Circuit elements of N1 and N2 samples obtained from high frequency part of EIS spectrum
Full size table

Capacitive semicircles correspond to the high frequency range. In this range, one can find circuit elements: RΩ, Rct, Q and n. The constant phase element (ZCPE) is a pseudocapacitance element that is between a resistance and a capacitance and can be written as [35]:

$$Z_{CPE} = \frac{1}{{Q\left( {j\omega } \right)^{n} }}$$
(3)

Here n is the initial slope of the Nyquist plot and determines the depression of the capacitive semicircle [36]. Table 3 shows nN1 = 0.85 and nN2 = 0.83.

The total impedance over the high frequency range can be written as Eq. (4):

$$Z = R_{\varOmega } + \frac{{R_{ct} Z_{CPE} }}{{R_{ct} + Z_{CPE} }}$$
(4)

where Z is the total impedance, RΩN1 = 28.6 Ohm and RΩN2 = 28.1 Ohm. Using Eq. (4) leads to RctN1 = 63.5 Ohm (50 < RctN1 < 80), QN1 = 5.76 μF s(n−1), RctN2 = 93.5 Ohm (82 < RctN2 < 116) and QN2 = 3.3 μF s(n−1). As expected, the charge transfer resistance (Rct) of N1 is lower than that of sample N2. Electron) transfer depends on the magnitude of the band-gap that is affected by maghemite particle size and defects. The lower charge-transfer resistance of N1 relative to N2 verifies the presence of more sub-band-gap states between the conduction and valence bands and explains the higher capacity of N1 relative to N2 cathode material.

Three main factors can affect the CPE impedance: (1) electrode surface roughness [37], (2) the distribution of reaction rate or current distribution [38] and (3) varying thickness and composition [39]. Surface roughness, defined as (D = (n + 1)/n), is the most important parameter and lies between 2 and 3. D = 2 implies a atomically smooth surface and D = 3 implies a fully rough surface that has a three dimensional accessibility [37]. For a uniform reaction rate, the same cathode thickness and a similar composition and current distribution, then DN1 = 2.17 and DN2 = 2.2, which represents increased homogeneity of sample N1 relative to N2. These results are in good agreement with the narrower particle size distribution of sample N1 compared to N2 (Fig. 2).

At low frequencies, the Warburg impedance represents the diffusion resistance of maghemite for the lithium insertion process. According to the Fig. 8, the total impedance of the circuit can be written as follows:

$$Z = R_{\varOmega } + \frac{{(R_{ct} + Z_{W} )Z_{CPE} }}{{(R_{ct} + Z_{W} ) + Z_{CPE} }}$$
(5)
Fig. 8
figure 8

Equivalent circuit of EIS spectra for the whole frequency range. RΩ: electrolyte resistance, Rct: charge transfer resistance, ZCPE: constant phase element and ZW: Warburg impedance

Full size image

Figure 9 shows the evolution of the diffusion resistance of samples N1 and N2 as a function of frequency in a ZW-ω diagram (7.24E−3 Hz < ω < 25 Hz) obtained from Eq. (5) and the values in Table 3. As expected, the diffusion resistance of the 19 nm material is greater than that of the 11 nm material (over all frequency ranges). This is in a good agreement with the results obtained in charge–discharge tests. The lower resistance of sample N1 is because of the more active reaction surface and the presence of more surface defects relative to the N2 sample. This causes easier lithium diffusion into the maghemite nanoparticles and increases Li+ capacity.

Fig. 9
figure 9

Diffusion resistance of N1 and N2 samples

Full size image

4 Conclusions

Different particle sizes of maghemite have been synthesized, characterized and employed as a Li-ion cathode material. Electrochemical results indicated that with a reduction in particle size of the maghemite, particularly towards the nanoscale, the lithium insertion capacity was found to be increased from 26 mAh g−1 for micro size to 186 and 206 mAh g−1 for nano size samples. EIS studies revealed a two-stage lithium insertion process. The first step of the discharge process is the surface reduction of Fe3+–Fe2+ and physical bonding of Li+ to the oxide particles without lithium insertion. The second step is Li+ diffusion and core reduction of maghemite particles. EIS and DRS verified that the higher capacity of maghemite with a lower particle size is because of the ease of electron transfer due to a smaller band gap and increased Li+ diffusion due to a higher surface area.