A hybrid inverse method for evaluating FC-PBGA material response to thermal cycles

Abstract

This study proposes a hybrid experimental-analytical inverse method that can be used to evaluate thermomechanical cyclic behavior of flip-chip plastic ball grid array modules and the constituent materials. Treating such a package as an adhesively bonded trilayer plate, the structural formulation follows and modifies an existing analytical model. A phase-shifted shadow moiré method is employed to obtain the package thermal warpage variation in responding to a temperature cycle. By correlating the modeling predicted and the experimentally measured package warpage, the application of the method leads to the determination of those uncertain material parameters including temperature dependent modulus of elasticity and coefficient of thermal expansion of the die attachment and the substrate materials. These parameters are difficult to determine otherwise due to the complexity involving the effect of package processing condition and extremely thin thickness of the adhesive layer. As the values of all material parameters are ascertained, shear and peel stresses in the module adhesive layer can also be evaluated based on the analytical model.

Appendix A: inverse method

The proposed HEAIM to evaluate the thermomechanical cyclic response of a FC-PBGA package is stepwised as:

• (1) Measuring strain/deformation

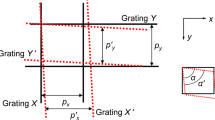
Out-of-plane strain/deformation of solid is measured within the area of interest under thermal load using phase-shifted shadow moiré technique. The obtained instantaneous strain/deformation data versus the controlled temperature are collected and stored based on the geometrical position of nodes within the surface area. The 3D profile of warpage w _expi (x _i,y _i) is characterized by nodes (x_i,y_i) within the area.

• (2) Formulating system of equations based on closed-form solutions for deformation

In order to obtain a mathematical equation of the strain/deformation, the equations of compatibility of displacements and equilibrium of forces and moments within the structure under a given applied load are first constructed. Stresses are then derived using materials constitutive relations within structure. A number of assumptions is used without compromising the universality of the achieved closed-form solution. The warpage equation was expressed in terms of materials constitutive parameters and used in the inverse method. Equation A1 presents warpage at each node with dimension of (x _i , l/2) over the length of the module.

$$ \begin{gathered} w_{i} \left( {x_{i} ,l/2} \right) = \hfill \\ {\frac{{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)\left( {\alpha_{3} - \alpha_{1} } \right)\left( {T_{2} - T_{1} } \right) \times \left( {{\frac{1}{2}}x_{i}^{2} - {\frac{{\cosh Kx_{i} - 1}}{{K^{2} \cosh Kl}}}} \right)}}{{\left( {2\sum\limits_{j = 1,3} {{\frac{{\left( {1 - 2\nu_{j} } \right)\left( {1 + \nu_{j} } \right)}}{{\left( {1 - \nu_{j} } \right)E_{j} h{}_{j}}}}} + {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } {2\sum\limits_{j = 1}^{3} {\left( {{\frac{{E_{j} h_{j}^{3} }}{{12\left( {1 - \nu_{j}^{2} } \right)}}}} \right)} }}} \right. \kern-\nulldelimiterspace} {2\sum\limits_{j = 1}^{3} {\left( {{\frac{{E_{j} h_{j}^{3} }}{{12\left( {1 - \nu_{j}^{2} } \right)}}}} \right)} }}} \right)\left( {\sum\limits_{j = 1}^{3} {\left( {{\frac{{E_{j} h_{j}^{3} }}{{12\left( {1 - \nu_{j}^{2} } \right)}}}} \right)} } \right)}}} \hfill \\ \end{gathered} $$

(A1)

where

$$ K = \sqrt {{\frac{{\sum\limits_{j = 1,3} {{\frac{{\left( {1 - 2\nu_{j} } \right)\left( {1 + \nu_{j} } \right)}}{{\left( {1 - \nu_{j} } \right)E_{j} h{}_{j}}}}} + {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } {4\sum\limits_{j = 1}^{3} {\left( {{\frac{{E_{j} h_{j}^{3} }}{{12\left( {1 - \nu_{j}^{2} } \right)}}}} \right)} }}} \right. \kern-\nulldelimiterspace} {4\sum\limits_{j = 1}^{3} {\left( {{\frac{{E_{j} h_{j}^{3} }}{{12\left( {1 - \nu_{j}^{2} } \right)}}}} \right)} }}}}{{\sum\limits_{j = 1}^{3} {\left( {{\frac{{h_{j} }}{{3\left( {{\frac{{E_{j} }}{{2\left( {1 + \nu_{j} } \right)}}}} \right)}}}} \right)} + {\frac{{h_{2} }}{{3\left( {{\frac{{E_{2} }}{{2\left( {1 + \nu_{2} } \right)}}}} \right)}}}}}}} $$

(A2)

and h and l are the height and length of the layers of the trilayer structure respectively.

• (3) Identifying known and unknown material parameters

A trilayer structure consists of three layers of composite and/or individual component layers with their distinct mechanical and thermal parameters (Eq. A3). Material properties are mainly the elastic modulus E, Poisson’s ratio υ and CTE α. A reasonable range is estimated from different sources including vendor/manufacturer, and literature for each unknown parameter. An unknown parameter is introduced as a vector (Eq. A4) with a number of divisions$\overline{K}$ (Eq. A5).

$$ \left[ m \right] = \left[ {\left( {E_{r} } \right)_{\text{o,1}} \, \left( {\alpha_{r} } \right)_{\text{o,2}} \, \left( {\nu_{r} } \right)_{\text{o,3}} } \right]_{3,3} $$

(A3)

$$ \left( m \right)_{o,d} \,=\, \left[ {\left( {m_{1} } \right)_{o,d} .. \, \left( {m_{r} } \right)_{o,d} .. \, \left( {m_{{\overline{K} }} } \right)_{o,d} } \right]_{{1,\overline{K} }} $$

(A4)

where

$$ \begin{gathered} \left( {m_{1} } \right)_{o,d} \,=\, \left( {m_{ \min } } \right)_{o,d} \hfill \\ \left( {m_{{\overline{K} }} } \right)_{o,d} \,=\, \left( {m_{ \max } } \right)_{o,d} \hfill \\ \end{gathered} $$

(A5)

$$ \left( {m_{r} } \right)_{o,d} \,=\, {\frac{{r\left( {\left( {m_{ \max } } \right)_{o,d} - \left( {m_{ \min } } \right)_{o,d} } \right)}}{{\overline{K} }}} $$

(A6)

• (4) Solving the system of equations using iterative method

The matrix with the materials parameters, ([m]) is generated at each iterative loop with all the parameters indexed by r.

By having n numbers of unknown parameters, there will be $\overline{K}^{n}$ number of iterations. During each iteration w _i,r (x _i, l/2) is generated for all nodes (index ‘i’) over the length of module as:

$$ \begin{gathered} w_{r,i} \left( {x_{i} ,l/2} \right) = \hfill \\ {\frac{{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)\left( {m_{r,3,2} - m_{r,1,2} } \right)\left( {T_{2} - T_{1} } \right) \times \left( {{\frac{1}{2}}x_{i}^{2} - {\frac{{\cosh K_{r} x_{i} - 1}}{{K_{r}^{2} \cosh K_{r} l}}}} \right)}}{{\left( {2\sum\limits_{j = 1,3} {{\frac{{\left( {1 - 2m_{r,j,3} } \right)\left( {1 + m_{r,j,3} } \right)}}{{\left( {1 - m_{r,j,3} } \right)m_{r,j,1} h{}_{j}}}}} + {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } {2\sum\limits_{j = 1}^{3} {\left( {{\frac{{m_{r,j,1} h_{j}^{3} }}{{12\left( {1 - m^{2}_{r,j,3} } \right)}}}} \right)} }}} \right. \kern-\nulldelimiterspace} {2\sum\limits_{j = 1}^{3} {\left( {{\frac{{m_{r,j,1} h_{j}^{3} }}{{12\left( {1 - m^{2}_{r,j,3} } \right)}}}} \right)} }}} \right)\left( {\sum\limits_{j = 1}^{3} {\left( {{\frac{{m_{r,j,1} h_{j}^{3} }}{{12\left( {1 - m^{2}_{r,j,3} } \right)}}}} \right)} } \right)}}} \hfill \\ \end{gathered} $$

(A7)

where

$$ K_{r} = \sqrt {{\frac{{\sum\limits_{j = 1,3} {{\frac{{\left( {1 - 2m_{r,j,3} } \right)\left( {1 + m_{r,j,3} } \right)}}{{\left( {1 - m_{r,j,3} } \right)m_{r,j,1} h{}_{j}}}}} + {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^{3} {h_{j} } } \right)^{2} } {4\sum\limits_{j = 1}^{3} {\left( {{\frac{{m_{r,j,1} h_{j}^{3} }}{{12\left( {1 - m^{2}_{r,j,3} } \right)}}}} \right)} }}} \right. \kern-\nulldelimiterspace} {4\sum\limits_{j = 1}^{3} {\left( {{\frac{{m_{r,j,1} h_{j}^{3} }}{{12\left( {1 - m^{2}_{r,j,3} } \right)}}}} \right)} }}}}{{\sum\limits_{j = 1}^{3} {\left( {{\frac{{h_{j} }}{{3\left( {{\frac{{m_{r,j,1} }}{{2\left( {1 + m_{r,j,3} } \right)}}}} \right)}}}} \right)} + {\frac{{h_{2} }}{{3\left( {{\frac{{m_{r,2,1} }}{{2\left( {1 + m_{r,2,3} } \right)}}}} \right)}}}}}}} $$

(A8)

• (5) Calculating the difference between the predicted and the measured deformation

Equation A7 is used to calculate the warpage/deformation for nodes. During an iteration loop, for every node, the calculated warpage is compared with the experimental data available for the same node (see step1). The correlation coefficient (Eq. A9) is calculated during each iteration denoted by index ‘r’ as follows:

$$ R_{r}^{2} = 1 - {\frac{{SSerr_{r} }}{{SStot_{r} }}} $$

(A9)

where

$$ SSerr_{r} = \sum\limits_{i = 1}^{n} {\Updelta_{r,i}^{2} } $$

(A10)

$$ SStot_{r} = \sum\limits_{i = 1}^{n} {\left( {w_{r,i} \left( {x_{i} ,l/2} \right) - {\frac{{\sum\limits_{i = 1}^{n} {w_{\exp i} \left( {x_{i} ,l/2} \right)} }}{n}}} \right)^{2} } $$

(A11)

The Δ _r,i denotes the difference between the calculated warpage and the experimental data for each node along the length of the module.

$$ \Updelta_{r,i}^{2} = \left( {w_{r,i} \left( {x_{i} ,l/2} \right) - w_{\exp i} \left( {x_{i} ,l/2} \right)} \right)^{2} $$

(A12)

• (6) Continue the iterative processing until reaching the maximum correlation between measured and the modeling obtained package deformation, indicating the predicted parameters are optimized

The inverse method solution is converged by maximizing the correlation coefficient among all the iterations (Eq. A13).

$$ { \max }\,R^{2} = { \max }\left( {R_{r}^{2} } \right) $$

(A13)

The maximum value offers a corresponding matrix of material parameters. These parameters were employed to calculate warpage data showed a good agreement with the experimentally obtained values of warpage. Calculated warpage values with a confidence level of 85% or higher has been aimed through iterative loops in the proposed inverse method. Depending on assumptions taken to achieve a closed-form solution, the ending results can be affected as compared with experimental data. This suggests that a more precise range of the material parameters leads to a higher confidence level.