Introduction

Titanium and its alloys are broadly used in different applications in the biomedical field such as orthopedic and dental implants due to their light weight, high corrosion resistance and low elastic modulus as compared with the other metallic biomaterials such as stainless steels and Co–Cr–based alloys [1,2,3]. Recently, in the dental field both low- and high-strength titanium alloys have been introduced [4, 5]. Anyway, the low-strength and high-strength titanium and its alloys have several disadvantages.

For the low strength, polishing is too difficult and poor wear resistance causes limitations in the high-stress conditions; the higher elastic modulus of high-strength titanium alloys has the higher effect on shielding stress between implant and bone for surgically implant parts [4, 6, 7].

Recently, we have fabricated a Ti–2.7Al–3Cu–2Fe (wt%) alloy by hot extrusion of a compact of TiH2, Al, Fe and Cu powder blend, and demonstrated that the alloy has a fully α/β lamellar microstructure with a high yield strength (YS) of 1072 MPa, high ultimate tensile strength (UTS) of 1220 MPa and a relatively low tensile ductility of 2.7% [8]. It was also shown that this alloy has a great potential for biomedical applications due to its high corrosion resistance [9]. Furthermore, the high-strength titanium alloys such as Ti-6Al-4 V with the releasing of V ions from the wear corrosion and passive film dissolution on the alloy surface have a toxic effect for the long-term performance, since high condensation of V ions in the blood causes health problems [10, 11]. Recently, the design trend moved to new biomedical titanium alloys through reducing elastic modulus and controlling the addition of toxic alloying elements [12,13,14].

Products belonging to cellular metabolism (as hydrogen peroxide, or bacterial products) tend to influence the corrosion behavior of titanium plants. These are absorbed on surfaces modifying the corrosion behavior and leading to the formation of further chemical species. In addition, cells and bacteria can act as biofilm producers contributing to influence the corrosion resistance of the plants. These features can be amplified once tribocorrosion or fretting corrosion takes place locally. So, in all these conditions, the corrosion/dissolution behavior of biomedical titanium alloys must be carefully analyzed.

To improve mechanical properties, corrosion resistance, high-temperature properties and formability of titanium, different alloying elements must be added [14,15,16]. A safe alloying element to improve the properties of titanium alloys to be applied in the biomedical field is Fe leading to low elastic modulus, high-strength, non-toxic, non-allergic and low-cost alloys [17]. The addition of copper to titanium can improve antibacterial properties. Antibacterial capability is dependent on the Cu content; for percentage lower than 5 wt %, antibacterial and mechanical properties are improved [18, 19]. The industries more likely accept the addition of Fe because of its low cost and the improvement of mechanical properties of Ti alloys by adding Fe [8, 20]. Fe is a β-eutectic, non-toxic and non-allergic element [8], and with an addition of 1–4 wt.% Fe to the Ti alloys, good mechanical properties can be obtained [9]. Besides what has been mentioned, various researches have been done in the direction of the optimization of the production process. Najafizade et al. [21] optimized siliconizing performance by using RSM method and experimental tests. Hoseinzade et al. [22] optimized the tube drawing performance with rectangular tubes to optimize the friction coefficient, drawing velocity, bearing length and die half angle. New developments in science and technology have significant impact on human health and life [23,24,25,26,27]. Since the mechanical properties of Ti alloys are important for the application in the biomedical field, in this paper, we tried to find the optimal combination of process parameters to have the best mechanical and microstructural properties that have not been carried out in the previous researches [28,29,30]. So, lack of this issue was the key motivation of this research. Based on the literature, there has not been a comprehensive study on the optimization of mechanical and biocorrosion properties of Ti alloys. This motivated the authors to carry out a research in this field.

The aim of the present paper is the optimization of the composition and processing parameters of a new developed Ti–XAl–2Fe–3Cu alloy in order to improve the mechanical properties and the biocorrosion behavior.

Experimental

Specimens preparation

Ti-Al-Fe-Cu alloy rods were fabricated by extruding a compact of a mixture of TiH2, Al, Fe and Cu powders, with a composition of Ti-2Fe-3Cu-XAl (X = 6, 4, 2 wt%), at 1200 °C and with 5 min of holding time. A hydraulic press with 200-ton capacity was employed. The purity and particle size of TiH2 powder were 99.5% and 75 µm (− 200 mesh), respectively. Al powder with particle sizes 40 µm (− 325 mesh), Cu powder of 40 µm (− 325 mesh) and Fe powder with particle sizes smaller than 53 µm (− 300 mesh) produced via gas atomization were employed. In order to reduce the moisture levels, all powders were heated in a vacuum oven for 2 h at 100 °C; tumbler mixing for 24 h was employed for the blending.

The powder mixture was then cold-pressed to produce cylindrical powder compacts with a relative density of around 85%. The powder compact was heated to 1200 °C by induction heating in an argon atmosphere with oxygen content below 200 ppm, held at this temperature for 5 min and then left to be cooled down at room temperature. The extrusion cylinder and stainless-steel die were heated to 500 °C before the extrusion process. The extrusion ratio was 9:1 in order to produce cylindrical roads of 100 mm in diameter. The overall schematic of the process is shown in Figs. 1a, b.

Figure 1
figure 1

a Flowchart of the experimental procedure and b Schematic diagram of the experimental setup

Full size image

The oxygen and hydrogen contents of the extruded rods were measured by using a LECO TCH-600 nitrogen/oxygen/hydrogen analyzer, as shown in Table 1. A Rigaku Ultima IV XRD was used to identify the phase structure of the extruded rods by applying Cu-Kα radiation at a precipitating voltage of 40 kV and a current of 40 mA with a scan step of 0.02. The microstructure of the as-extruded rods was characterized by using an OLYMPUS BX51M optical microscopy and FEI NOVA NanoSEM 230 scanning electron microscope. The cross sections of the extruded rods were polished with traditional metallographic techniques and etched with Kroll solution (2 ml HF, 6 ml HNO3, 92 ml H2O) for preparing them for microstructural analysis by optical microscopy. To check and recognize the average sizes of different phases in alloys, DT2000 software was used. The tensile test specimens with a gauge length of 15 mm and a thickness of 2 mm and a width of 3 mm were cut along the extrusion direction using an electrical discharge wire machine. The tensile tests were performed by using a Zwick/Roll Z20 universal testing machine at room temperature. The strain was measured by using an extensometer with a gauge length of 12 mm. The strain rate of the tests was set at 5 × 10–4 s−1. The fracture surfaces and the longitudinal cross section near the fracture of the tensile test specimens were examined using SEM.

Table 1 Level of process parameters
Full size table

Electrochemical test

Electrochemical measurements were performed by using a biologic vsp-300 potentiostat. In a conventional three-electrode cell configuration, Ti–Al–Cu–Fe samples were used as the working electrode, platinum electrode as the counter electrode (CE) and saturated calomel electrode (SCE), separated from the cell by a glass frit, as the reference electrode (RE). It is worth noting that all the reported potential in this text refers to SCE and the electrochemical cell was open to the air. The immersion time for electrochemical measurements was 1 h at 298 K. Electrochemical impedance spectroscopy (EIS) was performed with the frequency ranging from 100 kHz to 10 mHz at open-circuit potential. The sinusoidal potential perturbation was 5 mV in amplitude. Polarization tests were performed from − 250 mV to + 2 V around the OCP with a scan rate of 1 mV/s.

Result and discussion

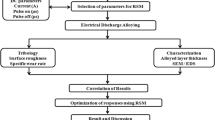
Optimization

Creation of the design matrix with response surface methodology (RSM)

Needless to say, having the best combination of process parameters would be highly beneficial for both industrial and academic purposes. To do so, in the current research, hydrogen, oxygen and Al percentage were considered to reach this aim. In addition, the four output parameters, namely elongation, UTS, YS and Icorr, were considered as fundamental to fulfill the optimization process. RSM is a method that combines mathematical and statistical evaluation of a model in order to analyze a specific process. The outputs (responses) are influenced by input parameters and the main goal of this method is to optimize or to find the optimal combination of process parameters based on the desired boundary conditions. RSM consists of two main models that are widely used in the studies and projects, namely CCD (central composite design) and Box–Behnken. The main difference between these two models is the range of selection for input parameters. The most important feature of RSM is DOE (design of experiment) which tries to find the most suitable point in which the outputs are examined.

Having determined the inputs and outputs, central composite design (CCD) approach was applied to run optimization. In the RSM approach, the values need to be sorted as the lowest, middle and highest value. In the RSM, the minimum, middle and maximum values are considered as (− 1), (0) and (1), respectively, and the alpha value has been considered as 1 in the optimization. It is worth noting that the key reason to run optimization is reducing the cost and time in the experimental test. The mentioned parameters and their considered ranges are shown in Table 1. For running test and achieving the results, a design matrix (Table 1) was set and the results are reported in Table 2.

Table 2 Design matrix and outputs
Full size table

In this stage and after collecting all data, the empirical equations for outputs are obtained. The empirical equations provide information about the relationships between outputs and process parameters.

$${\text{Elongation}} = \;{2}.0{8}0. - {27}00{\text{ A}} - 0.{16}00{\text{ B}} - 0.{66}00{\text{ C}} + 0.{1125} + {\text{ AB}} + 0.0{\text{375 AC}} + 0.0{\text{125 BC}} - 0.0{\text{591 A}} - 0.{1}0{\text{91 B}} + 0.{29}0{\text{9 C}}$$
(1)
$${\text{UTS}} = \;\; + {1231}.{98} + {13}.{9}0{\text{ A}} + {8}.{4}0{\text{ B}} + {33}.00{\text{ C}} - {6}.00{\text{ AB}} - {2}.{\text{25 AC}} - {4}.{\text{25 BC}} + {2}.0{\text{5 A}} - 0.{\text{4545 B}} + {29}.{\text{55 C}}$$
(2)
$${\text{YS}} = + {1152}.{1}0 + {11}.{2}0{\text{ A}} + {5}.{9}0{\text{ B}} + {71}.{9}0{\text{ C}}$$
(3)
$$I_{{{\text{corr}}}} = + 0.{1275} + 0.0000{\text{ A}} + 0.0000{\text{ B}} - 0.0{25}0{\text{ C}}$$
(4)

The above-mentioned Eqs. (1–4) were used to check the rate of accuracy of the models and to do this checking, ANOVA was used. Having checked the results and p values of the achieved results, the corresponding graphs are extracted. Table 3 (a, b, c, d) shows the analysis of the variance calculated through ANOVA for the outputs needed in the current research.

Table 3 Variance calculations for the analysed outputs. The data belong directly from the software ANOVA
Full size table

Figure 2 (a–d) indicates the input parameters and their effects on the respective outputs.

Figure 2
figure 2

a–d input parameters variations and their effects on the outputs (the left pictures indicate the variation, the rigth pictures indicate the comparison between the measured and predicted data)

Full size image

Effect of process parameters on UTS

Figure 3 shows the effect of the oxygen, hydrogen and aluminum content on the ultimate tensile strength (UTS). As can be seen from Fig. 3a, with the increase in the oxygen and hydrogen percentages in the alloy the UTS is slightly increased. On the other hand, Fig. 3b, c shows the combined effect of Al with O and H, respectively. With the increase in the percentage of the Al and O, the UTS significantly increased, as compared to the oxygen and hydrogen shown in Fig. 3a. Al content has a strong effect on the UTS because Al is α phase stabilizer in titanium alloys. With the increase in Al percentage, the α phase percentage increases in the Ti alloys. Anyway, the presence of a higher percentage of α phase inside the Ti alloys leads to brittleness as it will be shown in the analysis of elongation to failure of these alloys.

Figure 3
figure 3

Interaction between input a (oxygen–hydrogen), b (aluminum–hydrogen) and c (aluminum–oxygen)) and output (UTS) parameters

Full size image

Effect of process parameters on YS

Figure 4 shows the effect of the different alloying elements on yield stress (YS) of the Ti–XAl–2Fe–3Cu alloy. The main elements affecting the YS behavior are oxygen, hydrogen and aluminum. As can be seen from Fig. 4a, with the increase in the oxygen and hydrogen percentage the YS is marginally increased. The main reason for this phenomenon is due to the fact that O is α stabilizer and H is β stabilizer. However, both oxygen and hydrogen increase the brittleness of this kind of alloys. With the increase in oxygen, the α phase grows inside the Ti alloys, this leads to increase in the yield stress. Figure 4b shows the effect of H and Al content on the YS of the alloys. By enhancing H and Al percentage, the YS increased. As Al is a strong α stabilizer, the most efficient way to increase YS if the increasing of aluminum content.

Figure 4
figure 4

Interaction between input a (oxygen–hydrogen) and b (hydrogen–al)) and output (YS) parameters

Full size image

Effect of process parameters on Elongation

Figure 5 shows the effect of all the alloying elements on the elongation to failure of the Ti–XAl–2Fe–3Cu alloy. As can be seen from Fig. 5a, the elongation increased with the decrease in the O and H contents. Oxygen is an α stabilizer and with the increase in O and H in the titanium alloys, the TiO2 and TiH2 intermetallics percentages increase [20]. The development of these intermetallics leads to a decrease in the elongation to failure. Figures 5b, c shows how elongation to failure decreases as the aluminum percentage increases. Aluminum is one of the strongest α stabilizers, and α phase has an HCP structure. This structure is generally characterized by low ductility.

Figure 5
figure 5

Interaction between input a (oxygen–hydrogen), b (aluminum–hydrogen) and c (aluminum–oxygen)) and output (elongation) parameters

Full size image

Mechanical properties

The typical tensile stress–strain curves of the tensile test specimens, cut from the extruded rod of the Ti–XAl–2Fe–3Cu alloys, are shown in Figure 6. The average value of ultimate tensile strength (UTS), yield strength (YS) and percentage of elongation to fracture are given in Table 4; for comparison, the data belonging to CP-Ti, Ti–6Al–4V and Ti-5Al-2.5Fe are listed in the table. The UTS, YS and elongation percentage values of the Ti-4Al-2Fe-3Cu alloy were 1230 MPa, 1141 MPa and 2.2%, respectively, while the average UTS, YS and elongation to fracture of the Ti–2.7Al–2Fe–3Cu alloy were 1220 MPa, 1103 MPa and 2.5%. The results show that the Ti–XAl–2Fe–3Cu alloys possess relatively higher yield and ultimate tensile strengths than CP-Ti, Ti–6Al–4V and Ti-5Al-2.5Fe alloys [31].

Figure 6
figure 6

Engineering stress–strain curves of the Ti–XAl–2Fe–3Cu alloys at room temperature

Full size image
Table 4 Tensile properties of Ti–XAl–2Fe–3Cu alloys compared with the CP-Ti and other alloys
Full size table

Effect of the microstructure and different phases on mechanical properties

Figure 7 shows the optical microscopy structure of Ti–XAl–2Fe–3Cu with two different aluminum contents. Figure 7 a and b presents a typical microstructure of basket-wave morphology like the other α+β titanium alloys just similar to the commercial Ti–6Al–4V alloy characterized by transformed β phases with lamellar α phases [32,33,34].

Figure 7
figure 7

Optical micrographs of the Ti–XAl–2Fe–3Cu alloys: a Ti-2Al-2Fe-3Cu and b Ti-4Al-2Fe-3Cu

Full size image

The Ti–XAl–2Fe–3Cu alloys have a similar microstructure. The core parameters of the lamella structure, with relevant influence on the mechanical properties, are the average size of the cellular grains (dG), lamella thickness (λT) and lamella length (λL) (Fig. 8) [35]. To precisely define the effect of different Al percentage on the morphology of the phases, the size of the dG, λT and λL in 35 randomly chosen locations of the fabricated Ti–XAl–2Fe–3Cu alloys was analyzed (Fig. 8). The critical parameters in α + β titanium alloys with lamellar structure affecting the mechanical properties are cellular grains, lamella thickness and lamella length. The smaller the sizes of lamella are, the higher the material strength results [31]. The general strengthening mechanisms are related to the grain refinement strengthening, precipitation hardening, solid solution strengthening and dislocation strengthening. So, yield stress can be calculated by Eq. (5) [36]:

$$\sigma_{{\text{s}}} = \Delta \sigma_{{{\text{gb}}}} + M\left( {\tau_{{0}} + \Delta \tau_{{\text{p}}} + \Delta \tau_{{\text{s}}} + \Delta \tau_{{\text{d}}} } \right)$$
(5)

where \(\sigma_{{\text{s}}}\) is yield stress, \(\Delta \sigma_{{{\text{gb}}}}\) is grain refinement strengthening, \(M\) is Taylor factor, \(\tau_{0}\) is intrinsic critical resolved shear stress, \(\Delta \tau_{{\text{p}}}\) is precipitation hardening, \(\Delta \tau_{{\text{s}}}\) is solid solution strengthening, and \(\Delta \tau_{{\text{d}}}\) is dislocation strengthening, respectively.

Figure 8
figure 8

Schematic diagram of the fully lamellar microstructure of Ti–XAl–2Fe–3Cu alloy: dG cellular grains, λT-lamellar thickness and λL-lamellar length [35]

Full size image

The grain refinement strengthening can be calculated by the Hall–Petch relation Eq. (6) [37]:

$$\sigma = \sigma_{0} + kd^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}$$
(6)

where \(\sigma\) is yield stress, \({\sigma }_{0}\) is friction stress, \(k\) is Hall–Petch coefficient, and \(d\) is diameter of the grains, but for the current research, \(d\) was considered as average lamella thickness [8].

The lamella thickness in the alloys after heat treatment increases, and according to Eq. (6), the yield strength of the sample decreased.

The average values of these data are shown in Fig. 9. The average sizes of the dG, λT and λL in the Ti-4Al-2Fe-3Cu alloy were smaller than the Ti-2Al-2Fe-3Cu alloy, respectively.

Figure 9
figure 9

The average size of the cellular grains (dG), lamellar length (λL) and lamellar thickness (λT) of the Ti–XAl–2Fe–3Cu alloys

Full size image

Figure 10 shows the SEM images of Ti–XAl–2Fe–3Cu specimens with high magnification. The microstructure of the Ti-4Al-2Fe-3Cu has a lamellar α phase with the grain boundary of α phase and a trace of precipitation free zones inside the grain; the Ti-2Al-2Fe-3Cu alloy has a typical structure of α + β alloys with the lamellar α phase and continuous grain boundary of α phase. The microstructures of Ti-4Al-2Fe-3Cu alloy have some similarity with the Ti-6Al-5Fe-0.05B-0.05C [38] alloy; however, some segments in the structure of Ti-4Al-2Fe-3Cu alloy have a fraction of α phase, and they have lower ductility. The high strength of the new alloy can be attributed to the fine α platelets and ultra-fine α-phase precipitates as shown in Fig. 10a. During the extrusion process, most of the porosity is removed, but, as can be seen in Figs. 10a, b, a small amount of elongated pores are still present.

Figure 10
figure 10

SEM micrographs of Ti–XAl–2Fe–3Cu alloys: a Ti-2Al-2Fe-3Cu; b Ti-4Al-2Fe-3Cu

Full size image

The EDS point analysis results, in the locations shown in the SEM images in Fig. 10, are listed in Table 5. After extrusion with the Al content of 2 wt.%, the ratio of Fe content in β and α lamellar was approximately 6.52: 1.16, and increasing the Al content to 4 wt.% caused this ratio to decrease to 5.49: 1.11. On the other hand, almost all Cu atoms stayed in the β lamella and the Cu contents in the α lamella were below the detection limit of EDS.

Table 5 EDS analysis results of the as-extruded sample of Ti–XAl–2Fe–3Cu alloys
Full size table

The average size of α lamella and β phases in Ti-4Al-2Fe-3Cu is 5.2 ± 1 μm and 7.2 ± 1.4 μm, and the percentage of each phase in Ti-4Al-2Fe-3Cu is 34.51% and 65.49% as presented in Figs. 11 a and b. The average size of α lamella and β phases in Ti-2Al-2Fe-3Cu is 8.3 ± 1.1 μm and 7.6 ± 1.3 μm, and the percentage of each phase in Ti-2Al-2Fe-3Cu is 45.35% and 54.62% as shown in Fig. 11 c and d, respectively. The particle size and percentage of each phase are strongly related to the mechanical properties.

Figure 11
figure 11

Shows the aggregation of α lamellar and β phases in Ti–XAl–2Fe–3Cu a α lamellar in Ti-2Al-2Fe-3Cu; b β in Ti-2Al-2Fe-3Cu; c α lamellar in Ti-4Al-2Fe-3Cu; d β in Ti-4Al-2Fe-3Cu

Full size image

Figure 12 shows the comparison among the XRD patterns of Ti–XAl–2Fe–3Cu alloys. The XRD results of the Ti–XAl–2Fe–3Cu (X = 4, 2 wt %) alloys show that the phase constitution is a combination of both α-Ti and β-Ti phases. The intermetallic of Ti-Cu was detected, and those intermetallics have similar results as reported by Ren et al. [32] and Zhang et al. [33] for Ti-6Al–4 V-XCu and Ti-Cu alloys, respectively. They mentioned the existence of Ti2Cu phase, which increased with the increase in the Cu content. The intermetallics correlate with the mechanical property, intermetallics cause increased strength and decreased ductility. This phase is fundamental because its precipitation improves biocorrosion [34, 35, 39,40,41].

Figure 12
figure 12

XRD patterns of the Ti–XAl–2Fe–3Cu alloys

Full size image

Effect of the oxygen and hydrogen content on mechanical properties and fracture behavior

The oxygen and hydrogen contents have a direct connection with the mechanical properties. Based on Table 1, the oxygen content of the Ti-4Al-2Fe-3Cu rod was 0.3 wt%, the oxygen content of the Ti-2Al-2Fe-3Cu rod was 0.32 wt%, the hydrogen content of the Ti-4Al-2Fe-3Cu rod was 0.12 wt%, and the hydrogen content of the Ti-2Al-2Fe-3Cu rod was 0.13 wt%. Therefore, the oxygen content in rods was almost constant, but the hydrogen content in the samples is higher than standard. Hydrogen content makes Ti-2Fe-3Cu-XAl (X = 4–2.7) alloys brittle [31]. The hydrogen content in these alloys is higher than the standard of commercial titanium alloys value. This high percentage is the reason for the low ductility [31].

Figure 13 shows the fracture surfaces of Ti-4Al-2Fe-3Cu and Ti-2Al-2Fe-3Cu specimens, respectively. As can be seen in Fig. 13a, Ti-4Al-2Fe-3Cu alloy shows a combination of transgranular or brittle cleavage facets, the fracture surface presents the massive part of a cleavage structure with few microporous and dimples. Figure 13b represents the fracture surface of Ti-2Al-2Fe-3Cu. As can be seen, it has a structure similar to the Ti-4Al-2Fe-3Cu, but with more dimples and small micropores. The fracture surface of both alloys is related to the mechanical properties, demonstrating that the Ti-2Al-2Fe-3Cu is more ductile.

Figure 13
figure 13

SEM micrograph of fractured surfaces of Ti–XAl–2Fe–3Cu alloys: a Ti-2Al-2Fe-3Cu, b Ti-4Al-2Fe-3Cu

Full size image

Biocorrosion properties

Electrochemical impedance tests, carried out open-circuit potential (Eocp) after 1 h immersion, are shown in Fig. 14a. The Nyquist plot (Fig. 14a) for different values of Al in Ringer’s solution showed similar behavior which reported by other researchers for Ti alloys [42, 43]. It can be seen that the diameters of Nyquist curves of the Ti-4Al-2Fe-3Cu alloys are larger in comparison with Ti-2Al-2Fe-3Cu sample which indicates improvement on corrosion resistance. The EIS results were fitted by an equivalent circuit used in previous studies [44,45,46]. It showed that, by increasing aluminum content from 2 to 4%, the polarization resistance values increase from about 230 KΩcm2 to about 280 KΩcm2. Figure 14b compares the polarization curves of the titanium samples in Ringer’s solution. The corrosion current density estimated from these curves was 0.158 μA/cm2 for the Ti-2Al-2Fe-3Cu and 0.131 μA/cm2 for Ti-4Al-2Fe-3Cu sample. Furthermore, a clear decrease in passive current density with the increase in the Al content can be observed in all Ti- XAl-2Fe-3Cu alloys. This can be linked to the low-defects oxide layer on Ti-4Al-2Fe-3Cu alloy surface due to the addition of Al.

Figure 14
figure 14

a The Nyquist diagrams of Ti–XAl–2Fe–3Cu samples after 1-h immersion in the Ringer’s solution, b Polarization curves of the Ti–XAl–2Fe–3Cu samples in the Ringers’ solution

Full size image

Effect of process parameters on Icorr

From Fig. 15, it can be observed that the corrosion current density (Icorr) forms the polarization parameters in Ringer’s solution changing with the alloying elements. Aluminum contents have a strong effect on the corrosion resistivity of the alloys. By increasing Al content, Icorr is extremely reduced. The increase in corrosion current density reduces the corrosion resistivity. The total amount of ions released for Ti-4Al-3Fe-3Cu alloy in Ringer’s solution is lower if compared to Ti-2Al-2Fe-3Cu, hence signifying the lower toxicity of the Ti-4Al-3Fe-3Cu alloy. This can be linked to the low-defects diffusionless oxide layer on the high percentage of Al content surface due to the addition of Al. The Ti-Fe alloys have higher corrosion resistance in Hank’s solution than the CP-Ti [47]. Based on the literature, stability of the passive film is improved through the addition of iron [48].

Figure 15
figure 15

Interaction between input (hydrogen–al) and output (Icorr) parameters

Full size image

To run optimization, the range of the parameters is firstly determined. In the current research, range of used parameters was given in Table 6. To run the optimization, each parameter must have the importance and weight based on the project’s requirements.

Table 6 Weight and importance of parameters
Full size table

When the target is to find maximum [49]:

$$d_{{\text{i}}} = \left\{ {\begin{array}{*{20}c} {0\quad Y_{{\text{i}}} < {\text{Low}}_{{\text{i}}} } \\ \begin{gathered} \left( {\frac{{Y_{{\text{i}}} - {\text{Low}}_{{\text{i}}} }}{{{\text{High}}_{{\text{i}}} - {\text{Low}}_{{\text{i}}} }}} \right)^{w} \quad {\text{Low}}_{{\text{i}}} < Y_{{\text{i}}} < {\text{High}}_{{\text{i}}} \hfill \\ 1\quad Y_{{\text{i}}} > {\text{High}}_{{\text{i}}} \hfill \\ \end{gathered} \\ \end{array} } \right.$$
(7)

When the target is to find minimum [49]:

$$d_{{\text{i}}} = \left\{ {\begin{array}{*{20}c} {1\quad Y_{{\text{i}}} < {\text{Low}}_{{\text{i}}} } \\ \begin{gathered} \left( {\frac{{Y_{{\text{i}}} - {\text{Low}}_{{\text{i}}} }}{{{\text{High}}_{{\text{i}}} - {\text{Low}}_{{\text{i}}} }}} \right)^{w} \quad {\text{Low}}_{{\text{i}}} < Y_{{\text{i}}} < {\text{High}}_{{\text{i}}} \hfill \\ 0\quad Y_{{\text{i}}} > {\text{High}}_{{\text{i}}} \hfill \\ \end{gathered} \\ \end{array} } \right.$$
(8)
$$D = \left( {\prod\limits_{{{\text{i = }}1}}^{{\text{n}}} {d_{{\text{i}}}^{{{\text{r}}_{{\text{i}}} }} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sum {{\text{r}}_{{\text{i}}} } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sum {{\text{r}}_{{\text{i}}} } }$}}}}$$
(9)

The “di,” “wi,” “D” and “r” show the unique desirability of each response, weight field, desirability objective function and importance.

Once processed the data through the software, the optimal combination is extracted as shown in Table 7 and to check the accuracy of achieved results, a confirmatory test must be done.

Table 7 Desired parameters
Full size table

In Table 8, it can be seen that the achieved results are in the good correlation based on the project requirements.

Table 8 Confirmatory tests
Full size table

Conclusions

In the present research, it was tried to optimize the process parameters of Ti–XAl–2Fe–3Cu powder compact extrusion via RSM and experimental tests. Having done the microstructural analysis, the α/β lamellar structure was observed. Based on the achieved results, the size and morphology of the coarse plate-like α phase varied increasing aluminum content, and α structure became finer with the increase in the Al content. By enhancing the Al content, the YS of the Ti–XAl–2Fe–3Cu alloy increases, but its ductility slightly decreases. The key reason that supports this phenomenon is the amount of β phase. The highest percentage of oxygen and hydrogen content in Ti–XAl–2Fe–3Cu alloys reduces the ductility through the induction of a brittle cleavage structure appearing on the fracture surface. The corrosion resistivity of the Ti alloys is increased with the increase in the Al percentage. Also, oxygen and hydrogen do not have any crucial effect on the corrosion resistivity of Ti alloys [50].

Date availability

The data from this study are available from the corresponding author upon reasonable request.