Analysis of interpenetrating metal ceramic composite structures using an enhanced random sequential absorption microstructure generation algorithm

Abstract

In this paper, we present the analysis of an interpenetrating metal ceramic composite structure. We introduce a new generation algorithm for the modeling of interpenetrating composite microstructures with connected, spherical cavities embedded into an open-porous foam structure. The method uses a geometric ansatz and is designed to create structures of special topology, as the investigated metal ceramic composite structures consisting of a connected AlSi10Mg phase showing spherical shapes embedded into an Al₂O₃ preform. Based on the introduced enhanced random sequential absorption approach, the generated microstructures yield numerical insights into the material that are not accessible by experimental techniques. The generated microstructures are compared to structures reconstructed from experimental CT scan data considering microstructural features and mechanical behavior. We show that the proposed method is able to generate statistically equivalent microstructures by using only a small number of statistical descriptors. The numerical formulation is validated using compression tests including plastic yielding in the aluminum and damage progression in the ceramic phase. Both the composite material and the pure ceramic preform are considered in this analysis, and good agreement is found between reconstructed and generated microstructures. Furthermore, the observations reveal the importance of the local geometrical sphere arrangement with respect to the mechanical behavior. A validation with experimental results is presented and it is shown that the model predicts microstructural properties and gives meaningful insights into the structural and material interplay. Finally, we discuss the potential of the method for the investigation of failure mechanisms.

Introduction

The properties of a materials strongly depend on the fundamental mechanisms and features of its inner, often hierarchical structure [1]. Microstructural features may originate from the manufacturing and processing of the material (e.g., grain structure, internal domains, voids) or are part of its design (e.g., composite structures). These features can be of any size from the atomic (nanometer) scale up to the macroscopic (millimeter) scale and they have an influence on the material behavior from the chosen scale upwards [2]. Understanding the relationships between structure and properties is one of the key objectives in materials science in order to understand the materials internal processes, predict important material characteristics and design materials addressing property and performance requirements as pointed out by [3, 4].

Theoretically, closed form homogenization techniques as presented by [5,6,7] are able to predict the elastic properties of different porous and non-porous microstructures. This has been shown, e.g., by Roberts and Garboczi [8] for porous structures, by Kari [9] for particle reinforced composites and by Feng [10] and Horny et al. [11] for interpenetrating composite materials.

However, as microstructural features might change due to the mechanical or thermal loading going beyond the elastic range, in situ investigations are necessary to get profound understanding of the material behavior and its link to the underlying microstructure. Here, modeling approaches can give insights into internal processes of a material that are difficult-sometimes impossible-to gain with experimental methods. Therefore, many advancements in structure-property relations nowadays include computational materials science, especially multiscale materials modeling and computational homogenization [3, 12].

For brittle materials, going beyond the elastic range is associated with damage of the material. Various different computational approaches exist to model the fracture and damage in brittle or quasi-brittle materials in a discrete or a regularized continuum, as summarized by Rabczuk [13]. Finite element-based methods such as regularized continuum damage models [14, 15], interelement-separation methods [16, 17], techniques based on the Extended Finite Element Method (XFEM) [18], or variational concepts including phase fields [19, 20] are well suited to model discrete cracks in a consistent manner.

In order to model the damage of complex material with these methods, a proper digital representation of the microstructure is essential. In consequence, a lot of effort is made to either transfer the real microstructure of the investigated material into a computational model [11, 21,22,23,24] or to generate representative model microstructures [9, 25,26,27,28,29,30].

In this context, the term reconstruction is used with varying definitions depending on the respective community or the objective of the investigations as, e.g., shown in [2, 31, 32]. In the present paper, microstructure reconstruction is defined as the transfer of a real, physical material structure into a 3D numerical model by means of 2D imaging techniques such as X-ray computer tomography (CT) or focused ion beam combined with scanning electron microscopy (FIB-SEM), whereas the generation of representative model volumes is referred to as microstructure generation.

Especially X-ray CT has improved rapidly over the past years and is a commonly accepted tool in materials science for 3D tomography reconstruction to characterize the microstruture of a material. It can be used as a starting point for numerical modeling [32] and is well suited for materials with structural characteristics in the μm range [33]. As a high material contrast facilitates the distinction between different phases, it is preferably used for reconstructing porous or cellular materials such as foams, see, e.g., [11, 34], and different composite materials, like textiles [23], or fibre reinforced polymers, [22].

An advantage of the non-destructive X-ray CT technique is that it allows to investigate the same sample experimentally and simulatively. Wang et al. [21] and Li et al. [35] used this approach to model the damage behavior of interpenetrating SiC/Al composites under dynamic compression with volume fractions of $80\,\%$ SiC and $20\,\%$ Al. Advanced X-ray CT techniques even allow for in situ experiments as shown by Schukraft et al. [36] who investigated damage mechanisms in an Al₂O₃/AlSi10Mg interpenetrating composite with approx. $25\,$vol-$\%$ Al₂O₃. Further, these experimental techniques can be coupled with numerical investigations of the same specimen to get deeper insights into the ongoing material processes and to identify and understand the relevant mechanism as shown by Hanhan et al. [37] for a short fibre-reinforced composite.

Although microstructure reconstructions yield the most realistic geometrical description of a composite structure, they can be cumbersome due to time-consuming reconstruction and post-processing procedures as well as the fact that the structure has to physically exist. A much faster and more versatile approach is to generate microstructures and mimic the real structure as good as possible in a solely computational model. This can be done by either simulating the physical process chain that leads to the formation of the microstructure, see, e.g., [38], or by geometry-based methods that focus on the mathematical representation of the final morphology, see, e.g., [39]. A detailed review of the manifold of generation techniques is given by Bargmann et al. [2].

Geometrical generation algorithms are based on statistical descriptions and the main challenge is to meaningfully represent the geometries and distributions of all constituents (particles, pores, etc.) as well as the interfaces between them. Correlation functions, e.g., according to Torquato [25], can be used in pixel- or voxel-based approaches to create statistically equivalent representations of the real microsturcture. These structures are then used to simulate the mechanical behavior of the microstructure as shown in [26, 27]. Another approach is to describe at least one of the constituents with well-defined geometries like spheres [28], spheroids [29], or cylinders [30] and only use a reduced set of statistical descriptors such as volume fractions, size distributions, aspect ratios, and number of inclusions as an input for the generation process. This approach can lead to simple and robust algorithms, which only use closed form equations. A detailed reconstruction of the parent structure is not essentially necessary and the generation is possible even if only a small number of statistical descriptors of the desired microstructure is known. Periodicity of the structures can be incorporated easily if it is computationally favorable, e.g., for asymptotic homogenization, as shown in [29]. Further, the macroscopic mechanical behavior, as well as the damage mechanisms on the microscale, can be predicted well by geometrically generated microstructures as shown by Huang et al. [28] for cenosphere epoxy syntactic foams.

A widely used geometrical generation algorithm is the random sequential absorption (RSA) method [40] which successively places new inclusions in a pre-defined volume until a desired target fraction is reached. It classically includes a constraint avoiding an overlap of the inclusions. Thus, a continuous matrix with isolated reinforcements is generated. As a consequence of the randomized placement procedure, only relatively small volume fractions can be represented, i.e., up to about $38\,\%$ for monodisperse spheres [41]. The generation of higher volume fractions of inclusions is time consuming if not impossible.

In this paper, we present an extension of the RSA method to generate interpenetrating composite microstructures with connected, spherical inclusions. A key feature is the high volume fraction of the inclusion phase that can be considered by a formulation constraining the fully randomized sphere placement. The algorithm allows for obtaining numerical 3D models of interpenetrating microstructures without the need of an elaborated reconstruction process. It uses closed form equations and only needs basic information about the microstructure (volume fractions, size distributions) which is accessible by experimental measurements. Thus, it enables an easy and accelerated procedure for the numerical analysis of the considered example material, i.e., an Al₂O₃/AlSi10Mg composite. Based on the introduced method, we compare generated microstructures with reconstructed structures. The mechanical behavior of both the ceramic foam and the composite is studied in FEM simulations. The results are discussed in comparison with experimental investigations of the given material based on [11, 36, 42].

Microstructure reconstruction

Based on computer tomography (CT) data, we reconstruct the material microstructure to prepare it for a numerical analysis by choosing an region of interest (ROI) and subsequent segmentation, interface smoothing and meshing as described in the following.

In [11], X-ray CT scans on the ceramic preform ceramic preform cube with an edge length of $5\,$mm were conducted. Based on these CT scan images, we reconstruct and prepare the material microstructures for the numerical analysis of both the ceramic Al₂O₃ preform and as the interpenetrating Al₂O₃/AlSi10Mg composite.

The raw CT scan data consist of a stack of grayscale images, where the grayscale values depend on the density of the constituents. Beam artifacts occuring at the edge of the scanned volume are cut off by defining a region of interest (ROI) with an edge length of approx. $1.9\,$mm in the center of the scan. The ROI is chosen in a way that it represents the overall volume fractions and pore size distribution as characteristic features of the microstructure.

Then, the ROI grayscale images are segmented and transferred to a 3D array of black and white voxels representing the two components of the microstructure. Common challenges during the segmentation process as capturing different features with a low material contrast and detecting features that are close to the resolution limit are addressed by binarizing, segmenting and cleaning the images from segmentation errors according to the segmentation routine presented in [11]. The ready segmented 3D voxel reconstruction of the cubic ROI is shown in Fig. 1.

Figure 1

Reconstructued 3D microstructure ROI from binarized micro-CT scan images of the Al₂O₃ foam (white = ceramic, black = pore), see [11]

As numerical investigations of the whole ROI volume are too expensive, cubic subvolumes have been chosen randomly within the segmented ROI with the precondition to match the same volume fraction as the overall ceramic volume fraction of $30\,$%. Pre-studies have been conducted to evaluate the minimum size of an RVE based on the correct representation of microstructural geometry and volume fractions. A volume element with an edge length of $133$ μm is chosen as RVE edge length found to be a good compromise to minimize the trade-off between accuracy and computational cost. This complements the findings based on investigations on the effective elastic properties in [11]. An arbitrary example for such an RVE cutout is shown in Fig. 2. Here, only the ceramic foam is displayed to get a better insight into the interpenetrating structure and the reconstruction process.

For the composite, the porous volumes are filled with the aluminum alloy. To reduce artificial stress concentrations caused by the sharp edges of the voxel discretized microstructure in the simulation, the interface between the Al₂O₃ and the porous volume (or AlSi10Mg for the composite) is triangulated and smoothened. Therefore, the first-order Laplacian algorithm implemented in the Materialise 3-matic 14.0 software [43] is applied. Subsequently, the ceramic and the metal volume are meshed by tetrahedral finite elements for subsequent numerical investigation of the ceramic foam, as well as the Al₂O₃/AlSi10Mg composite. This is exemplarily shown in Fig. 2 for the ceramic foam containing a total of 731, 673 tetrahedral elements.

It is remarked that the CT scan was performed on the ceramic preform prior to the AlSi10Mg infiltration due to the higher material contrast between Al₂O₃ and the pores compared to the aluminum alloy. The composite is subsequently modeled with the assumption of a perfectly infiltrated ceramic foam, not taking into account possible residual pores within the aluminum or at the interface. Due to the CT scan resolution with voxels of a size around $2.6^{3}$ μm$^{3}$ also smaller pores within the delicate ceramic rods might be present but cannot be resolved. Potential pre-cracks in the Al₂O₃ phase that might have been introduced through the infiltration process are neglected in the present study.

Figure 2

Process of reconstruction from binarized 2D images to smooth 3D FEM mesh

Microstructure generation

In addition to the reconstruction, the generation of microstructures plays a significant role in analyzing microstructural behavior and in identifying fundamental mechanisms. The generation based on mathematical formulations allows for the investigation of a broad range of structural variations. This gives further insights into the behavior and the impact of individual material or geometry parameters.

For the composite material considered in this paper, the microstructure generation comprises several challenges: It consists of two components (Al₂O₃ and AlSi10Mg) with an interpenetrating (also called bi-continuous) structure, meaning that both phases are topologically interconnected throughout the whole volume. Here, the predominant shape of the aluminum phase results from connected spherical objects as described in detail in [11]. Even though the microstructure behaves homogeneously on a macroscopic scale, it is not ordered and shows randomness and heterogeneity on the microscale.

In the following, we propose a formulation for the microstructure generation that includes all functionalities and parameters to address these challenges.

Microstructure generation algorithm

Our approach is based on the random sequential absorption (RSA) method introduced by Widom [40]. We consider the pores of the ceramic foam to be perfectly spherical and create the final microstructure by sequentially adding spheres to a hexahedral volume cell. In the classical RSA algorithm, a non-overlapping condition is imposed resulting in a composite with isolated inclusions. However, to create an interpenetrating microstructure, the RSA formulation is modified with respect to the sphere placement.

The basic idea is to constrain the fully randomized sphere placement and restrict the positions for potential new spheres to certain volume areas to ensure an interconnection between both the spheres and the remaining volume. In the following, the extended RSA algorithm is described in detail.

First, an empty cell with the dimensions $L_{x}, L_{y}, L_{z}$ is initialized. The radius $r_{1}$ of the first sphere (like for any subsequent sphere) is chosen according to the defined probability density function of the sphere size distribution pdf. Characterizing the reconstructed CT data of the preform of the material considered in this paper, a generalized extreme value distribution (GEV) was found to best describe the distribution of the spherical pores, see [11], which is defined by the parameters c, loc, and scale as a function of a:

$$\begin{gathered} pdf(b,c) = \frac{1}{{scale}}\left\{ {\begin{array}{*{20}c} {\exp \left( { - \exp ( - b)} \right)\exp ( - b)} & {\quad ,{\text{for}}~c = 0} & {} \\ {\exp \left( { - (1 - cb)^{{\frac{1}{c}}} } \right)(1 - cb)^{{\frac{1}{{c - 1}}}} } & {\quad ,{\text{for}}~b \le \frac{1}{c},c} & { > 0} \\ \end{array} } \right. \hfill \\ {\text{with}}~b = \frac{{a - loc}}{{scale}}{\mkern 1mu} \hfill \\ \end{gathered}$$

(1)

Sphere 1 is placed at a random position $\varvec{p}_{1}$ within a cuboid of $L_{x}/2 \times L_{y}/2 \times L_{z}/2$ at the center of the cell to incite a homogeneous sphere distribution throughout the whole volume.

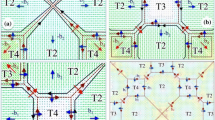
The second sphere is placed randomly within a certain distance range $d_{min} \ldots d_{max}$ around sphere 1 as shown in Fig. 3a (grey area). The position $\varvec{p}_{2}$ of sphere 2 can be calculated by making use of polar coordinates and randomly choosing the two angles $\theta$ and $\phi$ as well as the distance d:

$$\begin{aligned} \varvec{p}_{2} = \varvec{p}_{1} + d \begin{bmatrix} \sin {\theta } \cos {\phi } \\ \sin {\theta } \sin {\phi } \\ \cos {\theta } \\ \end{bmatrix} \quad , \text {with} \begin{array}{l} d \in [d_{min}; d_{max}] \\ \theta \in [0; 2\,\pi ] \\ \phi \in [0;\pi ] \end{array} \end{aligned}$$

(2)

The distances $d_{min}$ and $d_{max}$ depend on the radii $r_{1}$ and $r_{2}$ of the spheres involved and the overlap parameters $ovl_{min}$ and $ovl_{max}$ in order to ensure the interpenetrating character of the microstructure but avoiding small spheres to be placed fully within large sphere:

$$\begin{aligned} \begin{aligned} d_{min} = max\{r_{1}, r_{2}\} + (1-ovl_{max}) \cdot min\{r_{1}, r_{2}\} \\ d_{max} = max\{r_{1}, r_{2}\} + (1-ovl_{min}) \cdot min\{r_{1}, r_{2}\} \end{aligned} \end{aligned}$$

(3)

Starting from sphere 3, the sphere placement strategy is defined by the parameters $n_{min}\in \{1,2,3\}$ and bias (Boolean). Before adding the new sphere, one of the already existing old spheres within the spherelist is randomly chosen. In the most simple case of $n_{min}=1$, the new sphere is placed randomly around the old sphere as given in Eq. (2). This is shown exemplary in Fig. 3b for a third sphere which might be placed in the gray marked areas around sphere 1 ($p_{3}'$) or sphere 2 ($p_{3}''$) depending on which of the two spheres have been chosen initially.

Using $n_{min}=2$, one random neighbor of the picked old sphere is additionally taken into account and the new sphere can only be placed in the (blue marked) areas where it overlaps with both of them (e.g., $p_{3}'''$). Similarly, a new placed sphere overlaps with three existing spheres if $n_{min}=3$ (this can not be visualized in the simplified 2D scheme).

With $bias = True$, the number of random picks for each sphere is tracked and used as a bias for subsequent picks. The probability of choosing a specific sphere correlates with the inverse of this number in order to get a spatially homogeneous distribution of spheres.

Figure 3

Simplified 2D scheme of the modified random sequential absorption (RSA) algorithm with spheres of constant radius. a The fist sphere with radius $r_{1}$ is placed at position $p_{1}$ in the center quarter of the cell. The second can be placed at a certain distance range $d_{min} \ldots d_{min}$ around sphere 1 (marked in gray). b A third sphere can either intersect with the first ot the second sphere ($p_{3}'$, $p_{3}''$) when placed in the gray marked area or with both of them ($p_{3}'''$) if placed in the blue area. The probabilities of $p_{3}'$, $p_{3}''$ and $p_{3}'''$ can be specified

Admissibility checks are performed once the new position of the (i-th) sphere is defined. The distance $d_{ij}$ to all of the other spheres is calculated and the acceptable distance range $d_{min}<d_{ij}<d_{max}$ is checked according to Eq. (3) by replacing the indices $r_{1} \xrightarrow {} r_{i}$ (i = index of new sphere), $r_{2} \xrightarrow {} r_{j}$ (j = index of sphere from spherelist) and iterating over all j. Note that, the distance calculation differs for periodic and non-periodic microstructures (see Appendix A).

It is prescribed that a minimum distance for non-overlapping spheres

$$\begin{aligned} d_{non-ovl} \ge (1+dist_{min})(r_{i}+r_{j}) \end{aligned}$$

(4)

must be maintained in order to avoid very delicate geometries and to reduce subsequent meshing difficulties. For the same reason, an overlap check of the spheres with the cell boundaries is conducted. Spheres cannot be positioned at a defined distance range to the cell borders which avoid very small spherical cap cutoffs. Therefore, $\mathbf {p}_{i} = [p_{i}^{x}, p_{i}^{y}, p_{i}^{z}]^{\text {T}}$ can be anywhere inside the cell, except for

$$\begin{aligned} \begin{aligned} (1-ovl_{cell})\,r_{i} \nleq p_{i}^{k} \nleq r_{i} \\ L_{k}-(1-ovl_{cell})\,r_{i} \ngeq p_{i}^{k} \ngeq L_{k}-r_{i} \end{aligned} \quad , \text {for each}~k \in \{x,y,z\} \end{aligned}$$

(5)

with the cell overlap parameter $ovl_{cell}$ and the cell dimensions $\mathbf {L~}=~[L_{x}, L_{y}, L_{z}]^{\text {T}}$. In the case of non-periodic microstructures, ($periodic == False$) also sphere position $\mathbf {p}_{i}$ outside of the cell are allowed:

$$\begin{aligned} \begin{aligned} -(1-ovl_{cell})\,r_{i} \le p_{i}^{k} \le 0 \\ L_{k}+(1-ovl_{cell})\,r_{i} \ge p_{i}^{k} \ge L_{k} \end{aligned} \quad , \text {for each}~k \in \{x,y,z\} \end{aligned}$$

(6)

If any of the admissibility checks from Eqs. (4), (5) (6) is not passed, the sphere gets rejected and a new sphere placement is initialized. Otherwise, the volume of the sphere, that is added to the cell, has to be calculated.

While this volume can be easily determined for a sphere without overlaps placed fully inside the cell $V_{sphere}=\frac{3}{4}\pi r^{3}$, we further have to consider the intersection volume with other spheres. In the case of non-periodic microstructures, additionally, the volume cut off by the cell boundaries must be taken into account making the evaluation more difficult than for periodic ones. Sphere overlap and cell boundary overlap calculations are based on the volume of a spherical cap which results from a cut of the sphere with a plane

$$\begin{aligned} V_{cap} = \frac{\pi }{3} h^{2} \left( 3r-h\right) \,. \end{aligned}$$

(7)

Here, h is the height of the cap according to [44]. For the intersection of a sphere with a (plain) cell boundary, the determination of h is straightforward, but also the overlap volume of two intersecting spheres i and j can be expressed analytically. Here, the cap height $h_{i}$ of sphere i which is located at a distance d to sphere j can be described with

$$\begin{aligned} h_{i}(i,j) = r_{j}-\frac{(r_{j}^{2}-r_{i}^{2}+d^{2})}{2d}\,. \end{aligned}$$

(8)

Subsequently, the intersection volume of the two spheres is the sum of the respective spherical caps combining Eqs. (7) and (8). Summing over all neighbor spheres $j=1 \dots \,n$ that intersect with sphere i yields the intersection volume

$$\begin{aligned} \begin{aligned} V_{i,\,intersect}&= \sum _{j=1}^{n} V_{i,\,cap} + V_{j,\,cap} \\&= \sum _{j=1}^{n} \frac{\pi }{3} h_{i}^{2}\left( 3r_{i}-h_{i}\right) + \frac{\pi }{3} h_{j}^{2}\left( 3r_{j}-h_{j}\right) \,. \end{aligned} \end{aligned}$$

(9)

This is the volume already occupied by other spheres, when placing the new sphere i at position $\mathbf {p}_{i}$. For periodic microstructures, this volume is subtracted from the total sphere volume to get the newly added volume $V_{i,add}~=~V_{i,sphere}-V_{i,intersect}$.

For non-periodic structures, the cutoffs at the cell boundaries have to be taken into account as well. First, we have to determine with which of the six cell faces the sphere is in contact with, i.e., where the distance of the sphere to the cell boundary is smaller than its radius. Overlaps are tracked in an simple boolean array ($x_{min},~x_{max},~y_{min},~y_{max},~z_{min},~z_{max})$ where the entry values are equal 1 if the sphere intersects with the respective cell boundary and 0 otherwise. For each intersection, we have to compute the height of the overlap $\delta$ and further distinguish between the different overlap cases depending on total number of sphere/cell face overlaps $n_{\delta }~(\le 3)$ in order to compute the volume of the sphere remaining inside of the cell [45]. The following cases are considered:

• $n_{\delta }=0$: no cell overlaps

In this case, the sphere volume inside the cell is equal to the total sphere volume $V_{in}=V_{sphere}=\frac{3}{4}\pi r$.

• $n_{\delta }=1$: overlap with a single face

The volume of the cutoff by the cell face $V_{face}(\delta )$ can be calculated with the formula for the spherical cap according to Eq. (7), with a cap height $h=\delta$. An alternative, dimensionless form to calculate $V_{face}$ is given in the Appendix B. The volume of the sphere remaining inside the cell $V_{in}$ is given as

$$\begin{aligned} V_{in} = V_{sphere} - V_{face}\,. \end{aligned}$$

(10)

• $n_{\delta }=2$: overlap with two faces

Two face volumes $V_{face}(\delta _{1})$, $V_{face}(\delta _{2})$ and an edge volume $V_{edge}(\delta _{1}\, \delta _{2})$ depending on the distances to the two cell faces $\delta _{1}$, $\delta _{2}$ and the sphere radius r need to be considered. See Appendix B for the mathematical expression of $V_{edge}$. The sphere volume in the cell can then be calculated as

$$\begin{aligned} V_{in} = V_{sphere} - \sum V_{face} + V_{edge}\,. \end{aligned}$$

(11)

• $n_{\delta }=3$: overlap with three faces

In this case, three face volumes $V_{face}(\delta _{1})$, $V_{face}(\delta _{2})$, $V_{face}(\delta _{3})$, three edge volumes $V_{edge}(\delta _{1},\, \delta _{2})$, $V_{edge}(\delta _{1},\, \delta _{3})$, $V_{edge}(\delta _{2},\, \delta _{3})$ and the corner volume $V_{corner}(\delta _{1},\,\delta _{2},\,\delta _{3})$ have to be determined in order to calculate $V_{in}$. The equation to determine $V_{corner}$ is given in Appendix B.

$$\begin{aligned} V_{in} = V_{sphere} - \sum V_{face} + \sum V_{edge} - V_{corner}\,. \end{aligned}$$

(12)

With the volume $V_{i,in}$ of sphere i inside the cell, that is calculated in Eqs. (10), (11), (12) (depending on the position $\mathbf {p}_{i}$ and radius $r_i$) and the intersection volume $V_{i,intersect}$ from Eq. (9), the volume added to the cell in the non-periodic case can be determined with

$$\begin{aligned} V_{i,\;add} = V_{i,\;in} - V_{i,\;intersect}\,. \end{aligned}$$

(13)

Subsequently, an estimate of the volume fraction including the new sphere i using $estimate = fraction + V_{i,add}/V_{cell}$ is calculated. If the estimate volume fraction exceeds the target fraction plus tolerance, the sphere is rejected and a new sphere placement in initialized. Otherwise, the sphere is added to the spherelist and the current fraction is updated by the value of estimate. The procedure is repeated until the targeted volume fraction has been reached within defined tolerances. For a better visualization, the described overall algorithm is illustrated in Algorithm 1. The involved parameters are listed and described in Table 1.

Table 1 Input parameters for the modified RSA algorithm

Finite element modeling

To investigate and compare the reconstructed and generated microstructures numerically with respect to the mechanical behavior, FE-models of the structures were set up. The transfer of CT-scan reconstructions to a FE-meshes has been described in Sect. 2. For the generated microstructures, the information about the cell dimensions and the sphere arrangement stored in the spherelist output of Algorithm 1 was used together with the constructive solid geometry and meshing capabilities of Abaqus/CAE [46] software in order to create the model geometry.

Constitutive models

Al₂O₃ ceramic

We want to analyze the mechanical response of the foam and the composite under compressive load. With respect to material damage modeling, a main challenge is, that we do not know where damage initiates and propagates in advance. Thus, interelement-separation techniques are not suited for the problem. As the mesh of the complex microstructures already contains about one million elements (and more) and XFEM and variational approaches would need further mesh refinement along the crack paths, this is challenging for the considered microstructure. Therefore, we optimize between accuracy and computational efficiency and incorporate a regularized continuum damage model following the ficticious crack model of Hillerborg et al. [14] and the crack band model of Bažant and Oh [15].

A multi-directional fixed smeared cracking assumption according to [47] accounts for the brittle damage behavior of the Al₂O₃. Up to failure, linear elasticity is assumed.

The constitutive model for the ceramic phase is given as follows. First, the total strain rate $d\varepsilon$ is decomposed by

$$\begin{aligned} d\varvec{\varepsilon } = d\varvec{\varepsilon }^{el} + d\varvec{\varepsilon }^{ck} \end{aligned}$$

(14)

into elastic $d\varvec{\varepsilon }^{el}$ and cracking strain rates $d\varvec{\varepsilon }^{ck}$ in order to correctly represent the state of the damaged solid. In the elastic regime, before the initiation of damage, ${\varepsilon }^{ck}=0$ is assumed.

To detect the onset of cracking, a simple yet effective stress-based Rankine crack initiation criterion is chosen (see Fig. 4). Once the maximum principle tensile stress $\sigma _{1}$ exceeds the tensile strength of the material $\sigma _t^{I}$, the first crack has formed. A local orthonormal coordinate system (1, 2, 3) is introduced that aligns with the crack, i.e., the local 1-axis is the crack plane normal and the local 2- and 3-axis lie in the crack plane. The global strains $\varvec{\varepsilon }\,(x,y,z)$ can be transformed into the local coordinate system by a transformation matrix $\varvec{T}$ reading $\varvec{\varepsilon }\,(x,y,z)=\varvec{T}\,\varvec{\epsilon }\,(1,2,3)$. The same transformation holds for the global and local stresses $\varvec{\sigma }$ and $\varvec{\tau }$, respectively.

The local coordinate system and the transformation matrix $\varvec{T}$ are fixed at the time when the first crack occurs (see Appendix C for an example of $\varvec{T}$). Subsequent cracks can only form orthogonal to the first one leading to a maximum of three cracks per material point in a 3D configuration. The cracking condition can be written as

$$\begin{aligned} \tau _{ii} - \sigma _t^{I}\left( \epsilon _{ii}^{ck}\right) = 0 \quad \text {and} \quad \tau _{ij} - \sigma _s^{II}\left( \epsilon _{ij}^{ck},\epsilon _{ii}^{ck},\epsilon _{jj}^{ck}\right) =0 \end{aligned}$$

(15)

for Mode I and Mode II opening, respectively. No Einstein summation for the indices i and j is applied in Eq. (15)

The relations between local stresses and local strains are given in incremental form by

$$\begin{aligned} d\varvec{\tau } = \varvec{D}\,d\varvec{\epsilon }^{ck} \end{aligned}$$

(16)

with the diagonal cracking or damage matrix $\varvec{D}$ containing the secant stiffness (or damaged elasticity) values for tensile and shear components. Using the elasticity condition $d\varvec{\sigma }=\varvec{C}\,d\varvec{\varepsilon }$ with the elsatic stiffness matrix $\varvec{C}$ and Eq. (14), this can be re-written in the incremental stress-strain relation

$$\begin{aligned} d\varvec{\sigma } = \left[ \varvec{C}-\varvec{C}\varvec{T}\,\left( \varvec{D}+\varvec{T}^{T}\varvec{C}\varvec{T}\right) ^{-1}\,\varvec{T}^{T}\varvec{C}\right] \, d\varvec{\varepsilon }. \end{aligned}$$

(17)

Following the idea of Hillerborg et al. [14], the fracture energy $G_{f}^{I}$ required to from a unit crack area is a material property and can be calculated from the crack opening $du_{i}$ according to

$$\begin{aligned} G_{f}^{I} = \int \sigma _t^{I}\,du_{i} \, . \end{aligned}$$

(18)

Regularizing the crack strain by a characteristic length $l_{c}$ reading $u_{i}^{ck} = \varepsilon _{ii}^{ck}\,l_{c}$ allows us to rewrite the tension softening $\sigma _t^{I}(\epsilon _{ii}^{ck})$ in Eq. (15) as a stress-displacement relationship in order to use the fracture energy $G_{f}^{I}$ as a physical input parameter. Here, a linear softening as shown in Fig. 5a is assumed. The displacement, at which the materials shows no residual stiffness $u_{i,0}$, depends on the fracture energy and the tensile strength of the alumina. To avoid non-physical element distortions due to the applied compressive loads, elements are deleted after reaching zero stiffness at a relative displacement of $u_{i,0}$.

The Mode II shear-softening behavior shown in Eq. (15) depends on both the local shear strain $\epsilon _{ij}^{ck}$ and the amount of crack opening in the normal directions $u_{ii}^{ck}$ and $u_{jj}^{ck}$. In this case, the relation between local stresses and local strain is

$$\begin{aligned} \tau _{ij} = D_{ij}\left( u_{ii}^{ck},u_{jj}^{ck}\right) \epsilon _{ij}^{ck}. \end{aligned}$$

(19)

The damaged stiffness $D_{ij}$ can be expressed in form of a fraction of the shear modulus G as $D_{ij}=\alpha (u_{ii}^{ck},u_{jj}^{ck})\,G$. The factor $\alpha \rightarrow \infty$ before crack initiation and $\alpha \rightarrow 0$ in case of the fully damaged case. Fig. 5b shows the bilinear shear-retention model used in this study. Here, $\rho$ represents the shear retention factor $\rho =\alpha /(1+\alpha )$.

Figure 4

Rankine failure criterion a and coordinate system transformation after crack initiation b

Figure 5

Post-failure Mode I stress-displacement behavior a and Mode II shear retention b

A summary of the material input parameters for the alumina constitutive model is given in Table 2.

AlSi10Mg aluminum alloy

The AlSi10Mg aluminum alloy is modeled using an elasto-plastic material behavior with $J_{2}$ plasticity and isotropic hardening. The yield surface

$$\begin{aligned} f(\varvec{\sigma }, k) = \varvec{\bar{\sigma }} - k = 0 \end{aligned}$$

(20)

is defined by the equivalent stress $\varvec{\bar{\sigma }}=\sqrt{3\,J_{2}}$ and the yield stress k with the second invariant of the stress tensor $J_{2}=(\varvec{\sigma '}:\varvec{\sigma '})/2$ and the stress deviator $\varvec{\sigma '}=\varvec{\sigma }-tr\,(\varvec{\sigma })/3$. The associated flow with a rate independent Swift hardening law [48] is given by

$$\begin{aligned} k(\varvec{\bar{\varepsilon }}_{pl}) = A\left( \varvec{\bar{\varepsilon }}_{pl}-\varepsilon _{0}\right) ^{n}. \end{aligned}$$

(21)

It describes the yield stress k as a function of the equivalent plastic strain $\varvec{\bar{\varepsilon }}_{pl}$ and the hardening parameters $\{A,\varepsilon _{0},n\}$. All involved constitutive parameters are summarized in Table 2. It is remarked that no damage model is considered for the aluminum alloy.

Table 2 Material input parameter. Tensile strength $\sigma _t^I$ and yield strength $\sigma _y$ are uniquely defined for the Al₂O₃ and the AlSi10Mg, respectively. Yield strength $\sigma _y$ corresponds to yield stress at zero plastic strain $k(\varvec{\bar{\varepsilon }}_{pl}=0)$

Figure 6

Compression simulation boundary conditions. Frictionless contact $\mu =0$ was assumed between the investigated structure and the rigid plates on top (moving) and on the bottom (fixed). Same boundary conditions have been used for the ceramic foam and the MMC

Boundary conditions

We model compression tests of the ceramic foam, as well as the interpenetrating composite material by meshing the considered structures as described in Sect. 2. With the algorithm proposed in Sect. 3, periodic, as well a s non-periodic, structures can be generated. The consideration of periodic structures can be advantageous, e.g., for asymptotic homogenization matters in conjunction with periodic boundary conditions. However, in this study, we choose non-periodic structures and boundary conditions as reconstructed microstructures do not show a periodic geometry. Further, the damage of the complex microstructure is not considered to occur in an periodic manner.

As shown in Fig. 6, we apply a compressive load by rigid plates on top (moving) and on the bottom (fixed). This mimics the experimental test conditions described in [36] and [42]. We assume that the friction between the plates and the material is negligible (friction coefficient $\mu = 0$) and that the alumina and aluminum phases are perfectly tied at the interface. The latter simplifying assumption is based on the experimental results in [11] that show the excellent infiltration quality accomplished for the given composite with almost no residual porosity, especially at the alumina/aluminum interface. Investigations on the load transfer in similar structures showed firmly/materially bonded interfaces as presented, e.g., in [49, 50]. Analogously to other studies, e.g., [21, 51], we therefore assume a perfectly bonded interface knowing that we probably overestimate the stiffness or strength of the composite. The volume elements are compressed under displacement control in y-direction up to a total nominal strain of $6\,$%. The applied strain rate is approximately $1.2 \times 10^{-1}$. This is higher than in the experiments [36, 42], but, since only rate-independent constitutive models have been used, this has no influence on the comparability of the results. The simulations are performed with the Abaqus/Explicit solver [46] using an explicit central difference time integration scheme .

Figure 7

Sphere size distribution in the CT-scan ROI of the microstructure as described in [11]. The distribution function is used as an input for the microstructure generation algorithm

Results

Microstructure generation

The CT-scan reconstruction of the ROI shown in Fig. 1 has been analyzed regarding the sphere size distribution of the interpenetrating microstructure according to the procedure shown in [11]. The resuling sphere size distribution is given in Fig. 7. A probability density function can be derived according to Eq. (1) for the probability function of the sphere sizes.

Figure 8

Comparison of the $1-R^{2}$ error between input and output pore size distribution depending on the edge length of the volume element (left) as well as depending on the number of spheres $n_{spheres}$ placed in the volumen element (right)

The analysis shows that a general extreme value (GEV) distribution with the parameters $c=-0.413$, $loc=7.993$, $scale=5.087$ is best suited to describe the sphere distribution of the microstructure. These parameters were then chosen as input for the generation algorithm as shown in Table 1. In order to determine the minimum size of a statistically equivalent volume element, microstructures with cell edge lengths varying between $50 and 290$ μm have been studied considering steps of $30$ μm in the cell edge length. The input y and output $\hat{y}$ probability density functions have been compared and the error $1-R^{2}$ between the functions over the edge length of the volume element (VE) as well as the number of spheres $n_{spheres}$ is shown in Fig. 8.

In this context, $R^{2}$ is the coefficient of determination defined by

$$\begin{aligned} R^{2}(y, \hat{y}) = 1 - \frac{\sum _{i=1}^{m}\left( y_{i}-\hat{y}_{i}\right) ^{2}}{\sum _{i=1}^{m}\left( y_{i}-\bar{y}\right) ^{2}}\,. \end{aligned}$$

(22)

Here, $R^{2}=1$ means that the input and output probability density function are identical, $y_{i}$ is the i-th value of the input function and $\hat{y}_{i}$ is the i-th value of the output distribution. The mean input value is given by the normalized sum of m discrete values of the input distribution reading $\bar{y}=\frac{1}{m} \sum _{i=1}^{m} y_{i}$.

We evaluate the coefficient of determination by comparing the continuous input and output distribution functions at a total of $m=1000$ discrete values which are regularly distributed over the input and output distributions, respectively. The residual sum of squares $\sum _{i=1}^{m}(y_{i}-\hat{y}_{i})^{2}$ is then divided by the total sum of squares $\sum _{i=1}^{m}(y_{i}-\bar{y})^{2}$ as shown in Eq. (22)

We choose $1-R^{2}$ as a measure to quantify the error between the input and output distribution functions rather than the accordance $R^{2}$ between them. Thus, a value equal zero indicates the best possible match. It can be observed that a the error $1-R^{2}$ and the scattering reduces for increasing volume elements. For VEs larger than $120$ μm, the input and output distributions are in good accordance showing an error of $1-R^{2} < 2\,\%$. For VEs with an edge length $\ge 260$ μm, the error reduces below $1\,\%$.

The data points given in Fig. 8 (left) are displayed again in Fig. 8 (right) related to the number of placed spheres $n_{spheres}$. Here, the markers show the size of the respective volume element. Naturally, $n_{spheres}$ correlates with the edge length of the volume element, as a higher number of spheres can be placed in a larger volume element. As the choice of the sphere radius from the distribution function of possible sphere radii and the placement is randomized, it shows a more contiuous distribution of values along the x-axis. The error $R^{2}-1$ shows values of $<2\,\%$ for $n_{spheres}>150$ and converges to zero for a number of spheres $n_{spheres}>500$.

Figure 9

Reconstructed (left) and generated (right) volume elements with an edge length of $290$ μm. Only the ceramic part is displayed

A qualitative comparison of a generated microstructure with a given edge length of $290^{3}\,$ μm³ of the volume element with a reconstructed volume element of the same size is given in Fig. 9. For a better insight into the 3D-interpenetrating structure, only the ceramic phase is displayed.

Figure 10

Median neighboring sphere size versus sphere radius of the reconstructed and the generated microstructures. The figure shows the median neighbor sphere radius for each of the 10 equally sized bins extracted from the global size distribution. The different marker types represent three example volume elements investigated for reconstructed and generated microstructures, respectively

Isotropy is another key feature of the investigated material that should be covered by the generation algorithm. Therefore, generated microstructures have been investigated with statistical correlation descriptors according to Torquato [25] and exemplary results are shown in Appendix D. As shown in Fig. 13, isotropy can be assumed for the generated microstructures considering volume elements with an edge length of $133$ μm used in the compression simulations.

Local arrangement of spheres

Stress concentrations in the ceramic are significant for the onset of damage. As they originate from the local geometrical composition of the microstructure, not only the overall distribution of spheres within the volume but also the local arrangement of spheres might be of importance. Analyzing the the correlation of sphere size to the size of their neighboring pores in the microstructures leads to the results shown in Fig. 10. Here, the median neighbor sphere sizes are plotted over the sphere size (mean value of the bin) for both the reconstructed and generated microstructures. For each sphere, we first determine all spheres that are in direct contact or overlap with it, further called neighbor spheres. Then, we divide the spheres into 10 equally sized bins according to their radius. For each bin, we calculate the median size of all neighbor spheres related to the bin as an indicator for the neighborhood of a certain sphere size group.

In the case of the reconstructed microstructures, three randomly chosen sub-volumes with an edge length of $532$ μm are chosen for the analysis. This size of the volume has to ensure the statistical equivalence of the sphere size distribution compared to the whole ROI volume. Furthermore, boundary effects shall be minimized, as sphere sizes are underestimated if the sphere is cut by the boundary. For all investigated sub-volumes, a clear correlation between median neighboring radius and sphere radius can be observed as the median neighbor radius decreases with increasing pores size.

Regarding the generated microstructures, four different volume elements with an edge length of $200$ μm are analyzed. Based on the results in Fig. 8, here, this volume size is chosen as optimum of computation time and smallest statistical error in the analysis. It can be observed that-in contrast to the reconstructed microstructures-no correlation between median neighboring radius and sphere radius occurs in the generated structures. For the generated microstructures, the median neighboring sphere size varies randomly with the sphere size itself.

Figure 11

a Compressive stress-strain behavior of the reconstructed (red solid) and the generated microstructures (blue dashed) compared to experimental results (gray area) of the Al₂O₃ foam. bMaximum principal stress $\sigma _{1} > 150~\text {MPa}$ at a compressive strain of $\varepsilon _{yy} = 0.1 \%$ and damaged Al₂O₃ foams at a of strain of $\varepsilon _{yy} \ge 0.3$ for reconstructed (left) and the generated (right) examplary microstructures, respectively

Compression simulations

Compression simulations have been performed on both reconstructed and generated composite microstructures as well as the ceramic foams. Based on the boundary conditions and constitutive models described in "Finite element modeling" section, simulations of cubic VEs with an edge length of $133$ μm were chosen for the investigations. Pre-studies on the compression behavior have shown that the minimum representative size is mainly connected to the correct representaion of microstructural characteristics, i.e., geometries and volume fractions. Therefore, only microstructures with the same volume fractions have been investigated in the analyses. Studies on volume elements with double the size showed similar qualitative results with a slight tendency of smaller compressive strengths. Although the statistical investigations on the volume size suggest a slightly larger volume element as optimum, the measured error between input and output sphere distribution functions with $<2\,\%$ is decently small for VEs $>120$ μm, cp. Fig. 8. This is also supported by findings of a previous study of the authors given in [11], which shows good results for the determination of the effective elastic properties of a representative volume element using an edge length of at least $133$ μm. Despite the fact that RVE sizes for elastic and damage modeling usually do not coincide (i.e., $RVE\,(elastic) < RVE\,(damage)$ [52, 53], the considered system size is chosen to optimize the trade-off between accuracy and simulation time. In order to show the capabilities of the generation algorithm, a smaller VE size is considered reasonable.

For the reconstructed VEs, we again randomly choose the volumes within the CT-scan avoiding the boundary regions of the ROI. The ceramic fraction of the VEs is restricted to $30\,\%$ as according to [11] the correct volume fractions are an essential feature to meet the RVE conditions. In order to capture the variety of geometrical configurations that might occur in larger volumes, we displayed five different simulation results representing a statistical range for both reconstructed and generated microstructures. Simulation results for both the ceramic foam structure and the composite material are shown in Figs. 11 and 12, respectively. For both reconstructed and generated structures, five simulations results are displayed showing the statistical range for both structure types.

As it can be observed in Fig. 11a, the ceramic foam shows a linear followed by nonlinear behaviour in the stress-strain curves for strains up to the point of global failure. This behavior is observed for the generated, as well as the reconstructed, microstructures. Only one of the generated microstructures shows an almost linear behavior up to the compression strength and macroscopic failure. The elastic elastic moduli of $18-35\,$GPa for generated and $21-30\,$GPa for reconstructed microstructures are in good agreement with experimental fingings, where the stiffnes varies within $23-28\,$GPa.

Generated structures show compressive strengths of $45-69\,$MPa with failure strains of $\varepsilon = 0.2-0.35\,\%$. The compressive strength of reconstructed structures varies between $50 and 70\,$MPa occuring at strains of $\varepsilon = 0.25-0.35\,\%$. Both structure types are within the boundaries of experiments where a compressive strength between $30\,$MPa and $70\,$MPa for the foam is found.

Contour plots of the maximum principal stress $\sigma _{1}>150\,$MPa within example microstructures at a total strain of $\varepsilon _{yy} = 0.1\,\%$ and at a strain just after the macrosopic failure of the material are depicted in Fig. 11b. Stress concentrations can be observed preferably on top and on bottom of the spherical pores, especially in thin ceramic rods. These locations can also be identified for the initiation of damage causing the final failure of the foam structure. The final damage pattern for the reconstructed and the generated microstructures is shown in Fig. 11b (bottom) for strains higher than the maximum compression strength, i.e., $\varepsilon _{yy} > 0.3\,\%$.

For the interpenetrating composite, the results are shown in Fig. 12. The simulated stress-strain curves of five generated and reconstructed microstructures are displayed together with experimental data according to [36, 42] in Fig. 12a. Compared to the ceramic foam, the compressive stresses are a factor 10 higher and the strains at the compressive strength is 4-5 times larger. For the simulated structures, a linear elastic regime can be observed with that is followed by a nonlinear behavior. After reaching the compression strength, the stress drops and runs out into a plateau of residual strength. Comparing the different simulation results, the effective elastic properties with a elastic modulus of approx. $120\,$GPa are almost identical for all structures. Deviations between the different volume elements start at the end of the linear range at a macroscopic stress of approx. $270\,$MPa. For both reconstructed and generated microstructures, the compression strength is reached at a strain of approx. $1\%$ and varies between 400 and $580\,$MPa.

In the softening regime, slight differences between the individual VEs can be observed as some structures show a smooth asymptotic stress decrease whereas others reveal multiple, more pronounced drops followed by intermediate plateaus. Nonetheless, all structures tend to a level of residual strength between 250 and 350 MPa. Both reconstructed and generated composite microsturctures show results comparable to experimental findings, however, they exhibit an increased compression strength.

The contour plots of the maximum principal stress distributions with $\sigma _{1}>150\,$MPa within the ceramic phase of two example microstructures at a total strain of $\varepsilon _{yy} = 0.3\,\%$ as well as the equivalent plastic strain $\bar{\varepsilon }_{pl}>5\,\%$ in the AlSi10Mg phase at a total strain of $\varepsilon _{yy} = 3.5\,\%$ are shown in Fig. 12b. It can be observed that the principal stresses in the Al₂O₃ phase of the composite are distributed along the interface to the aluminum. No characteristic locations of stress concentrations can be determined. Considering a strain of $\varepsilon _{yy} = 3.5\,\%$, the overall behavior depends mainly on the metal phase. Here, the reconstructed as well as the generated microstructure shows an accumulation of plastic strain in a $45^{\circ }$ angle to the compression direction.

Figure 12

a Compressive stress-strain behavior of the reconstructed (red solid) and the generated microstructures (blue dashed) compared to experimental results (gray area) of the Al₂O₃ / AlSi10Mg interpenetrating composite. b Maximum principal stress $\sigma _{1} > 150~\text {MPa}$ within the Al₂O₃ phase at a compressive strain of $\varepsilon _{yy} = 0.3\,\%$ and plastic equivalent strain $\bar{\varepsilon }_{pl} > 5~\%$ within the AlSi10Mg phase at a compressive strain of $\varepsilon _{yy} = 3.5\,\%$ for reconstructed (left) and the generated (right) examplary microstructures, respectively

Discussion

We introduced a formulation for the generation of 3D foam structures as well as interpenetrating composites. The generated microstructures have been compared with reconstructed microstructures and evaluated in comparison with experimental results. It has been found that the proposed generation algorithm is able to create interpenetrating foam and composite structures with high volume fractions up to $70\,\%$ using an purely geometrical ansatz. Real microstuctures can be reproduced successfully regarding volume fractions and sphere size distribution starting from VEs with an edge length of about $120-140$ μm showing an error of less than $2\,\%$ (see Fig. 8). This result emphasizes previous investigations on an Al₂O₃-foam and Al₂O₃/AlSi10Mg composite RVEs for effective elastic properties shown in [11] and indicates that a sufficiently large CT-scan ROI has been chosen for this analysis.

Based on these investigations, compression simulations have been performed on reconstructed as well as generated microstructures with volume elements of $133$ μm edge length. This coincides with 50 voxels of the CT-scan reconstructions. For the FEM model, linear elasticity with a Rankine damage criterion and linear softening behavior is applied to the ceramic. For the aluminum, an elasto-plastic behavior with isotropic Swift hardening parametrized by experimental investigations is used. It is found that the overall stress-strain behavior agrees well with experimental findings for both the reconstructed and the generated microstructures as shown in Figs. 11 a and 12 a. This indicates that the generation algorithm can compensate for the time-consuming reconstruction process and enables a meaningful modeling process.

Considering the foam stuctures, a scattering of the elastic modulus between $18 \,\text{and} \;35\,$GPa for generated and $21 \,\text{and} \;30 \hbox { GPa}$ for reconstructed microstructres can be observed (cf. Fig. 11a). For the composite structures, the scattering which vanishes to a negligible amount and all simulations show a stiffness of approx. $120\,$GPa (cf. Fig. 12a). It can be observed that the maximum stresses within the ceramic phase are much more localized in the foam structure (see Fig. 11b) compared to the composite (see Fig. 12b). In the composite, the AlSi10Mg phase blocks lateral straining of the ceramic skeleton and helps to distribute the stresses more equally in the Al₂O₃. In more detailed investigations of the 3D structures, it can be observed that the aluminum phase prevents strong bending and buckling of the ceramic rods. Consequently, the foam structure elastic properties depend much more on the geometrical configuration of the ceramic as the composite. For the composites, the analysis of the elastic behavior shows that predominantly the volume fractions are decisive which is in good agreement with [11].

However, different stress-strain behavior of the composite structures is observed beyond the linear elastic range when damage and plasticity occur. Both mechanisms start to evolve in areas of high stress concentration and therefore are dependent of the local geometry. Since, the generated microstructures are statistically equivalent considering the overall fractions and sphere size distribution but still show a wider range of compressive and residual strengths compared to the reconstructions, the local sphere arrangement has been investigated.

As shown in Fig. 10, a clear correlation between spheres and their neighbors for the reconstructed microstructures can be observed as the neighbor sphere size decreases with increasing size of the considered sphere. However, this trend is not given for generated structures. They exhibit smaller neighbor sphere sizes for small spheres and higher scattering of median neighbor size increases for large spheres compared to the reconstructions. Although microstructures might be eqiuvalent considering the sphere size distribution, this difference in the local neighborhood can influence the local stress concentration and subsequently the mechanical behavior.

For the generated microstructures, much more randomized local geometical arrangements are possible, as shown in Fig. 10. This can lead to more of both thick and delicate ceramic rods and might explain the stronger scattering of the stress-strain behavior under compression in generated structures (cf. Figs. 11a and  12a). If the ceramic skeleton contains, e.g., a thick and continuous wall structure in compressing direction, this will increase the stiffness of the foam considerably and is an explanation for the topmost stress-strain curve shown in Fig. 11a. This indicates that additional sphere placement restrictions have to be implemented in the algorithm to account for the statistical equivalent description of neighbor sphere sizes.

The mechanical behavior of the composite structures can be explained on the same basis. The onset as well as the evolution of damage and plasticity that characterizes the stress-strain behavior of the material is mainly influenced by local geometrical features. Again, a solid, continuous ceramic wall leads to a delayed damage initiation and higher compression strengths. The connectivity of the aluminum phase (= spheres) is a characteristic quantity for how easily the VE can be sheared at higher strains when the mechanical properties are dominated by the metal phase (see Fig. 12).

Another reason for the difference between the reconstructed and generated microstructures might be the nature of the surfaces. Generated composites show a decreased stress concentration at the top and the bottom of the perfectly spherical aluminum-filled cavities due to the perfectly smooth surface, whereas reconstructions have a more jagged interface between the ceramic and the aluminum phase. However, the edges of the windows connecting two neighboring spheres are sharp in the generated structures, whereas they are smooth for reconstructions. These sharp edges can lead to stress peaks at these windows and to a premature damage initiation compared to compared to reconstructions. Nontheless, the generated mictrostructures can represent the results of reconstructed structures and experiments very well for both the foam and the composite. However, the scattering of the local sphere arrangement can lead to larger variations in the mechanical behavior compared to reconstructions. Despite of the different local sphere arrangement, the generated structures are isotropic as shown in Appendix D.

The simulation of the composite as shown in Figs. 11 and 12 shows higher stresses than experimental tests of the material. This seems plausible regarding the fact that no initial flaws in the ceramic and aluminum were considered in the model. This would decrease the stiffness, as well as the compression and residual strength. Further, the interface between the Al₂O₃ and the AlSi10Mg was considered to be perfectly tied, i.e., no debonding effects were modeled that further could reduce the strength of the material.

As the experimental results can be reproduced well, the generation algorithm can be used for controlled modifications of desired structural characteristics in the future. As it is based on closed form equations and only needs fundamental information of the desired microstructure, it is a fast and versatile alternative to the reconstruction procedure. This enables the optimization and tailoring of the desired material properties and might help to speed up the process of material development. If the algorithm needs to be applied for different microstructures containing non-spherical shapes, it can easily be extended to these other geometrical forms.

Conclusion

We introduced a microstructure generation algorithm based on a purely geometrical ansatz that is able to generate interpenetrating microstructures. The presented algorithm is based on the RSA approach but involves an extended formulation for the random sphere placement in order to achieve high sphere volume fractions and ensure the interpenetrating morphology of the microstructure. To mesh the microstructures for FEM simulations, additional conditions and parameters are introduced to avoid geometrically challenging areas. As all equations (sphere placement, determination of volumes, etc.) are analytical, the process of microstructures generation can be realized in reasonable time (seconds on a desktop PC) without exceptional computing power. The generation algorithm minimizes the amount of basic information about the microstructure. So, as volume fractions and sphere size distribution is known, the algorithm can well reproduce microstructures in a statistical sense.

For the exemplary distribution function used within this paper, a minimum statistically equivalent volume element with an edge length of approximately $130$ μm has been determined. Compression simulations including damage modeling in the ceramic and elastic-plastic behavior in the metal phase show that the mechanical response of the generated and reconstructed microstructures are in good accordance. Further, the numerical results are at the upper end of experimentally determined compression behavior of the composite material.

Consequently, the generation algorithm is well suited for further studies on interpenetrating composite materials to investigate the mechanical behavior depending on microstructural characteristics. The simulations can give insights into material microstructures that are not or only with high effort accessible by experimental investigations and allow to study controlled modifications that enable the optimization and tailoring of desired material properties.

Appendices

Appendix A: Distance calculation

The periodic distance $\mathbf {d}_{p}$ between two spheres with positions $\mathbf {p}_{1}$ and $\mathbf {p}_{2}$ is given by

$$\begin{aligned} \mathbf {d}_{p} = (\mathbf {p}_{1}-\mathbf {p}_{2}) - \mathbf {a} \odot \mathbf {L} \end{aligned}$$

where $\odot$ represents the Hadamard product (= element-wise mutliplication), $\mathbf {L}=[L_{x}, L_{y}, L_{z}]^{\text {T}}$ is the vector of cell dimensions and $\mathbf {a} = [a_{x}, a_{y}, a_{z}]^{\text {T}}$ is a vector with values $\in \{-1, 0,1\}$ according to

$$\begin{aligned} {a}_{k} = \left\{ \begin{array}{ccl} -1 &{} \text {if} &{} p_{1}^{k}-p_{2}^{k} < -L_{k}/2 \\ 0 &{} \text {if} &{} \mid p_{1}^{k}-p_{2}^{k} \mid \,\le L_{k}/2 \\ 1 &{} \text {if} &{} p_{1}^{k}-p_{2}^{k} > L_{k}/2 \end{array} \right. . \end{aligned}$$

Choosing $\mathbf {a}=\mathbf {0}$ we get the regular, non-periodic distance vector $\mathbf {d}_{r} = \mathbf {p}_{1}-\mathbf {p}_{2}$. The distance between the spheres in euclidean space is simply the 2-norm of the respective distance vector

$$\begin{aligned} d = \Vert \mathbf {d}_{r} \wedge \mathbf {d}_{p}\Vert _{2} \, . \end{aligned}$$

Appendix B: Overlap calculation

The calculation of sphere overlaps with one, two or three cell boundaries is performed depending on the relative overlap between sphere and cell $\delta /r$ in a dimensionless form according to [45], where r is the sphere radius and $\delta$ is the overlap.

For the overlap with one cell face ($n_{\delta }=1$), the volume cut off by the cell (spherical cap) is calculated with

$$\begin{aligned} V_{face} = \frac{1}{3} \pi r^{3} \left[ 3 \left( \frac{\delta }{r}\right) ^{2} - \left( \frac{\delta }{r}\right) ^{3} \right] \end{aligned}$$

For the overlap with two cell faces ($n_{\delta }=2$), a case distinction is needed in calculating $V_{edge}$ as the sphere can either intersect with the two faces independently or is additionally cut by the edge of the cell. The general form for $V_{edge}$ is

$$\begin{aligned} V_{edge} = \frac{4}{3} \pi r^{3} \, f_{edge}\left( \frac{\delta _{1}}{r}, \frac{\delta _{2}}{r} \right) \end{aligned}$$

and the case distinction is made within the function $f_{edge}$ given by Eq. (B1)

$$\begin{aligned}f_{edge} \left( \frac{\delta _{1}}{r}, \frac{\delta _{2}}{r} \right)=\left\{ \begin{array}{cl} \frac{1}{4\pi } \left\{ \begin{array}{c} 2\hat{a}\hat{b}\hat{x} - (3\hat{a}-\hat{a}^{3}) \tan ^{-1} \left( \frac{\hat{x}}{\hat{b}}\right) - (3\hat{b}-\hat{b}^{3}) \tan ^{-1} \left( \frac{\hat{x}}{\hat{a}}\right) \\ + 2 \tan ^{-1} \left( \hat{x} \frac{\hat{a}}{\hat{b}}\right) + 2 \tan ^{-1} \end{array} \right\} &{} \text {for} \, \hat{x}^{2} > 0 \\ \\ 0 &{} \text {for} \, \hat{x}^{2} \le 0 \end{array} \right. \end{aligned}$$

(B1)

where

$$\begin{aligned} \hat{a} = 1 - \frac{\delta _{1}}{r} \text {,} \quad \hat{b} = 1 - \frac{\delta _{2}}{r} \quad \text {and} \quad \hat{x}^{2} = 1 - \hat{a}^{2} - \hat{b}^{2} \, . \end{aligned}$$

and the edge intersects the sphere for $\hat{x}^{2} > 0$.

Similar to $n_{\delta }=2$, a case distinction for three overlaps ($n_{\delta }=3$) has to be made to account for a potential overlap of the sphere with the cell corner. The volume of the corner $V_{corner}$ can be expressed in a general way with

$$\begin{aligned} V_{corner} = \frac{4}{3} \pi r^{3} \, f_{corner}\left( \frac{\delta _{1}}{r}, \frac{\delta _{2}}{r} , \frac{\delta _{3}}{r} \right) \end{aligned}$$

where the function $f_{corner}$ is given by Eq. (B2)

$$\begin{aligned} f_{corner}\left( \frac{\delta _{1}}{r}, \frac{\delta _{2}}{r} , \frac{\delta _{3}}{r} \right)=\left\{ \begin{array}{cl} \begin{array}{c} \frac{1}{2} f_{edge} \left( \frac{\delta _{1}}{r}, \frac{\delta _{2}}{r}\right) \\ - \frac{1}{8\pi } \end{array} \left\{ \begin{array}{c} 6\hat{a}\hat{b}\hat{x} - 2\hat{a}\hat{A}\hat{c} - 2\hat{b}\hat{B}\hat{c} - (3\hat{a}-\hat{a}^{3})\tan ^{-1} \left( \frac{\hat{c}}{\hat{A}}\right) \\ - (3\hat{b}-\hat{b}^{3}) \tan ^{-1} \left( \frac{\hat{c}}{\hat{B}}\right) + 3(\hat{c}-\hat{c}^{3}) \left[ \tan ^{-1} \left( \frac{\hat{A}}{\hat{a}}\right) \right. \\ \left. - \tan ^{-1} \left( \frac{\hat{B}}{\hat{b}}\right) \right] + 2 \left[ \tan ^{-1} \left( \hat{c} \frac{\hat{a}}{\hat{A}}\right) \right. \left. + \tan ^{-1} \left( \hat{c} \frac{\hat{b}}{\hat{B}}\right) \right] \end{array} \right\} &{} \text {for} \, \hat{a}^{2} + \hat{b}^{2} + \hat{c}^{2} > 1 \\ \\ 0 &{} \text {for} \, \hat{a}^{2} + \hat{b}^{2} + \hat{c}^{2}\le 1 \end{array} \right. \end{aligned}$$

(B2)

with the relations

$$\begin{aligned} \hat{c} = 1 - \frac{\delta _{3}}{r} \text {,} \quad \hat{A} = \sqrt{1 - \hat{a}^{2} - \hat{c}^{2}} \quad \text {and} \quad \hat{B} = \sqrt{1 - \hat{b}^{2} - \hat{c}^{2}} \, . \end{aligned}$$

and the sphere intersects with the corner if $\hat{a}^{2} + \hat{b}^{2} + \hat{c}^{2} < 1$.

A more detailed explanation of the formula and their derivation is given by Freireich et al. [45].

Appendix C: Transformation matrix

The transformation matrix $\varvec{T}$ reflects the orientation of the crack and relates global and local quantities such as strains and stresses. As the first crack nucleates in the direction of maximum principle stress (local 1-direction) the corresponding transformation matrix to relate, i.e., the global crack strain $\varvec{\varepsilon }^{ck}=[\varepsilon _{xx}, \varepsilon _{yy}, \varepsilon _{zz}, \varepsilon _{xy}, \varepsilon _{yz}, \varepsilon _{zx}]^{T}$ to the relevant local crack strain $\varvec{\epsilon }^{ck}~=~[\epsilon _{11}, \epsilon _{12}, \epsilon _{13} ]^{T}$ reads

$$\begin{aligned} \varvec{T} = \begin{bmatrix} v_{1,x}^{2} &{} v_{1,x}v_{2,x} &{} v_{3,x}v_{1,x} \\ v_{1,y}^{2} &{} v_{1,y}v_{2,y} &{} v_{3,y}v_{1,y} \\ v_{1,z}^{2} &{} v_{1,z}v_{2,z} &{} v_{3,z}v_{1,z} \\ 2 v_{1,x}v_{1,y} &{} v_{1,x}v_{2,y} + v_{2,x}v_{1,y} &{} v_{3,x}v_{1,y} + v_{1,x}v_{3,y} \\ 2 v_{1,y}v_{1,z} &{} v_{1,y}v_{2,z} + v_{2,y}v_{1,z} &{} v_{3,y}v_{1,z} + v_{1,y}v_{3,z} \\ 2 v_{1,z}v_{1,x} &{} v_{1,z}v_{2,x} + v_{2,z}v_{1,x} &{} v_{3,z}v_{1,x} + v_{1,z}v_{3,x} \\ \end{bmatrix} \end{aligned}$$

with the vectors $\varvec{v}_{i} = [v_{i,x}, v_{i,y}, v_{i,z}]^{T}$ indicating the direction cosines of the local i-axis expressed in global coordinates (x, y, z) [47].

Appendix D: Isotropy of generated microstructures

The investigated, reconstructed microstructures exhibit profound isotropy as shown in [11]. In the microstructure generation algorithm introduced in Sect. 3, the outcome of an isotropic structure is forced by the initial sphere placement in the center and the constrained placement method using the bias parameter. However, isotropy is not necessarily guaranteed.

To prove the isotropy of the generated structures, lineal path functions according to [25] have been evaluated for different volume sizes. No remarkable difference between the statistical functions for each orthogonal direction (x,y,z) has been found for sample sizes of an edge length of $133$ μm and larger. Two exemplary results are displayed in Fig. 13 for volume element sizes of $133^{3}$ μm$^{3}$ (left) and $290^{3}$ μm$^{3}$ (rigth). The findings lead to the conclusion that isotropy can be assumed for the considered microstructures.

Figure 13

Lineal path functions of generated microstructures with a volume of $133^{3}$ μm$^{3}$ (left) and $290^{3}$ μm$^{3}$ (rigth), respectively. For each volume element size, the evaluation in three orthogonal directions (x,y,z) for two example structures ($\#1$ and $\#2$) is shown