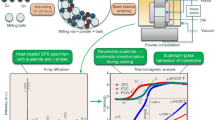
Abstract
Mn–Al–C is intended to be one of the “gap magnets” with magnetic performance in-between ferrites and Nd-Fe-B. These magnets are based on the metastable ferromagnetic \(\tau\)-phase with L1\(_0\) structure, which requires well controlled synthesis to prevent the formation of secondary phases, detrimental for magnetic properties. Here, we investigate the formation of \(\tau\)-phase in Mn–Al–C using Spark Plasma Sintering (SPS) and compare with conventional annealing. The effect of SPS parameters (pressure and electric current) on the phase formation is also studied. Single \(\tau\)-phase is obtained for annealing 5 min at \(500~^\circ \hbox {C}\) with SPS. In addition, we show that the initial grain size of the \(\epsilon\)-phase is influencing the \(\tau\)-phase transformation and fraction at a given annealing condition, independently of the annealing method used. A faster transformation was observed for smaller initial \(\epsilon\)-grains. The samples obtained by SPS showed comparable magnetic properties with the conventional annealed ones, reaching coercivity of 0.18 T and saturation magnetization of 114 Am\(^2\)/kg in the optimized samples. The similarity in coercivity is related to the microstructure, as we reveal the presence of structure defects like twin boundaries and dislocations in both materials.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Mn-Al alloys have been intensively studied since the 60’s as candidates for rare-earth free permanent magnets (PM) applications [1,2,3]. The renewed interest in this material system in the past years was triggered by the abrupt increase in the rare earth elements prices in 2010 and 2011 along with the ever growing demand and applications of PM [4]. This combination requires the development and improvement of sustainable and abundant materials for PMs. In this context, the Mn-Al alloy is characterized by the utilization of non-critical elements, low cost and reasonable magnetic properties. These characteristics are pointed as crucial to use and develop this material system as “gap magnets” with performance in between hexaferrites and Nd-Fe-B [5]. The magnetic properties of Mn-Al are related to the tetragonal \(\tau\)-phase (L1\(_{0}\) type structure), which is the unique ferromagnetic phase of this material system and yields in a theoretical maximum energy-product of approximately 101 kJ/m\(^{3}\) [6,7,8]. This phase was successfully produced in various form, e.g. powder, bulk, ribbon, particulate, and thin-films [8].
However, the \(\tau\)-phase is metastable and it is easy to form non-magnetic equilibrium phases like \(\gamma _{2}\) and \(\beta\)–Mn, which are detrimental for the magnetic properties [9, 10]. Thus, different processing strategies and parameters have to be optimized to obtain a maximum fraction of this ferromagnetic phase and prevent the stable ones. In the literature, two methods are commonly reported: (i) slow cooling from the high temperature \(\epsilon\)-phase or (ii) rapid cooling (i.e. quenching) from the melt or from the \(\epsilon\)-phase followed by an annealing process at moderate temperatures (450–600 \(^{\circ }\hbox {C}\)) [11,12,13]. It is worth mentioning that the cooling rate in (i) or a long time annealing in (ii) can lead to the decomposition of the \(\tau\)-phase into the stable phases. Two mechanisms have been proposed to explain the \(\epsilon \rightarrow \tau\) transformation, one is based on diffusional “massive” transformation, whereas the other one is a plate-like modification formed by a shear reaction, said “displacive”. Both have been observed simultaneously, and the mechanisms are known to depend on various aspect of the process like microstructure, chemical composition or annealing procedure [14,15,16]. In addition, carbon interstitial doping improves the stability of the \(\tau\)-phase and also enhances the saturation magnetization [17, 18].
Consequently, the necessity to optimize the processing window (temperature and time) is imperative to produce high purity \(\tau\)-phase with effective magnetic properties. For this purpose, techniques that allow fast heating and cooling could be beneficial to control the \(\epsilon \rightarrow \tau\) phase transition and prevent the decomposition to the stable phases. In this context, Spark Plasma Sintering (SPS) is an appealing annealing method as it is commonly related to decrease the process time and temperature for reactive and/or non-reactive sintering [19, 20]. These characteristics are due to the combination of pressure and electric current flow, which induces Joule heating during the SPS process, leading to the possibility of fast heating/cooling rates. Moreover, other side effects related to the presence of electric current were reported, including hot spots formation and electromigration. These side effects might give an additional degree of freedom to optimize the \(\tau\)-phase transition temperature, phase stability and microstructure, as reported for other material systems [20,21,22]. Previous studies have focused on the reactive sintering by SPS of the \(\tau\)-phase and, particularly, on the effect of the high SPS pressure on the texture and anisotropy of the sintered pellets [23, 24].
In this study, Mn–Al–C alloys were prepared by melt spinning at different quenching rates (20 and 50 m/s). We investigate the \(\epsilon \rightarrow \tau\) transformation by SPS and conventional annealing at different temperatures and dwelling times. The role of the pressure and electric current during the SPS process in the phase formation is disclosed. In addition, we reveal the influence of the initial grain size of the \(\epsilon\)-phase on the phase transition and \(\tau\)-phase fraction evolution upon annealing. Analysis of the phase fractions, microstructure, and magnetic properties for the SPS processed samples are compared with conventional annealed ones.
Experimental section
Mn\(_{54}\)Al\(_{44}\)C\(_2\) ingots were prepared by induction melting using high purity elements (>99.9%) under argon atmosphere. The C doping is used to enhance the stability of the \(\tau\)-phase as well as to improve the saturation magnetization. The resulting ingots were subjected to melt spinning (Edmund Bühler Melt Spinner-SC), by ejecting the molten alloy through an orifice (1 mm) from the bottom of a quartz tube onto a water-cooled copper wheel under argon atmosphere. To evaluate the influence of the quenching rate, two different tangential wheel velocities (\(\nu\)) were used: 20 and 50 m/s. It is possible that some ribbons have a mixed \(\epsilon\) and \(\tau\)-phase, so ribbons with single \(\epsilon\)-phase were selected by applying a magnetic field and selecting only the non-magnetic ones.
Spark Plasma Sintering (Dr. Sinter Lab - Fuji Electronic Industrial Co. Ltd.) experiments were carried out at the following temperatures: 450, 500 and 550 \(^{\circ }\hbox {C}\), with dwelling time of 5 and 15 minutes and heating rate of 100 \(^{\circ }\hbox {C}\)/min. The temperature was measured through K-type thermocouple placed in a radial hole inside the die. Prior to the SPS, the melt spun ribbons were manually ground and sieved to a particle size distribution below 100 \(\mu\)m. A constant uniaxial stress of 10 or 100 MPa was applied during the SPS process. The SPS tools used for the experiments were standard graphite punches and die with 10 mm diameter. Additionally, to investigate the effect of electric current during the SPS process, boron nitride (BN) spacers were used between the powder and the graphite punches, while the other parameters (pressure, time and temperature) were kept fixed. By employing this methodology, it is ensured that the electric current flows solely through the graphite tools and not through the sample [25]. For the SPS process, the ribbons are crushed into powder and since the temperature is not high enough to promote sintering, only porous cylindrical samples (around 70% relative density) were obtained. In addition, reference samples were prepared by conventional annealing the melt spun ribbons at 500–550 \(^{\circ }\hbox {C}\) for 5, 15 and 30 minutes using pre-heated oven.
X-ray diffraction (XRD) measurements were performed at room temperature using a Stoe Stadi P diffractometer in transmission geometry equipped with a Mo-K\(_{\alpha 1}\) source and an acceleration voltage of 45 kV. The step size is 0.01\(^{\circ }\), and the acquisition time per step is 180 seconds. The patterns were refined by the Rietveld method using the FullProf software [26]. The morphology and microstructure of the ribbons were studied using a Field Emission Gun-Scanning Electron Microscope (FEG-SEM JEOL 7600F) equipped with backscatter (BSE) and secondary electron (SE) detector under accelaration voltage of 15 kV. To evaluate the grain size distribution, electron backscatter diffraction (EBSD) was used in a FEG-SEM (Tescan Mira3) with additional four-quadrant BSE (4Q-BSE) detector for enhanced microstructural feature analysis through electron channeling contrast imaging (ECCI). The EBSD analysis was taken with 200 nm step size and 10 ms acquisition time per step. The resistivity was measured using a TCR600 from NAPSON corp. using the 4-points probe measurements with finite size corrections. Magnetic measurements were performed, at room temperature, using a Quantum Design PPMS-VSM with a maximum field up to 14 T.
Results and discussion
The structural properties of the melt spun ribbons, obtained for different wheel speeds (20 and 50 m/s), were evaluated through XRD analysis as shown in Fig. 1(a). Both materials consist of single \(\epsilon\)-phase (space group P6\(_3\)/mmc). BSE-SEM images (see in Fig. 1(b) and (c)) disclose the influence of the wheel speed on the grain sizes of the as-spun samples. Images are taken after etching the ribbons in the Kroll reagent (a mix of nitric and hydrofluoric acid). The average grain size estimated for the ribbons obtained at 20 m/s and 50 m/s is 5 \({\upmu }\hbox {m}\) and 2.5 \({\upmu }\hbox {m}\), respectively. This confirms the ability of the melt spinning technique to tune the grain size of the \(\epsilon\)-phase. However, the difference in grain size is rather small compared to the difference in the wheel speed, suggesting that even faster wheel speeds are necessary to reach submicrometer-sized grains.
The melt spun ribbons were then conventionally annealed or SPS processed at different temperatures and dwelling times. XRD patterns were recorded for all the samples after annealing. Using the Rietveld refinement, we determined the phase fractions (in wt.%) of \(\epsilon\) (space group P6\(_3\)/mmc), \(\tau\) (space group P4/mmm) and \(\beta\)-Mn (space group P4\(_1\)32) . The cumulative phase fraction for the different annealed samples is shown in Fig. 2. We distinguish the samples regarding their initial grain size, i.e. ribbons obtained from melt spinning at 20 m/s (a,b) or 50 m/s (c,d).
For ribbons melt spun at 20 m/s (see Fig. 2(a,b)) and after conventional annealing for 30 min at 500 \(^{\circ }\hbox {C}\), we obtain single \(\tau\)-phase. The transformation is not completed when lower dwelling times are used, consistent with the literature [18, 27,28,29]. By increasing the temperature to 550 \(^{\circ }\hbox {C}\) , one can obtain single \(\tau\)-phase in 5 min with conventional annealing. Regarding the SPS process, optimum conditions with a single \(\tau\)-phase are achieved in 5 min at 500 \(^{\circ }\hbox {C}\). At lower annealing temperatures, the transformation \(\epsilon \rightarrow \tau\) is uncompleted, and the \(\epsilon\)-phase is still present, independently of the dwell time. On the other hand, at higher temperatures or dwell time longer than 5 min, we observe the decomposition of the \(\tau\)–phase into equilibrium \(\beta\)–Mn-phase. It seems that SPS has a minor influence on the \(\tau\)–phase formation, as quasi-similar thermal process in SPS (500 \(^{\circ }\hbox {C}\)/5 min) and conventional annealing (550 \(^{\circ }\hbox {C}\)/5 min) provides single phases.
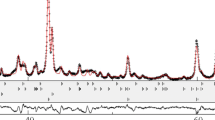
The influence of SPS parameters (pressure and current) on the phase transformation was studied. To assess the role of electric current, electrical resistivity measurements were conducted on the graphite punch and on a cold-compacted \(\epsilon\)–phase sample. The resistivity is 1.3 m\(\Omega\).cm and 5.7 m\(\Omega\).cm for the graphite and the \(\epsilon\)–phase, respectively. Thus, it is unlikely the current would flow in the Mn–Al–C sample during the SPS process. To ensure that, a SPS experiment has been conducted with BN-spacers in between the graphite punch and the Mn–Al–C powder. As BN is an electrical insulator, this configuration ensures that the electric current does not flow through the powder but only through the graphite die and pistons [25]. Similar annealing conditions (i.e. 500 \(^{\circ }\hbox {C}\) for 5 min) were used on the 20 m/s powder, and the XRD pattern (see Fig. 3) reveals a quasi-single \(\tau\)-phase (>98 wt%) with small formation of the \(\beta\)-phase. No traces of \(\epsilon\) are observed, which indicates a full \(\epsilon \rightarrow \tau\) transformation and a small influence of the current during the SPS process, in agreement with the resistivity measurements. Regarding the influence of pressure, an experiment using 10 MPa with graphite tools (500 \(^{\circ }\hbox {C}\) for 5 min) was done, and its XRD pattern is shown Fig. 3. The \(\epsilon \rightarrow \tau\) is also complete but with a slight formation of secondary \(\beta\)-phase. These results show that the SPS parameters have influence on the formation of the secondary \(\beta\)-phase but not on the \(\epsilon \rightarrow \tau\) transformation as no traces of \(\epsilon\) is observed.
The phase fraction obtained for ribbons melt spun at 50 m/s is shown in Fig. 2(c,d). Single \(\tau\)-phase is obtained at 500 \(^{\circ }\hbox {C}\)/30min or 550 \(^{\circ }\hbox {C}\)/5min for the conventional annealed samples. Regarding the SPS processed samples, the annealing at 450 \(^{\circ }\hbox {C}\) for 15 min results in an incomplete transformation, whereas the decomposition to the \(\beta\)–Mn is observed for samples annealed at temperatures equal or above 500 \(^{\circ }\hbox {C}\). The optimum process was found to be 475 \(^{\circ }\hbox {C}\)/15 min (see the yellow square in Fig. 2(c)). In addition, comparing the phase fractions for a given annealing condition, higher amount of \(\tau\)-phase is observed for the 50 m/s samples compared to the 20 m/s. This observation holds true for both annealing methods. As shown previously, the main difference between the ribbons melt spun at 20 and 50 m/s lies in the grain size, finer at higher wheel speed. Thus, a finer microstructure of \(\epsilon\)-phase eases the formation of the \(\tau\)-phase, where a reduced time and temperature is necessary to complete the transformation. As reported in previous studies [8, 16, 30, 31], this result supports that the \(\tau\)-phase in Mn–Al–C nucleation takes place at the grain boundaries, which are in higher density in finer microstructures. The grain boundary regions show higher energy when compared to the grain interior. During the nucleation of \(\tau\)-phase, there is an energy dissipation related to the removal of the parent \(\epsilon\)-phase grain boundaries. This energy term enhances the probability of creating stable nuclei of the \(\tau\)-phase through heterogeneous nucleation process. Given the higher grain boundary density, the samples with finer \(\epsilon\)-phase microstructure (50 m/s) have more nucleation sites for the \(\tau\)-phase formation, which is reflected on the higher phase fraction when compared to a \(\epsilon\)-phase coarser microstructure (20 m/s) at a given annealing condition. The heterogeneous nucleation at grain boundaries appears to be independent from the mechanism involved in the \(\epsilon \rightarrow \tau\) phase transformation (massive, displacive or a mixture of these two), as reported by Wiezorek et al. and Palanisamy et al. [16, 32]
It is of interest to understand how the \(\epsilon \rightarrow \tau\) transformation acts on the microstructure and, particularly, on the grain size. For this, the surface fracture of the 20 m/s ribbons in the as-spun and conventionally annealed states (500 \(^{\circ }\hbox {C}\) /30 min) were evaluated. The secondary electrons SEM images of both cases are shown in Fig. 4. The transgranular surface fracture features observed in the as-spun \(\epsilon\)–phase (Fig. 4(a)) show a faceted-like morphology related to cleavage steps/bands with slip traces. As for the case of the ribbons with \(\tau\)-phase (Fig. 4(b)), the surface also shows characteristics of transgranular fractures, however a change in morphology can be observed. Similar features were observed for the 50 m/s ribbons. Even though a clear difference of the surface fracture is observed after the \(\epsilon \rightarrow \tau\) transformation, the grain size for the annealed ribbons cannot be estimated based on these images. Thus, EBSD has been performed to investigate the grain size of the Mn–Al–C samples with the \(\tau\)-phase obtained from the 20 and 50 m/s melt spun ribbons conventional annealed, shown in Fig. 5. The EBSD analysis reveals a reduction in the grain size after the \(\epsilon \rightarrow \tau\) transformation, achieving an average grain size of 2.4 and 1.7 \({\upmu }\hbox {m}\) (initial \(\epsilon\)–phase grain size is estimated to 5 and 2.5 \({\upmu }\hbox {m}\)) for the 20 and 50 m/s ribbons, respectively. The microstructure is finer and quite similar, independently of the initial wheel speed used for quenching the material. Thus, the wheel speed seems to play a minor role in the final microstructure of the Mn–Al–C. This observation also holds true for the samples annealed using SPS, in which the average grain size is slightly smaller, around 1 \({\upmu }\hbox {m}\), for both wheel speeds.
The magnetic hysteresis loops were measured for all annealed samples, using a magnetic field up to 14 T. From the hysteresis loops, the coercive field (Hc) as well as the mass magnetization at 14 T is retrieved and plotted in Fig. 6. One can note that the mass magnetization values scales with the \(\tau\)-phase fraction, reaching maximum values for the samples without significant amount of secondary phases. For the single phase samples, the magnetization is very similar independently of the method used for annealing (SPS or conventional) and independently of the wheel speed (i.e. 20 or 50 m/s) used to produce the initial ribbons. The first quadrant of the M–H loops for the single \(\tau\)-phase melt spun at 20 m/s is shown in Fig. 7 as an example. The ferromagnetic Mn–Al–C material is known to be difficult to saturate [33], but our SPS and conventional annealed samples show a quasi-saturated magnetization (114 and 112 Am\(^2\)/kg at 14 T, respectively), as they are single phase [3, 34]. These values are comparable with previously reported saturation magnetization for Mn–Al–C ribbons [8, 35, 36].
Regarding coercivity, Fig. 6 shows that the \(\mu _0\)Hc does not depend on the phase fraction of the \(\tau\)-phase, as all values lies between 0.15 and 0.18 T, which are typical values for annealed ribbons [3, 34].The coercivity seems to be independent of the method used for annealing. It is worth mentioning that no improvement in coercivity is observed with the formation of \(\beta\)-phase, contrary to previous report [37].
By comparing the 20 and 50 m/s samples, slightly higher coercivity values are obtained for the sample melt spun at 20 m/s (see the horizontal dotted lines as guides to the eye). This result cannot be explained by the grain size, as a slightly finer microstructure has been revealed by EBSD for the samples melt spun at 50 m/s. Hence, the grain size of the \(\epsilon\) and \(\tau\)-phase does not seem to have a major influence on the coercivity of the transformed \(\tau\)-phase sample in our study due to the comparable grain size of both samples. However, it was shown by Jia et al. that when the difference in grain size is large (from 3 mm to 2 \({\upmu }\hbox {m}\)), it influences greatly the coercivity [31]. It is known that in the Mn-Al(C) system, the coercivity mechanism is not only dependent on the grain size, but also linked to the defects in the microstructure (e.g. twin and anti-phase boundaries, stacking faults, dislocations, etc.) [33, 34, 38, 39]. Recent studies have shown that the presence of twin boundaries is detrimental to coercivity, since they can be nucleation centres for reversal domains, while a high dislocation density can hinder the domains wall motion by pinning mechanism. This balance between the density and the different types of defects appears to be the key factor for the coercivity and the mechanism behind it. To observe this two types of defects, electron channeling contrast imaging (ECCI) was used to enhance the contrast between different grain orientations (twin boundaries) and to probe defects (dislocations) near the sample surface [40, 41]. As can be exemplified in Fig. 8, independently from the wheel speed used to produce the parent \(\epsilon\)-phase sample, twin boundaries are present in the \(\tau\)-phase sample. Additionally, it can be seen regions with low density dislocations close to grain boundaries in both samples, as highlighted in Fig. 8(c). This combination leads to the coercivity values in the range of 0.15-0.18 T, as shown previously.
Electron channeling contrast images (ECCI) of the conventional annealed samples of a 20 m/s and b 50 m/s, highlighting the twin boundaries (examples marked with “TB” in red) and dislocations (examples marked with “d” in yellow). A higher magnification micrograph of the 50 m/s sample is displayed in c to show dislocations in more detail
Conclusion
We investigated the \(\epsilon \rightarrow \tau\) transformation by fast annealing using the Spark Plasma Sintering (SPS) technique. Single \(\epsilon\)-phase was successfully produced by melt spinning at two different wheel speeds, which allows to tune the grain size of the material. We demonstrated that SPS yields single \(\tau\)-phase after 5 min at 500 \(^{\circ }\hbox {C}\). It is also pointed out that the \(\tau\)-phase fraction depends on the initial \(\epsilon\)-phase grain size at a given annealing condition. The sample obtained by SPS shows comparable magnetic properties (Ms and Hc) to the conventional annealing, which can be directly related to the similarities in the microstructure and defects. We show that pure \(\tau\)-phase can be obtained by fast annealing using SPS or conventional annealing when appropriate annealing conditions are used.
References
Koch AJJ, Hokkeling P, vd Steeg MG, de Vos KJ (1960) New material for permanent magnets on a base of Mn and Al. J Appl Phys 31(5):75–77. https://doi.org/10.1063/1.1984610
Ohtani T, Kato N, Kojima S, Kojima K, Sakamoto Y, Konno I, Tsukahara M, Kubo T (1977) Magnetic properties of Mn–Al–C permanent magnet alloys. IEEE Trans Magn 13(5):1328–1330. https://doi.org/10.1109/tmag.1977.1059574
Cui J, Kramer M, Zhou L, Liu F, Gabay A, Hadjipanayis G, Balasubramanian B, Sellmyer D (2018) Current progress and future challenges in rare-earth-free permanent magnets. Acta Mater 158:118–137. https://doi.org/10.1016/j.actamat.2018.07.049
Skokov KP, Gutfleisch O (2018) Heavy rare earth free, free rare earth and rare earth free magnets - Vision and reality. Scripta Mater 154:289–294. https://doi.org/10.1016/j.scriptamat.2018.01.032
Coey JMD (2012) Permanent magnets: plugging the gap. Scripta Mater 67(6):524–529. https://doi.org/10.1016/j.scriptamat.2012.04.036
Park J, Hong Y, Bae S, Lee J, Jalli J, Abo G, Neveu N, Kim S, Choi C, Lee J (2010) Saturation magnetization and crystalline anisotropy calculations for MnAl permanent magnet. J Appl Phys 107(9):09–731. https://doi.org/10.1063/1.3337640
Palanisamy D, Singh S, Srivastava C, Madras G, Chattopadhyay K (2016) Predicting pathways for synthesis of ferromagnetic \(\tau\) phase in binary Heusler alloy Al-55 pct Mn through understanding of the kinetics of \(\varepsilon\)-\(\tau\) transformation. Metall Mater Trans A 47(12):6555–6568. https://doi.org/10.1007/s11661-016-3756-4
Keller T, Baker I (2022) Manganese-based permanent magnet materials. Prog Mater Sci 124:100872. https://doi.org/10.1016/j.pmatsci.2021.100872
Bittner F, Schultz L, Woodcock TG (2017) The role of the interface distribution in the decomposition of metastable L1\(_{0}\)-Mn\(_{54}\)Al\(_{46}\). J Alloys Compd 727:1095–1099. https://doi.org/10.1016/j.jallcom.2017.08.197
Xiang Z, Deng Baiwen, Zhang X, Wang X, Cui E, Yu L, Song Y, Lu W (2020) Nanocrystalline MnAlV rare-earth-free permanent magnetic alloys with improved magnetization and thermal stability. Intermetallics 116:106638. https://doi.org/10.1016/j.intermet.2019.106638
Bittner F, Freudenberger J, Schultz L, Woodcock TG (2017) The impact of dislocations on coercivity in L1\(_{0}\)-MnAl. J Alloys Compd 704:528–536. https://doi.org/10.1016/j.jallcom.2017.02.028
Øygarden V, Rial J, Bollero A, Deledda S (2019) Phase-pure \(\tau\)-MnAlC produced by mechanical alloying and a one-step annealing route. J Alloys Compd 779:776–783. https://doi.org/10.1016/j.jallcom.2018.11.175
Popov VV, Maccari F, Radulov IA, Kovalevsky A, Katz-Demyanetz A, Bamberger M (2021) Microstructure and magnetic properties of Mn–Al–C permanent magnets produced by various techniques. Manufact Rev 8:10. https://doi.org/10.1051/mfreview/2021008
Si P-Z, Qian H-D, Choi C-J, Park J, Han S, Ge H-L, Shinde KP (2017) In situ observation of phase transformation in MnAl(C) magnetic materials. Materials 10(9):1016. https://doi.org/10.3390/ma10091016
Zhang C, Zhang T, Wang J, Zhao S, Wu Y, Jiang C (2018) Anisotropic single-variant of (Mn\(_{54}\)Al\(_{46}\))97C\(_3\). Scripta Materialia 143:72–76. https://doi.org/10.1016/j.scriptamat.2017.09.008
Palanisamy D, Raabe D, Gault B (2019) On the compositional partitioning during phase transformation in a binary ferromagnetic MnAl alloy. Acta Mater 174:227–236. https://doi.org/10.1016/j.actamat.2019.05.037
McCallum RW, Lewis L, Skomski R, Kramer MJ, Anderson IE (2014) Practical aspects of modern and future permanent magnets. Annu Rev Mater Sci 44(1):451–477. https://doi.org/10.1146/annurev-matsci-070813-113457
Zhao S, Wu Y, Zhang C, Wang J, Fu Z, Zhang R, Jiang C (2018) Stabilization of \(\tau\)-phase in carbon-doped MnAl magnetic alloys. J Alloys Compd 755:257–264. https://doi.org/10.1016/j.jallcom.2018.04.318
Aubert A, Loyau V, Mazaleyrat F, LoBue M (2017) Uniaxial anisotropy and enhanced magnetostriction of CoFe\(_2\)O\(_4\) induced by reaction under uniaxial pressure with SPS. J Eur Ceram Soc 37(9):3101. https://doi.org/10.1016/j.jeurceramsoc.2017.03.036
Guillon O, Elsässer C, Gutfleisch O, Janek J, Korte-Kerzel S, Raabe D, Volkert CA (2018) Manipulation of matter by electric and magnetic fields: toward novel synthesis and processing routes of inorganic materials. Mater Today 21(5):527–536. https://doi.org/10.1016/j.mattod.2018.03.026
Maccari F, Karpenkov DY, Semenova E, Karpenkov AY, Radulov IA, Skokov KP, Gutfleisch O (2020) Accelerated crystallization and phase formation in Fe\(_{40}\)Ni\(_{40}\)B\(_{20}\) by electric current assisted annealing technique. J Alloys Compd 836:155338. https://doi.org/10.1016/j.jallcom.2020.155338
Wang H, Kou R, Harrington T, Vecchio KS (2020) Electromigration effect in Fe-Al diffusion couples with field-assisted sintering. Acta Mater 186:631–643. https://doi.org/10.1016/j.actamat.2020.01.008
Tyrman M, Quetel-Weben S, Pasko A, Perrière L, Guillot I, Etgens V, Mazaleyrat F (2017) Ferromagnetic L1\(_{0}\) phase formation in the Mn–Al–C alloys induced by high-pressure spark plasma sintering. IEEE Trans Magn 53(11):1–5. https://doi.org/10.1109/TMAG.2017.2732500
Tyrman M, Ahmim S, Pasko A, Etgens V, Mazaleyrat F, Quetel-Weben S, Perrière L, Guillot I (2018) Anisotropy of the ferromagnetic L1\(_{0}\) phase in the Mn–Al–C alloys induced by high-pressure spark plasma sintering. AIP Adv 8(5):056217. https://doi.org/10.1063/1.5007241
Gorynski C, Anselmi-Tamburini U, Winterer M (2020) Controlling current flow in sintering: a facile method coupling flash with spark plasma sintering. Rev Sci Instrum 91(1):015112. https://doi.org/10.1063/1.5119059
Rodríguez-Carvajal J (1993) Recent advances in magnetic structure determination by neutron powder diffraction. Physica B Condens Matter 192(1–2):55–69. https://doi.org/10.1016/0921-4526(93)90108-i
Jian H, Skokov KP, Gutfleisch O (2015) Microstructure and magnetic properties of Mn–Al–C alloy powders prepared by ball milling. J Alloys Compounds 622:524–528. https://doi.org/10.1016/j.jallcom.2014.10.138
Zhao S, Wu Y, Jiao Z, Jia Y, Xu Y, Wang J, Zhang T, Jiang C (2019) Evolution of intrinsic magnetic properties in L1\(_{0}\) Mn–Al alloys doped with substitutional atoms and correlated mechanism: experimental and theoretical studies. Phys Rev Appl 11(6):064008. https://doi.org/10.1103/physrevapplied.11.064008
Liu Z, Su K, Cheng Y, Ramanujan R (2015) Structure and properties evolutions for hard magnetic MnAl and MnGa based alloys prepared by melt spinning or mechanical milling. Mater Sci Eng Adv Res 1(1):12–19
Yanar C, Wiezorek JMK, Soffa WA, Radmilovic V (2002) Massive transformation and the formation of the ferromagnetic L1\(_{0}\) phase in manganese-aluminium-based alloys. Metall Mater Trans A 33:2413–2423. https://doi.org/10.1007/s11661-002-0363-3
Jia Y, Wu Y, Zhao S, Wang J, Jiang C (2018) Relation between solidification microstructure and coercivity in MnAl permanent-magnet alloys. Intermetallics 96:41–48. https://doi.org/10.1016/j.intermet.2018.02.011
Wiezorek JMK, Kulovits AK, Yanar C, Soffa WA (2010) Grain boundary mediated displacive-diffusional formation of \(\tau\)-phase MnAl. Metall Mater Trans A 42(3):594–604. https://doi.org/10.1007/s11661-010-0308-1
Zhao P, Feng L, Nielsch K, Woodcock TG (2021) Microstructural defects in hot deformed and as-transformed \(\tau\)-Mn–Al–C. J Alloys Compd 852:156998. https://doi.org/10.1016/j.jallcom.2020.156998
Jia Y, Wu Y, Zhao S, Zuo S, Skokov KP, Gutfleisch O, Jiang C, Xu H (2020) L1\(_{0}\) rare-earth-free permanent magnets: the effects of twinning versus dislocations in Mn–Al magnets. Phys Rev Mater 4(9):094402. https://doi.org/10.1103/physrevmaterials.4.094402
Wei J, Song Z, Yang Y, Liu S, Du H, Han J, Zhou D, Wang C, Yang Y, Franz A et al (2014) \(\tau\)-MnAl with high coercivity and saturation magnetization. AIP Adv 4(12):127113. https://doi.org/10.1063/1.4903773
Si P, Qian H, Wang X, Yang Y, Park J, Ge H, Choi C-J (2019) High-pressure synthesis of high coercivity bulk mnal-c magnets from melt-spun ribbons. J Electron Mater 48(2):794–798. https://doi.org/10.1007/s11664-018-6798-0
Rial J, Palmero EM, Bollero A (2020) Efficient nanostructuring of isotropic gas-atomized MnAl powder by rapid milling (30 s). Engineering 6(2):173–177. https://doi.org/10.1016/j.eng.2019.03.013
Bance S, Bittner F, Woodcock TG, Schultz L, Schrefl T (2017) Role of twin and anti-phase defects in MnAl permanent magnets. Acta Mater 131:48–56. https://doi.org/10.1016/j.actamat.2017.04.004
Jakubovics JP, Jolly TW (1977) The effect of crystal defects on the domain structure of Mn–Al alloys. Phys B 86–88:1357–1359. https://doi.org/10.1016/0378-4363(77)90910-x
Gutierrez-Urrutia I, Zaefferer S, Raabe D (2013) Coupling of electron channeling with EBSD: toward the quantitative characterization of deformation structures in the SEM. JOM 65(9):1229–1236. https://doi.org/10.1007/s11837-013-0678-0
Zaefferer S, Elhami N-N (2014) Theory and application of electron channelling contrast imaging under controlled diffraction conditions. Acta Mater 75:20–50. https://doi.org/10.1016/j.actamat.2014.04.018
Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft DFG (German Research Foundation) under the Priority Programme SPP1959-Fields Matter and European Union’s Horizon 2020 research and innovation programme under grant agreement No 101003914 (PASSENGER).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Handling Editor M. Grant Norton.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maccari, F., Aubert, A., Ener, S. et al. Formation of pure \(\tau\)-phase in Mn–Al–C by fast annealing using spark plasma sintering. J Mater Sci 57, 6056–6065 (2022). https://doi.org/10.1007/s10853-022-07002-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-022-07002-4