Introduction

The electrical properties of glasses containing transition metal oxides (TMO) have been of great interest due to their semiconducting nature and potential of subsequent applications including erasable optical recording media, optical switching devices, laser hosts and second harmonic generation [1,2,3,4,5,6,7,8]. The conduction mechanism in these glasses can be analyzed by several models [9,10,11,12], one of which is the well-developed small polaron hopping theory proposed by Mott [9, 10]. The polaron is a quasiparticle of electron with the accompanying local lattice deformation. In this model, the hopping occurs from transition metal ion at lower oxidation state (Fe2+) to a neighboring ion at higher oxidation state (Fe3+). Therefore, the polaron conduction is correlated with the content of iron ions but also with the ratio of iron ions in different valence states and their proximity. However, some models give more satisfactory network parameters and can better explain the variation of conductivity with temperature [12, 13]. As the Mott theory seems to well-describe the conduction behavior of TMO-containing glasses at high temperatures (> θ/2, where θ is Debye temperature) [9], in the low temperature region, the Schnakenberg model can better clarify the variation of activation energy with temperature observed in many glass systems [12, 14]. Schnakenberg considered that an optical multiphonon assisted hopping process determines the D.C. (direct current) conductivity at high temperatures. As the temperature is lowered, multiphonon processes are replaced by a single optical phonon process and at the lowest temperatures the polaron hops with one or more acoustic phonons making up the difference between the sites [12]. This model was found to be in good agreement with the experimental data for many TMO glass systems and gives reasonable values for the phonon frequency, decay parameter, polaron hopping energy and disorder energy [14,15,16].

TeO2 glasses doped with high levels of TMO such as V2O5 or Fe2O3 are known to be good semiconductors [17]. These glasses showed relatively high conductivities of 10–4 Scm−1 above 400 K. Highly conductive tellurite glasses containing TMOs have potential applicability in electrical devices (e.g., memory switching and gas sensors) [18]. However, to our knowledge, there are so far no reports on electrical properties of BeO containing TeO2-Fe2O3 glasses and glass–ceramic composites. The Be2+ ion is a rather unique cation as it has the highest field strength (charge-to-radius ratio) and electronegativity among all alkaline-earth and alkali ions, and is also characterized by small electronic polarizability, α(Be2+) = 0.008 Å3 [19]. Therefore, the effect of the addition of BeO on the structure of TeO2–Fe2O3 glasses and the associated influence on electrical properties is a fascinating topic. In the present study, we report the synthesis and detailed analysis of electrical properties of Be–Fe–Al–Te–O glasses and glass–ceramics employing different theoretical models.

Materials and methods

Glass preparation

In the present work, five iron-tellurite glasses containing different levels of beryllium oxide were prepared. The glasses have the nominal composition of xBeO–10Fe2O3–(90-x)TeO2 in mol% (designated as 10FexBe), where x = 0, 10, 15, 20 and 25 mol%. Appropriate amounts of reagents BeO (99% Alfa Aesar), TeO2 (99.99% ChemPur GmbH) and Fe2O3 (99.9 + % ChemPur GmbH) were thoroughly mixed in a fume hood. Melting was performed in Al2O3 crucibles at 900 °C for 60 min, under air atmosphere. Melts were poured on a cold brass plate and then were annealed at a temperature of 370 °C for 48 h and cooled to room temperature during in 10 h. As shown by ICP OES analysis the uptake of Al2O3 is significant and will thus be taken under consideration when discussing the experimental results.

Moreover, the prepared samples will be compared with the glass–ceramic composites doped with two times higher Fe2O3 content (20FexBe). Such glass–ceramics were prepared in an analogous way, and the detailed description of their structure and magnetic properties was recently reported [20].

Glass characterization

The amorphous nature of the prepared materials was confirmed by powder X-ray diffraction (XRD). XRD data were collected on a PANalytical PRO MPD instrument with Bragg–Brentano geometry and CuKα1 radiation over a 2θ range of 10°–70° at a step size of 0.013° and step time of 52 s. The XRD measurements were conducted at room temperature.

The chemical composition of the samples was investigated using an inductively coupled plasma optical emission spectrometer (ICP OES, Aviro 200 PerkinElmer). Measurements were taken after dissolution of 0.05 g of the respective glass powders in 5 ml of aqueous solution of HF acid (40%). All ICP OES results are listed in Table 1, where the error margins of ICP-OES analysis were ± 3% for all elements. The oxygen content was determined from the charge requirements of the analyzed cations. In the case of iron ions, the contents of FeO and Fe2O3 were estimated based on XPS measurements. Periodic table mix 1 for ICP measurements (SIGMA-ALDRICH, Products number: 92091) containing Be, Fe, Te and Al ions was used as reference standard.

Table 1 Glasses ID, target and ICP OES analyzed compositions, optical basicity Λth, density ρ, iron-ions concentration NFe-ions and mean Fe–Fe ion spacing R
Full size table

X-ray photoelectron spectroscopy (XPS) was employed for the surface physicochemical examination of the studied samples. The high-resolution XPS analyses were performed using an Escalab 250Xi device (ThermoFisher Scientific, USA), equipped with a monochromatic AlKα source. The adventitious carbon C 1s peak at 284.6 eV was used for the X-axis calibration of the XPS spectra.

The topography of samples was observed by using an Olympus LEXT OLS4000 Confocal Scanning Laser Microscope (CSLM). Color imaging was performed under white LED light and 3D images were obtained using a 405 nm laser and photomultiplier detector. The maximum used objective lens and laser 3D image magnification was 100x, with optical magnification of 2160x. CSLM measurements were conducted on freshly fractured and alcohol cleaned samples.

The structure of the glasses was studied by Raman and IR spectroscopy. Raman spectra were measured at the backscattering geometry on a Renishaw inVia Raman Microscope equipped with a 2400 lines/mm diffraction grating, a high-sensitivity Peltier-cooled charge coupled device (CCD), a motorized xyz microscope stage and × 50 magnification lens. All measurements were taken in the range from 200 to 2000 cm−1 at room temperature with 2 cm−1 resolution. The 514.5 nm line of an Ar ion laser was used for excitation, employing ca. 0.10 mW/μm2 at the glass sample to avoid decomposition. Examination of the glasses after the end of each measurement showed no signs of laser-induced modifications when using the Raman microscope. The sample spot size of the Raman microscope is about 0.5 µm in diameter. Raman spectra were acquired for each glass under VV and VH polarizations, where the first letter indicates the polarization of the exciting laser beam and the second letter the polarization (V: vertical, H: horizontal) of the scattered light. Unpolarized Raman spectra, VV + VH, were also measured. The estimated error in Raman band position was ± 1 cm−1.

The infrared (IR) spectra were measured on a vacuum Fourier-transform spectrometer (Bruker, Vertex 80v) in quasi-specular reflectance mode (11° off-normal). For each spectrum, 400–2000 scans were collected at room temperature with 4 cm−1 resolution and averaged for evaluation. Reflectance spectra were measured separately in the far- and mid-IR ranges and then merged to form a continuous spectrum in the range 30–7000 cm−1. Analysis of the reflectance spectra by Kramers–Kronig transformation yielded the absorption coefficient spectra, α(ν) [21]. The estimated error in infrared band position was ± 2 cm−1.

Density and electrical properties measurements

Density was evaluated based on Archimedes principle with the use of distilled water as an immersion fluid. The density measurements were conducted three times for each sample. The iron ion concentration (NFe-ions) given as ions cm−3 was calculated based on the measured densities and composition, according to relation:

$$N_{{{\text{Fe}} - {\text{ions}}}} = \frac{{2*\rho *n_{{{\text{Fe}}_{2} {\text{O}}_{3} }} *N_{A} }}{{M_{{{\text{Fe}}_{2} {\text{O}}_{3} }} }}$$
(1)

Here ρ is the glass density (in gcm−3), MFe2O3 is the molar mass of the Fe2O3 (in gmol−1), nFe2O3 is the Fe2O3 mole ratio and NA is the Avogadro constant. The relationship between Ni and Ri, where Ri is the mean distance between i-ions, is generally described as follows:

$$R_{i} \approx N_{i}^{{ - \frac{1}{3}}}$$
(2)

This relation is a quite good approximation for calculating the mean distance between i-ions in homogenous glasses where ions are assumed to be distributed uniformly in the glass network. This condition is not fulfilled for samples 20FexBe in which Fe2O3 is accumulated in crystallites and, therefore, the R-value is taken here as a rough approximation.

Impedance spectroscopy measurements were conducted in the frequency range from 10 mHz to 1 MHz and the temperature range from 213 to 473 K, with an AC voltage of 1 Vrms, using the Novocontrol Concept 40 broadband dielectric spectrometer Alpha-A, equipped with ZG4 dielectric interface. The temperature step was 10 K. For the electrical measurements, gold electrodes were evaporated in vacuum at the polished plane parallel surfaces of circular samples. Measurements were taken under a nitrogen atmosphere using Quatro Cryosystem temperature-controlling system.

Results and discussion

Glass formation and reaction of aluminum crucible with the melt

Table 1 presents the target and measured compositions. The sample names are based on the Fe2O3 (10 or 20) and xBeO contents in mol% (x = 0, 10, 15, 20 or 20). A significant loss of Be is observed, especially in samples containing lower amount of iron (10FexBe). All melts dissolved also significant amount of aluminum, which originates from the crucible material and is included in the analyzed compositions (see Table 1). The highest amount of Al2O3 is observed for samples undoped with BeO in both series (10Fe0Be and 20Fe0Be) and it decreases with an increase in the BeO to the nominal composition as shown in Fig. 1. This phenomena is in contradiction with the observation made for sodium-silicate glasses doped with lithium and beryllium, where the dissolution of Al2O3 in the melts was found to be the highest for glasses with the highest BeO amount [22]. Moreover, the content of Al2O3 in the present samples is higher than for the ones containing a lower amount of Fe2O3 and consequently higher levels of TeO2. This can be explained by the high solubility of Al2O3 in TeO2 [23]. Figure 2 presents the density versus beryllium content for all samples. The density decreases with the increase in the Be content. Moreover, similar behavior was found also for the sum of Be and Al concentration as shown in the inset of Fig. 2. This observation can be explained by the light mass and low density of beryllium (1.85 g cm−3) and aluminum (2.7 g cm−3) in comparison with the higher mass and densities of Te (6.24 g cm−3) and Fe (7.87 g cm−3).

Figure 1
figure 1

Correlation between Al content and the nominal Be content of samples. Two confocal microscope pictures of freshly fractured glasses are also shown: 10Fe0Be (left) and 10Fe20Be (right)

Full size image
Figure 2
figure 2

Density as a function of Be content for 10FexBe glasses and 20FexBe glass–ceramics. Inset shows density as a function of the sum of Al and Be contents for 10FexBe glasses and 20FexBe glass–ceramics

Full size image

Quenching of the beryllium-iron-tellurite melt resulted in black and non-transparent glass samples when considering mm thick pieces. Figure 1 displays exemplar confocal microscope micrographs of the topography of glasses 10Fe0Be (left) and 10Fe20Be (right). The results for other 10FexBe samples are similar and show the homogenous surfaces typical for glassy materials. The amorphous nature of the synthesized 10FexBe samples was confirmed by X-ray diffraction. The absence of any crystalline phases is apparent from Fig. 3. For comparison, the XRD study of 20FexBe samples showed that they are glass–ceramic composites containing Fe2O3 crystallites dispersed in the glass matrix [20].

Figure 3
figure 3

X-ray diffraction spectra of the prepared 10FexBe materials

Full size image

Optical basicity, Λ, is a parameter that often correlates with the level of depolymerization of a conventional glass network where it will be higher as more non-bridging oxygen atoms and ionic bonds occur than for a more polymerized network with covalent bridging bonds between oxygen and network former atoms [24]. In our previous paper [25], we have shown a correlation between glass basicity calculated on the basis of the glass composition and its role on niobate dissolution from the crucible. Therefore, we examine here the presence of a similar dependence between optical basicity and Al dissolution from the crucible. The theoretical optical basicity for any oxide glass of composition aAxOy–bBpOq—… can be evaluated with the use of the Duffy and Ingram relation [26, 27]:

$${\Lambda }_{{{\text{th}}}} = \frac{{X_{A} }}{{\gamma_{A} }} + \frac{{X_{B} }}{{\gamma_{B} }} + \ldots = \frac{ya}{{ya + qb + \ldots }}{\Lambda }\left( {A_{x} O_{y} } \right) + \frac{qb}{{ya + qb + \ldots }}{\Lambda }\left( {B_{p} O_{q} } \right) + \ldots$$
(3)

where 1/γA = Λ(AxOy)… is the optical basicity of oxide AxOy, etc. As seen in Eq. (3), the oxide basicities are weighted by their oxygen equivalent fractions \(X_{A} , \,{\text{etc}}\)., to calculate the glass basicity. Values of Λ for single oxides have been tabulated by various research groups and are constantly expanded to oxides and nitrides of other elements, as well as refined and updated [19, 24, 27, 28]. The values of optical basicity of the studied samples were calculated according to relation (3), using the optical basicity values of the various oxides listed in ref. [29] with Λ(BeO) = 0.375, Λ(Fe2O3) = 0.8, Λ(FeO) = 0.93, Λ(Al2O3) = 0.61 and Λ(TeO2) = 0.93, and are reported in Table 1. As can be seen, despite being the network former, the large Te4+ cation has a much higher polarizability than the small high field strength modifier cation Be2+, possibly decoupling the polarizability and optical basicity from the degree of polymerization. According to our expectations, Fig. 4a presents an increasing content of dissolved Al with higher optical basicity, especially for the glass series 10FexBe. Therefore, the highest basicity was found for those glasses that ultimately dissolve the most aluminum indicating that TeO2 supports Al2O3 dissolution. Since higher cation mass (Te, Fe) is correlated to higher polarizability and optical basicity, we see a clear correlation density and optical basicity, as displayed.

Figure 4
figure 4

The correlation between optical basicity and Al content (a), and density (b) for all studied samples. Line in (b) is a guide for eyes

Full size image

Besides obtaining the total Fe content (Table 1), we have carried out XPS measurements for both series to estimate the ratio of iron in its different valence states Fe2+ and Fe3+. As an example, the XPS Fe 2p spectrum recorded for sample 20Fe25Be is displayed in Fig. 5a where the proposed deconvolution model consists of four peak doublets. The primary components, with Fe 2p3/2 located at 710.8 and 712.9 eV, respectively, should be ascribed to Fe3+ species like in oxides [30, 31]. Such compounds are always high-spin, leading to complex multiplet split spectra. The smaller component negatively shifted at 709.3 eV lies in the energy range characteristic of Fe2+ compounds [32]. Finally, the broad satellite Fe 2p3/2 feature typical for iron (III) oxides is distinguishable at approximately 719 eV. Based on the deconvolution results, it is possible to estimate Fe2+ and Fe3+ relative contents in each studied sample as listed in Table 2 in terms of the ratio [Fe2+]/([Fe2+] + [Fe3+]). It can be seen that iron is primarily present in the higher valence state and the content of Fe2+ varies between 6.5% (sample 20Fe15Be) and 11.4% (sample 10Fe25Be). This finding is in agreement with earlier studies that showed that a glass matrix of higher optical basicity favors higher oxidation states[33]. However, there is no direct correlation between the composition and the relative content of iron (II) in the studied samples. Moreover, the XPS results confirm that tellurium ions are present only in the Te4+ oxidation state in all samples (Fig. 5b). Also, the presence of Al3+ ions was confirmed (not shown in graphs), while the Be 1s signal cannot be properly evaluated as it is strongly overlapped by the Te 4d signal.

Figure 5
figure 5

High-resolution XPS spectra recorded in a Fe 2p and b Te 3d core-level binding energy range for sample 20Fe25Be

Full size image
Table 2 D.C. conductivity at 273 K σDC, and parameters obtained by fitting the conductivity data to the Schnakenberg polaron hopping model (Eq. 6): phonon frequency ν, Debye temperature θ, polaron hopping energy WH and disorder energy WD; mean activation energy at high temperature region W (Eq. 7), total content of Fe-ions [Fe] (from Table 1), the ratio of Fe-ions on different valence states C = [Fe2+]/([Fe2+] + [Fe3+]) (from XPS results), the effective content of Fe-ions which takes part in conduction process C(1-C), and information about structure of samples. The results are given with the mean accuracy of ± 95%
Full size table

Short-range-order structure by Raman and infrared spectroscopy

The detailed analysis of the short-range-order (SRO) structure of the 20FexBe series was conducted in our previous work [20]. Here, we will focus on the Raman and IR spectra of the 10FexBe series. The polarized Raman spectra are measured in parallel (VV) and cross (HV) polarization to assist the assignment of Raman bands to symmetric (polarized) or asymmetric (depolarized) vibrational modes [34]. The Raman results for the compositions with the lowest (10Fe0Be) and the highest (10Fe25Be) Be content are shown in Fig. 6 (top) and (bottom), respectively. The Raman spectra show three intensive and polarized bands at ~ 447, ~ 670 and ~ 765 cm−1 which are attributed to symmetric vibrational modes. The first and most intense band at ~ 447 cm−1 can be assigned to the symmetric stretching-bending mode of Te–O–Te single bridges, νs(Te–O–Te) [35, 36]. The ~ 670 cm−1 component can be attributed to the symmetric stretching/breathing mode of Te–O2–Te double bridges, νs(Te–O2–Te), connecting TeO4 trigonal bipyramids (tbp’s) sharing an edge, that is two bridging oxygen atoms [35]. The band at ~ 765 cm−1 is due to the symmetric stretching of TeO32– trigonal pyramids (tp’s) with three terminal oxygen atoms, without excluding some contribution from TeO3+1 polyhedra [23, 36]. The main difference in the Raman spectra of pure TeO2 glass [35, 36] and that doped with 5 at% Fe and 5 at% Al (10Fe0Be) is the dominant presence in the latter of the band at ~ 447 cm−1. This intensity enhancement for 10Fe0Be can be correlated with the formation of Al–O–Te and Fe–O–Te bridges, as it was found also for the 20Fe0Be sample [20]. Consequently, the tellurite network of glass 10Fe0Be is more depolymerized than TeO2 glass through transformation TeO4 → TeO3+1 → TeO32−, leading to the formation of Al–O–Te and Fe–O–Te bridges in addition to Te–O–Te bridges.

Figure 6
figure 6

Polarized Raman spectra in parallel (VV, red) and cross (HV, blue) polarization for samples: (a) 10Fe0Be and (b) 10Fe25Be

Full size image

Comparison in Fig. 6 of the VV polarized Raman spectra of samples before (10Fe0Be) and after doping with BeO (10Fe25Be) shows a slight increase of the relative intensity of the envelopes at ~ 670 cm−1 relative to those at ~ 765 cm−1 and 447 cm−1 after adding BeO. Also, the intensity of the ~ 670 cm−1 band was found to slightly increase relative to that at ~ 765 cm−1 in the order 10Fe15Be < 10Fe20Be < 10Fe25Be, suggesting the increase in content of TeO4 unit over the TeO32– and the TeO3+1 modified tellurite polyhedra [20]. Of interest is also the comparison between samples 10Fe0Be and 10Fe10Be which contain a similar amount of Fe-ions but part of Al3+ is substituted by Be2+ with a lower valence state. This substitution was found to result in a very slight increase in the polymerization of tellurite network, i.e., increase of the relative content of TeO4 units.

Unpolarized (VV + VH) Raman spectra for 10FexBe series are displayed in Fig. 7. The results were background corrected and normalized to the stronger band at ~ 447 cm−1 to facilitate comparison. The increase in the intensity of the band at ~ 670 cm−1 relative to that at ~ 765 cm−1 is noticeable. The observed changes are in accordance with the increase in Be content as well as the total content of all modifiers in glass (10Fe0Be < 10Fe10Be < 10Fe20Be < 10Fe15Be < 10Fe25Be). It suggests the increase in polymerization of the tellurite network for samples doped with BeO in comparison to the undoped one. A similar influence of BeO was observed for samples 20FexBe in which doping with BeO caused also the increase of tellurite network polymerization [20]. It was found that the presence of BeO supported the crystallization process of Fe2O3 and, consequently, the residual glass network was poorer in modifier oxides and became more polymerized. In the case of glasses 10FexBe no crystallinity was found, even for the glass with the highest content of BeO. However, a clear correlation between BeO addition and reduction of Al2O3 dissolution was noticed. Therefore, most probably the increased polymerization in this case is due to the decrease in the Al content found for beryllium-containing glasses.

Figure 7
figure 7

Unpolarized (VV + VH) Raman spectra of all 10FexBe glasses scaled on the 440 cm−1 band. Spectra were background corrected and normalized to the band at 440 cm−1

Full size image

To conduct the full analysis of glasses structure, the infrared spectra were also studied and are reported in Fig. 8. IR spectroscopy is complementary to Raman in that the asymmetric vibrational modes of the tellurite network are usually strongly active in the infrared. The main broad and asymmetric IR band is found at ~ 700 cm−1 and results from the convolution of the asymmetric stretching modes of TeO32–, TeO3+1 and TeO4 units [20, 23]. For the pure TeO2 glass, the strongest infrared absorption band was observed at ~ 655 cm−1 [35, 36]. For sample 10Fe0Be, the shift to higher frequencies (~ 702 cm−1) confirms the presence of the TeO32– and TeO3+1 units besides TeO4 units. Moreover, additional broadening at high frequencies may result from weaker contributions of the Al–O stretching in [AlO4/2]− tetrahedra which absorb above 700 cm−1 [22]. The slight shift of the main band envelope to lower frequencies is visible for all Be-doped glasses, with sample 10Fe20Be exhibiting the main band at the lowest frequency of ~ 680 cm−1. This is a confirmation of increasing tellurite network polymerization as observed by Raman spectroscopy. The small envelope at ~ 463 cm−1 can be correlated with the presence of the modifier Fe ions which in the tellurite network would probably form FeO6 octahedral units [37]. Finally, the broad and weak envelop at 310 cm−1 is mainly due to stretching-bending vibrations of O–Te–O and Te–O–Te bonding in various tellurite configurations [35].

Figure 8
figure 8

IR spectra of 10FexBe glasses. The spectra are off set for clarity

Full size image

Electrical properties

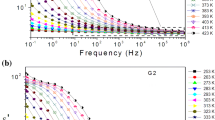
The conductivity behavior was measured for both series of samples 10FexBe and 20FexBe. Figure 9 presents the real part of conductivity as a function of frequency at different temperatures for samples: 10Fe25Be (Fig. 9a), 20Fe20Be (Fig. 9b) and 20Fe25Be (Fig. 9c). The conductivity spectra versus frequency demonstrate a D.C. (direct current) plateau at lower frequencies and an A.C. (alternating current) region of a linear (in log–log scale) increase of conductivity with frequency. Only sample 20Fe20Be was found to show an additional relaxation process in the A.C. part; its shift with temperature suggests that it is thermally activated (Fig. 9b).

Figure 9
figure 9

The real part of conductivity versus frequency shown for selected temperatures for (a) 10Fe25Be, (b) 20Fe20Be and (c) 20Fe25Be. The lines present the Jonscher relation fit (Eq. 4)

Full size image

The conductivity behavior of almost all tested samples (besides 20Fe20Be) can be analyzed using the Jonscher relation, known also as an universal dynamic response [38]:

$${\text{Re}}\sigma (\omega ) = \sigma_{{{\text{DC}}}} (T) + A(T)\omega^{{({\text{ST}})}}$$
(4)

Here Reσ(ω) is the frequency-dependent real part of conductivity, σDC is the frequency-independent D.C. conductivity, A is a coefficient and s is an exponent which depends on temperature and material properties. The part Aωs describes the A.C. dispersion. Elliott [39] examined the dependence of the exponent factor s on temperature for various conduction mechanisms in glasses. Here we compare this set of dependencies to values of s estimated from our experimental data by the means of nonlinear data fitting. The obtained values of exponent s are presented versus temperature in Fig. 10. As can be seen the values slightly decrease with the increase in temperature for all samples. In the case of samples 10FexBe and 20Fe0Be s varies between 0.7 and 0.5, while glass–ceramic composites 20Fe10Be, 20Fe15Be and 20Fe25Be exhibit higher values of s between 0.9 and 0.7. For the sample 20Fe20Be the estimation of the s parameter was impossible due to the additional relaxation process at the A.C. part. Comparing the values of exponent s and its temperature behavior to the models discussed by Elliott [39], we suggest that in our homogenous glasses the conduction process may be due to the overlap of polaron tunneling mechanism. In addition, for the glass–ceramics doped with higher content of Fe2O3 the quantum mechanical tunneling between semiconducting crystallites of iron oxides can be proposed.

Figure 10
figure 10

Temperature dependence of s parameter, obtained by fitting the Jonscher relation to conductivity spectra of the studied materials (Eq. 4, Fig. 9)

Full size image

Usually, when the A.C. conductivity of glass comprises relaxation processes the analysis of the impedance spectra can be helpful in determining the conduction mechanisms. Figure 11 (left) displays the Nyquist plot (imaginary versus real part of impedance Z) for sample 20Fe20Be measured at 333 K. Two semicircles are clearly visible, which indicate two relaxation processes. For all other samples, only one distinct and flattened semicircle was observed. The impedance spectra were modeled using the Cole–Cole empirical relation which describes a relaxation by the means of equivalent circuit consisting of a resistance and a CPE (constant phase element and CPE impedance Z−1CPE = \(\left( {j\omega \tau } \right)^{1 - \alpha }\)) connected in parallel [38, 40]:

$$Z^{*} = \frac{R}{{1 + \left( {j\omega \tau } \right)^{1 - \alpha } }}$$
(5)

where Z* is the complex impedance, R is the equivalent resistance of a process, τ is the mean dielectric relaxation time, ω is the angular frequency and α is a parameter which describes the width of the relaxation time distribution. For α = 0 there is no dispersion (Debye response) and CPE is equivalent to the capacitance, but when α > 0 the capacitor cannot be directly defined, reflecting the distributed nature of the response. Our modeling with the use of Cole–Cole relation allows separating components of the conductivity processes taking place through the different composite regions like the crystalline phase and the amorphous glass matrix. The best fitting results for the sample 20Fe20Be were obtained with a superposition of two Cole–Cole relaxation processes as shown in Fig. 11. The obtained resistivity values were converted to conductivities with the use of sample and electrode sizes and are shown in Fig. 11 (right) as a function of temperature. The conduction process which proceeded at high frequency region exhibits slightly higher conductivity values than the one found at low frequencies. The estimated conductivities do not follow the Arrhenius law suggesting that their activation energy changes with temperature. It was also confirmed based on the analysis of derivative conductivity which was found not to be constant.

Figure 11
figure 11

(left) Nyquist plot of sample 20Fe20Be at temperature of 333 K with the fitting results of 2 Cole–Cole relations. (right) Conductivities values of two relaxation processes obtained from fitting the Nyquist plots and the Schnakenberg relation fit results

Full size image

Schnakenberg has presented a model for non-adiabatic regime of polaron hopping [12]. According to his model, the activation energy of conductivity changes with temperature and the conductivity versus temperature may be described by [12]:

$$\sigma = \frac{A}{T}\sqrt {{\text{sin}}h\left( {\frac{h\vartheta }{{KT}}} \right)} {\text{exp}}^{{ - \frac{{4W_{{\text{H}}} }}{h\vartheta }{\text{tan}}h\frac{h\vartheta }{{4KT}}}} {\text{exp}}^{{ - \frac{{W_{{\text{D}}} }}{KT}}}$$
(6)

where A is a constant, ν is a phonon frequency, WH is a hopping energy and WD is a structural disorder energy between hopping sites. Equation (6) is fitted to the data at Fig. 11 (right) and the results are listed in the figure in frames. The fitting results are in good agreement with the experimental data. Interestingly, the obtained values of WH and WD of the two relaxation processes (conducted at high and low frequency regions), as well as ν and estimated Debye temperatures θ are close to each other. This suggests that these two conduction processes are due to a similar conduction mechanism: hopping of polarons between iron ions at lower valence state Fe2+ to neighboring ion with the higher oxidation level Fe3+. The structure of crystallites is more ordered than the structure of residual glass matrix, therefore slightly lower values of disorder energy and phonon frequency suggest that the high frequency process is due to conduction process within Fe2O3 nanocrystallites. The low frequency process is connected with the iron ions dispersed within the residual glass matrix.

The same fitting procedure of Nyquist plots was done for the other glass–ceramics using one and two Cole–Cole relaxations. Significantly better fitting was obtained for the two Cole–Cole relaxations. It suggests that impedance spectra of these materials result from two relaxation processes which strongly overlap. However, as the results of fitting the Schnakenberg relation to conductivity values show similar behavior as for sample 20Fe20Be, we decide to present and compare only the D.C. conductivity behavior to simplify the analysis.

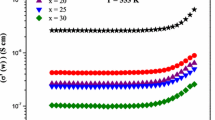
The D.C. conductivity was obtained by fitting the data in Fig. 9 with the Jonscher relation (4) and are plotted in Fig. 12. The D.C. conductivity was found to be higher for samples 20FexBe doped with the highest Fe content. Moreover, a clear correlation between Fe-ion concentration (estimated based on density and Fe content, see Table 1) and the D.C. conductivity values is observed, especially for the glass samples (Fig. 13a). In the case of glass–ceramics, the D.C. conductivity results from the conduction processes through nanocrystallites, the glass matrix and possible grain boundaries. In this case, the D.C. conductivity will not follow strictly the total content of iron ions. Mott [9] noticed that polaron jumps between nearest neighboring ions are possible when they are of different valence states. If C is the ratio between the concentration of transition metal ions in the low valence state to the total concentration of transition metal ions, C = [Fe2+]/[Fe2+] + [Fe3+] then concentration of hopping sites is proportional to C(1-C). A correlation between D.C. conductivity and C(1-C) multiplied by the Fe-ion concentration is visible (inset of Fig. 13a). It confirms that in our samples, the conductivity of homogenous glasses is mostly influenced by the effective concentration of carriers participating in charge transport. The D.C. conductivity shows good agreement with Schnakenberg relation (red lines in Fig. 12). Analysis of Schnakenberg relation (6) fitting results is listed in Table 2 for all samples. It is apparent that WH and WD values found for glass–ceramics are lower than for glasses, and this was associated to the higher amount of carriers. The highest value of disorder was achieved for glass 10Fe0Be which also showed the highest depolymerization of the tellurite network of all glasses. The lowest value of hopping energy was detected for the sample 20Fe20Be in which the effect of nanocrystallites was also clearly visible in the impedance spectra.

Figure 12
figure 12

D.C. conductivity estimated from Figs. 9 (Eq. 4) as a function of temperature. Lines shows the Schnakenberg model fit (Eq. 6). The mean adjusted R2 value of fitting was found to be 0.999 for all samples

Full size image
Figure 13
figure 13

(a) D.C. conductivity at 273 K as a function of iron ion concentration for all studied samples. Inset in (a) shows the correlation of D.C. conductivity and effective concentration of iron ions taking place in the conduction process for all samples. (b) Polaron hopping energy versus mean iron ions spacing. Inset in (b) displays the high temperature activation energy estimated on the basis of Eq. 7 as a function of effective concentration of iron ion taking place in conduction process

Full size image

It was shown by Mott that the hopping energy is WH ~ rp−1 − R−1, where R is a mean distance between iron ions (listed in Table 1) and rp is the polaron radius [9]. In the case of overlap polaron hopping rp << R, and therefore WH should show a dependence on R as found for our samples in Fig. 13b. The hopping energy decreases as the mean distance between iron ions decreases. At the high temperature region the activation energy W, arising from electron-lattice interactions and static disorder, is given by:

$$W = W_{{\text{H}}} + \frac{{W_{{\text{D}}} }}{2}, \;T > \frac{{\theta_{{\text{D}}} }}{2}$$
(7)

where θD is Debye temperature (θD = hν/K, h is the Plank´s constant). The values of estimated W values are listed in Table 2 and plotted in the inset of Fig. 13b as a function of the effective concentration of carriers taking place in the transport. It can be seen that the estimated activation energy decreases with the increase in carrier concentration for both series of samples. The values of phonon frequencies obtained from fitting the Schnakenberg relation (Table 2) appear to be larger than typical ones (1013 s−1 rather than 1012 s−1); however, similar high results were found for vanadate-tellurite glasses [15]. The phonon frequency was used to estimate the Debye temperature for all samples (Table 2). Like the phonon frequencies, the Debye temperatures were found to be rather high, i.e., between 979 and 1464 K. However, it is hard to define the meaning of a Debye temperature in disordered materials, in analogy to the temperature of a crystal corresponding to highest frequency normal mode of vibration.

Conclusions

Beryllium tellurite glasses with high iron content were prepared and studied for their structure and properties, with a special emphasis on their electrical properties. The glasses contained significant amounts of alumina from crucible dissolution. The series containing 10 mol% Fe2O3 was amorphous, while the earlier studies series with 20 mol% Fe2O3 was partially crystalized. Divalent Fe2+ was identified by XPS as a minority species with a ratio to the total Fe content less than 0.11. Infrared and Raman spectroscopy showed only minor structural changes as BeO replaces TeO2 in the xBeO–10Fe2O3–(90-x)TeO2 series. Contrary to conventional glasses, where the network modifier such as Si, B or P has a lower polarizability than the network modifier, is the high field strength cation Be2+ less polarizable than the large Te4+ network former cation. Alumina dissolution seems to be linked to the basicity of the melts rather than the number of non-bridging oxygen atoms, and through the dissolution of the crucible material Al2O3 is taken up by the melt, which in turn heightens the number of non-bridging oxygen in the BeO poor, high basicity glasses.

The comparison of Jonscher universal dielectric response and theoretical models collected by Elliott revealed that in glasses the conduction process is due to the overlap polaron tunneling. In glass–ceramics the quantum mechanical tunneling between semiconducting crystallites of iron oxides is proposed as a secondary mechanism. The D.C. conductivity behavior was analyzed based on the Schnakenberg model and the energy of polaron hopping and disorder were estimated. Fitting model parameters show that phonon frequency is rather high and polaron energy term due to disorder is larger in glasses than for glass–ceramics.