Introduction

In a computational material design (CMD) framework, quantitative modelling of precipitation kinetics has its essential position. Hence, significant effort has been devoted to the building of appropriate integrated computational material engineering (ICME) methodologies that tackle precipitation. Their successful implementation enabling predictive precipitation modelling for certain alloy systems would facilitate more efficient CMD for designing those alloys and their heat treatments. One alloy category where precipitation is critical is precipitation hardening (PH) stainless steels. They have a martensitic microstructure with excellent mechanical properties and considerable corrosion resistance. Their industrial applications span machine components, aircraft fittings and pressure vessels [1,2,3,4,5]. During manufacturing, the final heat treatment is quench-hardening to form the supersaturated martensite, followed by an ageing treatment at about 450–525 °C to stimulate precipitation from the supersaturated matrix [6,7,8]. These alloys can make use of multiple alloying elements for the precipitation [9,10,11,12,13,14,15], Cu being one of the most common elements. Cu has high solubility in the austenite and low solubility in the martensite, and its high supersaturation in the martensite enables the formation of a significant amount of very fine precipitates early during ageing [16, 17]. Furthermore, Cu is an inexpensive alloying element. The impact of Cu precipitation on mechanical properties of PH stainless steels such as 17-4 PH [4, 18] and 15-5 PH [5, 6, 19,20,21] has been extensively studied in the past few decades. For example, Habibi and co-workers [5, 6, 20] presented thorough experimental investigations of the microstructure, characterized mostly by transmission electron microscopy (TEM), and mechanical property evolution for various ageing treatments of 15-5 PH stainless steels. Later works have utilized atom probe tomography (APT), which enables also the quantification of the precipitate composition [4, 17, 19]. Wang et al. [17] used APT to investigate the Cu precipitation in 17-4 PH stainless steels aged at 450 °C from 0.5 h up to 200 h. They found that the Cu precipitates start to precipitate with a low Cu concentration and, moreover, they have a core–shell structure with Ni–Al–Mn-rich shells surrounding the core Cu-rich particles [22, 23]. Similar core–shell structures have also been found by Laurent et al. [19] and Yeli et al. [4].

As mentioned above, precipitation modelling is key for CMD, and there are several modelling tools available to simulate precipitation. These tools all have different capabilities and purposes, and the tool must be carefully chosen for the research at hand. Microscopic models such as Kinetic Monte Carlo (KMC) are useful for simulating early stages of the precipitation, i.e. nucleation. KMC can aid understanding of mechanisms acting on a very fine scale due to its inherent atomic-scale treatment [24, 25]. KMC is, however, somewhat limited when it comes to elasticity aspects of non-coherent precipitates. Cluster dynamics (CD) is also atomistic modelling, but it operates more on the mesoscopic level, allowing for slightly longer kinetic simulations [26]. However, CD is not suitable to describe the full precipitation kinetics. Both KMC and CD have been successfully applied to precipitation of Cu particles in Fe–Cu-based materials and can handle the enrichment of the initially diluted Cu precipitates with time [27, 28]. The drawbacks with these approaches, especially for CMD, are the computational cost and the parametrisation. They are not coupled with CALPHAD (CALculation of PHAse Diagram) types of databases that can provide parametric input on multicomponent thermodynamics and kinetics. On the other hand, mesoscopic scale modelling using the phase field (PF) method has been performed with CALPHAD database coupling. PF simulations of Cu precipitation in steels with nuclei diluted in Cu with respect to the equilibrium composition have been studied [27, 28]. However, PF method cannot naturally account for nucleation and is therefore not the most appropriate method for studying early stages of precipitation. The computational cost is also limiting in PF, especially when it is supposed to be used in CMD. In this case, macroscopic types of approaches like the Langer–Schwartz–Kampmann–Wagner (LSKW) [29] approach for precipitation modelling have the advantages that they can account concomitantly for nucleation, growth and coarsening of a distribution of precipitates, are fully coupled with CALPHAD databases and have been applied to numerous complex alloy systems, showing promising results [30,31,32]. However, the precipitation behaviour in multicomponent grades requires major attention because of the complex interconnection between capillary effects and diffusion fluxes couplings [33]. Prior works using LSKW precipitation modelling have been performed on binary Fe–Cu alloys and multicomponent steels with Cu precipitation [30, 34, 35]. For example, Stechauner et al. [35] modelled Cu precipitation in a Fe–Cu binary system, and the results were in good agreement with experimental details. Furthermore, Yang et al. [34] developed and applied a numerical model to simulate Cu precipitation in the Fe–C–Mn–Cu quaternary system, showing reasonable results by comparing with experimental works. Even though the modelling efforts in the literature have shown promising results, it appears as if one aspect has not been studied in detail. From the experimental literature, it is clear that the composition of the precipitates varies during the ageing treatment and this should be a key aspect to consider in the modelling to enable predictive simulations.

In the present work, we aim to evaluate state-of-the-art implementations of LSKW [29, 36] precipitation modelling for precipitation simulations in PH stainless steels. Different model implementations and assumptions are compared, and particular attention is paid to the treatment of the composition of the precipitates by comparing to new APT measurements. The modelling is furthermore compared to a few experimental datasets from the literature in order to evaluate the feasibility of using LSKW modelling for CMD in PH stainless steels where it will mostly be important to accurately predict trends with respect to alloying and heat treatment conditions. These trends, or inter-/extrapolations, will strongly depend on CALPHAD database reliability, and it is therefore also assessed.

Methodology

The assessment of LSKW modelling for predicting precipitation requires knowledge of the equations driving the models and their implementation in the mean-field framework as well as experimental data to compare with. The latter allows for validation (and calibration) of the modelling results, but equally important is the insights in the microstructure development that experiment brings and which is essential for making proper assumptions in the modelling. In this section, we describe the experimentally investigated materials and heat treatments (both from the literature and new APT experiments performed herein) as well as key aspects of mean-field LSKW modelling of precipitation.

Materials and heat treatments

Three sets of APT data on Cu precipitation in PH stainless steels are used to compare with the LSKW modelling in this work. APT analysis of Cu precipitation in a 15-5 PH steel (denoted as Alloy A) is performed here, and the other two sets of APT data for Cu precipitation in 17-4 PH steels originate from the works of Wang et al. [17] (Alloy B) and Yeli et al. [4] (Alloy C). All three alloys are exposed to solution treatment for 1 h at slightly different temperatures before quenching in water or oil. Thereafter, all three alloys are exposed to isothermal ageing at temperatures between 450 and 500 °C for different durations. The experimental conditions, including chemical compositions and heat treatments, are summarized in Table 1.

Table 1 Compositions and heat treatments of alloys investigated in the present work
Full size table

Atom probe tomography (APT)

APT specimens are prepared by first cutting 0.7 × 0.7 × 15 mm3 specimens from the aged samples, grinding to 0.5 × 0.5 × 15 mm3, before standard two-step electrolytic polishing. The samples are firstly polished using a 25 vol% perchloric/acetic acid solution at 12–16 V, followed by a second-step of polishing to suitable sharpness using 2 vol% perchloric acid in 2-butoxyethanol solution at 4–6 V. The APT measurements are performed using a local-electrode atom probe (CAMECA LEAP 4000X-HR) equipped with an energy-compensating reflectron for improved mass resolution. The measurements are conducted in laser-assisted mode using a UV laser power of 60 pJ at 50 K with a pulse frequency of 200 kHz, pulse fraction of 20% and detection rate of 0.5%. The data are reconstructed and analysed utilizing CAMECA Integrated Visualization and Analysis Software (IVAS) version 3.8.0. To quantitatively analyse the composition, mean radius, number density and volume fraction of Cu precipitates in each specimen and try to avoid bias, 10 at.% Cu isoconcentration is used to define the precipitate–matrix interface for all conditions. Thereafter, the mean radius of Cu precipitates in each sample condition is calculated by averaging the radii of all fully contained precipitates under assumption of a spheroidal shape. The number density is calculated by averaging the two values evaluated with and without counting the number of partially contained precipitates in the tip volume. The average volume fraction of Cu precipitates in each condition is firstly evaluated by averaging the volumes of fully contained precipitates, before the volume fraction of Cu precipitates is calculated based on the precipitate average volume and the aforementioned number density. Two methods are used to evaluate the Cu concentration in the precipitates in this work: (i) the Cu concentration in each fully contained precipitate is evaluated by proxigram analysis as exemplified in Fig. 1, and the average for all particles is calculated. This is denominated as ‘average composition’ from here on; (ii) the proxigram analysis of all the Cu precipitates is also carried out to estimate the Cu concentration in the centre of the precipitates, denominated as ‘core composition’.

Figure 1
figure 1

One proxigram analysis showing the method used to evaluate Cu concentration in a Cu precipitate

Full size image

Precipitation modelling

Langer–Schwartz–Kampmann–Wagner (LSKW) approach

The LSKW approach is implemented in the two software, TC-PRISMA and MatCalc [36,37,38,39,40,41], used in the present work. The modelling approach enables to track the precipitate size distribution (PSD) as a function of time during a given thermal treatment. It is a mean-field approach because all the precipitates share the same homogeneous environment, i.e. the same homogeneous matrix, and is based on the LSKW approach, also known as numerical Kampmann–Wagner (NKW) [36] method. We consider in the following that spherical precipitates of phase β are created from a supersaturated matrix α in a multicomponent alloy made of n elements, \(i = 1, \ldots ,n\). Despite that this method can simulate the precipitation of several precipitate phases at the same time, for the sake of simplicity and our own interest in this study we here only describe the models with one precipitate phase.

In the LSKW approach, the continuity equation describing the evolution of the size distribution of precipitates is expressed as:

$$\frac{\partial f(r,t)}{\partial t} =- \frac{\partial }{\partial r}(f(r,t)v) + j(r,t)$$
(1)

where \(f(r,t)\) is the size distribution of precipitates, \(j(r,t)\) is the nucleation rate, and \(v\), \(r\) and \(t\) are the velocity of the moving interface between a precipitate and the matrix, the precipitate radius and the time, respectively. The first term on the right-hand side accounts for the size change of precipitates due to their growth or coarsening, while the second term on the right-hand side accounts for the newly formed particles due to nucleation.

The main features of the LSKW model are:

  • The time integration of the size distribution evolution is performed with the precipitate distribution treated as discrete classes of precipitates of identical radius and chemical composition [42].

  • The entire simulation is discretized into small isothermal time increments.

  • Within these time intervals, the nucleation rate is evaluated for each precipitate class and new size classes are added to the list of existing classes if applicable.

  • In the same time step, for each existing class, the growth rate is evaluated and the radii and chemical compositions of the size classes are updated.

From the PSD, it is possible to evaluate the mean size, total number density and volume fraction of the precipitates and thus to track them as a function of time while solving Eq. 1. Also, the mass conservation law is used to compute the concentration of the matrix \(c_{i}^{\alpha }\) (Eq. 2) that is evolving due to the phase transformation and due to the presence of m precipitates in the material:

$$c_{i}^{0} = \left( {c_{i}^{\beta } - c_{i}^{\alpha } } \right) \cdot \sum\limits_{k} {N_{k} \times \frac{4\pi }{3}r^{3}_{k} + c_{i}^{\alpha } } \quad {\text{for}}\quad i = 1, \ldots ,n\quad {\text{and}}\quad k = 1, \ldots ,m$$
(2)

where \(c_{i}^{0}\) is the nominal composition of element \(i\), and \(c_{i}^{\beta }\) and \(c_{i}^{\alpha }\) are, respectively, the composition of element \(i\) in the precipitates and in the matrix phase. \(k\) represents a specific size class. The mass balance equation is necessary for computing at each time step the new chemical driving force that depends on the matrix composition as explained in the next section. The numerical approach allows to treat nucleation, growth and coarsening concurrently during the whole evolution providing that nucleation and growth models are known.

The nucleation models

The classical nucleation theory (CNT) [43,44,45,46,47,48] is utilized for modelling nucleation in multicomponent alloy systems in both software. The time-dependent nucleation rate is written as:

$$J(t) = J_{s} \exp \left( {\frac{ - \tau }{t}} \right)$$
(3)

where \(t\) is the time, \(J_{s}\) is the steady-state nucleation rate, and \(\tau\) is the incubation time, which is used to describe the flux of supercritical clusters increasing from zero to the point of stationary conditions within a certain period of time. It is given as:

$$\tau = \frac{1}{{4\pi \beta^{*} Z^{2} }}$$
(4)

where \(Z\) is the Zeldovich factor, and \(\beta^{*}\) is the atomic attachment rate. Based on the assumption that an equilibrium distribution of clusters is present at time \(t = 0\), \(J_{s}\) can be expressed as:

$$J_{s} = Z\beta^{*} N_{0} \exp \left( {\frac{{ - \Delta G^{*} }}{kT}} \right)$$
(5)

where \(N_{0}\) is the number of nucleation sites per unit volume; ΔG* is the Gibbs energy of formation of a critical nucleus, also known as the nucleation barrier; \(k\) is Boltzmann’s constant; and \(T\) is the temperature. ΔG*, \(\beta^{*}\) and \(r^{*}\) [49] from Eq. 4 are written as:

$$\Delta G^{*} = \frac{16\pi }{3}\frac{{\delta_{0}^{3} V_{m}^{2} }}{{\Delta G_{0}^{2} }}$$
(6)
$$\beta^{*} = \frac{{4\pi (r^{*} )^{2} }}{{a^{4} }}\left[ {\sum\limits_{i = 1}^{k} {\frac{{\left( {X_{i}^{\beta /\alpha } - X_{i}^{\alpha /\beta } } \right)^{2} }}{{X_{i}^{\alpha /\beta } D_{i} }}} } \right]^{ - 1}$$
(7)
$$r^{*} = \frac{{2\delta_{0} V_{m} }}{{\Delta G_{0} }}$$
(8)

In the above equations, \(\delta_{0}\) is the interfacial energy between the matrix and the precipitates; \(r^{*}\) is the critical radius; \(\Delta G_{0}\) is the driving force for precipitation; \(a\) is the lattice parameter; \(X_{i}^{\beta /\alpha }\) and \(X_{i}^{\alpha /\beta }\) are the mole fraction of component \(i\) at the interface in the precipitate and matrix, respectively; \(D_{i}\) is the diffusion coefficient of \(i\) in the matrix; and \(V_{m}^{{}}\) is the molar volume of the precipitate phase.

Interestingly, the method to obtain the chemical driving force, \(\Delta G_{0}\), in TC-PRISMA and MatCalc is different. In TC-PRISMA, the parallel tangent or surface, respectively, for binary or for ternary alloys, constructions are used [39]. It computes the tangent to the Gibbs energy of the matrix phase at the matrix composition, and it is parallel to the Gibbs energy curve of the precipitates at the same pressure as the matrix phase. With this set-up, we get the maximum driving force for precipitation, and the composition of the nucleus is fixed for a certain supersaturation. It is indeed the value where the tangent to the Gibbs energy curve of the precipitate crosses the curve. It is worth noting that this often gives a critical nucleus composition very close to the equilibrium one and cannot lead to composition smaller than the equilibrium in binary alloys. The expression for the driving force \(\Delta G_{0}\) is written as:

$$\Delta G_{0} = \sum\limits_{i} {X_{i}^{\beta } \left( {\mu_{i}^{\alpha } \left( {X_{i}^{0} ,P^{\alpha } } \right) - \mu_{i}^{\beta } \left( {X_{i}^{\beta } ,P^{\alpha } } \right)} \right)} ,\quad i = 1,2, \ldots ,n$$
(9)

where \(\mu_{i}^{\alpha }\) and \(\mu_{i}^{\beta }\) are the chemical potential of element \(i\) in the matrix and precipitates, respectively; \(X_{i}^{0}\) is the mole fraction of element \(i\) in the matrix; \(X_{i}^{\beta }\) is the mole fraction of element \(i\) in the precipitates; and \(P^{\alpha }\) is the pressure in the matrix.

In MatCalc, two other models for computing the nucleation rate have been derived by Kozeschnik et al. [40, 41]. They introduced the concept of minimum ΔG*, which corresponds to the saddle point of the work of formation of the nucleus in an energy landscape expressed as a function of the composition of the nucleus and its size. Instead of calculating the maximum driving force, they consider that the lowest nucleation barrier would have the highest possibility to form precipitates according to:

$$P^{*} \approx \exp \left( { - \frac{{\Delta G^{*} }}{kT}} \right)$$
(10)

\(P*\) is the probability of nucleation that depends both on the nominal composition and also on the composition of the nucleus. The composition giving the minimal value of ΔG* is the composition of the nucleus. Figure 2 schematically illustrates the fundamental differences of the nucleation in the two software for a binary alloy. Using the parallel tangent construction (dashed red lines), we get the driving force \(\Delta G_{0}\) that is calculated in TC-PRISMA; while using the minimum ΔG* model in MatCalc, several driving force \(\Delta G_{0}^{{\prime }}\) can be obtained depending on the nucleus composition. The other nucleation model in MatCalc uses the maximum nucleation rate (J) for evaluating nucleation. It is evaluated to provide the maximum nucleation rate, i.e. the composition of the nucleus as a function of time which yields the maximum value of J is evaluated and taken for the nuclei.

Figure 2
figure 2

Schematic illustrating the driving force calculations in TC-PRISMA and the minimum ΔG* model in MatCalc

Full size image

It is important to notice, when using the minimum ΔG* model, that the maximum driving force computed in TC-PRISMA will lead to the minimum nucleation barrier, ΔG*, if the interfacial energy is not a function of composition. Like in non-classical theory of nucleation [50,51,52], the minimum ΔG* value used in MatCalc is the result of the competition between the driving force and interfacial energy values.

The growth models

Precipitate growth occurs after nucleation. Different models are used in MatCalc and TC-PRISMA for deriving the growth rate equation. As mentioned above, only spherical particles are considered. The interface mobility is not taken into consideration because the diffusion of atoms in the matrix is considered as the limiting mechanism of the transformation. In this condition, in a multicomponent system, based on the flux balance equation, the growth of a precipitate writes:

$$\frac{{{\text{d}}r}}{{{\text{d}}t}}\left( {c_{i}^{\beta /\alpha } - c_{i}^{\alpha /\beta } } \right) = J_{i}^{\alpha } \quad {\text{for}}\quad i = 1, \ldots ,n$$
(11)

where \(c_{i}^{\beta /\alpha }\) and \(c_{i}^{\alpha /\beta }\) are the concentration of component \(i\) at the interface in the precipitate and matrix, respectively. \(J_{i}^{\alpha }\) is the diffusive flux of element \(i\) in the α matrix. Based on Fick’s first law in the volume-fixed frame of Ref. [53]:

$$J_{i}^{\alpha } = - \sum\limits_{m = 2}^{n} {D_{im} \frac{{\partial c_{m} }}{\partial r}}$$
(12)

where \(\frac{{\partial c_{m} }}{\partial r}\) is the gradient of the concentration in the matrix of element \(m\) around a precipitate. \(D_{im}\) is the diffusivity of element \(i\) in \(m\) with a reference element \(m = 1\), also called the interdiffusion coefficient. Using the stationary approximation, \(\Delta c_{i} = 0\), one can combine Eq. 11 with Eq. 12:

$$\frac{{{\text{d}}r}}{{{\text{d}}t}}\left( {c_{i}^{\beta /\alpha } - c_{i}^{\alpha /\beta } } \right) = \sum\limits_{m = 2}^{n} {\frac{{D_{mi} }}{r}\left( {c_{m}^{0} - c_{m}^{\alpha /\beta } } \right)}$$
(13)

where \(c_{m}^{0}\) is the concentration of component \(m\) in the matrix far from the interface.

The diffusivity is a composition-dependent parameter. To avoid further complexity to solve the equation, in TC-PRISMA, the diffusivity is replaced with a mobility-dependent relation which reads directly from the kinetic database and the chemical potentials. The equation is finally expressed as [54]:

$$\frac{{{\text{d}}r}}{{{\text{d}}t}}\left( {c_{i}^{\beta /\alpha } - c_{i}^{\alpha /\beta } } \right) = \sum\limits_{i = 2}^{n} {c_{i}^{\alpha /\beta } \frac{{M_{i} }}{{\xi_{i} r}}\left( {\mu_{i}^{0} - \mu_{i}^{\alpha /\beta } } \right)}$$
(14)

where \(\mu_{i}^{\alpha /\beta }\) is the chemical potential of element \(i\) in the matrix at the interface; \(\mu_{i}^{0}\) is the chemical potential of element \(i\) in the matrix far from the interface; and \(\xi_{i}\) is the effective diffusion distance factor. In the case of multicomponent alloys, the composition shift at the interface is not only due to capillarity but is also influenced by the diffusion process. That is why, when one wants to solve exactly the system of equations, Eq. 14 cannot be used alone. Two growth models are implemented in TC-PRISMA: the simplified and the advanced growth rate models, with different assumptions to solve Eq. 14. The advanced model was proposed by Chen et al. [54]. In this model, a local equilibrium condition at the interface between the matrix and precipitates is considered:

$$\mu_{i}^{\alpha /\beta } \left( {c_{2}^{\alpha /\beta } , \ldots ,c_{n}^{\alpha /\beta } ,P^{\alpha /\beta } } \right) = \mu_{i}^{\beta /\alpha } \left( {c_{2}^{\beta /\alpha } , \ldots ,c_{n}^{\beta /\alpha } ,P^{\beta /\alpha } } \right),\quad i = 2, \ldots ,n.$$
(15)

\(\mu_{i}^{\beta /\alpha }\) is the chemical potential at the interface in the precipitates; \(P^{\alpha /\beta }\) and \(P^{\beta /\alpha }\) are the pressures at the interface in the matrix and at the interface in the precipitates, respectively. It is worth noticing here that the pressures in both phases are not equal. Thus, Eq. 14 is not the equilibrium tie-line. With this assumption, the velocity of a moving phase interface and the operating tie-line can be computed solving Eqs. 14–15. The simplified growth rate model in TC-PRISMA instead assumes that the chemical potential at the interface of precipitates and matrix is only modified by the Gibbs–Thomson effect with a constant molar volume:

$$\mu_{i}^{\alpha /\beta } (P^{\alpha } ) = \mu_{i}^{\beta /\alpha } (P^{\alpha } ) + \frac{{2\delta V_{m} }}{r}$$
(16)

After further derivations, the equation of the simplified growth rate model in TC-PRISMA can be expressed as:

$$v = \frac{K}{r}\left( {\Delta G_{0} - \frac{{2\delta V_{m}^{\beta } }}{r}} \right),\quad {\text{and}}\quad K = \left[ {\sum\limits_{i} {\frac{{\left( {c_{i}^{\beta /\alpha } - c_{i}^{\alpha /\beta } } \right)^{2} }}{{c_{i}^{\alpha /\beta } D_{i} }}} } \right]^{ - 1} V_{m}^{\alpha }$$
(17)

The model is further simplified by replacing \(c_{i}^{\beta /\alpha }\) with the composition of the nucleus from the nucleation driving force calculation and \(c_{i}^{\alpha /\beta }\) with the matrix composition.

In MatCalc, the thermodynamic extremal principle (TEP) [55] approach is used to derive the velocity of the moving interface. The master equation in the TEP, when considering that the size and concentration of precipitates are the so-called characteristic parameters of the solid solution, is:

$$\frac{\partial G}{{\partial r_{k} }} = - \frac{1}{2}\frac{\partial Q}{{\partial \dot{r}_{k} }}$$
(18)
$${\text{And}}\quad \frac{\partial G}{{\partial c_{ki} }} = - \frac{1}{2}\frac{\partial Q}{{\partial \dot{c}_{ki} }},\quad {\text{for}}\quad k = 1,2, \ldots ,m\quad {\text{and}}\;{\text{for}}\quad i = 1,2, \ldots ,n$$
(19)

where \(G\) is the Gibbs energy of the system, \(Q\) is the Gibbs energy dissipation rate, \(\dot{r}_{k}\) is the growth rate, and \(\dot{c}_{ki}\) is the rate of concentration change of element \(i\) in precipitate k. \(r_{k}\) is the radius of precipitate \(k\). The total Gibbs energy of the solid solution \(G\) can be expressed as [49]:

$$G = \sum\limits_{i = 1}^{n} {N_{i}^{0} \mu_{i}^{0} + \sum\limits_{k = 1}^{m} {\frac{{4\pi r_{k}^{3} }}{3}\sum\limits_{i = 1}^{n} {c_{ki} \mu_{ki} + \sum\limits_{k = 1}^{m} {4\pi r_{k}^{2} \delta } } } }$$
(20)

where \(N_{i}^{0}\) is number of moles of component \(i\) in the matrix. The first term on the right-hand side is the sum of Gibbs energy of the matrix, the second term on the right-hand side is the Gibbs energy of the precipitates, and the third term is the total interfacial energy. If the transformation is limited by diffusion, the Gibbs energy dissipation rate can be divided into two terms: \(Q_{\text{prec}}\) and \(Q_{\text{matrix}}\). The former represents the dissipation rate due to the diffusion of atoms inside the precipitates and is given as [56]:

$$Q_{\text{prec}} = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\int\limits_{0}^{{r_{k} }} {\frac{RT}{{c_{ki} D_{ki} }}4\pi r^{2} J_{i}^{\beta 2} dr} } } \quad {\text{with}}\quad 0 < r \le r_{k}$$
(21)

where \(J_{i}^{\beta }\) is the diffusive flux in the precipitates, R is the universal gas constant, and \(D_{ki}\) here denotes the diffusivity of element \(i\) in a specific precipitate \(k\) which is different from \(D_{ik}\) that is used in TC-PRISMA. The dissipation rate caused by fluxes in the matrix, \(Q_{\text{matrix}}\), is written as [56]:

$$Q_{\text{matrix}} = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\int\limits_{{r_{k} }}^{Z} {\frac{RT}{{c_{i}^{0} D_{i0} }}4\pi r^{2} J_{i}^{\alpha 2} {\text{d}}r} } } \quad {\text{with}}\quad r_{k} < r \le Z$$
(22)

In order to obtain the Gibbs energy dissipation rate caused by fluxes in the matrix \(Q_{\text{matrix}}\), the diffusive flux in the matrix \(J_{i}^{\alpha }\) is required and explicitly described as [56]:

$$J_{i}^{\alpha } = J_{i}^{\alpha *} \frac{{r_{k}^{2} }}{{r^{2} }}\frac{{Z^{3} - r^{3} }}{{Z^{3} - r_{k}^{3} }}\quad {\text{with}}\quad r_{k} < r \le Z$$
(23)

where \(J_{i}^{\alpha *}\) is the diffusive flux in the matrix at the interface, and \(Z\) is the distance of atoms travelled within a sphere of radius due to the flux in the matrix. By solving the master equations (Eqs. 17 and 18), the growth rate can be derived as well as the rate of concentration change.

Interfacial energy modelling

The interfacial energy is an important factor affecting the precipitation significantly [57,58,59]. It is a key parameter in the nucleation, growth and coarsening stages. In TC-PRISMA, the extended Becker’s model function is used to estimate the coherent interfacial energy:

$$\delta_{c} = \frac{{n_{s} z_{s} }}{{N_{A} z_{l} }}\Delta E_{s}$$
(24)

where \(n_{s}\) is the number of atoms per unit area at the interface, \(z_{s}\) is the number of cross-bonds per atom at the interface, \(z_{l}\) is the coordination number of an atom within the bulk crystal lattice, \(N_{A}\) is the Avogadro constant, and \(\Delta E_{s}\) is the enthalpy of solution in a multicomponent system. The interfacial energy is calculated prior to the precipitation simulation and thereafter used as a constant parameter throughout the isothermal simulation. In MatCalc, the generalized broken-bond (GBB) model [49] is instead implemented to calculate the interfacial energy. It has the same foundation as the Becker’s model, but it considers additional factors. The GBB writes:

$$\delta_{c} = \alpha (r) \cdot \frac{{n_{s} z_{{s,{\text{effe}}}} }}{{N_{A} z_{{l,{\text{effe}}}} }} \cdot f(T/T_{C} ) \cdot \Delta E_{s}$$
(25)

where \(\alpha (r)\), which is a function of precipitate size, represents a factor for the curvature of the interface. It ranges from 0 to 1 and increases with increasing size of the precipitates. \(f(T/T_{C} )\) is a function representing the influence of a diffuse interface, \(T_{c}\) is the regular solution critical temperature, and the interface only appears as sharp at 0 K. For simplicity in the present work, we neglect the diffuse interface contribution. For details on the diffuse interface, see Kozeschnik et al. [35, 59]. For the second term on the right-hand side of Eq. 25, the ‘effective’ expression is added to the parameters of the broken bonds and coordination number. It means that instead of only counting the nearest-neighbour broken bonds, the second, third, etc., nearest broken bonds are evaluated. So with some evaluations of the \(\frac{{z_{{s,{\text{effe}}}} }}{{z_{{l,{\text{effe}}}} }}\) value, Eq. 25 can be further expressed as

$$\delta = \alpha (r) \cdot 0.329\left( {N_{A} V_{m}^{2} } \right)^{ - 1/3} \cdot f(T/T_{c} ) \cdot \Delta E_{s}$$
(26)

where \(V_{m}\) is the molar volume of the system.

Results and discussion

The methods presented in the previous section are applied to the materials given in Table 1 to discuss the assumptions, models and key features to properly account for in order to predict precipitation kinetics accurately. The focus of the simulations and experiments in this work is on precipitation occurring during a relatively short ageing time, i.e. technically relevant ageing times for PH stainless steels. For Cu precipitation in these types of alloys, it is well known that the nuclei are coherently precipitating in the matrix, i.e. precipitate and matrix have the same crystallographic structure, while at later stages, the Cu precipitates transform into the stable fcc phase [30]. Since only short ageing is considered here, we only treat the metastable Cu-rich bcc precipitate phase. For all the materials considered in this work, thermodynamic calculations of the equilibrium state at the ageing temperature are performed using two different databases: TCFE 9.1 [60] from ThermoCalc [61] and MC_Fe from MatCalc. Only the metastable Cu-rich precipitate phase is accounted for in both databases used.

Binary vs multicomponent precipitation modelling

Most often in precipitation modelling and especially for CMD a simplification of the alloy system is made. For example, the alloys considered in this work could plausibly be modelled by a binary Fe–Cu model alloy. The added complexity when dealing with a multicomponent system induces higher computational costs, but, on the other hand, accurate predictions may not be possible with too crude simplifications. It should also be noted that the modelling results clearly rely on the database accuracy, whether it is a binary or a multicomponent database. In this section, we compare simulations for Fe–Cu binary, the quaternary version of the real alloy and the multicomponent real alloy. Alloy B is used for this comparison. The compositions of the simulated materials as well as the results from the metastable equilibrium calculations are shown in Table 2. Comparing the two databases, the predictions of the metastable equilibrium fraction and concentration of bcc-Cu precipitates, of interest in this study, are found to be similar in MatCalc and in TC-PRISMA for all three cases studied here. The similarity of the databases will simplify the comparison of the models.

Table 2 The composition and metastable equilibrium calculation results for the three simulated versions (binary, quaternary, real) of Alloy B at 480 °C
Full size table

The simulations are performed at 480 °C for 108 s using the simplified growth rate model in TC-PRISMA and using the minimum ΔG* model in MatCalc. The input parameters of the simulation for both TC-PRISMA and MatCalc are given in Table 3. Figure 3 shows the volume fraction, number density and mean size of the precipitates as well as the Cu concentration evolution of the precipitates for the different grades (Table 2). Included in Fig. 3 are also experimental data from the literature [4], acquired using APT, and the experimental data are indicated by red filled circles.

Table 3 Precipitation modelling set-up in TC-PRISMA and MatCalc for alloy B in the binary, quaternary and full grade versions
Full size table
Figure 3
figure 3

The simulated precipitation parameters of a volume fraction, b number density, c mean radius and d Cu concentration in Cu precipitates of Alloy B using simplified growth rate and minimum ΔG* model

Full size image

In Fig. 3a1, the volume fraction for all the materials in TC-PRISMA simulations exhibits the classical shape and increases rapidly after a certain incubation time that is longer than the experimentally observed incubation time. The plateau in volume fraction that is reached after about 105 s is in good agreement with the MatCalc predictions, see Fig. 3a2, and the experimental data, which indicate that both databases used predict the metastable equilibrium volume fractions well. The number density and mean radius predictions are also in agreement with experiments for longer ageing times, see Fig. 3b1 and c1, respectively. The MatCalc simulations have a different shape for the volume fraction evolution, including a hump. The kinetics is also predicted to be faster by MatCalc as compared to TC-PRISMA. The origin of the hump in the volume fraction data and the different kinetic predictions in MatCalc will be discussed later. The number density evolution in MatCalc has a similar trend to the TC-PRISMA results, but MatCalc overestimates the maximum density as compared to the experimental results. This correlates with an underestimation of the mean radius predictions that are smaller in MatCalc as compared to both TC-PRISMA and experiments. On the other hand, the shape of the size evolution curve predicted from MatCalc is in good agreement with the experimental evolution. By collectively studying the data in Fig. 3 generated from the two software, it can be seen that the onset of precipitation is a major difference. The nucleation occurs faster in the MatCalc simulations, and this can be related to the precipitate composition and its evolution, as depicted in (d1) and (d2) for TC-PRISMA and MatCalc, respectively. The minimum ΔG* model allows for the nucleation of Cu particles with a low Cu concentration that increases with ageing time, as explained in 2.3.2. Comparing with (d1), it is clear that the maximum driving force model and the simplified growth rate model in TC-PRISMA with maintained local equilibrium condition (Eq. 15) lead to precipitate compositions close to the metastable equilibrium throughout the simulations. It is worth mentioning that ideally, the advanced growth rate model in TC-PRISMA is the better option than the simplified one since the operative tie-line for local equilibrium at the interface is computed. However, the advanced growth rate model only succeeds finding a solution for the binary grade but failed for quaternary and full grade.

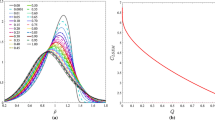
The chemical driving force for precipitation is another interesting aspect to study the different versions of Alloy B. Figure 4a and b shows the chemical driving force as a function of time in TC-PRISMA simplified model and MatCalc minimum ΔG* model, respectively. In Fig. 4a, a typical three-stage evolution can be observed for all three curves. The phase transformation kinetics is faster for the quaternary and full grades compared to the binary one, illustrated by the faster decrease in the chemical driving force. It is also clear that the initial chemical driving for precipitation in the binary model alloy is smaller than for the two other grades. This also infers slower kinetics and indicates the importance of accounting for a more complete alloy composition and not just simplifying to a binary case for the alloy of interest in this work. The utilization of the maximum driving force concept leads to a reduced chemical driving force during the course of ageing as the matrix becomes less and less supersaturated, as expected.

Figure 4
figure 4

The driving force of Cu precipitation in binary, quaternary and full grade material at 480 °C of Alloy B. The alloy composition is shown in Table 3, a simplified growth rate model in TC-PRISMA and b minimum ΔG* model in MatCalc

Full size image

On the other hand, using the minimum ΔG* model the driving force used for creating a nucleus is not monotonously changing in time; instead, all three curves exhibit a peak (Fig. 4b). The driving force remains small for an extended period of time because this value ensures the lowest nucleation barrier, see Eq. 6. Such a low driving force still leading to a low nucleation barrier is only possible because the interfacial energy is very low due to the low Cu concentration. Also in this case for the binary grade, a higher driving force is consumed at an early stage of precipitation since the precipitates are more Cu-rich and have higher interfacial energy in the binary alloy compared to the quaternary and the full grade alloys.

The multicomponent alloy version is preferred for the simulations, at least in this specific alloy system. Indeed, it is clear when looking at Fig. 3d2 that in the binary case even with a model allowing for low concentrated precipitates, the initial composition is still almost twice the one of the multicomponent alloy. In addition, other elements participating in the Cu precipitation will also affect the diffusivity of Cu in the system. An example for the effect on diffusivity can be taken from Alloy C [17] where it was found that the Cu particles are enriched with Ni, Cr and Mn during ageing. Similar observations in 15-5 PH stainless steel have also been published in other works by, for example, Laurent et al. [19]. The elastic strain energy or lattice misfit can be another important reason for considering the multicomponent alloy, but these factors are not considered in the present work. One clear observation from these initial simulations is the effect of the nuclei composition on the precipitation kinetics. This is thus investigated further in the next section.

Effect of nuclei composition on precipitation kinetics

Experimental view on chemical composition evolution of precipitates

Figure 5 shows the 3D reconstruction from APT measurement and highlights the distribution of Cu precipitates (cyan domains) together with Ni atoms (red spheres) and Mn atoms (green spheres) in aged specimens of Alloy A. A high number density of nanoscale Cu precipitates is found in all APT tips, except for the 5 min aged sample. The Cu precipitates grow with increasing ageing time, and the quantitative information is summarized in Table 4. It is noteworthy that the Cu concentration in the precipitates increases with ageing time, as other alloying elements are gradually rejected from the precipitates. This also explains the relatively high volume fraction of precipitates after 1–5 h of ageing compared to the specimens that are aged for 20 h and 50 h. In addition, segregations of Ni and Mn atoms to the interfaces of Cu precipitates and Bcc-Fe matrix are observed in all the specimens. This is consistent with the well-known core–shell structure found in similar systems. Figure 6 shows the Cu concentration evolution in different aged samples of Alloy A, where (a) is the result of concentration as a function of size and (b) demonstrates the concentration profile inside the Cu-rich precipitates.

Figure 5
figure 5

APT 3D reconstructions of aged specimens of Alloy A with 10 at.%Cu isoconcentration, red spheres indicating Mn atoms and green spheres indicating Ni atoms

Full size image
Table 4 The quantitative information of aged specimens of Alloy A analysed by APT
Full size table
Figure 6
figure 6

a The distribution of Cu composition of Cu precipitates versus size in 500 °C aged samples of Alloy A; b the core composition of Cu precipitates by proxigram analysis of the 500 °C aged samples of Alloy A

Full size image

Modelling view on chemical composition evolution of precipitates

In "The nucleation models" section, different models in MatCalc are introduced to evaluate the composition of the nuclei. It is important to emphasize that in both TC-PRISMA and MatCalc, a flat concentration profile from the interface to the core of the precipitate is considered. It is known [40] that, in MatCalc minimum ΔG* model, the chemical composition of Cu-rich precipitates can be far from the equilibrium during the precipitation. To further evaluate the model, the Cu concentration evolution in Cu-rich precipitates of Alloy A as a function of time obtained with the maximum J, minimum ΔG* and simplified growth rate models are plotted in Fig. 7 and compared with the experimental data collected from the APT analysis in Fig. 6a and b for Alloy A. The simulation parameters that are used in the software and the metastable equilibrium information are shown in Table 5. It is worth noting that the plotted concentration is the average concentration of all classes of precipitates in MatCalc. The open red circles represent the core composition of Cu in precipitates, while the filled red circles represent the average Cu composition from experimental measurements.

Figure 7
figure 7

Cu concentration in Cu-rich precipitates in Alloy A as a function of ageing time at 500 °C, with a comparison of experimental and computational results

Full size image
Table 5 Precipitation modelling set-ups and metastable equilibrium calculation for TC-PRISMA and MatCalc for Alloy A
Full size table

The simplified model in TC-PRISMA exhibits almost a constant Cu precipitate concentration and mean size of precipitates throughout the ageing as in the case of Alloy B treated earlier. It is logical because this concentration is only affected by the Gibbs–Thomson effect and the interfacial energy is constant. With the minimum ΔG* and maximum J models, we can observe a three-stage evolution of the precipitates composition. The Cu precipitates are created diluted and eventually reach the equilibrium composition. Despite that at the very early stages, the predicted Cu concentration matches perfectly the experimental one, and the concentration evolution seems shifted in time compared to the core data from APT except for the very end of the kinetics. For understanding the difference in terms of kinetics, it is important to keep in mind that in reality, the concentration profile is unlikely to appear as flat as assumed in the modelling. In this aspect, the precipitates in the simulations require more Cu atoms to diffuse in order to grow than experimentally. It might also explain why it takes longer to initiate nucleation in the simulation. This is also indicated in the previous section when observing the delayed kinetics of precipitation (Fig. 3). However, one needs to be reminded that a few limitations of the current APT measurements and analysis could also cause errors in the experimental data. For instance, the measured volume is very small. Each precipitate can be very small (less than 1 nm) at the beginning which leads to rather large uncertainties in the presented data. Also, very few precipitates are present at the large size end, see Fig. 6b. Additionally, the core data are acquired by analysing the core concentration of the largest few precipitates in the proxigram which creates a large error bar. The minor differences between maximum J and minimum ΔG* models shown in the results can possibly be considered negligible. However, it is worth mentioning that the maximum J model is a more complex assumption with its own limitations; for example, it is not clear that the nucleation follows a maximum nucleation rate path.

To understand why dilute Cu precipitates can be promoted in MatCalc, it is interesting to plot the evolution of the interfacial energy as a function of time. The interfacial energy indeed determines the nucleation barrier as shown in Eq. 6. Figure 8 shows the computed interfacial energy for the maximum J, in green, and minimum ΔG* model, in blue, as a function of time of Alloy A treated at 500 °C. The interfacial energy is low at the first stage, then increases rapidly in the middle stage and reaches a plateau by the end of the simulation. Of course, the interfacial energy evolution as a function of time goes hand in hand with the precipitate concentration as a function of time.

Figure 8
figure 8

The calculated interfacial energy of maximum J and minimum ΔG* models as a function of time at 500 °C using the composition of Alloy A

Full size image

To properly understand the overall impact of the non-monotonous evolution of the concentration, we simulate the precipitates volume fraction, number density and mean radius as a function of time using maximum J, minimum ΔG* and simplified growth rate model and compare with APT studies (Table 5) for Alloy A where concentration of the precipitates is measured. The results are plotted in Fig. 9a–c. The red filled circles represent the APT results. In Fig. 9a, the volume fraction evolution obtained from the minimum ΔG* and maximum J models shows an excellent fitting with the experimental data. The models are able to reproduce the volume fraction increase up to a value higher than the equilibrium one. This is because the precipitates are initially diluted and contain many other elements than Cu. Thus, from a mass balance point of view, the achievable volume fraction of precipitates can be higher than the equilibrium one. And with time, the depletion of not only Fe atoms but also other elements such as Cr and Ni from the precipitates to the matrix leads to a decreasing volume fraction. It is actually because the precipitates concentration is far from equilibrium that it is possible to reach a significantly higher volume fraction than the equilibrium one. In Fig. 9b, the number density evolutions show quantitatively that the maximum value of the simplified growth rate curve is two orders of magnitude smaller than both minimum ΔG* and maximum J models but takes longer time to be reached, the kinetics being slower when the precipitates are highly concentrated. In Fig. 9c, the size trend is in good agreement with the experimental data, but quantitatively the size is underestimated. It is believed that it is mostly related to the concentration evolution as shown in Fig. 7. As mentioned above, the precipitates in these implementations of LSKW exhibit a flat concentration profile. For the same amount of solute atoms, Cu in this work, the precipitate size is smaller in the simulations when a flat profile is assumed as compared to the experimental case when a diffuse concentration profile is found for the precipitates.

Figure 9
figure 9

The simulated a volume fraction, b number density and c mean radius as a function of time obtained with the three models, in comparison with APT results of Alloy A aged at 500 °C

Full size image

Considering the results from TC-PRISMA simplified model, it is clear that it cannot capture the nucleation kinetics well. It is the result of the high difference in Cu concentration between experiments and modelling. It is also interesting to note that in TC-PRISMA even if it is not possible to initiate precipitation early, when it starts, the size predictions rapidly approach a good agreement with the experimental results. This is because in TC-PRISMA, the high constant interfacial energy over the whole kinetic simulation promotes both the formation of larger precipitates, see Eq. 8, and a higher coarsening rate to minimize the surface/volume ratio of the precipitates.

The concentration of the precipitates explains both the early initiation of the transformation and the smaller size obtained with the models compared to the experimental ones. Because the concentration evolution in the precipitates explains the onset of the transformation and the shift in the kinetics and because this concentration is directly related to the interfacial energy pre-factor, the latter is an important parameter to calibrate for properly reproducing the concentration variation as a function of time.

Discussion on the use of LSKW modelling in computational materials design for PH stainless steels

In the previous sections, the different assumptions and models used in LSKW modelling for predicting precipitation kinetics are tested. It is clear that in the case of PH stainless steels with Cu-rich precipitates forming initially diluted and coherently with the surrounding matrix, it is important to use models accounting for a diluted precipitate concentration. Usage of LSKW modelling in CMD also requires handling of other aspects which are treated here.

Number of nucleation sites

The actual number of nucleation sites has a strong impact on nucleation. It is clear that the nucleation rate for a system with higher number of potential nucleation sites is larger than a system with a lower number of nucleation sites, in the case when all sites are equally energetic (Eq. 5). The number of nucleation sites can be determined by experimental measurements which can be useful when calibrating the modelling. The number of nucleation sites is affected by different factors. Normally in the same system, the number of nucleation sites on dislocations is significantly less than in bulk. And in the MatCalc software implementation, it is possible to change a pre-factor called nucleation constant for changing the number of nucleation sites.

Figure 10 shows the concentration and volume fraction of Cu-rich precipitates evolutions with time of Alloy A at 500 °C for nucleation in the bulk and at dislocations using minimum ΔG* model. In Fig. 10a, the concentration of Cu precipitates that nucleate on dislocations shows a delayed increase as compared to the bulk nucleation. A similar result is observed also for the volume fraction evolution, since fewer potential nucleation sites lower the nucleation rate. Therefore, increasing the number of potential nucleation sites can possibly allow calibration of the simulation and shift the curve towards the left-hand side. However, it is worth mentioning here that the available number of nucleation sites in bulk nucleation is the total number of atoms in the system per unit volume. It is therefore not physically found to increase this value. Thus, to further calibrate the modelling, the modification of other parameters is needed.

Figure 10
figure 10

a Concentration and b volume fraction of Cu-rich precipitates with nucleation sites of bulk and dislocations using minimum ΔG* model

Full size image

Interfacial energy modification and calibration with the concentration in the precipitates

As introduced in "Interfacial energy modelling" section, the interfacial energy has a strong impact on the nucleation but also on growth and coarsening. It is in fact complicated to evaluate a priori how the kinetics is affected by changing the interfacial energy values due to the strong interplay between the different precipitation stages. Therefore, it is vital to work with an interfacial energy calculation model that provides reasonable predictions or to calibrate the predictions by experiments. It is calculated as a constant value prior to the isothermal precipitation simulation in TC-PRISMA (Eq. 24), while in MatCalc, the interfacial energy evolves as a function of time (Eq. 26). As discussed earlier, it is possible to adjust the interfacial energy input by adding a pre-factor into the equation:

$$\delta = \delta_{0} \cdot \alpha$$

Precipitation kinetics changes with adjustments of the interfacial energy. Since the lower interfacial energy decreases the nucleation barrier, we expect that the concentration of precipitates will increase earlier with a lower interfacial energy. Tested values of the pre-factor are α = 0.5, 0.8, 1.0 and 1.5. Figure 11 shows the simulated Cu concentration of precipitates with modified interfacial energy of Alloy A using minimum ΔG* model. All curves show that the evolution of Cu concentration starts from a low value and reaches a plateau when the simulation ends at 108 s. With the interfacial energy pre-factor increasing from 0.5 to 1.5, the curve shifts from short to larger time as expected. Interfacial energies with lower pre-factor values give the best fitting with respect to APT data, due to invoked faster precipitation kinetics.

Figure 11
figure 11

Concentration of Cu-rich precipitates of Alloy A with various pre-factors of interfacial energy at 500 °C using minimum ΔG* model

Full size image

The lowering of the interfacial energy with a pre-factor of 0.5 or 0.8 might therefore allow for more accurate precipitation predictions in this case. Figure 12 represents the volume fraction, number density and mean radius evolution as a function of time at 500, 480 and 450 °C, respectively, of Alloys A, B and C using minimum ΔG* model. Apart from the interfacial energy set-ups, the other input parameters are the same as shown in Table 3. Consistent results between simulation and experiment are shown in general, but the mean radius is underestimated. This is mainly related to the flat concentration profile within precipitates as discussed in  "Results and discussion "section. Exceptionally, the volume fraction in Alloy B as shown in Fig. 12a2 does not agree with the simulation very well. It could be due to inaccuracies in the APT measurements.

Figure 12
figure 12

The simulated volume fraction (a1–a3), number density (b1–b3) and mean radius (c1–c3) as a function of ageing time under different interfacial energies obtained by minimum ΔG* model, in comparison with the corresponding APT results of Alloys A, B and C at 500, 480 and 450 °C ageing temperatures

Full size image

By reducing the interfacial energy, we see that the concentration evolution is more in agreement with the experiments. The predictions of volume fraction evolution also experience a faster increase with lower interfacial energy. Again, related to the flat concentration profile, the interfacial energy in a flat concentration profile costs more than a profile with gradients. That is why when we lower the interfacial energy, the concentration curve fits better with the experiment; however, the number of precipitates is also increased due to the lower nucleation barrier which leads to the faster increase in the volume fraction. To further explore that, a combination of the interfacial energy pre-factor and nucleation constant should be considered. Figure 13 shows the Cu concentration and volume fraction of the Cu-rich precipitates with 0.8 interfacial energy pre-factor and various nucleation constants. As shown in Fig. 13b, with the nucleation constant set as 0.01 in comparison with 1.0, the volume fraction evolution matches with the APT data better, but in return, the concentration curve is shifted to the right-hand side but to a slightly lesser extent than in Sect. 3 where no parameters are calibrated. These results emphasize the importance of finding the right balance between these two parameters in order to enable accurate predictions. The selection of the parameters should also follow the known physics, and in the present case, the precipitation is normally described as homogeneous precipitation, but it is clear that preferred nucleation will occur at highly energetic sites such as dislocations and high- and low-angle boundaries.

Figure 13
figure 13

a Cu concentration and b volume fraction of Cu-rich precipitates of Alloy A as a function of time with 0.8 interfacial energy pre-factor and nucleation constant set as 1.0 and 0.01

Full size image

From the present work, we can see that with proper settings and calibration, the minimum ΔG* model is able to predict precipitation in PH stainless steels at relevant ageing temperatures. A good agreement between simulations and experiments is found in the present work, but it is not easy to evaluate clear differences between the different alloying and ageing conditions, in part due to the large uncertainty and unclear trends in the experimental measurements, and thus, we believe more work is needed before widespread implementation of this calibrated modelling for CMD in PH stainless steels.

Conclusions

  1. (1)

    Langer–Schwartz–Kampmann–Wagner (LSKW) modelling considering off-equilibrium compositions of precipitates is critical for accurate predictions of precipitation kinetics for Cu precipitation in PH stainless steel. This is due to the fact that the Cu precipitates are diluted with Cu atoms at early stages.

  2. (2)

    A composition-dependent interfacial energy should be considered in the LSKW modelling of Cu precipitation in PH stainless steel.

  3. (3)

    Before applying the LSKW modelling in computational materials design, it is important to calibrate the modelling with respect to composition and size of particles.

  4. (4)

    The current modelling considering a flat diffusion profile in the precipitates leads to delayed precipitation which cannot fully capture the experimentally observed kinetics. This suggests that further improved LSKW modelling should treat the concentration profile within precipitates using a more sophisticated approach.