The brittle-to-ductile transition in cold-rolled tungsten sheets: the rate-limiting mechanism of plasticity controlling the BDT in ultrafine-grained tungsten

Abstract

Conventionally produced tungsten (W) sheets are brittle at room temperature. In contrast to that, severe deformation by cold rolling transforms W into a material exhibiting room-temperature ductility with a brittle-to-ductile transition (BDT) temperature far below room temperature. For such ultrafine-grained (UFG) and dislocation-rich materials, the mechanism controlling the BDT is still the subject of ongoing debates. In order to identify the mechanism controlling the BDT in room-temperature ductile W sheets with UFG microstructure, we conducted campaigns of fracture toughness tests accompanied by a thermodynamic analysis deducing Arrhenius BDT activation energies. Here, we show that plastic deformation induced by rolling reduces the BDT temperature and also the BDT activation energy. A comparison of BDT activation energies with the trend of Gibbs energy of kink-pair formation revealed a strong correlation between both quantities. This demonstrates that out of the three basic processes, nucleation, glide, and annihilation, crack tip plasticity in UFG W is still controlled by the glide of dislocations. The glide is dictated by the mobility of the screw segments and therefore by the underlying process of kink-pair formation. Reflecting this result, a change of the rate-limiting mechanism for plasticity of UFG W seems unlikely, even at deformation temperatures well below room temperature. As a result, kink-pair formation controls the BDT in W over a wide range of microstructural length scales, from single crystals and coarse-grained specimens down to UFG microstructures.

Introduction

The brittle-to-ductile transition (BDT) is a striking feature of body-centered cubic (bcc) materials [1]. Because of its impact on the safe operation of components, the BDT is the most critical property of bcc metals from an industrial point of view. Below the BDT temperature, the ductile nature of bcc metals changes fundamentally: They become brittle and shatter like glass [2]. Therefore, the utilization of bcc metals as construction materials is limited to applications with operating temperatures above their respective BDT temperature [3]. The decisive factor determining material behavior (whether brittle or ductile) is the ability to relieve the stresses in front of a crack tip by plastic deformation at a sufficiently high rate to match the applied loading rate [4,5,6,7]. In general, from the start of the lifespan of a single dislocation to its end, at least three mechanisms must be activated in sequence. These basic mechanisms are (i) the nucleation of a dislocation, (ii) the glide, and (iii) the storage or annihilation of this dislocation [8]. Out of these three atomic-scale processes, the one with the highest activation energy is usually by far the slowest and thus the rate-controlling mechanism that limits plastic deformation [9]. In general, the rate-controlling process of crack tip plasticity and the mechanism that controls the BDT have to be interpreted as thermally activated and must possess identical activation energies [10]. Contrasting models have been developed, describing the BDT as a phenomenon either controlled by dislocation nucleation [11, 12] or governed by the subsequent glide of the dislocations [13,14,15]. Experiments using the model material tungsten (W) [16] have suggested that the glide of dislocations controls the BDT [17]. For W this has been validated and specified to the glide of ½〈111〉 screw dislocations by studies performed on single crystals on the macroscale [18] and microscale [19], on a hot-deformed fine-grained [20], on coarse-grained recrystallized microstructures [21], and on hot-deformed materials that have undergone at least partial recrystallization [20, 22].

Ultrafine-grained (UFG) materials are at the cutting edge in materials science exhibiting outstanding properties. Recently, we have shown that severe deformation conducted by a close to the standard rolling process paves the way to create monolithic UFG W sheets in industrial quantity, showing a significantly improved room-temperature behavior. Whereas conventionally produced W is brittle at room temperature, UFG W produced by severe warm and cold rolling possesses room-temperature ductility [23, 24]. In this work, we are using the expression room-temperature ductility in terms of a BDT temperature below room temperature, i.e., stable crack propagation to a significant extent during tests at room temperature. In comparison with the studies quoted previously, room-temperature ductility of W represents a decrease in BDT temperature by several hundred Kelvin. This improvement has raised questions about the nature of the BDT in W sheets with UFG microstructure.

The great interest in the plasticity of UFG materials is related to a possible change in mechanisms [25]. For UFG W, the rate-controlling deformation mechanism that limits plasticity [26,27,28] and controls the transformation from a brittle state into a ductile and safe material behavior is still the subject of ongoing debates [20, 21, 29,30,31,32,33]. This paper has the objective to resolve the contradiction between a BDT that would be controlled by the glide of screw dislocations [31], or by the glide of edge dislocations [30], both hypotheses being suggested in recent works on UFG W. While below the knee temperature (and given stress) the glide of screw dislocations steadily slows down, edge and mixed dislocations maintain their high glide velocities even far below room temperature [34]. Consequently, an increased fraction of these (which has observed with decreasing grain size [35]) might control crack tip plasticity in UFG W [32]. Concerning this contradiction, we are aiming to generate a better knowledge of the following issues:

• (1) What is the impact of plastic deformation conducted by warm and cold rolling on the BDT Arrhenius activation energy compared to an undeformed microstructure?

• (2) Is room-temperature ductility of UFG W related to a change in the mechanism that controls the BDT?

This paper is organized as follows: The first section addresses the contamination during the single steps of rolling, well known to have a significant impact on the BDT temperature of W. Afterward, the evolution in BDT temperature induced by warm and cold rolling and the impact of rolling deformation on the BDT Arrhenius activation energy are discussed. Taking advantage of the derived trend of BDT activation energy, the observed BDT activation energies are linked with literature data.

Background

In this section, we recap the plastic properties of W derived in earlier works on high-purity single crystals [36,37,38]. We furthermore elucidate how the so-called Gibbs energy of activation needs to be comprehended with respect to experimentally derived BDT Arrhenius activation energies and address impact factors that affect the measured activation energy.

At first, we like to introduce the reader to the different notations this work is dealing with. Quantities owning the prefix effective or the extension of activation are used frequently further on. The ones that are supplemented by effective are related to short-ranging dislocation–lattice interactions. However, this prefix is only utilized in association with stresses and the activation volume, leaving aside the fact that in this work all the formulations of energy are related to short-range interactions. Instead, an appending asterisk highlights the link to dislocation–lattice interactions. Energies of activation are related to the occurrence of an event with a probability that is mandatory. This probability is determined by the externally forced strain rate and is mandatory to relieve the resulting stresses at the crack tip by the thermally activated glide of dislocations.

The energy of the Peierls barrier is expressed as Helmholtz energy of activation. The Helmholtz energy of activation for kink-pair formation corresponds to the difference in energy that is measured for a dislocation line that contains a kink pair compared to the line energy of a straight dislocation that is located in a Peierls valley without the formation of a kink pair [8]. For the glide of dislocations, the Helmholtz energy of activation ($\Delta F^{*}$) can be written as

$$ \Delta F^{*} = { }\Delta G^{*} + \tau^{*} V^{*} $$

(1)

and consists of two components [39]: (i) the Gibbs energy of activation ($\Delta G^{*}$) as the part that describes the supplied thermal energy and (ii) the mechanical work ($\tau^{*} V^{*}$), which is the product of effective critical resolved shear stress ($\tau^{*}$) and effective activation volume ($V^{*}$). Hence, two sources of energy need to be considered and distinguished during the later discussion of the results. Since for a given type of dislocation and glide system the height of the Peierls barrier is a constant (at least in a wide temperature regime), the contribution of both energies to the Helmholtz energy of activation are interdependent. In such inherently balanced system, the thermal part determines the remaining level of effective critical resolved shear stress that is required to reach the activated state (at a given strain rate). If the strain rate varies and the material temperature is held constant, the provided energy by heat is affected by the rate dependence of effective critical resolved shear stress [40]. Underlining this fact, we used the notation $\Delta G^{*} \left( {\tau^{*} } \right)$ instead $\Delta G^{*}$ hereinafter.

A last quantity describing an energy needs to be introduced for the later discussion on the rate-limiting mechanism controlling the BDT. This quantity is the BDT Arrhenius activation energy. The general postulation of activation energy (see Appendix) is based on the assumption that a thermally activated process is associated with an energy barrier along the reaction path hindering the occupation of an energetically more favorable state. The statistical duration for overcoming the energy barrier is related to the probability of a temporary increase in thermal energy in a given time. This situation is empirically described by the so-called Arrhenius law. Following Roberts et al. [41] and Hartmaier et al. [42], in the present work, we use an adapted formulation of the Arrhenius law

$$ {\text{d}}K/{\text{d}}t = A\exp \left( { - \frac{{E_{{\text{A}}} }}{{k_{{\text{B}}} { }T_{{{\text{BDT}}}} }}} \right) $$

(2)

where ${\text{d}}K/{\text{d}}t$ is the applied loading rate in the fracture toughness tests and $T_{{{\text{BDT}}}}$ is the related BDT temperature. Beside the BDT temperature, the so-called Arrhenius exponent consists of the BDT activation energy ($E_{{\text{A}}}$) and the Boltzmann constant ($k_{{\text{B}}}$). Furthermore, the exponential factor becomes multiplied by a prefactor (${\text{A}}$). Assuming that the stress-related mechanical part in the formulation of the Helmholtz energy of activation is not thermally activated, the rate sensitivity of the plastic deformation is directly linked with the Gibbs energy of activation [43]. Since in experiments with varying loading rates only the rate-sensitive component is measured, the Gibbs energy of activation for a given mechanism can be comprehended as a prediction of the BDT Arrhenius activation energy.

In this second part, we summarize the outcomes of the work by Brunner [38], Brunner et al. [36, 37], Ziebart [44], and Ziebart et al. [45] all on high-purity W single crystals [46]. At this point, we like to mention early fundamental work by Dorn et al. [47], also addressing the Helmholtz energy of activation for kink-pair formation in bcc metals. However, since the results for W are subjected to a considerable level of uncertainty, the provided data are not taken into account in the present work.

There is a lack of available data on the velocity of screw dislocations in W and related energies [21]. Available data about the plastic deformation of W refer to the process of kink-pair formation and were derived by conducting strain-relaxation tests and tensile test [36,37,38], as well as by the screening of the internal friction spectrum [44, 45], cf. Refs. [48, 49]. In the previous work on the BDT in W, the authors compared the calculated BDT activation energies with the Helmholtz energy of activation for kink-pair formation which was subsequently reduced by the mechanical part. Due to its simplicity, the elastic interaction model has been applied in this context, even though the fact that this model is only valid at low stress [8]. In Fig. 1 we provide a graphical alternative based on the data provided by Brunner [38] and Seeger’s kink-pair theory [50, 51] taking into account both elastic interaction and line tension model, respectively (see Appendix).

Figure 1

Kink-pair formation energies deduced for high-purity W. Between absolute zero and knee temperature ($T_{{\text{k}}}$) three regimes of constant Helmholtz energy ($\Delta F^{*}$, horizontal black line) and the related contributions by thermal energy ($\Delta G^{*} \left( {\tau^{*} } \right)$, solid and dashed red lines) and mechanical work ($\tau^{*} V^{*} { }$) are given. The numbering of the regimes is executed in roman numerals starting with the lowest number on the right-hand side: regime (iii) is spanning from 0 K to the lower bend temperature ($\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}$), (ii) from the lower bend to upper bend ($\hat{T}$), and (i) from the upper bend to the knee temperature ($T_{{\text{k}}}$). The solid red trend line representing $\Delta G^{*} \left( {\tau^{*} } \right)$ refers to a strain rate of plastic deformation (${\text{d}}\varepsilon_{{{\text{pl}}.}} /{\text{d}}t$) of 8.5 × 10⁻⁴ s⁻¹ [37]. Red dashed trend lines limit the light red area at the top and the lower end taking into account higher and lower plastic strain rates than 8.5 × 10⁻⁴ s⁻¹ (see text). It shall be noted that the transitions between the regimes are also affected by the applied strain rate [53] since the stress of the upper bend is invariant of the plastic strain rate [54]. However, in this figure, all transitions are related to the intermediate trend line based on the experimental results

In Fig. 1 the evolutions of the Helmholtz energy of activation ($\Delta F^{*}$), Gibbs energy of activation ($\Delta G^{*} \left( {\tau^{*} } \right)$), and the mechanical work ($\tau^{*} V^{*}$) are plotted against the deformation temperature ($T$) The displayed temperature regime spans between absolute zero and a critical temperature known as the athermal temperature or knee temperature ($T_{{\text{k}}}$). According to Seeger [52], the Peierls energy provided by Brunner [38] is subdivided into three regimes, whereby the Helmholtz energy of activation for regime (i) perfectly matches the energy of the γ-relaxation in W [44]. It is worth highlighting the fact, that the displayed partitioning of the Helmholtz energy of activation (Fig. 1) is only valid for a single plastic strain rate. The single plastic strain rate (${\text{d}}\varepsilon_{{{\text{pl}}.}} /{\text{d}}t$) of 8.5 × 10⁻⁴ s⁻¹ reflects the experimental conditions selected by Brunner [38].

To gain more flexibility, we furthermore approximated the impact of the plastic strain rate on the Gibbs energy of activation of kink-pair formation. The red dashed trend lines in Fig. 1 correspond to plastic strain rates that deviate by two orders of magnitude (each) from the above-mentioned one, i.e., predicts BDT Arrhenius activation energies for slower and faster loading rates, respectively. This approximation was made considering work by Kiener et al. [26], demonstrating that a normalization of the trends showing the effective critical resolved shear stress against the temperature by the Peierls stress and the knee temperature leads to a kind of master curve for pure bcc metals. To take advantage of this behavior, in this study, comprehensive data on high-purity Mo provided by Hollang et al. [53] were used to obtain a plausible region for Gibbs energies of activation in W. Our calculations show that the rate-dependent shifts in Gibbs energy of activation are more pronounced with increasing material temperature. Hence, knowledge about the actual plastic strain rate gains more importance with increasing BDT temperature. To make it even more complex, also the chemical composition might affect the dislocation–lattice interactions substantially [39].

In summary, the matching of Gibbs energy of activation for kink-pair formations [38] and BDT Arrhenius activation energy is expected to be obtained if all following aspects are fulfilled: (i) The glide of dislocations controls crack tip plasticity. (ii) Screw segments are limiting the mobility of dislocations. (iii) The plastic strain rate of the process zone in front of the crack tip meets the plastic strain rate (bulk) conducted in the experiments conducted by Brunner [38] using tensile specimens. (iv) The chemical composition does not differ significantly from the reference material [46]. This highlights that the interpretation of measured BDT activation energies is not straightforward and requires consideration of a variety of impact factors.

Materials and methods

In cooperation with Plansee SE, Austria, a set of W sheets was produced aiming to investigate the impact of pre-deformation on the BDT temperature and to study the evolution of the rate dependence of the transition temperature. A single W plate with technical purity [55], produced by a powder metallurgical route in combination with subsequent hot rolling (HR), was used as starting material for all materials.

Materials: production parameters

Material production was conducted by applying a proprietary rolling method. The warm-rolled (WR) materials, labeled 1.7WR, 2.5WR, 2.9WR, and 3.3WR, were produced in sequence. Rolling was conducted in a unidirectional manner during all passes. The label number indicates the logarithmic strain conducted by rolling and is referring to the plate thickness after hot rolling. The material denoted as 4.1CR was produced by applying to the material 3.3WR an additional thickness reduction of 0.8 logarithmic strain by cold rolling (CR). The cumulated total strain of 4.1 conducted by warm and cold rolling is equal to a thickness reduction of 98%. The single rolling steps are summarized in Table 1. For the distinction between hot-, warm- and cold-worked material states, we make use of the classification for bcc refractory metals as suggested by Trefilov et al. [56].

Table 1 Production parameters and microstructural properties

The sheets are highly textured. The respective orientation density functions (ODFs) possess an incomplete α-fiber, dominated by the rotated cube competent and orientations nearby. Along the γ-fiber, the orientation densities are less pronounced. The grains possess a typical pancake-like morphology, i.e., the grains are elongated parallel to the rolling direction and the transverse direction combined with short high-angle boundary (HAB) spacings parallel to the normal direction. Related to the short grain dimension, all materials in as-rolled condition can be classified as UFG, i.e., possessing a mean HAB spacing in the submicron regime [57]. For convenience, Table 1 provides information about grain size and morphology. A comprehensive treatise about the rolling-induced microstructural evolution is given in an earlier work [31].

As a reference, a section of 1.7WR was annealed at 2300 K for 1 h in H₂ atmosphere, generating a fully recrystallized microstructure, hereinafter referred to as material RX. Even after recrystallization, the rolling texture is still noticeable, but HAB spacing and grain morphology have fundamentally changed to a coarse-grained microstructure with almost equiaxed grains.

Chemical analysis: contamination during rolling

Specimens were sectioned from the rolled sheets by electrodischarge machining (EDM). To remove contamination originating from EDM cutting (in the first place Cu and Zn), thorough pickling of the specimens was conducted before the chemical analysis. The concentrations of C, N, O, and S were determined by carrier gas hot extraction (CGHE), using CS600 and TC 600, LECO Instrumente, Germany, respectively [60]. For the other screened elements, we applied inductively coupled plasma optical emission spectroscopy (ICP-OES) [61], iCAP 7000 Series, Thermo Fisher Scientific, USA.

Fracture mechanical testing: BDT temperatures

Except pickling, no further surface treatment was subjected to the sheets after rolling. Consequently, surface quality and thickness of the sample used for fracture mechanical testing are predetermined by the sheet properties. Single edge notched tensile SE(T) specimens with an L–T crack system [62] were used. The contour of the specimens and the pinning holes were machined by EDM. The notch was inserted by EDM as well. Sketches of the specimen geometry and used sample fixture are provided in a previous publication [23]. As it is an accepted practice for brittle materials, a fatigue pre-crack was not inserted [63,64,65]. Instead, crack propagation started at the tip of the EDM notch, which is decorated with multiple parallel-aligned, thermal-induced short cracks. The tips of these short cracks are located within the stress field of the notch, cf. Ref [66] for micrographs of the notch tip. Due to the presence of multiple cracks, shielding of the cracks by each other is suggested to take place. Furthermore, with a radius of about 0.07 mm, the notch tip is approximately one order of magnitude coarser than the relevant spacing of potential flaws in the microstructure, i.e., HABs [67]. The absence of a fatigue pre-crack is assumed to increase the measured critical stress intensity factor [63], which is already raised due to a significant material fraction in plane stress condition (thin sheets). At this point, we like to point out that our experiments do not have the objective to determine values of the plane strain fracture toughness ($K_{{{\text{Ic}}}}$), which is a material property. Instead, trends for the determination of BDT temperatures were recorded.

Fracture toughness tests were conducted using two universal testing machines, both manufactured by ZwickRoell, Germany. Up to a test temperature of 573 K, a ZwickRoell 1474 in combination with an environmental chamber, SFL 3119–400, Instron, USA, was utilized. For test temperatures above, experiments were conducted on a ZwickRoell Z150 equipped with a vacuum high-temperature radiation heater, MAYTEC, Germany. Both machines are electromechanical test devices driven by a step-motor propelled screw-based transmission. Specimens were applied to mode ${\text{I}}$ load, whereby the test machines were operated in a displacement-controlled mode. The crosshead speed was held constant during a single test campaign. The selected minimum temperature interval was 15 K using the environmental chamber and 25 K using the vacuum radiation heater, reflecting the less exact temperature control by radiation heating.

First information was derived from the single test records and was related to the shape of the force–displacement curves. Following Schwalbe et al. [68], material behavior was categorized as: (1) brittle: fracture unstable and force versus displacement plot to a great extent linear, (2) semi-ductile: fracture unstable and test record nonlinear (test record intersects with 95%-tangent), and (3) ductile: fracture stable and test record nonlinear.

In a subsequent procedure, we calculated the critical stress intensity factor ($K_{{\text{Q}}}$) following the procedure as given in ASTM E399 [62],

$$ K_{{\text{Q}}} = \frac{{F_{{\text{Q}}} }}{t W}\sqrt {{\uppi }a_{0} } Y $$

(3)

for the given material under the respective tests conditions (temperature and loading rate), where $F_{{\text{Q}}}$ is referred to as the critical force. The geometric parameters ${ }t$, $W$ are the thickness and width of the SE(T) specimen in an unnotched domain, respectively. Since the thermal-induced cracks are small compared to the notch length, the length of the starting notch ($a_{0}$) was taken as the crack length in the above formulation. With regard to Murakami’s tables [69], a boundary correction factor ($Y$) of 2.85 was selected. Finally, the critical stress intensity factors were plotted against the test temperature for determining the materials’ BDT temperature at the respective experimental condition.

Furthermore, we calculated the dissipated energy applying the approximate solution [70] of the J-integral ($J_{{{\text{tot}}.}}$) [71, 72],

$$ J_{{{\text{tot}}.}} = \frac{U}{{t\left( {W - a_{0} } \right)}} \eta { } $$

(4)

where $U$ is the integrated area below the complete force versus displacement curve and $\eta$ reflects sample geometry and loading mode. Taking advantage of the temperature-dependent nature of the J-integral, the evolution of the J-integral was plotted against the test temperature for determining BDT temperatures.

The literature does not provide a consistent methodology for determining BDT temperatures. In this work, we make use of two criteria: criterion (i) considers the shape of the respective test record and the following differentiation with regard to Schwalbe et al. [68]. The BDT temperature is set as the lowest test temperature in the respective campaign exhibiting only material behavior that is classified as semi-ductile or ductile. Or expressed in other words, the lowest test temperature that exhibits no brittle fracture in the respective campaign. Since this classification suggested by Schwalbe et al. [68] separates stable crack propagation below 2% of the ligament width in brittle and above 2% (where the record intersects the 95% tangent) in semi-ductile and ductile material behavior [2], respectively, criterion (i) is denoted as 2% criterion hereinafter.

For criterion (ii) the trends of the J-integral ($J_{{{\text{tot.}}}}$) versus the test temperature ($T$) were fitted using a hyperbolic tangent function, cf., e.g., Ref. [73],

$$ J_{{{\text{tot}}.}} = b + {\text{c}}\tanh \left( {\frac{T - d}{{2e}}} \right) $$

(5)

owning the fitting variables $b$, $c$, $d$, and $e$, where $b$ is the average value of the upper and lower shelf energy and $c$ the half of the difference between upper and lower shelf energy. For all fittings, the lower shelf energy was preset to be 5 J mm⁻². The parameter $e$ is a measure for the width of the transition regime. The fitting parameter $d$ represents the temperature at $b$, i.e., at the halfway between upper and lower shelf energy, which is handled as a preliminary BDT temperature in this work. The test temperature within the temperature interval that was the closest to the preliminary BDT temperature was then set as the BDT temperature. We name criterion (ii) as the halfway criterion hereinafter.

Independent on the applied criterion, please note that similar to the critical stress intensity factors, the deduced BDT temperatures presented in this work are believed to be non-conservative due to the absence of a sharp fatigue pre-crack [74]. Nevertheless, Giannattasio et al. [20] have demonstrated that the BDT activation energy for a given material is not measurably affected by the selected type of specimen, considering the specimen-dependent shift of the BDT temperature and the resulting modification of the prefactor of the Arrhenius law.

Results and discussion

In this study, we elucidate the impact of severe deformation conducted by warm and cold rolling on the mechanism controlling the BDT in room-temperature ductile W sheets with UFG microstructure. The following sections deal with the impact of rolling on the purity of the studied materials, the rolling-induced evolution of the BDT temperature, and BDT Arrhenius activation energy.

Comparison of the chemical compositions

The mechanical behavior of W is very sensitive to changes in the material’s chemical composition. Therefore, we used a single hot-rolled W plate as a starting material, aiming to produce a set of materials possessing similar chemical compositions. Here, we show that there is no relevant absorption of foreign elements during rolling.

Impurities significantly affect the BDT temperature of W [75, 76]. A comprehensive chemical analysis was conducted screening changes in concentration of foreign elements during material production. The evolution of the impurity content is given in Table 2 for each of the examined elements. We also give the total impurity level taking into account the detection limits if the single concentrations are below, achieving conservative results about material purity. Showing no clear increase in impurities with an increasing number of rolling steps, the sum concentration of foreign elements scatters at around 70 wt.-ppm. The level of the elements Fe, Ni, and Cr, which are most likely associated with the base material of the rollers, is also invariant over the whole rolling procedure. Rated as particularly critical [76], the interstitials C, N, and O are not detectable or slightly above their detection limits. Furthermore, P, S, and K are below the detection limits as well. As typical elements with a strong tendency to segregate to grain boundaries in W [77], the elements C, N, O, P, S, and K are believed to determine the cohesion of grain boundaries. Although the global concentration of these elements with grain boundary affinity is in a first-order approximation constant, the local impurity density at grain boundaries is expected to vary strongly in this study. Since the surface density of grain boundaries (def. as area per unit volume) is significantly raised with increasing rolling deformation, a globally constant impurity level of elements with grain boundary affinity will result in a lowered decoration of grain boundaries with these elements in consequence. In this work, however, all materials in as-rolled condition fractured in a predominantly transgranular manner if tested below the respective BDT temperature. We deduce that the decoration of the grain boundaries can be neglected for the rolling-induced reduction in BDT temperature evaluated in this study. Under the selected experimental conditions (specimens equipped with L–T crack system), the BDT needs to be comprehended as a competition between transgranular bond breaking and plastic deformation.

Table 2 Chemical compositions of W sheets with different degrees of deformation

A further contribution of foreign elements to plastic deformation that need to be addressed in the context of BDT temperature and BDT activation energy is their potential to enhance or decrease dislocation mobility by altering the Peierls barrier of the ½〈111〉 screw dislocations [78, 79]. Since the results provided by Brunner [38] for the Gibbs energy of activation for kink-pair formation in W have been derived from high-purity single crystals (99.9995 wt.-% W), we expect a shift towards higher BDT activation energies for materials with technical purity.

Reduction of the BDT temperature

Tungsten is known for showing improved mechanical behavior after pre-deformation. Our results reveal a stepwise reduction of BDT temperature with increased plastic strain conducted by rolling. The advantage gained by cold rolling is significantly stronger than the improvements achieved during the previous steps of warm rolling.

In Fig. 2 a compilation of single graphs is displayed, which is organized as follows: Each graph contains a single trend showing the evolution of the critical stress intensity factor ($K_{{\text{Q}}}$) against the test temperature ($T$) for a given material and loading rate. The fillings of the symbols reflect the observed material behavior for the respective experiment. Red vertical lines mark the BDT temperatures based on the 2% criterion. Along the vertical axis of the compilation trends for different materials are shown, which were acquired at similar loading rates. This is indicated by changes in the first part of the notation, which is located at the top left corner in each diagram. Horizontally aligned trends display the results of the same material but tested with different loading.

Figure 2

Evolution of the critical stress intensity factor. Trends of the critical stress intensity factor ($K_{{\text{Q}}}$) are plotted against the test temperature ($T$). Each subplot displays the results of one material condition tested at a constant loading rate. All materials were tested at three loading rates (${\text{d}}K/{\text{d}}t$) indicated by the number following the dash in the nomenclature (top left corner). The code − 0.01 refers to test campaigns carried out with a nominal loading rate of 0.01 MPa m^0.5 s⁻¹, − 1.0 for 1.0 MPa m^0.5 s⁻¹ and − 100 for 100 MPa m^0.5 s⁻¹. Additionally, the filling of the symbols reflects the material behavior observed in the respective single experiment. Filled symbols indicate brittle behavior, crossed and open symbols represent semi-ductile and ductile material behavior, respectively. The red vertical lines highlight the respective BDT temperatures derived by applying the 2% criterion. Evolution of the critical stress intensity factor. Please note the change in scaling of $K_{{\text{Q}}}$ and $T$ axes for the presentation of the results of the recrystallized material RX. For comparison purposes, additional to the vertical red lines, the vertical grey line shows the BDT temperatures of the material 1.7WR

At first, the fully recrystallized W sheet is discussed. The trends are shown at the bottom row of Fig. 2. An interpolated BDT temperature of 620 K for a loading rate of 1.0 MPa m^0.5 s⁻¹ is relatively low for hot-deformed W or W in undeformed conditions using EDM-notched specimens. To give numbers: Giannattasio et al. [20] have investigated a sintered compact without a subsequent hot-deformation step, reporting a BDT temperature above 1100 K. Rupp et al. [22, 80] have found for presumably hot-rolled rods, an orientation-dependent BDT temperature scattering around 800 K.

Next, we elucidate the impact of plastic deformation on the transition temperature. The rolled materials show a general tendency towards lower BDT temperatures with increasing logarithmic strain. This behavior is independent of the loading rate applied during the later experiments. Therefore, the evolution in BDT temperature is described using the experimental data that is related to the loading rate of 1.0 MPa m^0.5 s⁻¹ further on. With a BDT temperature of 398 K, even the less deformed material 1.7WR exhibits clearly improved material behavior, possessing a BDT temperature which is about 200 K lower than the reference material. Warm rolling up to a logarithmic strain of 2.5 lowers the transition temperature further, resulting in a BDT temperature of 348 K. However, the further reduction in BDT temperature by continued warm rolling becomes smaller the higher the level of plastic deformation becomes if expressed as gain per strain. Comparing 2.5WR, 2.9WR, and 3.3WR under consideration of all loading rates reveals that the BDT temperature of these materials is quite similar. In part, the determined BDT temperatures are identical, e.g., for 2.9WR and 3.3WR at 1.0 MPa m^0.5 s⁻¹ and 2.5WR and 2.9WR at 100 MPa m^0.5 s⁻¹ as well. The comparison of 2.5WR and 2.9WR at a loading rate of 0.01 MPa m^0.5 s⁻¹ even shows a slight increase in measured BDT temperature with increasing plastic deformation. We conclude that the differences in BDT temperature for these three materials smear up as a consequence of scattering material behavior and the existence of a minimum temperature interval that has to be selected for recording trends.

A further substantial reduction in BDT temperature was just achieved again after switching over from warm rolling to cold rolling. Compared with material 3.3WR, which underwent the maximum strain for the set of warm-rolled materials, the BDT temperature after cold rolling is improved by more than 100 K. This improvement was achieved by a thickness reduction that corresponds to logarithmic 0.8 only. With the decrease from 323 to 208 K, material 4.1CR possesses a BDT temperature significantly below room temperature. With a BDT temperature of 236 K, cold-rolled W even shows room-temperature ductility at a loading rate of 100 MPa m^0.5 s⁻¹. Extrapolating this trend, room-temperature ductility is expected to be retained far within the low-dynamic regime, which begins in the order of magnitude of 10⁴ MPa m^0.5 s⁻¹ and changes around 10⁶ MPa m^0.5 s⁻¹ to the high-dynamic regime [81]. We are convinced that these rolling-induced improvements in BDT temperature are solely related to the modification of the microstructure. This is justified by the facts that (i) all materials own similar chemical composition and (ii) the impact of the different sheet thicknesses is negligible (to be published). The latter statement is supported by the fact that the specimens used for testing material RX and 1.7WR possess an identical thickness, but exhibit a difference in BDT temperature of around 250 K.

Taking into account the varying criteria commonly used for determining BDT temperatures, a second attempt was made to assess the impact of rolling on the BDT temperature. Aiming to study the impact of the criterion on BDT temperature and BDT activation energy, we calculated the approximation of the J-integral after every experiment. The results are depicted in Fig. 3, which is composed of trends displaying the evolution of the J-integral ($J_{{{\text{tot}}.}}$) divided by a constant $\eta$ against the test temperature ($T$). The arrangement of the single diagrams is identical to the compilation displayed in Fig. 2. Red vertical lines display the position of BDT temperatures based on the halfway criterion. The transition temperatures determined by applying the halfway criterion are in good agreement with those based on the 2% criterion. For about one-half of the experimental campaigns, both criteria provide the same BDT temperature. In the case of the other half, the difference in BDT temperature between both criteria is in the range of neighbored test temperature of the selected test temperature interval. Consequently, the general tendencies described above using the 2% criterion and the tendencies derived by using the halfway criterion are quite similar and are not repeat at this point.

Figure 3

Evolution of the dissipated energy until fracture. Trends of the J-integral ($J_{{{\text{tot}}.}}$) divided by a constant ($\eta$) are plotted against the test temperature ($T$). The red dashed curve was fitted using a hyperbolic tangent function, cf. Equation (4). Vertical lines highlight the respective BDT temperatures (halfway criterion). Open symbols signalize that the respective data points were not considered during the fitting procedure. Due to the limited size of the dataset recorded for material RX, the fitting procedure for the J-integral was not feasible. Please note the change in the scaling of both axes. For comparison purposes, the vertical grey line shows the BDT temperature of material 1.7WR

Due to the limited size of the dataset acquired during the high-temperature test campaigns, a fitting procedure was not feasible for the trends recorded for material RX. Thus, the halfway criterion did not apply to the reference material. In order to give some idea about the BDT temperature of material RX based on the evolution of the J-integral, in Fig. 3 the lowest test temperature possessing a specimen in the upper shelf is provided. Since this is a very rough approximation, we do not consider these BDT temperatures for a later calculation of the BDT activation energy of material RX.

Table 3 BDT temperatures, loading rates, and BDT activation energies. Results obtained using the 2% criterion (i) and the halfway criterion (ii) are given

Evolution of BDT Arrhenius activation energies

Room-temperature ductility after cold rolling has raised questions about the rate-limiting mechanism controlling the BDT in UFG W. Our results show that in UFG W the BDT temperature is still rate dependent, even well below the room temperature. However, there is a tendency towards lower BDT activation energies with an increasing amount of pre-deformation.

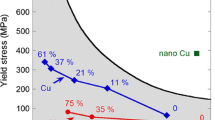
Based on the experimental data listed in Table 3, we derived Arrhenius plots, displaying the compatibility of the evolution in transition temperature in consequence of varying loading rates with the Arrhenius relationship. Regression lines in Fig. 4a refer to both 2% criterion and halfway criterion and related quantities, i.e., BDT temperatures ($T_{{{\text{BDT}}}}$) and respective loading rates (${\text{d}}K/{\text{d}}t$). Irrespective of the reciprocal character of the abscissa, the calculated values of $R^{2}$ are still sufficiently high to deduce Arrhenius behavior. After this verification, Arrhenius activation energies were derived based on the displayed regression lines. In Fig. 4b, these BDT activation energies ($E_{{\text{A}}}$) are displayed against the respective transition temperatures ($T_{{{\text{BDT}}}}$), whereby the horizontal dashed lines colored in the same fashion than the data points show the span of obtained BDT temperatures related to nominal loading rates in the regime between 0.01 and 100 MPa m^0.5 s⁻¹. A clear tendency can be observed, revealing a reduction in BDT activation energy with increasing strain, with a maximum BDT activation energy (1.27 ± 0.14 eV) for material 1.7WR and a minimum value (0.54 ± 0.10 eV) for the cold-rolled sheet. As a direct consequence of the small differences in BDT temperature of the materials 2.5WR, 2.9WR, and 3.3WR, this tendency appears to be blurred. Hereinafter, we treat this group of materials as a single material, having an activation energy of about 1.0 eV in the first approximation. In addition, Table 3 gives information about the BDT activation energies applying both criteria separately. Slight differences in BDT activation energies can be noticed, which scatter in a statistical way around the respective mean value calculated considering both criteria. However, we like to point out that the fundamental finding that cold-rolled W has a lower BDT activation energy than the warm-rolled materials is independent of the selected criterion. Hereinafter, we only discuss the values calculated by the combined approach, after obtaining the impression that the application of both criteria generates results that are more robust than using only one of both.

Figure 4

BDT Arrhenius activation energies. In a the logarithmic loading rate (${\text{d}}K/{\text{d}}t$) is plotted against the reciprocal value of the BDT temperature ($T_{{{\text{BDT}}}}$). Subplot b shows the BDT activation energies ($E_{{\text{A}}}$) against the BDT temperature ($T$) related to the 2% criterion and a nominal loading rate of 1.0 MPa m^0.5 s⁻¹. The vertical error bars reflect the agreement of the measured rate dependence of the BDT temperatures with the Arrhenius law, cf. subplot (a). The horizontal dashed lines represent shifts in the respective BDT temperature as a function of the loading rate (nominal 0.01–100 MPa m^0.5 s⁻¹). As a first reference, the evolution of the Gibbs energy of activation ($\Delta G^{*} \left( {\tau^{*} } \right)$ against the deformation temperature ($T$) is given by the solid black trend line as proposed by Brunner [38]. Further references are drawn as dashed black lines utilizing Eqs. (10) and (11). These trend lines vary in the assumption of the Helmholtz energy of activation (see text). Literature data are represented by grey symbols. Stars symbolize the Gibbs energy of activation derived from the measurement of the strain-rate sensitivity of the flow stress in polycrystalline warm- and cold-rolled W sheets, which were produced similarly to the materials of the present study. All other grey symbols show BDT Arrhenius activation energies from pre-cracked (notched) and unnotched specimens, respectively. BDT temperatures from notched samples (squares) are given for a nominal loading rate of 1.0 MPa m^0.5 s⁻¹, from unnotched samples (circles) for a total strain rate of 10⁻³ s⁻¹. From Refs. [18, 20]: filled square: single-crystalline; open square: polycrystalline hot-deformed; crossed square: polycrystalline as-sintered; Ref. [19]: half-filled square (bottom filled): single-crystalline; Refs. [17, 82]: half-filled square (top filled): single-crystalline; Ref. [83]: filled circle: polycrystalline as-swaged; Ref. [84]: open circle: polycrystalline recrystallized; Refs. [18, 20]: half-filled circle: polycrystalline hot-deformed; Ref. [85]: crossed circle: polycrystalline recrystallized. For more information, we refer the reader to Table 4

In order to verify or falsify glide of the screw dislocations and the underlying process of kink-pair formation as the rate-limiting process of plasticity by means of BDT activation energies, knowledge about Gibbs energy of activation in W is mandatory. Based on stress-relaxation experiments on high-purity W single crystals, Brunner [38] has proposed a piecewise linear evolution describing the Gibbs energy of activation for kink-pair formation against the deformation temperature showing a non-uniformity at the upper bend temperature. In Fig. 4b the dependence of the Gibbs energy of activation ($\Delta G^{*} \left( {\tau^{*} } \right)$) on the material temperature ($T$) as derived by Brunner is plotted as black solid lines, utilized as a first reference in the following discussion. A comparison of BDT activation energies obtained in the present study and Brunner’s results reveals a strong correlation between both. With a BDT activation energy of 0.54 ± 0.10 eV, material 4.1CR is almost on point, slightly (+ 0.1 eV) above the reference line (black solid line). However, there is a general tendency towards higher activation energies. This deviation between BDT activation energies and Gibbs energy of activation tends to grow continuously with raised BDT temperature, valid for the combined warm-rolled materials (+ 0.3 eV) and material 1.7WR (+ 0.5 eV) possessing the highest transition temperatures.

An accurate judgment about the quality of matching requires considering the rate dependence of the BDT temperature. As elucidated in the background section, the reference line (black solid, Fig. 4b) provides only correct solutions of the evolution in Gibbs energy of activation for a plastic strain rate of 8.5 × 10⁻⁴ s⁻¹, on which Brunner’s results [38] are based on (in combination with high-purity W to be precise). Taking into account the results of the present study achieved using SE(T) specimens, this rate dependence requires knowledge about the plastic strain rate in the process zone at the crack tip. However, the assessment of the plastic strain rate at the crack tip is not straightforward since plastic deformation is strongly localized [86]. Hahn et al. [87] have suggested that the strain rate in the process zone can be approximated under most circumstances by the expression

$$ {\text{d}}\varepsilon /{\text{d}}t \approx 10^{ - 3} {\text{ d}}K/{\text{d}}t $$

(6)

where the strain rate (${\text{d}}\varepsilon /{\text{d}}t$) is expressed in s⁻¹ and the global loading rate (${\text{d}}K/{\text{d}}t$) is given in ksi in^0.5 s⁻¹. However, this rule of thumb also holds for s⁻¹ and MPa m^0.5 s⁻¹ neglecting a failure below 10%. Due to the singularity, deformation at the crack tip starts to become reversible even at small global stress intensity factors [2]. Therefore, we further simplify that the total strain rate at the crack tip is equivalent to the plastic strain rate. Applying this relationship to the loading rates conducted during our experiments, it turns out that the intermediate nominal loading rate (1.0 MPa m^0.5 s⁻¹) corresponds to an approximated value for the plastic strain rate of 10⁻³ s⁻¹, well matching the experimental conditions in Brunner’s work, which was 8.5 × 10⁻⁴ s⁻¹. Consequently, it appears to be very likely that for comparing BDT activation energy and Gibbs energy of activation the activation energy has to be linked with the BDT temperatures obtained at a loading rate of 1.0 MPa m^0.5 s⁻¹. Irrespective of the remaining level of uncertainty in these assumptions, we also want to highlight the declining effect of the strain rate with decreasing test temperature, cf. Figure 1. We conclude that the match of BDT activation energy and Gibbs energy of activation for kink-pair formation, which is obtained for room-temperature ductile W (which is in the main focus of this work) gives strong evidence that the BDT is still controlled by the glide of the ½〈111〉 screw dislocation. Consequently, we deduce that room-temperature ductility in W is very likely not related to a change in the rate-limiting mechanism. In the investigated temperature regime, further accompanying processes like dislocation nucleation and dislocation annihilation or storage, must be significantly less energy-consuming than the glide of the ½〈111〉 screw dislocations. This also includes dislocation grain boundary interactions as frequently discussed in the context of the observed improvements originated from UFG microstructures [32].

After this first analysis, a more cautious formulation has to be picked for the warm-rolled materials if Brunner’s [38] results are chosen as reference. However, BDT activation energies for W provided by literature encourage to draw a more certain conclusion, also declaring kink-pair formation as the rate-limiting mechanism with a high level of certainty. The tendency to deviate from Brunner’s calculations as obtained in this study is also reflected by the comprehensive collection of BDT activation energies from literature, which is displayed in Fig. 4 as grey symbols. Grey squares reflect the fact that the specific activation energy has been obtained by a fracture mechanical approach (1.0 MPa m^0.5 s⁻¹). Results achieved using unnotched specimens (10⁻³ s⁻¹) are shown as grey circles. For more details, we refer the reader to the caption and Table 4. These data are furthermore extended by unpublished results of the Gibbs energy of activation obtained by measuring the strain-rate sensitivity of the flow stress of W sheets that have been produced similarly as the materials of the present study. If this data collection (all grey symbols) is considered as an empirical reference, the above-discussed deviation of our results towards higher energies is significantly mitigated. This emphasizes and supports the above conclusion about an unchanged controlling mechanism.

Table 4 BDT Arrhenius activation energies in W

Considering all BDT activation energies available for W today, the non-uniformity in Gibbs energy of activation at the upper bend as proposed by Brunner [38] appears to be questionable, at least for materials that possess a lower purity than the high-purity single crystals (99.9995 wt.-% W) examined by Brunner [38]. This assumption, however, incorporates the vast majority of materials, due to the very high-purity of Brunner’s material [46]. Based on the activation energies shown in Fig. 4b, we suggest a smooth evolution of the Gibbs energy of activation at the change from regime (i) to regime (ii) displayed as black dashed lines. These trend lines were calculated by applying a phenomenological approach as suggested by Kocks et al. [88]. More details are given in the appendix, cf. Eqs. (10) and (11) and also Ref. [89]. The plotted trend lines vary in the assumption of the Helmholtz energy of activation. The bottom trend line was calculated using a Helmholtz energy of activation of 2.06 eV and a Peierls stress of 980 MPa as reported by Brunner [38]. Both trend lines above were derived using a Helmholtz energy of activation, which was increased by 0.2 and 0.5 eV, which reflects solute atom-dislocation binding energy as described by Hull et al. [39]. During all calculations, the parameters $p$ and $q$ were set as 1 and 2, respectively. About the reason for the mismatch between Brunner’s results [38] and this suggested trend line, we can only speculate at this point. However, studies on Fe reveal a similar behavior. If less pure specimens are investigated instead of high-purity Fe, the non-uniformity disappears [90]. This issue should be focused on in future work.

Conclusions

Low BDT temperatures and ductile material behavior even far below room temperature have raised questions about the rate-limiting deformation mechanism in UFG W produced by cold rolling. Referring to the questions outlined in the introduction section, we want to highlight the following outcomes:

• (1) Plastic deformation conducted by warm and cold rolling decreases the BDT temperature and BDT activation energy of W sheets. On the other hand, the restoration of the microstructure by recrystallization increases the BDT temperature and BDT activation energy regarding the rolled materials.

• (2) Independent of the microstructure of W, whether UFG or coarse-grained, the glide of dislocations is the slowest process of crack tip plasticity.

• (3) Our experiments provide strong evidence that room-temperature ductility in UFG W sheets cannot be explained by a change in the BDT-controlling mechanism as frequently discussed. Instead, the BDT in UFG W is still controlled by the glide of screw dislocations and the underlying process of kink-pair formation. As a consequence, kink-pair formation controls the BDT in W over a wide range of microstructural length scales, from single crystals and coarse-grained specimens down to UFG microstructures.

• (4) The non-uniformity in Gibbs energy of activation at the upper bend as proposed by Brunner is questionable, at least for W with a lower purity than the high-purity single crystals studied by Brunner. For most materials, a smoother change from the regime (i) to the regime (ii) seems more likely.

This work reveals furthermore that the BDT in severely rolled W sheets equipped with an L–T crack system has to be comprehended as a competition between transgranular bond breaking and plastic deformation.

Appendix

Here, we extend the brief recap on the plastic deformation of W started in the background section and provide a more comprehensive overview. The appendix is organized as follows: At first, we give more information about the energies this work is dealing with. Later, experimental results on plastic deformation of W single crystals are discussed in the background of the kink-pair-mediated glide of ½〈111〉 screw dislocations.

The Helmholtz energy of activation ($\Delta F^{*}$) consists of two components [39]: (i) a thermal part denoted as Gibbs energy of activation ($\Delta G^{*}$) and (ii) mechanical work ($\tau^{*} V^{*}$). The latter is a function of the effective critical resolved shear stress ($\tau^{*}$) and activation volume ($V^{*}$) and balances, in fact, the energy delta between Helmholtz energy of activation and Gibbs energy of activation at relevant deformation temperature, i.e., in the so-called thermal regime that is addressed later in this section. As become clear by the following equation,

$$ \Delta F^{*} = \Delta G^{*} + \tau^{*} V^{*} $$

(7)

two kinds of activation energies need to be considered forming a thermodynamic quantity describing the energy of the Peierls barrier, i.e., the interaction of the dislocation line with the periodicity of the lattice, the so-called Helmholtz energy of activation. Here, notations owning the prefix effective or the extension of activation have been used and are used frequently further on. Quantities like Helmholtz energy of activation and Gibbs energy of activation are referring to the amount of energy that is needed to create a steady concentration of kink pairs (constrained equilibrium concentration, cf. Ref. [91] for more details). These energies of activation are mandatory to accommodate the externally forced strain rate by the glide of dislocations in the thermal regime, representing screw segment-controlled mobility of the dislocations. The prefix effective indicates that the respective quantity is describing a property related to a dislocation–lattice interaction. Transferred to the shear stress, the critical resolved shear stress is the sum of the resistance for the glide of dislocations caused by long-range interactions (starting at about 10 b, cf. Ref. [92]) and short-range interactions that are linked to the periodicity of the lattice, cf. Refs. [93, 94] for detailed information about this distinction. Unlike the critical resolved shear stress, the effective critical resolved shear stress considers only the impact of the Peierls barrier (short-range interactions) on the stress needed to initiate plastic deformation. However, although the energies discussed in this paper (Helmholtz energy of activation, Gibbs energy of activation, and the mechanical work) are related to the periodicity of the lattice, these quantities are not extended by this prefix (effective). Instead, the relation of a quantity describing an energy to short-range interactions is highlighted by using an asterisk. To keep attention on the impact of the effective resolved shear stress (and due to that of the applied strain rate as is demonstrated later in this chapter) on the Gibbs energy of activation, the notation $\Delta G^{*} \left( {\tau^{*} } \right)$ instead $\Delta G^{*}$ is used hereinafter. Furthermore, we like to point out that the activation entropy ($\Delta S^{*}$) is small for deformation of bcc metals at low temperatures [9, 40, 92]. Consequently, the assumption $\Delta G^{*} \cong \Delta H^{*} { }$ (enthalpy of activation) holds [91].

The last quantity that is addressed in this section is the Arrhenius activation energy. The postulation of activation energy is based on the assumption that an investigated process is associated with an energy barrier along the reaction path hindering the occupation of an energetically more favorable state, known as the ground state. But it is furthermore supposed that local fluctuations in thermal energy are sufficient to overcome this energy barrier [9]. The statistical waiting time for overcoming the energy barrier, achieving the so-called activated state, is related to the probability of a temporary increase in energy (in a given time). In solids, this increase is related to an increased local concentration of phonons, caused by interferences of wave packets [9]. By investigating the evolution of process kinetics (statistical rate of events exhibiting a successfully crossing of the energy barrier caused by thermal fluctuations) as an effect of changes in material temperature (or vice versa), the thermal energy that is required to surmount the energy barrier with a given probability can be deduced quantitatively. This empirically found relationship is known as Arrhenius law

$$ P = v^{*} \exp \left( { - \frac{{E_{{\text{A}}} }}{{k_{{\text{B}}} { }T}}} \right) $$

(8)

and describes the probability of the occurrence of an event ($P$) that is triggered by thermal fluctuations. As a consequence of Arrhenius law, also the kinetics of a process consisting of a large number of these thermally activated single events can be expressed as a function of an exponential term [9]. This so-called Arrhenius exponent consists of (Arrhenius) activation energy ($E_{{\text{A}}}$), the Boltzmann constant ($k_{{\text{B}}}$), and the material temperature ($T$). Furthermore, the exponential factor becomes multiplied by the effective frequency ($v^{*}$) [43].

Figure 

Figure 5

Gibbs energy of activation for kink-pair formation. A recap is shown referring to the subjects: Helmholtz free energy of activation ($\Delta F^{*}$, solid black line) for kink-pair formation, Gibbs energy of activation ($\Delta G^{*} \left( {\tau^{*} } \right)$, solid red line), and the related trend of the critical resolved shear stress ($\tau_{{{\text{crit}}}}$, crosses). Shown Gibbs energies of activation were calculated based on information given in Refs. [36, 38]. Steps in the trend line of $\Delta F^{*}$ indicate the position of the lower and upper bend temperature and the knee temperature as well (vertical dashed grey lines) for the applied strain rate (${\text{d}}\varepsilon_{{{\text{pl}}.}} /{\text{d}}t$)

5 shows trends representing the evolution of energy against the deformation temperature ($T$) for three quantities [38]: Helmholtz energy of activation ($\Delta F^{*}$), Gibbs energy of activation ($\Delta G^{*} \left( {\tau^{*} } \right)$), and mechanical work ($\tau^{*} V^{*}$, as the difference of both). The evolution of the Gibbs energy of activation for kink-pair formation is highlighted by squares. The different colors of the squares indicate different methods or parameter used for this recalculation of Brunner’s results [38]: results drawn in grey were calculated by using the elastic interaction (EI) model, whereas black symbols are indicating the use of the line tension (LT) model. The application of filled and open squares is motivated by highlighting the use of different parameter sets in regime (ii) and (i) for the calculations. Parameter sets are taken from Ref. [38]. The underlying evolution of the effective critical resolved shear stress ($\tau^{*}$) is displayed in Fig. 5 (crosses) as well. The plastic strain rate of (${\text{d}}\varepsilon_{{{\text{pl}}}} /{\text{d}}t$) of 8.5 × 10⁻⁴ s⁻¹ was applied in tension [37].

The displayed temperature regime spans between absolute zero and a critical temperature ($T_{{\text{k}}}$) related to the increasing amount of energy provided by the phonon spectrum with increasing material temperature [43] known as the athermal temperature or knee temperature. This critical temperature (not to be mistaken with the BDT temperature) is symbolizing the transition from a thermal to an athermal regime, where the lattice (i.e., the Peierls barrier) is no obstacle for the glide of bcc ½〈111〉 screw dislocations anymore [43]. In the athermal temperature regime, the glide of screw dislocations is controlled by phonon drag [16] and the mobility of non-screw dislocations is comparable with the mobility of edge-type dislocations [95]. Following the experimental work by Brunner on high-purity W [38], Fig. 5 exhibits a subdivision of the thermal regime in three temperature regimes. This subdivision (regimes are bordered by vertical dashed grey lines) has been suggested by Seeger [52] to be closely linked with inherent transformations of the kink-pair mechanism and is reflected by staggering levels of Helmholtz energy of activation (horizontal solid black lines) [38]. However, some of the conclusions about the origins of the partitioning of the thermal regime drawn by Seeger have been questioned later [96]. Additionally, recent simulations [97, 98] and Microlaue experiments [99] have not provided any evidence for the glide of ½〈111〉 screw dislocations on planes apart from the {110} plane.

As a consequence of the phonon spectrum, the Gibbs energy of activation (solid red line, Fig. 5) is decreasing with decreasing deformation temperature and the trend line is running through the coordinate’s origin at absolute zero. The evolution of the Gibbs energy of activation can be expressed as

$$ \Delta G^{*} \left( {\tau^{*} } \right) = m^{\prime } { }k_{{\text{B}}} T $$

(9)

where the product $m^{\prime } { }k_{{\text{B}}}$ consisting of a parameter and the Boltzmann constant is the slope, which is a function of the loading rate. Finally, $T$ is the material temperature. In regime (i) Brunner [38] has determined $m^{\prime }$ to be 30.6 whereas regime (ii) and (iii) possess a value of 24.

A further attempt has been proposed by Kocks et al. [88], please also cf. Ref. [89]. This phenomenological description of the Gibbs energy of activation for kink-pair formation ($\Delta G^{*} \left( {\tau^{*} } \right)$) includes the Helmholtz energy of activation ($\Delta F^{*}$), the Peierls stress ($\tau_{{\text{P}}}$), and the thermal part of the critical resolved shear stress ($\tau^{*}$). The remaining variables $p$ and $q$ are fitting parameters.

$$ \Delta G^{*} \left( {\tau^{*} } \right) = \Delta F^{*} \left[ {1 - \left( {\frac{{\tau^{*} }}{{\tau_{{\text{P}}} }}} \right)^{p} } \right]^{q} $$

(10)

Based on the data provided by Brunner for W [38], in regime (ii) and (iii), the thermal part of the critical resolved shear stress ($\tau^{*}$) can be expressed as a function of the temperature ($T$) using following parabolic formulation

$$ \tau^{*} = \left( {28.8 - 0.0294 T} \right)^{2} $$

(11)

with $\tau^{*}$ in MPa and $T$ in Kelvin. This allows a straightforward description of the Gibbs energy of activation for kink-pair formation as a function of the material temperature.

Assuming that in the considered temperature regime the atoms of the crystal lattice oscillate with the Debye frequency (cf., e.g., Refs. [100, 101] for general information and [102] for data on the Debye frequency regarding W), the frequency of attempts to overcome the Peierls barrier by thermal fluctuations is invariant. This latter frequency is typically in the region around 10¹² to 10¹³ Hz [91, 103]. In a stress-free material at a given Peierls energy and a constant material temperature, the probability for successful attempts in a given time can also be considered as a constant. However, with continuously increasing strain rate, this probability is at some point not sufficient anymore to ensure the glide velocity (i.e., the need for a specific number of successful attempts per time) that is required to accommodate the externally forced strain rate. This consideration can be seen as an analogy to the definition used above for describing the knee temperature, but instead of a constant strain rate and varying the deformation temperature, here the temperature is held constant and the strain rate is changed. In order to accommodate further on the increased and externally forced strain rate by the glide of dislocations, the number of successful attempts per time needs to be increased. At a given phonon spectrum (constant temperature), this mandatory increase in probability for overcoming the Peierls barrier needs to be comprehended as a reduction of the thermal energy (Gibbs energy of activation) that is needed to achieve a successful attempt. Independent of this deduction, the Helmholtz energy of activation, directly linked with the absolute height of the Peierls barrier, is supposed to remain unchanged. Compensating this energy delta, the amount of energy, which is related to mechanical work, has to be increased by the amount of the decrease in Gibbs energy of activation that is needed to achieve the mandatory increase in probability for successful attempts. This predicted increase in mechanical work with increasing strain rate has been directly observed in experiments on bcc metals acquiring the effective critical resolved shear stress of bcc metals at different strain rates, e.g., [53, 104], or in so-called strain-rate jump tests, e.g., [105, 106].