Measuring crystal orientation from etched surfaces via directional reflectance microscopy

Abstract

Mapping crystal orientation has always been the domain of diffraction-based techniques. However, these measurements have limited throughput and require specialized equipment. In this work, we demonstrate crystal orientation mapping on chemically etched aluminum samples using a simple and inexpensive optical technique called directional reflectance microscopy (DRM). DRM quantifies surface reflectance as a function of illumination angle. We identify directional reflectance characteristics of grains with (111) out-of-plane orientation and infer their surface topography to calculate their underlying crystal orientation. We confirm the surface topography using atomic force microscopy and validate DRM orientation measurements with electron backscatter diffraction.

Introduction

Optical microscopy (OM) is one of the most common characterization techniques to analyze the surface microstructure of metals and metal alloys. Researchers often rely on OM to rapidly characterize the geometry and distribution of microconstituents in polycrystalline solids—such as crystal grains [1, 2], phases [3], or precipitates [4]. However, the crystal structure and orientation of such features cannot be directly assessed through OM because of its diffraction-limited spatial resolution [5, 6]. To acquire this information and investigate the relationships between materials structure and properties, researchers usually rely on diffraction-based techniques such as electron backscatter diffraction (EBSD) [7] or X-ray diffraction (XRD) [8].

Several studies have explored the possibility of acquiring crystallographic information from polycrystalline solids using OM methods. The main motivation behind these research efforts is the higher throughput, simplicity, and flexibility of OM over conventional diffraction-based techniques. Spiedel et al. demonstrated the possibility of mapping the out-of-plane texture of etched polycrystalline nickel and aluminum (Al) by analyzing surface topography through laser confocal microscopy [9]. Favret et al. used a similar approach that relies on oblique laser illumination [10]. More recently, Oleksii et al. demonstrated grain orientation mapping on Raman-active materials using a polarized laser source [11].

Here, we demonstrate a new method for identifying and analyzing orientation in a subset of grains on etched Al surfaces using an inexpensive light source and a simple optical microscope. This technique, based on directional reflectance microscopy (DRM) [12], involves the acquisition of a sequence of optical micrographs taken under varying illumination conditions. As a result of etching, the grains on the sample surface exhibit different orientation-dependent facets, which reflect light in specific directions. The distribution of this directional reflectance has different characteristics depending on the grain’s crystallographic orientation. We analyze the directional reflectance and devise an algorithm to identify (111) out-of-plane oriented grains and compute their complete orientation. The spatial resolution of this method is sufficient to quantify the misorientation distribution within individual grains. We find good agreement between our results and EBSD orientation and misorientation measurements. Additionally, the relationship between surface structure and reflectance provides an efficient new path to assessing the topography of etched surfaces. Here, we identify intermediate Al facets that form in addition to thermodynamically preferred {111} or kinetically favored {100} crystallographic planes previously documented [13, 14].

Material and method

Samples were cut from 2-mm-thick Al foil (> 99.99%) by wire-based electrical discharge machining and then annealed at 400 °C for 6 h to induce grain growth to an average grain size of ~ 300 µm [15]. They were ground using a sequence of SiC paper from 320 grit to 4000 grit and then etched by immersion in Keller’s reagent (Best Chemical) for 6 min at room temperature [16]. After etching, the samples exhibited visible grain contrast and were suitable for DRM and EBSD measurements without further processing.

DRM measurements

The DRM apparatus consisted of an Olympus SZ6145 microscope equipped with an industrial monochrome CMOS camera, a custom-built motorized stage providing precise control over the incoming light direction, and a collimated white LED light source. The apparatus is shown in Fig. 1a. We collected a sequence of micrographs (2448 pixels × 2048 pixels) of the etched sample surface from different incoming light directions, $\varvec{I}$, defined by its corresponding azimuth ($\varphi$) and elevation $(\theta$) coordinates (Fig. 1b). We set the camera exposure time to ensure that most of the pixels are below the saturation limit of the CMOS sensor throughout the DRM dataset. One DRM dataset comprises a total of 1584 DRM micrographs, taken by varying $\varphi$ from $0^\circ$ to $355^\circ$ using step increments of $5^\circ$, and $\theta$ from $15^\circ$ to $67.5^\circ$ using step increments of $2.5^\circ$. For each DRM micrograph of the sample, we captured a set of corresponding background micrographs of a diffuse white surface to normalize DRM micrographs.

Figure 1

a Photograph of the DRM setup and b schematic illustration of the DRM coordinate system

This operation is performed in MATLAB and is similar, in principle, to the background subtraction process described in Ref. [12]. Here, however, the operation involves a division as opposed to a subtraction. The background division process is exemplified in Fig. 2.

Figure 2

Exemplary micrographs of a an etched Al sample under the illumination direction defined by $\varphi = 105^\circ$ and $\theta = 35^\circ$. b Corresponding DRM background micrograph taken using the same illumination direction. c Normalized DRM sample micrograph obtained via background division. To ease the display of illumination inhomogeneities, we have increased the image contrast in this figure

EBSD measurements

We acquired EBSD measurements using a step size of 21.4 μm and 6 μm to assess the mean grain orientation and the intragranular grain orientation distribution, respectively. We set the acceleration voltage for both measurements to 20 kV and enable pattern center correction to minimize distortions in the large area scans. We processed the EBSD raw data using MTEX 5.0.3 [17, 18] under MATLAB.

Analysis

Figure 3 illustrates the sequence of operations required to determine grain orientation from DRM measurements. First, we segment the sample surface (Fig. 3a) by identifying areas where changes in the directional reflectance occur [12]. The segmented image contains a network of grain boundaries that separate all grains that can be resolved by DRM (Fig. 3b). Using this image as a mask, we plot the directional reflectance profile (DRP) from each grain (Fig. 3c). A DRP is a stereographic projection of the reflection intensity measured as a function of the illumination angle, $\varvec{I}$ [12]. Each DRP contains 1584 intensity values—one for each DRM micrograph—computed as the average reflection intensity over the grain area in that micrograph and normalized between 0 and 1. Because of the faceted surface topography induced during the chemical etching process (Fig. 3d), grain reflectance changes with $\varvec{I}$. For a certain $\varvec{I}$, the etch-induced facets reflect light toward the microscope, making the grain appear bright in the corresponding micrograph, and causing the DRP to exhibit a reflectance peak at that illumination direction (Fig. 3c). Via this relationship, DRPs can be analyzed to infer the geometry of the etch-induced surface facets across the grain surface. By determining the relationship between facet geometry and crystallography, we calculate the grain orientation in terms of Euler angles (Fig. 3e).

Figure 3

DRM data processing. a One example micrograph from a DRM dataset. b High magnification view of the highlighted area in a showing the grain boundary map. c DRP corresponding to the grain highlighted in b. d Scanning electron micrograph of the etch-induced surface topography of the same grain. e Schematic of the unit cell orientation associated with this grain, and Euler angles

Grain directional reflectance originates from the specular reflection of light at etch-induced surface facets [12]. Therefore, it should be possible to uniquely derive the orientation and tilt of such facets by identifying the $\varphi$ and $\theta$ coordinates corresponding to the center of reflectance peaks in DRPs. Specifically, the peaks $\varphi$-coordiante describes the in-plane orientation of the facet, while the $\theta$-coordinate is used to compute the facet out-of-plane tilt, $t$, following [12]

$$ \theta { = }\frac{\pi }{2} - 2t $$

(1)

To connect surface facet geometry with the underlying grain orientation, we compute the crystallography of facets by examining the angles between reflectance peaks. The DRP in Fig. 3c shows three reflectance peaks that originate from three sets of facets on the surface of a (111) out-of-plane oriented grain. We hypothesize that the symmetry axis of these three peaks must lie along the [111] crystallographic direction because that is the only threefold symmetry axis in cubic crystals. The facets on the grain surface causing the reflections share the same threefold symmetry and must have Miller indices of the form {x11} where x takes some value larger than 1. Following Eq. 1, we measure facet tilts of ~ 35°, which are consistent with the angles between (111) and the three adjacent {411} surfaces. Grains with orientations other than (111) exhibit different facet geometry. However, all (111) grains give rise to DRPs with threefold symmetry. To confirm this relationship between surface structure and directional reflectance, we measured the topography of another (111) grain using atomic force microscopy (AFM) [19]. The AFM contour map and 3D reconstruction of the surface topography are shown in Fig. 4a, b, respectively. We find that the facet tilt in this grain is approximately 20°, which is consistent with {211} crystallographic planes. We speculate that the surface evolves during etching from flat, to increasingly angled facets as the depth of etching increases (as shown schematically in Fig. 4c). After sufficient time, we would expect the fully etched surface to be dominated by {100} facets, although none of the surfaces investigated here reached that state.

Figure 4

Topography of etched Al surfaces. a AFM contour map for an etched (111) surface. b Normal vectors of the three facets in the etch-pit computed from the AFM data. c Schematic illustration of the etch-pit facet evolution during etching of a (111) grain, seen along the cross section indicated in the 3D rendering of the etch-pit. d Secondary electron micrograph of the surface topography from a (111) out-of-plane oriented grain and e its corresponding DRP

The different facet crystallography found in the two (111) grains suggests that the facet crystallography may change from grain to grain and sample to sample as different surface structures evolve during the etching process, resulting in reflectance peaks with different $\theta$-coordinates. However, peaks $\varphi$-coordinates should remain relatively constants as {x11} surfaces with changing x share the same in-plane direction. This property provides the opportunity to develop a simple mathematical relationship between grain orientation and directional reflectance for grains around (111) orientation.

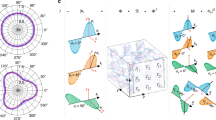
Since crystal orientation is defined by three independent angles, we select DRPs that exhibit threefold symmetry and compute the orientation of the corresponding (111) oriented grains using exclusively the three $\varphi$-coordinates of reflectance peaks. Figure 4d, e shows an electron micrograph of the surface structure on such a grain and its DRP, respectively. $\varphi_{x}$, $\varphi_{y}$, and $\varphi_{z}$ describe the in-plane orientation of the three facet groups covering the surface of the grain.

To compute the Euler angles, $\phi_{1} , \Phi , \phi_{2}$ [20], we must express them in terms of these three $\varphi$-coordinates. Thus, we write a system of equations to relate Euler angles to $\varphi$-coordinates. The rotations matrices used in the Euler angle parametrization are:

$$ R_{Z} (\phi_{1} ) = \left[ {\begin{array}{*{20}c} {\cos \phi_{1} } & {\sin \phi_{1} } & 0 \\ { - \sin \phi_{1} } & {\cos \phi_{1} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],\quad R_{X} (\Phi ) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \Phi } & {\sin \Phi } \\ 0 & { - \sin \Phi } & {\cos \Phi } \\ \end{array} } \right],\quad R_{Z} (\phi_{2} ) = \left[ {\begin{array}{*{20}c} {\cos \phi_{2} } & {\sin \phi_{2} } & 0 \\ { - \sin \phi_{2} } & {\cos \phi_{2} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] $$

(2)

Here, the rotation matrix $R_{i} \left( \alpha \right)$ describes a passive rotation of $\alpha$ degrees about the Cartesian axis, $i$, where $\alpha$ can be $\phi_{1}$,${{\Phi }}$, or $\phi_{2}$, and $i$ is either $X$ or $Z$. Any grain orientation, $O$, can be parametrized using these rotation matrices:

$$ O = R_{Z} (\phi_{2} )R_{Z} (\Phi )R_{Z} (\phi_{1} ) $$

(3)

Substituting Eq. (2) into Eq. (3), we obtain

$$ O = \left[ {\begin{array}{*{20}c} {{\text{c}}\phi_{1} {\text{c}}\phi_{2} - {\text{c}}\Phi {\text{s}}\phi_{1} {\text{s}}\phi_{2} } & { - c\phi_{2} {\text{c}}\Phi {\text{s}}\phi_{1} - c\phi_{1} {\text{s}}\phi_{2} } & {{\text{s}}\phi_{1} {\text{s}}\Phi } \\ {{\text{c}}\phi_{2} {\text{s}}\phi_{1} {\text{ + c}}\phi_{1} {\text{c}}\Phi {\text{s}}\phi_{2} } & {{\text{c}}\phi_{1} {\text{c}}\Phi {\text{c}}\phi_{2} - s\phi_{1} {\text{s}}\phi_{2} } & { - c\phi_{1} {\text{s}}\Phi } \\ {{\text{s}}\Phi {\text{s}}\phi_{2} } & {{\text{c}}\phi_{2} {\text{s}}\Phi } & {{\text{c}}\Phi } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {X_{x}^{'} } & {Y_{x}^{'} } & {Z_{x}^{'} } \\ {X_{y}^{'} } & {Y_{y}^{'} } & {Z_{y}^{'} } \\ {X_{z}^{'} } & {Y_{z}^{'} } & {Z_{z}^{'} } \\ \end{array} } \right]. $$

(4)

Here, $c$ and $s$ refer to cosine and sine, respectively. The $x$ and $y$ components of the rotated Cartesian basis vectors, $\left[ {\begin{array}{*{20}c} {X_{x}^{'} } & {Y_{x}^{'} } & {Z_{x}^{'} } \\ \end{array} } \right]$ and $\left[ {\begin{array}{*{20}c} {X_{y}^{'} } & {Y_{y}^{'} } & {Z_{y}^{'} } \\ \end{array} } \right]$, define the projections of the $X^{'}$, $Y^{'}$, and $Z^{'}$ vectors onto the sample surface. These projections can be also expressed in terms of $\varphi_{x}$, $\varphi_{y}$, and $\varphi_{z}$ as:

$$ \begin{aligned} \frac{{X'_{x} }}{{X'_{y} }} & = \frac{{{ \cos }\phi_{1} { \cos }\phi_{2} - { \cos }\Phi { \sin }\phi_{1} { \sin }\phi_{2} }}{{{ \cos }_{2} { \sin }\phi_{1} + { \cos }\phi_{1} { \cos }\Phi { \sin }\phi_{2} }}{ = }\cot (\varphi_{x} ) \\ \frac{{Y'_{x} }}{{Y'_{y} }} & = \frac{{-{\text{cos}}\Phi { \cos }\phi_{2} { \sin }\phi_{1} -{\text{cos}}\phi_{1} { \sin }\phi_{2} }}{{{ \cos }\phi_{1} { \cos }\Phi { \cos }\phi_{2} -{\text{sin}}\phi_{1} { \sin }\phi_{2} }} = \cot (\varphi_{y} ) \\ \frac{{Z_{x}^{'} }}{{Z_{y}^{'} }} & = \frac{{\sin \phi_{1} \sin \Phi }}{{ - \cos \phi_{1} \sin \Phi }} = - \tan \phi_{1} = \cot (\varphi_{z} ) \\ \end{aligned} $$

(5)

The solution of this system is rather involved since ${{\Phi }}$ and $\phi_{2}$ are coupled. To simplify the solution, we first impose $\varphi_{z}^{'} = 90^\circ$ for all DRPs (which corresponds to an in-plane rotation of the crystal and a rotation about the center of the DRP), solve the system of equations as a function of a rotated set of $\varphi '$-coordinates, and then rotate the in-plane orientation of the crystal back by an angle $\varphi_{z} - 90^\circ$. Setting $\varphi_{z}^{'} = 90^\circ$ yields $\phi_{1}$ = 180° (from Eq. 5), which results in the new system of equations

$$ \begin{aligned} \frac{{X'_{x} }}{{X'_{y} }} & = \frac{{ - \cos \phi_{2} }}{{ - \cos \Phi \sin \phi_{2} }} = \frac{1}{{\cos \Phi \tan \phi_{2} }} = \cot (\varphi_{x} ') \\ \frac{{Y'_{x} }}{{Y'_{y} }} & = \frac{{\sin \phi_{2} }}{{ - \cos \Phi \cos \phi_{2} }} = \frac{{ - \tan \phi_{2} }}{\cos \Phi } = \cot (\varphi_{y} ') \\ \frac{{Z'_{x} }}{{Z'_{y} }} & = 0 \\ \end{aligned} $$

(6)

Multiplying the first two expressions in Eq. (6) yields:

$$ \cos^{2} (\Phi ) = - \tan (\varphi_{x} ')\tan (\varphi_{y} ') $$

(7)

We note that $\varphi_{x}^{'}$ and $\varphi_{y}^{'}$ can also be written as a function of $\varphi_{z} - 90^\circ$ as:

$$ \begin{aligned} \varphi_{x} ' & = \varphi_{x} - (\varphi_{z} - 90^\circ ) \\ \varphi_{y} ' & = \varphi_{y} - (\varphi_{z} - 90^\circ ) \\ \end{aligned} $$

(8)

Thus, by substituting Eq. (8) into Eq. (7) and correcting the in-plane orientation by $\varphi_{z} - 90^\circ$, we obtain:

$$ \begin{aligned} \phi_{1} & = 180^\circ + (\varphi_{z} - 90^\circ ) = \varphi_{z} + 90^\circ \\ \Phi & = \arccos \left( {\sqrt { - \tan (\varphi_{x} { - }\varphi_{z} + 90^\circ )\tan (\varphi_{y} { - }\varphi_{z} + 90^\circ )} } \right) \\ \phi_{2} & = \arctan \left( { - \cos (\Phi )\cot (\varphi_{x} { - }\varphi_{z} + 90^\circ )} \right) \\ \end{aligned} $$

(9)

We use Eq. (9) to derive the Euler angles from the measured $\varphi$-coordinates of directional reflectance peaks in the DRPs of (111) oriented grains.

To compute $\varphi_{x}$, $\varphi_{y}$, and $\varphi_{z}$ from DRPs, we determine the center of reflection peaks in DRPs by applying an intensity threshold to binarize the reflectance distribution and calculating the centroids of the resulting peaks. Figure 5 shows comparison an example DRP before and after binarization using a threshold of 0.5. We find that the actual threshold value does not affect the accuracy of the $\varphi$-coordinates computation significantly. One problem associated with this method is that peaks occurring in proximity of $\varphi = 0^\circ$ may be counted twice, yielding errors in the computation of the $\varphi$-coordinate. With reference to Fig. 5a, the peak that intersect the $\varphi = 0^\circ$ is split in two halves, each one with a distinct—and incorrect—centers of mass (see Fig. 5c). To solve this issue, we impose periodic boundary conditions along the $\varphi$-axis and avoid a miscount of peaks (Fig. 5b, d).

Figure 5

a DRP from a (111)-oriented grain and b corresponding “periodic DRP”. c The binarized versions of the DRP in a. d The binarized versions of the “periodic DRP” in b showing the reflectance peak centroids

Using binarized DRPs is a simple, computationally inexpensive process to estimate the centroids of reflectance peaks. The centroid of the high-reflectance peak area may not always coincide with the actual peak center (i.e., the position of the intensity maximum). However, re-computing the crystal orientation using a peak-fitting algorithm that identifies the peak local maximum, increased the average measurement error (not shown here), suggesting that simple binary peak estimation is sufficient.

Results

Figure 6a shows comparison DRM and EBSD grain orientation maps along the z- and x-axis. Here, grains are color-coded according to the inverse pole figure (IPF) color scheme used in EBSD measurements [17]. The comparison between the maps qualitatively demonstrates that we identify all grains vicinal to (111) and determine their orientation correctly. We also compute the angular difference between the orientation measured by DRM and EBSD for each grain in Fig. 6a, which is ~ 4° on average. Figure 6b displays this difference for one representative (111) grain on a {100} pole figure.

Figure 6

Comparison of DRM and EBSD orientation measurements. a IPF grain map along x and z for the same area compiled by DRM and EBSD. Only grains that can be indexed using Eq. (9) are colored in the DRM map. b Comparison between the orientation of a representative grain (marked with a yellow triangle) measured by DRM and EBSD in a {100} pole figure. The <100> axes from DRM (circles) and EBSD (crosses) measurements differ by ~ 2.6°

The mean orientation of a grain may vary depending on the spatial resolution of the technique that is used to measure it. DRM measurements were made with a 12-µm step size, with each pixel averaging the reflectivity of the area, whereas EBSD measurements were made with a similar step size (6 µm), but measuring only from a much smaller spot in the middle of each step rather than averaging the area. Due to differences in spatial resolution and coverage, DRM and EBSD may have different sensitivity to local intragranular misorientations and thus may yield different but equally valid mean orientations. We also compare DRM and EBSD measurements of the grain orientation spread (GOS) [21], which describes the average misorientation between measurement points. Using Eq. (9), we compute the Euler angles at each pixel within the (111) oriented grains, map the intragranular orientation distribution, and compute the GOS. Figure 7a shows qualitatively that the top and bottom sides of a grain have different orientations. DRPs from the two areas show that surface structures differ by a slight out-of-plane rotation (Fig. 7b, c), which is also confirmed by the EBSD pole figures (Fig. 7d). The GOS values we measure from DRM (3.45°) and EBSD (3.15°) differ by ~ 8.5%, but these values are susceptible to the same type of sampling variations as the mean orientation measurements.

Figure 7

Intragranular misorientation measurement. a Pixel-wise DRM texture map within a single (111) Al grain. b DRP from point A and c point B in the grain shown in a showing a peak shift of a few degrees. d EBSD pole figure for measurements at point A (circles) and point B (crosses) showing a lattice rotation of 7.05°. e DRM and f EBSD maps of intragranular misorientation angle

The discrepancies between DRM and EBSD orientation measurements (~ 4° on average) may be related to the inherent angular resolution of the DRM illumination apparatus. However, mis-registration between the EBSD and DRM dataset can also introduce systematic differences in the measurements. We register DRM and EBSD datasets manually, by identifying common triple junction points in the sample microstructure. We believe that this approach minimizes in-plane mis-registrations such as a dataset rotation.

Discussion

The results presented here demonstrate the capability of measuring crystal orientation by a simple and inexpensive optical technique that quantifies surface reflectance as a function of the direction of the incoming light. In Al, this technique is limited to (111) oriented grains because the analysis requires the centers of three reflectance peaks to solve for a Euler angle triplet. Al is known to form {100} surface facets during chemical etching, in contrast to the {111} facets formed on most other metals with the face-centered cubic crystal structure [14]. However, our DRM and AFM analysis revealed that (111) grains in different samples exhibit facets consistent with both {211} and {411} crystallographic planes. DRM provides a new tool to rapidly evaluate this kind of surface crystallography. It could be a key to new experiments that elucidate the details of Al surface evolution. By solving remaining uncertainty in facet crystallography DRM would in turn become a powerful tool for measuring general crystallographic orientation in Al.

The combination of spatial resolution, sample throughput, and low cost make DRM a potentially valuable technique for large-scale surface analysis of materials [22]. The DRM apparatus used for this study consisted of a commercial light source, an optical microscope, and a motorized stage to control incoming light direction. DRM measurement time (i.e., data acquisition and analysis) at the angular resolution used in this study took less than 30 min. By contrast to scanning surface analysis techniques, this time does not scale with sample size if the sample area (~ 2 cm × 2 cm in this work) fits within the microscope field of view. Because DRM does not require vacuum, it is more flexible than electron-based techniques such as EBSD with regard to sample size and material. DRM orientation measurements have the potential to be performed on any crystalline material, so long as a suitable crystallographic etchant can be found. In addition to applications as a technique purely for mapping crystallographic orientation, DRM can be used in a more specialized role to study interactions between crystallography, surface structure, and processing. These measurements are typically possible using AFM, but they are generally low in throughput. In this context, DRM could have important consequences for the study of corrosion mechanisms and the design of new corrosion resistant materials [23].

The study of surface directional reflectance is an emerging field with broad promise for several types of surface characterization. The rich amount of information that can be extracted from a single directional reflectance measurement provides unique insights into the relationships between topography, crystallography, and surface structure in polycrystalline materials.

Conclusions

• We show the possibility of performing crystal orientation and misorientation measurements on chemically etched Al polycrystals using an optical technique called directional reflectance microscopy (DRM).

• We demonstrate these measurements on a subset of grains with out-of-plane orientation vicinal to (111), whose directional reflectance exhibits enough features (namely specular reflection peaks) to compute the underlying crystal orientation.

• We compare DRM orientation measurements against EBSD and find a difference of ~ 4° on average.