Abstract
The evolution of texture components for two experimental 0.06 wt% C steels, one containing 0.03 wt% Nb (Nb steel) and the second containing both 0.03 wt% Nb and 0.02 wt% Ti (Nb–Ti steel), was investigated following a new thermomechanical controlled process route, comprising first deformation, rapid reheat to 1200 °C and final deformation to various strains. Typical deformation textures were observed after first deformation for both steels. Following subsequent reheating to 1200 °C for various times, the recrystallisation textures consisted primarily of the α-\( \left\langle {011} \right\rangle \)//RD texture fibre with a weak γ-{111}//ND texture fibre, similar to deformation textures, indicative of the dominance of a strain-induced boundary migration mechanism. The texture components after finish deformation were different from the rough deformation textures, with a strong α-\( \left\langle {011} \right\rangle \)//RD texture fibre at the beginning, and then the strong peaks move to (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) textures due to the deformation-induced ferrite (DIF) transformation. The effect of Ti on the recrystallisation textures and deformation textures has also been analysed in this study. The results illustrate that Ti significantly influences the γ-{111}//ND texture fibre. Finally, the textures after deformation and recrystallisation in the austenite were calculated based on the K–S orientation relationship between the austenite and ferrite. This allowed the understanding of the mechanism of recrystallisation between first and final deformation and the DIF textures during phase transformation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Microalloyed steels have been widely used in a variety of industrial sectors, such as construction, energy and automotive [1,2,3]. This is a result of optimised thermomechanical controlled processing (TMCP) to provide the desired microstructure and crystallographic texture, leading to steels with excellent formability, strength and toughness [3, 4]. TMCP, consisting of controlled hot deformation followed by controlled cooling, are used to maximise the benefits of the microalloy additions to the steels [5, 6]. The main improvement in mechanical properties by TMCP is a result of ferrite grain refinement, which is maximised by having a high surface area-to-volume ratio (Sv) of austenite grain boundaries and the deformation band density [7].
Numerous studies on the effect of temperature on the deformation and recrystallisation focus on the conditions in the fully ferritic phase field, to avoid the complexities associated with a phase transformation [8,9,10,11,12,13]. The observed texture is then a result of the recrystallised texture in the austenite and the resultant transformation to ferrite. Recently, using processing conditions that result in the formation of deformation-induced ferrite (DIF), this strategy has become a favoured method to obtain ultrafine ferrite grains in microalloyed low carbon steels [10,11,12,13,14,15,16]. Most of these investigations into DIF have focused on the effect of chemical composition, the cooling rate and the deformation parameters (strain, strain rate). But little attention has been paid as to how the textures arising from processing that leads to DIF effect the final texture. This is no doubt because of the complexities associated with its rapid formation during deformation resulting in the formation of the deformation-induced ferrite, the subsequent deformation and recrystallisation of that ferrite and finally its ensuing evolution during cooling to room temperature. Moreover, a key issue is to differentiate the DIF from the ferrite that was formed by transformation from the austenite during cooling.
In this study, the deformation textures after initial deformation (the ‘roughing stage’), solution heat treatment recrystallisation textures and finish deformation textures have been investigated in the BCC ferrite using detailed electron backscatter diffraction (EBSD), to separate the DIF textures from the texture arising from the normal transformation on cooling. Moreover, depending on the observation of the BCC textures and the Kurdjumov–Sachs (K–S) orientation relationship, the recrystallisation and deformation textures in the FCC matrix have been calculated to understand how the DIF and deformed austenite textures formed during final deformation. The effect of a Ti addition to the Nb microalloyed steel on the texture evolution has also been analysed and compared to the base Nb microalloyed steel.
Experimental methods
Compositions and processing conditions
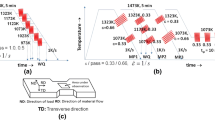
The materials used in the research consisted of two laboratory cast microalloyed steels containing Nb (designated as Nb steel) and Nb and Ti (designated as Nb–Ti steel), which were made by vacuum induction melting and cast into 220 mm × 65 mm × 28 mm square ingots at ArcelorMittal. The compositions of these steels were analysed by Sheffield Testing Laboratories and are listed in Table 1. The ingots were soaked at 1300 °C for 2 h and hot-rolled from 28- to 12-mm-thick plates in two passes in a 2-high experimental 50 tonne Hille rolling mill. The finishing temperature was 1100 °C, followed by quenching in iced water. Specimens with the dimensions of 60 mm × 30 mm × 10 mm were removed from this plate for controlled deformation using plane strain compression (PSC), performed using the thermomechanical compression (TMC) machine at the University of Sheffield [18]. Prior to deformation via PSC, the samples were reheated to 1100 °C, held for 30 s and then force air cooled to the deformation temperature of 850 °C, which was achieved in a single pass using a strain of 0.3 at a constant true strain rate of 10 s−1. Following this, the steels were rapidly reheated at a rate of 10 °C/s to a temperature of 1200 °C, isothermally held for 0, 10, 100 and 1000 s followed by an immediate water quenching as illustrated in Fig. 1a. Based on an assessment of the microstructures of these samples, 10 s for 1200 °C was chosen for this study and subjected to final rolling. The final deformation passes were performed with different rolling parameters and hold times, as shown in Fig. 1b, which provided materials deformed to strains of 0.3 and 0.6, both with and without a 10-s hold after rolling.
The electron backscatter diffraction (EBSD)
Electron backscatter diffraction (EBSD) specimens were prepared from the PSC samples with dimensions of about 10 mm × 10 mm × 5 mm. In order to obtain the best possible surface finish for EBSD, after polishing by 1-μm diamond suspension, the specimens had a final polish using colloidal silica for an extended period followed by water cleaning. EBSD investigations were performed using the FEI Sirion FEG SEM with 20 kV. The orientation mapping was processed on a square grid with step sizes of 0.25 μm and the pattern solving efficiencies of 80–90%. Data analysis was processed using HKL Channel 5 software. The observed texture was identified using pole figures and orientation distribution function (ODF) in the Euler space [19]. The analysis of ODF is based on the individual crystallite orientations and utilising the angular notation given by Bunge [20]. The EBSD maps were subdivided into subsets, namely those containing only deformation-induced ferrite (DIF) and deformed prior-austenite grains that had transformed to ferrite using HKL Channel 5 software. The calculation of the parent orientations (FCC) from each of the product components (BCC) was carried out in MATLAB using the reconstruction procedure outlined elsewhere [21].
Results
Deformation textures in the BCC matrix during the first deformation at 850 °C, followed by immediate water quenching
Before the first deformation at 850 °C, the steel was first heat-treated at 1100 °C for 30 s. Figure 2 shows the recrystallised structure in the Nb and Nb–Ti steels, with a similar grain size for the Nb and Nb–Ti steels. The ODFs in the φ2 = 45° section were taken from the samples after heat treatment at 1100 °C for 30 s, before the first deformation at 850 °C, Fig. 3. The results show the strong γ-{111}//ND recrystallisation texture fibre for the Nb and Nb–Ti steels in the BCC matrix. The deformed structure of the prior-austenite grains could be seen after the first rolling at 850 °C, Fig. 4. There was no evidence of DIF on the prior-austenite grain boundaries after the first deformation and the grain size in the RD direction were also similar for the two steels. Figure 5 gives the ODFs after heat treatment at 1100 °C for 30 s followed by the first deformation at 850 °C and water quenching. Two important fibre textures were present: α-\( \left\langle {011} \right\rangle \)//RD texture fibre and γ-{111}//ND texture fibre, with the major texture component of {112} \( \left\langle {110} \right\rangle \) (5.5 random and 6.8 random for Nb and Nb–Ti steels) together with a minor component of {111} \( \left\langle {110} \right\rangle \). The textures shown in Figs. 3 and 5 demonstrated that the recrystallisation textures during heat treatment at 1100 °C were different from the deformation textures after subsequent deformation at 850 °C.
Recrystallisation textures in the BCC matrix after heat treatment at 1200 °C followed by immediate water quenching
Figures 6 and 7 show the prior-austenite grains during heating at 1200 °C for different times in Nb and Nb–Ti steels. The recrystallisation of the prior-austenite grains and subsequent grain growth can be seen with increasing holding time. Compared with the microstructure in Fig. 2, the recrystallised grain size in the Nb and Nb–Ti steels at 1200 °C was both larger than that of 1100 °C for 30 s, even for the sample heated to 1200 °C and immediately cooled. The grain size was larger in the Nb steel compared to that in the Nb–Ti steel for the same holding time.
The (111) and (110) pole figures and φ2 = 45° ODF section from recrystallised samples after rolling at 850 °C followed by heat treatment at 1200 °C for 0, 10, 100 and 1000 s and immediate water quenching are shown in Fig. 8 for the Nb steel. At 1200 °C for 0 s, the major texture components were {112}\( \left\langle {1\bar{1}0} \right\rangle \) with minor components of {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), {114}\( \left\langle {1\bar{1}0} \right\rangle \), {112}\( \left\langle {1\bar{3}1} \right\rangle \) and {111}\( \left\langle {0\bar{1}1} \right\rangle \). With an isothermal hold for 10 s at 1200 °C, the major texture components changed to (112)\( \left\langle {1\bar{1}0} \right\rangle \) and {111}\( \left\langle {0\bar{1}1} \right\rangle \) with minor components of {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) and {112}\( \left\langle {1\bar{3}1} \right\rangle \). After 1200 °C for 100 s, the minor components of {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) disappeared and moved to {001}\( \left\langle {0\bar{1}0} \right\rangle \) with the major texture components of {111}\( \left\langle {1\bar{1}0} \right\rangle \). With a further increase in the holding time to 1000 s at 1200 °C, the major texture components consisted of (112)\( \left\langle {1\bar{1}0} \right\rangle \) and {111}\( \left\langle {0\bar{1}1} \right\rangle \) with minor components of {001}\( \left\langle {0\bar{1}0} \right\rangle \).
The texture components for the Nb–Ti steel after rough rolling followed by heat treatment at 1200 °C for 0, 10, 100 and 1000 s and immediate water quenching are presented in Fig. 9. The major texture components are {112}\( \left\langle {1\bar{1}0} \right\rangle \) for all four specimens during the whole period of the heat treatment. The different minor texture components during heat treatment for each specimen are the {221}\( \left\langle {1\bar{2}2} \right\rangle \), {111}\( \left\langle {1\bar{1}2} \right\rangle \), {112}\( \left\langle {1\bar{3}1} \right\rangle \) and {001}\( \left\langle {1\bar{1}0} \right\rangle \) at 0, 10 and 100 s, and {001}\( \left\langle {0\bar{1}0} \right\rangle \), {112}\( \left\langle {1\bar{3}1} \right\rangle \) for 1000 s.
The recrystallisation texture components for Nb and Nb–Ti steels were different [22], as the intensity of {111}\( \left\langle {1\bar{1}0} \right\rangle \) texture continually increased for the Nb steel, while the {111}\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) texture changed to a stronger {111}\( \left\langle {1\bar{1}0} \right\rangle \) texture component for Nb–Ti steel as a result of the Ti addition. As the isothermal holding time increased, the {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) disappeared and changed to {001}\( \left\langle {0\bar{1}0} \right\rangle \).
To further analyse the differences of the recrystallisation fibres in these two steels, Fig. 10 shows the orientation distribution function along the section of Φ = 55° and φ2 = 45° as a function of φ1 with rotation of the normal direction parallel to the [111] (γ fibre). The strong f(g) peaks in Fig. 10 for Nb and Nb–Ti steels correspond to the ideal orientations given in Figs. 4 and 5. Meanwhile, for the γ fibre, the f(g) peak was around φ1 = 0° and 60° for the Nb steel for the entire period, but the orientation density peak in the Nb–Ti steel was around 20°–30° and 70°–90°, Fig. 10. The orientation density was a minimum in the Nb at φ1 = 30° and for the Nb–Ti at φ1 = 60° for the whole period. Thus, the addition of Ti to the steel changed the texture distribution significantly compared to the Nb steel.
Deformation-induced ferrite (DIF) microstructures during finish deformation for the Nb and Nb–Ti steels
For the study of deformation-induced ferrite during hot working, Figs. 11 and 12 show IPF maps taken from the Nb and Nb–Ti steel samples that had a final deformation at a temperature of 850 °C, which is above the Ar3 for the various strains and holding times given in Fig. 1b. For schedule A-10, deformation-induced ferrite formation was observed along the austenite grain boundaries, Figs. 11a and 12a. After the same deformation and with a subsequent isothermal hold for 10 s (schedule B-10), the ferrite that had formed through deformation began to coarsen along the prior-austenite grain boundaries (Figs. 11b, 12b). The volume fraction of the DIF along the prior-austenite grain boundaries increased with increased isothermal holding after deformation as a result of this grain growth (as illustrated by the white lines in Fig. 11). Following a second deformation to a strain of 0.6 (schedule C-10), the interior of austenite grains became active as nucleation sites for DIF (Figs. 11c, 12c) (as illustrated by the white ring).
Figure 13 gives the average size of the deformation-induced ferrite grains. Not surprisingly, the size of the DIF was larger after a hold after deformation (B-10 vs A-10 and D-10 vs C-10). Equally, the second deformation at 850 °C (C-10) resulted in a finer DIF grain size compared to the strain of 0.3 (A-10). Moreover, the grain size of the DIF in the Nb steel is slightly smaller than that found in the Nb–Ti steel.
The average DIF grain size measured from Fig. 8 in the Nb steel specimens after finish deformation with the isothermal holding time of schedule A-10: ε = 0.3, 0 s, schedule B-10: ε = 0.3, 10 s, schedule C-10 ε = 0.6, 10 s, schedule D-10 ε = 0.6, 10 s +10 s hold
The φ2 = 45° ODF sections for the Nb and Nb–Ti steels with a finishing deformation at 850 °C are presented in Fig. 14. There is only one peak and a few weaker components shown in Fig. 14a, e with a total strain of 0.3 for Nb and Nb–Ti steels (schedule A-10). The strongest peak was along (112)\( \left\langle {1\bar{1}0} \right\rangle \). Weaker components exist at (111)\( \left\langle {1\bar{2}1} \right\rangle \), (111)\( \left\langle {0\bar{1}1} \right\rangle \). After deformation to a strain of 0.3 and then an isothermal hold for 10 s (schedule B-10), three strong peaks were observed at (112)\( \left\langle {1\bar{1}0} \right\rangle \), (111)\( \left\langle {0\bar{1}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \) for Nb steel (Fig. 14b) and two speaks for Nb–Ti steel at (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \) (Fig. 14f). The intensity of (112)\( \left\langle {1\bar{1}0} \right\rangle \) decreased after a 10-s hold, due to the ferrite recrystallisation. The two orientation components along (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) with the intensity became weaker than that in the sample deformed without isothermal holding (schedule A-10) for both Nb and Nb–Ti steels. Increasing the strain to 0.6 (schedule C-10) (Fig. 14c, g), the strong peak at (112)\( \left\langle {1\bar{1}0} \right\rangle \) had an intensity slightly higher than that of the strong peak for those samples deformed to a strain of 0.3 with 10-s holding (schedule B-10), but much less than that at schedule A-10 for both steels. Three orientation components were observed along (111)\( \left\langle {1\bar{2}1} \right\rangle \), (111)\( \left\langle {0\bar{1}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \) with a similar intensity to each other. Finally, after isothermal holding for 10 s after a total strain of 0.6 (schedule D-10) (Fig. 14d, h), the strong peaks moved to (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) with the components at (112)\( \left\langle {1\bar{1}0} \right\rangle \) becoming weaker for both steels. There were also weaker components at (001)\( \left\langle {1\bar{1}0} \right\rangle \) and (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) in all ODFs.
(111) and (110) φ2 = 45° ODF sections from the Nb and Nb–Ti steel specimens after finish deformation with the isothermal holding time of a, e ε = 0.3, 0 s (schedule A-10), b, f ε = 0.3, 10 s (schedule B-10), c, g ε = 0.6, 10 s (schedule C-10), d, h ε = 0.6, 10 s +10 s hold (schedule D-10), while a–d took from Nb steel and e–h took from Nb–Ti steel
Discussion
The effect of heat treatment at 1200 °C for different holding time between the first and final rolling on the deformation and the recrystallisation textures in the Nb and Nb–Ti steels
Considering the recrystallisation textures at 1100 and 1200 °C (Figs. 3, 8, 9), and the deformation textures at the first and final rolling (Figs. 5, 14), the results show that the recrystallisation textures at 1200 °C (Figs. 8, 9) are closely related to the first deformation textures at 850 °C (Fig. 5), but they are different from the recrystallisation textures at 1100 °C (Fig. 3) for both steels [23, 24]. This suggests that the strain-induced boundary migration (SIBM) mechanism was dominant during recrystallisation at 1200 °C, as reported by several researchers [23, 25, 26]. A characteristic feature of this mechanism is that the new grains have similar orientations to the old grains from which they have grown [27]. Therefore, after the first deformation followed by a rapid increase in the temperature to 1200 °C, the mechanism of recrystallisation is different from the recrystallisation at 1100 °C for both steels, due to the SIBM.
After reheating at 1200 °C for 10 s, both steels were then subject to a final deformation schedule using different strains and interpass holding times (Fig. 1b). For the rolling schedule A-10, which has the same rolling parameters as the first deformation, similar texture components were observed, namely (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \), Figs. 5 and 14. However, the intensity of those two orientations was stronger after the final rolling compared to after the first rolling. Moreover, with a 10-s isothermal hold after the final deformation, the peak of the orientations changed to (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \). Then, following further deformation (schedule of C-10, which has the same rolling parameters with A-10), the intensity of the (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) was still lower after C-10 compared to after final rolling at A-10. Thus, the heat treatment at 1200 °C between the first and finish deformations had a clear effect on the texture.
Simulation of texture
It is known that the phase transformation from austenite to ferrite obeys the K–S orientation relationship [28]; therefore, the deformation and the recrystallisation textures in the FCC matrix, which transformed to the BCC textures after water quenching to room temperature, can be calculated through the K–S orientation relationship [29]. The simulations were conducted on the Nb steel.
The calculation of the parent orientations (FCC) from each of the product components (BCC) was carried out in MATLAB using the reconstruction procedure outlined elsewhere [21]. The transformation from ferrite to austenite is characterised by the K–S orientation relationship, which defined a rotation of 90° around each of the twelve possible \( \left\langle {112} \right\rangle \) axes; therefore, 24 rotations are necessary to obtain the 24 variants. The complete procedure for the calculation of a parent orientation has been analysed through ODFs presented in Fig. 15.
The deformation textures in the austenite after the first deformation were Goss/Brass and Cube textures shown in Fig. 15a. After reheating to 1200 °C for 0, 10 and 100 s, the recrystallised austenite texture components were mainly Brass for three different holding times (Fig. 15b–d) and weak orientation of Goss and {236}\( \left\langle {358} \right\rangle \) that begin at 10 s and increased at 100 s (Fig. 15c, d). With increasing holding time to 100 s, the weak Cube texture appeared at 100 s (Fig. 15d).
After the first deformation in the austenite, there was also a weak Brass texture shown in Fig. 15a. With the isothermal holding time increased to 10 s, a weak {236}\( \left\langle {358} \right\rangle \) texture formed. The intensity of the {236}\( \left\langle {358} \right\rangle \) orientation increased with increasing holding time to 100 s. The Brass recrystallisation orientation of {236}\( \left\langle {358} \right\rangle \) produced by the Brass deformation texture rotated by an approximate 30°–40° \( \left\langle {111} \right\rangle \) rotation. Virnich [30] and Gottstein [31] reported similar recrystallisation behaviour in the FCC metal, and the intensity of {236}\( \left\langle {358} \right\rangle \) also appeared after holding for a period and then increased with the increasing holding time [32].
The recrystallisation textures at 1200 °C (Figs. 8, 9) in this investigation are similar to the deformation textures after the first deformation (Fig. 5), but different from the typical recrystallisation texture with strong γ-{111}//ND texture fibre, as shown in Fig. 2. The evolution of recrystallisation textures (Fig. 15b–d) in the austenite is also different from the typical austenite recrystallisation textures, but similar to the deformed textures in austenite (Fig. 15a), which also support the SIBM recrystallisation theory [33]. Moreover, the calculated recrystallisation textures at 1200 °C in the austenite indicated that the Brass deformation texture after first rolling with orientation of {011}\( \left\langle {211} \right\rangle \) also rotated to the Brass recrystallisation orientation. The solute drag during high-temperature heat treatment promoted the retention of the Cube texture during recrystallisation to 100 s.
There are weaker {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) and {112}\( \left\langle {1\bar{3}1} \right\rangle \) textures shown in Fig. 8a–c after isothermal holding from 0 and 10 s, which could also have been produced from Brass textures shown in Fig. 15b, c. Moreover, there is a weak Goss texture only shown in Fig. 15d after holding for 100 s at 1200 °C in the austenite. As reported by Guillén [34], the (001)\( \left\langle {0\bar{1}0} \right\rangle \) texture component in the BCC matrix shown in Fig. 8d can have transformed from the Goss recrystallisation texture, which only appeared after isothermal holding for 100 s. Therefore, the calculated FCC textures shown in Fig. 15 fitted well with the produced textures after transformation to BCC matrix.
The effect of Ti on the recrystallisation and deformation textures as well as the microstructures
The γ-fibre plots shown in Fig. 10, taken from the heat treatment samples at 1200 °C (Fig. 1a), indicated that the Nb steel exhibited the maximum orientation density at (111)\( \left\langle {1\bar{1}0} \right\rangle \). However, for the Nb–Ti steel, the reverse was true in that the texture component of (111)\( \left\langle {1\bar{1}0} \right\rangle \) disappeared when recrystallisation occurred. Moreover, Fig. 5 shows that there was no difference in the deformation textures for the Nb and Nb–Ti steels after the first deformation. However, after heat treatment at 1200 °C, the recrystallisation textures in the Nb and Nb–Ti steels were different from first deformation textures. With the Ti addition in the Nb–Ti steel, the recrystallisation textures at 1200 °C changed significantly, when compared with the Nb steel.
A similar phenomenon has also been observed by Ghosh et al. [22] in continuously annealed steels which showed that the (111)\( \left\langle {1\bar{1}0} \right\rangle \) orientation is favoured in the Nb steel. This is because of the differences in dissolution kinetics. In the Nb steel, all microalloy elements and carbon would have been in solution after reheating to 1200 °C, whereas for the Nb–Ti steel, full dissolution would not have occurred [20,21,22]. The solute drag from the Nb is known to influence the recrystallisation textures during heat treatment [35, 36].
The final deformation textures shown in Fig. 14 were similar γ-fibre deformation textures for both Nb and Nb–Ti steels. As shown in Figs. 11 and 12, the DIF formed mainly on the prior-austenite grain boundaries during final deformation, which are not observed on the first deformation (Fig. 4). It is shown that the addition of Ti did not influence the DIF textures during final deformation.
The mechanism of the DIF during final deformation depending on the simulation of FCC textures
DIF was observed at the prior-austenite grain boundaries during final deformation (Figs. 11, 12), although the average prior-austenite grain size was larger than that during holding at 1100 °C. It has been observed that a finer prior-austenite grain size before deformation increases the extent of DIF [37]. In the present study, in contrast to the observations of [13, 17, 38,39,40,41,42,43,44,45,46], DIF was promoted by a larger prior-austenite grain size, arising from the reheating process between first and final deformation. As shown in Fig. 14, for both Nb and Nb–Ti steels, the peak components of the orientation were at (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) with the final rolling schedule of A-10. Then, with 10-s holding after finishing deformation (B-10), the peak components of the orientation changed to (111)\( \left\langle {1\bar{2}1} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \), (111)\( \left\langle {0\bar{1}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \). With increasing the finishing deformation strain to 0.6 (C-10), the maximum peak orientation changed back to (112)\( \left\langle {1\bar{1}0} \right\rangle \). But again, with a subsequent hold of 10 s, the peak reverts to (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \). During holding for 10 s the DIF grains grew, increasing their overall volume fraction. Nevertheless, it is clear that the DIF textures are mainly (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {1\bar{1}2} \right\rangle \).
Furthermore, the previous work [34, 47,48,49,50,51] about the relationship between FCC and BCC textures has indicated that the Goss texture from deformed austenite (FCC) would produce components of (112)\( \left\langle {1\bar{1}0} \right\rangle \), (111)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) in the BCC ferrite matrix after phase transformation. The Brass texture from deformed and recrystallised austenite (FCC) was transformed to the components of (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) in ferrite matrix (BCC). The DIF rapidly formed on the prior-austenite grain boundaries during final deformation. Then, after final deformation, the residual deformed austenite will be transformed directly to ferrite without producing DIF [50, 52,53,54].
Therefore, the (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) in the resultant ferrite matrix, shown in Fig. 14, come from Goss deformed austenite textures (Fig. 15a). The (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) shown in Fig. 14 come from Brass recrystallised austenite textures. Figure 16 shows IPF subset maps of the (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) textures that are the DIF components [55]. It is clear that most of the DIF occurred on the prior-austenite grain boundaries and the number density increased with the increasing strain and isothermal holding time after deformation. The results show that the DIF textures were mainly (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \), which come from the recrystallisation austenite textures.
IPF images from (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}\bar{1}0} \right\rangle \), (111) \(\left\langle {1-21} \right\rangle\) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \) orientation of DIF in the Nb steel specimens after finish deformation with the isothermal holding time of a ε = 0.3, 0 s (schedule A-10), b ε = 0.3, 10 s (schedule B-10), c ε = 0.6, 10 s (schedule C-10), d ε = 0.6, 10 s + 10 s hold (schedule D-10)
Conclusions
-
1.
Both Nb and Nb–Ti steels after heat treatment at 1100 °C for 30 s and the first deformation at 850 °C show the typical strong recrystallisation and deformation textures in the BCC matrix.
-
2.
The recrystallisation textures after heat treatment at 1200 °C for different times were studied for both Nb and Nb–Ti steels. The observed texture was different from the typical recrystallisation textures, but similar to the deformation textures after first rolling at 850 °C. The difference was believed to be due to SIBM recrystallisation occurring at 1200 °C.
-
3.
The effect of Ti on the recrystallisation textures has been analysed. The results indicated that Ti significantly influences the γ-{111}//ND texture fibre due to the lower solid solution in the Nb–Ti steel. The solute drag effect benefited the nucleation of the (111)\( \left\langle {1\bar{1}0} \right\rangle \) orientation for the Nb steel. However, the effect of Ti on the DIF textures is not obvious. The rapid formation of DIF supports the view that DIF occurred through a massive transformation.
-
4.
The DIF textures were mainly (001)\( \left\langle {1\bar{1}0} \right\rangle \), (001)\( \left\langle {\bar{1}10} \right\rangle \), (111)\( \left\langle {1\bar{2}1} \right\rangle \), {112}\( \left\langle {1\bar{3}1} \right\rangle \) and (111)\( \left\langle {\bar{1}\bar{1}2} \right\rangle \), which were produced from the Brass recrystallised FCC texture. The (112)\( \left\langle {1\bar{1}0} \right\rangle \) and (111)\( \left\langle {0\bar{1}1} \right\rangle \) in the ferrite matrix were produced from the Goss deformed texture in the austenite.
-
5.
The (001)\( \left\langle {0\bar{1}0} \right\rangle \) instead of {001}\( \left\langle {\bar{1}\bar{1}0} \right\rangle \) appeared after isothermal holding until 100 s at 1200 °C, which arose from the Goss recrystallisation texture which only formed in the austenite after a 100-s hold.
References
Timokhina IB, Hodgson PD, Ringer SP, Zheng RK, Pereloma EV (2007) Precipitate characterisation of an advanced high-strength low-alloy (HSLA) steel using atom probe tomography. Scr Mater 56:601–604
Patel JK, Wilshire B (2002) The challenge to produce consistent mechanical properties in Nb–HSLA strip steels. J Mater Process Technol 120:316–321
Ghosh A, Mishra B, Das S, Chatterjee S (2004) An ultra low carbon Cu bearing steel: influence of thermomechanical processing and aging heat treatment on structure and properties. Mater Sci Eng A 374:43–55
Gomez M, Valles P, Medina SF (2015) Evolution of microstructure and precipitation state during thermomechanical processing of a X80 microalloyed steel. Mater Sci Eng A 528:4761–6773
Shukla R, Ghosh SK, Chakrabarti D, Chatterjee S (2013) Microstructure, texture, property relationship in thermo-mechanically processed ultra-low carbon microalloyed steel for pipeline application. Mater Sci Eng A 587:201–208
Jahazi M, Egbali B (2000) The influence of hot rolling parameters on the microstructure and mechanical properties of an ultra-high strength steel. J Mater Process Technol 103:276–279
Park S (1991) Modelling and measurement of the continuous-cooling-precipitation kinetics of Nb(CN) in HSLA steels. McGill University, Montreal, Canada
Ray RK, Jonas JJ (1990) Transformation textures in steels. Int Mater Rev 35:1–36
Lee DN (1995) The evolution of recrystallization textures from deformation textures. Scr Metall Mater 32:1689–1694
Lücke K, Hölscher M (1991) Rolling and recrystallization textures of BCC steels. Texture Microstruct 14:585–596
Equihua F, Salinas A, Nava E (2010) Effect of aluminum content on austenite-ferrite transformation temperature in low carbon (Si–Al) hot rolled GNO electrical steels. Rev Metal 46:78–85
Chen J, Li F, Liu Z, Tang S, Wang G (2013) Influence of deformation temperature on γ–α phase transformation in Nb–Ti microalloyed steel during continuous cooling. ISIJ Int 53:1070–1075
Imandoust A, Zarei-Hanzaki A, Abedi HR (2012) Low-temperature strain-induced ferrite transformation in twinning-induced plasticity steel. Scr Mater 67:995–998
Eghbali B, Abdollah-zadeh A (2006) Strain-induced transformation in a low carbon microalloyed steel during hot compression testing. Scr Mater 54:1205–1209
Ohmori A, Torizuka S, Nagai K, Koseki N, Kogo Y (2004) Effect of deformation temperature and strain rate on evolution of ultrafine grained structure through single-pass large-strain warm deformation in a low carbon steel. Mater Trans 45:2224–2231
Song R, Ponge D, Raabe D, Speer JG, Matlock DK (2006) Overview of processing, microstructure and mechanical properties of ultrafine grained bcc steels. Mater Sci Eng A 441:1–17
Hodgson P, Hickson M, Gibbs R (1999) Ultrafine ferrite in low carbon steel. Scr Mater 40:1179–1184
Loveday MS, Mahon GJ, Roebuck B, Lacey AJ, Palmiere EJ, Sellars CM, van der Winden MR (2006) Measurement of flow stress in hot plane strain compression tests. Mater High Temp 23:85–118
Randle V, Engler O (2010) Introduction to texture analysis: macrotexture, microtexture and orientation mapping. CRC Press, Taylor and Francis Group, New York
Bunge HJ (1982) Texture analysis in materials science: mathematical methods. Butterworth & Co, UK
Davies PS (2009) An investigation of microstructure and texture evolution in the near titanium alloy timetal 834. The University of Sheffield
Ghosh P, Ray RK, Ghosh C, Bhattacharjee D (2008) Comparative study of precipitation behavior and texture formation in continuously annealed Ti and Ti + Nb added interstitial-free high-strength steels. Scr Mater 58:939–942
Kashihara K, Takeuchi Y, Shibayanagi T (2010) Characteristics of strain-induced boundary migration as evaluated by the crystal rotation axis method in (001) [100] and (112) [11\(\bar{1}\)] aluminum bicrystal deformed by plane-strain compression. Mater Trans 51:607–613
Lee DN, Han HN (2013) Recrystallization textures of metals and alloys. In: Wilson P (ed) Recent developments in the study of recrystallization. InTech, Croatia
Theyssier MC, Driver JH (1999) Recrystallization nucleation mechanism along boundaries in hot deformed Al bicrystals. Mater Sci Eng A 272:73–82
Bellier SP, Doherty RD (1977) The structure of deformed aluminium and its recrystallization-investigations with transmission Kossel diffraction. Acta Metall 25(5):521–538
Gong P, Palmiere EJ, Rainforth WM (2016) Thermomechanical processing route to achieve ultrafine grains in low carbon microalloyed steels. Acta Mater 119:43–54
Kitahara H, Ueji R, Tsuji N, Minamino Y (2006) Crystallographic features of lath martensite in low-carbon steel. Acta Mater 54:1279–1288
Gong P, Palmiere EJ, Rainforth WM (2017) Characterisation of strain-induced precipitation behaviour in microalloyed steels during thermomechanical controlled processing. Mater Charact 124:83–89
Donadille C, Valle R, Dervin P, Penelle R (1989) Development of texture and microstructure during cold-rolling and annealing of F.C.C. alloys: example of austenitic stainless steel. Acta Mater 37:1547–1571
Escher C, Nevesa S, Gottstein G (1998) Recrystallization texture evolution in Ni3Al. Acta Mater 46:441–450
Rollett A, Humphreys F, Rohrer G, Hatherly M (2014) Recrystallization and related annealing phenomena. Elsevier, New York
Von Schlippenbach U, Emren F, Lücke K (1986) Investigation of the development of the cold rolling texture in deep drawing steels by ODF-analysis. Acta Metall 34:2105–2117
Guillén MPB (1995) Transformation textures in hot rolled steels. Ph.D. Dissertation, McGill University
Gong P, Palmiere E, Rainforth W (2015) Dissolution and precipitation behaviour in steels microalloyed with niobium during thermomechanical processing. Acta Mater. 97:392–403
Show BK, Veerababu R, Balamuralikrishnan R, Malakondaiah G (2010) Effect of vanadium and titanium modification on the microstructure and mechanical properties of a microalloyed HSLA steel. Mater Sci Eng A 527:1595–1604
Zheng C, Xiao N, Hao L, Li D, Li Y (2009) Numerical simulation of dynamic strain-induced austenite-ferrite transformation in a low carbon steel. Acta Mater 57:2956–2968
Zheng C, Raabe D, Li D (2012) Prediction of post-dynamic austenite-to-ferrite transformation and reverse transformation in a low-carbon steel by cellular automaton modeling. Acta Mater 60:4768–4779
Zheng C, Li D, Lu S, Li Y (2008) On the ferrite refinement during the dynamic strain-induced transformation: a cellular automaton modeling. Scr Mater 58:838–841
Song R, Ponge D, Raabe D, Kaspar R (2005) Microstructure and crystallographic texture of an ultrafine grained C–Mn steel and their evolution during warm deformation and annealing. Acta Mater 53:845–858
Loginova I, Odqvist J, Amberg G, Ågren J (2003) The phase-field approach and solute drag modeling of the transition to massive γ → α transformation in binary Fe–C alloys. Acta Mater 51:1327–1339
Lan YJ, Xiao NM, Li DZ, Li YY (2005) Mesoscale simulation of deformed austenite decomposition into ferrite by coupling a cellular automaton method with a crystal plasticity finite element model. Acta Mater 53:991–1003
Jones S, Bhadeshia H (1997) Kinetics of the simultaneous decomposition of austenite into several transformation products. Acta Mater 6454:2911–2920
Ion J, Easterling K, Ashby M (1984) A second report on diagrams of microstructure and hardness for heat-affected zones in welds. Acta Metall 32:1949–1962
Hurley PJ, Hodgson PD, Muddle BC (1999) Analysis and characterisation of ultra-fine ferrite produced during a new steel strip rolling process. Scr Mater 40:433–438
Dong H, Sun X (2005) Deformation induced ferrite transformation in low carbon steels. Curr Opin Solid State Mater Sci 9:269–276
Lloyd GE, Schmidt NH, Mainprice D, Prior DJ (1991) Crystallographic textures. Miner Mag 55:331–345
Witkowska M, Rys J, Ratuszek W (2005) Annealing textures and precipitation behaviour in ferritic austenitic duplex type steels. Arch Metall Mater 50:471–478
Oh KH, Jeong JS, Koo YM, Lee DN (2015) The evolution of the rolling and recrystallization textures in cold-rolled Al containing high Mn austenitic steels. Mater Chem Phys 161:9–18
Raabe D, Lücke K (1992) Texture and microstructure of hot rolled steel. Scr Metall Mater 26:1221–1226
Xu P, Akita K, Suzuki T, Yamanaka K (2011) Texture evolution of ferrite steel during anisotropic tensile deformation studied by neutron diffraction 1242:1117–1118
Al-Fadhalah KJ (2012) Texture and grain boundary character distribution in a thermomechanically processed OFHC copper. J Eng Mater Technol 134:011001-1–011001-9
Gazder AA, Saleh AA, Nancarrow MJB, Mitchell DRG, Pereloma EV, Transmission A (2015) Kikuchi diffraction study of a cold-rolled and annealed Fe–17Mn–2Si–3Al–1Ni–0.06C wt% steel. Steel Res Int 86:1204–1214
Vercammen S, Blanpain B, De Cooman BC, Wollants P (2004) Cold rolling behaviour of an austenitic Fe–30Mn–3Al–3Si TWIP-steel: the importance of deformation twinning. Acta Mater 52:2005–2012
Xiong ZP, Saleh AA, Kostryzhev AG, Pereloma EV (2017) Strain-induced ferrite formation and its effect on mechanical properties of a dual phase steel produced using laboratory simulated strip casting. J Alloy Compd 721:291–306
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gong, P., Sun, L., Wynne, B.P. et al. The effect of thermomechanical controlled processing on recrystallisation and subsequent deformation-induced ferrite transformation textures in microalloyed steels. J Mater Sci 53, 6922–6938 (2018). https://doi.org/10.1007/s10853-018-2029-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-018-2029-6