Abstract
A comprehensive model was developed to simulate manganese sulfide formation during the solidification of steel. This model coupled the formation kinetics of manganese sulfide with a microsegregation model linked to thermodynamic databases. Classical nucleation theory and a diffusion-controlled growth model were applied to describe the formation process. Particle size distribution (PSD) and particle-size-grouping (PSG) methods were used to model the size evolution. An adjustable parameter was introduced to consider collisions and was calibrated using the experimental results. With the determined parameters, the influences of the sulfur content and cooling rate on manganese sulfide formation were well predicted and in line with the experimental results. Combining the calculated and experimental results, it was found that with a decreasing cooling rate, the size distribution shifted entirely to larger values and the total inclusion number clearly decreased; however, with increasing sulfur content, the inclusion size increased, while the total inclusion number remained relatively constant.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Non-metallic inclusions formed during solidification processes can essentially influence the final product quality. On the one hand, their presence can negatively affect steel properties [1–3]. On the other hand, they can contribute to a beneficial microstructure by acting as heterogeneous nucleation sites. To combine a preferably high steel cleanness with the creation of specific inclusion types and sizes for microstructure evolution, comprehensive knowledge of the inclusion formation is needed.
A typical inclusion type that is formed in nearly every steel grade is manganese sulfide (MnS). The latter can lead to anisotropy of the steel matrix and act as a possible starting point for crack formation or corrosion [2, 3]. Apart from these negative effects, in the field of ‘Oxide Metallurgy’ [4, 5], MnS, whether as single-phase inclusion or together with titanium oxides, is known to act as a potential nucleation agent for the formation of acicular ferrite [6–8]. In addition, the formation of MnS prevents internal cracks resulting from the appearance of FeS and reduces hot tearing segregation [9]. Two factors have a significant impact on number density, size distribution, and total amount of formed MnS: the cooling rate and the sulfur content. Both parameters play an important role in process control and optimization, especially during casting, and can therefore directly affect the final product quality. Thus, it is not surprising that MnS formation has been extensively studied over the last several decades.
Mathematical modeling provides a useful tool to investigate the formation of inclusions during the solidification of steel. Different researchers [10–13] developed several models describing MnS formation. MnS is normally generated from the enrichment of Mn and S in the residual liquid during the solidification process. Thus, it is important to consider the microsegregation of solutes when simulating MnS formation. Ueshima et al. [10] thermodynamically evaluated MnS formation based on an analysis of the interdendritic segregation. Imagumbai [11] applied a Solidification-Unit-Cell method to calculate the mean diameter of MnS, which depends on the cell volume, temperature gradient, and solidification speed. Valdez et al. [12] coupled Scheil’s model [14] and MnS growth to predict the size evolution. In their mean size prediction, Diederichs and Bleck [13] modified the empirical equation from Schwerdtfeger [15] into a function of manganese and sulfur contents, cooling rate, and secondary dendrite arm spacing. In this model, the concentrations of manganese and sulfur were calculated using the model of Clyne–Kurz [16]. In total, an enhanced model covering microsegregation, thermodynamics, and kinetics to describe the MnS size distribution has not been published thus far.
The present paper proposes a comprehensive model of MnS formation during the solidification of steel. A deeper understanding of the nucleation and growth of manganese sulfide during the solidification of steels is desirable to reduce, control, and even benefit from the formation of MnS. For that purpose, the development of a comprehensive modeling approach for inclusion formation is continued. As a first step, a microsegregation model linked to thermodynamic databases has been developed [17, 18]. Second, coupled with the proposed microsegregation model, the thermodynamics of inclusion formation during the solidification process has been simulated [19]. In the present case, the modeling of inclusion formation is conducted by simultaneously considering the kinetics, microsegregation, and thermodynamics.
Microsegregation is estimated using Ohnaka’s model [20]. The thermodynamic equilibrium is calculated with ChemApp [21] to determine the liquidus temperature and solute partition coefficients at the solidification interface based on commercial databases. MnS trapping at the solidification interface in the residual liquid is assumed to be proportional to the step value of the solid fraction. The kinetics of MnS formation are described using classical nucleation theory [22, 23] and a diffusion-controlled growth model. Particle size distribution (PSD) [24] and particle-size-grouping (PSG) [25] methods are applied to model the size evolution process. An adjustable parameter is introduced to consider collisions and is calibrated using the experimental results. Steels with different cooling rates and sulfur contents are calculated. The size distribution and evolution, as well as the amount of manganese sulfide, are obtained and compared with the experimental results. The influences of the cooling rate and sulfur content on MnS formation are summarized.
Modeling
Model background
Figure 1 describes the flow chart of the proposed model. In the coupled model, the solute enrichment in the residual liquid steel was estimated using Ohnaka’s model [20]. The thermodynamic equilibrium at the solidification interface was calculated using ChemApp [21] and the ChemSage datafile. The datafile was created from FactSage 7.0 based on the FSstel database. ChemApp [21] is an interface software. FactSage, ChemSage, and ChemApp are products of GTT Technologies, Herzogenrath, Germany. The particle size distribution (PSD) and particle-size-grouping (PSG) methodologies were used to describe the size evolution of MnS. For each solidification step, in the residual liquid, the number density of the nuclei was calculated by Becker’s theory [23]; the growth of the existing particles was calculated with Zener’s model [26]; the collision of the particles was treated in a simple way based on Brownian motion. After each step, the particle size distribution of MnS and its total amount were obtained. The concentrations of solutes accounting for the consumption of inclusion formation were used in the next microsegregation calculation. The model was programmed using FORTRAN and compiled within the Microsoft Visual Studio 2013 environment. Microsoft Visual Studio 2013 is provided by Microsoft Corporation, Redmond, United States.
The flow chart of the model: steel compositions, cooling rate (R c), and estimated solidification time (t f) are input parameters for the calculation; the solidification process is recorded using the solid fraction (f s) and the step value (Δf s); at each step, microsegregation, entrapment of inclusions, and an equilibrium calculation are performed; when the activity equals one (a = 1.0) and the number of inclusions gets larger than one (N > 1), further inclusion behavior (nucleation, growth, and collision) is considered; the new concentrations in the residual liquid are obtained through mass balance calculation
To simplify the calculations, the physical assumptions of the model are as follows:
-
Only MnS formed in the residual liquid is considered in this work. The particles trapped in the solid are assumed to be inert. The particles are distributed homogeneously in liquid steel.
-
MnS particles are independent. The formation behaviors of nucleation, growth, and collision occur independently for the particles.
-
The morphology of the particles is spherical.
-
Diffusion-controlled growth is assumed. A local equilibrium exists at the interface of the inclusions and liquid steel.
Microsegregation
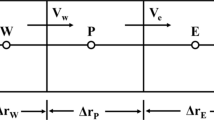
Microsegregation was calculated using Ohnaka’s model [20] with local partition coefficients. In the calculations, the analytical solution of Ohnaka’s model [20] was integrated into Eq. (1). The partition coefficients, liquidus temperature, and diffusion coefficients were calculated at each solidification step based on a thermodynamic equilibrium, while they were assumed to be constants with the increase of the solid fraction by Δf s . The thermodynamic equilibrium was calculated using ChemApp [21] and ChemSage datafiles. A detailed description of the microsegregation calculation can be found in a previous publication by the authors [17],
where f s represents the solid fraction; \( C_{\text{L}}^{ + } \) and C L are the concentrations of solutes in the residual liquid at solid fractions of f s and f s + Δf s, respectively; k is the equilibrium partition coefficient between the solid and the liquid; α is the back diffusion coefficient, which can be calculated using Eq. (2); D s is the solute diffusion coefficient in the solid; t f is the local solidification time; and λ2 is the secondary dendrite arm spacing.
Thermodynamics
Due to the microsegregation of manganese (Mn) and sulfur (S), MnS forms in the residual liquid as given in Eq. (3). It is believed that MnS is thermodynamically stable when the real concentration product (K) is larger than the solubility product (K eq). The solubility and real concentration products can be calculated using Eq. (4) [27] and Eq. (5), respectively, which are further used to calculate the chemical driving force of nucleation. The nucleation possibility will be evaluated because MnS is thermodynamically stable.
where [Mn] and [S] represent the soluble manganese and sulfur in the residual liquid; MnS represents solid manganese sulfide formed in the liquid steel; and C S and C Mn are segregated concentrations in the liquid.
Nucleation
Classical nucleation theory is applied to the model. For simplicity, homogeneous nucleation is considered in the current case. The inclusion nucleation rate is calculated using equation Eq. (6) [28, 29]:
where I hom is the homogeneous nucleation rate; I A is a pre-exponent factor that is assumed to be constant; \( \Delta G_{ \hom }^{*} \) is the activation energy for the homogeneous nucleation of inclusions, which is given in Eq. (7); k b is the Boltzmann constant; T is the temperature; σ is the interfacial energy between inclusions and liquid steel; ΔG V stands for the change in the free energy per unit volume of the inclusion, which can be calculated by ΔG m/V m; and ΔG m [Eq. (8)] and V m are the molar free energy change and the volume of the inclusion, respectively.
Combining Eq. (3) to Eq. (8), the nucleation number density of the system at each solidification step is determined by Eq. (9):
where N(f s) is the number density at the solid fraction of f s; ρ Fe is the density of liquid steel; and Δt is the time period for one solidification step. m s represents the mass of the investigated system. All calculations were performed assuming 100 g of steel.
Growth
The growth of the spherical particle is assumed to be controlled by diffusion of the solutes in liquid steel. Zener’s equation [26], as given in Eq. (10), is used to calculate the growth rate.
where dr/dt is the growth rate of the particle with a radius of r; D l is the solute diffusion coefficient in the liquid steel; C l, C i, and C il are the solute concentrations in liquid steel, the inclusion, and at the inclusion-liquid steel interface, respectively.
There exists a local equilibrium at the inclusion-liquid steel interface. According to previous studies [30, 31], the diffusion flux (J) toward the inclusion is proportional to the concentration gradient and can be calculated using Eq. (11). For the given reaction of MnS formation [Eq. (3)], it is assumed that at the interface, the diffusion fluxes of Mn and S are equal, as shown in Eq. (12). From Eqs. (11) and (12), Eq. (13) is derived. Equation (14) is from the thermodynamic equilibrium at the inclusion-liquid steel interface. Combining Eqs. (13) and (14), the interfacial concentrations of the solutes can be solved.
where J is the diffusion flux of solute; M is the molar weight of the solutes; and the superscripts Mn and S stand for manganese and sulfur, respectively.
Collisions
Collisions of the particles in liquid steel have important effects on the inclusion size distribution. Brownian motion, Stokes collisions, and turbulent collisions are normally considered when studying the inclusion coalescence in steelmaking vessels, such as an RH degasser and a casting tundish [32, 33]. However, during the solidification process at the dendritic scale, it is difficult to calculate the collision frequencies in the same way as in metallurgical vessels due to the lack of corresponding parameters. Particularly, for turbulent collisions, it is impossible to determine the turbulent energy caused by the solidification interface movement, which is non-negligible. Therefore, to reasonably consider a collision, a collision factor (f) is introduced based on Brownian motion collision. This is a factor for enhancing the collision frequency by considering other types of collisions in a simple way. Brownian motion collision is more representative in the studied radius range compared with Stokes collision, as shown in Fig. 2.
In Fig. 2, the collision frequencies of Brownian motion and Stokes collision are calculated using Eqs. (15) and (16) [32, 33]. It is assumed that the average radius of MnS is 0.3 µm and the size ranges from 0 to 1.0 µm in the targeted system. It is found that Brownian motion causes a collision that is several times stronger than a Stokes collision in the particle size range. Hence, the total collision frequency in the model is calculated based on the Brownian motion collision frequency together with the collision factor as given in Eq. (17). The number density of the particles formed by the collisions is calculated with Eq. (18). Note that the collision factor is an adjustable parameter and will be fitted to the experimental results.
where \( \beta_{\text{B}} \left( {r_{i} , r_{j} } \right) \), \( \beta_{\text{S}} \left( {r_{i} , r_{j} } \right) \) , and \( \beta^{\prime}\left( {r_{i} , r_{j} } \right) \) are the Brownian motion, the Stokes collision, and the total collision frequencies, respectively, for particles with radii of r i and r j ; μ is the dynamic viscosity of liquid steel; π is the circumference ratio; g is the gravitational acceleration; ρ in is the density of the inclusion; and N ij is the number density of the particle formed by the collisions of the particles with number densities of n i and n j .
Class model
Particle size distribution (PSD) is a useful and widely applied method to describe the evolution process of inclusion formation and precipitation. In this method, the size histogram is characterized by the size classes and corresponding number density of each class. For the classification of size during nucleation and growth, Maugis and Gouné [34] suggested an approach in which each radius defines one size class. At each calculation step, a new size class is generated due to nucleation and existing classes of particles that grow simultaneously. However, for a phenomenon involving collision, it is difficult to consider each radius as one size class because of the breadth of the particle size distribution. Fortunately, it has been illustrated that the particle-size-grouping (PSG) method is effective for solving this problem [25]. Inspired by the aforementioned approaches, the following method (Fig. 3) is applied to treat size classes for MnS formation in the solidification process:
-
The size of the particles is classified into several groups (G i ) according to the boundary values (R i ) in both solid and liquid steel. The groups are characterized by the average radius (r i ) and related number density (n i ). The superscripts S1 and L1 indicate that it is in the solid state and liquid state at the current (‘1’) calculation step, respectively. S2 and L2 are for the subsequent (‘2’) step after a series of activities, such as trapping, nucleation, and growth.
-
Nucleation: The particles created by nucleation with the radius and number density (r 0, n 0) are classified into the first group (G 1). As given by Eq. (19), the number density (\( n_{1}^{{{\text{L}}2}} \)) of G 1 at the second step is the sum of n 0 and existing number density (\( n_{1}^{{{\text{L}}1}} \)). The average radius changes to \( r_{1}^{{{\text{L}}2}} \) based on the calculation with total volume and number [Eq. (20)].
$$ n_{1}^{{{\text{L}}2}} = n_{1}^{{{\text{L}}1}} + n_{0} $$(19)$$ r_{1}^{{{\text{L}}2}} = \sqrt[3]{{\frac{{(r_{1}^{{{\text{L}}1}} )^{3} \cdot n_{1}^{{{\text{L}}1}} + r_{0}^{3} \cdot n_{0} }}{{n_{1}^{{{\text{L}}1}} + n_{0} }}}} $$(20) -
Growth: The particles after growing from (\( r_{i - 1}^{{{\text{L}}1}} \), \( n_{i - 1}^{{{\text{L}}1}} \)) to (r g , n g ) can be grouped into G i−1 or G i . If R i−2 < r g ≤ R i−1 they belong to G i−1 (the same group before growing); the size of this group is r g (\( r_{i - 1}^{{{\text{L}}2}} \) = r g ) and the number is n g (\( n_{i - 1}^{{{\text{L}}2}} \) = n g ). If R i−1 < r g ≤ R i , they upgrade to the larger group G i ; the number of the group (\( n_{i}^{{{\text{L}}2}} \)) becomes the sum of \( n_{i}^{{{\text{L}}1}} \) and n g (\( n_{i}^{{{\text{L}}2}} = n_{i}^{{{\text{L}}1}} + n_{g} \)); and the radius of this group renews to \( r_{i}^{{{\text{L}}2}} \) as calculated in Eq. (21).
$$ r_{i}^{{{\text{L}}2}} = \sqrt[3]{{\frac{{(r_{i}^{{{\text{L}}1}} )^{3} \cdot n_{i}^{{{\text{L}}1}} + r_{g}^{3} \cdot n_{g} }}{{n_{i}^{{{\text{L}}1}} + n_{g} }}}} $$(21) -
Collision: The new size class (G i+2) is easier to create due to collision compared with diffusion-controlled growth. The calculation of the radius and number are similar to calculations described in the nucleation and growth processes. The number of particles contributing to the collisions is reduced.
-
The inclusions in solid steel are trapped particles and inert in the following solidification process. Therefore, at each calculation step, the number densities of the particles in different classes increase according to the trapped number (dark volumes in Fig. 3) in the corresponding classes. The trapped number or amount of each group in the liquid is proportional to the step value of the solid fraction as given in Eq. (22) [35]. The average radius of each class is obtained based on the total volume and number of particles in the group.
$$ {\text{Amount}}_{\text{trapped}} = {\text{Amount}}_{{{\text{in}}\;{\text{liquid}}}} \times \Delta f_{\text{s}} /(1 - f_{\text{s}} ) $$(22) -
-
At one solidification step, the radius and number of particles in different size groups, as well the size classes, are refreshed once after the inclusions experience all of the activities (trapped, nucleation, growth, and collision). Note that the boundary values of the size group (R i ) are settled during the calculation. Hence, the particles can be classified into the appropriate group according to their own radius (r i ) and the boundary values.
Figure 3 Schematic illustration of the particle-size-grouping: the particles are divided into j groups (G 1…G i to G j ) and each group has its radius range defined by R; the groups are characterized by the corresponding mean radius (r 1…r i to r j ) and the total number (n 1…n i to n j ); in the calculation, the size and number changes of the groups in the solid (with the superscript S) resulted from particle entrapment; and changes of groups in the residual liquid (with the superscript L) are caused by inclusion nucleation, growth, and collision
At each solidification step, after the nucleation and growth of inclusions, the increase of inclusion amount is recorded. This further causes decrease of the amount of Mn and S in the residual liquid. The changes of solute concentration are accounted for, and the new concentrations of solutes in the residual liquid are used for the next calculation.
Experiments
In the present work, the submerged split chill tensile (SSCT) experiment was used to simulate the solidification process of steel. The SSCT experiment was initially developed to investigate the high-temperature mechanical properties of alloys [36–38]. The schematics of the SSCT experimental and sampling process are explained in Fig. 4.
Schematic illustration of the a submerged split chill tensile (SSCT) test: an in situ solidification experiment where a cylindrical test body is submerged into the melt in an induction furnace. The steel shell solidifies around the test body; b sample preparation procedure: the solid shell is separated from the cylindrical body for preparing a metallographic specimen for subsequent SEM analysis [39]
As shown in Fig. 4a, liquid steel is pre-melted in an induction furnace (25 kg). A cylindrical chill body is submerged into liquid steel. A steel shell starts to solidify on the cylindrical body with the Zr-oxide coating surface. The crystallographic growth of the shell mainly originates perpendicular to the cylinder. After approximately 30 s, the sample is lifted out of the liquid melt. The temperature changes during shell solidification are measured by thermocouples inside the test body. The measured temperatures serve as input data for thermal analysis and heat flux calculation. Furthermore, shell growth, cooling rates, solid fractions, and temperature distributions are obtained using an in-house developed solidification model. The detailed descriptions of SSCT and the interpretation of the results can be found elsewhere [37, 38]. Figure 4b displays the sample preparation procedure. The solidified shell is cut into 16 pieces at room temperature. The piece with a relatively even shell thickness is selected. Then, the sample is metallographically prepared for observation.
In the current case, three steels with different sulfur contents are melted and solidified using an SSCT experiment. The chemical compositions of the steels are listed in Table 1. After the aforementioned sample preparation process, the inclusions in the samples are measured using automated SEM/EDS analysis. This method has been widely applied to investigate the steel cleanness [40–42]. These measurements employed a Scanning Electron Microscope (SEM) (ZEISS Ultra55) equipped with an Energy Dispersive X-ray Spectrometer (EDS) (Oxford Instruments).
In the SEM measurements inclusions are detected due to material contrast differences in the backscattered electron (BSE) image. Usually, non-metallic inclusions are displayed as darker compared to the steel matrix. This method enables the definition of a measurement field on the specimen which is automatically scanned for inclusions. The output consists of the position and the morphological data of every detected particle as well as its chemical composition. Thus, in contrast to manual SEM/EDS analysis, a huge amount of data is obtained that enables statistical evaluation. With this method, the size distribution and number density of inclusions on a defined area can be determined.
The measured fields and corresponding cooling rates are shown in Fig. 5. For sample S1, three fields (A, B, and C) of different shell thicknesses, but with the same height, are measured to study the influence of the cooling rate on MnS formation. In samples S2 and S3, each has a field with the same thickness and height as field B to investigate the influence of the sulfur content. For each field, an area of 1.02 mm2 is measured. The minimum detectable particle size in the measurements is 0.1 µm equivalent circle diameter (ECD). While the measured area is relatively small to keep inclusions from forming under similar cooling conditions, at least 1000 particles are checked to ensure quality. From the cooling curve calculated based on the measured temperature, the cooling rates of the measured fields are defined as shown in Fig. 5b.
Parameter fitting
Table 2 lists the parameters used in the model for the present calculations. To fit the adjustable parameter collision factor (f), MnS formation in S1 under a cooling rate of 25.4 K s−1 (corresponding to field B) is calculated. The solidification temperature ranges from 1713 to 1783 K. A series of calculations are performed with varying collision factors. The influence of the collision factor on the size distribution of MnS is shown in Fig. 6. It is found that the size ranges become broader and the peak number densities decrease with an increasing collision factor. This means that stronger collisions result in larger particles and smaller amounts. In addition, all of the size distributions are in a reasonable lognormal arrangement. In Table 3, the calculated mean diameters and total number densities with different collision factors are compared with the measured value of field B.
Note that for the comparison between measurements and calculations, the measured 2-dimensional diameter and number density from the analyzed cross section are converted into volumetric values using the program CSD Corrections v.1.50 [47, 48]. In this program, corrections are made for the intersection probability and cut section effects. The measured 2D diameters and area are input into the software. Before conversion, the morphology information of the particles should be defined by ‘short,’ ‘intermediate,’ and ‘long’ aspect ratios and roundness. In the case of MnS particles, they are assumed to be isotropic. The bin size settings for the histogram are also needed. Different choices of bin size settings vary the converted results. The last row of Table 3 gives the range of the mean diameters and number densities estimated with different bin settings. In Table 3, we find that both the mean diameter and the number density predicted with a collision factor of 200 agree well with the experimental values. As an output, in addition to the 3D size distribution, its Population Density Function [PDF, described in Eq. (23)] can be obtained from the CSD Corrections to minimize the influence of the bin size selection, which has already been applied in the study of the inclusion size distribution [49, 50]. Figure 7 compares both the 3D size distribution and PDF of MnS from the measurement and calculation with a collision factor of 200.
In Fig. 7a, the predicted and measured size distributions are reclassified with a lognormal bin size. It is found that the calculated size distribution of MnS is in good agreement with the experimental one. The diameter class of 0.75 µm contains the most particles for both calculation and measurement. The predicted and measured maximum particle sizes are also similar, with a diameter of approximately 2.5 µm. The measured number densities of the particles in the first several size classes (smaller than 0.12 µm) are higher than the predicted ones. This relatively larger discrepancy is attributed to the measured limitation (0.1 µm) and the further conversion to the 3D size distribution. For the population density shown in Fig. 7b, the situation is similar to the number density, that is, the distributions fit well with each other, except for the first several size classes. Note that the present model cannot consider MnS precipitations in the solid steel, which can be smaller than 0.1 µm, and may lead to discrepancies in the comparison.
where n v is the volume number density of a bin and Δl is the bin width.
Figure 8 displays the MnS formation process, including the size and amount evolutions as well as the concentration changes of Mn and S. In Fig. 8a, the entire distribution shifts to the direction of a larger size when solidification proceeds. The size distribution at a solid fraction of 0.980 has a narrow range from 0 to 0.5 µm and a high number density when MnS begins to form. The distribution curve subsequently becomes flatter and broader due to growth and collision. At the end of solidification (solid fraction of 1), the maximum size reaches 2.5 µm and the maximum number density is approximately 3.0 × 106 mm−3 with a diameter of 0.75 µm. From Fig. 8b, it can be seen that MnS precipitates at a solid fraction of 0.98 and the amount soars. The concentration of sulfur decreases due to the relatively lower content and small liquid fraction, while the Mn concentration continues to increase but at a slower speed. During the late stage of precipitation, MnS grows slowly due to the consumption of S and the reduction of liquid steel.
As a whole, a collision factor equal to 200 is regarded to be effective for simulating MnS formation using the present model under the SSCT experimental conditions. Therefore, in the following calculations, a collision factor of 200 is applied to study the influence of cooling rate and sulfur content.
Influence of the cooling rate and sulfur content
After fitting the parameters to the experimental results, the present model gives high-quality predictions for MnS formation during the solidification process. Furthermore, the model is utilized to investigate the influences of two important process parameters on MnS formation: the cooling rate and sulfur content. For reasonable comparisons of the calculated and experimental results, the measured 2D size distributions from the SSCT samples are also converted into 3D ones using the described CSD Corrections v. 1.5 with the lognormal bin size setting; size classes smaller than 0.1 µm are not considered to avoid differences caused by the measurement limitations and precipitation in the solid steel.
Influence of cooling rate
Sample S1 is calculated for three different cooling rates (42.3, 25.4, and 13.5 K s−1), which correspond to the measured fields A, B, and C, respectively. The influence of the cooling rate on size distributions from the calculations and experiments is shown in Fig. 9a and b, respectively.
From Fig. 9a, it is found that the size of the inclusions has an increasing trend with a decreasing cooling rate. When the cooling rate slows from 42.3 to 13.5 K s−1, the maximum particle size class increases from approximately 1.3 to 2.5 µm; the diameter of particles with peak frequencies enlarges from 0.42 to 0.76 µm; the frequency of particles with diameters of approximately 0.25 µm (the smallest size class) decreases from 20 to 5 %. In Fig. 9b, the experimental size distributions display similar trends with the predicted results with decreasing cooling rates. The calculated and predicted size ranges and the diameter of the particles with the largest proportion are the same.
Figure 10 shows the calculated changes of the total number, mean diameter, and amount of MnS, as well as the concentrations of Mn and S, with different cooling rates. In Fig. 10a, it is found that the number density decreases, while the mean diameter increases with the decreasing rate. The amount of MnS decreases slightly when the cooling rate slows down, which is attributed to fewer segregations of Mn and S, as shown in Fig. 10b. The simulations together with the experimental results demonstrate that the variations of cooling rate will significantly change the MnS size distributions, mean diameter, and total number. At the same time, this indicates that the preferable features of MnS are achievable by controlling the cooling conditions and referring the corresponding predictions.
Influence of sulfur content
In addition to the cooling rate, the sulfur content is another key factor for MnS formation. Three samples with different sulfur contents (S1, S2, and S3) are calculated under a cooling rate of 25.4 K s−1. Figure 11 shows the influence of the sulfur content on the size distributions from the simulations and experiments.
As shown in Fig. 11a, the size significantly increases with the increase of sulfur content from 20 ppm to 50 and 60 ppm. In the sample containing 20 ppm sulfur (S3), a diameter of approximately 0.25 µm, that is, the smallest size class, has a peak frequency of 80 %, which is only approximately 15 % in the other two samples with higher sulfur contents; the maximum size of the particles is approximately 0.76 µm, while it is 2.5 µm in the higher sulfur samples. The size distributions of the samples with 50 and 60 ppm sulfur are close to each other. Comparing the predicted size distributions with experimental ones (Fig. 11b), the agreement can be considered satisfactory when bearing in mind the complexity of the phenomenon and the uncertainty of the physical properties and measurements.
In Fig. 12, the influence of the sulfur content on the number density, mean diameter, and amount of MnS is predicted. Figure 12a shows that with increasing sulfur content, the number density of MnS in the samples is comparable, while the mean diameter increases. The amount of MnS decreases considerably due to the decreasing sulfur content and fewer segregations. In the meantime, MnS in the sample containing higher sulfur content precipitates earlier than that in the sample with lower sulfur content.
Based on the above discussion in this section, the cooling rate and sulfur content are important process parameters on deciding the MnS formation, final size distribution, and number density. Finely dispersed MnS is desirable for both controlling and utilizing the inclusions. For instance, the small size can effectively relieve the steel anisotropy due to MnS elongation after rolling; meanwhile, it can retain the austenite growth through pinging grain boundaries and further improve the steel properties. Faster cooling and reducing the sulfur content are two approaches for obtaining finer particles. At the same time, the other effects of these two methods should be considered, such as the increasingly serious manganese microsegregation, as shown in Fig. 10b and Fig. 12b, which is detrimental to steel properties. Additionally, there is a favorable diameter, ranging from approximately 0.3 to 0.9 µm when utilizing inclusions such as heterogeneous nucleation sites for acicular ferrite [51, 52]. In industrial solidification processes, the local cooling rate varies between several hundred degrees per second for welding and strip casting, whereas for continuous casting or ingot casting the local cooling rate might decrease to less than 0.1 degree per second close to the center of the cast part. The presented model allows the precise evaluation of solidification processes with respect to the formation of sulfides with prescribed diameter or—vice versa—the adjustment of the manganese and sulfur content for the cooling conditions of a certain solidification process. Thus, the model provides a valuable tool for further activities in the field of inclusion metallurgy.
Summary
MnS formation in the solidification of steels influences both the final product quality and the casting process. In addition to the negative effect on mechanical steel properties, MnS is also known to improve the machinability of free cutting steel, enhance the hot ductility during continuous casting, and promote the acicular ferrite formation. For detailed studies of these aspects, apart from thermodynamics and the mean diameters, considering the formation kinetics of MnS including the number density, the size evolution, and distribution, as well as the amount and the resultant concentrations of the reactants is necessary.
In the present paper, a comprehensive model coupling of microsegregation and MnS formation thermodynamics and kinetics was proposed. Microsegregation was predicted using the stepwise Ohnaka’s model [20] based on thermodynamic databases. With segregated concentrations in the residual liquid, the PSD method was applied to describe the size and number evolution of manganese sulfides. Inclusion trapping and collisions were treated in simple ways. The parameters determined by comparing the simulations and experiments were further applied to study the influence of the sulfur content and cooling rate. Combining the calculated and experimental results, the following conclusions are drawn:
-
The suggested comprehensive model can be applied to simulate the formation of manganese sulfide during solidification. The calculated size distribution of manganese sulfide fits well with the experimental results. The influences of the sulfur content and cooling rate on manganese sulfide formation were well predicted and in line with the experimental results.
-
With the decreasing cooling rate, the size distribution shifted entirely to a larger size direction and the total number clearly decreased. The content of manganese sulfides decreased slightly due to the lesser enrichment of the solutes.
-
With the increasing sulfur content, the MnS size increased, while the total number was similar. The overall inclusion amount significantly increased. Finer manganese sulfides can be achieved via faster cooling or reducing the sulfur content.
It is common to find heterogeneous nucleation inclusions in an alloyed steel. In the meantime, compound inclusions play indispensable roles in inclusion metallurgy. So in the future, based on the current work, heterogeneous nucleation of inclusions, such as sulfides and nitrides, on oxides will be the primary dedicated object. Additionally, the competitive formation thermodynamics and kinetics of multi-oxides during cooling and solidification will be simulated. As a whole, a comprehensive model of the both homogeneous and heterogeneous types of inclusions accounting for microsegregation, thermodynamics, and kinetics is the final target. A further ambitious idea is connecting the inclusion formation to the microstructure evolutions in the following metallurgical process.
References
Thornton PA (1971) The influence of nonmetallic inclusions on the mechanical properties of steel. J Mater Sci 6:347–356. doi:10.1007/BF02403103
Raghupathy VP, Srinivasan V, Krishnan H, Chandrasekharaiah MN (1982) The effect of sulphide inclusions on fracture toughness and fatigue crack growth in 12 wt% Cr steels. J Mater Sci 17:2112–2126. doi:10.1007/BF00540430
Ray GP, Jarman RA, Thomas JGN (1994) Some aspects of crack initiation in mild steel under corrosion fatigue condition. J Mater Sci 29:47–53. doi:10.1007/BF00356571
Takamura JI, Mizoguchi S (1990) Metallurgy of oxides in steels. I: roles of oxides in steels performance. In: Proceedings of the 6th international iron and steel congress, ISIJ, Tokyo, pp 591–597
Mizoguchi S, Takamura JI (1990) Metallurgy of oxides in steels. II: Control of oxides as inoculants. In: Proceedings of the 6th international iron and steel congress, ISIJ, Tokyo, pp 598–604
Mu W, Jönsson PG, Nakajima K (2016) Prediction of intragranular ferrite nucleation from TiO, TiN, and VN inclusions. J Mater Sci 51:2168–2180. doi:10.1007/s10853-015-9527-6
Byun JS, Shim JH, Cho YW, Lee DN (2003) Non-metallic inclusion and intragranular nucleation of ferrite in Ti-killed C–Mn steel. Acta Mater 51:1593–1606
Shim JH, Oh YJ, Suh JY, Cho Y, Shim JD, Byun JS, Lee DN (2001) Ferrite nucleation potency of non-metallic inclusions in medium carbon steels. Acta Mater 49:2115–2122
Alvarez de Toledo G, Campo O, Lainez E (1993) Influence of sulfur and Mn/S ratio on the hot ductility of steels during continuous casting. Steel Res 64:292–299
Ueshima Y, Isobe K, Mizoguchi S, Maede H, Kajioka H (1988) Analysis of the rate of crystallization and precipitation of MnS in a resulphurized free-cutting steel. Tetsu-to-Hagane 74:465–472
Imagumbai M (1994) Behaviors of manganese-sulfide in aluminum-killed steel solidified uni-directionally in steady state. Dendrite structure and inclusions. ISIJ Int 34:896–905
Valdez ME, Wang Y, Sridhar S (2004) In-situ observation of the formation of MnS during solidification of high sulphur steels. Steel Res Int 75:247–256
Diederichs R, Bleck W (2006) Modelling of manganese sulphide formation during solidification. Part I: Description of MnS formation parameters. Steel Res Int 77:202–209
Scheil E (1942) Bemerkungen zur schichtkristallbildung. Z Metall 34:70–72
Schwerdtfeger K (1972) Einfluss der Erstarrungsgeschwindigkeit und des Schwefelgehaltes auf die durchschnittliche Grösse von Mangansulfideinschlüssen in einem Mangan und Kohlenstoff enthaltenden Stahl. Arch Eisenhüttenwes 43:201–205
Clyne TW, Kurz W (1981) Solute redistribution during solidification with rapid solid state diffusion. Metall Trans A 12:965–971
You D, Bernhard C, Wieser G, Michelic S (2016) Microsegregation model with local equilibrium partition coefficients during solidification of steels. Steel Res Int 87:840–849
You D, Bernhard C, Michelic S, Wieser G, Presoly P (2016) On the modelling of microsegregation in steels involving thermodynamic databases. Mater Sci Eng 119:1–8
You D, Michelic SK, Bernhard C, Loder D, Wieser G (2016) Modeling of inclusion formation during the solidification of steel. ISIJ Int. doi:10.2355/isijinternational.ISIJINT-2016-243
Ohnaka I (1986) Mathematical analysis of solute redistribution during solidification with diffusion in solid phase. Trans ISIJ 26:1045–1051
Petersen S, Hack K (2007) The thermochemistry library ChemApp and its applications. J Mater Res 98:935–945
Volmer M, Weber A (1926) Keimbildung in übersättigen gebilden. Z Phys Chem 119:277–301
Becker R, Döring W (1935) Kinetische behandlung der keimbildung in übersättigten dämpfen. Ann Phys 416:719–752
Perez M, Dumont M, Acevedo D (2008) Implementation of classical nucleation and growth theories for precipitation. Acta Mater 56:2119–2132
Nakaoka T, Taniguchi S, Matsumoto K, Johansen ST (2001) Particle-size-grouping method of inclusion agglomeration and its application to water model experiments. ISIJ Int 41:1103–1111
Zener C (1949) Theory of growth of spherical precipitates from solid solution. J Appl Phys 20:950–953
Xia G (1992) Untersuchungen über das mechanische Verhalten von erstarrendem Stahl unter stranggußähnlichen Bedingungen. PhD Dissertation, Montanuniversität Leoben
Turpin ML, Elliott JF (1966) Nucleation of oxide inclusions in iron melts. J Iron Steel Inst 204:217–225
Turnbull D (1950) Kinetics of solidification of supercooled liquid mercury droplets. J Chem Phys 18:411–424
Atkins P, De Paula J (2002) Atkins’ physical chemistry. Oxford University Press, Oxford
Wang YN, Yang J, Xin XL, Wang RZ, Xu LY (2016) The effect of cooling conditions on the evolution of non-metallic inclusions in high manganese TWIP steels. Metall Mater Trans B 47:1378–1389
Tozawa H, Kato Y, Sorimachi K, Nakanishi T (1999) Agglomeration and flotation of alumina clusters in molten steel. ISIJ Int 39:426–434
Lei H, Nakajima K, He JC (2010) Mathematical model for nucleation, Ostwald ripening and growth of inclusion in molten steel. ISIJ Int 50:1735–1745
Maugis P, Gouné M (2005) Kinetics of vanadium carbonitride precipitation in steel: a computer model. Acta Mater 53:3359–3367
Yamada W, Matsumiya T, Ito A (1990) Development of simulation model for composition change of nonmetallic inclusions during solidification of steels. In: Proceedings of the 6th international iron and steel congress, ISIJ, Tokyo, pp 618–625
Ackermann P, Kurz W, Heinemann W (1985) In situ tensile testing of solidifying aluminium and Al–Mg shells. Mater Sci Eng 75:79–86
Bernhard C, Hiebler H, Wolf MM (1996) Simulation of shell strength properties by the SSCT test. ISIJ Int 36:S163–S166
Arth G, Ilie S, Pierer R, Bernhard C (2015) Experimental and numerical investigations on hot tearing during continuous casting of steel. Berg Huettenmaenn Monatsh 160:103–108
Pierer R, Bernhard C (2008) On the influence of carbon on secondary dendrite arm spacing in steel. J Mater Sci 43:6938–6943. doi:10.1007/s10853-008-2985-3
Nuspl M, Wegscheider W, Angeli J, Posch W, Mayr M (2004) Qualitative and quantitative determination of micro-inclusions by automated SEM/EDX analysis. Anal Bioanal Chem 379:640–645
Pistorius PC, Patadia A (2012) The steel matrix affects microanalysis of CaO-Al2O3-CaS inclusions, Clean Steel Conference Proceedings, Hungarian Mining and Metallurgical Society (OMBKE), Budapest
Michelic SK, Wieser G, Bernhard C (2011) On the representativeness of automated SEM/EDS analyses for inclusion characterisation with special regard to the measured sample area. ISIJ Int 51:769–775
Zhang J, Lee HG (2004) Numerical modeling of nucleation and growth of inclusions in molten steel based on mean processing parameters. ISIJ Int 44:1629–1638
Zhang J, Xing X, Song B, Guo X, Xiang C (2004) Metallurgical physical chemistry. Metallurgical Industry Press, Beijing
Lehmann J, Rocabois P, Gaye H (2001) Kinetic model of non-metallic inclusions’ precipitation during steel solidification. J Non-Cryst Solids 282:61–71
Oikawa K, Ohtani H, Ishida K, Nishizawa T (1995) The control of the morphology of MnS inclusions in steel during solidification. ISIJ Int 35:402–408
Higgins MD (2000) Measurement of crystal size distributions. Am Miner 85:1105–1116
Higgins MD (2002) Closure in crystal size distributions (CSD), verification of CSD calculations, and the significance of CSD fans. Am Miner 87:171–175
Zinngrebe E, Van Hoek C, Visser H, Westendorp A, Jung IH (2012) Inclusion population evolution in Ti-alloyed Al-killed steel during secondary steelmaking process. ISIJ Int 52:52–61
Van Ende MA, Guo M, Zinngrebe E, Blanpain B, Jung IH (2013) Evolution of non-metallic inclusions in secondary steelmaking. ISIJ Int 53:1974–1982
Lee JL (1994) Evaluation of the nucleation potential of intragranular acicular ferrite in steel weldments. Acta Metall Mater 42:3291–3298
Zhang Z, Farrar RA (1996) Role of non-metallic inclusions in formation of acicular ferrite in low alloy weld metals. Mater Sci Technol 12:237–260
Acknowledgements
Open access funding provided by Montanuniversität Leoben. The authors are grateful for financial support from the Federal Ministry for Transport, Innovation and Technology (bmvit) and the Austrian Science Fund (FWF) [TRP 266-N19]. The authors also sincerely acknowledge the laboratories at voestalpine Stahl GmbH in Linz for assistance in the analysis of samples. Michael Higgins is thanked for offering the program of CSD Corrections v. 1.5 and answering questions during usage.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
You, D., Michelic, S.K., Wieser, G. et al. Modeling of manganese sulfide formation during the solidification of steel. J Mater Sci 52, 1797–1812 (2017). https://doi.org/10.1007/s10853-016-0470-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-016-0470-y