Abstract
Perovskites in the ternary system PbTiO3 (PT)–PbZrO3 (PZ)–Pb(Fe0.5Nb0.5)O3 (PFN) have attracted close interest because they can display simultaneous ferroelectric, magnetic and ferroelastic properties. Those with the most sensitive response to external fields are likely to have compositions near the morphotropic phase boundary (MPB) which lies close to the binary join Pb(Zr0.53Ti0.47)O3 (PZT)–PFN. In the present study, the strength and dynamics of strain coupling behaviour which accompanies the development of ferroelectricity and (anti)ferromagnetism in ceramic PZT–PFN samples have been investigated by resonant ultrasound spectroscopy. Elastic softening ahead of the cubic–tetragonal transition does not fit with models based on dispersion of the soft mode or relaxor characteristics but is attributed, instead, to coupling between acoustic modes and a central peak mode from correlated relaxations and/or microstructure dynamics. Softening of the shear modulus through the transition by up to ~50 % fits with the expected pattern for linear/quadratic strain/order parameter coupling at an improper ferroelastic transition and close to tricritical evolution for the order parameter. Superattenuation of acoustic resonances in a temperature interval of ~100 K below the transition point is indicative of mobile ferroelastic twin walls. By way of contrast, the first-order tetragonal–monoclinic transition involves only a small change in the shear modulus and is not accompanied by significant changes in acoustic dissipation. The dominant feature of the elastic and anelastic properties at low temperatures is a concave-up variation of the shear modulus and relatively high loss down to the lowest temperature, which appears to be the signature of materials with substantial local strain heterogeneity and a spectrum of strain relaxation times. No evidence of magnetoelastic coupling has been found, in spite of the samples displaying ferromagnetism below ~550 K and possible spin glass ordering below ~50 K. For the important multiferroic perovskite ceramics with compositions close to the MPB of ternary PT-PZ-PFN, there must be some focus in future on the role of strain heterogeneity.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
A characteristic approach for tailoring desirable properties of materials for device applications is to make use of solid solutions. This is achievable in the case of multiferroic perovskites, for example, by combining the ferroelectric properties of Pb(Zr,Ti)O3 (PZT) with the ferro/antiferromagnetic properties of Pb(Fe0.5Nb0.5)O3 (PFN) or Pb(Fe0.5Ta0.5)O3 (PFT) [1–6], producing a successful demonstration of magnetic switching of ferroelectric domains at room temperature in single crystals with nominal composition [Pb(Zr0.53Ti0.47)O3]0.6[Pb(Fe0.5Ta0.5)O3]0.4 [7–9]. The same approach has been successful also in the development of magnetoelectric thin films with compositions between Pb(Fe0.67W0.33)O3 and Pb(Zr0.53Ti0.47)O3 [10, 11]. In other magnetoelectric perovskites, the ferroelectricity often arises from Pb or Bi at the A-site and magnetism from Fe or Mn at the B-site, but in PZT–PFN and PZT–PFT, the ferromagnetism and the ferroelectricity both arise from the same ion (Fe3+) at the B-site [12]. This leads to an unusually high magnetoelectric coupling and a high-temperature multiferroic state.
An important coupling mechanism between magnetic and electric dipoles in PZT–PFT could be by strain mediation [7]. Applying the magnetic field induces a change in magnetic moments, and a strain due to magnetoelastic coupling would then cause a change in the ferroelectric moment, or vice versa, with the implication that the elastic strain relaxations might be as important as the primary ferroic properties. The ferroelectric transition(s) involve changes in symmetry from cubic to tetragonal, rhombohedral or monoclinic so that they are also ferroelastic, which means that the dielectric properties are necessarily coupled with shear strain. Much less is known about strain coupling with the ferromagnetic and/or antiferromagnetic order parameters.
The purpose of the present study was to characterise the overall strain relaxation behaviour of selected members of the PZT–PFN and PZT–PFT solid solutions by experimental determination of elastic and anelastic properties. Variations of the shear modulus provide a highly sensitive measure of the strength of intrinsic strain coupling effects associated with phase transitions, while acoustic losses are indicative of dynamical relaxation behaviour of defects such as twin walls or the boundaries between polar nano regions. In part I (this paper), we report results for Pb(Zr0.53Ti0.47)O3-PFN, and in part II [13], we report results for Pb(Zr0.53Ti0.47)O3-PFT.
Phase transitions and location of the morphotropic phase boundary within the PT-PZ-PFN ternary system
Following the long established understanding of PZT, the expectation is that the largest variations in dielectric properties for PZT–PFN solid solutions could occur in the vicinity of the MPB, hence the focus on compositions close to this within the ternary system PbTiO3 (PT)–PbZrO3 (PZ)–PFN. Structural relationships in the ternary system have not been fully investigated, but their form can be sketched out from the known behaviour of the three binaries and a limited number of experimental results for ternary compositions.
PT-PFN
PT has a cubic (\( Pm\bar{3}m \))–tetragonal (ferroelectric, P4mm) transition at ~760 K which is weakly first order but close to a tricritical point [14–19]. The same transition extends along the PT-PFN binary [20]. The sequence of structural transitions with falling temperature in PFN is cubic (\( Pm\bar{3}m \), or \( Fm\bar{3}m \) if there is B-site ordering)–tetragonal (P4mm)–monoclinic (Cm). At least in some samples, the low temperature structure may be rhombohedral (R3m) [21]. The first transition is close to tricritical in character and typically occurs at ~380–390 K. The second, 20–40 K lower, is generally considered to be first order in character [21–31]. With increasing PT content along the PFN–PT binary join, the stability field of the monoclinic structure diminishes such that the P4mm–Cm transition point extrapolates to 0 K at ~8–12 % PT [32, 33].
PZ–PFN
PZ has a first-order transition from cubic (paraelectric, \( Pm\bar{3}m \)) to orthorhombic (antiferroelectric, Pbam) at ~500 K, sometimes with and sometimes without a small intermediate stability field of a few degrees for the rhombohedral (ferroelectric, R3m) structure [34–37]. The Pbam structure is restricted to low PT and low PFN contents (i.e. near to PZ) [38–42]). It is likely that the cubic (\( Pm\bar{3}m \))–rhombohedral (R3m) transition is close to tricritical since it passes through a tricritical point with increasing PT content along the PT–PZ join [43].
For most of the PZ–PFN solid solution, the ferroelectric structure is rhombohedral [39–41]. Additional transitions between rhombohedral phases at compositions close to the Pbam—rhombohedral phase boundary and near the 50:50 composition have been proposed [40, 41], but the structures involved were not fully characterised. By analogy with the topology of the PZ-rich side of the PZ–PT phase diagram shown by Cordero et al. [44], one possibility is that high temperature and lower temperature ferroelectric phases labelled by Lovkova et al. [41] as FE2 and FE3 correspond to R3m and R3c structures, respectively. This would have the R3m–R3c transition temperature increasing from ~300 K at 10 % PFN to ~330 K at 20 % PFN. Whatmore and Bell [45] appear to have placed the transition at ~300 K for 5 % PFN and ~330 K for 10 % PFN, but the trend of increasing transition temperature with increasing PFN content is the same.
Ternary compositions
The P4mm structure that extends along most of the PT–PFN join and along the PT–PZ boundary towards the MPB is expected to occur all across the PT-rich side of the MPB in the ternary system. Tetragonal lattice geometry has been confirmed at room temperature for three compositions in the middle of this field [46], at three compositions along the join Pb(Zr0.44Ti0.56)O3-PFN [47] and close to the ternary MPB [48].
The PZ-rich side of the binary MPB in PT–PZ has an additional octahedral tilting transition with a maximum transition temperature of ~420 K at ~15 % PT [38]. This phase boundary extrapolates to the location of the MPB at ~160 K, ~50 % PT [38, 44, 49], though extrapolation to ~0 K at ~50 % PT has also been shown in some phase diagrams [50, 51]. Diffraction and dielectric evidence for a tilting transition at ~210 K in Pb(Zr0.52Ti0.48)O3 [52, 53] is consistent with the topology given by Cordero et al. [44] and calculated from first principles by Kornev et al. [54]. Away from the MPB, the change in space group is R3m–R3c, for which second-order character is allowed. Data for PbZr0.9Ti0.1O3 appear to show that this transition is weakly first order [55], but it is continuous with varying composition at room temperature [56]. As discussed above, this same transition may also occur along the PZ–PFN binary join and would give a stability field for the R3c structure extending into the ternary system at room temperature. In the stability field of the monoclinic structure below the MPB of PZT, the same octahedral tilting transition involves the symmetry change Cm–Cc [57–62], but no information is yet available to determine whether this occurs in the ternary system as well. In (Pb0.94Sr0.06)(Zr0.55Ti0.45)O3, the Cm–Cc transition is thermodynamically continuous [63].
The stability limit of the Cm structure of PFN within the ternary system is not known but, just as for PZT, is presumed to be closely linked to the position of the MPB. Fang et al. [48] reported that they were expecting to find a rhombohedral structure at compositions on the PZ side of the MPB but that the distortion from cubic lattice geometry was below the limit of resolution of their diffraction data. PFN-rich compositions along the join Pb(Zr0.44Ti0.56)O3-PFN were reported by Amonpattaratkit et al. [47] as being cubic at room temperature but could presumably have been rhombohedral or monoclinic with only very small lattice distortions. The same applies to PFN-rich compositions along the join Pb(Zr0.53Ti0.47)O3–PFN, with a two phase mixture (cubic + tetragonal) at 30 % PFN [64].
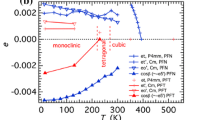
The location of the room temperature MPB has been determined at three ternary compositions in ceramic samples by Fang et al. [46, 48, 65]. These three compositions, the binary phase diagram for PZT from Jaffe et al. [38] and the position of the tetragonal–monoclinic boundary in PT–PFN [32, 66] lead to the estimated location of the room temperature MPB shown in Fig. 1. Note that it is shown specifically as the limit of the stability field for the tetragonal structure. The composition dependence of this MPB in PZT is such that compositions just on the tetragonal side at room temperature would be expected to cross it at some lower temperature, while compositions on the rhombohedral side would be expected to be monoclinic close to it. Prasatkhetragarn [67] claimed that a tetragonal–rhombohedral transition occurs with falling temperature at 423 K in a sample with composition [Pb(Zr0.44Ti0.56)O3]0.9[PFN]0.1, but the reported room temperature diffraction pattern is that of the tetragonal structure and is therefore shown as such in Fig. 1.
Section of the ternary PT–PZ–PFN system at room temperature. Solid bars location of ternary MPB from Fang et al. [48]; solid circles location of MPB in PT–PZ from Jaffe et al. [38], and in PT–PFN from Singh et al. [33], Sitalo et al. [32]. Blue squares tetragonal samples at room temperature [3, 46, 47, 64, 68–70]. Brown squares ternary compositions described as cubic by Amonpattaratkit et al. [47] but which are most likely rhombohedral or monoclinic with small strains. Filled green squares ternary compositions described as cubic by Yu et al. [64] but which are most likely rhombohedral or monoclinic with small strains. Open green square ternary composition described as containing both cubic and tetragonal phases [64]. The sample at [Pb(Zr0.44Ti0.56)O3]0.9[PFN]0.1 is shown as tetragonal, based on the reported diffraction pattern [67]. Other boundaries in PT–PZ from Jaffe [38], Cordero et al. [49], PZ–PFN from Lovkova et al. [41] and Blazhievskii et al. [40]. Red crosses mark nominal compositions of samples used in the present study, along the join Pb(Zr0.53Ti0.47)O3–PFN. The rhombohedral structure type at room temperature for most of the PZ-rich side of the ternary MPB is not known
The binary PZT solid solution may consist more widely of intergrowths of the rhombohedral + monoclinic or tetragonal + monoclinic structures [50, 51, 71]. Coexistence of tetragonal and rhombohedral phases near the MPB has been reported for samples doped with 5–6 % Fe3+ and 5.5 % Nb [72] and of cubic plus tetragonal phases at [Pb(Zr0.53Ti0.47)O3]0.3[PFN]0.7 [64], but these aspects of the stability relations remain to be explored more fully for the ternary system.
Pb(Zr0.53Ti0.47)O3-PFN
The topology of Fig. 1 shows that end member PFN itself and samples used in the present study along the binary join between Pb(Zr0.53Ti0.47)O3 and PFN are all close to the MPB. It is consistent with tetragonal structures reported by Kumar et al. [70] at 50 % PFN and by Sanchez et al. [3] for four compositions with 10, 20, 30 and 40 % PFN. Known structural transitions along this join are shown in Fig. 2. Based on the phase diagrams of Jaffe et al. [38] and Cordero et al. [44], the expectation for Pb(Zr0.53Ti0.47)O3 is \( Pm\bar{3}m - P4mm - Cm - Cc \), with transitions at ~650, ~315 and ~190 K which are permitted by symmetry to be thermodynamically continuous. The temperatures of a peak in the dielectric constant, T m, at three compositions along the binary join [48] and at one composition close to it [70] fall along a linear trend between the transition temperatures for \( Pm\bar{3}m - P4mm \) in the two end members (Fig. 2). T m values at five compositions given by Sanchez et al. [3] fall somewhat above this line and are not shown. The P4mm–Cm and Cm–Cc transitions in Pb(Zr0.52Ti0.48)O3 are accompanied by small dielectric anomalies (e.g. [52]), but there appears to be no analogous evidence for these in data reported for samples within the PZT–PFN binary being considered here [3, 48, 65, 68]. A further constraint on the topology of the binary system comes from the fact that it cuts the expected location of the room temperature MPB at two compositions, corresponding to ~1–7 and ~69–75 % PFN. These two points are shown in Fig. 2 as marking the position of the P4mm–Cm transition at room temperature, assuming that the stability field of the monoclinic structure extends into the ternary field.
Binary phase diagram for Pb(Zr0.53Ti0.47)O3–PFN. Locations of the \( Pm\bar{3}m - P4mm \) and P4mm–Cm transitions in PZT are taken from the phase diagram of Jaffe et al. [38] and for the Cm–Cc transition from Cordero et al. [44]. Transition temperatures shown for PFN are based on a review of the literature in Carpenter et al. [28]. Values of T m for \( Pm\bar{3}m - P4mm \) at intermediate temperatures from the literature for nearby compositions [48, 70] fall on the straight line drawn between T c values of the pure end members. Open circles with a broken straight line drawn through them are estimates for the onset of precursor elastic softening (T ps) ahead of the cubic–tetragonal transition. Filled diamonds are estimates for the P4mm–Cm transition. Estimates of the onset of possible spin glass behaviour (T g) are from the present study
A tricritical point, marking the change from continuous (Zr-rich compositions) to discontinuous (Ti-rich compositions) character for the ferroelectric transition, exists close to the 50:50 composition in PZT (Pb(Zr0.49Ti0.51)O3 [14, 15, 19, 73], between Pb(Zr0.55Ti0.45)O3 and Pb(Zr0.58Ti0.42)O3 [74]). It is not accidental that this occurs close to the MPB because the crossover between stability fields for tetragonal and rhombohedral structures is also determined by one of the fourth-order coefficients in the Landau 246 potential tending to zero ([75–77] and see Appendix of this paper). There is likely to be of a line of tricritical points near the ternary MPB, and the ferroelectric transition in ceramics with compositions between Pb(Zr0.53Ti0.47)O3 and PFN is expected to be close to tricritical in character.
Magnetic properties
Rather less is known about magnetic transitions across the PT–PZ–PFN ternary. T N for the antiferromagnetic ordering transition in PFN diminishes from ~ 143 K with increasing PT content along the PT-PFN binary join and would extrapolate to 0 K at ~13 % PT [33]. From the same work [33], it appears that a magnetic anomaly attributed to a spin glass transition (T g ≈ 10–30 K [78–86]) extends to at least 15 % PT. A closely similar pattern is seen with increasing PZ content along the PZ–PFN join in Li-doped samples [42]. There is, however, great variability between samples, and weak ferromagnetism has been reported both at room temperature and at temperatures up to ~530–580 K [28, 86–89]. Weak ferromagnetism was detected at room temperature in ternary compositions along the Pb(Zr0.53Ti0.47)O3–PFN join by Sanchez et al. [3] and along the Pb(Zr0.44Ti0.56)O3–PFN join by Amonpattaratkit et al. [47]. It remains possible that the weak room temperature ferromagnetism in PFN and PZT–PFN is due to the presence of some minor impurity phase, but Kuzian et al. [90, 91] have shown that ferrimagnetic ordering might occur in PFN, while Glinchuk et al. [4] have shown how a nanodomain structure of local chemical ordering could lead to ferromagnetism in PZT–PFN.
B-site ordering
Even though there appears to be no direct diffraction evidence for long-range B-site ordering of Fe3+ and Nb5+ in PFN, Mössbauer and NMR spectroscopy suggest a degree of short-range order or clustering [92–94]. Alternating Fe/Nb in three dimensions would change the symmetry of the cubic phase from \( Pm\bar{3}m \) to \( Fm\bar{3}m \) [95]. If this can occur during the preparation of end member PFN samples, the same local ordering might be expected in samples with compositions extending into the ternary system.
Besides affecting the consequent magnetic ordering, B-site order is an important potential influence on relaxor ferroelectric properties. The temperature of the maximum of the real part of the dielectric permittivity related to the ferroelectric transition in PFN is typically broad but independent of frequency [96–100]. It can be weakly dispersive in some samples [101–103], however, with variability of the local order responsible for relaxor as opposed to classical ferroelectric behaviour. Evidence for a temperature below which polar nanoregions (PNR’s) might be present is provided by acoustic emission (564–603 K [30]), thermal expansion data (~690 K [104]) and the onset of elastic softening (~550 K [28]). No information is yet available for local ordering in ternary PZT-PFN, but ceramics near the MPB have dielectric maxima related to the ferroelectric transition which are reported to be generally broad and independent of frequency [65, 67, 68, 70].
Strain and elasticity
Elastic and anelastic relaxation phenomena associated with phase transitions are due to coupling of the driving order parameter(s) with strain. There are as yet no data for strain relaxation effects in PZT–PFN multiferroics, but lattice parameters and elasticity data from the literature for Pb(Zr0.52Ti0.48)O3 give a clear picture of what is expected for a sequence \( Pm{\bar{\text{3}}}m\,\, - P 4mm{-}Cm{-}Cc \). A formal analysis of the spontaneous strains is given in the Appendix, and these are compared with PFN in Appendix Fig. 10. The cubic–tetragonal transition in Pb(Zr0.52Ti0.48)O3 is accompanied by a tetragonal shear strain, e t, amounting to ~3 %, in comparison with only ~0.3 % for PFN. In both cases, the strain variations can be well represented as conforming to Landau tricritical \( \left( {q^{ 4} \alpha \left( {T_{\text{c}} {-}T} \right)} \right) \). The tetragonal–monoclinic transition is weakly first order and is accompanied by much smaller additional shear strains that are similar in form for both PZT and PFN. The Cm–Cc transition is accompanied principally by a small, negative volume strain. Even more obviously than for PFN, the \( Pm\bar{3}m\, - \,P4mm \) and P4mm–Cm transitions in Pb(Zr0.52Ti0.48)O3 are quite distinct instabilities with different critical temperatures, implying that there are two separate driving mechanisms.
Changes in elastic properties have been studied extensively for PZT [44, 49, 105–109]. As expected for improper ferroelastic cubic–tetragonal and cubic–rhombohedral transitions with strong coupling between symmetry breaking shear strains and the order parameter, measurements at Hz and kHz frequencies on ceramic samples with compositions close to the MPB show large (~50 %) softening of the Young’s modulus, 1/S 11, and shear modulus, G [44, 105–107, 109]. A sample doped with Nb has also shown the same pattern of elastic softening [110]. Characteristic peaks in acoustic loss, expressed in terms of the inverse mechanical quality factor, \( Q^{ - 1} \), show dispersion with respect to frequency and are attributed to the motion under stress of the ferroelastic twin walls [106, 107, 109, 111]. From the measurements of Bourim et al. [107] at Hz frequencies, it appears that the twin walls become pinned by oxygen vacancies in the vicinity of ~400 K, below which the loss returns to low values.
There is a rounded minimum in the Young’s and shear moduli at temperatures corresponding to the expected location of the tetragonal–monoclinic transition in PZT [49, 105–109, 112]. The transition appears to be reversible for Pb(Zr0.52Ti0.48)O3 but displays a small hysteresis between heating and cooling at Pb(Zr0.535Ti0.465)O3 and Pb(Zr0.545Ti0.455)O3 [106, 109]. If there is any associated anomaly in \( Q^{ - 1} \), it is perhaps only a slight increase with falling temperature through the transition at both Hz and kHz frequencies [49, 105–107, 109]. By way of contrast, a poled sample of Pb(Zr0.52Ti0.48)O3 displayed a sharp minimum in the Young’s modulus measured at ~150 kHz [52, 60, 113, 114]. The difference is presumed to reflect a difference in microstructure, with the unpoled sample having a higher density of nanoscale twinning.
The octahedral tilting transition (R3m–R3c) in Zr-rich samples away from the MPB in PZT is accompanied by a small step-like softening of the Young’s modulus and a small peak in acoustic loss [44, 49, 108]. This is the expected pattern for a co-elastic, displacive transition with second-order character and weak strain/order parameter coupling. The loss peak measured at kHz frequencies remains discernible in the vicinity of the MPB, but its influence on the Young’s modulus is much harder to see [44, 49, 109]. The minimum in Young’s modulus is sharp when measurements are made on poled samples [52, 60, 113, 114]. A single measurement of longitudinal acoustic velocity through a sample of Pb(Zr0.53Ti0.47)O3 showed a small rounded minimum with a slight hysteresis [61]. In this case, the measuring frequency was not specified but is presumed to be in the MHz range.
Sample preparation and characterisation
The ceramic samples used in the present study with nominal compositions [PbZr0.53Ti0.47O3](1−x)[PbFe0.5Nb0.5O3] x , x = 0.6, 0.4, 0.3 were the same as those described in Sanchez et al. [3]. They are referred to below as PZTFN6, PZTFN4 and PZTFN3, respectively. As described in Sanchez et al. [3] and in more detail by Carpenter et al. [28] for PFN, they were prepared from oxide starting materials by a conventional solid-state reaction route. The final stage was heating of pressed pellets to 1250 °C (PZTFN4, PZTFN3) or 1100 °C (PZTFN6) at 10 °C min−1, annealing at this temperature for 4 h and cooling back to room temperature, again at 10 °C min−1. The resulting ceramic discs, ~9 mm in diameter and ~0.5–0.65 mm thick, were sawn into smaller pieces for the different measurements described below. An additional sample with x = 0.2 (PZTFN2) was prepared in a second batch. Ferroelectric hysteresis loops measured at room temperature for PZTFN2, PZTFN3 and PZTFN4 are given in Fig. 3a of Sanchez et al. [3].
Room-temperature FORC diagrams and hysteresis loops (insets) for a PFN, b PZTFN6, c PZTFN4, d PFZTFN3, e PZTFN2. The dashed line delimits regions of the FORC distribution (ρ) significant at the 0.05 level [124]. All samples exhibit a low coercivity component, indicated by the strong positive feature at low values of B u and B c. PFN a also contains a high coercivity component, indicated by the ridge-like feature along the horizontal axis at high values of B c and the extended statistically significant area below the horizontal axis. A very low coercivity component appears in PZTFN6, indicated by the high intensities at the origin
A ceramic sample of PbZr0.53Ti0.47O3 (PZTFN0) was also prepared by a conventional solid-state route. PbO, ZrO2, TiO2 powders were mixed and calcined at 1000 °C for 2.5 h). The calcined powders were ground for 10 min and again ball milled for 1 h. Poly(vinyl alcohol) solution (1 wt%) was added to the calcined powder as a binder, and the powder was again dried in an oven at about 80 °C for 5 h. The dried powder was granulated by passing it through a mesh and pressed into a pellet. The pressed pellet was heat treated at 600 °C for the removal of organic binders followed by sintering at 1250 °C for 4 h. All the heating treatments were performed in air.
Average compositions, based on point analyses obtained for the final ceramic sample using a Cameca SX-100 electron microprobe, are given in Table 1. In general, the perovskite was homogeneous with respect to Fe and Nb, but with was some variation in Zr:Ti across individual grains. Several impurity phases were also detected in chemical map images. Expressed with respect to one lead atom, their compositions can be given as
and
in PZTFN2, PZTFN3, PZTFN4 and PZTFN6, respectively. These all belong essentially to the system PbO–Fe2O3–Al2O3 with Al coming from the crucibles or Al2O3 powder which was placed around the pellets to ensure an even temperature distribution. PZTFN2 contained some ZrO2 and PZTFN4 contained a second impurity, ~Pb1(Zr0.20Ti0.30Fe1.06Nb0.17Al1.35W0.54)3.62O6.51, which has a stoichiometry close to that of pyrochlore, PbA4O7. The traces of W are presumed to be from the WC ball mill. A small amount of excess PbO appears to occur along grain boundaries.
Higher resolution X-ray diffraction data than reported by Sanchez et al. [3] were obtained with a Bruker D8 Advance Bragg–Brentano diffractometer (PZTFN3, PZTFN2, PZTFN0) or a PANalytical Empyrean diffractometer (PZTFN6, PZTFN4). These revealed the presence of some impurity phase(s) at low concentrations perhaps up to a few %, as for PFN prepared in the same way [28]. The PZTFN2 sample, prepared separately, had a higher concentration of impurities and a second perovskite phase. Rietveld refinements [115] using the FULLPROF suite of programs [116] showed the dominant phase to be tetragonal perovskite with lattice parameters given in Table 2, consistent with bulk compositions being just to the PT side of the ternary MPB at room temperature (Fig. 1). Values of the tetragonal shear strain, e t, calculated from the lattice parameters, a and c, with an approximation for the cubic reference parameter a o as (a 2 c)1/3, are also given in Table 2.
Magnetic hysteresis loops and first-order reversal curve (FORC) diagrams were obtained at room temperature using a Princeton Measurements Company alternating gradient magnetometer manufactured by Lake Shore Cryotronics, which is housed in the Nanopaleomagnetism Lab at the University of Cambridge. Hysteresis loops were measured using a saturating field of 1.8 T, a field step of 5 mT, and a time constant of 100 ms. FORC diagrams are obtained by plotting the FORC distribution (\( \rho \)), which is the mixed second derivative of the magnetisation with respect to the reversal and measurement fields [117, 118]. The FORC diagram is a contour plot of ρ in a space defined by B c (coercive field) in the horizontal dimension and B u (interaction field) in the vertical dimension. In effect, FORC diagrams can be thought of as maps of the magnetic response of all particles in a sample in terms of coercivity and magnetic interaction field distributions [118]. This approach to characterization of magnetic samples is very useful in discriminating between components with different magnetic states and is widely used in rock and mineral magnetism and solid-state physics [118–121]. FORC diagrams were calculated from >300 FORCs measured on each sample using a saturating field of 2.2 T, time constants of 100–300 ms, field steps of 4–6 mT, and maximum coercivities (B c) of 1–1.95 T, depending on the characteristics of the hysteresis loops. The FORCs were processed with the program FORCinel [122] using the VARIFORC method for variable smoothing [123].
The magnetic hysteresis loops show small openings, indicative of a weakly ferromagnetic component present in all the samples (insets Fig. 3). The FORC diagrams are characterised by the presence of a low coercivity (0.05–0.1 T) magnetic component, implied by the strong maximum at low values of B u and B c, vertical spreading, together with the pairing of the stronger positive and weaker negative areas and the displacement below the horizontal axis (Fig. 3). These features are indicative of discrete particles consisting of single magnetic domains with inter-particle magnetostatic interactions that are creating a net positive mean interaction field. The interactions are weaker in PZTFN2, PZTFN3 and PZTFN4, as shown by less vertical spreading and relatively minor displacement of the peak below the horizontal axis, compared to PFN and PZTFN6. PFN contains a second, high coercivity (~2 T) component, indicated by the ridge-like feature along the horizontal axis at high values of B c and the extended statistically significant area below the horizontal axis [28]. PZTFN6 exhibits a second, very low coercivity (<0.02 T) component, seen as a triangular positive feature near the origin, which is responsible for the constriction in the hysteresis loop.
Experimental methods
Resonant ultrasound spectroscopy (RUS)
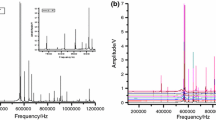
RUS data were collected using slightly irregular, but almost parallelepiped-shaped samples with dimensions and masses given in Table 2. The high-temperature (HT) RUS measurements were performed after the low temperature (LT) measurements and the larger samples from the LT measurements were subdivided in-between these two experiments and hence the lower masses in Table 2 for the HT experiments. The instrument used for measurements above room temperature has been described by McKnight et al. [125] and uses Stanford electronics [126]. Temperature was determined with a thermocouple located within a few mm of the sample, subject to an additional small calibration based on the transition temperature for the \( \alpha \, - \,\beta \) transition in quartz (846 K), the cubic–tetragonal transition in BaTiO3 (405 K) and the R3m → C2/c transition in Pb3PO4 (453.6 K). The helium flow cryostat used for measurements below room temperature has been described by McKnight et al. [127]. In each case, spectra were collected in heating and cooling cycles, generally in steps of 3, 5 or 10 K, with a settle time of 20 min for thermal equilibration at each temperature. The spectra were analysed offline using the software package Igor Pro (WaveMetrics). Selected resonance peaks were fit with an asymmetric Lorentzian function to obtain the peak frequency, f, and width at half maximum height, ∆f. f 2 scales with the elastic modulus that determines the particular resonance mode and for most modes this is dominated by the shear modulus. In order to follow variations of the shear modulus over wide temperature intervals, it is sometimes necessary to combine data from different resonance peaks by scaling their values to overlap. The inverse mechanical quality factor, \( Q^{ - 1} \), is a measure of acoustic loss and has been calculated as Δf/f. Values of \( Q^{ - 1} \) measured in the low temperature instrument tend to be higher than those measured in the high-temperature instrument because the sample sits directly between the transducers rather than being separated from them by buffer rods.
Temperature dependence of dielectric properties
Dielectric measurements were made using an Agilent HP4294a Precision Impedance Analyzer, with the sample held in the same horizontal Netzsch furnace as used for the high-temperature RUS measurements. Electrodes were created on opposite sides of the RUS samples using high-temperature silver paste and these were connected by platinum wires to coaxial cables outside the furnace. The temperature and impedance analyzer were controlled using LabView software. Data were collected in both heating and cooling cycles, with a temperature ramp of 0.2 K min−1 and each measurement taking approximately 10 s. The results are presented as capacitance and dielectric loss tangent. The capacitance is not calibrated, with some parasitic component expected due to some unshielded length of wire.
Temperature dependence of magnetic properties
Magnetic properties were measured in two different quantum design MPMS XL squid magnetometers, one in Cambridge (SQUID 1) and the other in Dresden (SQUID 2). Data were collected at low temperatures in both instruments, while high-temperature data were collected only in SQUID 2. In each case, the sample measured was the RUS sample, a portion of the RUS sample or a portion of the pressed pellet from which the RUS sample was taken. For the SQUID 2 measurements, the sample was held in an open quartz tube. For low temperature measurements, the sample was placed in an evacuated capsule and held in a straw.
The first magnetic investigation was carried out on SQUID 1 in order to study the magnetic behaviour under very low fields. This involved two sequences of data collection during heating from 5 K up to room temperature with the moment measured in the residual field of the magnet. The first measurement was preceded by cooling in “zero” field, labelled ZFC (i.e. cooling in the residual field of the magnet), while the second was preceded by cooling in a field of 20 kOe, labelled FC, from room temperature down to 5 K. These showed significant features that were absent in similar measurements run with probe fields of 0.01 kOe on heating, demonstrating that some part of the history-dependent behaviour in these materials has very low coercivity values. The magnetisation values were scaled to 1 at room temperature, as the magnitude and direction of the residual field were not controlled and the absolute value of the measured moment cannot readily be compared. In SQUID 1, magnetic hysteresis curves were also collected at selected temperatures during cooling with applied fields between +50 and −50 kOe.
In SQUID 2, both low temperature and high temperature measurements were performed using a more conventional zero field cooled-field cooled sequence, comprising cooling in the residual field of the SQUID, followed by measurement of the moment in 0.1 kOe applied field on heating (ZFC measurement), followed again by measurement in 0.1 kOe on cooling (FC measurement). This was most effective when performed in the full temperature range, from ~5 to ~700 K, although it required a change from the cryostat to the furnace and back. To determine the total evolution of the moment provided by the field, the most reasonable approach was to do a ZFC measurement from 700 K to room temperature, then a FC measurement from 700 K to room temperature, followed by a FC measurement in the cryostat. Generally, this was combined with a ZFC/FC cycle in the cryostat alone, but the exact sequence differed between samples and is clear from an examination of the relevant figures, below. Hysteresis loops between −2 and −20 kOe were also performed at selected temperatures in SQUID 2 for PZTFN4 to check whether the loop opening closed at high temperatures.
Heat capacity
The heat capacity of an irregularly shaped piece of PZTFN3 with mass 0.00586 g, held in Apiezon H grease, was measured between 3 and 400 K by a relaxation method with the HC option of a Quantum Design model 6000 PPMS. Data were collected in three sequences on heating with temperature steps of 2–5 K and three pulses per temperature point.
Results
Variations with temperature of elasticity, dielectric and magnetic data are shown for PZTFN6–PZTFN0 in Figs. 4–9, respectively. They display a number of features in common:
PZTFN6. a RUS analysed data showing f 2 and \( Q^{ - 1} \), with scaling applied to match frequencies at room temperature. b SQUID 2 temperature dependence of the magnetic moment between ~2 and 700 K under an applied field of 0.01 T, with triangular markers (one marker displayed per four data points) showing ZFC and FC data below room temperature; crosses (one marker displayed per two data points) show ZFC data above room temperature and FC data for the full temperature range. c SQUID 1 temperature dependence of magnetic moment measured in the residual field of the magnet between 2 and 300 K, with ZFC data scaled to match FC data at room temperature. d SQUID 1 magnetic hysteresis loops collected at selected temperatures in a cooling sequence (one marker displayed per four data points). e Capacitance and f dielectric loss at selected frequencies (one marker displayed per 200 data points)
-
(i)
Reductions in f 2, corresponding essentially to precursor softening of the shear modulus, start at a temperature, T ps, which is ~100 K above the expected cubic–tetragonal transition. A narrow temperature interval of steep softening then follows, with a minimum that is generally not seen due to strong attenuation. Below the temperature where this steep softening ends, T cRUS, there are further relatively minor variations and these are followed at the lowest temperatures by a concave-up pattern of stiffening.
-
(ii)
The first increase in \( Q^{ - 1} \) with falling temperature, marking the onset of acoustic loss relating to the phase transition, occurs at a temperature, labelled as T* (see Table 3), which is ~30–60 K above T cRUS. There is then a 50–100 K interval in which the attenuation can be sufficiently high that the resonance peaks disappear from the RUS spectra (superattenuation). Below this interval, \( Q^{ - 1} \) remains relatively high until the lowest temperatures, but with minor peaks that differ between samples.
Table 3 Values of the temperature at which precursor elastic softening starts, T ps, \( Q^{ - 1} \) starts to increase, T*, the steep reduction of f 2 ends, T cRUS, and the dielectric constant or capacitance has a maximum, T m -
(iii)
A broad, asymmetric and frequency-independent peak occurs in capacitance at a temperature, T m (see dashed lines in Figs. 4–9). This is clearly related to the ferroelectric transition and is similar to the variation in dielectric constant observed for other ceramic samples with nearby compositions in the ternary system [48, 65, 67, 68, 70].
-
(iv)
Slight stiffening with falling temperature accompanied by hysteresis between heating and cooling occurs between ~200 and ~250 K in samples with intermediate compositions and appears to correspond with the tetragonal–monoclinic transition.
-
(v)
Magnetic hysteresis loops all show a small opening at room temperature and below, indicative of a weak ferromagnetic moment. Magnetisation data show that this moment tends to zero in the vicinity of 500 K. There is no overt evidence for a magnetic transition below room temperature, but there are additional anomalies in the data for all three samples below ~50 K. The high-temperature ferromagnetism is most likely due to the impurity phases but the low temperature effects are more likely to be intrinsic to the perovskite.
Values of T ps, T cRUS, T* and T m are listed in Table 3.
PZTFN6
Results for f 2 and \( Q^{ - 1} \) from the RUS spectra of PZTFN6 are shown in Fig. 4a. Analysed peaks in the high-temperature spectra had frequencies of 230 and 650 kHz at room temperature. Resonances from the low temperature spectra had frequencies of ~66 and ~400 kHz. Other peaks were used to refine the variation of \( Q^{ - 1} \) above the high-temperature transition point. The onset of softening with falling temperature, T ps, is at ~650 K (see Fig. 2a). An increase in \( Q^{ - 1} \) starts at ~510 K, and the interval of superattenuation (no detectable resonances) is ~410–490 K. A shallow minimum occurs in f 2 at ~325 K, and there is a distinct hysteresis between heating and cooling centred on ~220 K. \( Q^{ - 1} \) has relatively high values below the superattenuation interval and shows small peaks at ~165 K and below ~100 K, which are accompanied by changes in slope of f 2, before falling off to low values at the lowest temperatures. (The apparent hysteresis near 100 K is an artefact arising from difficulties in measuring weak peaks).
Measurements of magnetic moment as a function of temperature at low and high temperature in SQUID 2 (Fig. 4b), in residual field in SQUID 1 (Fig. 4c) and as a function of field in SQUID 1 (Fig. 4d) give patterns that are similar to those seen for PFN [28]. Significant curvature of the reciprocal susceptibility in the temperature-dependent magnetic data precludes Curie–Weiss analysis. There is a steep increase in the low applied field magnetic moment (Fig. 4c) in the field cooled data below ~ 20 K as well as a separation between FC and ZFC data across the temperature range examined in that measurement. The measured magnetic moments do not show evidence for an antiferromagnetic transition in either low or high field conditions. Higher field, temperature-dependent magnetic data from SQUID 2 (Fig. 4b) clearly show the ferromagnetic transition occurring at ~560 K, as well as replicating the 20 K anomaly seen in the low-field data. Magnetic hysteresis loops show a small opening at every temperature. The change in shape of the loop at 5 K relative to that at 30 K suggests that there is some kind of transition between the two.
The dielectric data (Fig. 4e, f) show a broad peak in capacitance at ~500 K. The amplitude varies systematically with frequency but T m does not, and there is a very slight maximum in loss tangent, tanδ. Although the form of variations of both capacitance and tanδ remains the same between heating and cooling, there is a marked reduction in their absolute values in the cooling sequence relative to heating. A steep reduction in capacitance occurs just below T m, at ~484 K, and there is a further subtle maximum at ~380 K. Neither of these features appears to correlate systematically with variations in tanδ but f 2 would extrapolate to its lowest value at ~480 K (T cRUS).
PZTFN4
Results for f 2 and \( Q^{ - 1} \) from the RUS spectra of PZTFN4 are shown in Fig. 5a. f 2 values are again a compilation from different resonances, scaled to match up at room temperature (peaks from the high-temperature spectra at 330 and 180 kHz and a peak from the low temperature spectra at 81 kHz). The onset of softening with falling temperature ahead of the cubic–tetragonal transition occurs at ~700 K, superattenuation occurs in the interval ~440–550 K, the shallow minimum in f 2 is at ~250 K, the slight hysteresis is centred on ~190 K, and a steep upturn occurs below ~85 K. \( Q^{ - 1} \) remains high below the superattenuation interval and only diminishes below ~ 40 K. Well-resolved \( Q^{ - 1} \) values at low temperatures reveal a small Debye-like peak at ~165 K and another maximum at ~70 K.
PZTFN4. a RUS analysed data showing f 2 and \( Q^{ - 1} \), with scaling applied to match f2 values at room temperature. b SQUID 2 temperature dependence of the magnetic moment between ~2 and 700 K measured under an applied field of 0.01 T. Triangular markers (one marker displayed per four data points) show ZFC and FC data below room temperature; crosses (one marker displayed per two data points) show ZFC data above room temperature and FC data for the full temperature range. c SQUID 1 temperature dependence of magnetic moment measured in the residual field of the magnet between 2 and 300 K, with ZFC data scaled to match FC data at room temperature. d SQUID 1 magnetic hysteresis loops collected at various temperatures (one marker displayed per four data points). e Capacitance and f dielectric loss at selected frequencies (one marker displayed per 200 data points)
Higher field temperature-dependent magnetic data from SQUID 2 (Fig. 5b) clearly show the ferromagnetic transition occurring at ~450 K, with a tail up to ~500 K, as well as a steep upturn in magnetisation below ~45 K. Although most of the low temperature behaviour is considered in terms of some paramagnetism, there is a divergence in trends of the evolution of FC and ZFC magnetisation in the low-field data below ~ 150 K (Fig. 5c). The higher field data do not show any anomaly at 160 K. The low field, SQUID 1, FC data go sharply in the opposite direction to the ZFC data at T < 15 K; a maximum occurs at ~50 K in the FC data and at ~160 K in the ZFC data. Significant curvature of the reciprocal susceptibility precludes any Curie–Weiss analysis. Magnetic hysteresis loops from SQUID 1 (Fig. 5d) show small openings. Also for the 300 and 400 K curves taken on SQUID 2, the opening gets significantly smaller at 400 K but is still visible. The change in shape of the loop at 5 K relative to that at 30 K again suggests that there is some kind of transition between the two.
The dielectric data (Fig. 5e,f) show a broad peak in capacitance at ~550 K. The amplitude again varies systematically with frequency, but T m does not, and there are slight anomalies in the loss tangent, tanδ. At low frequency and high temperature, an additional anomaly is most likely due to the influence of conductivity.
PZTFN3
Results for f 2 and \( Q^{ - 1} \) from the RUS spectra of PZTFN3 are shown in Fig. 6a. f 2 values are a compilation from peaks from the high-temperature spectra with frequencies of 184, 219, 310, 590, 593 kHz at room temperature, and a peak from the low temperature spectra with frequency 510 kHz. The onset of elastic softening is above the highest temperature reached, ~700 K, and the superattenuation interval is ~450–560 K. Resonance peaks were detectable in the high-temperature RUS spectra below ~450 K but were too weak to allow reliable fitting. The shallow minimum in f 2 appears to occur at ~410 K. This sample has the most clearly defined hysteresis in the whole series, with a small step (increasing stiffness with falling temperature) occurring at 205 K during cooling, and at 240 K during heating. There is also a clear break in slope at ~165 K and the onset of relatively steep stiffening with falling temperatures occurs at ~65 K. \( Q^{ - 1} \) remains high below room temperature, reducing steadily with falling temperature and with a peak at ~165 K. There may be a broad peak in \( Q^{ - 1} \) at around 50–70 K, but the data are noisy.
PZTFN3. a RUS analysed data showing f 2 and \( Q^{ - 1} \), with scaling applied to match f 2 values at room temperature. b SQUID 2 temperature dependence of the magnetic moment between ~2 and 700 K under an applied field of 0.01 T, with triangular markers (one marker displayed per two data points) showing ZFC and FC data below room temperature; crosses (one marker displayed per two data points) show ZFC data above room temperature and FC data for the full temperature range. Note that the high-temperature ZFC result indicate that the probe field of 0.01 T is above the coercive field for this sample above 300 K. c SQUID 1 temperature dependence of magnetic moment measured in the residual field of the magnet between 2 and 300 K, with ZFC data scaled to match FC data at room temperature. d SQUID 1 magnetic hysteresis loops collected at various temperatures (one marker displayed per four data points). e Capacitance and f dielectric loss at selected frequencies (one marker displayed per 200 data points)
Higher field temperature-dependent magnetic data from SQUID 2 (Fig. 6b) clearly show the ferromagnetic transition occurring at ~500 K, and a steep upturn in moment below ~22 K. Low-field temperature-dependent magnetic data from SQUID 1 (Fig. 6c) again show significant differences between FC and ZFC values, but the additional anomalies below ~25 K are not observed. ZFC data have slightly reducing moment with falling temperature below ~50 K. Magnetic hysteresis loops from SQUID 1 (Fig. 6d) show a small opening at every temperature. As with the other samples, the change in shape of the loop at 5 K relative to that at 30 K suggests that there is some kind of transition between the two.
Capacitance variations show a frequency-independent maximum at ~572 K (Fig. 6e). This is accompanied by a minimum in tanδ measured at 1.1 and 12.7 kHz and a maximum in tanδ measured at 1 MHz (Fig. 6f). The steep drop in capacitance at 559 K is more obvious than for either PZTFN6 or PZTFN4 and is accompanied by a steep change also in tanδ. In contrast with the data for PZTFN6 and PZTFN4, there are almost no differences in the values of either capacitance or dielectric loss between heating and cooling. The more subtle maximum in capacitance occurs at ~390 K.
Specific heat data were collected in heating sequences for PZTFN3 in order to check for independent evidence of a tilting transition. They show a smooth variation up to 155 K followed by a series of small anomalies, in particular at ~175,~217,~300 and ~338 K (Fig. 7). The drop with increasing temperature between 155 and 175 K resembles the typical form associated with a second-order phase transition, and its location correlates with the small anomalies seen in the RUS data at ~165 K. The irregularity at 210 K is close to the measured thermal hysteresis, but those at 300 and 338 K fall in regions of very high \( Q^{ - 1} \).
PZTFN2
Results for f 2 and \( Q^{ - 1} \) from the RUS spectra of PZTFN2 are shown in Fig. 8a. The f 2 values are a compilation from a resonance peak in the high-temperature spectra which had frequency 162 kHz at room temperature, the same peak in the low temperature spectra and another resonance in the low temperature spectra which had frequency 80 kHz at room temperature. The onset of elastic softening with falling temperature is at ~820 K, there is a relatively sharp minimum at ~575 K, a rounded minimum at ~110 K and steep stiffening below this. \( Q^{ - 1} \) starts to increase below ~635 K, and the strongest attenuation is between ~500 and ~600 K. \( Q^{ - 1} \) values remain relatively high down to ~150 K, below which there is a distinct peak at ~60 K. Weak ferromagnetism evident from the field cooled data extends up to ~500 K (Fig. 8b), but there is no overt evidence for an antiferromagnetic transition at lower temperatures (Fig. 8b, c). Open hysteresis loops extend at least from room temperature down to 5 K with a clear increase in the maximum magnetisation below 30 K (Fig. 8d). The asymmetric maximum in the dielectric constant is at ~596 K. This value of T m is independent of frequency though the amplitude reduces with increasing frequency and shows some hysteresis (Fig. 8e). There is a further increase in amplitude with increasing temperature at the lowest frequencies and the ferroelectric transition is marked also by an anomaly in the dielectric loss (Fig. 8f).
PZTFN2. a RUS analysed data showing f 2 and \( Q^{ - 1} \), with scaling applied to match f 2 values at room temperature. b SQUID 2 temperature dependence of the magnetic moment between ~5 and 700 K under an applied field of 0.005 T. c SQUID 1 temperature dependence of magnetic moment measured in the residual field of the magnet between 2 and 300 K, with ZFC data scaled to match FC data at room temperature. d SQUID 1 magnetic hysteresis loops collected at various temperatures (one marker displayed per four data points). e Capacitance and f dielectric loss at selected frequencies (one marker displayed per 200 data points)
PZTFN0
Results for f 2 and \( Q^{ - 1} \) from the RUS spectra of PZTFN0 are shown in Fig. 9a. f 2 values are from a peak with frequency 672 kHz at room temperature in the high-temperature spectra and a peak at 108 kHz from the low temperature spectra. Elastic softening starts above the highest temperature reached, i.e. above 700 K, and reaches a well-defined minimum at ~640 K. The total softening amounts to ~45 %. Subsequent variations are small, with shallow minima at ~220 and ~360 K. There is a clear hysteresis between heating and cooling below ~350 K in the high-temperature data for f 2. High-temperature data for \( Q^{ - 1} \) come from peaks with frequencies of 540 kHz (cooling) and 310 kHz (heating). High loss occurs between ~700 and 550 K, but it was possible to observe resonance peaks reasonably clearly throughout this interval, and there is then a smaller maximum at ~505 K. Data for \( Q^{ - 1} \) at low temperatures are from the 108 kHz peak and have well-defined Debye-like maxima at ~190 and ~260 K. There is a trend of increasing stiffness and decreasing loss below ~ 200 K but no sign of the steep upturn below 50–100 K seen in data for the ternary PZTFN samples.
PZTFN0. a RUS data. Different pieces of sample were used for the low and high-temperature experiment, but they came from the same original pressed pellet. f 2 values have been scaled to match at room temperature on heating. (The break in absolute \( Q^{ - 1} \) values at 300 K is an artefact arising from the different experimental set up for low and high-temperature RUS instruments). b Capacitance and c dielectric loss at selected frequencies (one marker displayed per 200 data points)
As with intermediate members of the solid solution, the maximum in capacitance occurs a few degrees above the minimum of f 2 (T cRUS ≈ 651, T m = 665 K). The steep fall in capacitance occurs at ~655 K and tanδ has an anomaly in the same temperature range (Fig. 9c).
Discussion
The rounded maximum in capacitance and lack of frequency dependence for T m are closely similar to reported results for the dielectric properties of other PZT–PFN ceramics [48, 65, 67, 68, 70]. Minor impurity phases do not appear to affect the main conclusions which can be drawn from elastic and dielectric properties measured at a macroscopic scale, but it would be incautious to relate any of the observed ferromagnetic properties to the perovskite.
From the perspective of strain and elasticity, intermediate members of the PZT–PFN solid solution show features typical of a classical improper ferroelastic phase transition followed by more complicated structural evolution that can be understood in terms of interaction of multiple order parameters. There is clearly strong coupling between strain and the ferroelectric order parameter. No evidence has been found for magnetoelastic effects.
Improper ferroelastic transition
The ferroelectric transition is marked by a broad, asymmetric peak in capacitance and, within reasonable experimental uncertainties, values of T m fall on a linear trend between the known cubic–tetragonal transition temperatures of Pb(Zr0.53Ti0.47)O3 and PFN (Fig. 2). A few degrees below this is a steep decline in the capacitance and a few degrees lower still is the temperature at which the steep elastic softening ceases. The pattern is similar to that observed from a sample of Pb(Zr0.52Ti0.48)0.975Nb0.025O3 for which heat capacity was also measured and the main peak in enthalpy change reported to occur at ~24 K below T m [128]. Taking the transition point, T c, as being marked by the maximum in heat capacity would imply that the maximum in dielectric constant occurs above T c, while the end of the steep softening occurs at or just below T c.
Differences between the dielectric and elastic properties reflect differences between proper ferroelectric and improper ferroelastic character. Application of an ac electric field produces, predominantly, reversals in the orientation of electric dipoles and displacement of 180° twin walls, whereas a dynamic stress field induces, predominantly, displacements of the 90° twin walls in a tetragonal crystal. The differences between T m and T cRUS are also likely to relate to the longer length scale of correlations mediated by strain in comparison with correlations mediated by polarisation.
The interval just below T c is not recorded in the RUS data due to superattenuation, but the general form of softening of the shear modulus is consistent with classical relaxation effects of linear/quadratic strain/order parameter coupling. From considerations of the phase diagram, the pattern is expected to be that of a tricritical transition. The steep and non-linear stiffening with falling temperature below T c is characteristic of tricritical character, as seen, for example, in association with tilting transitions in SrZrO3 [129], KMnF3 [130, 131], BaCeO3 [132] and quartz [125]. Also as expected in this context, there is a correlation between the magnitudes of the reduction in f 2, measuring softening of the shear modulus, and the magnitudes of the tetragonal shear strains. In Pb(Zr0.52Ti0.48)O3 e t reaches ~0.03 (Appendix Fig. 10a) and the softening in PZTFN0 amounts to at least 40 %. (The shear modulus of Pb(Zr0.54Ti0.46)O3 softens by ~60 % [109].) For PFN e t reaches ~0.002 and the amount of softening is ~35 % [28]. The corresponding strains and softening for intermediate members of the solid solution are ~0.01 (Table 2) and ~40–50 % (Figs. 4a, 5a, 6a, 8a).
a Strain variations for Pb(Zr0.52Ti0.48)O3 determined from lattice parameters given in Fig. 3 of Noheda et al. [153]. Strain values for PFN are reproduced from Carpenter et al. [28] (note: \( e^{\prime}_{5} \) in Appendix Fig. 10 of that work was given with the wrong sign). b Both \( e_{\text{a}}^{2} \) and \( e_{\text{t}}^{2} \) vary linearly with temperature, consistent with the \( Pm\bar{3}m - P4mm \) transition being close to tricritical in character. c Detail from b showing that the temperature dependence of \( e^{\prime}_{5} \) can be represented by Eq. 8 for both PFN and PZT, consistent with close to tricritical character for the \( P4mm - Cm \) transition if \( e^{\prime}_{5} \) scales with the square of the driving order parameter. d The trajectory across order parameter space can be represented by the variation with falling temperature of \( e^{\prime}_{\text{o}} \) and ea; arrows indicate the direction of falling temperature
Precursor softening
Precursor elastic softening occurs from about ~100 K above the transition point across the entire solid solution (Fig. 2). If this is due to fluctuations of the soft mode, it would be expected to fit with a phenomenological description of the form
where \( \Delta C_{{ik}} \) is the amount of softening of single crystal elastic constants away from the trend for the cubic parent structure and A ik are material constants. The value of the exponent κ, between 1/2 and 2, depends on the anisotropy and dispersion of soft branches round the critical point of the soft mode [133–137] as has been found for precursor softening in SrTiO3, LaAlO3 and KMnF3, for example [138–140]. If, on the other hand, the softening is due to relaxor-like freezing processes, it would be better represented by a Vogel–Fulcher equation
where E a is an effective activation energy and T VF is the zero-frequency freezing temperature. This was found to provide good descriptions of precursor softening of the shear modulus in PbMg1/3Nb2/3O3 [141] and PbSc0.5Ta0.5O3 [142], and it also describes softening ahead of the cubic–tetragonal transition in BaTiO3 [143]. These models have been tested for PZTFN6 but neither provides a quantitative fit to the precursor softening.
Additional softening not due to classical strain/order parameter coupling might alternatively be considered in terms of coupling of acoustic modes with a central peak mode, as seen, for example, below the cubic–rhombohedral octahedral tilting transition in LaAlO3 [144]. A central peak mode has been seen in Brillouin spectra from single crystals of Pb(Zr0.55Ti0.45)O3 and Pb(Zr0.58Ti0.42)O3 by Kim et al. [74] and has relaxation times in the range ~1–3 ps. It extends up to ~70 K above the transition point, which is more or less where the onset of softening occurs for PZT–PFN samples (Fig. 2). Kim et al. [74] showed also that it couples strongly with acoustic modes immediately below the transition point. The microscopic origin of the central peak is understood as being from polarisation fluctuations which slow down as the transition point is approached with increasing or decreasing temperature. Development of a central peak is characteristic of relaxors [145], and observations by inelastic neutron scattering or Brillouin scattering should also provide closer insights into the nature of dynamic microstructures in PZT-PFN. The onset of increasing \( Q^{ - 1} \) labelled as T* represents the temperature at which a strain-coupled microstructure starts to relax on a time scale of ~10−5–10−6 s and might represent the onset of a quasi-static tweed microstructure.
Twin wall dynamics and evidence for local strain heterogeneity
High acoustic attenuation in a temperature interval of ~100 K through and below the cubic–tetragonal transition is due to mobile ferroelastic twin walls and has been characterised at lower frequencies by Bourim et al. [107]. They observed two Debye loss peaks associated with pinning of the twin walls, probably by oxygen vacancies. Extrapolation of Arrhenius solutions for the frequency and temperature dependence would put the equivalent freezing process near 800 K when measured at ~500 kHz, however, implying that the same loss mechanism will not be detected in RUS data. It has been argued elsewhere, firstly, that displacements of ferroelastic twin walls can occur by at least two mechanisms, the advance/retraction of needle tips or the sideways migration of small ledges, and, secondly, that the latter will dominate under the relatively low stress and high-frequency conditions characteristic of RUS measurements [138, 146, 147]. On this basis, the low-frequency Debye peaks would be due to freezing of the needle tip motion, while the loss mechanism responsible for the superattenuation observed here is motion of ledges along the twin walls.
It is notable that there is no discrete Debye loss peak of the type seen for \( Q^{ - 1} \) at ~110 K in PIN–PMN–PT [148] which could be indicative of a discrete freezing process for the mobile twin walls. Instead, relatively high values of \( Q^{ - 1} \) continue to lower temperatures and aspects of the ferroelastic microstructures must remain mobile down to at least ~50 K. The steep increase in f 2 below ~80 K and a decline in values of \( Q^{ - 1} \) only below ~40 K, which occurs in PZT–PFN samples (Figs. 4a, 5a, 6a), has been seen also in PFN [28] and in Pb(Zr0.53Ti0.47)0.6(Fe0.5Ta0.5)0.4O3 [149]. This appears to be a signature for freezing of defects which are coupled to shear strains and which have a spectrum of relaxation times, as would occur in a material with significant local strain heterogeneity. Some of the irregularity of the structural evolution, in comparison with materials which have single structural, magnetic or ferroelectric transitions, seems to correlate with the irregular pattern of small anomalies in heat capacity seen for PZTFN3 in the temperature interval ~ 180–400 K (Fig. 7). PFN itself is known to have a tweed microstructure over a wide temperature interval [150].
Defect dynamics at high temperatures
Irreversibility and the high dielectric loss above the transition temperature for each of the PZT–PFN samples do not appear in the elasticity data and are therefore attributed to defects which are not coupled with strain. The sensitivity to heating in air implies that the concentrations of Fe2+ and oxygen vacancies are important in this and that some oxidation/reduction occurs at the highest temperatures. Furthermore, the irreversible changes depend on the total iron content in that they are substantial in PTZFN6 and PTZFN4 but do not occur in PTZFN3. The loss mechanism perhaps relates to conductivity at grain boundaries, as discussed for PFN by Raymond et al. [98, 99]. Frequency-dispersive dielectric properties unrelated to the phase transitions have also been attributed to a conduction mechanism depending on partial reduction of Fe3+ to Fe2+ [48, 65, 68].
Multiple instabilities
The first-order transition between tetragonal (P4mm) and monoclinic (Cm) structures in PZT samples with compositions close to the MPB is recognised by a rounded minimum in the Young’s modulus and a hysteresis of up to ~100 K between heating and cooling [106, 109]. A comparable hysteresis is seen, as expected, near 300 K in the high-temperature RUS data for PZTFN0 (Fig. 9a). The same pattern is not seen in the data for PZTFN2 (Fig. 8a) because the actual Zr:Ti of this sample, ~49:51, puts it further from the MPB, but it seems safe to attribute the hysteresis in f 2 between heating and cooling near 200 K for PZTFN6, PZTFN4 and PZTFN3 to the same transition. Estimates of the transition temperatures produce a boundary in the binary phase diagram which is consistent with the estimated position of the ternary MPB at room temperature (Figs. 1, 2). The rounded minimum of the Young’s modulus and shear modulus of PZT [49, 105–107, 109], becomes sharper in poled ceramics with compositions Pb(Zr0.515Ti0.485)O3 and Pb(Zr0.52Ti0.48)O3 [52, 60, 113, 114], though hysteresis in the present study on ternary compositions occurs at temperatures below the minimum in f 2. In none of the published data for PZT [44, 49, 105–107, 109], or in the present study, is there any evidence of the transition being accompanied by a significant anomaly in acoustic loss. Nor is there any precursor softening as it is approached from either side. It therefore appears that the weakly first-order transition is between structures with only slightly different shear moduli, and without any additional effects associated with strain/order parameter relaxation.
Strain analysis for Pb(Zr0.52Ti0.48)O3 in Appendix has been used to imply that the transition sequence \( Pm\bar{3}m - P4mm - Cm \) involves two separate instabilities with different order parameters. The effect of two separate order parameters is seen in SrZrO3, where the sequence \( Pm\bar{3}m - I4/mcm -Imma - Pnma \) is due to tilting and involves two order parameters with different (R-point and M-point) symmetries. The two M-point structures, I4/mcm and Imma, differ only in the combination of non-zero components, while the Pnma structure has both tilts. RUS measurements give minima in shear and bulk moduli at the I4/mcm → Imma transition, but only stiffening at the Imma → Pnma transition [129]. In BaTiO3, the sequence P4mm → Amm2 → R3m involves only changes in orientation of a single (Γ-point) order parameter and the two transitions give sharp minima in the shear modulus [147]. The evidence of stiffening associated with development of a second tilt system is that interactions between two separate driving order parameters hinder the strain relaxation mechanism responsible for elastic softening at displacive transitions when measured at high frequencies and with low applied stress. If this is the case, stiffening below the tetragonal–monoclinic transition rather than a sharp minimum, as observed here, would provide a further argument in favour of the monoclinic structure being stabilised by two separate order parameters with different critical temperatures. In this context, it is interesting to note the close similarity between order parameter evolution for Pb(Zr0.52Ti0.48)O3 indicated by the strain analysis in Appendix Fig. 10b and the evolution of two separate order parameters calculated from first principles by Kornev et al. [54].
Tilting transition
The temperature for a tilting transition will depend, qualitatively, on the average radii of cations on the crystallographic B-site. This decreases with increasing substitution of Ti4+ (~0.61 \(\AA\)) for Zr4+ (~0.71 \(\AA\)) across the PZT solid solution and is ~200 K when the average reaches ~0.67 \(\AA\) at Pb(Zr0.53Ti0.47)O3 in the phase diagram of Cordero et al. [44] (ionic radii from [151]). The average of Fe3+ (~0.65 \(\AA\)) and Nb5+ (~0.64 \(\AA\)) is close to, but slightly lower than the average for the B-site cations in Pb(Zr0.53Ti0.47)O3, so the tilting transition would be expected to extend along the PZT–PFN join at progressively lower temperatures with increasing PFN content.
Location of the tilting transition in elasticity data collected at kHz frequencies is possible through the existence of a small anomaly in modulus and a peak in the acoustic loss [44, 49, 106, 109]. For PZTN0, the expected Cm–Cc transition temperature is ~200 K, and this is marked by an increase in \( Q^{ - 1} \), the end of softening and onset of stiffening (Fig. 9a). There is no separate evidence for the origin of the small Debye-like peak in \( Q^{ - 1} \) near 165 K in all three of the PZT–PFN samples being due to octahedral tilting but, in the case of PZTFN3, at least, it is accompanied by a slight break in slope of f 2 (Fig. 6a) and an anomaly in heat capacity (Fig. 7). By analogy with the small loss anomaly seen in unpoled PZT close to the MPB [44, 49, 106, 109], it may correspond to the Cm–Cc tilting transition.
A striking feature of the elastic anomalies associated with the R3m–R3c transition at Zr-rich compositions in PZT shown by Cordero et al. [49] is that they have the typical pattern of softening and loss associated with linear/quadratic strain/order parameter coupling in other perovskites. Close to the MPB, however, this signature essentially disappears, implying that the strain relaxation no longer occurs. By analogy with other systems, this provides further evidence for strain heterogeneity on a mesoscopic length scale. For example, a tilting transition in La0.6Sr0.1TiO3 with cation/vacancy order is accompanied by changes in lattice parameters which represent normal spontaneous strains. The tilting transition still occurs if the cations and vacancies are disordered, but development of the long-range macroscopic strain is disrupted by the influence of heterogeneous strains on a unit cell scale [152]. Cation disorder, an adaptive microstructure of nanodomains and/or tweed would contribute to similar local strain heterogeneity in PZT–PFN and have the same effect in suppressing the macroscopic strain without suppressing the tilting transition itself.
Magnetism and magnetoelastic behaviour
There is no evidence in any of the dielectric, magnetic or elasticity data presented here that the antiferromagnetic ordering in PFN (T N ~ 150 K) extends across to PZT–PFN compositions. Magnetic hysteresis loops in the PZT–PFN samples show small openings at every temperature, but values of the coercivity and remnant moment at room temperature vary between samples. This weak ferromagnetism extends up to ~ 500-600 K and is most likely due to the impurity phases, though some contributions might also come from variable concentration of oxygen vacancies and, hence, the possible presence of Ti3+, in the vicinity of grain boundaries. While the FORC analysis also indicates properties that are not uniform, there is a systematic trend observable in the diagrams, which suggests that inter-particle magnetostatic interactions (responsible for the vertical spreading and peak displacement below the horizontal axis) increase going from PZTFN2 to PFN (Fig. 3). It appears that the single domain particles are more randomly dispersed in PZTFN2, PZTFN3 and PZTFN4, while in the PFN-rich samples they are packed closer together and are arranged in a specific configuration, which results in a local anisotropy that gives rise to the positive mean interaction field.
On the other hand, the magnetic data for PZT–PFN show a distinct change in properties between 5 and 30 K, which is more likely to be intrinsic to the perovskite. In particular, the moments in applied field increase with falling temperature and simultaneously the coercive field for the small loop openings decrease for all the samples. There is a systematic lowering of the measured saturation magnetisation, given in μB Fe−1, at both low and high temperature upon addition of PFN. This goes from ~2 μB Fe−1 for PZTFN2 to ~0.5 μB Fe−1 for PZTFN6 and ~0.2 μB Fe−1 for pure PFN. The pattern of evolution of the magnetic moment between FC and ZFC measurements is not totally consistent between samples, however. The origin of the low temperature anomalies is presumed to be essentially the same as the ordering which gives weak ferromagnetism in PFN and occurs within crystals which are now believed to have significant local strain heterogeneity. If there is even weak magnetoelastic coupling, a spin glass type of magnetic ordering and glassy strain could be interdependent.
Multiferroicity
The PZT–PFN samples produced for this study are truly multiferroic in displaying ferroelasticity, ferromagnetism and ferroelectricity to high temperatures. It seems likely that the impurity phases are responsible for the ferromagnetism, but this could still contribute significantly to the overall multiferroicity. The magnetic field from a strongly ferromagnetic impurity phase present even in small proportions would influence the magnetic properties of the perovskite. Conversely, electrostriction from the perovskite is likely to influence the magnetic properties of the impurity. In this sense, samples with chemical and structural heterogeneity could turn out to have advantageous multiferroic properties which remain to be explored.
Conclusions
The elastic and anelastic properties of perovskites with compositions close to the ternary MPB of PbZrO3-PbTiO3-PbFe0.5Nb0.5O3 are dominated by large softening of the shear modulus associated with the \( Pm\bar{3}m - P4mm \) transition and high acoustic attenuation in a temperature interval of ~ 100 K below the transition point due to the mobility of ferroelastic twin walls. In this respect, the tetragonal ferroelectric structure has all the characteristic features of a typical improper ferroelastic. Evidence for a first-order transition, provisionally attributed to P4mm–Cm, and an octahedral tilting (Cm–Cc) transition has also been found, but the influence of these on elastic/anelastic properties is much more subtle. These additional instabilities do not yield the classical softening response expected from linear/quadratic strain order parameter coupling. Similarly, they are not accompanied by acoustic loss that would signify twin wall mobility. It appears both that the multiple order parameters lock in together in some way that prevents strain relaxation and that the expected adaptive microstructure also does not relax under external loading, at least when measured at frequencies of ~0.1–1 MHz.
The second dominant feature of the elastic behaviour is precursor softening in a temperature interval of up to ~100 K above the cubic–tetragonal transition point. The form of softening does not fit descriptions arising from phenomenological models of soft mode dispersion or of relaxor ferroelectrics. It is instead considered in terms of coupling of acoustic phonons with a central peak mode due to local correlations and/or dynamic microstructure.
Finally, concave-up stiffening with falling temperature and reductions in attenuation below ~ 100 K appear to be signatures of a material with heterogeneous local strains which have a spectrum of relaxation times. Such heterogeneity must then have a bearing on the magnetoelectric properties when PFN is added in solid solution. Although no direct evidence for significant magnetoelastic coupling has been found, strain heterogeneity may well have some influence both on the magnetic ordering and the development of spin glass.
References
Sanchez DA, Ortega N, Kumar A, Roque-Malherbe R, Polanco R, Scott JF, Katiyar RS (2011) Symmetries and multiferroic properties of novel room-temperature magnetoelectrics: lead iron tantalate–lead zirconate titanate (PFT/PZT). AIP Adv 1:42169. doi:10.1063/1.3670361
Sanchez DA, Kumar A, Ortega N, Martinez R, Katiyar RS (2011) Investigation of multiferroic properties of (PbZr0.53Ti0.47O3)(1-x)-(PbFe0.5Ta0.5O3) x ceramics. Integr Ferroelectr 124:61–72. doi:10.1080/10584587.2011.573720
Sanchez DA, Ortega N, Kumar A, Sreenivasulu G, Katiyar RS, Scott JF, Evans DM, Arredondo-Arechavala M, Schilling A, Gregg JM (2013) Room-temperature single phase multiferroic magnetoelectrics: Pb(Fe, M)x(Zr, Ti)(1-x)O3 [M = Ta, Nb]. J Appl Phys 113:074105. doi:10.1063/1.4790317
Glinchuk MD, Eliseev EA, Morozovska AN (2014) Novel room temperature multiferroics on the base of single-phase nanostructured perovskites. J Appl Phys 116:054101. doi:10.1063/1.4891459
Scott JF (2013) Room-temperature multiferroic magnetoelectrics. NPG Asia Mater 5:e72. doi:10.1038/am.2013.58
Glinchuk MD, Eliseev EA, Morozovska AN (2016) Landau-Ginzburg description of anomalous properties of novel room temperature multiferroics Pb(Fe1/2Ta1/2) x (Zr0.53Ti0.47)1-x O3 and Pb(Fe1/2Nb1/2) x (Zr0.53Ti0.47)1-x O3. J Appl Phys 119:024102. doi:10.1063/1.4939584
Evans DM, Schilling A, Kumar A, Sanchez D, Ortega N, Arredondo M, Katiyar RS, Gregg JF, Scott JF (2013) Magnetic switching of ferroelectric domains at room temperature in multiferroic PZTFT. Nat Commun 4:1534. doi:10.1038/ncomms2548
Evans DM, Schilling A, Kumar A, Sanchez D, Ortega N, Katiyar RS, Scott JF, Gregg JM (2014) Switching ferroelectric domain configurations using both electric and magnetic fields in Pb(Zr, Ti)O3-Pb(Fe, Ta)O3 single-crystal lamellae. Philos Trans A Math Phys Eng Sci 372:20120450. doi:10.1098/rsta.2012.0450
Evans DM, Alexe M, Schilling A, Kumar A, Sanchez D, Ortega N, Katiyar RS, Scott JF, Gregg JM (2015) The nature of magnetoelectric coupling in Pb(Zr, Ti)O3-Pb(Fe, Ta)O3. Adv Mater 27:6068–6073. doi:10.1002/adma.201501749
Kumar A, Sharma GL, Katiyar RS, Pirc R, Blinc R, Scott JF (2009) Magnetic control of large room-temperature polarization. J Phys: Condens Matter 21:382204. doi:10.1088/0953-8984/21/38/382204
Katiyar RS, Kumar A, Scott JF (2014) US Patent No. 8,803,264
Stock C, Dunsiger SR, Mole RA, Li X, Luo H (2013) Coupled short-range ferroelectric and magnetic order in PbFe1/2Nb1/2O3. Phys Rev B 88:094105. doi:10.1103/PhysRevB.88.094105
Schiemer JA, Lascu I, Harrison RJ, Kumar A, Katiyar RS, Sanchez DA, Ortega N, Salazar Mejia C, Schnelle W, Echizen M, Shinohara H, Heap AJF, Nagaratnam R, Dutton SE, Scott JF, Nair B, Mathur ND, Carpenter MA (2015) Elastic and anelastic relaxation behaviour of perovskite multiferroics II: PbZr0.53Ti0.47O3 (PZT) - PbFe0.5Ta0.5O3 (PFT). J Mater Sci (in press)
Eremkin VV, Smotrakov VG, Fesenko EG (1990) Structural phase-transitions in PbZr1-x Ti x O3 crystals. Ferroelectrics 110:137–144
Noheda B, Cereceda N, Iglesias T, Lifante G, Gonzalo JA, Wang YL (1995) Composition dependence of the ferroelectric-paraelectric transition in the mixed system PbZ1-x Ti x O3. Phys Rev B 51:16388–16391. doi:10.1103/PhysRevB.51.16388
Rossetti GA, Navrotsky A (1999) Calorimetric investigation of tricritical behavior in tetragonal Pb(Zr x Ti1−x )O3. J Solid State Chem 144:188–194. doi:10.1006/jssc.1999.8146
Rossetti GA, Maffei N (2005) Specific heat study and Landau analysis of the phase transition in PbTiO3 single crystals. J Phys: Condens Matter 17:3953–3963. doi:10.1088/0953-8984/17/25/021
Mikhaleva EA, Flerov IN, Gorev MV, Molokeev MS, Cherepakhin AV, Kartashev AV, Mikhashenok NV, Sablina KA (2012) Caloric characteristics of PbTiO3 in the temperature range of the ferroelectric phase transition. Phys Solid State 54:1832–1840. doi:10.1134/S1063783412090181
Chung C-C (2014) Microstructural evolution in lead zirconate titanate (PZT) piezoelectric ceramics. PhD, University of Connecticut
Sai Sunder VVSS, Umarji AM (1995) Thermal expansion studies in the lead iron niobiate - lead titanate system. Mater Res Bull 30:427–434. doi:10.1016/0025-5408(95)00016-X
Ivanov SA, Tellgren R, Rundlof H, Thomas NW, Ananta S (2000) Investigation of the structure of the relaxor ferroelectric Pb(Fe1/2Nb1/2)O3 by neutron powder diffraction. J Phys: Condens Matter 12:2393–2400. doi:10.1088/0953-8984/12/11/305
Bokov VAA, Myl’nikova IEE, Smolenskii GA (1962) Ferroelectric antiferromagnetics. Sov Phys JETP 15:447–449
Ehses KH, Schmid H (1983) Die Hochtemperaturphasenumwandlungen von PbFe0.5Nb0.5O3. Z Krist 162:64–66
Bonny V, Bonin M, Sciau P, Schenk KJ, Chapuis G (1997) Phase transitions in disordered lead iron niobate: X-ray and synchrotron radiation diffraction experiments. Sol State Commun 102:347–352. doi:10.1016/S0038-1098(97)00022-7
Lampis N, Sciau P, Geddo Lehmann A (1999) Rietveld refinements of the paraelectric and ferroelectric structures of PbFe0.5Nb0.5O3. J Phys: Condens Matter 11:3489–3500. doi:10.1088/0953-8984/11/17/307
Brunskill IH, Schmid H, Tissot P (1981) The characterization of high temperature solution-grown single crystals of Pb(Fe1/2Nb1/2)O3. Ferroelectrics 37:547–550. doi:10.1080/00150198108223482
Raevski IP, Kubrin SP, Raevskaya SI, Prosandeev SA, Malitskaya MA, Titov VV, Sarychev DA, Blazhevich AV, Zakharchenko IN (2012) Dielectric and Mossbauer studies of ferroelectric and magnetic phase transitions in A-site and B-site substituted multiferroic PbFe0.5Nb0.5O3. IEEE Trans Ultrason Ferroelectr Freq Control 59:1872–1878. doi:10.1109/TUFFC.2012.2399
Carpenter MA, Schiemer JA, Lascu I, Harrison RJ, Kumar A, Katiyar RS, Ortega N, Sanchez DA, Mejia CS, Schnelle W, Echizen M, Shinohara H, Heap AJ, Nagaratnam R, Dutton SE, Scott JF (2015) Elastic and magnetoelastic relaxation behaviour of multiferroic (ferromagnetic + ferroelectric + ferroelastic) Pb(Fe0.5Nb0.5)O3 perovskite. J Phys: Condens Matter 27:285901. doi:10.1088/0953-8984/27/28/285901
Matteppanavar S, Angadi B, Rayaprol S (2013) Single phase synthesis and room temperature neutron diffraction studies on multiferroic PbFe0.5Nb0.5O3. In: AIP Conference Proceedings. doi:10.1063/1.4791496
Dul’kin E, Kania A, Roth M (2014) Characteristic temperatures of PbFe1/2Nb1/2O3 ferroelectric crystals seen via acoustic emission. Mater Res Express 1:016105. doi:10.1088/2053-1591/1/1/016105
Levstik A, Filipič C, Holc J (2008) The magnetoelectric coefficients of Pb(Fe1/2Nb1/2)O3 and 0.8Pb(Fe1/2Nb1/2)O3-0.2Pb(Mg1/2W1/2)O3. J Appl Phys 103:066106. doi:10.1063/1.2896639
Sitalo EI, Raevski IP, Lutokhin AG, Blazhevich AV, Kubrin SP, Raevskaya SI, Zakharov YN, Maliskaya MA, Titov VV, Zakharchenko IN (2011) Dielectric and piezoelectric properties of PbFe1/2Nb1/2O3-PbTiO3 ceramics from the morphotropic phase boundary compositional range. IEEE Trans Ultrason Ferroelectr Freq Control 58:1914–1919. doi:10.1109/TUFFC.2011.2031
Singh SP, Yusuf SM, Yoon S, Baik S, Shin N, Pandey D (2010) Ferroic transitions in the multiferroic (1 − x)Pb(Fe1/2Nb1/2)O3–xPbTiO3 system and its phase diagram. Acta Mater 58:5381–5392. doi:10.1016/j.actamat.2010.06.014
Whatmore RW, Glazer AM (1979) Structural phase transitions in lead zirconate. J Phys C: Solid State Phys 12:1505–1519. doi:10.1088/0022-3719/12/8/012
Corker DL, Glazer AM, Dec J, Roelder K, Whatmore RW (1997) A re-investigation of the crystal structure of the perovskite PbZrO3 by X-ray and neutron diffraction. Acta Cryst B 53:135–142. doi:10.1107/S0108768196012414
Fujishita H, Ishikawa Y, Tanaka S, Ogawaguchi A, Katano S (2003) Crystal structure and order parameters in the phase transition of antiferroelectric PbZrO3. J Phys Soc Jpn 72:1426–1435. doi:10.1143/JPSJ.72.1426
Yoshida T, Moriya Y, Tojo T, Kawaji H, Atake T, Kuroiwa Y (2009) Heat capacity at constant pressure and thermodynamic properties of phase transitions in PbMO3 (M = Ti, Zr and Hf). J Therm Anal Calorim 95:675–683. doi:10.1007/s10973-008-9220-y
Jaffe B, Cook WR, Jaffe HL (1971) Piezoelectric ceramics. Academic Press, Cambridge
Marbeuf A, Ravez J, Demazeau G (1974) Nature de transitions dans le système PbZrO3-PbFe x/2Nb x/2O3. Rev Chim Miner 11:198–206
Blazhievskii BP, Isupov VA, Kozlovskii LV et al (1986) Ferroelectric properties of the ceramic lead zirconate-orthoniobate. Inorg Mater 22:418
Lovkova EV, Prutchenko SG, Politova ED (2000) Phase diagram and dielectric properties of Pb[Zr1-x (Fe0.5Nb0.5) x ]O3 (0 < x<0.2) solid solutions. Inorg Mater 36:1264–1267
Raevski IP, Molokeev MS, Misyul SV, Eremin EV, Blazhevich AV, Kubrin SP, Sarychev DA, Titov VV, Chen H, Chou C-C, Raevskaya SI, Malitskaya MA (2015) Studies of ferroelectric and magnetic phase transitions in multiferroic PbFe0.5Ta0.5O3. Ferroelectrics 475:52–60. doi:10.1080/00150193.2015.995009
Whatmore RW, Clarke R, Glazer AM (1978) Tricritical behaviour in PbZr x Ti1-x O3 solid solutions. J Phys C: Solid State Phys 11:3089–3102. doi:10.1088/0022-3719/11/14/029
Cordero F, Trequattrini F, Craciun F, Galassi C (2013) Merging of the polar and tilt instability lines near the respective morphotropic phase boundaries of PbZr1-x Ti x O3. Phys Rev B 87:094108. doi:10.1103/PhysRevB.87.094108
Whatmore RW, Bell AJ (1981) Pyroelectric ceramics in the lead zirconate-lead titanate-lead iron niobate system. Ferroelectrics 35:155–160. doi:10.1080/00150198108017679
Fang B-J, Ding C-L, Liu W, Li L-Q, Tang L (2009) Preparation and electrical properties of high-Curie temperature ferroelectrics. Eur Phys J Appl Phys 45:20302. doi:10.1051/epjap/2009004
Amonpattaratkit P, Jantaratana P, Ananta S (2015) Influences of PZT addition on phase formation and magnetic properties of perovskite Pb(Fe0.5Nb0.5)O3-based ceramics. J Magn Magn Mater 389:95–100. doi:10.1016/j.jmmm.2015.04.053
Fang B, Shan Y, Tezuka K, Imoto H (2005) Synthesis and characterization of pseudo-ternary Pb(Fe1/2Nb1/2)O3-PbZrO3-PbTiO3 ferroelectric ceramics via a B-site oxide mixing route. J Mater Sci 40:6445–6451. doi:10.1007/s10853-005-1711-7
Cordero F, Trequattrini F, Craciun F, Galassi C (2011) Octahedral tilting, monoclinic phase and the phase diagram of PZT. J Phys: Condens Matter 23:415901. doi:10.1088/0953-8984/23/41/415901
Zhang N, Yokota H, Glazer AM, Thomas PA (2011) Neutron powder diffraction refinement of PbZr(1-x)Ti(x)O3. Acta Cryst B 67:386–398. doi:10.1107/S0108768111028631
Zhang N, Yokota H, Glazer AM, Ren Z, Keen DA, Keeble DS, Thomas PA, Ye ZG (2014) The missing boundary in the phase diagram of PbZr(1-x)Ti x O3. Nat Commun 5:5231. doi:10.1038/ncomms6231
Mishra SK, Pandey D, Lemmens HJ, Van Tendeloo G (2001) Evidence for another low temperature phase transition in tetragonal Pb(Zr x Ti1-x )O3 (x = 0.515,0.520). Phys Rev B 64:054101. doi:10.1103/PhysRevB.64.054101
Ranjan R, Mishra SK, Pandey D, Kennedy BJ (2002) Antiferrodistortive phase transition in PbTi0.48Zr0.52O3: a powder neutron diffraction study. Phys Rev B 65:60102. doi:10.1103/PhysRevB.65.060102
Kornev IA, Bellaiche L, Janolin P-E, Dkhil B, Suard E (2006) Phase diagram of Pb(Zr, Ti)O3 solid solutions from first principles. Phys Rev Lett 97:157601. doi:10.1103/PhysRevLett.97.157601
Clarke R, Glazer AM (1976) The ferroelectric-ferroelectric transition in rhombohedral lead zirconate-titanate. Ferroelectrics 12:207–209. doi:10.1080/00150197608241429
Corker DL, Glazer AM, Whatmore RW, Stallard A, Fauth F (1998) A neutron diffraction investigation into the rhombohedral phases of the perovskite series PbZr1-x Ti x O3. J Phys: Condens Matter 10:6251–6269. doi:10.1088/0953-8984/10/28/007
Noheda B, Wu L, Zhu Y (2002) Low-temperature superlattice in monoclinic PbZr0.52Ti0.48O3. Phys Rev B 66:060103. doi:10.1103/PhysRevB.66.060103
Hatch DM, Stokes HT, Ranjan R, Mishra SK, Pandey D, Kennedy BJ (2002) Antiferrodistortive phase transition in Pb(Ti0.48Zr0.52)O3: space group of the lowest temperature monoclinic phase. Phys Rev B 65:212101. doi:10.1103/PhysRevB.65.212101
Woodward DI, Knudsen J, Reaney IM (2005) Review of crystal and domain structures in the PbZr x Ti1−x O3 solid solution. Phys Rev B 72:104110. doi:10.1103/PhysRevB.72.104110
Pandey D, Singh AK, Baik S (2008) Stability of ferroic phases in the highly piezoelectric Pb(Zr x Ti1-x )O3 ceramics. Acta Cryst A 64:192–203. doi:10.1107/S0108767307055511
Solanki RS, Singh AK, Mishra SK, Kennedy SJ, Suzuki T, Kuroiwa Y, Moriyoshi C, Panday D (2011) Ground state of (Pb0.94Sr0.06)(Zr0.530Ti0.470)O3 in the morphotropic phase boundary region: evidence for a monoclinic Cc space group. Phys Rev B 84:144116. doi:10.1103/PhysRevB.84.144116
Solanki RS, Mishra SK, Senyshyn A, Yoon S, Baik S, Shin N, Pandey D (2013) Confirmation of the monoclinic Cc space group for the ground state phase of Pb(Zr0.525Ti0.475)O3: a combined synchrotron X-ray and neutron powder diffraction study. Appl Phys Lett 102:052903. doi:10.1063/1.4790569
Solanki RS, Mishra SK, Senyshyn A, Ishii I, Senyshyn A, Ishii I, Moriyoshi C, Suzuki T, Kuroiwa Y, Pandey D (2012) Antiferrodistortive phase transition in pseudorhombohedral (Pb0.94Sr0.06)(Zr0.550Ti0.450)O3: a combined synchrotron x-ray and neutron powder diffraction study: a combined synchrotron x-ray and neutron powder diffraction study. Phys Rev B 86:174117. doi:10.1103/PhysRevB.86:174117
Yu L, Deng H, Zhou W, Cao H, Zheng T, Yang P, Chu J (2016) Modified structure and optical properties of multiferroic Pb(Zr0.53Ti0.47) x (Fe0.5Nb0.5)(1−x)O3 ceramics. Ceram Int 42:917–922. doi:10.1016/j.ceramint.2015.09.019
Fang B, Shan Y, Tezuka K, Imoto H (2005) Reduction of dielectric losses in Pb(Fe1/2Nb1/2)O3-based ferroelectric ceramics. Jpn J Appl Phys 44:5035–5039. doi:10.1143/JJAP.44.5035
Singh SP, Singh AK, Pandey D (2007) Evidence for a monoclinic MA to tetragonal morphotropic phase transition in (1 − x)[Pb(Fe1/2Nb1/2)O3]–xPbTiO3 ceramics. J Phys: Condens Matter 19:036217. doi:10.1088/0953-8984/19/3/036217
Prasatkhetragarn A (2011) Synthesis and Dielectric properties of 0.9Pb(Zr1/2Ti1/2)O3–0.1Pb(Fe1/3Nb2/3)O3 ceramics. Ferroelectrics 416:35–39. doi:10.1080/00150193.2011.577661
Fang B, Shan Y, Tezuka K, Imoto H (2005) High Curie temperature Pb(Fe1/2Nb1/2)O3-based ferroelectrics: 0.40Pb(Fe1/2Nb1/2)O3-0.34PbZrO3-0.26PbTiO3. Phys Status Solidi 202:481–489. doi:10.1002/pssa.200406921
Tu C-S, Tseng C-T, Chien RR, Schmidt VH, Hsieh C-M (2008) Nanotwin and phase transformation in tetragonal Pb(Fe1/2Nb1/2)1−xTixO3 single crystal. J Appl Phys 104:054106. doi:10.1063/1.2974791
Kumar N, Ghosh A, Choudhary RNP (2011) Electrical behavior of Pb(Zr0.52Ti0.48)0.5(Fe0.5Nb0.5)0.5O3 ceramics. Mater Chem Phys 130:381–386. doi:10.1016/j.matchemphys.2011.06.059
Yokota H, Zhang N, Taylor A, Thomas PA, Glazer AM (2009) Crystal structure of the rhombohedral phase of PbZr1−x Ti x O3 ceramics at room temperature. Phys Rev B 80:104109. doi:10.1103/PhysRevB.80.104109
Kumar A, Mishra SK (2014) Structural and dielectric properties of Nb and Fe co-doped PZT ceramic prepared by a semi-wet route. Adv Mater Lett 5:479–484. doi:10.5185/amlett.2014.564
Mishra SK, Pandey D (1997) Thermodynamic nature of phase transitions in Pb(Zr x Ti1−x )O3 ceramics near the morphotropic phase boundary. II. Dielectric and piezoelectric studies. Philos Mag B 76:227–240. doi:10.1080/01418639708241087
Kim TH, Ko J-H, Kojima S, Bokov AA, Long X, Ye Z-G (2012) Phase transition behaviors of PbZr1−x Ti x O3 single crystals as revealed by elastic anomalies and central peaks. Appl Phys Lett 100:082903. doi:10.1063/1.3688050
Vanderbilt D, Cohen M (2001) Monoclinic and triclinic phases in higher-order Devonshire theory. Phys Rev B 63:094108. doi:10.1103/PhysRevB.63.094108
Rossetti GA, Khachaturyan AG, Akcay G, Ni Y (2008) Ferroelectric solid solutions with morphotropic boundaries: vanishing polarization anisotropy, adaptive, polar glass, and two-phase states. J Appl Phys 103:114113. doi:10.1063/1.2930883
Spivakov AA, Zakharov YuN, Ter-Oganessian NV, Lutokhin AG, Panchenko EM, Sakhenko VP (2015) Interrelation of ferroelectricity and tilting in perovskites using the phase transitions in PbZr1−x TixO3 as an example. Solid State Sci 40:105–110. doi:10.1016/j.solidstatesciences.2015.01.004
Kumar A, Katiyar RS, Rinaldi C, Rinaldi C, Lushnikov SG, Shaplygina TA (2008) Glasslike state in PbFe1/2Nb1/2O3 single crystal. Appl Phys Lett 93:232902. doi:10.1063/1.3043686
Laguta VV, Glinchuk MD, Maryško M, Kuzian RO, Prosandeev SA, Raevskaya SI, Smotrakov VG, Eremkin VV, Raevski IP (2013) Effect of Ba and Ti doping on magnetic properties of multiferroic Pb(Fe1/2Nb1/2)O3. Phys Rev B 87:064403. doi:10.1103/PhysRevB.87.064403
Falqui A, Lampis N, Geddo-Lehmann A, Pinna G (2005) Low-temperature magnetic behavior of perovskite compounds PbFe1/2Ta1/2O3 and PbFe1/2Nb1/2O3. J Phys Chem B 109:22967–22970. doi:10.1021/jp0551014
Rotaru GM, Roessli B, Amato A, Gvasaliya SN, Mudry C, Lushnikov SG, Shaplygina TA (2009) Spin-glass state and long-range magnetic order in Pb(Fe1/2Nb1/2)O3 seen via neutron scattering and muon spin rotation. Phys Rev B 79:184430. doi:10.1103/PhysRevB.79.184430
Havlicek R, Vejpravova JP, Bochenek D (2010) Structure and magnetic properties of perovskite-like multiferroic PbFe0.5Nb0.5O3. J Phys: Conf Ser 200:012058. doi:10.1088/1742-6596/200/1/012058
Kleemann W, Shvartsman VV, Borisov P, Kania A (2010) Coexistence of antiferromagnetic and spin cluster glass order in the magnetoelectric relaxor multiferroic PbFe0.5Nb0.5O3. Phys Rev Lett 105:257202. doi:10.1103/PhysRevLett.105.257202
Chillal S, Thede M, Litterst FJ, Gvasaliya SN, Shaplygina TA, Lushnikov SG, Zheludev A (2013) Microscopic coexistence of antiferromagnetic and spin-glass states. Phys Rev B 87:220403. doi:10.1103/PhysRevB.87.220403
Matteppanavar S, Rayaprol S, Singh K, Reddy VR, Angadi B (2015) Evidence for magneto-electric and spin–lattice coupling in PbFe0.5Nb0.5O3 through structural and magneto-electric studies. J Mater Sci 50:4980–4993. doi:10.1007/s10853-015-9046-5
Matteppanavar S, Rayaprol S, Anupama AV, Sahoo B, Angadi B (2015) On the room temperature ferromagnetic and ferroelectric properties of Pb(Fe1/2Nb1/2)O3. J Supercond Nov Magn 28:2465–2472. doi:10.1007/s10948-015-3058-x
Majumder SB, Bhattacharyya S, Katiyar RS, Manivannan A, Dutta P, Seehra M (2006) Dielectric and magnetic properties of sol-gel-derived lead iron niobate ceramics. J Appl Phys 99:024108. doi:10.1063/1.2158131
Blinc R, Cevc P, Zorko A, Holc J, Kosec M, Trontelj A, Pirnat J, Dalal N, Ramachandran V, Krzystek J (2007) Electron paramagnetic resonance of magnetoelectric Pb(Fe1/2Nb1/2)O3. J Appl Phys 101:033901. doi:10.1063/1.2432309
Fraygola B, Nascimento WJ, Coelho AA, Garcia D, Eiras JA (2013) Evidence of new magnetic ordering at high temperatures in Pb-based multiferroics perovskites. Phys Status Solidi A 210:1856–1860. doi:10.1002/pssa.201329011
Kuzian RO, Kondakova IV, Daré AM, Laguta VV (2014) Magnetic interactions in disordered perovskite PbFe1/2Nb1/2O3. Phys Rev B 89:024402. doi:10.1103/PhysRevB.89.024402
Kuzian RO, Laguta VV, Richter J (2014) Lieb-Mattis ferrimagnetic superstructure and superparamagnetism in Fe-based double perovskite multiferroics. Phys Rev B 90:134415. doi:10.1103/PhysRevB.90.134415
Raevski IP, Kubrin SP, Raevskaya SI, Sarychev DA, Prosandeev SA, Malitskaya MA (2012) Magnetic properties of PbFe1/2Nb1/2O3: Mössbauer spectroscopy and first-principles calculations. Phys Rev B 85:224412. doi:10.1103/PhysRevB.85.224412
Raevskii IP, Sarychev DA, Bryugeman SA, Reznichenko LA, Shilkina LA, Razumovskaya ON, Nikolaev VS, Vyshatko NP, Salak AN (2002) Study of cation ordering and magnetic phase transitions in ternary Fe-containing perovskite oxides by Mössbauer spectroscopy. Crystallogr Rep 47:1012–1015. doi:10.1134/1.1523519
Laguta VV, Rosa J, Jastrabik L, Blinc R, Cevc P, Zalar B, Remskar M, Raevskaya SI, Raevski IP (2010) 93Nb NMR and Fe3+ EPR study of local magnetic properties of magnetoelectric Pb(Fe1/2Nb1/2)O3. Mater Res Bull 45:1720–1727. doi:10.1016/j.materresbull.2010.06.060
Correa M, Kumar A, Priya S, Katiyar RS, Scott JF (2011) Phonon anomalies and phonon-spin coupling in oriented PbFe0.5Nb0.5O3 thin films. Phys Rev B 83:014302. doi:10.1103/PhysRevB.83.014302
Gao XS, Chen XY, Yin J, Wu J, Liu ZG, Wang M (2000) Ferroelectric and dielectric properties of ferroelectromagnet Pb(Fe1/2Nb1/2)O3 ceramics and thin films. J Mater Sci 35:5421–5425. doi:10.1023/A:1004815416774
Bochenek D, Surowiak Z, Krok-Kowalski J, Poltierova-Vejpravova J (2010) Influence of the sintering conditions on the physical proprieties of the ceramic PFN multiferroics. J Electroceramic 25:122–129. doi:10.1007/s10832-010-9599-2
Raymond O, Font R, Suárez-Almodovar N, Portelles J, Siqueiros JM (2005) Frequency-temperature response of ferroelectromagnetic Pb(Fe1/2Nb1/2)O3 ceramics obtained by different precursors. Part I. Structural and thermo-electrical characterization. J Appl Phys 97:084107. doi:10.1063/1.1870099
Raymond O, Font R, Portelles J, Suárez-Almodovar N, Siqueiros JM (2006) Frequency-temperature response of ferroelectromagnetic Pb(Fe1/2Nb1/2)O3 ceramics obtained by different precursors. III. Dielectric relaxation near the transition temperature. J Appl Phys 99:124101. doi:10.1063/1.2201853
Mishra RK, Choudhary RNP, Banerjee A (2010) Bulk permittivity, low frequency relaxation and the magnetic properties of Pb(Fe1/2Nb1/2)O3 ceramics. J Phys: Condens Matter 22:025901. doi:10.1088/0953-8984/22/2/025901
Bokov AA, Emelyanov SM (1995) Electrical properties of Pb(Fe0.5Nb0.5)O3 crystals. Phys Status Solidi B 164:K109–K112. doi:10.1002/pssb.2221640239
Fundora A, Vázquez A, Portelles J, Calderón F, Siqueiros JM (1998) Diffuse phase transitions in ferroelectric ceramics. J Non Cryst Solids 235–237:567–569. doi:10.1016/S0022-3093(98)00567-5
Bharti C, Choudhary SN, Sinha TP (2008) Relaxor behaviour in Pb(Fe0.5Nb0.5)O3. J Surf Sci Technol 24:1–10
Dkhil B, Gemeiner P, Al-Barakaty A, Bellaiche L, Dul’kin E, Mojaev E, Roth M (2009) Intermediate temperature scale T* in lead-based relaxor systems. Phys Rev B 80:064103. doi:10.1103/PhysRevB.80.064103
Bouzid A, Bourim EM, Gabbay M, Fantozzi G (2005) PZT phase diagram determination by measurement of elastic moduli. J Eur Ceram Soc 25:3213–3221. doi:10.1016/j.jeurceramsoc.2004.07.018
Cordero F, Craciun F, Galassi C (2007) Low-temperature phase transformations of PbZr1−x Ti x O3 in the morphotropic phase-boundary region. Phys Rev Lett 98:255701. doi:10.1103/PhysRevLett.98.255701
Bourim EM, Tanaka H, Gabbay M, Fantozzi G (2000) Internal friction and dielectric measurements in lead zirconate titanate ferroelectric ceramics. Jpn J Appl Phys 39:5542–5547. doi:10.1143/JJAP.39.5542
Zachariasz R, Czerwiec M, Ilczuk J, Brus B, Zarycka A, Bartowska J (2005) Mechanical loss associated with the grain size in lead zirconate titanate ceramics. J Phys IV France 129:185–187. doi:10.1051/jp4:2005129039
Cordero F, Craciun F, Galassi C (2008) Anelastic and dielectric study of the phase transformations of around the morphotropic phase boundary. J Phys Chem Solids 69:2172–2176. doi:10.1016/j.jpcs.2008.03.025
Franke I, Roleder K, Mitoseriu L et al (2006) High-temperature macroscopic piezoelectricity in Nb-doped PbZr1−x Ti x O3 ceramics driven by the existence of polar regions. Phys Rev B 73:144114. doi:10.1103/PhysRevB.73.144114
Postnikov VS, Pavlov VS, Turkov SK (1970) Internal friction in ferroelectrics due to interaction of domain boundaries and point defects. J Phys Chem Solids 31:1785–1791. doi:10.1016/0022-3697(70)90168-X
Arlt G (1990) Domain contributions to piezoelectricity in ceramics. In: IEEE proceedings in Ultrasonics Symposium pp 733–742
Singh AK, Mishra SK, Ragini Pandey D, Yoon S, Baik S, Shin N (2008) Origin of high piezoelectric response of Pb(ZrxTi1−x)O3 at the morphotropic phase boundary: role of elastic instability. Appl Phys Lett 92:022910. doi:10.1063/1.2836269
Pandey D, Singh AK, Ranjan R (2005) Monoclinic phases in the Pb(Zr x Ti1-x )O3 ceramics. Ferroelectrics 325:35–42. doi:10.1080/00150190500326761
Rietveld HM (1969) A profile refinement method for nuclear and magnetic structures. J Appl Cryst 2:65–71. doi:10.1107/S0021889869006558
Rodriguez-Carvajal J, Fernandez-Diaz MT, Martinez JL (1991) Neutron diffraction study on structural and magnetic properties of La2NiO4. J Phys: Condens Matter 3:3215–3234. doi:10.1088/0953-8984/3/19/002
Mayergoyz I (1986) Mathematical models of hysteresis. IEEE Trans Magn 22:603–608. doi:10.1109/TMAG.1986.1064347
Roberts AP, Pike CR, Verosub KL (2000) First-order reversal curve diagrams: a new tool for characterizing the magnetic properties of natural samples. J Geophys Res 105:28461–28475. doi:10.1029/2000JB900326
Roberts AP, Heslop D, Zhao X, Pike CR (2014) Understanding fine magnetic particle systems through use of first-order reversal curve diagrams. Rev Geophys 52:557–602. doi:10.1002/2014RG000462
Pike CR, Roberts AP, Verosub KL (2001) First-order reversal curve diagrams and thermal relaxation effects in magnetic particles. Geophys J Int 145:721–730. doi:10.1046/j.0956-540x.2001.01419.x
Pike CR, Roberts AP, Dekkers MJ, Verosub KL (2001) An investigation of multi-domain hysteresis mechanisms using FORC diagrams. Phys Earth Planet Inter 126:11–25. doi:10.1016/S0031-9201(01)00241-2
Harrison RJ, Feinberg JM (2008) FORCinel: an improved algorithm for calculating first-order reversal curve (FORC) distributions using locally weighted regression smoothing. Geochem Geophys Geosys 9:Q05016. doi:10.1029/2008GC001987
Egli R (2013) VARIFORC: an optimized protocol for calculating non-regular first-order reversal curve (FORC) diagrams. Glob Planet Change 110:302–320. doi:10.1016/j.gloplacha.2013.08.003
Heslop D, Robertss AP (2012) Estimation of significance levels and confidence intervals for first-order reversal curve distributions. Geochem Geophys Geosys 13:Q12Z40. doi:10.1029/2012GC004115
McKnight REA, Moxon T, Buckley A, Taylor PA, Darling T, Carpenter MA (2008) Grain size dependence of elastic anomalies accompanying the α–β phase transition in polycrystalline quartz. J Phys: Condens Matter 20:75229. doi:10.1088/0953-8984/20/7/075229
Migliori A, Maynard JD (2005) Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev Sci Instrum 76:121301. doi:10.1063/1.2140494
McKnight REA, Carpenter MA, Darling TW, Buckley A, Taylor PA (2007) Acoustic dissipation associated with phase transitions in lawsonite, CaAl2Si2O7(OH)2·H2O. Am Mineral 92:1665–1672. doi:10.2138/am.2007.2568
Piticescu RM, Mitoseriu L, Viviani M, Poladian VM (2005) Preparation and characterisation of Pb(Zr0.52Ti0.48)0.975Nb0.025O3 ceramics. J Eur Ceram Soc 25:2491–2494. doi:10.1016/j.jeurceramsoc.2005.03.088
McKnight REA, Howard CJ, Carpenter MA (2009) Elastic anomalies associated with transformation sequences in perovskites: I. Strontium zirconate, SrZrO3. J Phys: Condens Matter 21:015901. doi:10.1088/0953-8984/21/1/015901
Schranz W, Sondergeld P, Kityk AV, Salje EKH (2009) Dynamic elastic response of KMn1-xCaxF3: elastic softening and domain freezing. Phys Rev B 80:094110. doi:10.1103/PhysRevB.80.094110
Carpenter MA, Salje EKH, Howard CJ (2012) Magnetoelastic coupling and multiferroic ferroelastic/magnetic phase transitions in the perovskite KMnF3. Phys Rev B 85:224430. doi:10.1103/PhysRevB.85.224430
Zhang Z, Koppensteiner J, Schranz W, Betts JB, Migliori A, Carpenter MA (2010) Microstructure dynamics in orthorhombic perovskites. Phys Rev B 82:014113. doi:10.1103/PhysRevB.82.014113
Axe JD, Shirane G (1970) Study of the α − β quartz phase transformation by inelastic neutron scattering. Phys Rev B 1:342–348. doi:10.1103/PhysRevB.1.342
Pytte E (1970) Soft-mode damping and ultrasonic attenuation at a structural phase transition. Phys Rev B 1:924–930. doi:10.1103/PhysRevB.1.924
Pytte E (1971) Acoustic anomalies as structural phase transitions. In: Samuelsen EJ, Aanderson E, Feder J (eds) NATO ASI, Norway. Scandinavian University Books, Oslo, pp 151–169
Höchli UT (1972) Elastic constants and soft optical modes in gadolinium molybdate. Phys Rev B 6:1814–1823. doi:10.1103/PhysRevB.6.1814
Carpenter MA, Salje EKH (1998) Elastic anomalies in minerals due to structural phase transitions. Eur J Mineral 10:693–812. doi:10.1127/ejm/10/4/0693
Carpenter MA, Buckley A, Taylor PA, Darling TW (2010) Elastic relaxations associated with the \({Pm{\bar{3}}m} - {\hbox{R}}{\bar{3}}{\hbox{c}}\) transition in LaAlO3: III. Superattenuation of acoustic resonances. J Phys: Condens Matter 22:35405. doi:10.1088/0953-8984/22/3/035405
Salje EKH, Zhang H (2009) Domain boundary pinning and elastic softening in KMnF3 and KMn1-xCaxF3. J Phys: Condens Matter 21:035901. doi:10.1088/0953-8984/21/3/035901
Carpenter MA (2007) Elastic anomalies accompanying phase transitions in (Ca, Sr)TiO3 perovskites: Part I. Landau theory and a calibration for SrTiO3. Am Mineral 92:309–327. doi:10.2138/am.2007.2295
Carpenter MA, Bryson JFJ, Catalan G, Zhang SJ, Donnelly NJ (2012) Elastic and anelastic relaxations in the relaxor ferroelectric Pb(Mg1/3Nb2/3)O3: II. Strain–order parameter coupling and dynamic softening mechanisms. J Phys: Condens Matter 24:45902. doi:10.1088/0953-8984/24/4/045902
Aktas O, Salje EKH, Crossley S, Lampronti GI, Whatmore RW, Mathur ND, Carpenter MA (2013) Ferroelectric precursor behavior in PbSc0.5Ta0.5O3 detected by field-induced resonant piezoelectric spectroscopy. Phys Rev B 88:174112. doi:10.1103/PhysRevB.88.174112
Salje EKH, Carpenter MA, Nataf GF, Picht G, Webber K, Weerasinghe J, Lisenkov S, Bellaiche L (2013) Elastic excitations in BaTiO3 single crystals and ceramics: mobile domain boundaries and polar nanoregions observed by resonant ultrasonic spectroscopy. Phys Rev B 87:14106. doi:10.1103/PhysRevB.87.014106
Carpenter MA, Sinogeikin SV, Bass JD (2010) Elastic relaxations associated with the \({Pm{\bar{3}}m} - {\hbox{R}}{\bar{3}}{\hbox{c}}\) transition in LaAlO3: II. Mechanisms of static and dynamical softening. J Phys: Condens Matter 22:35404. doi:10.1088/0953-8984/22/3/035404
Bokov AA, Ye Z-G (2006) Recent progress in relaxor ferroelectrics with perovskite structure. J Mater Sci 41:31–52. doi:10.1007/s10853-005-5915-7
Carpenter MA, Zhang Z (2011) Anelasticity maps for acoustic dissipation associated with phase transitions in minerals. Geophys J Int 186:279–295. doi:10.1111/j.1365-246X.2011.05028.x
Carpenter MA (2015) Static and dynamic strain coupling behaviour of ferroic and multiferroic perovskites from resonant ultrasound spectroscopy. J Phys: Condens Matter 27:263201. doi:10.1088/0953-8984/27/26/263201
Nataf GF, Li Q, Liu Y, Withers RL, Driver SL, Carpenter MA (2013) Ferroelastic aspects of relaxor ferroelectric behaviour in Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 perovskite. J Appl Phys 113:124102. doi:10.1063/1.4794027
Schiemer J, Carpenter MA, Evans DM, Gregg JM, Schilling A, Arredondo M, Alexe M, Sanchez D, Ortega N, Katiyar RS, Echizen M, Colliver E, Dutton S, Scott JF (2014) Studies of the room-temperature multiferroic Pb(Fe0.5Ta0.5)0.4(Zr0.53Ti0.47)0.6O3: resonant ultrasound spectroscopy, dielectric, and magnetic phenomena. Adv Funct Mater 24:2993–3002. doi:10.1002/adfm.201303492
Meng X, Baba-Kishi KZ, Chan HL, Choy CL, Luo HS (2004) Study of domain morphology in Pb(Fe1/2, Nb1/2)O3 and (0.94)Pb(Fe1/2Nb1/2)O3:(0.06)PbTiO3 by transmission electron microscopy. Ferroelectrics 303:69–73. doi:10.1080/00150190490456600
Shannon RD (1976) Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst A 32:751–767. doi:10.1107/S0567739476001551
Howard CJ, Zhang Z, Carpenter MA, Knight KS (2007) Suppression of strain coupling in perovskite La0.6Sr0.1TiO3 by cation disorder. Phys Rev B 76:054108. doi:10.1103/PhysRevB.76.054108
Noheda B, Gonzalo JA, Cross LE, Guo R, Park S-E, Cox DE, Shirane G (2000) Tetragonal-to-monoclinic phase transition in a ferroelectric perovskite: the structure of PbZr0.52Ti0.48O3. Phys Rev B 61:8687–8695. doi:10.1103/PhysRevB.61.8687
Pérez-Mato JM, Salje EKH (2001) Order-parameter saturation at low temperatures: displacive phase transitions with coupled Einstein oscillators. Philos Mag Lett 81:885–891. doi:10.1080/09500830110089961
Carpenter MA, Meyer HW, Sondergeld P, Marion S, Knight KS (2003) Spontaneous strain variations through the low temperature phase transitions of deuterated lawsonite. Am Mineral 88:534–546. doi:10.2138/am-2003-0407
Noheda B, Gonzalo JA, Caballero AC, Moure C, Cox DE, Shirane G (2000) New features of the morphotropic phase boundary in the Pb(Zr1−x Ti x )O3 system. Ferroelectrics 237:237–244. doi:10.1080/00150190008216254
Noheda B, Cox DE, Shirane G, Guo R, Jones B, Cross LE (2000) Stability of the monoclinic phase in the ferroelectric perovskite PbZr1−x TixO3. Phys Rev B 63:014103. doi:10.1103/PhysRevB.63.014103
Viehland DD, Salje EKH (2014) Domain boundary-dominated systems: adaptive structures and functional twin boundaries. Adv Phys 63:267–326. doi:10.1080/00018732.2014.974304
Souza Filho AG, Lima KCV, Ayala AP, Guedes I, Freire PTC, Mendes Filho J, Araújo EB, Eiras JA (2000) Monoclinic phase of PbZr0.52Ti0.48O3 ceramics: Raman and phenomenological thermodynamic studies. Phys Rev B 61:14283–14286. doi:10.1103/PhysRevB.61.14283
Carpenter MA, Bryson JFJ, Catalan G, Howard CJ (2012) Elastic and anelastic relaxations in the relaxor ferroelectric Pb(Mg1/3Nb2/3)O3: I. Strain analysis and a static order parameter. J Phys: Condens Matter 24:045901. doi:10.1088/0953-8984/24/4/045901
Thomas H, Müller KA (1968) Structural phase transitions in perovskite-type crystals. Phys Rev Lett 21:1256–1259. doi:10.1103/PhysRevLett.21.1256
Devonshire AF (1949) Theory of barium titanate. Philos Mag 40:1040–1063. doi:10.1080/14786444908561372
Acknowledgements
RUS facilities in Cambridge were established with funding from the Natural Environment Research Council (Grants NE/B505738/1, NE/F017081/1). The present work was supported by Grant No. EP/I036079/1 from the Engineering and Physical Sciences Research Council. We thank Dr. Sam Crossley for his assistance with dielectric analysis and the use of his software to run those measurements. JAS gratefully acknowledges the hospitality of the Max Planck Institute for Chemical Physics of Solids. The Nanaopaleomagnetism lab has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement 320750. SED and HS acknowledge support from the Winton Programme for the physics of sustainability. HS also acknowledges support from the Funai Foundation for Information Technology and the British Council Japan Association. Original data from this work can be found at http://eprints.esc.cam.ac.uk/3748/.
Author information
Authors and Affiliations
Corresponding author
Appendix: Formal Strain Analysis
Appendix: Formal Strain Analysis
The \( \Gamma_{4}^{ - } \) order parameter for the P4mm and Cm structures contains three components, with q 1 = q 2 = 0, q 3 ≠ 0 and q 1 = q 2 ≠ q 3 ≠ 0, respectively. As set out in Carpenter et al. [28], spontaneous strains, e, for the tetragonal structure depend on their variations according to
and for the monoclinic structure as
e a is the volume strain, \( e^{\prime}_{\text{t}} \) is the tetragonal shear strain, \( e^{\prime}_{\text{o}} \) the orthorhombic shear strain and \( e^{\prime}_{5} \) a monoclinic shear strain. Reference axes, X, Y and Z, for strains of the P4mm structure are parallel to [100], [010] and [001] of the cubic parent structure. Addition of the prime for the Cm structure signifies reference axes parallel to [110], [\( \bar{1}10 \)] and [001].
Variations of strains calculated using expressions in Carpenter et al. [28] and the lattice parameters in Fig. 3 of Noheda et al. [153] for Pb(Zr0.52Ti0.48)O3 are given in Appendix Fig. 10a. A baseline for the cell dimension, a o, of the reference cubic structure was taken as \(a_{{\text{o}}} {\mkern 1mu} = {\mkern 1mu} a_{1} {\mkern 1mu} + {\mkern 1mu} a_{2} {\mkern 1mu} \coth {\mkern 1mu} \left( {\Theta _{{{\text{so}}}} /T} \right) \) with the saturation temperature, \( \Theta_{\text{so}} \) set at 150 K. As has already been found for the cubic–tetragonal or cubic–rhombohedral transitions in PZT and PFN, the \( Pm\bar{3}m - P4mm \) transition is close to tricritical in character, i.e. \( e_{\text{a}}^{2} \, \propto \,e{^\prime}_{\text{t}}^{2} \, \propto \,q^{4} \, \propto \,\left( {T_{\text{c}} - T} \right), \) with T c = 651 K (Appendix Fig. 10b).
The variation of \( e^{\prime}_{5} \) for the P4mm–Cm transition can be well represented by
which is the standard solution to a Landau expansion with saturation temperature, \( \Theta_{\text{s}} \), for the order parameter [154, 155]. If \( e^{\prime}_{5} \) scales with the square of the driving order parameter for this transition, the data are also consistent with close to tricritical character; the fit shown in Appendix Fig. 10c has T c = 298 ± 1 K, Θs = 132 ± 5 K. Using components of only one order parameter, as set out for PFN [28], would lead to the expectation of only one instability such that the evolution of (ferroelectric) order parameter components for both the P4mm and Cm structures would extrapolate to zero at the same value of T c. However, the shear strains for Pb(Zr0.52Ti0.48)O3 clearly indicate two instabilities, separated by ~300 K (Appendix Fig. 10b). Data have been added to Fig. 10a, c to show that the tetragonal strain in PFN does not exceed ~0.003, that the magnitudes of displacements associated with q 1 and q 3 are likely to both be small and more nearly equal, in contrast with PZT, and that the two instability temperatures are closer together. The overall pattern of evolution is otherwise the same, however.
Observed strain variations of the monoclinic structure are at least qualitatively compatible with the predictions from linear/quadratic strain/order parameter coupling and a single order parameter, for which Eqs. 3–7 were derived. Firstly, the large tetragonal strain (\( e^{\prime}_{\text{t}} \) values up to 3 %) and small orthorhombic strain (\( e^{\prime}_{\text{o}} \) values up to 0.3 %) for Pb(Zr0.52Ti0.48)O3 imply that the structural changes associated with q 1 are small relative to those associated with q 3, i.e. the dominant ferroelectric displacement is that of the P4mm structure. Below the P4mm–Cm transition, \( e^{\prime}_{\text{t}} \) and \( e_{\text{a}} \) are at first barely deflected from the trend established in the P4mm stability field, consistent with Eqs. 4 and 5 if the contribution of q 1 is small. On the same basis, from Eqs. 6 and 7, it would be expected that \( e^{\prime}_{ 5} \) should be substantially larger than \( e^{\prime}_{\text{o}} \) and this is as observed (Fig. 10a). \( e^{\prime}_{\text{o}} \) is expected to scale with \( q_{1}^{2} \) and, to reasonable approximation, \( e_{\text{a}} \) appears to be determined primarily by \( q_{3}^{2} \). A plot of \( e^{\prime}_{\text{o}} \) against \( e_{\text{a}} \) therefore provides a representation of the trajectory across order parameter space with falling temperature (Fig. 10d). This appears to be simply the successive development of P4mm (00q 3) displacements below ~651 K and R3m (q 1 q 1 q 1) displacements below ~298 K.
Below ~200–250 K, the trend of \( e^{\prime}_{\text{t}} \) reverses, so as to decrease with falling temperature, which is most likely due mainly to the contribution from q 3 in the Cm and Cc structures. While \( e^{\prime}_{ 5} \) and \( e^{\prime}_{\text{o}} \) are not obviously affected, the volume strain, \( e_{\text{a}} \), has a small change in trend that would constitute a negative volume strain associated with the Cm–Cc transition expected in this temperature interval [44, 52, 53]. Based on lattice parameters of Clarke and Glazer [55], the analogous R3m–R3c transition in Pb(Zr0.9Ti0.1)O3 is also accompanied by a volume strain of~−0.001, without any change in the trend of shear strain arising from the \( Pm\bar{3}m - R3m \) transition. In (Pb0.94Sr0.06)(Zr0.55Ti0.45)O3 the Cm–Cc transition is clearly accompanied by a small, negative volume strain [63].
The focus here is on strain evolution because of its implications for the form of variations of the elastic constants. This treats the average structures without consideration of the possibility that the tetragonal and monoclinic or tetragonal and rhombohedral phases coexist over some temperature interval near the MPB of PZT (e.g. [105, 156, 157]). MPB transitions are also known to be complicated by the possible presence of nanotwinning, as has considered in the context of adaptive structures (e.g. [76, 158]).
The requirement for two critical temperatures follows the view of Souza Filho et al. [159] but is not considered further here. Cordero et al. [106] and Cordero et al. [109] suggested that the second instability could have bilinear coupling between the monoclinic shear strain, \( e^{\prime}_{ 5} \) and the driving order parameter, which is allowed by symmetry for a discrete P4mm–Cm transition with \( \Gamma_{5} \) of the parent P4mm space group as the active representation. If this were correct, \( e^{\prime}_{\text{o}} \) would be an improper ferroelastic strain occurring by linear/quadratic coupling with the driving order parameter while \( e^{\prime}_{ 5} \) would be proper and the expected relationship between them would be \( e^{\prime}_{\text{o}}\, \propto \,e{^\prime}_{5}^{2} \). This possibility appears to be ruled out by the linear relationship between \( e^{\prime}_{\text{o}} \) and \( e^{\prime}_{ 5} \) for both Pb(Zr0.52Ti0.48)O3 and PFN shown in Appendix Fig. 11.
Finally, it is well understood that the boundary between stability fields for R3m and P4mm structures with respect to a \( Pm\bar{3}m \) parent structure can be considered in terms of the changing values of the coefficients for fourth-order terms in the full Landau free energy expansion. The usual expansion can be written in the form (from [160]).
Setting the equilibrium condition, \( \partial G/\partial e\, = \,0 \), and substituting for strains gives
This is essentially the same as the general 246 potential considered by Vanderbilt and Cohen [75], except that the effects of saturation are included and the higher order terms are grouped slightly differently. The renormalised fourth-order coefficients are
In this form the condition of Thomas and Muller [161] is that \( b{^\prime}^{*} < \,\,0 \) gives the tetragonal structure as the stable form and \( b{^\prime}^{*} > \,\,0 \) gives the rhombohedral structure as the stable form. With sixth-order terms and following [140, 162], \( (b^{*} \, + \,b{^\prime}^{*} ) < \,\,0 \) and \( b{^\prime}^{*} > \,\,0 \) can give the sequence of stability with falling temperature to be cubic–tetragonal–orthorhombic–rhombohedral. The strain data confirm that in the vicinity of the MPB, at least, the system is close also to the tricritical limit, \( (b^{*} \, + \,b{^\prime}^{*} ) = \,\,0 \), as expected from the known proximity of the tricritical point [14, 15, 19, 73, 106].
According to Cordero et al. [106], the tetragonal–monoclinic transition appears to be reversible at Pb(Zr0.52Ti0.48)O3 but displays a hysteresis between heating and cooling at Pb(Zr0.535Ti0.465)O3 and Pb(Zr0.545Ti0.455)O3. This would place a tricritical point near Pb(Zr0.52Ti0.48)O3, as for the ferroelectric transition, and is consistent with tricritical character implied by the strain analysis. In this case, however, the transition would appear to be first order at Zr-rich compositions and continuous at Ti–rich compositions, which is the reverse of what is observed for the tricritical point of the ferroelectric transition at higher temperatures.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schiemer, J.A., Lascu, I., Harrison, R.J. et al. Elastic and anelastic relaxation behaviour of perovskite multiferroics I: PbZr0.53Ti0.47O3 (PZT)–PbFe0.5Nb0.5O3 (PFN). J Mater Sci 51, 10727–10760 (2016). https://doi.org/10.1007/s10853-016-0280-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-016-0280-2