Introduction

Graphene has attracted significant interest since it was first isolated in 2004 [1–3] due to its extraordinary physical properties [4, 5] which make it ideal for a wide range of applications including sensors, batteries, supercapacitors, hydrogen storage and composites [6–10]. In particular, graphene is a promising reinforcement for polymer matrices due to its mechanical, thermal, electrical and gas barrier properties [2, 4, 5]. For such bulk applications, the development of methods for the mass production and processing of homogeneously distributed graphene into solvents/polymers is a priority. At present, one route for producing bulk quantities of graphene is the chemical conversion of graphite to graphite oxide via either Hummers’ [11], Brodie’s [12] or Staudenmaier’s [13] methods. The resultant graphite oxide is a strongly oxygenated, highly hydrophilic layered material that can be easily exfoliated either in water [14] or organic solvents [15, 16] through stirring or mild sonication to yield stable dispersions predominantly consisting of monolayers. These dispersions are a convenient starting material for the processing of films [17] and paper-like materials [18]. The graphene oxide (GO) can then be converted to graphene through a chemical reduction using hydrazine [14, 19] or sodium borohydride [20] to restore the sp2 network and thus increases the conductivity. Rourke et al. [21] recently showed that GO can be washed with NaOH to remove the strongly bound oxidative debris to give “clean” graphene, considerably reducing the oxygen content and improving the conductivity of films made from the material by five orders of magnitude. GO can alternatively be reduced thermally [22] which also decreases the number of functional groups present on the surface of the flakes.

There is currently a small amount of research on the rheology of graphene or GO in the literature. The rheological properties of systems such as microwave-exfoliated graphite oxide–polycarbonate [23], polycarbonate composites reinforced with graphite and functionalized graphene sheets [24], or graphene-based polypropylene nanocomposites [25] have been investigated. The effect of the oxygen content on the surface of the GO on the rheological and electrical properties of poly(methyl methacrylate) (PMMA) composites has also been reported recently [26]. These papers have shown that the rheological properties of graphene systems can be controlled through matrix–filler interactions as discussed later in this paper.

Herein, the rheological properties of aqueous GO dispersions are studied as a model system in order to understand how graphene may affect the processing of more complex graphene–polymer systems. Aqueous dispersions were chosen since water is a Newtonian fluid, making the effect of the graphene obvious and because the dispersions are stable up to high loadings, albeit as a hydrogel at >8 vol%. Such dispersions were well described in the recent work of Tesfai et al. [27], who studied the dilute regime in which the GO dispersions were at a sufficiently low concentration that they did not interact. Hence, the dispersions were well fitted by the Einstein–Stokes equation. Recently, Naficy et al. [28] found unique viscoelastic properties for higher concentrated dispersions of GO, being classified as a new class of soft materials. Here, we study very high concentrations which are more relevant to bulk applications and behave as concentrated dispersions where the GO sheets interact with each other. The results obtained for the aqueous dispersion of GO can then be correlated with more complex graphene–polymer systems with different interactions between the graphene and matrix. Comparisons are then made to 1D nanotube systems which had been studied previously [29].

Experimental

Preparation of graphene oxide

Graphite oxide was prepared from natural graphite (Graphexel, 2369) using a modified Hummers’ method as described in Rourke et al. [21]. This graphite oxide was then exfoliated in water under mild sonication to give an aqueous dispersions of GO with a concentration of ~0.20 vol%. Aqueous dispersions with concentrations from 0.03 to 8 vol% were prepared by either dilution or concentration. It should be noted that similar rheological behaviour was found independently of whether the samples were prepared by re-dispersion (from the concentrated dispersion) or by concentration (from the diluted dispersion). The weight percentage concentrations of the dispersions were determined by weighing, drying and re-weighing the sample. The volume percentage concentrations were calculated using 2 mg/mL as the density of the GO.

Preparation of GO/PMMA composites

GO was dispersed into a PMMA matrix (Perspex, PMMA CP-75) at different loadings by melt mixing using a twin-screw extruder (Thermo Scientific HAAKE MiniLab micro compounder) following the procedure described elsewhere [30]. Extruded samples were processed by pressure moulding at 180 °C into 1 mm thick discs.

Rheological tests

A TA Discovery HR-3 rheometer with parallel plate geometry (1000 µm gap and 60 mm diameter) was used to analyse the dispersions. The sample was allowed to stand for 60 min between rheological tests conducted on the same sample. For the aqueous samples, the exposed surfaces of the sample were surrounded by low molecular weight silicone oil to prevent the evaporation of the water and measurements were taken at 25 °C. The GO–PMMA samples were measured using heated plates with a sample temperature of 230 °C. Dynamic strain sweeps at a constant frequency of 1 rad/s were used to find the linear viscoelastic region (LVR) in which the storage modulus (G′) and the loss modulus (G″) are independent of strain amplitude. Dynamic frequency sweeps were conducted at a constant strain of 0.1 % within the LVR to investigate the structure of the dispersions. Steady shear sweeps were used to investigate the flow properties of the material by recording the shear stress (σ) and viscosity (η) at increasing shear rates (\( \dot{\gamma } \)). The data obtained were scaled using the Peclet number (Pe), which gives the relative time scales for Brownian motion of, and the hydrodynamic forces on, the particles. The GO was approximated to circular hard discs, such that the Pe is defined by Eq. (1) [31]:

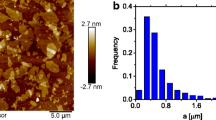
$$ Pe = \frac{\text{Timescale for Brownian motion}}{\text{Timescale for convection motion}} = \frac{{\dot{\gamma }}}{{D_{\rm r} }} = \dot{\gamma }\frac{{32\eta_{\rm s} b^{3} }}{{3kT}} $$
(1)

where D r is the rotary Brownian diffusion coefficient, k, Boltzmann’s constant, T, temperature, b the radius of the disc (atomic force microscopy performed on deposits of aqueous dispersions of GO on silicon oxide revealed an average diameter of the flakes of 0.6 µm (n > 50), as shown in the Supplementary Material) and η s is the viscosity of the solvent [31, 32].

The Bingham and Herschel–Bulkley models were fitted to the flow data. These models are widely used in the industrial field for pastes, slurries and suspensions [33]. The Bingham model has a zero strain rate at stresses beneath the yield stress and acts as a Newtonian fluid above the yield stress. The Herschel–Bulkley model is an Ostwald–de Waele (or power law) model with a yield stress added. The models were expressed as:

$$ {\text{Bingham model}}:\,\tau = \tau_{\rm y} + \eta_{\infty } \cdot \dot{\gamma } $$
(2)
$$ {\text{Herschel-Bulkley}}\, {\text{model:}}\,\tau = \tau_{\rm y} + K \cdot \dot{\gamma}^{n} $$
(3)

where τ is the shear stress, η ∞ is the infinite shear rate viscosity, n and K are constants, and τ y is the yield stress.

Recovery experiments

It was important to establish the timescale over which the recovery of the structure occurred. If the structure recovered instantly, the dispersions were shear-thinning, while if it occurred over a measurable time period, the dispersions were thixotropic. The recovery was investigated by conducting a series of dynamic strain sweeps on a sample and varying the rest time between the sweeps [34]. In another experiment, samples were sheared up to rates of 1000 s−1 followed by the application of a dynamic stress of 1 Pa, at a rate of 10 rad/s, to record the re-building of the structure. This stress was chosen since it was sufficiently high to measure the recovery but sufficiently low not to impede the recovery completely.

Results and discussion

Aqueous dispersions

Dynamic shear properties

The dispersions of GO sheets showed linear viscoelastic behaviour under dynamic shear up to a critical strain of between 0.1 and 10 % depending on the concentration, with G′ higher than G″ (Fig. 1). Above this critical strain, the structure of the dispersions broke down and the values for G′ and G″ became highly strain sensitive. A solid–liquid transition region was entered with the G′ and G″ crossover tending to occur at higher strains for higher GO concentrations, except for the highest concentration at which the sample had physically gelled and the crossover occurred at a lower strain.

Fig. 1
figure 1

Oscillatory shear measurements on the dispersions conducted at a constant frequency of 1 rad/s and increasing strain amplitude

Full size image

Dynamic frequency sweeps on the aqueous GO dispersions studied were conducted within the LVR at a constant strain amplitude of 0.1 % (Fig. 2). Within the LVR, the behaviour of samples under dynamic frequency sweeps could be categorised into three regimes depending on the concentration of GO:

Fig. 2
figure 2

Dynamic frequency sweep on the studied aqueous graphene oxide dispersions conducted within the LVR (at a constant strain amplitude of 0.1 %). Dependence of a G′, b G″ and c η* with the applied frequency. d Values of the moduli G′ and G″ within the LVR at a constant frequency of 0.1 rad/s as a function of the concentration of graphene oxide

Full size image
  1. 1.

    For very low concentrations of GO (0.03 vol%), the moduli increased with increasing frequency (Fig. 2a, b), while η* remained constant (Fig. 2c), which revealed a typical fluid behaviour.

  2. 2.

    At medium concentrations (0.03–1.2 vol%), an intermediate response between fluid behaviour and gel behaviour was found. At low frequencies, G′ and G″ were independent of frequency, with G′ larger than G″ (Fig. 2a, b), and η* (Fig. 2c) decreasing with a gradient of ~(−1) on the log–log plot (typical strong-gel spectrum). However, at higher frequencies G′ and G″ became frequency dependent, suggesting that the elastic structure had broken down.

  3. 3.

    Finally, at high concentrations of GO (>1.2 vol%) G′ and G″ were independent of the applied frequency (Fig. 2a, b), with η* decreasing with a gradient of ~(−1) on the log–log plot at all studied frequencies (Fig. 2c), which corresponds to a classic strong-gel spectrum. Similar types of behaviour have also been found previously for space-filling networks of particles with the elasticity resulting from the electrostatic interaction between the particles [31].

Figure 2d shows the dependence of the moduli values with concentration within the LVR. G′ and G″ were found to increase with the concentration of GO following a power law. The relationships of the data are given by the following expressions:

$$ G^{{\prime }} \, = 7 9 1\cdot c^{ 2. 7} {\text{with the quality of fit as }}R^{ 2} = \, 0. 9 9 { }(G^{{\prime }} {\text{in Pa}},c\,{\text{in vol}}\% ) $$
(4)
$$ G^{{\prime \prime }} = { 2}0 6\cdot c^{ 3} {\text{with the quality of fit as }}R^{ 2} = \, 0. 9 4 { }(G^{{\prime \prime }} {\text{ in Pa}},c\,{\text{in vol}}\% ) $$
(5)

The dispersions studied were found to behave like percolated networks. Similar power law relationships have also been found experimentally in other percolated networks with index values in the range of 2–3.5 being typical for random 3D networks [31].

Steady shear properties

As seen from Fig. 3, the steady shear behaviour observed for these GO dispersions could be characterised into two regions depending on the applied shear rate. A first region was observed at low shear rates, where the dispersions were found to significantly shear thin (i.e., the viscosity decreased very rapidly) while the stress remained approximately constant with increasing shear rates (e.g. a pseudo-yield stress) at 10−1–103 Pa depending on the concentration. This observed pseudo-yield stress suggested that in this first region the network reformed as it was sheared, as the Brownian motion of the particles was dominating over the hydrodynamic forces, with a Pe < 0.1. A second region was observed at higher shear rates where the shear stress was described by a power law relationship with at some loadings, n ~ 1. The transition between these two regions occurred at a certain Pe number (≥0.1) which depended on the concentration of GO and indicated the moment from which the hydrodynamic forces on the particles started to dominate over their Brownian motion. At high concentrations of GO (≥1.2 vol%), the first region extended until very high shear rates and the dispersions were found not to enter the second region for the shear rates applied in this work.

Fig. 3
figure 3

a Steady shear rate flow behaviour of the GO dispersions at different concentrations. b The fit of the models to the steady shear flow data. (The dashed lines show the fit of the Bingham model, and the solid lines show the fit of the Herschel–Bulkley model)

Full size image

The Bingham and Herschel–Bulkley models were applied to the experimental steady shear flow data as both of these incorporate a yield stress. The fits are plotted with the shear data in Fig. 3b and the parameters from the fitting are summarised in Table 1 together with the qualities of the fit. Although both models fit the data quite well at concentrations below 1.2 vol%, they failed to fit the experimental data at higher concentrations (≥1.2 vol%) where the samples had gelled and never entered the viscous flow region, i.e. the behaviour was within the pseudo-yield stress.

Table 1 Parameters obtained from the fitting of the experimental data using the Bingham and Herschel–Bulkley models
Full size table

Application of the Cox–Merz rule

The Cox–Merz rule is an empirical observation that states that the steady shear rate viscosity and the complex viscosity are closely super-imposable for numerically equivalent values of shear and frequency [35], allowing the prediction of the steady shear viscosity from dynamic data and vice versa. This rule only holds, however, for isotropic polymeric solutions and polymer melts, not for liquid crystals or flocculated systems. As shown in Fig. 4, the dispersions of GO studied did not obey the Cox–Merz rule, which means that the behaviour of the GO sheets cannot be elucidated directly from dynamic tests. In addition, it confirms that the GO flakes are interacting and behaving as a concentrated dispersion.

Fig. 4
figure 4

Comparison of the complex and steady shear viscosities of the 1.2 and 8 vol% dispersions. The two viscosities would be closely super-imposable if the Cox–Merz rule was obeyed

Full size image

Recovery of the structure

In order to evaluate the recovery and determine if there was any permanent damage to their structure dynamic strain sweeps from 0.1 to 100 % at a frequency of 1 rad/s were conducted on the samples, followed by identical dynamic strain sweeps after rest periods of 0, 30, 60 and 70 min after the initial sweep. The results obtained for the recovery of the 0.64 vol% dispersion (Fig. 5) revealed that it took between 30 and 60 min for both the G′ and G″ moduli to recover their initial values, which means that these dispersions were thixotropic. However, as it can be seen from Fig. 5, the original structure was not fully recovered as the G″ values for the final structure were higher than those observed initially, suggesting a more viscous structure after resting. We observed similar recovery behaviour for different concentrations of the dispersion.

Fig. 5
figure 5

Dynamic strain sweeps (G′ (a), G″ (b)) conducted on a 0.64 vol% dispersion of graphene oxide at 1 rad/s with different rest periods after the initial sweep

Full size image

The recovery behaviour of the structure after steady shear rate sweeps on the dispersions of GO was also evaluated. The steady shear rate sweeps were found to break down the structure of the samples more severely than the dynamic strain sweeps. Figure 6 shows the recovery of G′ and G″ for a 3.5 vol% dispersion after a strain sweep of 1–1000 s−1. The values of G′ and G″ immediately after shearing were much lower than those observed in the dispersion prior to the shear, suggesting that the structure was broken down considerably by the shear sweep. The recovery of the structure was found not to be linear, there was an initial slow increase in both moduli with time, followed by a significant increase in their values after ~70 min after shearing. The moduli became close to their initial values after ~6 h after shearing, although they were not completely recovered.

Fig. 6
figure 6

Recovery of a 3.5 vol% dispersion after it had been sheared in a steady shear rate sweep from 1 to 1000 s−1. The recovery was observed by applying a dynamic 1 Pa stress at a frequency of 10 rad/s to the sample

Full size image

Microstructure of the dispersions of GO

The dispersions of GO in the concentrated regime were found to act as reversible flocculated networks. The observed rheological behaviour can be thus discussed in terms of their microstructure (Fig. 7). At rest, the GO flakes formed a space-filling network with the electrostatic forces between them providing the observed elastic behaviour. At very low strain rates (Pe ≪ 1), the network was thought to creep with the majority of the network remaining intact and being reformed as quickly as it is broken (Fig. 7a).

Fig. 7
figure 7

Schematic representation of the breakdown of the structure into flocs, with decreasing sizes as the shear rates increase

Full size image

At strain rates outside the LVR, the structure of the network breaks down, causing the very rapid decrease of the viscosity and moduli observed in the system with increasing rates. The apparent yield stress observed in the experimental data in this region can be explained in terms of the flocculated networks proposed by Barnes [36]. He argued that under shear the existing flocculated network broke down into floccs (Fig. 7b) with decreasing sizes as the shear rates increased. The sizes of the floccs depend on the competition between the Brownian motion, which forms the floccs, and the shear forces, which break them apart. This competition is given by the Pe (Eq. 1) and leads to an equilibrium flocc size for each applied shear rate. With increasing shear rates, the floccs break into smaller ones, which require less stress to flow, keeping thus the stress virtually constant with increasing shear rates. At a sufficiently high shear rate, the floccs break up into the primary particles, i.e. fully dispersed GO flakes (Fig. 7c), and in this region the stress climbs with increasing rates. The Barnes explanation [36] appears here appropriate to discuss the behaviour of the aqueous dispersions of GO sheets. It should be noted that the formation and rheological strength of this flocculation and hence the system viscosity can be tuned through controlling the degree of interaction between the GO particles and matrix, as will be discussed in the next section.

For low concentrations of GO (0.03 vol%), we found the typical fluid behaviour, with the particles not interacting between them. The classic equation of Einstein-Stokes, typically used to describe the behaviour of diluted spheres [37, 38], predicts considerably lower viscosities for such low concentration of particles than those observed in the GO system studied here for such low concentrations. The classic Brenner prediction for dilute spheres [39] similarly underestimates the viscosities for the GO system in the dilute regime. This difference between the values of the viscosities and the predictions of these classic theories must be related to the very high aspect ratio of the GO sheets with respect to the spheres typically assumed by the models. Also in these theoretical models, the particles were assumed to be hard and rigid spheres, uncharged and without attractive forces.

Comparison of aqueous and polymer matrix systems

The storage modulus (G′) and loss modulus (G″) of the PMMA and the GO/PMMA composites at different loadings as a function of the frequency determined by dynamic tests are shown in Fig. 8a–c. Gradual increases of both G′ and G″ with increasing GO content were found, which suggested a reinforcement of the polymer melt. The presence of low-frequency plateau of G′ indicated the existence of a percolating particulate network. A graphene network was then observed to be gradually developed as the graphene content in the matrix is increased. The values of G″ were found to increase with increasing frequencies reaching a plateau at high frequencies.

Fig. 8
figure 8

Rheological properties of graphene oxide/PMMA composites at 230 °C with different concentrations of graphene oxide. Dynamic frequency behaviour at a constant strain amplitude of 1 %: Dependence of a G′, b G″ and c η* with the applied frequency. d Steady shear behaviour

Full size image

The viscosity values for PMMA and the composites determined from steady shear experiments (Fig. 8d) were found to increase with loading, and decrease with incrementing shear rates. An initial Newtonian plateau, in which the viscosity does not depend on the frequency, was observed for all the studied composites, and corresponds to the formation of the network of GO in the matrix. Then, a shear-thinning region was found, which corresponds to the breakage of the network of GO formed in the polymer matrix.

The addition of GO to the PMMA leads to the formation of an interconnected GO network that remains intact at rest and very low shear rates resulting in an overall increase of the viscosity of the composite with respect to the polymer. As the filler content is increased, higher values of viscosities were found, which is indicative of a more solid-like behaviour. The percolation threshold was found to be around a 1.2 vol% content of GO.

The viscosities and rheological percolation thresholds in graphene–polymer systems are known to be strongly dependent on the interactions between graphene and polymer, and the dispersion of the flakes in the matrix. The viscosity of the PMMA increased upon the addition of 0.6 vol%, after which it remained virtually constant with loading (Fig. 8). This initial increase in viscosity was relatively small compared to those observed in the GO/H2O system, due to the absence of hydrogen bonding between GO and PMMA. The very small increase in viscosity with loadings above 0.6 vol%. may be due to aggregation between the GO flakes. Optical microscopy did observe such aggregation (S2, Supplementary Material). However, in our previous studies, we have found that there is a mechanical percolation of 0.6 vol% above which the mechanical properties were independent of loading. The similarity between the rheological and mechanical behaviour strongly suggests that agglomerates of GO form at concentrations above 0.6 vol% through Van der Waals forces and π–π interactions. The interactions between GO and PMMA can be modified by changing either the surface chemistry of the flakes or the nature of the polymer, and hence, the viscosities and percolation thresholds of the system can be tuned. Zhang et al. [26] reported that the influence of the oxygen content at the surface of graphene on the rheological properties of PMMA composites resulted from the polarity matching between GO and matrix and the quality of the dispersion of the GO sheets. They proved that graphene with a higher C/O ratio provided a more homogeneous dispersion in PMMA showing a more effective impact on the viscoelasticity of PMMA, which was evidenced by a lower rheological percolation threshold and higher storage moduli and viscosities.

As well as modifying the surface chemistry of the graphene or GO, the rheological properties of these systems could be tuned alternatively by changing the matrix to one which will show different interactions with graphene. Recently, the influence of the addition of chemically reduced GO in PP on the rheological properties of composites has been reported [25]. They found a larger increase in viscosity and a transition from liquid- to solid-like behaviour occurring at lower concentrations (0.2–0.4 vol% of graphene) relative to those found here for the GO/PMMA system (~1.2 vol%). These results can be attributed to a higher degree of interaction between reduced GO and PP relative to GO and PMMA. Similarly, microwave-exfoliated graphite oxide/polycarbonate composites showed modest increases in viscosities with respect to the neat polycarbonate, with a rheological percolation threshold of 2.1 wt% [23].

These examples show the possibility of adapting the rheological model of the aqueous GO described herein, to more complex graphene–polymer systems with similar concentrations and controlling the degree of interaction between graphene and matrix. Hence, the viscosities and liquid–solid behaviour transitions of graphene–polymer systems can be controlled and tuned, which is of considerable importance for practical applications.

Comparison between aqueous dispersions of GO and oxidised carbon nanotubes

The aqueous GO dispersions are comparable to those reported by Kinloch et al. [29] for aqueous dispersions of oxidised carbon nanotubes as both systems were in water, which is a Newtonian fluid and rely on electrostatic dispersion from activate groups on the nanomaterials. The length of the nanotubes was also similar to the diameter of the GO flakes. However, the oxygen content and hence the degree of inter-particle interaction is higher for the GO (~33 at.% oxygen) than for the nanotubes (<20 at.% oxygen).

Both the GO and nanotube dispersions were reversible concentrated flocculated networks, with an LVR up to a critical strain, above which the values for G′, G″ and viscosity were highly strain sensitive. The values found for G′, G″ and viscosity within the LVR were found to be slightly higher for GO than for carbon nanotubes with similar concentrations (G′ and G″ ~105 Pa, η* ~106 Pa for aqueous dispersions of 8 vol% of GO and 9.2 vol% of CNTs). The LVR extended to higher strains for GO (up to ~10 % strain) than for nanotube (up to ~1 % strain) dispersions. Also solid–liquid transitions were found to occur at higher strains for dispersions of GO than for oxidised nanotubes at similar concentrations. The transition from the diluted polymer dispersion to the strong-gel mechanical spectrum (shown by dynamic frequency sweeps conducted within the LVR) occurred at lower concentrations for GO than for CNTs (1.2 vol% for GO, 4 vol% for CNTs). All these observations suggested that the structure of the GO networks formed in these aqueous dispersions required higher strains to break than those of oxidised carbon nanotubes at similar concentrations. The dispersions of GO were found to start behaving as a solid at lower concentrations than those of carbon nanotubes. The differences between these two systems revealed by the dynamic sweeps data must be related to the higher oxygen content present in the GO (~33 at.%) relative to the carbon nanotubes (<20 at.%), which provides a higher degree of inter-particle interactions for similar concentrations. Considering this difference in charge concentration, the results reveal a comparable rheological behaviour between aqueous dispersions of GO and oxidised carbon nanotubes under dynamic sweeps.

Under steady shear conditions, the observed apparent yield stress occurs at a much lower Pe for GO than for CNTs (Pe ~ 1–10 for CNTs, and Pe < 1 for GO), which suggests that the floccs of GO are smaller than those of CNTs for similar shear rates, i.e. the equilibrium flocc sizes for GO are smaller than those for nanotubes for identical shear rates. Hence, the final reduction of the floccs into the primary particles (i.e. fully dispersed graphene flakes or nanotubes) occurs at lower shear rates for the graphene than for CNTs. Both systems were found to be thixotropic, albeit the nanotube networks were found to recover slightly quicker than those of GO after similar resting times since shearing. These observations could be attributed to the different aspect ratio of both systems that allow the 1D tubes to retain an entangled network up to higher shear rates relative to a system composed of 2D flakes (as the lengths are comparable).

Conclusions

A rheological study of aqueous suspensions of GO at concentrations up to 8 vol% was performed. Three concentration regimes were observed in dynamic behaviour: (1) weak dispersion behaviour at concentration ≤0.03 vol%; (2) a transitional behaviour at concentrations in the range 0.03–1.2 vol%; and (3) concentrated behaviour with strong-gel behaviour at concentrations >1.2 vol%. Under steady shear, the dispersions rapidly shear thinned, with an apparent yield stress at very low Pe numbers (<1). At higher Pe numbers, the dispersions shear thinned following a power law model. Both the Bingham and the Herschel–Bulkley models described the experimental steady shear flow data well at low and medium concentrations (<1.2 vol%) before the samples had gelled, and both failed to fit the data at higher concentrations due to the experimental data not being at sufficiently high shear rates to access the power law region. The dispersions were found to be thixotropic and recovered their structure upon ~60 min rest.

The dispersions behave as a reversible flocculated system and it can be discussed in terms of their microstructure. These results found for this GO model system in the concentrated regime were then transferred to GO/polymer systems with similar concentrations, of interest for industrial applications. The rheological behaviour observed for the aqueous dispersions of GO sheets was compared to that previously reported for aqueous dispersions of oxidised carbon nanotubes.