Generalised Diffusion Probabilistic Scale-Spaces

Abstract

Diffusion probabilistic models excel at sampling new images from learned distributions. Originally motivated by drift-diffusion concepts from physics, they apply image perturbations such as noise and blur in a forward process that results in a tractable probability distribution. A corresponding learned reverse process generates images and can be conditioned on side information, which leads to a wide variety of practical applications. Most of the research focus currently lies on practice-oriented extensions. In contrast, the theoretical background remains largely unexplored, in particular the relations to drift-diffusion. In order to shed light on these connections to classical image filtering, we propose a generalised scale-space theory for diffusion probabilistic models. Moreover, we show conceptual and empirical connections to diffusion and osmosis filters.

1 Introduction

Diffusion probabilistic models [1] have recently risen to the state-of-the-art in image generation, surpassing generative adversarial networks [2] in popularity. In addition to significant research activity, the availability of pre-trained latent diffusion networks [3] has also brought diffusion models to widespread public attention [4]. Practical applications are numerous, including the generation of convincing, high-fidelity images from text prompts or partial image data.

Initial diffusion probabilistic models [1, 5,6,7,8,9,10] relied on a forward drift-diffusion process that gradually perturbs input images with noise and can be reversed by deep learning. Recently, it has been shown that the concrete mechanism that gradually destroys information in the forward process has a significant impact on the image generation by the reverse process. Alternative proposed image degradations include blur [11], combinations of noise and blur [12,13,14], or image masking [12].

So far, diffusion probabilistic research was mostly of practical nature. Some theoretical contributions established connections to other fields such as score-matching [7,8,9,10], variational autoencoders [6], or normalising flows [15]. Diffusion probabilistic models have been initially motivated [1] by drift-diffusion, a well-known process in physics. However, its connections to other physics-inspired methods remain mostly unexplored. Closely related concepts have a long tradition in model-based visual computing, such as osmosis filtering proposed by Weickert et al. [16]. In addition, there is a wide variety of diffusion-based scale-spaces [17,18,19,20]. Conceptually, these scale-spaces embed given images into a family of simplified versions. This resembles the gradual removal of image features in the forward process of diffusion probabilistic models.

Despite this multitude of connections, there is a distinct lack of systematic analysis of diffusion probabilistic models from a scale-space perspective. This is particularly surprising due to the impact of the forward process on the generative performance [13, 14]. It indicates that a deeper understanding of the information reduction could also lead to further practical improvements in the future.

1.1 Our Contribution

With our previous conference publication [21], we made first steps to bridge this gap between the scale-space and deep learning communities. To this end, we introduced first generalised scale-space concepts for diffusion probabilistic models. In this work, we further explore the theoretical background of this successful paradigm in deep learning. In contrast to traditional scale-spaces, we consider the evolution of probability distributions instead of images. Despite this departure from conventional families of images, we can show scale-space properties in the sense of Alvarez et al. [17]. These include architectural properties, invariances, and entropy-based measures of simplification.

In addition to our previous findings [21], our novel contributions include

• A generalisation of our scale-space theory for diffusion probabilistic models (DPMs) which includes both variance-preserving and variance-exploding approaches,

• Generalised scale-space properties for the reverse process of DPM,

• A scale-space theory for inverse heat dissipation [13] and blurring diffusion [14],

• And a significantly extended theoretical and empirical comparison of three diffusion probabilistic models to homogeneous diffusion [18] and osmosis filtering [16].

2 Related Work

Besides diffusion probabilistic models themselves, two additional research areas are relevant for our own work. Since we adopt a scale-space perspective, classical scale-space research acts as the foundation for our generalised theory. Furthermore, we discuss connections to osmosis filters, which have a tradition in model-based visual computing.

2.1 Diffusion Probabilistic Models

Large parts of our scale-space theory are based on the work of Sohl-Dickstein et al. [1], which pioneered diffusion probabilistic models (DPMs). The latent diffusion model by Rombach et al. [3] was integral for the gain of popularity of this approach. The public availability of code and trained models sparked many practical applications and caused a shift [4] away from generative adversarial networks [2]. Applications range from image generation [1, 3,4,5] over image inpainting [22, 23], super-resolution [24], segmentation [25], and deblurring [26] to the generation of different types of media, including video [24] and audio [27].

Following the same principles as early DPMs, most approaches rely on adding noise in the forward process. Since coarse-to-fine strategies were shown to improve DPMs [24, 28], they inspired Lee et al. [29] to use blurring with Gaussian convolution instead. Rissanen et al. [13] leveraged the equivalence of Gaussian blur to homogeneous diffusion [18] to establish inverse heat dissipation models. They only add small amounts of observation noise, while the model of Hoogeboom and Salimans [14] generalises this process and allows more substantial contributions of noise. Due to the close relations to both classical diffusion and osmosis filtering, we address both of these models in detail in Sect. 5.3. Image masking was recently also proposed as an alternative degradation in the forward process by Daras et al. [12].

We also rely on a more general version of the original DPM model that was proposed by Kingma et al. [6]. In addition, they introduced the notion of variational diffusion models and showed connections to variational autoencoders. Interestingly, early results of Vincent [30] established connections between denoising autoencoders and score-matching. Later publications showed more direct relations of score-based approaches to DPM [5]. Song and Ermon [7] related diffusion models to score-based Langevin dynamics with later follow-up results [8,9,10] that also include continuous time processes.

Theoretical contributions that are related to our own work are rare. Recently, Hagemann et al. [15] connected diffusion probabilistic models to a multitude of different concepts under the common framework of normalising flows. This includes relations to osmosis filtering, but not from a scale-space perspective. Franzese et al. [31] have investigated functional diffusion processes as a time-continuous generalisation of classical DPMs. They also allow both noise and blur as image degradations. In contrast, our models are time- and space-discrete.

2.2 Scale-Spaces

The second major field of research that forms the foundation of our contribution is scale-space theory. Scale-spaces have a long tradition in visual computing. Most of them rely on partial differential [17,18,19,20, 32] or pseudo-differential equations [33, 34], but they have also been considered for wavelets [35], sparse inpainting-based image representations [36], or hierarchical quantisation operators [37]. Such classical scale-spaces describe the evolution of an input image over multiple scales, which gradually simplifies the image. Since they obey a hierarchical structure and provide guarantees for simplification, they allow to analyse image features that are specific to individual scales. This makes them useful for tasks such as corner detection [38], modern invariant feature descriptors [39, 40], or motion estimation [41,42,43].

General principles for classical scale-spaces are vital for our contributions. They form the foundation for our generalised scale-space theory for DPM. We establish architectural, invariance, and information reduction properties in the sense of Alvarez et al. [17] for this new setting. In Sect. 5, we also mention where we drew inspiration from this contribution and other sources [18, 20] in more detail.

There are many different classes of scale-spaces, originating from the early work by Iijima [18], which was later popularised by Witkin [44]. They proposed a scale-space that can be interpreted as evolutions according to homogeneous diffusion. These initial Gaussian scale-spaces [17, 18, 44,45,46,47] have been generalised with pseudodifferential operators [33, 34, 48, 49] or nonlinear diffusion equations [19, 20]. Moreover, a comprehensive theory for shape analysis exists in the form of morphological scale-spaces [17, 50,51,52,53,54]. Wavelet shrinkage as a form of blurring [35] and sparse image representations [36, 37] have been considered from a scale-space perspective as well. Among this wide variety of different options, for us, the original Gaussian scale-space is still the most relevant. It is closely related to the blurring diffusion processes we consider in Sect. 5.3.

Our novel class of stochastic scale-spaces considers families of probability distributions instead of sequences of images. Conceptually similar approaches are rare. The Ph.D. thesis of Majer [55] proposes a stochastic concept, which also considers drift-diffusion. However, it is not related to deep learning and simplifies images in a different way. Instead of adding noise or blur, it shuffles image pixels. Similarly, Koenderink and Van Doorn [56] proposed “locally orderless images”, a local pixel shuffling as an alternative to blur. Other probabilistic scale-space concepts are only broadly related. There have been theoretical considerations of connections between diffusion filters and the statistics of natural images [57] and practical applications in stem cell differentiation [58].

In parallel to our conference publication [21], Zach et al. [59] have used homogeneous diffusion scale-spaces on probability densities. However, they learn image priors via denoising score matching with practical applications to image denoising. We on the other hand focus on the scale-space theory of generative diffusion probabilistic models.

2.3 Osmosis Filtering

In visual computing, osmosis filtering is a successful class of filters that has been introduced by Weickert et al. [16] and generalises diffusion filtering [20]. Even though it creates deterministic image evolutions, it is connected to statistical physics. Namely, it is closely related to the Fokker-Planck equation [60] and by extension also to Langevin formulations and the Beltrami flow [61]. This suggests that there could also be connections to diffusion probabilistic models.

Since such connections to drift-diffusion also apply to diffusion probabilistic models, we investigate connections between these approaches in Sect. 6.1. There, we also discuss the continuous theory for osmosis filters as it was originally proposed by Weickert et al. [16] and later extended by Schmidt [62]. Vogel et al. [63] introduced both the corresponding discrete theory and a fast implicit solver which we use for our experiments.

Osmosis filters are well suited to integrate conflicting information from multiple images, which makes them an excellent tool for image editing [16, 63, 64]. Additionally, they have been successfully used for shadow removal [16, 64, 65], the fusion of spectral images [66, 67], and image blending [68]. There are also applications for osmosis that do not deal with images. Notably, Hagenburg et al. [69] used osmosis to enhance numerical methods and considered a Markov chain formulation. While we deal with Markov processes in this paper, our interpretation of osmosis and the context in which we use it is significantly different.

There are also conceptually similar methods in visual computing that are also connected to drift–diffusion and predate osmosis. Namely, Hagenburg et al. [70] proposed a lattice Boltzmann model for dithering. Other broadly related filters are the directed diffusion models of Illner and Neunzert [71] and the covariant derivative approach of Georgiev [72].

3 Organisation of the Paper

We introduce the basic ideas of diffusion probabilistic models in Sect. 4, including Markov formulations for the forward and reverse processes. Based on these foundations, we propose generalised scale-space properties for three classes of probabilistic forward diffusion processes in Sect. 5 and briefly address reverse processes as well. As a link to classical scale-spaces and deterministic image filters, we investigate relations of diffusion probabilistic models to homogeneous diffusion and osmosis filtering in Sect. 6. We conclude with a discussion and an outlook in Sect. 7.

4 Diffusion Probabilistic Models

Diffusion probabilistic models [1] are generative approaches which have the goal to create new samples from a desired distribution. This distribution is unknown except for a set of given representatives. For image processing purposes, this training data typically consists of a set of images $\varvec{f}_1,...,\varvec{f}_{n_t} \in {\mathbb {R}}^{n_x n_y n_c}$ with $n_c$ colour channels of size $n_x \times n_y$ and $n=n_x n_y n_c$ pixels. From a stochastic point of view, these images are realisations of a random variable $\varvec{F}$ with an unknown probability density function $p(\varvec{F})$. DPMs aim to sample from this target distribution.

Fig. 1

Forward DPM Trajectory. Starting from each sample of the initial distribution $p(\varvec{u}_0)$, infinitely many trajectories exist. In each step of the trajectory, noise is added according to the transition probability $p(\varvec{u}_i | \varvec{u}_{i-1})$

4.1 The Forward Process

In a first step, the so-called forward process, diffusion probabilistic models map from the target distribution to a simpler distribution. While there are many alternatives, the standard normal distribution ${\mathcal {N}}(\varvec{0}, \varvec{I})$ is a typical choice. Here, $\varvec{I} \in {\mathbb {R}}^{n \times n}$ denotes the unit matrix. Thus, the forward process takes training images as an input and maps them to samples of multivariate Gaussian noise. These noise samples act as seeds for the reverse process. Like other generative models such as generative adversarial networks [2], it maps from samples of this simple distribution back to the approximate target distribution. These diffusion probabilistic models (DPMs) create image structures from pure noise.

In Sect. 5.3, we also present alternatives to purely noise-based forward processes. Typically, the forward process is straightforward both conceptually and in its implementation. For practical tasks, a major challenge is the estimation of the corresponding reverse process, which is implemented with deep learning. Our focus lies mostly on a theoretical analysis of the forward process from a scale-space perspective. We also discuss the reverse process in Sect. 5.2, but due to its approximate nature, theoretical results are less comprehensive. The design of the forward process also has significant impact on the performance of the generative model [13, 14]. Thus, it also constitutes a more attractive direction for a scale-space focused investigation: Understanding the nature of existing forward processes might allow to carry over useful properties from existing classical scale-spaces.

Therefore, in Sect. 5, we show that a wide variety of existing diffusion probabilistic models fulfil generalised scale-space properties. This new class of scale-spaces differs significantly from classical approaches, since it does not consider the evolution of images, but of probability distributions instead. First, we need to establish a mathematical definition of the probabilistic forward process on a time-dependent random variable $\varvec{U}(t)$.

At time $t=0$, this random variable has the initial distribution $p(\varvec{F})$. For subsequent times $t_1< t_2<... < t_m$ a trajectory is defined as a sequence of temporal realisations $\varvec{u}_1,..., \varvec{u}_m$ of $\varvec{U}(t)$. It represents one possible evolution according to random additions of noise in each time step and is visualised in Fig. 1. Importantly, each image $\varvec{u}_i$ in a trajectory only depends on $\varvec{u}_{i-1}$. This implies that the corresponding conditional transition probabilities fulfil the Markov property

$$\begin{aligned} p(\varvec{u}_i | \varvec{u}_{i-1}, ..., \varvec{u}_0) \;=\; p(\varvec{u}_i | \varvec{u}_{i-1}) \, . \end{aligned}$$

(1)

Here, we consider the probability of observing $\varvec{u}_i$ as a realisation of $\varvec{U}(t)$ at time $t_i$ given $\varvec{U}(t_{i-1})=\varvec{u}_{i-1}$. Thus, the stochastic forward evolution is a Markov process [73] and we can write the probability density of the trajectory in terms of the transition probabilities from (1) and the initial distribution $p(\varvec{u}_0)=p(\varvec{F})$:

$$\begin{aligned} p(\varvec{u}_0, ..., \varvec{u}_m) \;=\; p(\varvec{u}_0) \prod _{i=1}^m p(\varvec{u}_i | \varvec{u}_{i-1}) \, . \end{aligned}$$

(2)

This property is also integral to establishing central architectural properties of our generalised scale-space in Sect. 5. In contrast to our earlier conference publication [21], we consider a more general transition probability than the original model of Sohl-Dickstein et al. [1]. Relying on the model of Kingma et al. [6], we use Gaussian distributions of the type

$$\begin{aligned} p(\varvec{u}_i | \varvec{u}_{i-1}) \;=\; {\mathcal {N}}\left( \alpha _i \, \varvec{u}_{i-1}, \, \beta _i^2 \varvec{I} \right) \, . \end{aligned}$$

(3)

Since $\varvec{I} \in {\mathbb {R}}^{n \times n}$ denotes the unit matrix, the covariance matrix of this multivariate Gaussian is diagonal. Thus, for every pixel j, we consider independent, identically distributed Gaussian noise with mean $\alpha _i u_{i-1,j}$ and standard deviation $\beta _i$. Overall, the forward process has the free parameters $\alpha _i > 0$ and $\beta _i \in (0,1)$. In practice, these parameters can be learned or chosen by a user. Often $\alpha _i$ is also defined as a function of $\beta _i$, which we discuss in more detail in Sect. 5.

4.2 The Reverse Process

Sohl-Dickstein et al. [1] motivate the reverse process by a partial differential equation (PDE) that is associated to the forward process. In particular, they rely on the results of Feller [74]. These require the existence of the stochastic moments

$$\begin{aligned} m_k(\varvec{u}_t, t) \;=\; \lim _{h \rightarrow 0} \frac{1}{h} \int p(\varvec{u}_{t+h} , \varvec{u}_t) (\varvec{u}_{t+h} - \varvec{u}_t)^k \, {\textrm{d}} \varvec{u}_{t+h} \end{aligned}$$

(4)

with $k\in \{1,2\}$. Under this assumption, the probability density of the Markov process from Eq. (2) is a solution of the partial differential equation

$$\begin{aligned} \frac{\partial }{\partial t} p= & {} \frac{1}{2} \frac{\partial ^2}{\partial \varvec{u}_t \partial \varvec{u}_t} \left( m_2(\varvec{u}_t, t) p(\varvec{u}_\tau , \varvec{u}_t) \right) \nonumber \\+ & {} \frac{\partial }{\partial \varvec{u}_t} \left( m_1(\varvec{u}_t, t) p(\varvec{u}_\tau , \varvec{u}_t) \right) \, . \end{aligned}$$

(5)

Here, $p(\varvec{u}_\tau , \varvec{u}_t)$ denotes the probability density for a transition from $\varvec{u}_\tau$ to $\varvec{u}_t$ with $\tau < t$. In Sect. 6.1, we use the fact that Eq. (5) is a drift-diffusion equation to discuss connections to osmosis filtering.

For practical purposes, it is important that Feller has proven that a solution of Eq. (5) also solves the backward equation

$$\begin{aligned} \frac{\partial }{\partial \tau } p \;=\; \frac{1}{2} m_2(\varvec{u}_\tau , \tau ) \frac{\partial ^2}{\partial \varvec{u}_\tau \partial \varvec{u}_\tau } p + m_1(\varvec{u}_\tau , \tau ) \frac{\partial }{\partial \varvec{u}_\tau } p \, . \end{aligned}$$

(6)

Here, the backward perspective is obtained due to the exchange of roles of the earlier time $\tau$ with the later time t. Sohl-Dickstein et al. [1] exploit the close similarity of the backward equation to the forward equation. It implies that the reverse process from the normal distribution to the target distribution also has Gaussian transition probabilities. However, the mean and standard deviation are unknown and are estimated with a neural network instead. In particular, the training minimises the cross entropy to the target distribution $p(\varvec{F})$. We discuss the reverse process in more detail in Sect. 5.2.

The capabilities of diffusion probabilistic models go beyond merely using the reverse process to sample from the target distribution. Additionally, it is possible to condition this distribution with side information such as partial image information or textual descriptions of the image content. This is useful for restoring missing image parts with inpainting [1, 3] or for text-to-image models [3]. However, our main focus are theoretical properties of multiple different forward processes. Since the estimation of the parameters for the reverse process is not relevant for our contributions, we refer to [3, 5, 6, 9] for more details.

5 Generalised Diffusion Probabilistic Scale-Spaces

In our previous conference publication [21], we introduced scale-space properties for the original forward diffusion probabilistic model (DPM) of Sohl-Dickstein et al. [1]. We generalise these results in Sect. 5.1 to a wider variety of noise schedules. Moreover, we introduce a generalised scale-space theory for the corresponding backward direction in Sect. 5.2. Finally, we address the recent inverse heat dissipation [13] and blurring diffusion models [14] in Sect. 5.3.

Before we discuss scale-space properties, we need to establish some preliminaries that allow us to rewrite transition probabilities in a useful way. The transition probabilities from Eq. (3) allow us to express the random variable at time $t_i$ in terms of the random variable at time $t_{i-1}$ according to

$$\begin{aligned} \varvec{U}_i \; = \; \alpha _i \, \varvec{U}_{i-1} + \beta _i \, \varvec{G} \, . \end{aligned}$$

(7)

Here, $\varvec{G}$ denotes Gaussian noise from the standard normal distribution ${\mathcal {N}}(\varvec{0}, \varvec{I})$. This generalises the model of Sohl-Dickstein et al. [1] who use $\alpha _i = \sqrt{1-\beta _i^2}$. Kingma et al. [6] also investigate variance-exploding diffusion [7] with $\alpha _i^2 = 1$. We discuss both types of models in Sect. 5.1.

Proposition 1

(Transition Probability from the Initial Distribution) We can directly transition from $\varvec{U}_0$ to $\varvec{U}_i$ by

$$\begin{aligned} \varvec{U}_i \; = \; \varvec{U}_0 \prod _{\ell = 1}^{i} \alpha _\ell + \left( \sum _{k=1}^{i-1} \beta _k \prod _{\ell = k+1}^{i} \alpha _\ell + \beta _i \right) \varvec{G} \end{aligned}$$

(8)

Fig. 2

Semigroup Property for Forward DPM. Due to the Markov property, each intermediate scale i can be reached either from the training distribution $p(\varvec{u}_0)$ in i steps, or from $p(\varvec{u}_{i-k})$ in k steps. Note that this property does not apply to individual images as in classical scale-spaces. Instead, it refers to probability distributions which are visualised by samples from four different trajectories

Proof

For $i=1$, the statement is fulfilled according to

$$\begin{aligned} \varvec{U}_{1} \;=\; \alpha _{1} \, \varvec{U}_{0} + \beta _1 \, \varvec{G} \, . \end{aligned}$$

(9)

We prove the statement by induction. Applying the hypothesis for the step from i to $i+1$, we obtain

$$\begin{aligned} \varvec{U}_{i+1}&\;=\; \alpha _{i+1} \, \varvec{U}_{i} + \beta _{i+1} \, \varvec{G} \end{aligned}$$

(10)

$$\begin{aligned}&\;=\; \alpha _{i+1} \Bigg ( \varvec{U}_0 \prod _{\ell = 1}^{i} \alpha _\ell + \Bigg (\sum _{k=1}^{i-1} \beta _k \prod _{\ell = k+1}^{i} \alpha _\ell + \beta _i \Bigg ) \varvec{G} \Bigg )+ \beta _{i+1} \varvec{G} \end{aligned}$$

(11)

$$\begin{aligned}&\;=\; \varvec{U}_0 \prod _{\ell = 1}^{i+1} \alpha _\ell + \left( \sum _{k=1}^{i} \beta _k \prod _{\ell = k+1}^{i+1} \alpha _\ell + \beta _{i+1} \right) \varvec{G} \, . \end{aligned}$$

(12)

$\square$

Thereby, we have established the transition probability from time 0 to time $t_i$ as

$$\begin{aligned} p(\varvec{u}_i | \varvec{u}_0) = {\mathcal {N}}(\lambda _i \varvec{u}_0, \gamma _i^2 \varvec{I}) \end{aligned}$$

(13)

where the mean $\lambda _i$ and standard deviation $\gamma _i$ of this multivariate Gaussian distribution are

$$\begin{aligned} \lambda _i := \prod _{\ell = 1}^{i} \alpha _\ell \, , \qquad \gamma _i := \sum _{k=1}^{i-1} \beta _k \prod _{\ell = k+1}^{i} \alpha _\ell + \beta _i \, . \end{aligned}$$

(14)

An interesting special case of the proposition above arises for the parameter choice $\alpha _i = \sqrt{1-\beta _i^2}$ of the variance-preserving case [1]. Ho et al. [5] have shown that under this condition, the transition probability becomes

$$\begin{aligned} p(\varvec{u}_i | \varvec{u}_0) \;=\; {\mathcal {N}} \left( \sqrt{\prod _{j=1}^i (1 - \beta _j^2)} \, \varvec{u}_0, \, \varvec{I} - \prod _{j=1}^i (1-\beta _j^2) \varvec{I} \right) \, . \end{aligned}$$

(15)

These insights are helpful for establishing a generalised scale-space theory for diffusion probabilistic models.

5.1 Generalised-Scale-Space Properties for Forward DPM

In the following, we propose central architectural properties for a generalised DPM scale-space and also discuss invariances. To this end, we consider the sequence of the marginal distributions of the random variable $\varvec{U}(t)$. These can be obtained by integrating over all possible paths from the starting distribution to scale i according to

$$\begin{aligned} p(\varvec{u}_i) \;=\; \int p(\varvec{u}_0, ..., \varvec{u}_i) \, \, {\textrm{d}} \varvec{u}_0 \cdots \, {\textrm{d}} \varvec{u}_{i-1} \, . \end{aligned}$$

(16)

Thus at each scale i, we consider the marginal distribution of $\varvec{U}(t_i)$. Individual images are samples from the distributions at a given scale.

5.1.1 Property 1: Initial State

By definition, the initial distribution for the Markov process is the distribution $p(\varvec{F})$ of the training database. Thus, it also defines the initial state $p(\varvec{u}_0)$ of the scale-space.

5.1.2 Property 2: Semigroup Property

One central architectural property of scale-spaces is the ability to recursively construct a coarse scale from finer scales, i.e. the path from the initial state can be split into intermediate scales. This concept has been already established by Iijima [18] in the pioneering works on Gaussian scale-spaces. Intuitively, diffusion probabilistic models fulfil this property since they are Markov processes. The property is visualised in Fig. 2.

Proposition 2

(Semigroup Property) The distribution $p(\varvec{u}_i)$ at scale i can be reached equivalently in i steps from $p(\varvec{u}_0)$ or in $\ell$ steps from $p(\varvec{u}_{i-\ell })$.

Proof

The probability density of the forward trajectory is defined in a recursive way in Eq. (2). Thus, we have to show that this property also carries over to the marginal distributions of the scale-space. We can reach $p(\varvec{u}_{i})$ either directly from $\varvec{u}_0$ or from an intermediate scale $\ell$ by using the definition of the joint probability density of the Markov process:

$$\begin{aligned} p(\varvec{u}_i)&\;=\; \int p(\varvec{u}_0) \prod _{j=1}^{i} p(\varvec{u}_j |\varvec{u}_{j-1}) \, \, {\textrm{d}} \varvec{u}_0 \cdots \, {\textrm{d}} \varvec{u}_{i-1} \, \end{aligned}$$

(17)

$$\begin{aligned}&\;=\; \int p(\varvec{u}_{i-\ell }) \prod _{j=i-\ell +1}^{i} p(\varvec{u}_j |\varvec{u}_{j-1}) \, \, {\textrm{d}} \varvec{u}_{i-\ell } \!\cdots \! \, {\textrm{d}} \varvec{u}_{i-1} \, . \end{aligned}$$

(18)

$\square$

5.1.3 Property 3: Lyapunov Sequences

In classical scale-spaces (e.g. with diffusion), Lyapunov sequences quantify the change in the evolving image with increasing scale parameter. They constitute a measure of image simplification [20] in terms of monotonic functions. In practice, they often represent the information content of an image at a given scale. Here, we define a Lyapunov sequence on the evolving probability density instead.

To this end, we consider the conditional entropy of the random variable $\varvec{U}_i$ at time $t_i$ given the random variable $\varvec{U}_0$. It constitutes a measure for the gradual removal of the image information from the initial distribution $p(\varvec{u}_0)$.

Proposition 3

(Increasing Conditional Entropy) The conditional entropy

$$\begin{aligned} H_p(\varvec{U}_i | \varvec{U}_0)&\;=\; - \iint p(\varvec{u}_i, \varvec{u}_0) \ln p(\varvec{u}_i | \varvec{u}_0) \, \, {\textrm{d}} \varvec{u}_0 \, {\textrm{d}} \varvec{u}_i \, . \end{aligned}$$

(19)

increases with i under the assumption $\beta _j \in (0,1)$ for all j with $\beta _{j+1} \ge (1-\alpha _{j+1}) \gamma _j$ with $\gamma _j$ as defined in Eq. (14).

Proof

We can reduce the problem of showing that the conditional entropy is monotonically increasing to a statement on the differential entropy of $p(\varvec{u}_i | \varvec{u}_0)$ since

$$\begin{aligned} H_p(\varvec{U}_i | \varvec{U}_0)&= \int p(\varvec{u}_0) {\Big (}\underbrace{- \int p(\varvec{u}_i | \varvec{u}_0) \ln p(\varvec{u}_i | \varvec{u}_0) \, {\textrm{d}} \varvec{u}_i}_{=: H_p(\varvec{W}_i)} {\Big )} \, {\textrm{d}} \varvec{u}_0 \ge H_p(\varvec{U}_{i-1} | \varvec{U}_0) \end{aligned}$$

(20)

$$\begin{aligned}&\Leftrightarrow H_p(\varvec{W}_i) \ge H_p(\varvec{W}_{i-1}) \, . \end{aligned}$$

(21)

According to Eq. (13), $\varvec{W}_i$ is from ${\mathcal {N}}(\lambda _i \varvec{u}_0, \gamma _i^2 \varvec{I})$. Therefore, the entropy of $\varvec{W}_i$ only depends on the covariance matrix $\gamma _i \varvec{I}$ and yields

$$\begin{aligned} H_p(\varvec{W}_i) \;=\; \frac{1}{2} \ln \Big (\big (2\pi \, {\textrm{e}} \, \gamma _i^2\big )^n\Big ) \, . \end{aligned}$$

(22)

Thus, the entropy is increasing if $\gamma _{i+1} \ge \gamma _i$. Furthermore, due to Eq. (14) we have

$$\begin{aligned} \gamma _{i+1}&= \sum _{k=1}^{i} \beta _k \prod _{\ell = k+1}^{i+1} \hspace{-2mm} \alpha _\ell + \beta _{i+1} = \alpha _{i+1} \left( \sum _{k=1}^{i-1} \beta _k \prod _{\ell = k+1}^{i} \hspace{-2mm} \alpha _\ell + \beta _i\right) \nonumber \\&\quad + \beta _{i+1} = \alpha _{i+1} \gamma _i + \beta _{i+1} \, . \end{aligned}$$

(23)

Since $\beta _i > 0$ and $\gamma _i > 0$, we require

$$\begin{aligned} \alpha _{i+1} \gamma _i + \beta _{i+1} \ge \gamma _i \quad \Leftrightarrow \quad \beta _{i+1} \ge (1-\alpha _{i+1}) \gamma _i \, . \end{aligned}$$

(24)

Again, we can also consider $\alpha _i = \sqrt{1-\sigma _i}$, $\beta _i = \sqrt{\sigma _i}$ as in [1]. This gives us more concrete expressions for $\gamma _i$ according to Eq. (15). With this we obtain

$$\begin{aligned} \gamma _{i+1} = \sqrt{1 - \prod _{j=1}^{i+1} (1-\beta _j^2)} = \sqrt{1 - (1-\beta _{i+1}^2) \prod _{j=1}^{i} (1-\beta _j^2)} > \gamma _i \, . \end{aligned}$$

(25)

Since $\beta _{i+1} \in (0,1)$, this holds without further conditions with the noise schedule of Sohl-Dickstein et al. [1]. $\square$

5.1.4 Property 4: Permutation Invariance

The 1-D drift-diffusion process acts independently on each image pixel. Therefore, the spatial configuration of the pixels does not matter for the process. In the following we provide formal arguments for a permutation invariance of all distributions created by the trajectories of the drift-diffusion.

Let $P(\varvec{f})$ denote a permutation function that arbitrarily shuffles the position of the pixels in the image $\varvec{f}$ from the initial database. In particular, such permutations also include cyclic translations as well as rotations by $90^\circ$ increments.

Proposition 4

(Permutation Invariant Trajectories) Let $\varvec{u}_0$ denote an image from the initial distribution and $\varvec{v}_0:= P(\varvec{u}_0)$ its permutation. Then, any trajectory $\varvec{v}_0,... \varvec{v}_m$ obtained from the process in Eq. (7) is given by $\varvec{v}_i = P(\varvec{u}_i)$ for a trajectory $\varvec{u}_0,..., \varvec{u}_m$ starting with the original image $\varvec{u}_0$.

Proof

Consider the transition of $\varvec{v}_{i-1}$ to $\varvec{v}_i$ via a realisation $\varvec{g}_i$ of the random variable $\varvec{G}$ in Eq. (7). Then $\tilde{\varvec{g}}_i:= P^{-1}(\varvec{g}_i)$ is also from the distribution ${\mathcal {N}}(\varvec{0}, \varvec{I})$ and we can obtain $\varvec{u}_i$ from $\varvec{u}_{i-1}$ by using this permuted transition noise.

Since $\varvec{v}_0 = P(\varvec{u}_0)$ holds by definition, we can inductively show the claim by considering

$$\begin{aligned} \varvec{v}_i = \alpha _i \varvec{v}_{i-1} + \beta _i \varvec{g}_i = \alpha _i P(\varvec{u}_{i-1}) + \beta _i P(\tilde{\varvec{g}}_i) \;=\; P(\varvec{u}_i) \,.\nonumber \\ \end{aligned}$$

(26)

$\square$

Any permutation P is a bijection. Thus every trajectory from a permuted image corresponds exactly to one trajectory starting from the original image. This directly implies permutation invariance of the corresponding distributions.

Corollary 5

(Permutation Invariant Distributions) Let $\varvec{u}_0$ denote an image from the initial distribution and $\varvec{v}_0:= P(\varvec{u}_0)$ its permutation. Then, for any image $\varvec{v}$ from $p(\varvec{v}_i)$ there exists exactly one image $\varvec{u}$ from $p(\varvec{u}_i)$ such that $\varvec{v} = P(\varvec{u})$.

5.1.5 Property 5: Steady State

The steady-state distribution for $i \rightarrow \infty$ is a multivariate Gaussian distribution ${\mathcal {N}}(\varvec{0}, \beta ^2 \varvec{I})$ with mean $\varvec{0}$ and a covariance matrix $\beta ^2 \varvec{I}$ with $\beta < 2$. Convergence to a noise distribution is a cornerstone of diffusion probabilistic models and thus well known. For the sake of completeness, we provide formal arguments for this property. Moreover, we verify that for the noise schedule of Sohl-Dickstein et al. [1], we obtain $\beta =1$. Thus, we verify that their steady state is the normal distribution.

Proposition 6

(Convergences to a Normal Distribution) Let $\alpha _i$ and $\beta _i$ be bounded from above by $a, b \in (0,1)$, i.e. $\alpha _i \in (0,a]$ and $\beta _i \in (0,b]$. Moreover, let the assumptions of Proposition 3 be fulfilled. Then, for $i \rightarrow \infty$, the forward process from Eq. (2) converges to a normal distribution ${\mathcal {N}}(\varvec{0}, {\gamma }^2 \varvec{I})$ with ${\gamma } \le \frac{b}{1-a}$.

Proof

According to Eqs. (8) and (14), we have

$$\begin{aligned} \varvec{U}_{i} \;=\; \lambda _i \varvec{U}_0 + \gamma _i \varvec{G} \end{aligned}$$

(27)

with $\varvec{G}$ from ${\mathcal {N}}(\varvec{0}, \varvec{I})$. For $i \rightarrow \infty$, we can immediately conclude $\lambda _i \rightarrow 0$ for the mean of the steady-state distribution since it is the product of i factors $\alpha _\ell < 1$.

Under the assumptions of Proposition 3, we have already shown that $\gamma _i$ is increasing. Now let us consider the boundedness of $\gamma _i$, starting with definition Eq. (14) and using the assumptions $0<\alpha _i \le a$ and $0<\beta _i \le b$:

$$\begin{aligned} \ \gamma _i&= \sum _{k=1}^{i-1} \beta _k \prod _{\ell = k+1}^{i} \alpha _\ell + \beta _i \; \le \; \sum _{k=1}^{i-1} b \prod _{\ell = k+1}^{i} a + b \end{aligned}$$

(28)

$$\begin{aligned}&= b \left( \sum _{k=1}^{i-1} \prod _{\ell = k+1}^{i}a + 1 \right) \; = \; b \sum _{k=0}^{i-1} a^k \; \xrightarrow {i \rightarrow \infty } \; \frac{b}{1-a} \, . \end{aligned}$$

(29)

Overall, this shows that for $i \rightarrow \infty$, every trajectory converges to ${\gamma } \varvec{G}$ with a $\gamma \le \frac{b}{1-a}$ and $\varvec{G}$ from ${\mathcal {N}}(\varvec{0}, \varvec{I})$. $\square$

We have only specified an upper bound for the variance $\gamma ^2$ of the steady-state distribution so far. The original DPM model [1] with $\alpha _i = \sqrt{1-\beta _i^2}$ does not only act as an example that verifies reasonable parameter choices are possible under the assumptions of our proposition. Additionally, we can also explicitly infer that $\gamma =1$ in this special case. Due to

$$\begin{aligned} \gamma _i \;=\; \sqrt{1-\prod _{j=1}^{i} (1-\beta _j^2)} \end{aligned}$$

(30)

and $0< 1-\beta _j^2 < 1$, we obtain $\gamma _i \xrightarrow {i \rightarrow \infty } 1$. Thus, the original DPM model convergences to the standard normal distribution.

Note that the variance-exploding model is not covered by the steady-state criterion without additional assumptions. Due to the parameter choice $\alpha _\ell = 1$, the sequence $\gamma _i$ is given by

$$\begin{aligned} \gamma _i = \sum _{k=1}^{i} \beta _k \, . \end{aligned}$$

(31)

As the name of the model suggests, the variance is thus not necessarily bounded for $i \rightarrow \infty$. For special choices of $\beta _i$, e.g. $\beta _i = \beta _0^{i-1}$ with $\beta _0 = 1$, we can however still get convergence to a normal distribution with a fixed variance. In the case of the example it would be $(1-\beta _0)^{-1}$. Also note that due to $\alpha _\ell =1$ in Eq. (14), $\lambda _i=1$ for all i. Thus, the mean remains constant in this case.

The noisy steady state marks a clear difference to traditional scale-spaces. For instance, diffusion scale-spaces on images [20] converge to a flat steady state instead. However, the new class of diffusion probabilistic scale-spaces still underlies the same core concept: It removes information from the initial state recursively and hierarchically, leading to a state of minimal information w.r.t. the initial distribution.

5.2 Generalised Scale-Space Properties for Reverse DPM

Sohl-Dickstein et al. [1] argue via results of Feller [74] that for infinitesimal $\beta _t$, the distribution of forward and reverse trajectories becomes identical. However, these results are also tied in an inverse proportional way to the length of the trajectory. For arbitrary small $\beta _t$, the number of steps goes to infinity. For such a case of identical distributions, our results for the forward process would carry over to the reverse process: Initial and steady state are swapped and our Lyapunov sequences are decreasing instead of increasing. The remainder of the properties carry over verbatim.

In practice, however, the time-discrete reverse process used for DPMs is an approximation. Neural networks estimate the parameters for this reverse process. In the following, we comment on properties that can be established under these conditions.

To this end, we consider the reverse process of Sohl-Dickstein et al. [1] and denote its distributions with q. It takes the normal distribution ${\mathcal {N}}(\varvec{0}, \varvec{I})$ as a starting distribution $q(\varvec{u}_M)$. Transitions in the reverse direction from $t_i$ to $t_{i-1}$ fulfil

$$\begin{aligned} q(\varvec{u}_{i-1} | \varvec{u}_i) \;=\; {\mathcal {N}}\left( \varvec{\mu }(\varvec{u}_i, i), \varvec{\Sigma } (\varvec{u}_i, i) \right) \, . \end{aligned}$$

(32)

While these learned distributions are still Gaussian, they are significantly more complex than in the forward process. Both the learned mean and variance do not reduce to common scalars for all pixels. Furthermore, they depend on the current time step and on the image $\varvec{u}_i$ itself. Therefore, we can establish less properties for the reverse process than before, but central ones still carry over.

5.2.1 Property 1: Normal Distribution as Initial State

By definition, the distribution $q(\varvec{u}_M)$ at time $t_M$ is given by ${\mathcal {N}}(\varvec{0}, \varvec{I})$.

5.2.2 Property 2: Semigroup Property

The distribution $q(\varvec{u}_i)$ at time $t_i$, $i<M$ can be reached in $M-i$ steps from $p(\varvec{u}_M)$ or in ${M-\ell -i}$ steps from $p(\varvec{u}_{M-\ell })$ with ${M - \ell } > i$. Since the Markov property is fulfilled, the proof for the semigroup property is analogous to the forward case in Sect. 5.1.

5.2.3 Property 3: Lyapunov Sequence

As a by-product of their derivation of conditional bounds for the reverse process, Sohl-Dickstein et al. [1] have already concluded that both the entropy $H_q(\varvec{u}_i)$ and the conditional entropy $H_q(\varvec{u}_0 | \varvec{u}_i)$ are decreasing for the backward direction, i.e.

$$\begin{aligned} H_q(\varvec{u}_{i-1}) \le H_q(\varvec{u}_{i}) \,. \end{aligned}$$

This is plausible, since the evolution starts with noise, a state of maximum entropy, and sequentially introduces more structure to it.

5.2.4 Property 4: Steady State

DPM reverse processes have the goal to enable sampling from the unknown initial distribution $p(\varvec{u}_0)$. Convergence to this distribution is only guaranteed for the ideal case with identical distributions p and q. However, even if this is not strictly fulfilled, the parameters $\varvec{\mu }$ and $\varvec{\Sigma }$ are chosen such that they maximise a lower bound of the log likelihood

$$\begin{aligned} \int q(\varvec{u}_0) \log p(\varvec{u}_0) \, \, {\textrm{d}} \varvec{u}_0 \, . \end{aligned}$$

(33)

In this sense, the reverse process approximates the distribution of the training data at time $t=0$.

Property 4 from Sect. 5.1, the permutation invariance, does in general not apply to the reverse process. Since the parameters $\varvec{\mu }$ and $\varvec{\Sigma }$ depend on the previous steps $\varvec{u}_i$ of the trajectory, the configuration of the pixels matters. Invariances will only be present if the network that estimates the parameters enforces them in its architecture.

5.3 Generalised Scale-Space Properties for Blurring Diffusion

Inverse heat dissipation [13] and blurring diffusion [14] models do not solely rely on adding noise in order to destroy features of the original image. Instead, they combine it with a deterministic homogeneous diffusion filter [18] to gradually blur this image. Such diffusion filters are well known as the origin of scale-space theory [18] and also constitute a special case of the osmosis filters we consider in more detail in Sect. 6.1. First, we discuss equivalent formulations of blurring diffusion in the spatial and transform domain [13, 14]. These allow us to transfer our scale-space results for DPM to this new setting.

A discrete linear diffusion operator can be interpreted either as the discretisation of a continuous time evolution described by a partial differential equation (see also Sect. 6.1) or as a Gaussian convolution. In the following, we consider only greyscale images with $N=n_x n_y$ pixels. Colour images can be processed by filtering each channel separately. Rissanen et al. [13] use an operator ${\varvec{A}_i = \exp (t_i \varvec{\Delta })}$, where $\varvec{\Delta } \in {\mathbb {R}}^{N \times N}$ is a discretisation of the Laplacian $\Delta u = \partial _{xx} u + \partial _{yy} u$ with reflecting boundary conditions. By adding Gaussian noise, they turn the deterministic diffusion evolution into a probabilistic process given by

$$\begin{aligned} \varvec{u}_{i} \;=\; \varvec{A}_i \varvec{u}_{0} + \varvec{\epsilon }_i, \qquad \varvec{\epsilon }_i \in {\mathcal {N}}(\varvec{0}, \beta _i^2 \varvec{I}) \end{aligned}$$

(34)

In particular, they make use of a change of basis. To this end, let $\varvec{V} \in {\mathbb {R}}^{N \times N}$ denote the basis transform operator of the orthogonal discrete cosine transform (DCT). Furthermore, we use the notation $\tilde{\varvec{u}} = \varvec{V} \varvec{u}$ to denote the DCT representation of a spatial variable $\varvec{u}$. Then, the diffusion operator $\varvec{A}_t = \varvec{V}^\top \varvec{B}_t \varvec{V}$ reduces to a diagonal matrix $\varvec{B}_t = \text {diag} (\varvec{\alpha }_1,..., \varvec{\alpha }_N)$ in the DCT domain. The entries of ${\varvec{B}_t}$ result from the eigendecomposition of the Laplacian. Let the vector index ${j} \in \{1,...,N\}$ correspond to the position $(k,\ell ) \in \{0,...,n_x-1\} \times \{0,...,n_y-1\}$ in the two-dimensional frequency domain. Then the entries of $\varvec{B}_t$ are given by

$$\begin{aligned} \alpha _{{j}} \;=\; \exp \left( - t \pi ^2 \left( \frac{k^2}{n_x} + \frac{\ell ^2}{n_y} \right) \right) \, . \end{aligned}$$

(35)

Note that for the frequency $(k,\ell )^\top =(0,0)^\top$, $\alpha _0 = 1$. Hence, the average grey value of the image is preserved. Moreover, for all ${j} \ne 0$, we have $\alpha _{{j}} < 1$ for $t > 0$. Additionally, since $\varvec{V}$ is orthogonal and $\varvec{V}^T \varvec{V} = \varvec{I}$, it also preserves Gaussian noise: For a sample $\varvec{\epsilon }$ from the normal distribution ${\mathcal {N}}(\varvec{0}, \varvec{I})$, the transform $\tilde{\varvec{\epsilon }}$ is from the same distribution. These properties are important for some of our scale-space considerations later on.

Rissanen et al. [13] proposed the DCT representation of their process for a fast implementation. However, Hoogeboom and Salimans [14] used it to derive a more general formulation in the DCT domain. Since $\varvec{B}_t$ is diagonal, a step from time $t_i$ to time $t_{i+1}$ can be considered for individual scalar frequencies j:

$$\begin{aligned} {\tilde{u}}_{i+1,j} \;=\; \alpha _{i,j} {\tilde{u}}_{i,j} + \beta _i \epsilon \, . \end{aligned}$$

(36)

Here, $\epsilon$ is from ${\mathcal {N}}(0,1)$. In contrast to Rissanen et al. [13], they do not limit the noise variance $\sigma _t$ to minimal observation noise, but also allow to choose a noise schedule as in the DPM from Sect. 5.1. This formulation is particularly useful for us since it constitutes another 1-D drift-diffusion process as in Eq. (7). It allows us to transfer some of our previous findings to the new setting. However, note that compared to the model in Eq. (7) we operate on frequencies instead of images as realisations of the random variable. Moreover, each frequency has its own individual parameters $\alpha _{i,j}$. In addition, $\beta _i$ could be made frequency specific. However, in practice, Hoogeboom and Salimans [14] choose the same $\beta _i$ for all frequencies. This also entails that the Markov criterion for this process in DCT space is given by

$$\begin{aligned} p(\tilde{\varvec{u}}_{i+1} |\tilde{\varvec{u}}_{i}) \;=\; {\mathcal {N}}(\tilde{\varvec{u}}_i | \varvec{B}_i \tilde{\varvec{u}}_{i-1}, \beta _i^2 \varvec{I}) \, . \end{aligned}$$

(37)

In the following we consider a scale-space that is defined by the marginal distributions of the random variable $\varvec{U}_t:= \varvec{V}^\top \tilde{\varvec{U}}_t$, i.e. the backtransform of the trajectories in DCT space. Note that every trajectory in the frequency domain has exactly one corresponding trajectory in the spatial domain. Therefore, we can argue equivalently in the DCT domain or the spatial domain, depending on what is more convenient. As in Sect. 5.1, the process starts with the distribution of the training data or, respectively, the distribution of its discrete cosine transform.

5.3.1 Property 1: Initial State

By definition, the distribution $p(\varvec{u}_0)$ at time $t_0=0$ is given by the distribution $p(\varvec{F})$ of the training data.

5.3.2 Property 2: Semigroup Property

The distribution $p(\varvec{u}_i)$ at scale i can be reached equivalently in i steps from $p(\varvec{u}_0)$ or in $\ell$ steps from $p(\varvec{u}_{i-\ell })$. The Markov property is fulfilled in the DCT domain. Thus, the proof for the semigroup property is analogous to the DPM model in Sect. 5.1. For each intermediate scale, we can switch back to the spatial domain by multiplication with $\varvec{V}^\top$.

5.3.3 Property 3: Lyapunov Sequence

To establish this information reduction property, we require an analogous statement to Eq. (8). By using a similar induction proof for each frequency, we obtain

$$\begin{aligned} \tilde{\varvec{U}}_i \; = \; \varvec{M}_i \tilde{\varvec{U}}_0 + \varvec{\Sigma }_i \varvec{G} \, . \end{aligned}$$

(38)

Here, $\varvec{G}$ is from ${\mathcal {N}}(\varvec{0}, \varvec{I})$, $\varvec{M}_i = \text {diag}({\lambda _{i,0},...,\lambda _{i,N}})$ with

$$\begin{aligned} \lambda _{i,j} \;=\; \prod _{\ell = 1}^{i} \alpha _{\ell , j} \, , \end{aligned}$$

(39)

and $\varvec{\Sigma }_u = \text {diag}({\gamma _{i,0},...,\gamma _{i,N}})$ with

$$\begin{aligned} \gamma _{i,j} \;=\; \left( \sum _{k=1}^{i-1} \beta _{i} \prod _{\ell = k+1}^{i} \alpha _{\ell ,j} + \beta _{i} \right) \, . \end{aligned}$$

(40)

This is a frequency-dependent analogue statement to the direct transition from time $t_0$ to time $t_i$ in the DPM setting in Eq. (14).

Proposition 7

(Increasing Conditional Entropy) The conditional entropy

$$\begin{aligned} H_p(\tilde{\varvec{U}}_i | \tilde{\varvec{U}}_0)&\;=\; - \int \int p(\varvec{\tilde{u}}_i, \tilde{\varvec{u}}_0) \ln p(\varvec{\tilde{u}}_i | \varvec{\tilde{u}}_0) \, \, {\textrm{d}} \varvec{\tilde{u}}_0 \, {\textrm{d}} \varvec{\tilde{u}}_i \end{aligned}$$

(41)

increases with i under the assumption that for all frequencies j and $\beta _{i} \in (0,1)$ we have $\beta _{i+1} \ge (1-\alpha _{i+1,j}) \gamma _{i,j}$.

Proof

As in Sect. 5.1, the statement is equivalent to showing that the entropy $H_p(\varvec{W}_i)$ of the distribution $p(\tilde{\varvec{u}}_i | \tilde{\varvec{u}}_0)$ is increasing. Thus, we need to show that $H_p(\varvec{W}_i) \ge H_p(\varvec{W}_{i-1})$. The probability distribution of $p(\tilde{\varvec{u}}_i | \tilde{\varvec{u}}_0)$ can be inferred from Eq. (13), but it is more complex than in the DPM case due to the frequency dependent parameters.

Fortunately, the entropy of the multivariate Gaussian distribution ${\mathcal {N}}(\varvec{M}_t \tilde{\varvec{u}}_0, \varvec{\Sigma }_t)$ only depends on its covariance matrix $\varvec{\Sigma }_t$ and is given by

$$\begin{aligned} H_p(\varvec{W}_i) = \frac{1}{2} \ln \Big (\big (2\pi \, {\textrm{e}} \, \big )^n \det {\varvec{\Sigma }_i}\Big ) = \frac{1}{2} \ln \Bigg (\big (2\pi \, {\textrm{e}} \,\big )^n \prod _{j=1}^N \gamma _{i,j} \Bigg ) \end{aligned}$$

(42)

If $\gamma _{i+1,j} \ge \gamma _{i,j}$ holds for all frequencies j, the entropy is increasing. For a fixed frequency j, we can transfer the previous result from Eq. (23) to the scalar setting:

$$\begin{aligned} \gamma _{i+1, j} = \alpha _{{i}+1,j} \gamma _{i,j} + \beta _{i+1} \, . \end{aligned}$$

(43)

Since $\beta _i > 0$ and $\gamma _i > 0$, we require

$$\begin{aligned} \alpha _{i+1,j} \gamma _{i,j} + \beta _{i+1} \ge \gamma _{i,j} \quad \Leftrightarrow \quad \beta _{i+1} \ge (1-\alpha _{i+1,j}) \gamma _{i,j} \end{aligned}$$

(44)

This is a direct extension of our previous result in Sect. 5.1 to the frequency setting. $\square$

Note that there are also previous results for deterministic diffusion filters that use entropy as a Lyapunov sequence [20]. However, there the entropy is defined on the pixel values of the image instead of an evolving probability distribution. Individual trajectories rely on a deterministic diffusion filter. However, due to the added noise, the entropy statements of classical scale-spaces do not transfer to the trajectories of blurring diffusion.

5.3.4 Property 3: Preservation of the Average Grey Value

The DPM scale-space from Sect. 5.1 ensures convergence to Gaussian noise with zero mean, independently of the initial image. This requires the mean of the image to change. The behaviour of blurring diffusion scale-spaces is significantly different.

Proposition 8

(Preservation of the Average Grey Value) Let $\varvec{u}_0$ denote an image from the initial distribution $p(\varvec{f})$. Then, all images in the trajectory $\varvec{u}_0,..., \varvec{u}_m$ have the same average grey value.

This statement directly follows from an observation on the spatial version of the process. In every step, we add Gaussian noise with mean zero to a diffusion filtered image. Since diffusion filtering preserves the average grey value [20], this also holds for blurring diffusion. In colour images, the preservation of the average colour value applies for each channel.

5.3.5 Property 4: Rotation Invariance

In contrast to the forward DPM scale-space, blurring diffusion takes into account the neighbourhood configuration in the spatial domain due to the blurring of the homogeneous diffusion operator. Thus, permutation invariance does not apply to blurring diffusion scale-spaces.

However, in a space-continuous setting, the diffusion operator is rotationally invariant. The same applies to Gaussian noise samples: Under rotation, they remain samples from the same noise distribution. In the fully discrete setting, this rotation invariance is typically partially lost since only $90^\circ$ rotations align perfectly with the pixel grid. However, this depends on the concrete implementation of the process. From this observation, we can directly deduce the following statement.

Proposition 9

(Rotation Invariant Trajectories) Let $\varvec{u}_0$ denote an image from the initial distribution and $\varvec{v}_0:= R(\varvec{u}_0)$ a rotation by a multiple of $90^\circ$. Then, any trajectory $\varvec{v}_0,... \varvec{v}_m$ obtained from the process in Eq. (7) is given by $\varvec{v}_i = R(\varvec{u}_i)$ for a trajectory $\varvec{u}_0,..., \varvec{u}_m$ starting with the original image $\varvec{u}_0$.

5.3.6 Property 5: Steady State

Due to the preservation of the average grey value in Property 3, a blurring diffusion scale-space cannot converge to a noise distribution with zero mean unless the initial image already had a zero mean. Images typically have nonnegative pixel values (e.g. a range of [0, 255] or [0, 1]). Thus, a zero mean would be only possible for a flat image or after a transformation to a range that is symmetric to zero (e.g. $[-1,1]$). We do not make any such assumption. However, for the sake of simplicity, we consider greyscale images in the following. For colour images, the same statements apply for each channel.

Proposition 10

(Convergence to a Mixture of Normal Distributions) Under the assumptions of Proposition 7, $\alpha _{i,j} \in (0,a_j]$ with $0<a_j<1$, $\beta _i \in (0,b]$ with $0<b<1$, and $i \rightarrow \infty$, the forward process from Eq. (2) converges to a mixture of normal distributions ${\mathcal {N}}(\mu _k \varvec{I}, \varvec{\Sigma })$ with $\varvec{\Sigma } = \text {diag}(\sigma _1,...,\sigma _N)$ and $\sigma _i \le {\frac{b}{1-a_j}}$. The value $\mu _k$ with $k \in \{0,...,n_f\}$ assumes all possible average grey levels from the training database.

Proof

Consider a trajectory starting from an arbitrary image $\varvec{u}_0$ from the training database with mean $\mu$. As in the proof for Proposition 7, the findings from Eq. (8) and Eq. (14) for DPM carry over to our setting in the scalar case for each frequency j:

$$\begin{aligned} {\tilde{u}}_{i,j} \;=\; \lambda _{i,j} {\tilde{u}}_{0,j} + \gamma _{i,j} \epsilon \end{aligned}$$

(45)

with $\epsilon$ from ${\mathcal {N}}(0, 1)$. For the convergence of $\lambda _{i,j}$, we have to consider the product of all frequency specific $\alpha _{i,j}$ according to Eq. (39). Here we have the special case $\alpha _{i,0} = 1$ for the lowest frequency, i.e. $\lambda _{i,0}=1$ for all i. This is consistent with our previous findings in Proposition 8: The lowest frequency represents the average grey level, which remains unchanged.

For $j>0$, we have $\alpha _{i,j} < 1$ and thus $\lambda _{i,j} \rightarrow 0$ for $i \rightarrow \infty$. Thus, for all other frequencies the contribution of $\varvec{u}_i$ vanishes and only its mean $\mu$ is preserved. The convergence of $\gamma _{i,j}$ to $\sigma _i \le {\frac{b}{1-a_j}}$ is analogous to the proof of Proposition 6. This determines the standard deviation of the noise for each frequency. $\square$

Overall, blurring diffusion constitutes a scale-space that resembles the DPM scale-space in its architectural properties. The key difference lies in the incorporation of 2-D neighbourhood relationships between pixel values in the spatial domain. In the DCT domain, this translates to an individual set of process parameters for each frequency.

6 Diffusion Probabilistic Models and Osmosis

All diffusion probabilistic models considered in Sect. 5 have in common that they are connected to drift-diffusion processes. In image processing with partial differential equations (PDEs), osmosis filters proposed by Weickert et al. [16] are successfully applied to image editing and restoration tasks [16, 63,64,65]. Since they share their origin with diffusion probabilistic models, namely the Fokker-Planck equation [60], we discuss connections in the following. First, we briefly review the PDE formulation of osmosis filtering. Afterwards, we discuss common properties as well as differences between both classes of models. Finally, we compare all four models experimentally.

6.1 Continuous Osmosis Filtering

Unlike the first part of the manuscript, we consider a grey value image as a function $f: \Omega \rightarrow {\mathbb {R}}_+$ defined on the image domain $\Omega \subset {\mathbb {R}}^2$. It maps each coordinate $\varvec{x} \in \Omega$ to a positive grey value. In the following we limit our description to grey value images for the sake of simplicity. The filter can be extended to colour or arbitrary other multi-channel images (e.g. hyperspectral) by applying it channel-wise.

As in diffusion probabilistic models, osmosis filters consider the evolution of an image $u: \Omega \times [0,\infty ) \rightarrow {\mathbb {R}}_+$ over time. However, here the evolution is entirely deterministic. Its initial state is given by a starting image f, i.e. for all $\varvec{x}$ we have $u(\varvec{x}, 0) = f(\varvec{x})$. In addition, the second major factor that influences the evolution is the drift vector field $\varvec{d}: \Omega \rightarrow {\mathbb {R}}^2$ that can be chosen independently of the initial image and is typically used for filter design.

Given these two degrees of freedom, the image evolution fulfils the PDE [16]

$$\begin{aligned} \partial _t u&\;=\; \Delta u - {{{\textbf {div\,}}}}(\varvec{d} u)&\quad \text {on } \Omega \times (0,T] \, . \end{aligned}$$

(46)

At the boundaries of $\Omega$, reflecting boundary conditions avoid any exchange of information with areas outside of the image domain. There is a direct connection of this model to the inverse heat dissipation [13] and blurring diffusion [14]: All of these processes build on homogeneous diffusion [18], which is a special case of osmosis with $\varvec{d} = \varvec{0}$.

However, a non-trivial drift vector field enables to describe evolutions that do not merely smooth an image. The Laplacian $\Delta u$, which corresponds to the diffusion part of the PDE in Eq. (46), represents a symmetric exchange of information between neighbouring pixels. This symmetry can be broken by the drift component $-{{{\textbf {div\,}}}}(\varvec{d} u) = -\partial _x (d_1 u) - \partial _y (d_2 u)$. This is also vital for our own goal of relating osmosis image evolutions to diffusion probabilistic models and will allow us to introduce stochastic elements without any need to modify the PDE above.

6.2 Relating Osmosis and Diffusion Probabilistic Models

As noted in the previous section, for $\varvec{d}=\varvec{0}$, osmosis is directly connected to blurring diffusion. For the original DPM model, the connection is less obvious, but equally close. To this end, it is instructive to consider a 1-D osmosis process. Its evolution is described by the PDE

$$\begin{aligned} \partial _t u&\;=\; \partial _{xx} u - \partial _x (d u)&\quad \text {on } \Omega \subset {{\mathbb {R}}} \times (0,T] \, . \end{aligned}$$

(47)

A comparison with the PDE formulation of the DPM forward process in Eq. (5) reveals a significant structural similarity. Both equations describe an evolution w.r.t. the time t: 1-D osmosis considers an evolving image u, while the DPM evolution is defined on a probability density p. The derivative $\partial _{\varvec{u}_t}$ w.r.t. positions of individual particles in the diffusion probabilistic model corresponds to the spatial derivative $\partial _x$ in Eq. (47). The moments correspond to diffusivity and drift factors for the osmosis PDE and thus we can interpret 1-D osmosis as the deterministic counterpart to the probabilistic drift-diffusion process of DPM.

While both models are derived from the same physical principle, a 1-D osmosis filter would typically act on a 1-D signal instead of an image. In this 1-D setting, it also considers neighbourhood relations and exchanges information between neighbouring signal elements. In contrast, the 1-D drift-diffusion of DPM acts on individual pixels of a 2-D image which correspond to positions of individual particles. Thus, 1-D osmosis creates evolving 1-D signals, while a DPM trajectory consists of 2-D images.

For a meaningful comparison between the properties of osmosis filtering and the three diffusion probabilistic models, we require 2-D osmosis as in Eq. (46). Moreover, we need to add a stochastic component. Ideally, every trajectory of this new probabilistic osmosis process should inherit the theoretical properties of the deterministic model. Inverse heat dissipation [13] can be seen as a similar approach in that it provides a stochastic counter part to homogeneous diffusion [18]. However, there the addition of noise marks a clear departure from the PDE model and also implies that properties of the deterministic model do not carry over to the trajectory.

Instead of adding noise, we design the drift vector field $\varvec{d}$ in such a way that the osmosis evolution naturally converges to a noise sample. Weickert et al. [16] have shown that osmosis preserves the average grey value. Thus, for a given image f from the training data, we choose a noise image $\epsilon$, where at every location $x \in \Omega$, $\epsilon (x)$ is from ${\mathcal {N}}(\mu _{f}, \sigma ^2)$. Here, $\mu _{f}$ is the average grey value of f. Note that osmosis requires positive images. In practice, we clip the noise sample to $[10^{-6},1]$. While this truncates the tails of the Gaussian distribution, it has little impact for small standard deviation $\sigma$.

Now we can use another result of Weickert et al. [16] and consider the compatible case for osmosis. Our noise sample $\epsilon$ acts as guidance image for the osmosis process. The corresponding canonical drift vector field is defined by

$$\begin{aligned} \varvec{d} = \frac{\varvec{\nabla }\epsilon }{\epsilon } \end{aligned}$$

(48)

with the spatial gradient $\varvec{\nabla }$. Since $\mu _f=\mu _\epsilon$, the osmosis process converges to

$$\begin{aligned} \frac{\mu _{f}}{\mu _{\epsilon }} \epsilon = \epsilon \,. \end{aligned}$$

(49)

Considering intermediate results of the evolution at times $t_i$ yields a trajectory $u_0,..., u_m$ of the probabilistic osmosis process with $u_0 = f$. Even though the intermediate marginal probabilities or the transition probabilities are not known, the process starts with the target distribution $p(\varvec{F})$ and converges to an approximation to a normal distribution. In the following, we can empirically compare trajectories of this osmosis process to trajectories of diffusion probabilistic models.

Fig. 3

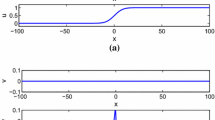
Visual comparison of trajectories. The diffusion probabilistic model (a) behaves distinctively different compared to the other approaches since it does not perform blurring in the image domain. Due to the minimal amounts of added noise, inverse heat dissipation (b) closely resembles homogeneous diffusion (c). With a suitable noise schedule, blurring diffusion (d) closely resembles osmosis filtering (e)

6.3 Comparing Osmosis Filters and Diffusion Probabilistic Models

For concrete experiments, we require a discrete implementation of the continuous osmosis model from Sect. 6.1. As Vogel et al. [63], we use a stabilised BiCGSTAB solver [75]. For the noise guidance images, we use a standard deviation of $\sigma =0.1$. All experiments are conducted on the Berkeley segmentation data set BSDS500 [76].

We compare to the three models from Sect. 5. According to Eq. (7), we implement forward DPM [1] by successively adding Gaussian noise with the standard parameter choice ${\alpha _i = \sqrt{1-\beta _i^2}}$ and $\beta _i=0.1$. Inverse heat dissipation [13] and blurring diffusion [14] can be implemented in many equivalent ways. We based our implementation on the reference code of Rissanen et al. [13], which implements the Laplacian in the DCT domain according to Eq. (35). For inverse heat dissipation, we use the standard parameter $\beta _i = 0.01$. For blurring diffusion, we choose $\beta _i = 0.1$ such that it coincides with the guidance noise of our probabilistic osmosis. Furthermore, we also include homogeneous diffusion [18] without any added noise in our comparisons.

6.3.1 Visual Comparison

Figure 3 reveals visual similarities and differences between model trajectories. All five models successively remove features of the initial training sample: They are drowned out by noise, by blur, or a combination of both. For the probabilistic models, we have shown that this information reduction is quantified by entropy-based Lyapunov sequences. A similar statement holds for images in an osmosis trajectory. As shown by Schmidt [62], the relative entropy of u w.r.t. the noise sample $\epsilon$ is increasing:

$$\begin{aligned} L(t) \;:=\; -\int _\Omega u(\varvec{x},t)\ln \left( \frac{u(\varvec{x},t)}{w(\varvec{x})}\right) \, \, {\textrm{d}} \varvec{x} \, . \end{aligned}$$

(50)

This also reflects the transition from the initial image $\varvec{f}$ to the steady state $\epsilon$. Similar statements on an unconditioned entropy apply to homogeneous diffusion [20].

Notably, only DPM does not preserve the average colour value of the initial image and converges to noise with mean zero. For visualisation purposes, the images of the DPM trajectory have therefore been affinely mapped to [0, 1]. DPM is also the only process that does not take neighbourhood relations between pixels into account. Therefore, edge features, such as the stripe pattern in Fig. 3a, remain sharp until they are completely overcome by noise.

This observation directly results from the 1-D drift-diffusion: DPM models the microscopic aspect of Brownian motion with colour values as particle positions. All other models consider the macroscopic aspect of drift-diffusion instead which considers colour values as particle concentrations per pixel cell. Consequentially, all other models apply 2-D blur in the image domain. Due to the very small amount of observation noise added by Rissanen et al. [13], the trajectory of heat dissipation is visually very similar to homogeneous diffusion.

Similarly, osmosis and blurring diffusion lead to visually almost identical trajectories. They mainly differ in the way how noise is added: Blurring diffusion uses explicit addition, while osmosis transitions to noise due to the drift vector field. In the following, we verify these observations quantitatively.

Fig. 4

Quantitative Comparison of Diffusion Probabilistic Models and Model-based Filters. Both the variance evolution over time in (a) and the FID w.r.t. the osmosis distributions in (b) suggest that DPM differs significantly from the classical diffusion and osmosis filters. Heat dissipation approximates diffusion, while blurring diffusion approximates osmosis

6.3.2 Variance Comparison

On the entire BSDS500 database, we evaluate the evolution of the image variance over time in Fig. 4a. As expected, the pairs homogeneous diffusion/heat dissipation and osmosis/blurring diffusion exhibit very similar evolutions of the variance. On the way to the flat steady state, homogeneous diffusion and heat dissipation approach zero variance. Osmosis and blurring diffusion converge to a noise variance defined by the input parameters while DPM very slowly converges to the standard distribution. These observations coincide with the expectations from our theoretical results.

6.3.3 FID Comparison

Additionally, we can judge the similarity of intermediate distributions in the scale-space with the Fréchet-Inception distance (FID) [77]. It is widely used to judge the quality of generative models in terms of the approximation quality towards the target distribution. We use the implementation clean-fid [78] that avoids discretisation artefacts due to sampling and quantisation. Note that we measure the FID of probabilistic osmosis distributions relative to results of the other four models. Thus, a low FID indicates how closely each filter approximates osmosis.

Figure 4b also confirms our previous hypothesis: Heat dissipation and blurring diffusion consistently differ most from osmosis results since they rely mostly on blur and not on noise. DPM comes close to osmosis in its noisy steady state, but differs significantly in the initial evolution due the lack of 2-D smoothing. Blurring diffusion approximates osmosis surprisingly closely over the whole evolution.

Hoogeboom and Salimans [14] have found that heat dissipation improves the overall quality of generative models compared to DPM. Blurring diffusion yields even better results. Given our findings, we can interpret these observations from a scale-space perspective: The integration of 2-D neighbourhood relationships in the scale-space evolution is important for good diffusion probabilistic models. However, also the addition of sufficient amounts of stochastic perturbations is vital. Overall, recent advances can be interpreted as an increasingly accurate approximation of osmosis filtering, with an approximation to diffusion scale-spaces as an intermediate model. Using such an approximation instead of directly applying 2-D osmosis is convenient due to the more straightforward relation to the reverse process.

7 Conclusions and Outlook

Inspired by diffusion probabilistic filters, we have proposed the first class of generalised stochastic scale-spaces that describe evolutions of probability distributions instead of images. While the setting differs significantly from classical scale-spaces, central properties such as gradual, quantifiable simplification and causality still apply. These results suggest that in general, sequential generative models from deep learning are closely connected to scale-space theory. Therefore, we hope that in the future, the scale-space community will benefit from the discovery of new scale-spaces that might also be used in different contexts. In particular, existing generative models are mostly focused on the steady states as the practically relevant output. The intermediate results of the associated scale-spaces could however also be useful in future applications.

On the flip side, trajectories of recent diffusion probabilistic models approximate well-known classical scale-space evolutions. This suggests that in the opposite direction, the deep learning community can potentially benefit from existing knowledge about scale-spaces by incorporating them into deep learning approaches.