A Tighter Relaxation for the Relative Pose Problem Between Cameras

Abstract

This paper tackles the resolution of the Relative Pose problem with optimality guarantees by stating it as an optimization problem over the set of essential matrices that minimizes the squared epipolar error. We relax this non-convex problem with its Shor’s relaxation, a convex program that can be solved by off-the-shelf tools. We follow the empirical observation that redundant but independent constraints tighten the relaxation. For that, we leverage equivalent definitions of the set of essential matrices based on the translation vectors between the cameras. Overconstrained characterizations of the set of essential matrices are derived by the combination of these definitions. Through extensive experiments on synthetic and real data, our proposal is empirically proved to remain tight and to require only 7 milliseconds to be solved even for the overconstrained formulations, finding the optimal solution under a wide variety of configurations, including highly noisy data and outliers. The solver cannot certify the solution only in very extreme cases, e.g.noise $100~{\texttt {pix}}$ and number of pair-wise correspondences under 15. The proposal is thus faster than other overconstrained formulations while being faster than the minimal ones, making it suitable for real-world applications that require optimality certification.

1 Introduction

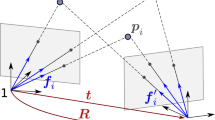
This work tackles the central, calibrated Relative Pose problem (RPp), in which given a set of N pair-wise feature correspondences between two images coming from two (central and calibrated) cameras, we seek the relative rotation ${\varvec{R}}$ and baseline $\varvec{b}$ (line joining the two camera centers [1]) between these two cameras, as it is shown in Fig. 1.

Solving the RPp is the cornerstone of visual odometry applications [2,3,4] and other more complex computer vision tasks, such as Simultaneous Localization and Mapping [5, 6] or Structure from Motion [7,8,9]. Although the gold standard for RPp poses it as a 2-view Bundle Adjustment (that minimizes the re-projection error [1, 10]), it is also a hard, non-convex problem which suffers from local minima. Therefore, it is a common and recommended practice to initialize it with the estimate obtained from a simpler formulation, typically based on the squared epipolar error. This algebraic error is related to the epipolar constraint [1] that associates a pair-wise feature correspondence $({\varvec{f}}_{i}, {\varvec{f}}_i')$ with the unknown relative baseline $\varvec{b}$ (as a 3D vector) and the rotation ${\varvec{R}}$ (as a $3 \times 3$ matrix), and it is defined by the expression ${\varvec{f}}_{i}^T ([\varvec{b}]_{\text {x}} {\varvec{R}}) {\varvec{f}}_i'= 0$, where $[\varvec{b}]_{\text {x}}$ denotes the cross-product with $\varvec{b}$ (see Eq. (1)). In the noiseless case the equality holds exactly; however, in the presence of noise ${\varvec{f}}_{i}^T ([\varvec{b}]_{\text {x}} {\varvec{R}}) {\varvec{f}}_i'= \epsilon _i \ne 0$, which is defined as the epipolar error.

Fig. 1

Given a set of N pair-wise correspondences $({\varvec{f}}_{i}, {\varvec{f}}_i')$ between two central and calibrated cameras $1-2$, in this work we aim to estimate the relative rotation ${\varvec{R}}$ and baseline (position) $\varvec{b}$ between these two frames

One common approach to the resolution of this simplified RPp based on the epipolar error relies on the introduction of the so-called essential matrix $\varvec{E}= [\varvec{b}]_{\text {x}} {\varvec{R}}$ [1, 11], that allows us to write the epipolar error for each observation $\epsilon _i$, which is quadratic in the entries of the unknowns (rotation and baseline), as a linear constraint in the entries of the essential matrix, i.e.$\epsilon _i = {\varvec{f}}_{i}^T \varvec{E}{\varvec{f}}_i'$ [1]. Due to the scale ambiguity, this problem has only five degrees of freedom. Hence, five correspondences in general position suffice to obtain a solution to the problem (the so-called five-points algorithm). Although this minimal approach can be embedded into robust frameworks, e.g.RANSAC, it is not guaranteed that the computed solution is optimal in the presence of noise. Introducing more correspondences has been shown to improve the accuracy of the solution [12,13,14,15]. In particular, the direct linear transformation (DLT) method requires eight or more pair of observations to estimate a solution. This solution, however, is not necessarily an essential matrix, since this method obviates its internal constraints [1, 16]. A (potential suboptimal) solution can be achieved by projecting the estimate onto the set of essential matrices [1]. Other methods [13, 17,18,19,20] propose to refine an initial estimate, e.g.from the five points algorithm, directly on the manifold of essential matrices. However, given the non-convexity of the problem, these approaches cannot guarantee the optimality of the solution.

A common approach to the global resolution of a non-convex problem consists of the description of a relaxation for the given problem, whose global optimum is easier to reach in general. The solution to this relaxation usually provides with all the information required to estimate an approximation of the actual global solution to the original problem. The quality of this approximation, however, depends on the own relaxation. If the relaxation happens to be tight, meaning it approximates well the original problem, then it provides also with a certificate of optimality for the solution to the original non-convex problem. This was the approach followed by Briales et al.in [14] and Zhao in [15], where two different convex semidefinite relaxations were derived for the RPp. This was also the underlying process followed in [21], where we proposed an algorithm to certify if a solution to the RPp is optimal. That work, however, builds upon a specific relaxation of the original problem that may happen to not be tight for some problem instances. In those cases, the proposal is unable to certify the optimality of the solution, even if it is the optimum. To overcome this limitation, previous works [14, 22, 23] have shown that the introduction of additional, independent constraints leads to tighter relaxations. Overconstrained formulations for the RPp, such as the one in [14], empirically remain tight under challenging scenes, even with high noise and low number of correspondences. However, the computational time required by the off-the-shelf tools to solve the problem depends on the number of constraints and variables. Therefore, special care must be paid when selecting redundant formulations since they may become too slow to be employed in real applications. Further, these redundant constraints are highly dependent on the problem variables and the intrinsic nature of the search space. If the domain can be defined in different forms potentially with different variables, as the set of essential matrices does, then the combination of those definitions can be leveraged to obtain a redundant set of constraints.

1.1 Contributions

In this work we leverage and combine different characterizations of the set of normalized essential matrices as the feasible set of the RPp based on the minimization of the squared normalized epipolar error. The final problem has 15 variables and 28 (redundant) constraints and presents a convex SDP relaxation that is proved empirically to remain tight in almost all the problem instances tested and can be solved in less than 7 milliseconds on a standard computer, hence being faster than other overconstrained formulations [14]. We first employ separately two different minimal set of constraints (LEFT and RIGHT) in Sect. 4 that fully define the essential matrix set. Although they tend to remain tight, each of them fails to estimate the optimal solution in some common scenarios. The combination of these independent sets of constraints leads to a redundant formulation (named BOTH) in Sect. 5.1 which empirically proves to be tighter than any of the two previous ones. We incorporate another characterization of the set of essential matrices, obtaining the last redundant problem (ADJ) with only 15 variables and 28 constraints in Sect. 5.2.

Last, we carry out extensive experiments on both synthetic and real data in Sect. 6, covering a broad set of problem regimes, including problem instances with corrupted random correspondences (high noise or $100\%$ outliers). These experiments support the claims of this work regarding the tightness and show that our last redundant characterization (ADJ) is able to maintain the tightness in almost all the cases, failing only (in less than $10\%$ of the cases) in very unrealistic cases, when the number of correspondences is very low (under 15) and very high noise (more than 50 pix). All the proposed solvers are able to estimate and certify the solution to the RPp in less than 7 milliseconds.

Although Sect. 6 shows empirically that strong duality holds in most of the cases for all the proposed formulations, a formal demonstration of this behavior is not provided. Please, notice that while we approach the Relative Pose problem through the essential matrix, the relative rotation and baseline can be easily recovered from it by any classic computer vision algorithm [1].

2 Related Work

Local optimization methods, as the one presented in Sect. 1, are not the only option when tackling the non-minimal N-point problem. There exist other approaches for this non-convex optimization that are able to obtain and/or certify the optimality of the solution. Some of the most relevant are commented next.

Hartley and Kahl [10] decouple the rotation from the translation while estimating the essential matrix with a cost function that minimizes the $L_{\infty }$ norm and solve the problem by a globally optimal Branch-and-Bound. Kneip and Lynen [24] enforce the coplanarity of the epipolar plane (an algebraic error), which serves to determine the relative rotation independently of the translation. The proposed eigenvalue formulation was solved by an efficient Levenberg-Marquardt and Branch-and-Bound scheme. In [19], Yang et al., based on [10], incorporate outliers and solve an inlier-set maximization problem via Branch-and-Bound. Nevertheless, due to its exploratory nature, Branch-and-Bound presents slow performance and an exponential computational time in worst-case scenarios.

Other approaches rely on the re-formulation of the original problem as a Quadratically Constrained Quadratic Problem (QCQP). Although these problems are still NP-hard to solve in most of the cases, we can find relaxations that can be actually solved and that may provide some useful information about the global optimal solution to the original problem. Of interest are those relaxations that are tight, which means we can recover from them the exact optimal solution to the original non-convex QCQP with an optimality certificate. One of these relaxations is the so-called Shor’s relaxation [25], in which we relax the QCQP onto a Semidefinite Positive problem (SDP), which can be actually solved up to arbitrary accuracy in polynomial time by off-the-shelf tools. These relaxations have been exploited for different problems in the literature, e.g.Rotation Synchronization [26,27,28] and Pose Synchronization [29, 30]. This was also the approach followed recently by Zhao in [15], in which a minimal QCQP formulation (12 variables and 7 constraints) leads to a small SDP relaxation that can be solved in 4ms. Another relaxation that has been exploited previously in the literature for other problems is the dual problem [31]. Recently, Garcia-Salguero et al.[21] leverage this relaxation (a convex SDP problem) and propose an algorithm that is able to certify the solution to the non-minimal N-point Relative Pose problem (RPp). This certifier is based on a specific formulation of the original problem, with a minimally constrained definition of the set of essential matrices. Although these minimal formulations enjoy the advantages of small convex relaxations, they turn out to be not always tight in practice. Nevertheless, these relaxations and their behavior depend on the specific parameterization of the search space, in this case the set of essential matrices; changing the explicit expressions, i.e.the constraints, that define this set lead to different relaxations, that could potentially work when others do not.

It has been shown in previous works, see e.g.[32,33,34], that the introduction of independent but redundant constraints [35, Ch.3] strengthens the SDP relaxations (both Shor’s and the dual problem). This was the approach followed by Briales et al.in [14]. The authors formulate the non-minimal Relative Pose problem based on the epipolar error through the rotation and translation components. The introduction of redundant constraints leads to an empirically always tight Shor’s relaxation. However, the high number of variables and constraints yields a quite large SDP problem which requires 1–2 seconds to be solved under a matlab implementation. Recently, Zhao et al.in [23] also introduce redundant constraints for the generalized essential matrix problem.

However, finding a good relaxation that remains tight in most of the problem instances while still being able to be efficiently solved (reduced number of variables and constraints) is not trivial. A limited number of variables hinder the applications of some “tricks”, e.g.constraints that relate the variables of the problem but do not define the search space, as the ones cleverly exploited in [14, 34] and [23]. Still, multiple definitions of the same search space under the same set of variables are usually not available. A notorious exception, widely reported in the literature, see e.g.[14, 33, 36], is that of exploiting the orthogonality of both rows and columns of orthogonal, square matrices, i.e.elements of $\text {O}(d)$.

For the essential matrices, there exist just a few global definitions. Faugeras et al.[11] proposed a cubic characterization of the set of essential matrices that does not require the introduction of new variables, i.e.the definition only depends on the entries of $\varvec{E}$. A similar derivation, also cubic and in terms of the own essential matrix, was shown by Zhao [15]. The constraints associated with these definitions must be quadratic in order to be able to formulate the problem as a QCQP. A common approach for this is to introduce auxiliary variables, as in [11].

3 Notation

In order to make clearer the mathematical formulation in the paper, we first introduce the notation used hereafter. Bold, upper-case letters denote matrices e.g.$\varvec{E}, {\varvec{Q}}$, while bold, lower-case denotes (column) vector e.g., ${\varvec{t}}, \varvec{x}$ and normal font letters e.g., a, b denote scalar. Additionally, we will denote with $\mathbb {N}$ the set of natural numbers (including the zero), with $\mathbb {R}^{n \times m}$ the set of $n \times m$ real-valued matrices, $\mathbb {S}^{n} \subset \mathbb {R}^{n \times n}$ the set of symmetric matrices of dimension $n \times n$ and $\mathbb {S}_+ ^{n}$ the cone of positive semidefinite (PSD) matrices of dimension $n \times n$. A PSD matrix will be also denoted by $\succeq$ , i.e., ${\varvec{Q}}\succeq 0 \Leftrightarrow {\varvec{Q}}\in \mathbb {S}_+ ^{n}$. We denote by $\oplus$ the direct sum such that $\varvec{A}_1 \oplus \varvec{A}_2 \oplus \dots \oplus \varvec{A}_r$ is a block-diagonal matrix with (block) diagonal terms given by $\varvec{A}_i \in \mathbb {R}^{n_i \times m_i}, \ n_i, m_i \in \mathbb {N}, \ \ i=1,\dots , r$. The $3 \times 3$ skew-symmetric matrix $[\varvec{t}]_{\times }$ is the equivalent matrix form for the cross-product with a 3D vector ${\varvec{t}}= [t_1, t_2, t_3]^T$, i.e., ${\varvec{t}}\times (\bullet ) = [\varvec{t}]_{\times } (\bullet )$ with

$$\begin{aligned}{}[\varvec{t}]_{\times } = \begin{bmatrix} 0 &{} -t_3 &{} t_2 \\ t_3 &{} 0 &{} -t_1 \\ - t_2 &{} t_1 &{} 0 \end{bmatrix} \end{aligned}$$

(1)

The columns of a matrix $\varvec{A}\in \mathbb {R}^{m \times n}$ are denoted by ¹, and its rows as $\varvec{a}_{i} \in \mathbb {R}^{n}, i = 1, \dots , m$. The operator ${\text {vec}}(\varvec{E})$ vectorizes the given matrix $\varvec{E}\in \mathbb {R}^{m \times n}$ column-wise, i.e. and $j = 1, \dots , n$. That is,

$$\begin{aligned} \varvec{E}= \begin{pmatrix} e_1 &{} e_2 &{} e_3 \\ e_4 &{} e_5 &{} e_6 \\ e_7 &{} e_8 &{} e_9 \\ \end{pmatrix} \end{aligned}$$

(2)

and so and $\varvec{e}_{1} = [e_1, e_2, e_3]^T$.

The Kronecker product is denoted as $\otimes$. We will denote the trace of a matrix as ${\text {tr}}(\varvec{A}) = \sum _{i=1}^n a_{ii}, \ \varvec{A}= [a_{ij}] \in \mathbb {R}^{n \times n}$. Further, for simplicity we will employ ${\text {tr}}({\varvec{A}}{\varvec{B}}) = \varvec{A}\bullet \varvec{B}, \forall \varvec{A}, \varvec{B}\in \mathbb {S}^{n}$. In this work we identify rotations with points in the rotation group $\text {SO}(3)\doteq \{ {\varvec{R}}\in \mathbb {R}^{3 \times 3} | {\varvec{R}}^T {\varvec{R}}= \varvec{I}_{3},\ \det ({\varvec{R}}) = 1$ } and define the 2-sphere as $\mathcal {S}^2\doteq \{ {\varvec{t}}\in \mathbb {R}^{3} | {\varvec{t}}^T {\varvec{t}}= 1 \}$. We will denote by $\mathcal {A} \setminus \mathcal {B}$ the classic difference or relative complement of the sets $\mathcal {A}$ and $\mathcal {B}$, i.e.$\mathcal {A} \setminus \mathcal {B} \doteq \{\varvec{x}\mid \varvec{x}\in \mathcal {A} \text { and } \varvec{x}\notin \mathcal {B}\}$ and by $\mathcal {A} \cup \mathcal {B}$ the union of the sets $\mathcal {A}$ and $\mathcal {B}$ defined as $\mathcal {A} \cup \mathcal {B} \doteq \{ \varvec{x}\mid \varvec{x}\in \mathcal {A} \text { or } \varvec{x}\in \mathcal {B} \}$. We will denote the cardinality of the set $\mathcal {A}$ (the number of elements in the set) by $|\mathcal {A}|$. Last, and always trying to keep the notation and ideas as clear as possible, we will use the same letter (e.g.L) to denote a set ($\mathcal {L}$, font: mathcal), the set of indices associated with this set ($\mathscr {L}$, font: mathscr (rsfso)) and the specific elements of the original set (${\mathbf {L}_j}$, font: mathbf) but with different fonts, that is: $\mathcal {L}\equiv \{{\mathbf {L}_j}, j \in \mathscr {L}\}$.

Fig. 2

Maximum error in rotation (Fig. 2a) and translation (Fig. 2b) in $90 \%$ of the problem instances between the solution obtained by minimizing the epipolar and the reprojection error for different level of noise (see legend) and number of correspondences (X-axis)

4 Minimal Relative Pose problem Formulation Based on Nullspaces

We follow previous works in the literature that introduce the essential matrix $\varvec{E}$ into the problem and minimize the sum of normalized squared epipolar errors $\epsilon _i^2$ [13, 15, 17, 21]. This error is algebraic and represents only an approximation of the (geometric) reprojection error. Nevertheless, as we show in Fig. 2, the solution obtained by this approximation tends to the one estimated with the reprojection error when the number of correspondences is large, even for highly noisy observations. This figure shows the maximum error in rotation and translation (in degrees) obtained in $90\%$ of the problem instances between both solutions for different level of noise and number of correspondences. To obtain the solution with the geometric error, we iteratively minimize (implemented with Ceres [37]) the reprojection error initializing the algorithm with the ground truth and the solution from our solver, and keeping the result with the lowest cost.

The cost function $f(\varvec{E})= \sum _{i=1}^N \epsilon _i^2$ can be written as a quadratic form on the elements in $\varvec{E}$ by defining the positive semi-definite (PSD) matrix $\mathbb {S}_+ ^{9} \ni {\varvec{Q}}= \sum _{i=1} ^N {\varvec{Q}}_i$, with ${\varvec{Q}}_i = ({\varvec{f}}_i'\otimes \varvec{f}_i)({\varvec{f}}_i'\otimes {\varvec{f}}_{i})^T \in \mathbb {S}_+ ^{9}$. Formally, the RPp reads:

$$\begin{aligned} f^{\star }= \min _{\varvec{E}\in \mathbb {E}} \sum _{i = 1} ^N ({\varvec{f}}_i'^T \varvec{E}{\varvec{f}}_{i}) ^2 = \min _{\varvec{E}\in \mathbb {E}} {\text {vec}}(\varvec{E})^T {\varvec{Q}}{\text {vec}}(\varvec{E}), \end{aligned}$$

(O)

that, for non-minimal problems with $N \ge 8$ correspondences and except in degenerate cases [1] has an unique global minimizer up to sign. In problem O, $\mathbb {E}$ stands for the set formed by the normalized essential matrices:

$$\begin{aligned} \mathbb {E}\doteq \{ \varvec{E}\in \mathbb {R}^{3 \times 3} \ \vert \ \varvec{E}= [\varvec{t}]_{\times } {\varvec{R}}, \ {\varvec{R}}\in \text {SO}(3), \ \varvec{t}\in \mathcal {S}^2\}. \end{aligned}$$

(3)

Fig. 3

Nullspaces ${\varvec{t}}, \varvec{q}\doteq {\varvec{R}}^T {\varvec{t}}$ of the essential matrix $\varvec{E}$. For any pair of correspondences $({\varvec{f}}_{i}, {\varvec{f}}_i')$, the “calibrated“ epipolar lines $\varvec{E}{\varvec{f}}_{i}, \varvec{E}^T {\varvec{f}}_i'$ vanish at the homogeneous coordinates of ${\varvec{t}}, \varvec{q}$, respectively

This set admits different parameterizations (see Sect. 2). In the context of building problem relaxations, the chosen definition of the set has a drastic effect on the performance of the method. In practice, we always seek a minimal parameterization of the search space that still assures the robustness of the algorithm.

4.1 Minimal Definition of the Essential Matrix Set

From the definition in (3) we see that the left nullspace of any essential matrix is one-dimensional (non-null) and it is identified with the translation vector ${\varvec{t}}$ (see Fig. 3). Further, we can define also the essential matrix as $\varvec{E}= {\varvec{R}}[{\varvec{R}}^T \varvec{t}]_x$ and so its right nullspace is also one-dimensional and it is identified with the translation (unit) vector $\varvec{q}\doteq {\varvec{R}}^T {\varvec{t}}$. These elements are the calibrated epipoles [1], and hence, they are endowed with geometric meaning, as it is shown in Fig. 3. The next two minimal characterizations arise naturally from these two equivalent definitions and the nullspaces ${\varvec{t}}, \varvec{q}$.

Definition 1

(Description $\mathcal {R}$ of the Essential Matrix Set) We can exploit the unitary condition of the rotation matrix ${\varvec{R}}$ to obtain the characterization:

$$\begin{aligned} \mathbb {E}_{\text {right}}\doteq \{ \varvec{E}\in \mathbb {R}^{3 \times 3} \vert \varvec{E}^T \varvec{E}= [\varvec{q}]_{\times }[\varvec{q}]_{\times }^T , \varvec{q}^T \varvec{q}= 1\}, \end{aligned}$$

(4)

where $\varvec{q}$ is the right nullspace of $\varvec{E}$.

Fig. 4

Pattern of the constraint matrices employed in a problem (SDP-R); b problem (SDP-L); c problem (SDP-B); d problem (SDP-ALL). In d, we mark in a lighter shade the anti-block-diagonal constraints $\mathbf {A}_k, \forall k \in (\mathscr {A}_{\text {left}}\cup \mathscr {A}_{\text {right}})$

Definition 2

(Description $\mathcal {L}$ of the Essential Matrix Set) [11, Prop. 2] The following description of the essential matrix set exploits also the unitary condition of the rotation matrix ${\varvec{R}}$ for its derivation:

$$\begin{aligned} \mathbb {E}_{\text {left}}\doteq \{ \varvec{E}\in \mathbb {R}^{3 \times 3} \vert \varvec{E}\varvec{E}^T = [\varvec{t}]_{\times }[\varvec{t}]_{\times }^T , {\varvec{t}}^T {\varvec{t}}= 1, {\varvec{t}}\in \mathbb {R}^{3}\} \end{aligned}$$

(5)

where ${\varvec{t}}$ is defined as the left nullspace of $\varvec{E}$. Note the symmetry between this parameterization and the one proposed in Def. 1.

The derivation of this definition is found in Theorem 1 in [15] and/or by noting that $\varvec{E}^T$ is essential iff $\varvec{E}$ is.

Each definition provides with different sets of seven independent and distinct constraints. The set $\mathcal {R}$ is formed by the definition in Def. 1 as:

(6)

where is the i-th column of the essential matrix $\varvec{E}$. For simplicity, we will denote by $\mathscr {R}_{\text {norm}}\doteq \{1\},\ \mathscr {R}_{\text {diag}}\doteq \{2, 3, 4\}, \ \mathscr {R}_{\text {odiag}}\doteq \{5, 6, 7\}$ the set of indices for the unitary norm, diagonal and off-diagonal constraints, respectively, and its union as $\mathscr {R}\doteq \{ \mathscr {R}_{\text {norm}}\cup \mathscr {R}_{\text {diag}}\cup \mathscr {R}_{\text {odiag}}\}$.

On the other hand, the description given in Def. 2 provides with the set $\mathcal {L}$ as:

$$\begin{aligned} \mathcal {L}\equiv {\left\{ \begin{array}{ll} &{} \text {(1): }t_1 ^2 + t_2 ^2 + t_3 ^2 = 1 \\ &{} \text {(2): }{\varvec{e}_{1}}^T \varvec{e}_{1} - t_2^2 - t_3 ^2 = 0 \\ &{} \text {(3): }{\varvec{e}_{2}}^T \varvec{e}_{2} - t_1^2 - t_3 ^2 = 0\\ &{} \text {(4): }{\varvec{e}_{3}}^T \varvec{e}_{3} - t_1^2 - t_2 ^2 = 0\\ &{} \text {(5): }{\varvec{e}_{1}}^T \varvec{e}_{2} + t_1 t_2 = 0\\ &{} \text {(6): }{\varvec{e}_{1}}^T \varvec{e}_{3} + t_1 t_3 = 0\\ &{} \text {(7): }{\varvec{e}_{2}}^T \varvec{e}_{3} + t_2 t_3 = 0 \end{array}\right. }, \end{aligned}$$

(7)

where $\varvec{e}_{i} \in \mathbb {R}^{3}$ denotes the i-th row of the essential matrix $\varvec{E}$. Let us denote by $\mathscr {L}_{\text {norm}}\doteq \{1\}, \mathscr {L}_{\text {diag}}\doteq \{2, 3, 4\},\mathscr {L}_{\text {odiag}}\doteq \{5, 6, 7\}$ the sets of indices for the unitary norm, the diagonal and off-diagonal constraints, respectively, and its union as the set of indices $\mathscr {L}\doteq \{ \mathscr {L}_{\text {norm}}\cup \mathscr {L}_{\text {diag}}\cup \mathscr {L}_{\text {odiag}}\}$. These equations were first given in [15].

4.2 Block SDP Relaxations for the Nullspace-Based Minimal Parameterizations

We obtain then two equivalent problems to original problem O by writing explicitly the set $\mathbb {E}$ with the two set of constraints $\mathbb {E}_{\text {left}}$ and $\mathbb {E}_{\text {right}}$, respectively. However problems like Prob. O are instances of QCQP, which in general are non-convex due to the number of quadratic constraints and NP-hard to solve in most cases [31]. Nevertheless, under certain conditions it is possible to derive tractable relaxations that allow us to obtain and certify the optimal solution to the original, non-convex problem. These relaxations have been proposed previously for other problems (see Sect. 2), showcasing a good performance and proving its usability. Empirically we show in Sect. 6 that this relaxation, which we introduce next, is also able to solve this non-convex problem for most problem instances, hence making it solvable in practice. For that, we first re-formulate our problems as the standard QCQP by introducing the vector with all the unknowns: the essential matrix and the corresponding translation vector (depending on the chosen definition of the set of essential matrices). Since both are similar, let us call this vector by $\varvec{x}= [\varvec{e}^T , \varvec{u}^T]^T \in \mathbb {R}^{12}$, where $\varvec{e}\in \mathbb {R}^{9}$ is the essential matrix $\varvec{E}$ vectorized by columns and $\varvec{u}$ is the corresponding translation vector. Problem O is written as

$$\begin{aligned} f^{\star }= \min _{\varvec{x}\in \mathbb {R}^{12}} \varvec{x}^T \varvec{C}\varvec{x}, \text { subject to } \varvec{x}^T \varvec{A}_i \varvec{x}= c_i, i=1, \dots , 7 \end{aligned}$$

(QCQP)

where the $12 \times 12$ matrix $\varvec{C}$ is the data matrix ${\varvec{Q}}$ padded with zeros and the forms $\varvec{x}^T \varvec{A}_i \varvec{x}= c_i, i=1, \dots , 7$ define the different constraints. By introducing the PSD matrix $\varvec{X}\in \mathbb {R}^{12 \times 12}$ we obtain the so-called Shor’s relaxation of problem QCQP:

$$\begin{aligned} g^{\star }= \min _{\varvec{X}\in \mathbb {R}^{12 \times 12}} \varvec{C}\bullet \varvec{X}, \text { subject to } \varvec{A}_i \bullet \varvec{X}= c_i, i=1, \dots , 7. \end{aligned}$$

(SDP)

As we show in Fig. 4 and explain in the Supplementary material A, for the definitions considered in this work, all the relaxations of the form in problem SDP have a block-diagonal pattern that is leveraged to simplify the optimization without losing information.

Remark 1

The sparsity of the problem and its effect on the optimal solution to the SDPs is related to the notion of chordal sparsity, as it was pointed out previously in [15]. We refer the reader to this work and references therein for more details, and to the recent work [38] for a similar application to polynomial problems through moment relaxations.²

Right-Nullspace-based formulation: We can define the vector variable for the standard QCQP as $\varvec{x}_{\text {Right}}= [\varvec{e}^T , \varvec{q}^T]^T \in \mathbb {R}^{12}$. With respect to this vector, the problem with the constraint set in Eq.  (6) is block-diagonal with two blocks of size $9 \times 9$ and $3 \times 3$, see Fig. 4a. Let us define the lifted matrices as: $\varvec{X}_{\varvec{e}} \doteq \varvec{e}\varvec{e}^T \in \mathbb {S}_+ ^{9}$ and $\varvec{X}_{\varvec{q}} \doteq \varvec{q}\varvec{q}^T \in \mathbb {S}_+ ^{3}$. The block SDP that is actually solved is

$$\begin{aligned} g^{\star }_{\text {R}}&= \min _{\varvec{X}_{\varvec{e}} \in \mathbb {R}^{9 \times 9}, \varvec{X}_{\varvec{q}} \in \mathbb {R}^{3 \times 3}} {\varvec{Q}}\bullet \varvec{X}_{\varvec{e}} \\&\text { subject to } \begin{aligned}&{{\mathbf {R}_i}^{\varvec{q}}}\bullet \varvec{X}_{\varvec{q}} = 1,&i \in \mathscr {R}_{\text {norm}}\\&{{\mathbf {R}_i}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + {{\mathbf {R}_i}^{\varvec{q}}}\bullet \varvec{X}_{\varvec{q}} = 0,&i \in \mathscr {R}\setminus \mathscr {R}_{\text {norm}}\\&\varvec{X}_{\varvec{e}} \succeq 0 \\&\varvec{X}_{\varvec{q}} \succeq 0 \end{aligned}, \end{aligned}$$

(SDP-R)

where we have defined the quadratic forms associated with the set $\mathcal {R}$ given in (6) as $\{ \mathbb {S}^{12} \ni {{\mathbf {R}_i}^{\varvec{e}}}\oplus {{\mathbf {R}_i}^{\varvec{q}}}\}_{i \in \mathscr {R}}$, such that each constraint is of the general form: $\varvec{e}^T {{\mathbf {R}_i}^{\varvec{e}}}\varvec{e}+ \varvec{q}^T {{\mathbf {R}_i}^{\varvec{q}}}\varvec{q}= r_i, \ i \in \mathscr {R}$, where $r_i \in \mathbb {R}^{}$.

Left-Nullspace-based formulation: Similarly, the vector variable for the standard QCQP is $\varvec{x}_{\text {Left}}= [\varvec{e}^T, {\varvec{t}}^T]^T \in \mathbb {R}^{12}$, and again, the problem with this variable and the constraint set in (7) is block-diagonal with two blocks of size $9 \times 9$ and $3 \times 3$, see Fig. 4b. Similarly, we define the lifted matrices as $\varvec{X}_{\varvec{e}} \doteq \varvec{e}\varvec{e}^T \in \mathbb {S}_+ ^{9}$ and $\varvec{X}_{{\varvec{t}}} \doteq {\varvec{t}}{\varvec{t}}^T \in \mathbb {S}_+ ^{3}$, and the block SDP that is actually solved by the solver is

$$\begin{aligned} g^{\star }_{\text {L}}&= \min _{\varvec{X}_{\varvec{e}} \in \mathbb {R}^{9 \times 9}, \varvec{X}_{{\varvec{t}}} \in \mathbb {R}^{3 \times 3}} {\varvec{Q}}\bullet \varvec{X}_{\varvec{e}} \\&\text { subject to } \begin{aligned}&{\mathbf {L}_j}^ {{\varvec{t}}} \bullet \varvec{X}_{{\varvec{t}}} = 1,&j \in \mathscr {L}_{\text {norm}}\\&{{\mathbf {L}_j}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + {\mathbf {L}_j}^ {{\varvec{t}}} \bullet \varvec{X}_{{\varvec{t}}} = 0,&j \in \mathscr {L}\setminus \mathscr {L}_{\text {norm}}\\&\varvec{X}_{\varvec{e}} \succeq 0 \\&\varvec{X}_{{\varvec{t}}} \succeq 0 \end{aligned}, \end{aligned}$$

(SDP-L)

where we have defined the quadratic forms associated with the set $\mathcal {L}$ given in (6) as $\{ \mathbb {S}^{12} \ni {{\mathbf {L}_j}^{\varvec{e}}}\oplus {{\mathbf {L}_j}^{{\varvec{t}}}}\}_{j \in \mathscr {L}}$ , such that each constraint is of the general form: $\varvec{e}^T {{\mathbf {L}_j}^{\varvec{e}}}\varvec{e}+ {\varvec{t}}^T {{\mathbf {L}_j}^{{\varvec{t}}}}{\varvec{t}}= l_j, \ j \in \mathscr {L}$, where $l_j \in \mathbb {R}^{}$.

Tight solution: Note that in both problems, each block has a norm constraint applied implying that the block cannot be the null matrix, i.e.it cannot have zero rank: the norms for the blocks $\varvec{X}_{{\varvec{t}}} , \varvec{X}_{\varvec{q}}$ are specified by the constraints in $\mathscr {L}_{\text {norm}}, \mathscr {R}_{\text {norm}}$, respectively, while the norm for the block $\varvec{X}_{\varvec{e}}$ is inferred by its relation with the other terms for both characterizations. Since original problem O has a unique solution (up to sign), we know that in order to consider the relaxation as tight, each block must have rank 1 for both problems (see Supplementary material A).

Nevertheless, while the formulations in Eq. (7) and (6) enjoy the benefit of having a minimal number of constraints, they lose tightness in certain scenarios, even in common scenarios, as we will show in Sect. 6.

Table 1 Set of constraints for each problem, the set of indices associated with each set of constraints and the cardinality of both sets, e.g.$|\mathcal {R}| = |\mathscr {R}| = 7$ in Problems SDP-R, SDP-L and equal to 6 in Problems SDP-B and SDP-ALL

5 Redundant Set of Constraints and Tighter Relaxations

With the only goal of finding a tighter SDP relaxation associated with the relative pose problem, we introduce redundant constraints in the problem.

5.1 Joining Left and Right-Nullspace-Based Definitions

Since we already have two different definitions of the essential matrix set in Def. 1 and Def. 2, we propose here to fuse them into a joint (redundant) characterization of the same set. This characterization requires, however, more variables (15: $\varvec{E}, {\varvec{t}}, \varvec{q}$) than those that leverage the minimal parameterizations in sets in Def. 1 (13: $\varvec{E}, \varvec{q}$) and in Def. 2 (13: $\varvec{E}, {\varvec{t}}$). While each set of constraints $\mathcal {R}, \mathcal {L}$ provides with seven independent expressions, the joint of both feasible sets does have a linearly dependent constraint in the expressions associated with the diagonal entries of $\varvec{E}\varvec{E}^T$ or $\varvec{E}^T \varvec{E}$. We discard one of these constraints in the set $\mathscr {L}$  ³. With a little abuse of notation and to keep the results clear, let us denote this reduced set once again as $\mathscr {L}$, whose cardinality is now 6 (c.f.Table 1). Therefore our joint characterization has only 13 independent constraints and 15 variables.

Sparse SDP Relaxation: As it was mentioned above, the set of constraints in Eq. (6) and (7) present a block-diagonal structure in terms of the vectors $\varvec{x}_{\text {Right}}$ and $\varvec{x}_{\text {Left}}$, respectively. Their union in terms of $\varvec{x}_{\text {Both}}= [\varvec{e}^T, {\varvec{t}}^T, \varvec{q}^T]^T \in \mathbb {R}^{15}$ is, therefore, also block-diagonal, see Fig. 4c. In this case, the lifted matrices in terms of the vector $\varvec{x}_{\text {Both}}$ are defined as $\varvec{X}_{\varvec{e}} \doteq \varvec{e}\varvec{e}^T \in \mathbb {S}_+ ^{9}, \ \varvec{X}_{\varvec{q}} \doteq \varvec{q}\varvec{q}^T \in \mathbb {S}_+ ^{3}, \ \varvec{X}_{{\varvec{t}}} \doteq {\varvec{t}}{\varvec{t}}^T \in \mathbb {S}_+ ^{3}$. The SDP is written in its block-diagonal form in terms of these lifted blocks as:

$$\begin{aligned} g^{\star }_{\text {B}}&= \min _{\varvec{X}_{\varvec{e}} \in \mathbb {R}^{9 \times 9}, \varvec{X}_{{\varvec{t}}} , \varvec{X}_{\varvec{q}} \in \mathbb {R}^{3 \times 3}} {\varvec{Q}}\bullet \varvec{X}_{\varvec{e}} \\&\text { subject to } \begin{aligned}&{{\mathbf {L}_j}^{{\varvec{t}}}}\bullet \varvec{X}_{{\varvec{t}}} = 1,&j \in \mathscr {L}_{\text {norm}}\\&{{\mathbf {R}_i}^{\varvec{q}}}\bullet \varvec{X}_{\varvec{q}} = 1,&i \in \mathscr {R}_{\text {norm}}\\&{{\mathbf {R}_i}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + {{\mathbf {R}_i}^{\varvec{q}}}\bullet \varvec{X}_{\varvec{q}} = 0,&i \in \mathscr {R}\setminus \mathscr {R}_{\text {norm}}\\&{{\mathbf {L}_j}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + {{\mathbf {L}_j}^{{\varvec{t}}}}\bullet \varvec{X}_{{\varvec{t}}} = 0,&j \in \mathscr {L}\setminus \mathscr {L}_{\text {norm}}\\&\varvec{X}_{\varvec{e}} \succeq 0 \\&\varvec{X}_{{\varvec{t}}} \succeq 0 \\&\varvec{X}_{\varvec{q}} \succeq 0. \end{aligned}, \end{aligned}$$

(SDP-B)

where all the data matrices ${\varvec{Q}}, {{\mathbf {L}_j}^{\varvec{e}}}, {{\mathbf {R}_i}^{\varvec{e}}}, ...$ are the same than those in problems SDP-R and SDP-L.

Tight solution: Since each block has a norm applied, i.e.their rank is strictly positive (see previous problems SDP-R and SDP-L) and the solution is still unique, we say that the relaxation in problem SDP-B is tight iff each block has rank 1.

Unfortunately, this extended problem is still not always tight, as showcased by the experiments in Sect. 6, although it is tighter than previous problems SDP-R and SDP-L.

5.2 Introducing More Constraints: SVD-Based Approach

The different parameterizations employed so far are defined in terms of geometric variables such as the baseline $\varvec{b}$ and the rotation ${\varvec{R}}$. The essential matrix, however, admits a second yet equivalent definition in terms of its singular value decomposition (SVD) [11, 39]. Concretely, any essential matrix can be decomposed as $\varvec{E}= \varvec{U}{\text {diag}}(\sigma , \sigma , 0) \varvec{V}^T$ where $\varvec{U}, \varvec{V}\in \text {SO}(3)$, ${\text {diag}}(\varvec{a}) \in \mathbb {R}^{n \times n}$ denotes the diagonal matrix whose diagonal is formed by the entries of $\varvec{a}\in \mathbb {R}^{n}$ and $\sigma \in \mathbb {R}^{}_ +$ (non-negative reals). Given the scale ambiguity of $\varvec{E}$ w.l.o.g we can fix $\sigma = 1$.

Theorem 1

(Polynomial Description of the Essential Matrix Set) A $3 \times 3$ real matrix has two non-null singular values equal to one and one zero singular value, i.e.it is an element of the set of normalized essential matrices [11, 39], iff it fulfills the following set of polynomial constraints:

$$\begin{aligned}&\mathbb {E}_{\text {adj}}\doteq \Bigg \{ \varvec{E}\in \mathbb {R}^{3 \times 3} \Bigg \vert \begin{aligned}&{\text {tr}}(\varvec{E}\varvec{E}^ T) = 2, \\&\det (\varvec{E}) = 0, \\&{\text {tr}}\big ({\text {Adj}}{(\varvec{E}\varvec{E}^T)}\big ) = 1 \\ \end{aligned} \Bigg \}, \end{aligned}$$

(8)

where ${\text {Adj}}{(\varvec{E})}$ denotes the adjugate of the matrix $\varvec{E}$. Proof in Supplementary material Section B.

The constraints in Th. 1 are equivalent to those proposed by Faugeras and Maybank [11, Prop. 3]. We provide the proof in the Supplementary material Section C and thanks an anonymous reviewer for pointing out this relation. Before continue, the reader may notice that only three constraints are provided in Th. 1 . Since the set of constraints are equivalent to those in [11, Prop. 3], the proof provided in the same paper in Section 4.2 also applies here, and the constraints in Th. 1 are restricted to real matrices.

Whereas Th 1 defines the set of normalized essential matrices, it can be generalized to the non-normalized set (the non-null singular values do not need to be equal to one) by scaling the constraints, that is: ${\text {tr}}(\varvec{E}\varvec{E}^ T) = 2 \sigma ^2$ and ${\text {tr}}( {\text {Adj}}{(\varvec{E}\varvec{E}^ T)})= \sigma ^4$, for any matrix $\varvec{E}$ with singular value $\sigma$. The sufficient condition is similar to that in Th. 1.

Still, the constraints in Th. 1 are polynomial and, thus, cannot be directly incorporated into our primal QCQP problem in order to derive the associated SDP. We provide next a set of quadratic constraints equivalent to Th. 1.

Definition 3

(Description $\mathcal {A}$ of the Essential Matrix Set) The following set of quadratic constraints is equivalent to the set proposed in Th. 1.

$$\begin{aligned}&{\text {tr}}(\varvec{E}\varvec{E}^ T) = 2 \qquad \varvec{E}\varvec{q}= \varvec{0}_{3 \times 1} \qquad \varvec{q}^T\varvec{q}= 1 \end{aligned}$$

(9)

$$\begin{aligned}&{\text {Adj}}{(\varvec{E})} = \varvec{q}{\varvec{t}}^T \qquad {\varvec{t}}^T \varvec{E}= \varvec{0}_{1 \times 3} \qquad {\varvec{t}}^T{\varvec{t}}= 1 , \end{aligned}$$

(10)

where ${\varvec{t}}, \varvec{q}$ are the left and right nullspaces of $\varvec{E}$, respectively, and ${\text {Adj}}{(\varvec{E})}$ is the adjugate matrix of $\varvec{E}$.

Supplementary material Section D includes the relation between Def. 3 and the one in Th. 1. Notice that, in general, ${\text {Adj}}{(\varvec{E})} =\pm \varvec{q}{\varvec{t}}^T$, but since $\varvec{q}$ and ${\varvec{t}}$ are identified with points in $\mathcal {S}^2$, the sign ambiguity is absorbed by any of the vectors and we can simply the expression to ${\text {Adj}}{(\varvec{E})} = \varvec{q}{\varvec{t}}^T$.

Thus, a $3 \times 3$ real matrix $\varvec{E}$ is a normalized essential matrix iff it fulfills the constraints in Definition 3 since these quadratic constraints are equivalent to the polynomial set in Th. 1 and the latter defines the set of normalized essential matrices.

The explicit forms of the constraints in Def. 3 are given as:

(11)

where $e_i$ is the i-th element of the 9D vector $\varvec{e}= {\text {vec}}(\varvec{E})$. Let us for simplicity define the set of indices $\mathscr {A}_{\text {norm}}\doteq \{1\}$, $\mathscr {A}_{\text {adj}}\doteq \{2, \dots , 10\}$, $\mathscr {A}_{\text {right}}\doteq \{11, 12, 13\}$, $\mathscr {A}_{\text {left}}\doteq \{14, 15, 16\}$ corresponding with the norm of the essential matrix (${\text {tr}}(\varvec{E}\varvec{E}^ T) = 2$), the adjugate expression (${\text {Adj}}{(\varvec{E})} = \varvec{q}{\varvec{t}}^T$) and the right and left nullspaces ($\varvec{E}\varvec{q}= \varvec{0}_{3 \times 1},\ {\varvec{t}}^T \varvec{E}= \varvec{0}_{1 \times 3}$), respectively. We define its union as $\mathscr {A}\doteq \{ \mathscr {A}_{\text {norm}}\cup \mathscr {A}_{\text {right}}\cup \mathscr {A}_{\text {left}}\cup \mathscr {A}_{\text {adj}}\}$.

See that this equivalent characterization only depends on the nullspaces of $\varvec{E}$. This means we can combine the constraints of this parameterization with those from our previous characterization with both nullspaces in Problem SDP-B without introducing new variables. We note that two of the constraints associated with the diagonal terms $\varvec{E}\varvec{E}^T$ and $\varvec{E}^T \varvec{E}$ in sets Def. 2 and Def. 1 became dependent when introducing the constraints in Def. 3. Without confusion, let us denote these sets of linear independent constraints⁴ by $\mathcal {L}, \mathcal {R}, \mathcal {A}$, with cardinality 6, 6 and 16, respectively (see Table 1). Therefore, this characterization has only 28 independent constraints and 15 variables.

Remark 2

Here we introduce redundant constraints to the RPp that define the set of normalized essential matrices. Note that this procedure is different to the (automatically) generated constraints by Lassarre’s moment relaxations for polynomial problems with available tools such as Gloptipoly 3 [40]. Our approach follows the idea exploited in previous works (see Section 2) with rotation matrices.

By writing explicitly the set of constraints in Def. 3 in terms of the vector variable $\varvec{x}_{\text {Adj}}\doteq [\varvec{e}^T, {\varvec{t}}^T, \varvec{q}^T ]^T \in \mathbb {R}^{15}$ we can re-formulate the original problem in Eq. (O) as a standard QCQP. Unlike other problems SDP-R, SDP-L and SDP-B where the sparsity pattern was easily identified in terms of the corresponding variable vectors (see Fig. 4a–c), the definition in $\mathcal {A}$ presents six equations associated with the nullspaces (with indices in $\mathscr {A}_{\text {left}}, \mathscr {A}_{\text {right}}$) that do not follow the same pattern as the other constraints and the objective function (which have a well-defined block-diagonal structure). These constraints have an anti-block-diagonal structure, as shown in Fig. 4d. In practice, however, the problem is also block-diagonal for any optimal solution. Notice that the anti-block-diagonal constraints are trivially satisfied by the zero blocks. Further, this block-diagonal solution will have rank greater than one even when the relaxation is tight, as the previous formulations. Central-path algorithms, as the one leveraged by off-the-shelf tools such as SeDuMi and SDPT3, will return this solution [41] instead of the rank one. Therefore, we can restrict, as in the previous formulations, the feasible points to be block-diagonal. Empirically we verify that removing the anti-block diagonal constraints $(\mathscr {A}_{\text {left}}\cup \mathscr {A}_{\text {right}})$ does not affect the tightness of the relaxation nor affects the computational cost of the resolution of the problem. Please, notice that in the solvers are actually dropping the off-diagonal constraints, i.e.the determinant requirement, without notice. Since these constraints are employed with the previous ones, we known that the returned solution will have null determinant if the relaxation is tight. Nevertheless, the constraints alone may yield solutions with non-null determinant. This is an interesting behavior which we pretend to study on the future since it may jeopardize convex relaxations with this structure.

In what follows, we drop the anti-block diagonal constraints in the set of constraints $\mathcal {A}$ for clarity. This allows to directly write the SDP relaxation with this feasible set as a block problem. Note that the SDP relaxation with all the constraints can be derived in a similar manner. As before, let us define the lifted matrices as $\varvec{X}_{\varvec{e}} \doteq \varvec{e}\varvec{e}^T \in \mathbb {S}_+ ^{9}$ and $\varvec{X}_{\text {null}} \doteq [{\varvec{t}}^T, \varvec{q}^T]^T [{\varvec{t}}^T, \varvec{q}^T] \in \mathbb {S}_+ ^{6}$. See that the adjugate constraints in Def. 3 relate both nullspaces and hence, only one block is defined for them, in contrast with the two blocks in Problem SDP-B. The block SDP relaxation is written in terms of these matrices as

$$\begin{aligned} g^{\star }_{\text {Adj}}&= \min _{ \begin{array}{c} \varvec{X}_{\varvec{e}} \in \mathbb {R}^{9 \times 9}, \varvec{X}_{\text {null}} \in \mathbb {R}^{6 \times 6} \end{array}} {\varvec{Q}}\bullet \varvec{X}_{\varvec{e}} \end{aligned}$$

(SDP-ALL)

$$\begin{aligned}&\text { subject to } \nonumber \\&\begin{aligned}&({{\mathbf {L}_j}^{{\varvec{t}}}}\oplus \varvec{0}_{3 \times 3} ) \bullet \varvec{X}_{\text {null}} = 1,&j \in \mathscr {L}_{\text {norm}}\\&(\varvec{0}_{3 \times 3} \oplus {{\mathbf {R}_i}^{\varvec{q}}}) \bullet \varvec{X}_{\text {null}} = 1,&i \in \mathscr {R}_{\text {norm}}\\&{\mathbf {A}_k^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} = 2,&k \in \mathscr {A}_{\text {norm}}\\&{{\mathbf {R}_i}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + (\varvec{0}_{3 \times 3} \oplus {{\mathbf {R}_i}^{\varvec{q}}}) \bullet \varvec{X}_{\text {null}} = 0,&i \in \mathscr {R}\setminus \mathscr {R}_{\text {norm}}\\&{{\mathbf {R}_i}^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + ({{\mathbf {L}_j}^{{\varvec{t}}}}\oplus \varvec{0}_{3 \times 3} ) \bullet \varvec{X}_{\text {null}} = 0,&j \in \mathscr {L}\setminus \mathscr {L}_{\text {norm}}\\&{\mathbf {A}_k^{\varvec{e}}}\bullet \varvec{X}_{\varvec{e}} + {\mathbf {A}_k^{{\varvec{t}}, \varvec{q}}}\bullet \varvec{X}_{\text {null}} = 0,&k \in \mathscr {A}_{\text {adj}}\\&\varvec{X}_{\varvec{e}} \succeq 0 \\&\varvec{X}_{\text {null}} \succeq 0 \end{aligned} \end{aligned}$$

(12)

where we have defined the quadratic forms associated with the set $\mathcal {A}$ as ${\mathbf {A}_k^{\varvec{e}}}\oplus {\mathbf {A}_k^{{\varvec{t}}, \varvec{q}}}\in \mathbb {S}^{15}$ for $k \in \mathscr {A}_{\text {norm}}\cup \mathscr {A}_{\text {adj}}$ such that each constraint is of the general form $\varvec{e}^T {\mathbf {A}_k^{\varvec{e}}}\varvec{e}+ [{\varvec{t}}^T, \varvec{q}^T] {\mathbf {A}_k^{{\varvec{t}}, \varvec{q}}}[{\varvec{t}}^T, \varvec{q}^T ] ^T = a_k, \ k \in \mathscr {A}_{\text {norm}}\cup \mathscr {A}_{\text {adj}}$ where $a_k \in \mathbb {R}^{}$. The remaining matrices have the same form than in previous problems SDP-R, SDP-L.

Tight solution: Note that both blocks, $\varvec{X}_{\varvec{e}} , \varvec{X}_{\text {null}}$ have norm constraints: in this case, the norm of $\varvec{X}_{\varvec{e}}$ is given by the constraint $\mathscr {A}_{\text {norm}}$ and the norm for $\varvec{X}_{\text {null}}$ is given by the constraints $\mathscr {L}_{\text {norm}}, \mathscr {R}_{\text {norm}}$. Since the problem still admits only a unique global minimizer, the tight solution has two blocks of rank 1 each.

6 Experimental Validation

In this section we prove through extensive experiments on both synthetic and real data the claims stated in this work.

6.1 Experiments on Synthetic Data

We carried out two types of experiments. In Sect. 6.1.1 we generate random instances of the RPp with “usual“ parameters. In Sect. 6.1.2 we increase the noise and include outliers in order to show that our final formulation in problem SDP-ALL remains tight in almost all the cases, while maintaining an attractive computation time.

Generation of Random Data: We generate random problem instances by following the procedure given in previous works [14, 21], which we summarize it here for completeness. We place the first camera frame at the origin (identity orientation and zero translation) and generate a set of random 3D points within a frustum with depth ranging from one to eight meters measured from the first camera frame and inside its Field of View (FOV). Then, we generate a random pose for the second camera whose translation magnitude is constrained within a spherical shell with minimum radio $||{\varvec{t}}||_{\text {min}}$, maximum radio $||{\varvec{t}}||_{\text {max}}$ and centered at the origin. We also enforce that all the 3D points lie within the second camera’s FOV. Next, we create the correspondences as unit bearing vectors and add noise by assuming a spherical camera, computing the tangential plane at each bearing vector (point on the sphere) and introducing a random error in pix sampled from the standard uniform distribution, considering a focal length of 800 pixels for both cameras. Outliers are generated by assigning a random unit vector to the correspondence associated with the second frame.

Compared methods: We compare the four different formulations proposed in this work (LEFT coincides with the proposal in [15]) and includes that by Briales et al.in [14]. The different formulations will be denoted by: LEFT (Problem SDP-L); RIGHT (Problem SDP-R); BOTH (Problem SDP-B); ADJ (Problem SDP-ALL); and [14] as BKG. Although BKG employs a different formulation for the RPp based on the rotation and the position components (in this work, the translation vector denoted by ${\varvec{t}}$), the underlying problem is the same.

Note that other certifiable approaches for the RPp do exist, as we illustrate in Sect. 2. Here, however, we compare only the above-mentioned certifiable solvers based on SDP relaxations [14, 15]. Our reasons behind this are the following. First, in [15] and [14] the authors independently reported that their, respectively, SDP solvers consistently attain lower rotation errors than the minimal methods (five, six and eight points algorithms, see Sect. 2) and the non-minimal solver by Kneip and Lynen in [24] w.r.t.the ground truth relative pose, which can be considered as the state-of-the-art solvers both for accuracy and efficiency. The different formulations proposed in this work have the same or more number of constraints than the minimal SDP in [15]; hence, we expect to, at least, observe the same performance in terms of accuracy, if not better. The computational times are also similar under a C++ implementation with SDPA [42] as IPM on a standard PC with CPU $i7-4702$MQ, $2.2$GHz and $8$ GB RAM: LEFT takes 5 milliseconds, RIGHT goes to 4.7 milliseconds, BOTH to 7.4 milliseconds and ADJ to 7 milliseconds. These times include the creation of the data matrix ${\varvec{Q}}$, the extraction of the solution $\varvec{x}$ from $\varvec{X}^{\star }$ (the optimal solution of the SDP) and the projection of $\varvec{x}$ onto the space of essential matrices.

Fig. 5

Synthetic data: common parameters: Dual gap for the obtained solution after projection onto the set of essential matrices (a), error in rotation in degrees (b), error in translation in degrees (c) and cost normalized by the one obtained by BKG (d) for the set of experiments with noise 0.5 pix (noise $6e-04$ in normalized coordinates). Similar graphics for noise 2.5 pix (noise $3e-03$ in normalized coordinates) can be found in Supplementary material 2 Fig. 6

6.1.1 Experiments on Usual Synthetic Data

In this set of experiments, we fix the available parameters when generating the data (FOV, parallax, noise and number of correspondences) and vary one of them each time to show the influence of each individual parameter. By default, we fix the FOV to 100 degrees, the translation parallax to $||\varvec{t}||_2 \in [0.5, 2.0] \;(\text {meters})$, the noise level to 0.5 pix and the number of correspondences to 100. In the experiments we let the focal length fixed, since it was shown in [21] that varying the focal length has the same effect of varying the noise level and field of view (changes in the signal-to-noise ratio). We generate problem instances with number of correspondence in $N \in \{8, 9, 10, 11, 12, 13, 14, 15, 20, 40, 100, 150, 200 \}$ and varying noise $\sigma _{\text {noise}} \in \{0.1, 0.5, 1.0, 2.5\}\;{\texttt {pix}}$, parallax $||{\varvec{t}}||_{max} \in \{0.7, 1.0, 2.5, 4.0\}$ and $\text {FOV}\in \{70, 90, 120, 160 \}$. Please, notice that in this work we consider only non-minimal problem instances with more than $N = 8$ correspondences. For each configuration of number of correspondences and parameters, we generate 200 random problem instances. Due to space restrictions and the similarity on the conclusions, we only include in Fig. 5 the results for noise 0.5 pix (results for noise 2.5 pix can be found in Supplementary material 2 Fig. 6). Figure 5a shows the dual gap between the optimal dual cost and the essential matrix obtained after projection on the feasible set [1]. Observe that for ADJ, the dual gap is constant, while for the smallest formulations it decreases with the number of correspondences and noise level. A more intuitive metric of this behavior is the error $\epsilon _{\text {rot}}$ of the estimated rotation $\hat{{\varvec{R}}}$ w.r.t.the ground truth ${\varvec{R}}_{gt}$ measured in terms of geodesic distance, and the translation error $\epsilon _{\text {trans}}$ as the angle (in degrees) between the (normalized) translation vector $\hat{{\varvec{t}}}$ and the ground truth ${\varvec{t}}_{gt}$, i.e.

$$\begin{aligned} \epsilon _{\text {rot}}&= \arccos \Big ( \frac{{\text {tr}}(\hat{{\varvec{R}}}^T {\varvec{R}}_{\text {gt}}) - 1}{2}\Big ) \frac{180}{\pi } ~[\text {degrees}] \end{aligned}$$

(13)

$$\begin{aligned} \epsilon _{\text {trans}}&= \arccos \Big ( \hat{{\varvec{t}}}^T {\varvec{t}}_{\text {gt}}\Big ) \frac{180}{\pi } ~[\text {degrees}] \end{aligned}$$

(14)

Figure 5b shows the rotation error and Fig. 5c the translation error for the four proposed solvers. Last, we compare the obtained solution with that from BKG and plot the ratio between each cost in Fig. 5d. Notice the tendency of the cost being closer to the one by BKG when the number of constraints is non-minimal. From this last figure we notice that the redundant formulation ADJ performs in most cases similarly to BKG, which can be considered as the state-of-the art given the obtained results, while requires less computational time for its resolution.

6.1.2 Experiments on Extreme Synthetic Data

In this set of synthetic experiments we show the performance of the proposed formulations in the presence of high noise level (up to $100~{\texttt {pix}}$) and high ratio of outliers (up to $100\%$). First, we fix the FOV and maximum parallax to their default values and vary the noise level as $\sigma \in \{ 5, 10, 50, 100 \}$ together with the number of correspondences (outliers are zero). Second, we let the noise be 0.5 pixels, fix the number of correspondences to 100 and introduce an increasing percentage of outliers (with step $10 \%$) up to $100\%$. For each combination of parameters, we generate 200 random problems. We want to remark that in these experiments we do not filter the outlier and simply feed the algorithms with all the correspondences. Due to space limits, we move the graphics to the Supplementary material 2 Section G Figure 7 and include here the main conclusions from them. In these cases, the dual gap is large for the minimal formulations LEFT and RIGHT, and the redundant BOTH, even when the number of correspondences is non-minimal. For ADJ, though, the dual gap is similar to the “normal“ problem instances in Fig. 5 except for a few problem instances with $N < 15$. The poor performance of the minimal solvers and BOTH is also reflected in the costs attained by their solution w.r.t.BKG. A similar conclusion is derived from the problem instances with outliers, and the smaller solvers fail to return the global optimum even with only $10\%$ of outliers.

6.2 Experiments on Real Data

To conclude our experimental validation, we evaluate the performance of the above-mentioned methods on real data. We sample pairs of images from 18 different sequences of the ETH3D dataset [43], which covers both indoor and outdoor scenes. They also provided with ground truth data and intrinsic calibration parameters. To generate the correspondences, we extract and match 100 SURF [44] features. The corresponding bearing vectors are computed by employing the pin-hole camera model with the provided intrinsic parameters for each image. We conduct two types of experiments with the same sequences of images and extracted features. Since the results are similar to those obtained in the synthetic experiments, we move the graphics to the Supplementary material 2 Section H Figure 8 and include only the main conclusions.

6.2.1 Experiments on Real Data with Outliers

The first set pretends to show the performance of the different methods under real data, including outliers, i.e.we feed the methods with all the points. Since the data contain outliers, LEFT, RIGHT and BOTH fail to return the optimal solutions for some problem instances (large normalized cost). ADJ, on the other side, shows the same robust performance.

6.2.2 Experiments of Real Data with Pre-filtered Outliers

The goal of this set is to reflect the performance of the different formulations only under real noise, without outliers. To discard outliers, we filter the matches with the provided ground truth and keep only those correspondences whose associated squared epipolar error w.r.t.the ground truth essential matrix is lower than a fixed threshold $\epsilon _{\text {error}}$, i.e.we consider as inliers all the correspondences (${\varvec{f}}_{i}, {\varvec{f}}_i'$) such that $({\varvec{f}}_i'^T \varvec{E}_{\text {gt}} {\varvec{f}}_{i}) ^2 < \epsilon _{\text {error}}$. We avoid the explicit used of a filtering stage (e.g.RANSAC) to decouple the performance of said stage and the different methods tested in this work. In this case, the costs are lower but the minimal solvers still fail to estimate the optimal solution (the percentage of suboptimal solutions remains above $20\%$). ADJ and BKG always return the optimal solution.

7 Conclusions and Future Work

In this work we have leveraged equivalent quadratic (global) definitions of the set of essential matrices which rely on the translation vectors of the relative pose between cameras. The Relative Pose problem is stated as an optimization problem over the set of essential matrices that minimizes the (squared) normalized epipolar error. We have combined these definitions to derive overconstrained problems. Despite the number of variables and constraints, all our formulations were solved in less 7 milliseconds on a standard computer, making our proposal suitable for real-world applications. The final formulation with 28 constraints and 15 variables allowed to derive a convex relaxation that remained tight under a wide variety of configurations, even with random correspondences (noise level of 100 pix and $100\%$ of outliers). Thus, our proposal is tighter than smaller formulations while being faster than overconstrained formulations.

Our results show that these formulations can be leveraged in other certifiable approaches, such as certifiers, which could potentially perform better than those based on minimal representations [21]. Since the tightness of the formulations is maintained even with outliers, our proposal is also suitable to be included in robust schemes, such as the combination of Graduated Non-Convexity [45] and the Black-Rangarajan duality between outlier rejection and line processes [46].