A Multi-view Camera Model for Line-Scan Cameras with Telecentric Lenses

Abstract

We propose a novel multi-view camera model for line-scan cameras with telecentric lenses. The camera model supports an arbitrary number of cameras and assumes a linear relative motion with constant velocity between the cameras and the object. We distinguish two motion configurations. In the first configuration, all cameras move with independent motion vectors. In the second configuration, the cameras are mounted rigidly with respect to each other and therefore share a common motion vector. The camera model can model arbitrary lens distortions by supporting arbitrary positions of the line sensor with respect to the optical axis. We propose an algorithm to calibrate a multi-view telecentric line-scan camera setup. To facilitate a 3D reconstruction, we prove that an image pair acquired with two telecentric line-scan cameras can always be rectified to the epipolar standard configuration, in contrast to line-scan cameras with entocentric lenses, for which this is possible only under very restricted conditions. The rectification allows an arbitrary stereo algorithm to be used to calculate disparity images. We propose an efficient algorithm to compute 3D coordinates from these disparities. Experiments on real images show the validity of the proposed multi-view telecentric line-scan camera model.

1 Introduction

Line-scan cameras play an important role in machine vision applications. The main reason is the lower cost per resolution in comparison to area-scan cameras. Since the image height only depends on the number of acquired lines, it is essentially unlimited. Because line-scan cameras with lines of up to 16 384 pixels are currently available [43, Chapter 2.3.4], images with several hundred megapixels can be easily acquired. Line-scan cameras are therefore used, for example, in applications in which small objects must be inspected over a large field of view or very high accuracy is required.

A 2D image is obtained from a line-scan camera by moving the sensor with respect to the object. Each line of the 2D image is acquired separately during the relative motion of the sensor. The acquired lines are stored in the 2D image from top to bottom as they are acquired, i.e., the row coordinate is directly related to the time at which a line was acquired.

In machine vision applications, the relative motion is realized either by mounting the camera above the moving object or by moving the camera across the stationary object [43, Chapter 2.3.1.1]. In most applications, the motion is carried out by a conveyor belt, a linear motion slide, or other linear actuators. As these examples show, in almost all machine vision applications, a linear motion is applied. Hence, the camera moves with constant velocity along a straight line relative to the object while the orientation of the camera is constant with respect to the object [14]. In practice, a linear motion can be realized by using appropriate encoders that ensure a constant speed [43, Chapter 2.3.1.1], [1, Chapter 6.8]. We will assume a linear motion of the camera in this paper.

For stereo reconstruction, the rectification of the stereo image pair into the epipolar standard configuration is essential for an efficient search for corresponding points. Unfortunately, for line-scan cameras with entocentric (i.e., perspective) lenses, no such rectification exists in general (see below). Machine vision applications generally are performed online. Therefore, an efficient epipolar rectification is essential.

A camera model for setups with a single line-scan camera with a telecentric lens has been recently proposed in [42]. In contrast to entocentric lenses, which perform a perspective projection, telecentric lenses perform a parallel projection of the world into the image.

In this paper, we extend the single-view telecentric line-scan camera model proposed in [42] to the multi-view case with an arbitrary number of cameras. Since there currently are no multi-view camera models for telecentric line-scan cameras that we are aware of, we discuss the most closely related work on two-view camera models for entocentric line-scan cameras in Sect. 2. We then propose our novel multi-view camera model for telecentric line-scan cameras in Sect. 3. In Sect. 4, we propose an algorithm to calibrate a multi-view setup. In Sect. 5.1, we describe a novel geometric algorithm that can be used to rectify a telecentric line-scan stereo image pair to the epipolar standard configuration. In Sect. 5.2, we describe how distances can be computed efficiently from a rectified telecentric line-scan stereo image pair. The experiments in Sect. 6 show the validity of the proposed multi-view telecentric line-scan camera on real-world images. Finally, Sect. 7 concludes the paper.

2 Related Work

We have been unable to find any publications that describe a multi-view camera model for line-scan cameras with telecentric lenses and for a corresponding 3D reconstruction. The closest approaches we have found are publications that describe a two-view stereo reconstruction with line-scan cameras with entocentric lenses. We will discuss these approaches in this section.

Gupta and Hartley [14] considered the uncalibrated two-view case and showed that for two entocentric line-scan cameras without lens distortions, the epipolar lines are actually not straight lines but hyperbolic arcs. Kim [21] examined the epipolar geometry for calibrated cameras in a remote-sensing context in more detail and also showed that the epipolar lines are hyperbolic arcs. Furthermore, he showed that the epipolar arcs are not even conjugate, i.e., if the epipolar arc in the second image of one point in the first image is computed and then the epipolar arcs in the first image for different points on the epipolar arc in the second image are computed, in general, they will be different. This shows that entocentric stereo images generally cannot be rectified rigorously. Rectification in this context means that the stereo image pair is transformed in such a way that the epipolar lines are straight and horizontal and that corresponding epipolar lines are located at the same row coordinate in both rectified images. This epipolar standard configuration is extremely important to achieve a high computation speed in stereo reconstruction algorithms.

Because of the importance of the epipolar standard configuration, Habib et al. [15, 16] examined under which conditions entocentric line-scan stereo images without lens distortions can be rectified to this configuration. They derived that there are exactly two configurations for which this is possible:

• The ideal across-track configuration, for which there must be a certain time at which the base (the vector between the projection centers of the two cameras) and the line sensor of the second camera are coplanar with the line sensor of the first camera at a particular (potentially different) instance of time. In simplified terms, this means that the base and the two line sensors must be coplanar (modulo the fact that one camera may be ahead or behind in time). In this configuration, the epipolar lines are given by corresponding rows in both images.

• The ideal along-track configuration, for which the base and the motion vector must be parallel. In this configuration, one camera is ahead and looks backward onto the scene, while the other camera is behind and looks forward onto the scene. The base refers to the separation on the track of the two projection centers at a particular instance of time. In this configuration, the epipolar lines are given by corresponding columns in both images.

Habib et al. [15, 16] also conclude that for all other configurations, a rigorous rectification requires that a 3D reconstruction of the scene is already available. We would like to add to this analysis that this is also the case if lens distortions are allowed and if the principal point does not lie exactly on the sensor line. Requiring a 3D reconstruction to be available for the purpose of epipolar rectification, of course, defeats the entire purpose of the rectification. Finally, Habib et al. [15, 16] derive that an epipolar rectification would always be possible if the cameras performed a parallel projection because the epipolar lines would be straight in this case. This idea is picked up by Morgan et al. [32], who approximate the epipolar geometry of two entocentric line-scan cameras by that of two virtual cameras that perform a parallel projection. Since the actual cameras are entocentric, this causes a geometric error in the rectified images. Another approach to approximate the epipolar arcs of entocentric line-scan cameras by straight line segments is described by Wang et al. [48, 49]. Finally, an approximate epipolar rectification approach that uses a local approximation by a parallel projection in image tiles is described by de Franchis et al. [7]. All of these approximate rectification approaches make use of the fact that the lenses of spaceborne line-scan cameras have large focal lengths and, therefore, a narrow field of view. These approximations no longer work for line-scan cameras with short focal lengths, i.e., a wide field of view, which are used in close-range applications.

A few entocentric line-scan stereo systems for industrial applications have been described in the literature, both for the across-track as well as the along-track configuration. The system by Calow et al. [6] and Ilchev et al. [19] uses two line-scan cameras that are aligned manually using a suitable mechanical device so that the sensor lines are approximately coplanar. The papers do not disclose in detail how this alignment is achieved, i.e., how it is determined that the sensor lines are coplanar, and how much effort must be spent to align the sensor lines. The system by Lilienblum and Al-Hamadi [27] also uses coplanar sensor lines. The authors describe that they constructed an adjustment device with which they could align the sensor lines to be coplanar within 10% of a pixel using differential micrometer screws that have an adjustment accuracy of 0.5 ${\upmu }\mathrm{m}$. Unfortunately, they neither disclose the costs of the adjustment device nor how the alignment was actually performed and how much time it took them to align the sensor lines. The system by Sun et al. [44, 45] also uses the across-track configuration. The authors mention that their sensor lines must be aligned to within a few arc seconds in order to have a misalignment between the epipolar lines that is small enough for the stereo matching to succeed. Like in the other papers, the authors unfortunately do not disclose how the alignment is achieved and how much time is necessary to align the sensors. Finally, the system by Godber et al. [12] uses the along-track configuration. The authors state that the epipolar lines are vertical in their configuration without explicitly deriving that this only is true for the ideal along-track case. They also do not describe how their cameras are aligned to achieve this configuration.

As can be seen from the above discussion, stereo reconstruction with entocentric line-scan cameras is complex. To be able to perform an epipolar rectification, we need to bring the cameras into one of the two ideal configurations and we need to ensure that the sensor line is mounted exactly behind the principal point. This requires expensive precision equipment and cumbersome manual labor. In contrast, we will show in this paper that stereo reconstruction is much simpler and, therefore, cheaper and more user-friendly if line-scan cameras with telecentric lenses are used.

3 Multi-view Camera Model

3.1 Exterior and Relative Orientation

To define a multi-view camera model for telecentric line-scan cameras, we use the same approach as [40, Section 6.1] to define the exterior and relative orientations, which we summarize here briefly.

We assume that there are $n_{\mathrm {c}}$ telecentric line-scan cameras in the multi-view setup. Furthermore, we use $n_{\mathrm {o}}$ images of a calibration object in different poses acquired by the $n_{\mathrm {c}}$ cameras for calibration. We enumerate the calibration object poses with the variable l ($l = 1, \ldots , n_{\mathrm {o}}$) and the cameras with the variable k ($k = 1, \ldots , n_{\mathrm {c}}$).

The exterior orientation of the calibration object with respect to a reference camera coordinate system is specified by a rigid 3D transformation. It transforms a point ${\varvec{{p}}}_{\mathrm {o}} = (x_{\mathrm {o}}, y_{\mathrm {o}}, z_{\mathrm {o}})^\top$ in the calibration object coordinate system into a point ${\varvec{{p}}}_l$ in the reference camera coordinate system as follows:

$$\begin{aligned} {\varvec{{p}}}_l = {{{\mathbf {\mathtt{{{R}}}}}}}_l {\varvec{{p}}}_{\mathrm {o}} + {\varvec{{t}}}_l \quad . \end{aligned}$$

(1)

Here, ${\varvec{{t}}}_l = (t_{l,x}, t_{l,y}, t_{l,z})^\top$ is a translation vector and ${{{\mathbf {\mathtt{{{R}}}}}}}_l$ is a rotation matrix that is parameterized by Euler angles: ${{{\mathbf {\mathtt{{{R}}}}}}}_l = {{{\mathbf {\mathtt{{{R}}}}}}}_x(\alpha _l) {{{\mathbf {\mathtt{{{R}}}}}}}_y(\beta _l) {{{\mathbf {\mathtt{{{R}}}}}}}_z(\gamma _l)$. Without loss of generality, we assume that the camera coordinate system of camera 1 is the reference camera coordinate system.

The point ${\varvec{{p}}}_l$ is then transformed into the camera coordinate system of camera k using

$$\begin{aligned} {\varvec{{p}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_k {\varvec{{p}}}_l + {\varvec{{t}}}_k \quad , \end{aligned}$$

(2)

where ${{{\mathbf {\mathtt{{{R}}}}}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_x(\alpha _k) {{{\mathbf {\mathtt{{{R}}}}}}}_y(\beta _k) {{{\mathbf {\mathtt{{{R}}}}}}}_z(\gamma _k)$ and ${\varvec{{t}}}_k = (t_{k,x}, t_{k,y}, t_{k,z})^\top$ describe the relative orientation of camera k with respect to the reference camera. With the above convention that camera 1 is the reference camera, for $k = 1$ we have ${{{\mathbf {\mathtt{{{R}}}}}}}_k = {{{\mathbf {\mathtt{{{I}}}}}}}$ and ${\varvec{{t}}}_k = {\varvec{{0}}}$.

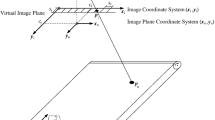
Figure 1 visualizes the exterior orientation for the single-camera case. As discussed immediately above, in this case, the relative orientation is trivial and therefore not visualized. The calibration object, placed on a conveyor belt in Fig. 1, defines the calibration object coordinate system $({\varvec{{x}}}_\mathrm {o}, {\varvec{{y}}}_\mathrm {o}, {\varvec{{z}}}_\mathrm {o})$, as described in detail in Fig. 5. The reference coordinate system coincides with the camera coordinate system of the camera for the single-camera case. The next section describes the conventions that are used to define the camera coordinate system $({\varvec{{x}}}_k, {\varvec{{y}}}_k, {\varvec{{z}}}_k)$. The notation ${\varvec{{p}}}_\mathrm {o} \equiv {\varvec{{p}}}_k$ in the figure indicates that the point ${\varvec{{p}}}_\mathrm {o}$, specified in the calibration object coordinate system, is transformed to the point ${\varvec{{p}}}_k$, specified in the camera coordinate system by (1) and (2). Thus, ${\varvec{{p}}}_\mathrm {o}$ and ${\varvec{{p}}}_k$ represent the same point on the object (hence, ${\varvec{{p}}}_\mathrm {o} \equiv {\varvec{{p}}}_k$) and are merely expressed in different coordinate systems.

The visualization of the relative orientation in Fig. 3 requires us to describe the interior orientation first and is therefore deferred to the end of Sect. 3.2.

3.2 Interior Orientation

Our model of the interior orientation of telecentric line-scan cameras is derived in [42, Section 4.1]. In this section, we will give a concise description of the model.

Fig. 1

Visualization of the exterior and interior orientation of the camera model for telecentric line-scan cameras. For simplicity, only a single camera is shown. Refer to the text for details

The camera coordinate system of any camera and therefore, in particular, a telecentric camera, is defined by the center of its entrance pupil [40, Section 6.1], [47, Section 3]. Since for telecentric lenses the center of the entrance pupil lies at infinity [40, Section 4], we move it to some arbitrary finite location on the optical axis of the lens. This is possible and correct since this relocation does not change the projection geometry because all optical rays are parallel. The ${\varvec{{z}}}$ axis of the camera coordinate system is identical to the optical axis and is oriented such that points in front of the camera have positive z coordinates. The ${\varvec{{x}}}$ axis is parallel to the sensor line and perpendicular to the ${\varvec{{z}}}$ axis. The ${\varvec{{y}}}$ axis is perpendicular to the sensor line and to the ${\varvec{{z}}}$ axis and is oriented such that a right-hand coordinate system results. Figure 1 visualizes the camera coordinate system of a single telecentric line-scan camera in the top part of the figure.

The exterior orientation of the camera refers to the first line of the line-scan image. We will index the lines that are acquired by the line-scan camera by a parameter t, starting at 0 for the first line of the image. The units of t are scan lines. Consequently, the row coordinates in the aggregate line-scan image are given by t. Since the cameras move relative to the object, the exterior orientation is different for each line of each camera. Furthermore, since the cameras may move with respect to each other, the relative orientation may be different for each line. However, because we assume a linear motion, a single relative and exterior orientation per camera or calibration image, respectively, is sufficient to model the exterior and relative camera geometries.

The constant linear velocity of the cameras can be ensured in practice using encoders to trigger the line-scan camera [42, Section 1], [43, Chapter 2.3.1.1], [1, Chapter 6.8]. Because of the linear camera motion, a point ${\varvec{{p}}}_k = (x_k, y_k, z_k)^\top$, specified in the camera coordinate system of camera k, moves along the straight line ${\varvec{{p}}}_k - t {\varvec{{v}}}_k$, where ${\varvec{{v}}}_k = (v_{k,x}, v_{k,y}, v_{k,z})^\top$ is the motion vector of camera k. The vector ${\varvec{{v}}}_k$ is described in units of meters per scan line in the camera coordinate system (i.e., its units are m Pixel$^{-1}$).

Note that ${\varvec{{v}}}_k$ describes the motion of the camera with respect to the objects. If the objects are moved with respect to a stationary camera by a linear motion system with a certain motion vector ${\varvec{{w}}}_k$, the camera motion vector is given by ${\varvec{{v}}}_k = -{\varvec{{w}}}_k$. This situation is visualized in Fig. 1. Here, objects are moved in front of the camera by a linear motion system. Thus, the motion vector of the linear motion system is displayed as $-{\varvec{{v}}}_k$ in the lower left corner of the figure.

One of the goals of our camera model is the ability to model arbitrary lens distortions. In particular, the model does not assume that the sensor line is aligned with the center of the lens distortions. We achieve this goal as follows. Conceptually, we model the sensor line as a particular line of a virtual area-scan camera. This allows us to model the misalignment of the line sensor with the center of the lens distortions by using the principal point of the virtual area-scan camera. This, in turn, allows us to use well-established lens distortion models for area-scan cameras that have proven their capability to model arbitrary lens distortions. In our model, we define the principal point as the intersection of the optical axis with the virtual image plane.¹ Furthermore, we assume that radial lens distortions are centered with respect to the optical axis, i.e., the principal point [40, Sections 6 and 7].

Fig. 2

Visualization of the line-scan lens distortion model. a An image of a square grid that is perpendicular to the optical axis, imaged by a lens without any distortions. b An image of a square grid that is perpendicular to the optical axis, imaged by a lens with barrel distortions. c A line sensor, visualized by the gray line, has been placed behind the lens of b. The gray cross visualizes the location of the optical axis. Note that the sensor line reprojects to a curved surface in the world, as can be seen by its position relative to the square grid. d The resulting distortion of the square grid in a line-sensor image, i.e., in an image that results from moving the sensor line in c in the direction of the vertical grid axis

Figure 2 visualizes this model for lens distortions. In Fig. 2a, an image of a square grid that is perpendicular to the optical axis, as imaged by a lens without any distortions, is shown.² The squares of the grid are imaged as squares by the distortion-free lens. In contrast, Fig. 2b shows the same square grid, this time imaged by a lens with barrel distortions. The images of the squares are no longer squares. Now, we place a line sensor behind the lens of Fig. 2b. This is shown in Fig. 2c, in which the sensor line is visualized by the gray line and the optical axis is visualized by the gray cross. Since the sensor line is not aligned with the optical axis, it appears bent with respect to the square grid in the world, i.e., the sensor line reprojects to a curved surface in the world. Hence, we can see that it is essential to model the offset of the sensor line to the optical axis to be able to model the apparent bend of the sensor line. From Fig. 2c, it is clear that the sensor line can be regarded as one particular line of a virtual area-scan sensor.³ This allows us to model the offset between the optical axis and the sensor line by the same mechanism as in area-scan cameras, i.e., by the principal point. This, in turn, allows us to model the distortion of the sensor line, i.e., the bend of the sensor line and the lateral distortion within the sensor line, by well established 2D distortion models, as described in detail below. Hence, the 2D distortion models provide the means to model the distortions of the sensor line, and, thus, the distortion in line-scan images: If we move the sensor line of Fig. 2c in the direction of the vertical axis of the square grid and assemble a line-scan image, we obtain the image in Fig. 2d, in which all lines are bent in the same direction.

We now turn to the detailed description of our interior orientation model. Its geometric basis is the fact that if a point ${\varvec{{p}}}_k$ projects to some point ${\varvec{{p}}}_\mathrm {s}$ on the sensor line, the optical ray of ${\varvec{{p}}}_\mathrm {s}$ and the line ${\varvec{{p}}}_k - t {\varvec{{v}}}_k$ on which ${\varvec{{p}}}_k$ moves must intersect. Figure 1 displays the points ${\varvec{{p}}}_k$ and ${\varvec{{p}}}_\mathrm {s}$ as filled circles. Furthermore, the optical ray that connects them is displayed as a solid line. The line shows two refraction-like bends in the lens to visualize the optical magnification that occurs within the lens. The line is parallel to the optical axis in its upper and lower parts to visualize the parallel projection that is effected by the telecentric lens. The line ${\varvec{{p}}}_k - t {\varvec{{v}}}_k$ on which the point ${\varvec{{p}}}_k$ is moving is also displayed as an arrow in the figure.

In the following, we will discuss how the optical ray of ${\varvec{{p}}}_\mathrm {s}$ can be computed.

First, we model that the sensor line may not be perfectly aligned with the optical axis by using the principal point $(c_x, c_y)^\top$ to model the offset between the optical axis and the sensor line.⁴ In the sensor line coordinate system, the pixels have coordinates ${\varvec{{p}}}_\mathrm {s} = (x_\mathrm {s}, 0)^\top$. Therefore, the ${\varvec{{x}}}$ coordinate $c_x$ specifies the horizontal coordinate of the principal point with respect to the left edge of the sensor line (which is also the left edge of the image) in units of pixels. This is identical to the usual convention for area-scan cameras. The ${\varvec{{y}}}$ coordinate $c_y$ has a slightly different interpretation: it measures the distance of the principal point to the optical axis in the vertical direction in units of pixels. Consequently, a value of $c_y = 0$ indicates that the line sensor is perfectly aligned with the optical axis in the vertical direction. Figure 1 displays the sensor line along with its sensor line coordinate system and the principal point $(c_x, c_y)^\top$ as the offset to the optical axis in units of pixels in the upper part of the figure.

To convert pixel coordinates into metric coordinates, we use two scaling factors: $s_x$ and $s_y$. The value of $s_x$ specifies the pixel pitch on the line sensor in meters. The value of $s_y$ has no physical meaning on the sensor. It is merely used as a convenience to be able to specify both coordinates of the principal point in units of pixels. Typically, $s_y = s_x$ is used. Figure 1 displays the pixel pitches $s_y$ and $s_x$ at the left edge of the sensor line.

With the principal point and the scaling factors, we can transform the pixel coordinates ${\varvec{{p}}}_\mathrm {s} = (x_\mathrm {s}, 0)^\top$ to intermediate coordinates in a virtual image plane as follows:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {d} \\ y_\mathrm {d} \end{array} \right) = \left( \begin{array}{c} s_x (x_\mathrm {s} - c_x) \\ - s_y c_y \end{array} \right) \quad . \end{aligned}$$

(3)

The transformed point ${\varvec{{p}}}_\mathrm {d} = (x_\mathrm {d}, y_\mathrm {d})^\top$ is visualized by ${\varvec{{p}}}_\mathrm {d} \equiv {\varvec{{p}}}_\mathrm {s}$ in Fig. 1 to indicate that both points refer to the same point in two different coordinate systems (the virtual image plane coordinate system and the sensor line coordinate system, respectively). Note that ${\varvec{{p}}}_\mathrm {d}$ is specified in units of meters.

The coordinates $(x_\mathrm {d}, y_\mathrm {d})^\top$ in (3) are affected by lens distortions. Therefore, in the next step, we rectify these distortions. We support two distortion models [42, Section 4.1], [40, Section 6.1], [47, Section 3], [43, Chapter 3.9.1.3]: the division model [2, 10, 22,23,24,25,26, 39] and the polynomial model [3, 4].

In the division model, which only supports radial distortions, the undistorted point $(x_\mathrm {u}, y_\mathrm {u})^\top$ is computed from the distorted point by:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) = \frac{1}{1 + \kappa r_\mathrm {d}^2} \left( \begin{array}{c} x_\mathrm {d} \\ y_\mathrm {d} \end{array} \right) \quad , \end{aligned}$$

(4)

where $r_\mathrm {d}^2 = x_\mathrm {d}^2 + y_\mathrm {d}^2$.

In the polynomial model, which supports radial as well as decentering distortions, the undistorted point is computed by:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) = \left( \begin{array}{l} x_\mathrm {d} (1 + K_1 r_\mathrm {d}^2 + K_2 r_\mathrm {d}^4 + K_3 r_\mathrm {d}^6) \\ \quad + (P_1 (r_\mathrm {d}^2 + 2 x_\mathrm {d}^2) + 2 P_2 x_\mathrm {d} y_\mathrm {d}) \\[2ex] y_\mathrm {d} (1 + K_1 r_\mathrm {d}^2 + K_2 r_\mathrm {d}^4 + K_3 r_\mathrm {d}^6) \\ \quad + (2 P_1 x_\mathrm {d} y_\mathrm {d} + P_2 (r_\mathrm {d}^2 + 2 y_\mathrm {d}^2)) \end{array} \right) \quad . \end{aligned}$$

(5)

In Fig. 1, the undistorted point ${\varvec{{p}}}_\mathrm {u} = (x_\mathrm {u}, y_\mathrm {u})^\top$ is visualized by an unfilled circle. Furthermore, it is visualized by a dashed line that represents the optical ray that would connect ${\varvec{{p}}}_\mathrm {u}$ and ${\varvec{{p}}}_\mathrm {s}$ if the lens didn’t have any distortions. Like ${\varvec{{p}}}_\mathrm {d}$, ${\varvec{{p}}}_\mathrm {u}$ is specified in units of meters. Note that, as is visualized in Fig. 1, our camera model can handle lateral distortions along the sensor line as well as longitudinal distortions perpendicular to the sensor line. This is the reason why it can handle arbitrary distortions. This also means that the reprojection of the sensor line into 3D, i.e., the set of all optical rays emanating from the sensor line, will not be a plane but a curved surface if $c_y \ne 0$.

Finally, we undo the magnification that is effected by the telecentric lens:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {c} \\ y_\mathrm {c} \end{array} \right) = \frac{1}{m} \left( \begin{array}{c} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) \quad . \end{aligned}$$

(6)

Here, $(x_\mathrm {c}, y_\mathrm {c})^\top$ are the metric coordinates of the point in the camera coordinate system and m is the magnification of the telecentric lens. As was already noted previously, the magnification of the lens is visualized in Fig. 1 by the line that connects ${\varvec{{p}}}_k$ and ${\varvec{{p}}}_\mathrm {s}$. The point ${\varvec{{p}}}_\mathrm {c} = (x_\mathrm {c}, y_\mathrm {c})^\top$ is not explicitly visualized. It can be visualized by the projection of the lower part of the line that connects ${\varvec{{p}}}_k$ and ${\varvec{{p}}}_\mathrm {s}$ into the ${\varvec{{xy}}}$ plane of the camera coordinate system.

Based on the above discussion, the optical ray corresponding to the point ${\varvec{{p}}}_\mathrm {s}$ on the sensor line is given by

$$\begin{aligned} (x_\mathrm {c}, y_\mathrm {c}, 0)^\top + \lambda (0, 0, 1)^\top= & {} (x_\mathrm {u} / m, y_\mathrm {u} / m, 0)^\top + \lambda (0, 0, 1)^\top .\nonumber \\ \end{aligned}$$

(7)

We now have determined the optical ray of ${\varvec{{p}}}_\mathrm {s}$ and the line along which a point ${\varvec{{p}}}_k$ moves. As described previously, these two lines must intersect if ${\varvec{{p}}}_k$ projects to ${\varvec{{p}}}_\mathrm {s}$. To compute the intersection, let us assume that we have transformed the point ${\varvec{{p}}}_\mathrm {s}$ to a distorted image point ${\varvec{{p}}}_\mathrm {d}$ by (3). Furthermore, let us call the undistortion function in (4) or (5) ${\varvec{{u}}}({\varvec{{p}}}) = (u_x(x_\mathrm {d}, y_\mathrm {d}), u_y(x_\mathrm {d}, y_\mathrm {d}))^\top$. Then, the intersection of the moving point ${\varvec{{p}}}_k - t {\varvec{{v}}}_k$ and the optical ray (7) results in the following equation system:

$$\begin{aligned} u_x(x_\mathrm {d}, y_\mathrm {d}) / m&= x_k - t v_{k,x} \end{aligned}$$

(8)

$$\begin{aligned} u_y(x_\mathrm {d}, y_\mathrm {d}) / m&= y_k - t v_{k,y} \end{aligned}$$

(9)

$$\begin{aligned} \lambda&= z_k - t v_{k,z} \quad . \end{aligned}$$

(10)

It can be seen that $\lambda$ does not occur in (8) and (9). Therefore, neither $z_k$ nor $v_{k,z}$ influence the projection and we can omit (10). The remaining equations (8) and (9) must be solved for t and $x_\mathrm {d}$. For the polynomial model, they define a polynomial equation system of degree 7 in the unknowns $x_\mathrm {d}$ and t. Therefore, the equations cannot be solved analytically. Hence, a numerical root finding algorithm must be used to solve them. For the division model, an analytical solution is possible, as described in [42, Section 4.1].

Once t and $x_\mathrm {d}$ have been determined, the point is transformed into the image coordinate system of the aggregate line-scan image by:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {i} \\ y_\mathrm {i} \end{array} \right) = \left( \begin{array}{c} x_\mathrm {d} / s_x + c_x \\ t \end{array} \right) \quad . \end{aligned}$$

(11)

Having described the interior orientation of the telecentric line-scan camera model, we conclude this section with the discussion of the visualization of the relative orientations that we had deferred at the end of Sect. 3.1. Figure 3 shows a setup with three telecentric line-scan cameras. The cameras are moving along the motion vectors ${\varvec{{v}}}_k$ ($k \in \{1,2,3\}$). As was described above, the camera coordinate systems, and therefore, the exterior and relative orientations, refer to the first line of each camera image, i.e., to the position of the sensor line at $t=0$. The camera coordinate systems of all three cameras are shown in Fig. 3. It also displays the exterior orientation ${{{\mathbf {\mathtt{{{R}}}}}}}_l$, ${\varvec{{t}}}_l$ of a particular observation of the calibration object shown at the bottom of the figure. Furthermore, the figure displays the relative orientations ${{{\mathbf {\mathtt{{{R}}}}}}}_k$, ${\varvec{{t}}}_k$ for cameras 2 and 3 (i.e., $k \in \{2,3\}$) with respect to the reference camera (camera 1). In addition, Fig. 3 shows the position of the sensor line for different values of t as the cameras move along their linear motion trajectories. Note that for illustration purposes, the images are only seven pixels high. Finally, Fig. 3 displays the footprint of the sensor line in the world for camera 1 as the camera moves. To avoid cluttering up the figure, the footprint is only hinted at by the arrows that emanate from the sensor lines for cameras 2 and 3.

Fig. 3

Visualization of the relative and exterior orientations of the camera model for telecentric line-scan cameras. Refer to the text for details

3.3 Model Degeneracies

The telecentric line-scan camera model that we have described has a few important degeneracies, which have been investigated in detail for the single-view case in [42, Section 4.4]. Almost all of them also apply to the multi-view case. Furthermore, some of the degeneracies that occur for multi-view telecentric area-scan camera setups that were described in [40, Section 6.2] also apply to multi-view telecentric line-scan setups. In this section, we list the degeneracies that affect the discussion in the remainder of the paper.

Remark 1

The model is overparameterized. The values of m and $s_x$ cannot be determined simultaneously. This can be solved by fixing $s_x$ at the initial value that was specified by the user. The value of $s_x$ is known from the specification of the sensor. Furthermore, $s_y$ is only used to specify the principal point in pixels and is therefore kept fixed at the initial value specified by the user [42, Remark 19]. The next remark discusses the reasons for our choice of this overparameterization.

Remark 2

The parameterization of the camera model is very intuitive for machine vision users [40, Section 6.1]. All parameters have a physical meaning that is easy to understand. Approximate initial values for the interior orientation parameters simply can be read off the data sheets of the camera ($s_x$ and $s_y$) and the lens (m) or can be obtained easily otherwise (the initial values for the principal point can be set to the center of the image horizontally and 0 vertically and the distortion coefficients can typically be set to 0). Furthermore, the calibration results are easy to check for validity.

Remark 3

The principal point $(c_x, c_y)^\top$ is solely defined by the lens distortions. Therefore, the smaller the lens distortions are, the less well defined the principal point is. In the extreme, i.e., if there are no lens distortions, $(c_x, c_y)^\top$ and $(t_{l,x}, t_{l,y})^\top$ have the same effect. Therefore, in this case $(c_x, c_y)^\top$ should remain fixed at the initial value specified by the user (typically, $c_x$ is set to the horizontal image center and $c_y$ is set to 0) [42, Remark 20].

Remark 4

The relative orientation parameters $(t_{k,x}, t_{k,y}, t_{k,z})^\top$ cannot be determined uniquely since all cameras can be moved arbitrarily along their optical axes without changing the image geometry because of the parallel projection that telecentric lenses effect [40, Section 4]. To provide a well-defined relative orientation, we move the origins of the camera coordinate systems along the respective optical axes to a sphere with radius 1 m when we compute the initial relative orientations. The center of the sphere is given by a point that lies at a distance of 1 m on the optical axis in front of the reference camera. The translation parameters $(t_{k,x}, t_{k,y})^\top$ are optimized in the calibration. Therefore, their final values may differ slightly from the sphere with radius 1 m. In this respect, multi-view telecentric line-scan setups behave in an identical manner as multi-view telecentric area-scan setups [40, Remark 4].

Remark 5

For planar calibration objects, the rotation part of the exterior orientation can only be determined up to a twofold ambiguity from a single camera. For example, a plane rotated by $\alpha _l = 20^\circ$ looks identical to a plane rotated by $\alpha _l = -20^\circ$. This is a special case of a Necker reversal when the object is planar [36, Section 4.1], [17, Chapter 14.6]. In a multi-view setup, these individual exterior orientation ambiguities can be resolved, albeit only up to an overall Necker reversal, which also affects the relative orientations. This ambiguity must be resolved manually by the user. In this respect, multi-view telecentric line-scan setups behave in an identical manner as multi-view telecentric area-scan setups [40, Remark 5].

3.4 Motion Configurations

The telecentric line-scan camera model we have discussed so far has assumed an individual motion vector ${\varvec{{v}}}_k$ per camera. This corresponds to the situation shown in Fig. 4a, in which the cameras move independently from each other across the object to acquire the images. While this setup is possible, and we therefore support it in our camera model, the much more common configuration is displayed in Fig. 4b, c. In Fig. 4b, the cameras are mounted rigidly above a linear motion system that moves the object in front of the cameras, while in Fig. 4c, the cameras are mounted rigidly on a linear motion system that moves the cameras across the object. In both cases, the motion vectors of the two cameras are coupled and thus not independent from each other.

Fig. 4

Different motion configurations for telecentric line-scan cameras. The figures show two line-scan cameras, each of which acquires an image of a calibration object. The cameras’ motion vectors are indicated by arrows. a Two cameras that acquire the images independently with independent motion vectors. b, c Two cameras with common motion vectors. b The cameras are mounted rigidly above a linear motion system that moves the object in front of the cameras. c The cameras are mounted rigidly on a linear motion system that moves the cameras across the object

In Fig. 4b, c, we can see that there is only a single common motion vector. Without loss of generality, we can assume the common motion vector is given in the coordinate system of the reference camera. As described in Sect. 3.1, we can assume that camera 1 is the reference camera. Let us call the common motion vector of the reference camera ${\varvec{{v}}}$. Then, it can be seen that the motion vectors ${\varvec{{v}}}_k$ of the remaining cameras can be obtained via the rotation of the relative orientations (2) as follows:

$$\begin{aligned} {\varvec{{v}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_k {\varvec{{v}}} \quad . \end{aligned}$$

(12)

Remark 6

Remark 22 in [42] and (10) show that $v_{k,z}$ has no effect on the projection of a point into the image of camera k. Therefore, for cameras with independent motion vectors, $v_{k,z}$ cannot be determined. In this configuration, we leave $v_{k,z}$ at the initial value specified by the user. The situation is different for cameras with a common motion vector, as the following proposition shows.

Proposition 1

In a setup with at least two telecentric line-scan cameras that have a common motion vector, the common motion vector ${\varvec{{v}}}$ can be determined uniquely if and only if there are at least two cameras that have a rotation in their relative orientation that is not purely around the ${\varvec{{z}}}$ axis (of either camera).

Proof

Without loss of generality, let us denote the two cameras that have a rotation in their relative orientation that is not purely around the ${\varvec{{z}}}$ axis by 1 and 2. As before, we assume that camera 1 is the reference camera, i.e., the rotation part of its relative orientation is given by the identity matrix ${{{\mathbf {\mathtt{{{I}}}}}}}$. Then, we can denote the rotation part of the relative orientation of camera 2 by ${{{\mathbf {\mathtt{{{R}}}}}}}$. According to (12), we have

$$\begin{aligned} {\varvec{{v}}}_1&= {{{\mathbf {\mathtt{{{I}}}}}}} {\varvec{{v}}} \end{aligned}$$

(13)

$$\begin{aligned} {\varvec{{v}}}_2&= {{{\mathbf {\mathtt{{{R}}}}}}} {\varvec{{v}}} \end{aligned}$$

(14)

Because of Remark 6, we can only infer the x and y components of the motion vector in each camera coordinate system. Hence, we have

$$\begin{aligned} \left( \begin{array}{c} v_{1,x} \\ v_{1,y} \end{array} \right)&= \left( \begin{array}{c} v_x \\ v_y \end{array} \right) \end{aligned}$$

(15)

$$\begin{aligned} \left( \begin{array}{c} v_{2,x} \\ v_{2,y} \end{array} \right)&= \left( \begin{array}{c} r_{11} v_x + r_{12} v_y + r_{13} v_z \\ r_{21} v_x + r_{22} v_y + r_{23} v_z \end{array} \right) \quad . \end{aligned}$$

(16)

Since $v_{1,x}$, $v_{1,y}$, $v_{2,x}$, $v_{2,y}$, and ${{{\mathbf {\mathtt{{{R}}}}}}}$ can be determined in principle (in practice, through calibration with independent motion vectors; see Sect. 4) and therefore can be considered as known, (15) and (16) constitute an equation system for ${\varvec{{v}}}$ that can be written as follows:

$$\begin{aligned} \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ r_{11} &{} r_{12} &{} r_{13} \\ r_{21} &{} r_{22} &{} r_{23} \end{array} \right) \left( \begin{array}{c} v_x \\ v_y \\ v_z \end{array} \right) = \left( \begin{array}{c} v_{1,x} \\ v_{1,y} \\ v_{2,x} \\ v_{2,y} \end{array} \right) \quad . \end{aligned}$$

(17)

Thus, we have four equations for the three unknowns of ${\varvec{{v}}}$. This system is non-degenerate if the matrix on the left-hand side has rank 3. This is the case if and only if the rotation ${{{\mathbf {\mathtt{{{R}}}}}}}$ is not purely around the ${\varvec{{z}}}$ axis, i.e., if $r_{13} \ne 0$ or $r_{23} \ne 0$. $\square$

Remark 7

The equation system in (17) is actually overdetermined. Therefore, in practice, we can solve for ${\varvec{{v}}}$ in a least-squares fashion using the singular value decomposition (SVD) [34, Chapter 2.6]. In fact, this approach extends to a setup with an arbitrary number of cameras. The reference camera results in an equation set of the form (15), while each additional camera results in an equation set of the form (16). Therefore, with $n_{\mathrm {c}}$ cameras, we obtain a $2 n_{\mathrm {c}} \times 3$ matrix that we can use to solve for ${\varvec{{v}}}$ using the SVD.

Remark 8

The case in which all relative orientations solely contain rotations around the ${\varvec{{z}}}$ axis is irrelevant in practice. If this were the case, all optical rays would be in the direction of the common ${\varvec{{z}}}$ axis. Hence, they would all be parallel and there would be no parallaxes from which a 3D reconstruction could be obtained.

Remark 9

For the two-view case, the equation system (17) can be solved analytically for the pure along-track and across-track cases.

In the pure along-track case, the rotation part of the relative orientation is a rotation around the ${\varvec{{x}}}$ axis by an angle $\alpha$. Therefore, the design matrix ${{{\mathbf {\mathtt{{{D}}}}}}}$ of the left-hand side of (17) has the following form:

$$\begin{aligned} {{{\mathbf {\mathtt{{{D}}}}}}} = \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} \cos \alpha &{} -\sin \alpha \end{array} \right) \quad . \end{aligned}$$

(18)

Let us denote the vector on the right-hand side of (17) by ${\varvec{{w}}}$. The solution of (17) can be computed based on the normal equations as

$$\begin{aligned} {\varvec{{v}}} = {\left( {{{\mathbf {\mathtt{{{D}}}}}}}^\top {{{\mathbf {\mathtt{{{D}}}}}}} \right) }^{-1} {{{\mathbf {\mathtt{{{D}}}}}}}^\top {\varvec{{w}}} \quad . \end{aligned}$$

(19)

Hence, for the pure along-track case, we have

$$\begin{aligned} {\varvec{{v}}} = \left( \begin{array}{c} (v_{1,x} + v_{2,x}) / 2 \\ v_{1,y} \\ (v_{1,y} \cos \alpha - v_{2,y}) / \sin \alpha \end{array} \right) \quad . \end{aligned}$$

(20)

Consequently, it can be seen that the value of $v_z$ only depends on the $v_y$ components of the individual cameras. Since $v_{2,y}$ linearly depends on $v_{1,y}$ via the relative orientation, we can see that $v_z$ depends on $v_{1,y} = v_y$. Therefore, we can expect $v_z$ to be highly correlated with $v_y$ in the two-view along-track case.

For the pure across-track case, the rotation part of the relative orientation is a rotation around the ${\varvec{{y}}}$ axis by an angle $\beta$. Using the same approach, it can be shown that

$$\begin{aligned} {\varvec{{v}}} = \left( \begin{array}{c} v_{1,x} \\ (v_{1,y} + v_{2,y}) / 2 \\ (- v_{1,x} \cos \beta + v_{2,x}) / \sin \beta \end{array} \right) \quad . \end{aligned}$$

(21)

Hence, $v_z$ only depends on the $v_x$ components of the individual cameras. Therefore, we can expect $v_z$ to be highly correlated with $v_x$ in the two-view across-track case.

3.5 Summary

Summarizing, the camera model for a multi-view setup with telecentric line-scan cameras consists of the following parameters:

• The six parameters of the exterior orientation (modeling the pose of the calibration objects in the $n_{\mathrm {o}}$ images): $\alpha _l$, $\beta _l$, $\gamma _l$, $t_{l,x}$, $t_{l,y}$, and $t_{l,z}$.

• The six parameters of the relative orientation of the $n_{\mathrm {c}}$ cameras with respect to camera 1: $\alpha _k$, $\beta _k$, $\gamma _k$, $t_{k,x}$, $t_{k,y}$, and $t_{k,z}$.

• The interior orientation of each camera: $m_k$; $\kappa _k$ or $K_{k,1}$, $K_{k,2}$, $K_{k,3}$, $P_{k,1}$, $P_{k,2}$; $s_{k,x}$, $s_{k,y}$, $c_{k,x}$, and $c_{k,y}$.

• For setups with independent motion vectors: the independent motion vectors given by $v_{k,x}$, $v_{k,y}$, and $v_{k,z}$.

• For setups with a common motion vector: the common motion vector $v_x$, $v_y$, and $v_z$.

4 Calibration

To calibrate the cameras, we use an extension of the calibration algorithms that we have used previously for other camera models [40, 42, 47]. We will describe this extended algorithm in the following.

We use the planar calibration object with circular control points in a hexagonal layout that is described in [40, Section 9]. Figure 5 shows an image of this type of calibration object. Planar calibration objects have the advantage that they can be manufactured very accurately and that they can be handled more easily by the users than 3D calibration objects. Another distinctive advantage of planar calibration objects is that they can be used conveniently in backlight applications if the calibration object is opaque and the control points are transparent [43, Chapter 4.7]. Further advantages of this kind of calibration object are discussed in [40, Section 9].

Fig. 5

An image of the planar calibration object. The calibration object coordinate system is defined by the five fiducial patterns that are defined by the circles that contain small black dots. Each fiducial pattern can be regarded as a hexagon with certain filled and dotted circles. The fiducial pattern in the center that contains six adjacent circles with black dots defines the origin of the calibration object coordinate system and its orientation. The origin is defined by the right circle in the middle row (i.e., by the center of the hexagon). The ${\varvec{{x}}}$ axis points horizontally to the right from the origin in the image, i.e., toward the adjacent filled circle. The ${\varvec{{y}}}$ axis points vertically downward, i.e., toward the middle of the two dotted circles below. The ${\varvec{{z}}}$ axis forms a right-handed coordinate system with the ${\varvec{{x}}}$ and ${\varvec{{y}}}$ axes, i.e., it points away from the viewer through the calibration object

The calibration object is manufactured with micrometer accuracy. Therefore, the 3D coordinates of the centers of the control points are known very accurately. We denote them by ${\varvec{{p}}}_j$ ($j = 1, \ldots , n_{\mathrm {m}}$), where $n_{\mathrm {m}}$ denotes the number of control points on the calibration object.

To calibrate the camera setup, the user acquires $n_{\mathrm {o}}$ images of the calibration object with each of the $n_{\mathrm {c}}$ cameras (cf. Sect. 3.1). It is not necessary that the calibration object is visible in all images simultaneously. Furthermore, it is not necessary that all control points are visible in any particular image. We will model this below by a variable $v_{jkl}$ that is 1 if the control point j of the observation l of the calibration object is visible with camera k, and 0 otherwise. Overall, however, there must be a chain of observations of the calibration object in multiple cameras that connects all the cameras.

As described in Sect. 3.1, we denote the exterior orientation of the calibration object in the reference camera by ${{{\mathbf {\mathtt{{{R}}}}}}}_l$ and ${\varvec{{t}}}_l$ ($l = 1, \ldots , n_{\mathrm {o}}$) and the relative orientation of the cameras with respect to the reference camera by ${{{\mathbf {\mathtt{{{R}}}}}}}_k$ and ${\varvec{{t}}}_k$ ($k = 1, \ldots , n_{\mathrm {c}}$). We denote the corresponding parameters by the vectors ${\varvec{{e}}}_l$ and ${\varvec{{r}}}_k$.

Moreover, we denote the interior orientation of camera k by the vector ${\varvec{{i}}}_k$ and the motion vector of camera k by ${\varvec{{v}}}_k$. For setups with independent motion vectors, this is the motion vector of camera k, while for cameras with a common motion vector, ${\varvec{{v}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_k {\varvec{{v}}}$ (cf. (12)). Hence, for cameras with a common motion, there is only one global motion vector ${\varvec{{v}}}$.

Furthermore, we denote the projection from world coordinates to pixel coordinates by $\varvec{\pi }({\varvec{{p}}}_j, {\varvec{{e}}}_l, {\varvec{{r}}}_k, {\varvec{{i}}}_k, {\varvec{{v}}}_k)$.⁵ Finally, we denote the image coordinates of the centers of the control points that have been extracted from the calibration images by ${\varvec{{p}}}_{jkl}$.

Then, to calibrate the multi-view camera setup, the following function is minimized:

$$\begin{aligned} \varepsilon ^2 = \sum _{l=1}^{n_{\mathrm {o}}} \sum _{k=1}^{n_{\mathrm {c}}} \sum _{j=1}^{n_{\mathrm {m}}} v_{jkl} \Vert \varvec{\pi }( {\varvec{{p}}}_j, {\varvec{{e}}}_l, {\varvec{{r}}}_k, {\varvec{{i}}}_k, {\varvec{{v}}}_k) - {\varvec{{p}}}_{jkl} \Vert _2^2 \quad . \end{aligned}$$

(22)

For setups with independent motion vectors, (22) can be minimized using the standard sparse Levenberg–Marquardt algorithm with a bipartite parameter set (Algorithm A6.4) that is described in [17, Appendix A6]. For setups with a common motion vector, however, we obtain a tripartite parameter set because the common motion vector ${\varvec{{v}}}$ creates a global parameter set that is influenced by all observations. This changes the structure of the Jacobians in a material way and requires an extension of the sparse Levenberg–Marquardt algorithm that we describe in Appendix A. From the results of the optimization, we can calculate the covariances of the optimized parameters in the usual manner [17, Chapter 5], [11, Chapter 4]. In particular, we use (Algorithm A6.4) of [17, Appendix A6] and, for setups with a common motion vector, the extension we propose in Appendix A.

The control point locations in the images ${\varvec{{p}}}_{jkl}$ are extracted by fitting ellipses [9] to edges extracted with a subpixel-accurate edge extractor [37, Chapter 3.3], [38]. As discussed in [40, Section 5.2] and [30], this causes a bias in the point positions. Since telecentric line-scan cameras perform an affine projection, there is no perspective bias, i.e., the bias consists solely of distortion bias. The bias can be removed with the approach for entocentric line-scan cameras described in [40, Section 10].

Minimizing (22) requires initial values for the unknown parameters. Initial values for the interior orientation parameters ${\varvec{{i}}}_k$ can be obtained from the specification of the camera and the lens (see Remarks 1 and 2 and [42, Section 4.2]). An approximate value for $v_{k,y}$ usually will be known from the considerations that led to the line-scan camera setup.⁶ The initial value of $v_{k,x}$ typically can be set to 0. The initial value of $v_{k,z}$ usually can also be set to 0. With known initial values for the interior orientation, the control point coordinates ${\varvec{{p}}}_j$ and their corresponding image point coordinates ${\varvec{{p}}}_{jkl}$ can be used as input for the OnP algorithm described in [41] to obtain estimates for the exterior orientations ${\varvec{{e}}}_l$ of the calibration object. These, in turn, can be used to compute initial estimates for the relative orientations ${\varvec{{r}}}_k$.⁷

For setups with a common motion vector, the user-specified initial estimates of ${\varvec{{v}}}_k$ are typically not accurate enough to be able to reconstruct initial estimates for ${\varvec{{v}}}$ and ${{{\mathbf {\mathtt{{{R}}}}}}}_k$ that are accurate enough to ensure convergence of the minimization. Therefore, we first calibrate the setup as if it were a setup with independent motion vectors. We can then use the algorithm described in Remark 7 to compute the initial estimate for ${\varvec{{v}}}$ and subsequently use this estimate to calibrate the setup as a setup with a common motion vector.

5 Stereo Rectification and Reconstruction

5.1 Stereo Rectification

As discussed in Sect. 2, stereo rectification for line-scan cameras with entocentric lenses is only possible in very restricted circumstances. In contrast, for line-scan cameras with telecentric lenses, stereo rectification can always be performed, as we will discuss in this section.

Proposition 2

In contrast to line-scan cameras with entocentric lenses, for line-scan cameras with telecentric lenses, lens distortions can be removed without knowledge of the 3D geometry of the scene.

Proof

This was shown in [42, Remarks 13 and 14]. We briefly describe the proof here.

As discussed previously, (8) and (9) do not depend on $z_\mathrm {c}$. Therefore, given an image point $(x_\mathrm {i}, y_\mathrm {i})^\top$, the corresponding point $(x_\mathrm {c}, y_\mathrm {c}, 0)^\top$ in the camera coordinate system can be computed as follows. First, (11) is inverted:

$$\begin{aligned} \left( \begin{array}{c} x_\mathrm {d} \\ t \end{array} \right) = \left( \begin{array}{c} s_x ( x_\mathrm {i} - c_x) \\ y_\mathrm {i} \end{array} \right) \quad . \end{aligned}$$

(23)

Next, (8) and (9) are solved for $(x_\mathrm {c}, y_\mathrm {c})^\top$:

$$\begin{aligned} x_\mathrm {c}&= u_x(x_\mathrm {d}, y_\mathrm {d}) / m + t v_x \end{aligned}$$

(24)

$$\begin{aligned} y_\mathrm {c}&= u_y(x_\mathrm {d}, y_\mathrm {d}) / m + t v_y \quad , \end{aligned}$$

(25)

where $y_\mathrm {d} = -s_y c_y$ [42, Remark 13].

The point $(x_\mathrm {c}, y_\mathrm {c}, 0)^\top$ can then be projected into a rectified camera for which all distortion coefficients have been set to 0. Moreover, any skew in the pixels can be removed by setting $v_x$ to 0 in the rectified camera. Finally, square pixels can be enforced by setting $s_x$ to $\min (s_x, m v_y)$ and then setting $v_y$ to $s_x / m$ [42, Remark 14]. $\square$

Figure 6 visualizes the image distortion rectification of Proposition 2. The gray lines represent the back transformation of the distorted image into camera coordinates, i.e., the result of applying (23)– (25) to the original, unrectified image. The vector ${\varvec{{v}}}_\mathrm {u}$ represents the motion vector of the unrectified image. It has a motion component $v_x \ne 0$, resulting in skewed pixels. Furthermore, the value of $v_y$ is not commensurate with $s_x$, i.e., the image has non-square pixels. The rectified image is represented by the black lines. The vector ${\varvec{{v}}}_\mathrm {r}$ represents the motion vector in the rectified image. It has $v_x = 0$ and $v_y$ is commensurate with $s_x$, i.e., the image has square pixels.

Fig. 6

Visualization of the image distortion rectification of Proposition 2. Refer to the text for details

It is shown in [42, Remark 18] that telecentric line-scan cameras without lens distortions are equivalent to telecentric area-scan cameras. A telecentric line-scan camera that has been rectified with the approach described in the proof of Proposition 2 has no distortions. Since telecentric area-scan cameras can always be stereo-rectified with lens distortions [33, operator reference of gen_binocular_rectification_map] or without lens distortions [18, 28], this shows that stereo rectification of telecentric line-scan cameras is always possible without knowing the 3D geometry of the scene, in contrast to entocentric line-scan cameras, where this is impossible in general. In the following, we will describe an explicit stereo rectification algorithm for telecentric line-scan cameras.

As shown in [42, Theorem 1], telecentric line-scan cameras without lens distortions are affine cameras. Therefore, once we have removed the lens distortions, the epipolar lines and planes are already parallel to each other in each image [17, Chapter 14.1]. This situation is depicted in Fig. 7, which shows unrectified images of two telecentric line-scan cameras. We have used two cameras with independent motion vectors in a relative orientation that includes a large rotation around the ${\varvec{{z}}}$ axes to make the visualization of the rectification algorithm clearer. The figure assumes that any lens distortions have been removed by the algorithm of Proposition 2. Therefore, the motion vectors of the unrectified images are in the same direction as the ${\varvec{{y}}}$ axes of the two camera coordinate systems and thus are not shown explicitly. Figure 7 visualizes the camera coordinate systems of the two unrectified cameras as well as the optical axes of the two cameras, which coincide with the ${\varvec{{z}}}$ directions of the two camera coordinate systems. Note that the optical axes of the two cameras do not intersect but are skew. Figure 7 also shows two homologous points in each image, their corresponding optical rays, the corresponding 3D points, and the epipolar lines corresponding to the two points in the other image. Since the optical rays are parallel, since the epipolar lines are the projections of the optical rays into the other images, and since the telecentric line-scan cameras perform a parallel projection, the epipolar lines are parallel to each other. However, they are not aligned with the rows of the images, i.e., with the ${\varvec{{x}}}$ axes. Consequently, the only steps that we need to perform geometrically to rectify the images are to rotate them around their ${\varvec{{z}}}$ axes to make the epipolar lines horizontal, to scale the images appropriately to make the epipolar lines equidistant, and to translate the images to make corresponding epipolar lines have the same row coordinate. We will discuss in the following how this can be achieved by a suitable modification of the interior and relative orientation parameters of the cameras.

Fig. 7

Visualization of the epipolar rectification of two telecentric line-scan images. Refer to the text for details

First of all, we note that the direction of the ${\varvec{{z}}}$ axes of the two cameras must remain invariant since they define the direction of the optical rays in the two cameras. Let us denote the two ${\varvec{{z}}}$ axes of the unrectified cameras by ${\varvec{{z}}}_{1;\mathrm {u}}$ and ${\varvec{{z}}}_{2;\mathrm {u}}$ (or ${\varvec{{z}}}_{1,2;\mathrm {u}}$ for short). They are given by the third column of the respective rotation matrices ${{{\mathbf {\mathtt{{{R}}}}}}}_1$ and ${{{\mathbf {\mathtt{{{R}}}}}}}_2$ of the relative orientation of the two cameras with respect to the reference camera. Therefore, the ${\varvec{{z}}}$ axes of the rectified cameras are given by

$$\begin{aligned} {\varvec{{z}}}_{1,2;\mathrm {r}} = {\varvec{{z}}}_{1,2;\mathrm {u}} \quad . \end{aligned}$$

(26)

To make the epipolar lines horizontal, we can define a common ${\varvec{{y}}}$ axis for the two cameras as the vector product of the two ${\varvec{{z}}}$ axes:

$$\begin{aligned} {\varvec{{y}}}_{1,2;\mathrm {r}} = \frac{{\varvec{{z}}}_{1;\mathrm {r}} \times {\varvec{{z}}}_{2;\mathrm {r}}}{{\Vert {\varvec{{z}}}_{1;\mathrm {r}} \times {\varvec{{z}}}_{2;\mathrm {r}} \Vert }_2} \quad . \end{aligned}$$

(27)

Note that the vector product never vanishes in practice because ${\varvec{{z}}}_{1;\mathrm {r}}$ and ${\varvec{{z}}}_{2;\mathrm {r}}$ cannot be parallel for there to be parallaxes.

Finally, the rotated ${\varvec{{x}}}$ axes are given by

$$\begin{aligned} {\varvec{{x}}}_{1,2;\mathrm {r}} = \frac{{\varvec{{y}}}_{1,2;\mathrm {r}} \times {\varvec{{z}}}_{1,2;\mathrm {r}}}{{\Vert {\varvec{{y}}}_{1,2;\mathrm {r}} \times {\varvec{{z}}}_{1,2;\mathrm {r}} \Vert }_2} \quad . \end{aligned}$$

(28)

Figure 7 displays the result of computing the camera coordinate systems of the rectified images as well as the rectified image planes, which lie in the ${\varvec{{xy}}}$ plane of the rectified camera coordinate systems. The rectified images are larger than the original images because they include the entire projection of the unrectified images. They are displayed at a relatively large distance behind the unrectified images to avoid cluttering up the figure. Note that, according to Remark 4, we can move the cameras arbitrarily along their optical axes. Therefore, the figure displays the geometry of the rectified images correctly. Furthermore, note that the rectified camera coordinate system axes have completely different directions than the unrectified camera coordinate system axes. Since the motion vector of the rectified images is in the ${\varvec{{y}}}$ direction of the rectified camera coordinate system, it is not shown. Note that the rectified images thus have a completely different (virtual) scanning direction than the unrectified images.

As was noted above, in general the optical axes of the two cameras do not intersect. Therefore, we determine the distance $d_{{\varvec{{y}}}}$ in the ${\varvec{{y}}}$ direction of the two optical axes of the rotated cameras (see Fig. 7). We then shift the lower camera upward and the upper camera downward by $\pm d_{{\varvec{{y}}}}/2$, where the sign is chosen appropriately for each camera. We then must compensate this shift of the camera in 3D by an appropriate offset of the principal point in the ${\varvec{{y}}}$ direction to obtain the original 3D ray geometry. The shifts in the principal points are given by

$$\begin{aligned} o_{1,2;y} = \pm (d_{{\varvec{{y}}}}/2) (m_{1,2} / s_{1,2;y}) \quad , \end{aligned}$$

(29)

with the sign chosen appropriately for each camera, depending on which direction the camera was shifted in the relative orientation. This ensures that $c_{1;y} = c_{2;y}$. Figure 7 displays the shifted optical axes of the rectified images. Note that they intersect at the center of the line segment that connects the two unrectified optical axes with the shortest distance, i.e., the line segment that corresponds to $d_{{\varvec{{y}}}}$. Furthermore, Fig. 7 displays the vertical offsets $o_{1,2;y}$ of the principal points. Finally, Fig. 7 displays the rectified points that correspond to the two points in each unrectified image as well as their corresponding epipolar lines. Note that the epipolar lines are horizontal in the rectified images.

After performing the above steps, we have ensured that the epipolar lines have the same ${\varvec{{y}}}$ coordinates in both rectified cameras. We now must ensure that that the epipolar lines have the same row coordinates in both rectified images. To achieve this, we set the magnification of both cameras to their mean value $(m_1 + m_2) / 2$. Furthermore, we make the pixels of both cameras the same size by setting them to their mean values $(s_{1;x} + s_{2;x}) / 2$ and $(s_{1;y} + s_{2;y}) / 2$ and adapt $v_{1,2;y}$ accordingly to preserve the squareness of the pixels that was achieved by the approach in the proof of Proposition 2. Moreover, we set $v_{1,2;z}$ to 0.⁸ Finally, we shift both rectified cameras along their ${\varvec{{z}}}$ axes such that their distance is 1 m. These last steps are not visualized in Fig. 7 because they would clutter up the figure too much.

Both rectification transformations, the removal of the lens distortions and the stereo rectification can be combined into a single overall transformation that can be computed offline and stored in a 2D transformation lookup table to facilitate a rapid image rectification. This is useful because especially the removal of lens distortions is computationally expensive.

5.2 Stereo Reconstruction

With the rectified images, we can use any two-view stereo algorithm to compute the disparities in a stereo image pair. Reviews of dense stereo reconstruction algorithms are given, for example, in [5, 35, 46]. What is still required, however, is an efficient algorithm to convert the disparities to 3D coordinates.

To construct an efficient algorithm, we assume that the two-view camera geometry is described with the first camera as the reference camera and that the relative orientation of the second camera is specified with respect to the first camera. The relative orientations of any two cameras in a multi-view setup can be transformed into this convention in a straightforward manner. In addition, we make use of the fact that for rectified telecentric line-scan cameras, the relative orientation only consists of a rotation around the ${\varvec{{y}}}$ axis (i.e., the relative orientation angles $\alpha$ and $\gamma$ are 0) and a translation of the form $(t_x, 0, t_z)^\top$ (i.e., the translation $t_y$ of the relative orientation is 0). Furthermore, we make use of the fact that both magnifications are identical ($m_1 = m_2 = m$), that $c_y$ is identical for both cameras ($c_{1;y} = c_{2;y} = c_y$), that $s_x$ is identical for both cameras ($s_{1;x} = s_{2;x} = s_x$), and that $s_{1,2;x} = m v_{1,2;y}$.

Let us suppose that we have a point correspondence $c_1 \leftrightarrow c_2 = c_1 + d$ in row 0 of the image, where $c_{1,2}$ are the column coordinates of the corresponding points and d is the disparity of the points. A point correspondence in any other row obviously will only influence the ${\varvec{{y}}}$ coordinate and not the ${\varvec{{x}}}$ and ${\varvec{{z}}}$ coordinates of the reconstructed point.

Then, the optical ray in the first camera is given by

$$\begin{aligned} \left( \begin{array}{c} x_1 \\ 0 \\ 0 \end{array} \right) + \lambda \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \quad , \end{aligned}$$

(30)

where $x_1 = (c_1 - c_{1;x}) s_x/m$. The direction of the ${\varvec{{x}}}$ axis of the second camera is given by $(r_{11}, r_{21}, r_{31})^\top$ in the coordinate system of the first camera, where $(r_{11}, r_{21}, r_{31})^\top = (\cos \beta , 0, -\sin \beta )^\top$ is the first column of the relative orientation matrix. The direction of the ${\varvec{{z}}}$ axis of the second camera is given by $(r_{13}, r_{23}, r_{33})^\top$ in the coordinate system of the first camera, where $(r_{13}, r_{23}, r_{33})^\top = (\sin \beta , 0, \cos \beta )^\top$ is the third column of the relative orientation matrix. Consequently, the optical ray in the second camera is given in the coordinate system of the first camera by

$$\begin{aligned} \left( \begin{array}{c} t_x + x_2 \cos \beta \\ 0 \\ t_z - x_2 \sin \beta \end{array} \right) + \mu \left( \begin{array}{c} \sin \beta \\ 0 \\ \cos \beta \end{array} \right) \quad , \end{aligned}$$

(31)

where $x_2 = (c_2 - c_{2;x}) s_x/m = (c_1 + d - c_{2;x}) s_x/m$.

We can now equate (30) and (31) and solve for $\mu$ and $\lambda$. Note that $\lambda$ is the ${\varvec{{z}}}$ coordinate of the reconstructed point in the camera coordinate system of camera 1. This results in

$$\begin{aligned} z = t_z - \frac{t_x}{\tan \beta } + \frac{(c_1 - c_{1;x}) s_x}{m \tan \beta } - \frac{(c_1 + d - c_{2;x}) s_x}{m \sin \beta } \quad . \end{aligned}$$

(32)

The ${\varvec{{x}}}$ coordinate of the reconstructed point is given by

$$\begin{aligned} x = x_1 = \frac{(c_1 - c_{1;x}) s_x}{m} \quad . \end{aligned}$$

(33)

Finally, the ${\varvec{{y}}}$ coordinate of a point correspondence in an arbitrary row r is given by:

$$\begin{aligned} y = y_1 = \frac{(r - c_y) s_y}{m} \quad . \end{aligned}$$

(34)

The only variables in (32)–(34) are $c_1$, d, and r. The remaining terms are constant for all points in a disparity image. Consequently, they can be factored out as constant factors or summands. Therefore, the 3D coordinates can be reconstructed very efficiently.

Fig. 8

The geometry of the stereo reconstruction from rectified images. Refer to the text for details

The geometry of the stereo reconstruction from rectified images is shown in Fig. 8. It displays a top view of the two cameras. Hence, the image planes are visualized by lines. The figure shows the two camera coordinate systems and their relative orientation. The ${\varvec{{y}}}$ axes are not shown since the view is along the common ${\varvec{{y}}}$ direction of both cameras.⁹ Figure 8 also shows the ${\varvec{{x}}}$ coordinates $c_{1,2;x}$ of the principal points and the homologous points $c_{1,2}$. As before, $c_{1,2} \equiv x_{1,2}$ indicates that these points are the same points represented in different coordinate systems. Finally, the figure shows the optical rays (30) and (31).

6 Experiments

In this section, we will perform experiments for a two-view telecentric line-scan camera setup. The setup is depicted in Fig. 9. It consists of two Basler raL2048-48gm line-scan cameras (14.3 mm sensor size, CMOS, 7.0 ${\upmu }\mathrm{m}$ pixel pitch, $2048 \times 1$) in an along-track configuration.¹⁰ The back camera looks forward and was equipped with an Opto Engineering TC2MHR058-F telecentric lens (nominal magnification: 0.228, working distance: 158 mm), while the front camera looks backward and was equipped with an Opto Engineering TC2MHR048-F telecentric lens (nominal magnification: 0.268, working distance: 133 mm). The back camera was selected as the reference camera. A line-shaped light source was used to illuminate the footprint of both sensor lines. A linear stage was used to move the objects in front of the two rigidly mounted cameras. An encoder triggered the image acquisition to ensure a constant speed and a simultaneous acquisition with both cameras.

Fig. 9

Stereo setup with two telecentric line-scan cameras. a Image of the setup. b Drawing of the setup. The cameras were mounted in an along-track configuration. A line-shaped light source was used to cover the footprint of both sensor lines. An encoder triggered the image acquisition to ensure a constant speed and a simultaneous acquisition with both cameras

6.1 Camera Calibration

The cameras were calibrated by acquiring 16 image pairs of an $8 \times 6$ cm$^2$ planar calibration object (i.e., 32 images in total, 16 per camera). Care was taken to use all degrees of freedom of the exterior orientation as well as possible. In particular, the calibration object was rotated around the ${\varvec{{z}}}$ axis to make full use of the 360$^\circ$ angle range. Furthermore, the calibration object was tilted with respect to the ${\varvec{{z}}}$ axis to cover the depth of field of the cameras as well as possible. Since the cameras were mounted rigidly with respect to each other, a common motion vector was assumed in the calibration. The results of calibrating the setup using the division distortion model are shown in Table 1. The polynomial distortion model resulted in root mean square (RMS) errors that were insignificantly smaller and are therefore not shown. It can be seen that the calibration returns magnification values that are relatively close to their nominal values. Furthermore, the results show that both lenses have relatively small distortions. Because of the small distortions, the principal points have relative large standard deviations, which is to be expected according to Remark 3. Nevertheless, the principal point is significantly different from the center of the sensor line for both cameras. A significance test based on the approach in [13] like the one performed in [42, Section 5.2] showed that all distortion parameters ($c_x$, $c_y$, and $\kappa$) are highly significant and, therefore, no over-fitting occurs, even for these small distortions.

Table 1 Calibration results for a stereo setup with two Basler raL2048-48gm line-scan cameras in an along-track configuration with a common motion vector

Table 2 Correlations of the optimized interior orientation parameters of the back camera of Table 1 rounded to three significant figures

Table 3 Correlations of the optimized interior orientation parameters of the front camera of Table 1 rounded to three significant figures

Fig. 10

One pair of images of the planar calibration object that were used to calibrate the line-scan cameras. Residuals are overlaid for each circular calibration mark as white lines. The residuals were scaled by a factor of 70 for better visibility. The predominant part of the residuals is a systematic periodic error in the direction of the movement, i.e., in vertical direction in the images. It is very similar for corresponding control points

In addition to examining the standard deviations of the interior orientation parameters in Table 1, we also examine their correlations. These can be computed from (62) as

$$\begin{aligned} c_{ij} = \frac{\sigma _{ij}}{\sigma _i \sigma _j} \quad \end{aligned}$$

(35)

where $\sigma _{ij}$ denotes the corresponding element of ${\varvec{{\Sigma }}_k}$ and $\sigma _l = \sqrt{\sigma _{ll}}$ for $l \in \{i,j\}$.

The correlations for the back camera are shown in Table 2, while those of the front camera are shown in Table 3. It can be seen that there are only very small correlations between almost all interior orientation parameters, with the following exceptions:

• There is a high correlation between m and $\kappa$. This is not surprising since the distortions in both cameras are quite small and a small change in m can be exchanged for a small change in $\kappa$ in this case.

• There is a high correlation between $c_x$ and $\kappa$. This is not surprising in light of Remark 3. What is surprising, however, is the relatively small correlation between $c_y$ and $\kappa$. We believe this is caused by the systematic errors that we will discuss immediately below.

• There is a very high correlation between $v_z$ and $v_y$. This is not surprising in light of Remark 9.

Fig. 11

a, b Stereo image pair of a PCB acquired with two telecentric line-scan cameras. c, d Stereo image pair of a, b rectified to the epipolar standard configuration. e Disparity image of a cropped part of c. f Final textured 3D reconstruction of the PCB in e

The results in Table 1 show that there is a relatively large RMS error of 0.5418. To examine the reason for these errors, it is instructive to investigate the individual residuals. The residuals are the differences between the extracted centers of the calibration marks in the image and the projections of the corresponding points on the calibration object into the image. The projection is performed by using the calibrated camera parameters of the interior and exterior orientation. The residuals are shown for one of the image pairs that were used for calibration in Fig. 10. The residuals were scaled by a factor of 70 for better visibility. It can be seen that the predominant part of the residuals is a systematic periodic error in the direction of the movement, i.e., in vertical direction in the images. The errors are very similar in magnitude and direction for corresponding control points in both images. Similar results were obtained in the experiments performed in [42, Section 5.2] for the single-view case, in which the camera was mounted perpendicularly above the linear stage. The encoder we used reacts to the angle position of the electric motor of the linear stage. Therefore, we assume that the major part of the residuals is caused by the circular actuator that is not perfectly centered. Another reason for this assumption is the fact that the periodicity of the error corresponds to one full revolution of the actuator. Therefore, we assume that the calibration error could be further reduced by using a higher-quality actuator that better realizes a constant speed. In comparison, the residuals in horizontal direction are very small, which shows that the proposed camera model represents the true projection very well.

6.2 Stereo Reconstruction

In this section, we test the validity of the proposed approach by discussing two examples of stereo reconstructions of printed circuit boards (PCBs). Our goal in this section is to validate the camera model only with respect to its ability to obtain qualitatively correct results. This indirectly tests the validity of the calibration and the stereo rectification in the sense that no qualitatively correct reconstruction would result if the calibrated camera parameters were incorrect or the stereo rectification would work incorrectly. Conversely, our goal is not to test the metric accuracy of the reconstruction for two reasons. First, the accuracy of the reconstruction to a large extent depends on the accuracy of the disparity calculations in the stereo algorithm. Second, testing quantitative results would require us to use a standard measurand or measurement system with a superior accuracy to obtain the ground truth [20, Chapter 2.2.1]. Unfortunately, we currently do not have such a measurand or measurement system at our disposal.

Figure 11a, b shows a stereo image pair of a PCB that was obtained with the two-view telecentric line-scan setup. Both images have a size of 2048 $\times$ 3584 pixels. The back image is the image in Fig. 11a, while the front image is the image in Fig. 11b. Because the magnifications of the two lenses were slightly different, the overlap between the fields of view of the two images is not perfect. We will take this into account during the reconstruction and perform the reconstruction only in the overlapping parts of the fields of view.

Table 4 displays the interior orientation parameters, the motion vectors, and the relative orientation that were computed with the stereo rectification algorithm of Sect. 5.1. It can be seen that the magnifications of both rectified cameras as well as their pixel sizes are identical and that both cameras have square pixels (since $v_y = s_x / m$). Furthermore, as should be the case, the relative orientation solely consists of a rotation around the ${\varvec{{y}}}$ axis and a translation in the ${\varvec{{x}}}$ and ${\varvec{{z}}}$ directions. Table 4 also shows the parameters of the rectifying camera pose transformations. These are transformations that transform points from the original camera coordinate systems to the rectified camera coordinate systems. As can be seen, both cameras have been rotated by approximately -90$^\circ$ around their ${\varvec{{z}}}$ axes. This corresponds to a counterclockwise rotation of the rectified images with respect to the original images. This is the behavior that is to be expected for an along-track configuration. Finally, it can be seen that both cameras have been shifted by the same amount in opposite directions along their ${\varvec{{y}}}$ axes, as described in Sect. 5.1.

Table 4 Camera parameters of the rectified cameras that were computed from the calibrated camera parameters in Table 1

The rectified images corresponding to the images in Fig. 11a, b are shown in Fig. 11c, d. The rectified image of the back camera has a size of 3460 $\times$ 2307 pixels, while the rectified image of the front camera has a size of 3709 $\times$ 2307 pixels. Note that there are severe occlusions in some parts of the images owing to the 60$^\circ$ angle between the viewing directions of both cameras.

Figure 11e displays the disparities that were computed using the variational stereo algorithm proposed in [8], while Fig. 11f displays a 3D view of a part of the reconstructed PCB. It can be seen that the large integrated circuits (ICs) have been reconstructed correctly in the places where there is texture on the ICs. For the parts in the image where there is no texture and for which, consequently, no valid disparities can be determined, the approach in [8] smoothly interpolates the reconstruction. This is especially noticeable on the large AMCC IC and between the two ICs to the right of the AMCC IC. In addition to the ICs, the large resistor RE3 in the lower right-hand corner has been reconstructed very well. Furthermore, many of the small surface mount devices (SMDs) are visible in the disparities. On the other hand, the large capacitor C13 has not been reconstructed well. The reason for this is its specular top, which has reflected the light of the illumination to the camera in the back image but not the front image. It might be worthwhile to investigate whether this problem could be alleviated through the use of a more diffuse illumination or through the use of polarizing filters [43, Chapter 2.1]. Furthermore, it can be seen that the ICs at the bottom right of the scene are reconstructed erroneously because they have a relatively weak and dark texture, which causes the algorithm in [8] to interpolate from neighboring areas, in particular, from the areas to the right of the rectified images, for which, unfortunately, there is no overlap. Therefore, the reconstruction results in the lower right corner basically are an artifact of the stereo algorithm.

Figure 12a, b shows a stereo image pair of a PCB with different characteristics. It contains fewer ICs but many more SMD components. The corresponding rectified images are depicted in Fig. 12c, d.

Fig. 12

a, b Stereo image pair of a PCB acquired with two telecentric line-scan cameras. c, d Stereo image pair of a, b rectified to the epipolar standard configuration. e Disparity image of a cropped part of c. f Final textured 3D reconstruction of the PCB in e

The disparities obtained from the rectified images are shown in Fig. 12e, while a 3D view of a part of the reconstruction is displayed in Fig. 12f. It can be seen that the large Altera IC has been reconstructed well in the area in which there is sufficient texture. Furthermore, it can be seen that all of the resistors and capacitors on the PCB have been reconstructed well and can be clearly seen in the disparities and the 3D reconstruction. It is also interesting to note that there are erroneous reconstructions at the places on the PCB where there is bare solder on which no SMD has been mounted, e.g., R96, R105, or R123. Again, the culprit is the fact that the bare solder specularly reflects the light of the illumination (to the left in the rectified back image and to the right in the rectified front image). Since these reflections create an erroneous pseudo-texture that the algorithm in [8] can match very well, an erroneous indentation is reconstructed. Again, it might be worthwhile to investigate whether this problem could be alleviated through the use of a more diffuse illumination or through the use of polarizing filters.

In summary, these examples show that the proposed 3D reconstruction algorithm using line-scan cameras with telecentric lenses works robustly in the areas in which there is sufficient diffuse texture to enable valid point correspondences to be determined. They also show that the multi-view camera model and the corresponding calibration algorithm return valid results.

Like all stereo algorithms, the algorithm in [8] may return erroneous results if the surface is not cooperative (i.e., where it has specular reflections or has no texture). As a topic for future research, it might be interesting to investigate whether these problems can be circumvented by an appropriate illumination. As mentioned previously, the specular reflections might be avoided through the use of a diffuse illumination or through polarizing filters. To circumvent the problems caused by a lack of texture, it might be interesting to investigate whether some kind of texture can be projected onto the objects that should be reconstructed, similar to the approach in [27].

7 Conclusions

We have proposed a multi-view camera model for line-scan cameras with telecentric lenses that can model an arbitrary number of cameras. The model assumes a linear relative motion with constant velocity between the cameras and the object. We have identified two different motion configurations. The first configuration allows each camera to move along a linear trajectory that is independent of all the other camera trajectories. The second, more common, configuration models cameras that are rigidly mounted with respect to each other and therefore possess a common motion vector. For the common motion configuration, we also have proved that the full 3D motion vector can be reconstructed uniquely, in contrast to the independent motion case, where the ${\varvec{{z}}}$ components of the motion vectors cannot be reconstructed. By allowing the principal point to have an arbitrary 2D location with respect to the sensor line and by supporting two distortion models (the division and polynomial models), the camera model can model arbitrary lens distortions.

Moreover, we have proposed a calibration algorithm that can calibrate an arbitrary multi-view telecentric line-scan camera setup.

We additionally have proved that an image pair that is acquired with two telecentric line-scan cameras can always be rectified to the epipolar standard configuration. This is in stark contrast to images that are acquired with line-scan cameras with entocentric (perspective) lenses, for which such a rectification is possible only under extremely restricted circumstances that are difficult, cumbersome, and expensive to achieve in practice. The fact that epipolar rectification is always possible makes a telecentric line-scan stereo system much easier to use in practice than an entocentric line-scan stereo system.

Furthermore, we have proposed an efficient algorithm to compute 3D coordinates from the disparities that can be obtained using an arbitrary stereo algorithm on the rectified images.

Finally, we have performed experiments on real images that have shown the validity of the proposed multi-view telecentric line-scan camera model.

An idea for future research is based on the following characteristics of line-scan applications. Line-scan cameras have readout rates in the range of 10–200 kHz [43, Chapter 2.3.1.1]. Therefore, the exposure time of each line must be very short. Hence, line-scan applications often require a very bright illumination. Furthermore, often an open diaphragm, i.e., a large aperture, is used to maximize the amount of light that passes through the lens. Large apertures, in turn, can severely limit the depth of field. This might cause problems in across-track configurations, where a common depth of field might be hard to achieve because the telecentric line-scan cameras must look onto the scene at an angle. As discussed in [40, Section 3], an overlapping depth of field can be achieved more easily by using tilt lenses (Scheimpflug optics). Therefore, a topic for future research might be to investigate whether the tilt lens camera model that was proposed in [40, Section 7] for area-scan cameras can be extended to telecentric line-scan cameras.

Sparse Levenberg–Marquardt Algorithm with Common Parameters

As mentioned in Sect. 4, minimizing (22) for setups with a common motion vector results in a sparse Levenberg–Marquardt algorithm with a tripartite parameter set. Specifically, the third part of the parameter set constitutes global parameters that are affected by all observations. In this section, we will describe how Algorithm A6.4 in [17] can be extended to handle this case.

For common motion vectors, we have parameters ${\varvec{{a}}}_k$ that depend solely on the camera, parameters ${\varvec{{b}}}_l$ that depend solely on the calibration object pose, and global parameters ${\varvec{{c}}}$. The parameters ${\varvec{{a}}}_k$ are given by the interior orientation ${\varvec{{i}}}_k$ and the relative orientation ${\varvec{{r}}}_k$ of camera k. The parameters ${\varvec{{b}}}_l$ are given by the exterior orientation ${\varvec{{e}}}_l$ of the calibration object with respect to the reference camera. Finally, the global parameters ${\varvec{{c}}}$ are given by the common motion vector ${\varvec{{v}}}$. In the Levenberg–Marquardt algorithm, we must compute the Jacobian ${{{\mathbf {\mathtt{{{J}}}}}}}$ of $\varvec{\pi }( {\varvec{{p}}}_j, {\varvec{{e}}}_l, {\varvec{{r}}}_k, {\varvec{{i}}}_k, {\varvec{{v}}} )$ with respect to its parameters. To improve the readability of the equations in the following, we will avoid double subscripts and use the abbreviations $m = n_{\mathrm {c}}$ and $n = n_{\mathrm {o}}$. For m cameras and n poses of the calibration object, the Jacobian ${{{\mathbf {\mathtt{{{J}}}}}}}$ has the following structure:

Here, ${{{\mathbf {\mathtt{{{A}}}}}}}_{kl}$ denotes the Jacobians of $\varvec{\pi }$ with respect to ${\varvec{{a}}}_k$, ${{{\mathbf {\mathtt{{{B}}}}}}}_{kl}$ the Jacobians of $\varvec{\pi }$ with respect to ${\varvec{{b}}}_l$, and ${{{\mathbf {\mathtt{{{C}}}}}}}_{kl}$ the Jacobians of $\varvec{\pi }$ with respect to ${\varvec{{c}}}$, all for a particular camera k and a particular calibration pose l for all j for which $v_{jkl} = 1$.¹¹ Hence, in our implementation, the height of these individual matrices depends on the number of control points that are visible in each respective calibration image. The heights $h_{kl}$ of the matrices are given by

$$\begin{aligned} h_{kl} = 2 \sum _{j=1}^{n_\mathrm {m}} v_{jkl} \quad , \end{aligned}$$

(37)

i.e., each control point visible in a particular image for a particular pose of the calibration object leads to two measurements. Note that $h_{kl}$ may be 0, in which case, we simply omit the corresponding matrices. Furthermore, the width of the individual matrices may also vary arbitrarily, depending on which parameters are optimized. We allow the user complete control over which parameters are optimized globally and for each individual camera. For example, by default, the width of the matrices ${{{\mathbf {\mathtt{{{A}}}}}}}_{1l}$ will be 6 elements smaller than that of the remaining matrices ${{{\mathbf {\mathtt{{{A}}}}}}}_{kl}$ ($k \ge 2$) since we do not optimize the relative orientation for the reference camera (camera 1).

The corresponding error vector $\varvec{\varepsilon }$ has an analogous structure:

$$\begin{aligned} \varvec{\varepsilon } = \left( \begin{array}{c} \varvec{\varepsilon }_{11} \\ \varvec{\varepsilon }_{21} \\ \vdots \\ \varvec{\varepsilon }_{m1} \\ \hline \varvec{\varepsilon }_{12} \\ \varvec{\varepsilon }_{22} \\ \vdots \\ \varvec{\varepsilon }_{m2} \\ \hline \vdots \\ \hline \varvec{\varepsilon }_{1n} \\ \varvec{\varepsilon }_{2n} \\ \vdots \\ \varvec{\varepsilon }_{mn} \\ \end{array} \right) \quad . \end{aligned}$$

(38)

Here, $\varvec{\varepsilon }_{kl}$ denotes the error vector for a particular camera k and a particular calibration pose l, i.e., the vector containing all errors $\varvec{\varepsilon }_{jkl} = \varvec{\pi }( {\varvec{{p}}}_j, {\varvec{{e}}}_l, {\varvec{{r}}}_k, {\varvec{{i}}}_k, {\varvec{{v}}}) - {\varvec{{p}}}_{jkl}$ for all j for which $v_{jkl} = 1$.

During the optimization in the Levenberg–Marquardt algorithm, we solve the following equation set for the parameter increments $\varvec{\delta }$:¹²

$$\begin{aligned} {{{\mathbf {\mathtt{{{N}}}}}}}^* \varvec{\delta } = ({{{\mathbf {\mathtt{{{J}}}}}}}^\top {{{\mathbf {\mathtt{{{J}}}}}}})^* \varvec{\delta } = -{{{\mathbf {\mathtt{{{J}}}}}}}^\top \varvec{\varepsilon } \quad . \end{aligned}$$

(39)

Here, the $*$ denotes the augmentation of the normal equations, i.e., the multiplication of the diagonal elements of ${{{\mathbf {\mathtt{{{N}}}}}}}$ by $1 + \lambda$ [34, Chapter 15.5.2].¹³

Because of the sparsity of ${{{\mathbf {\mathtt{{{J}}}}}}}$, the matrix ${{{\mathbf {\mathtt{{{N}}}}}}} = {{{\mathbf {\mathtt{{{J}}}}}}}^\top {{{\mathbf {\mathtt{{{J}}}}}}}$ has the following structure:

$$\begin{aligned} {{{\mathbf {\mathtt{{{N}}}}}}} = \left( \begin{array}{c|cccc|cccc} {{{\mathbf {\mathtt{{{M}}}}}}} &{} {{{\mathbf {\mathtt{{{P}}}}}}}_1 &{} {{{\mathbf {\mathtt{{{P}}}}}}}_2 &{} \cdots &{} {{{\mathbf {\mathtt{{{P}}}}}}}_m &{} {{{\mathbf {\mathtt{{{Q}}}}}}}_1 &{} {{{\mathbf {\mathtt{{{Q}}}}}}}_2 &{} \cdots &{} {{{\mathbf {\mathtt{{{Q}}}}}}}_n \\ \hline {{{\mathbf {\mathtt{{{P}}}}}}}_1^\top &{} {{{\mathbf {\mathtt{{{U}}}}}}}_1 &{} &{} &{} &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{11} &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{12} &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{1n} \\ {{{\mathbf {\mathtt{{{P}}}}}}}_2^\top &{} &{} {{{\mathbf {\mathtt{{{U}}}}}}}_2 &{} &{} &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{21} &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{22} &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{2n} \\ \vdots &{} &{} &{} \ddots &{} &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{{\mathbf {\mathtt{{{P}}}}}}}_m^\top &{} &{} &{} &{} {{{\mathbf {\mathtt{{{U}}}}}}}_m &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{m1} &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{m2} &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{mn} \\ \hline {{{\mathbf {\mathtt{{{Q}}}}}}}_1^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{11}^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{21}^\top &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{m1}^\top &{} {{{\mathbf {\mathtt{{{V}}}}}}}_1 &{} &{} &{} \\ {{{\mathbf {\mathtt{{{Q}}}}}}}_2^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{12}^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{22}^\top &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{m2}^\top &{} &{} {{{\mathbf {\mathtt{{{V}}}}}}}_2 &{} &{} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} &{} \ddots &{} \\ {{{\mathbf {\mathtt{{{Q}}}}}}}_n^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{1n}^\top &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{2n}^\top &{} \cdots &{} {{{\mathbf {\mathtt{{{W}}}}}}}_{mn}^\top &{} &{} &{} &{} {{{\mathbf {\mathtt{{{V}}}}}}}_n \end{array} \right) \quad , \end{aligned}$$

(40)

Analogously, the error vector ${{{\mathbf {\mathtt{{{J}}}}}}}^\top \varvec{\varepsilon }$ has the following structure:

$$\begin{aligned} {{{\mathbf {\mathtt{{{J}}}}}}}^\top \varvec{\varepsilon } = \left( \begin{array}{c} \varvec{\varepsilon }_{{\varvec{{c}}}} \\ \hline \varvec{\varepsilon }_{{\varvec{{a}}}_1} \\ \varvec{\varepsilon }_{{\varvec{{a}}}_2} \\ \vdots \\ \varvec{\varepsilon }_{{\varvec{{a}}}_m} \\ \hline \varvec{\varepsilon }_{{\varvec{{b}}}_1} \\ \varvec{\varepsilon }_{{\varvec{{b}}}_2} \\ \vdots \\ \varvec{\varepsilon }_{{\varvec{{b}}}_n} \\ \end{array} \right) \quad . \end{aligned}$$

(41)

We have:

$$\begin{aligned} {{{\mathbf {\mathtt{{{M}}}}}}}&= \sum _{i=1}^m \sum _{j=1}^n {{{\mathbf {\mathtt{{{C}}}}}}}_{ij}^\top {{{\mathbf {\mathtt{{{C}}}}}}}_{ij} \end{aligned}$$

(42)

$$\begin{aligned} {{{\mathbf {\mathtt{{{P}}}}}}}_k&= \sum _{j=1}^n {{{\mathbf {\mathtt{{{C}}}}}}}_{kj}^\top {{{\mathbf {\mathtt{{{A}}}}}}}_{kj} \end{aligned}$$

(43)

$$\begin{aligned} {{{\mathbf {\mathtt{{{Q}}}}}}}_l&= \sum _{i=1}^m {{{\mathbf {\mathtt{{{C}}}}}}}_{il}^\top {{{\mathbf {\mathtt{{{B}}}}}}}_{il} \end{aligned}$$

(44)

$$\begin{aligned} {{{\mathbf {\mathtt{{{U}}}}}}}_k&= \sum _{j=1}^n {{{\mathbf {\mathtt{{{A}}}}}}}_{kj}^\top {{{\mathbf {\mathtt{{{A}}}}}}}_{kj} \end{aligned}$$

(45)

$$\begin{aligned} {{{\mathbf {\mathtt{{{V}}}}}}}_l&= \sum _{i=1}^m {{{\mathbf {\mathtt{{{B}}}}}}}_{il}^\top {{{\mathbf {\mathtt{{{B}}}}}}}_{il} \end{aligned}$$

(46)

$$\begin{aligned} {{{\mathbf {\mathtt{{{W}}}}}}}_{kl}&= {{{\mathbf {\mathtt{{{A}}}}}}}_{kl}^\top {{{\mathbf {\mathtt{{{B}}}}}}}_{kl} \end{aligned}$$

(47)

$$\begin{aligned} \varvec{\varepsilon }_{{\varvec{{c}}}}&= \sum _{i=1}^m \sum _{j=1}^n {{{\mathbf {\mathtt{{{C}}}}}}}_{ij}^\top \varvec{\varepsilon }_{ij} \end{aligned}$$

(48)

$$\begin{aligned} \varvec{\varepsilon }_{{\varvec{{a}}}_k}&= \sum _{j=1}^n {{{\mathbf {\mathtt{{{A}}}}}}}_{kj}^\top \varvec{\varepsilon }_{kj} \end{aligned}$$

(49)

$$\begin{aligned} \varvec{\varepsilon }_{{\varvec{{b}}}_l}&= \sum _{i=1}^m {{{\mathbf {\mathtt{{{B}}}}}}}_{il}^\top \varvec{\varepsilon }_{il} \quad , \end{aligned}$$

(50)

where $k = 1, \ldots , m$ and $l = 1, \ldots , n$. To increase the numerical stability of the equation system, we additionally use the normalization and denormalization procedure described in [31, Section “Scale of measurement”].

Let us call the upper left matrix in ${{{\mathbf {\mathtt{{{N}}}}}}}$ that consists of the matrices ${{{\mathbf {\mathtt{{{M}}}}}}}$, ${{{\mathbf {\mathtt{{{P}}}}}}}_k$, and ${{{\mathbf {\mathtt{{{U}}}}}}}_k$ by ${{{\mathbf {\mathtt{{{U}}}}}}}$, the lower right matrix consisting of the matrices ${{{\mathbf {\mathtt{{{V}}}}}}}_l$ by ${{{\mathbf {\mathtt{{{V}}}}}}}$, and the upper right block consisting of the matrices ${{{\mathbf {\mathtt{{{Q}}}}}}}_l$ and ${{{\mathbf {\mathtt{{{W}}}}}}}_{kl}$ by ${{{\mathbf {\mathtt{{{W}}}}}}}$ (and, therefore, the lower left block by ${{{\mathbf {\mathtt{{{W}}}}}}}^\top$). Furthermore, let us call the upper part of ${{{\mathbf {\mathtt{{{J}}}}}}}^\top \varvec{\varepsilon }$ consisting of the vectors $\varvec{\varepsilon }_{{\varvec{{c}}}}$ and $\varvec{\varepsilon }_{{\varvec{{a}}}_k}$ by $\varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{U}}}}}}}}$ and the lower part consisting of the vectors $\varvec{\varepsilon }_{{\varvec{{b}}}_l}$ by $\varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{V}}}}}}}}$. As is usual in sparse Levenberg–Marquardt algorithms, we will compute the Schur complement ${{{\mathbf {\mathtt{{{S}}}}}}} = {{{\mathbf {\mathtt{{{U}}}}}}}^* - {{{\mathbf {\mathtt{{{W}}}}}}} {{{{\mathbf {\mathtt{{{V}}}}}}}^*}^{-1} {{{\mathbf {\mathtt{{{W}}}}}}}^\top$ and $\varvec{\varepsilon }_{{{\mathbf {\mathtt{{{S}}}}}}} = \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{U}}}}}}}} - {{{\mathbf {\mathtt{{{W}}}}}}} {{{{\mathbf {\mathtt{{{V}}}}}}}^*}^{-1} \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{V}}}}}}}}$. In our case, ${{{\mathbf {\mathtt{{{S}}}}}}}$ has the following structure:

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}} = \left( \begin{array}{c|cccc} {{{\mathbf {\mathtt{{{S}}}}}}}_{00} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{01} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{02} &{} \cdots &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{0m} \\ \hline {{{\mathbf {\mathtt{{{S}}}}}}}_{10} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{11} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{12} &{} \cdots &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{1m} \\ {{{\mathbf {\mathtt{{{S}}}}}}}_{20} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{21} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{22} &{} \cdots &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{2m} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{{\mathbf {\mathtt{{{S}}}}}}}_{m0} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{m1} &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{m2} &{} \cdots &{} {{{\mathbf {\mathtt{{{S}}}}}}}_{mm} \end{array} \right) \quad . \end{aligned}$$

(51)

Furthermore, $\varvec{\varepsilon }_{{{\mathbf {\mathtt{{{S}}}}}}}$ has the following structure:

$$\begin{aligned} \varvec{\varepsilon }_{{{\mathbf {\mathtt{{{S}}}}}}} = \left( \begin{array}{c} \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_0} \\ \hline \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_1} \\ \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_2} \\ \vdots \\ \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_m} \end{array} \right) \quad . \end{aligned}$$

(52)

We have:

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}}_{00}&= {{{\mathbf {\mathtt{{{M}}}}}}}^* - \sum _{j=1}^n {{{\mathbf {\mathtt{{{Q}}}}}}}_j {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} {{{\mathbf {\mathtt{{{Q}}}}}}}_j^\top \end{aligned}$$

(53)

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}}_{0k}&= {{{\mathbf {\mathtt{{{P}}}}}}}_k - \sum _{j=1}^n {{{\mathbf {\mathtt{{{Q}}}}}}}_j {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} {{{\mathbf {\mathtt{{{W}}}}}}}_{kj}^\top \end{aligned}$$

(54)

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}}_{k0}&= {{{\mathbf {\mathtt{{{S}}}}}}}_{0k}^\top \end{aligned}$$

(55)

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}}_{kk}&= {{{\mathbf {\mathtt{{{U}}}}}}}_k^* - \sum _{j=1}^n {{{\mathbf {\mathtt{{{W}}}}}}}_{kj} {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} {{{\mathbf {\mathtt{{{W}}}}}}}_{kj}^\top \end{aligned}$$

(56)

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}}_{kl}&= - \sum _{j=1}^n {{{\mathbf {\mathtt{{{W}}}}}}}_{kj} {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} {{{\mathbf {\mathtt{{{W}}}}}}}_{lj}^\top \end{aligned}$$

(57)

$$\begin{aligned} \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_0}&= \varvec{\varepsilon }_{{\varvec{{c}}}} - \sum _{j=1}^n {{{\mathbf {\mathtt{{{Q}}}}}}}_j {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} \varvec{\varepsilon }_{{\varvec{{b}}}_j} \end{aligned}$$

(58)

$$\begin{aligned} \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}_k}&= \varvec{\varepsilon }_{{\varvec{{a}}}_k} - \sum _{j=1}^n {{{\mathbf {\mathtt{{{W}}}}}}}_{kj} {{{{\mathbf {\mathtt{{{V}}}}}}}_j^*}^{-1} \varvec{\varepsilon }_{{\varvec{{b}}}_j} \quad . \end{aligned}$$

(59)

where $k = 1, \ldots , m$ and $l = 1, \ldots , m$.

We then solve

$$\begin{aligned} {{{\mathbf {\mathtt{{{S}}}}}}} \, \varvec{\delta }_{{{{\mathbf {\mathtt{{{S}}}}}}}} = \varvec{\varepsilon }_{{{{\mathbf {\mathtt{{{S}}}}}}}} \end{aligned}$$

(60)

for $\varvec{\delta }_{{{{\mathbf {\mathtt{{{S}}}}}}}}$ using the Cholesky decomposition.¹⁴ This gives us the parameter increments $\varvec{\delta }_{{\varvec{{c}}}}$ and $\varvec{\delta }_{{\varvec{{a}}}_k}$ ($k = 1, \ldots , m$), which we can back-substitute to obtain the parameter increments for $\varvec{\delta }_{{\varvec{{b}}}_l}$ ($l = 1, \ldots , n$):

$$\begin{aligned} \varvec{\delta }_{{\varvec{{b}}}_l} = {{{{\mathbf {\mathtt{{{V}}}}}}}_l^*}^{-1} \left( \varvec{\varepsilon }_{{\varvec{{b}}}_l} - {{{\mathbf {\mathtt{{{Q}}}}}}}_l \, \varvec{\delta }_{{\varvec{{c}}}} - \sum _{i=1}^m {{{\mathbf {\mathtt{{{W}}}}}}}_{il} \, \varvec{\delta }_{{\varvec{{a}}}_i} \right) \quad . \end{aligned}$$

(61)

The only thing that remains to be described is the computation of the covariances of the camera parameters. As described in [42, Section 3.2], we subsume the motion vector under the interior orientation of the respective camera. In particular, we use the convention that the motion vector is given by the last three elements of the interior orientation. We store the transformed common motion vector ${\varvec{{v}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_k {\varvec{{v}}}$ with the interior orientation of camera k. To compute the covariances of the interior orientation of camera k, we compute the inverse of the matrix ${{{\mathbf {\mathtt{{{S}}}}}}}$ without the augmentation of the matrices ${{{\mathbf {\mathtt{{{M}}}}}}}$, ${{{\mathbf {\mathtt{{{U}}}}}}}_k$ and ${{{\mathbf {\mathtt{{{V}}}}}}}_l$. This gives us (scaled) covariance block matrices ${\varvec{{\Sigma }}_{00}}$, ${\varvec{{\Sigma }}_{k0}}$, ${\varvec{{\Sigma }}_{0k}}$, and ${\varvec{{\Sigma }}_{kk}}$. We must reorder these blocks appropriately. Furthermore, since ${\varvec{{v}}}_k = {{{\mathbf {\mathtt{{{R}}}}}}}_k {\varvec{{v}}}$, we must propagate the covariances of ${\varvec{{v}}}$ to the covariances of ${\varvec{{v}}}_k$ appropriately [17, Result 5.3]. With this, the covariances ${\varvec{{\Sigma }}_k}$ of the interior orientation parameters of camera k are given by:

$$\begin{aligned} {\varvec{{\Sigma }}_k = \sigma _0^2 \left( \begin{array}{cc} {{{\mathbf {\mathtt{{{I}}}}}}} &{} {{{\mathbf {\mathtt{{{0}}}}}}} \\ {{{\mathbf {\mathtt{{{0}}}}}}} &{} {{{\mathbf {\mathtt{{{R}}}}}}} \end{array} \right) \left( \begin{array}{cc} \varvec{{\Sigma }}_{kk} &{} \varvec{{\Sigma }}_{k0} \\ \varvec{{\Sigma }}_{0k} &{} \varvec{{\Sigma }}_{00} \end{array} \right) \left( \begin{array}{cc} {{{\mathbf {\mathtt{{{I}}}}}}} &{} {{{\mathbf {\mathtt{{{0}}}}}}} \\ {{{\mathbf {\mathtt{{{0}}}}}}} &{} {{{\mathbf {\mathtt{{{R}}}}}}}^\top \end{array} \right) \quad ,} \end{aligned}$$

(62)

where $\sigma _0^2 = \varepsilon _{\mathrm {o}}/r$ is the variance of unit weight, $\varepsilon _{\mathrm {o}} = \varvec{\varepsilon }^\top \varvec{\varepsilon }$ is the optimized error obtained by the Levenberg–Marquardt algorithm, $r = l_{\varvec{\varepsilon }} - l_{{\varvec{{c}}}} - l_{{\varvec{{a}}}} - l_{{\varvec{{b}}}}$ is the redundancy of the system, $l_{\varvec{\varepsilon }}$ denotes the length of the error vector $\varvec{\varepsilon }$, $l_{{\varvec{{c}}}}$ denotes the length of the common parameter vector ${\varvec{{c}}}$ (in our case, the common motion vector ${\varvec{{v}}}$), $l_{{\varvec{{a}}}}$ denotes the length of the vector that contains all the ${\varvec{{a}}}$ parameters (in our case, the vector that contains all interior orientation parameters ${\varvec{{i}}}_k$ and all relative orientation parameters ${\varvec{{r}}}_k$), and $l_{{\varvec{{b}}}}$ denotes the length of the vector that contains all the ${\varvec{{b}}}$ parameters (in our case, the vector that contains all exterior orientation parameters ${\varvec{{e}}}_l$). The lengths $l_{{\varvec{{c}}}}$, $l_{{\varvec{{a}}}}$, and $l_{{\varvec{{b}}}}$ only take into account the parameters that are actually optimized.

We close this section by remarking that the sparse Levenberg–Marquardt algorithm we have described in this section can be used whenever the parameters can be split into the three classes of parameters ${\varvec{{c}}}$ (common parameters), ${\varvec{{a}}}_k$ (e.g., per-camera parameters), and ${\varvec{{b}}}_l$ (e.g., per-observation parameters). In particular, the proposed algorithm can be used as to implement a sparse bundle adjustment algorithm that reconstructs the 3D positions of tie points extracted from a set of images. In this case, the common parameters ${\varvec{{c}}}$ would remain identical (i.e., the common motion vector). Furthermore, the per-camera parameters ${\varvec{{a}}}_k$ would remain identical (i.e., the interior and relative orientations of the cameras). However, the per-observation parameters ${\varvec{{b}}}_l$ now would contain the reconstructed 3D points corresponding to the matched tie points (instead of the exterior orientations of the calibration object, as in our camera calibration algorithm).