Abstract
Studying the changes of shape is a common concern in many scientific fields. We address here two problems: (1) quantifying the deformation between two given shapes and (2) transporting this deformation to morph a third shape. These operations can be done with or without point correspondence, depending on the availability of a surface matching algorithm, and on the type of mathematical procedure adopted. In computer vision, the re-targeting of emotions mapped on faces is a common application. We contrast here four different methods used for transporting the deformation toward a target once it was estimated upon the matching of two shapes. These methods come from very different fields such as computational anatomy, computer vision and biology. We used the large diffeomorphic deformation metric mapping and thin plate spline, in order to estimate deformations in a deformational trajectory of a human face experiencing different emotions. Then we use naive transport (NT), linear shift (LS), direct transport (DT) and fanning scheme (FS) to transport the estimated deformations toward four alien faces constituted by 240 homologous points and identifying a triangulation structure of 416 triangles. We used both local and global criteria for evaluating the performance of the 4 methods, e.g., the maintenance of the original deformation. We found DT, LS and FS very effective in recovering the original deformation while NT fails under several aspects in transporting the shape change. As the best method may differ depending on the application, we recommend carefully testing different methods in order to choose the best one for any specific application.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Shape theory is used in several fields, from computer vision to biomedical engineering for object tracking, image segmentation or categorization and probabilistic modeling. While most biological applications usually analyze shapes and forms utilizing a discrete set of homologous anatomical landmarks (cf. [33]), the use of continuous surfaces without a pointwise correspondence is faced by exploiting the potential of a plethora of diffeomorphic techniques ([26, 38] and references therein). Shapes are embedded in curved Riemannian manifolds defined by a metric and a compatible connection, as detailed in [7]. Both properties permit analyses on manifolds by allowing the computations of distances between points, i.e., metrical properties and moving on the manifold along paths called geodesics. The parallel transport (PT) allows transporting geometrical data along curves on the manifold. Nevertheless, when defining geodesics by means of landmarks defined on two shapes, important features can be neglected by this PT (cf. [48]). Diffeomorphic approaches gained prominence in recent years, especially for shape analysis on magnetic resonance or CT scans (see [27]). Morphometrics has been applied to single human organs, for instance the heart in [25, 32, 36, 37], and the brain as in [4]. Cardiological examinations have been conducted on the left ventricle by shape analysis by means of statistical methods, such as principal component analysis (PCA) and generalized procrustes analysis (GPA), and only recently there have been results obtained by investigation on trajectories [25, 34, 35, 41]. Very recently , [49] proposed a new type of parallel transport that is independent from the path and partially reviewed the main methods currently adopted in different fields for (a) estimating the deformation and (b) for transporting it toward a template. Their method can be applied only in presence of homologous landmarks.
Here we present a comparison among different approaches for the estimation of the deformation, that is, for probing a deformation between two shapes \(X,X'\), and for a subsequent deformation transport, a method to use the measured deformation between a pair of shapes to deform a third different shape Y in \(Y'\). We consider the following methods:
-
1.
Deformation estimation: building a map from X to \(X'\). Here we consider three methods: ordinary procrustes analysis (OPA), thin plate spline (TPS), and large diffeomorphic deformation metric mapping (LDDMM).
-
2.
Deformation Transport: the deformation measured between a pair of shapes, considered as a source, is applied to a different shape to generate another pair, the target pair. Here we use four transport methods: naive transport (NT), linear shift (LS), direct transport (DT), fanning scheme (FS).
-
3.
Post-processing: the performance of the various methods will be assessed quantitatively, by using different metrics and statistical tools.
Please note that NT and DT are based on TPS, LS is based on OPA, while FS is based on LDDMM (see Table 1).
OPA and TPS are mostly used in geometric morphometrics [2]; the LDDMM represents, today, one of the most used approach for estimating shape differences and surface matching both in absence of homologous landmarks [12], or in the presence of them [19]. NT is the name we introduce here to label the simplest way, commonly used in geometric morphometric, to use the TPS for transporting deformations. The LS is an Euclidean version of the Levi Civita parallel transport recently proposed in [37]; the DT is a new Riemannian approach described by [49]; FS is a transport method introduced in [23, 24], based on the parallel transport along geodesics of the LDDMM. Recently, many methods have been proposed for transporting deformations, based upon different techniques of deformations estimation: OPA [17, 18, 20, 48], TPS [49], LDDMM [5, 15, 24, 27, 29, 31, 40], active contour [45, 46], parametrized surfaces [50], stationary velocity field (SVF) [22]. The characteristics of most of these have been discussed in [49] and therein summarized in Table 1. Nevertheless, we think that the techniques we compare here are typical of a broad spectrum of distant disciplines. In this paper, instead of common biological/clinical applications, we perform this comparison on a set of shapes typical in computer vision-oriented applications, i.e., deformations of human faces. In particular, we focus on a set of human emotions, i.e., neutral, scared and happy. Starting from the neutral expression, we built a sequence of expressions running through the scared and to the happy one. The change in expression of the human sequence of faces is first matched and then transported to alien faces, in order to generate a sequence of expressions similar to the human one.
2 Material and Methods
Let \(\mathcal {B}\) be a body, i.e., an open subset of the m-dimensional Euclidean space \(\mathcal {E}^m\), and \(\partial \mathcal {B}\) its boundary. Given k points \(x \in \mathcal {E}^m\) called landmarks, we may represent a k-configuration of the body as the \(k \times m\) matrix \(X = (x_1, \ldots , x_k)\), and we may define the Configuration Space \(\mathcal {C}^k_m\) as the set of all possible k-configurations. (Note that in this work a k-configuration X is used to indicate a discrete representation of the configuration \(\mathcal {B}_X\).)
Hence, the Shape Space \(\Sigma _m^k\) can be defined as the quotient of \(\mathcal {C}^k_m\) under the action of the group \(\mathcal {S}(m)\) of the Euclidean similarity transformations in \(\mathcal {E}^m\). The \(\mathcal {S}(m)\) group can be decomposed as \(\mathcal {S}(m) = \mathcal {T}(m) \times SO(m) \times \mathcal {D}\), where \(\mathcal {T}(m)\) is the translation group, SO(m) is the rotation group, and \(\mathcal {D}\) is the dilation group. In this paper \(m=3\).
2.1 The Geometry of the Kendall Shape Space
The Kendall shape space can be conveniently generated by removing similarity transformations one by one; the first step is to remove location, translating each configuration in such a way that the centroid lies on the origin o of the m dimentional Euclidean space. This brings us to the centered configuration space \(\mathcal {C}\mathcal {C}^k_m\). A centered configuration is then defined as a configuration whose centroid lies on o. The successive filtering can be done removing rotations—thus obtaining the size-and-shape space \(S\Sigma ^k_m\) and then removing size to obtain the shape space as \(\Sigma ^k_m=S\Sigma ^k_m/SO(m)\) [10]. To summarize, we consider the following spaces:
\(\mathcal {C}\mathcal {C}^k_m\) can be parametrized by centered landmarks or by Helmertized landmarks through a pre-multiplication of the matrix X. \(X_c\) is the \(k\times m\) matrix of the centered landmarks:
where \(C=I_k-\frac{1}{k}1_k 1_k^T\), \(1_k\) is the \(k\times k\) identity matrix and \(1_k\) is a \(k\times 1\) column of ones. We define the Helmertized landmarks \(X_H\) as the \((k-1)\times m\) matrix:
where H is the so called Helmert sub-matrix. The jth row of the Helmert sub-matrix H is given by
and so the jth row consists of \(h_j\) repeated j times, followed by \(j\,h_j\) and then \(k-j-1\) zeros, \(j= 1,\ldots , k-1\). The form \([X]_S\in S\Sigma ^k_m\), otherwise called size-and-shape, and the shape \([X]\in S\Sigma ^k_m\) of a centered configuration X are equivalence classes defined by
Given two configurations \(X, X' \in \mathcal {E}^m\), a deformation map \(\Phi : \mathcal {E}^m \rightarrow \mathcal {E}^m\) is the map such that
we shall write \(X' = \Phi (X)\) to indicate that \(X'\) is a deformation of X, i.e.. Note that, depending on the used method, such map can be considered as acting on the whole Euclidean space \(\mathcal {E}^m\) or just on the set of landmarks.
2.2 Methods for Estimating Deformations: OPA, TPS and LDDMM
The most used approaches to estimate a deformation in shape analysis are OPA, TPS and LDDMM. The first is the simplest way to align a pair of k-configurations, and it does not give an interpolation of the deformation in the whole space. The second has the advantage that it furnishes an explicit representation of an interpolation but is not immune from folding and non-invertibility; moreover, as explained in [11, 47] the TPS can be considered as a linearization of a smooth deformation. The last yields a real diffeomorphism; however, it requires computationally intensive numerical integrations of PDE. Moreover, the Riemannian structure of LDDMM allows the definition of a formal parallel transport and the measurement of distances between shapes. Furthermore, LDDMM can be used as an effective matching method that is very useful in absence of homologous landmarks.
We stress here that LDDMM is agnostic w.r.t. the presence or absence of homologous landmarks. As example, when LDDMM is endowed with specific distances such as current- or varifold-based distances, it can be used with non-homologous landmarks.
2.2.1 Ordinary Procrustes Analysis (OPA)
The Euclidean distance between two configurations is defined as:
where \(U\cdot V=\text {trace}(U^T V)\). The induced distance on the size-and-shape space \(S\Sigma ^k_m\) is then:
This definition allows us to give a procedure to align a configuration Y onto a configuration X. In particular, the aligned configuration \(Y_X\) is obtained by means of an optimal rotation \(R_{YX}\) minimizing the Euclidean distance \(||Y\,R-X||\).
It is possible to prove that \(R_{YX}\) is the rotational component coming from a polar decomposition of \(Y^T X\) (see [10]). That is, \(Y^T X=R_{YX}\,U\) with \(U\in \mathrm{Sym}(\mathbb {R}^{m\times m})\) and \(R_{YX}\in SO(m)\). It follows,
As a consequence, we can say that two configurations \({Y_X}, X\) are optimally aligned if and only if the matrix \(Y_X^T X\) is symmetric, i.e., \(Y_X^T X\in \mathrm{Sym}(\mathbb {R}^{m\, m})\). This pairwise alignment is called OPA without scaling. Given two aligned configurations X and \(X'\), i.e., such that \((X')^TX\) s symmetric, the deformation \(\Phi (X)\) is characterized simply by
where \(V=X'-X\). Please note that here the deformation is defined only on the k landmarks.
2.2.2 Thin Plate Spline (TPS)
By following the notation of [10], we summarize the construction of the TPS, and we refer to [2, 10] for further details. In the Euclidean space \(\mathcal {E}^m\), the m-tuple of interpolating TPS is a function \(\Psi \) represented by the triplet \((c_X,A_X,W_X)\), where \(c_X\in \mathcal {E}^m\) is a point represented by \((m \times 1)\) matrix; \(A_X\) is a linear transformation of \(\mathcal {E}^m\), represented by a \((m \times m)\) matrix; \(W_X\) is a \((k \times m)\) matrix. Given a point \(x\in \mathcal {E}^m\), and a configuration \(X\in \mathcal {C}^k_m\), we have
where \(s(x)=(\sigma (x-x_1),\ldots , \sigma (x-x_k))^T\) a is \((k \times 1)\) matrix, \(x_i \in X\) is the position of the ith landmark, and \(\sigma \) is the interpolating function. For a 3D shape, \(m=3\), the function \(\sigma \) is given by
Given two configurations X, and \(X'\), we can apply Eq. (2.4) landmark-wise, yielding to
There are 2k interpolation constraints in Eq. (2.5), and we introduce \(m\times (m +1)\) more constraints on W in order to uncouple the affine and non-affine parts:
For a given pair (X, Y), there exists a unique set of \(m(1+m+k)=m+m^2+mk\) parameters for the triplet \(\left( c_X,A_X,W_X\right) \) that solve the problem (2.5), constrained with (2.6). Please note that here the deformation is defined on the whole \(\mathcal {E}\). The quantity
is called bending energy, and it corresponds to the integral:
It has been proved that TPS is the interpolation function that minimize the bending energy [2].
2.2.3 Large Deformation Diffeomorphic Metric Mapping (LDDMM)
The LDDMM framework [28, 51] proposes to compare shapes via the action of diffeomorphisms \(\phi :{\mathcal {E}}^m \rightarrow {\mathcal {E}}^m\) of the ambient space. A convenient way to generate such diffeomorphisms is to compute flows of time varying smooth vector fields of \({\mathcal {E}}^m\).
Thence, the fundamental idea in LDDMM is to choose a priori a Reproducible Kernel Hilbert Space (RKHS) V of smooth vector fields on \({\mathcal {E}}^m\), containing all the admissible infinitesimal deformations of the ambient space. Following [12], a convenient choice for V is the RKHS containing vector fields \(w\in V\) of the form:
where \(p \in {\mathbb {N}}\) is fixed, \((q_i)_{i=1,\ldots ,p} \in \mathcal C^p_m\) is a set of control points, \((\mu _i)_{i=1,\ldots ,p} \in {\mathcal {C}}^p_m\) is a set of momenta and \(K(x,y) = \exp (\Vert x-y\Vert ^2 / \sigma ^2)\) is an isotropic radial Gaussian kernel of fixed bandwidth \(\sigma \). This bandwidth depends on the problem at hand and controls the smoothness of the deformations. The space V is endowed with the following scalar product:
Given an initial vector field w defined by formula (2.8), one can show (see e.g., [12]) that there is a unique square integrable time-varying vector field \(w(t,\cdot )\) such that \(w(0,\cdot ) = w\) which minimizes the energy \(\int _{0}^1 \Vert w(t,\cdot )\Vert ^2_K\). Its control points q(t) and momenta \( \mu (t)\) are given by a system of Hamiltonian equations:
Considering only such geodesics, the corresponding diffeomorphisms \(\phi _{q_0,\mu _0}\) are fully parametrized by the initial set of control points and momenta \(q_0, \mu _0\). Following this construction, we get the a finite-dimensional Riemannian manifold of diffeomorphisms. We denote \(\langle \cdot , \cdot \rangle _K\) and \(\Vert \cdot \Vert _K\) the metric scalar product and norm. We denote \(\phi _{q_0,\mu _0} \cdot M\) the action of the diffeomorphism parametrized by the initial control points and momenta \(q_0,\mu _0\) on a shape M. If M is a mesh embedded in \({\mathcal {E}}^m\), then \(\phi _{q_0,\mu _0}\) acts on the points of the meshes directly, namely \(\phi _{q_0,\mu _0} \cdot M \doteq \phi _{q_0,\mu _0} (M)\).
Then, registration to a target shape M of a template T is done by optimization with respect to \(q_0, \mu _0\) so as to minimize a criterion of the form:
where \(\Vert \cdot \Vert _s\) is a measure of distance between shapes and \(\beta >0\) controls the tradeoff between the deformation energy and the data attachment.
2.3 Methods for Transporting Deformations
Strictly speaking, none of the following applications is a PT, because, while the definition of PT of a vector is a precise notion of differential geometry (once built an appropriate connection on the manifold) the procedure of transporting a curve starting from a point X toward a different starting point Y is not a precise notion of differential geometry. Despite this, three methods (LS, DT, FS) make use of PT techniques to transport trajectories.
In general, the result of a PT on a manifold depends on the curve along which one transports a vector from a point X toward a point Y, but this happens only if the Riemannian curvature of the manifold does not vanish, i.e., the space is not flat. The Euclidean space is not the only flat space, because a space can have a vanishing curvature and a nonvanishing torsion (typical examples are the left (right) invariant connections in Lie Groups). For example, the TPS space introduced [49] is flat, but it has torsion. Then the DT depends only upon the starting and the target points.
Thus, we have to distinguish between at least three different cases:
-
1.
The Riemannian distances between X and each point of the curve are small, while the Riemannian distance between X and Y is large. Here the whole curve can be thought as a curve lying on the tangent space on X. Each point of the curve is then represented by a vector of the tangent space \(T_X\). (Formally, this can be obtained by means of the inverse exponential map.) In this particular case, we can parallel transport the whole curve by performing a PT of these vectors (and then shooting them on the manifold via exponential map). In this case, the use the term parallel transport of a curve could be acceptable. Furthermore, for manifold that are embedded in an Euclidean space (as the Kendall Shape Space and the TPS Space) the tangent vectors representing the whole curve can be built simply as differences between configurations, without using the inverse and direct exponential map.
-
2.
The Riemannian distances between X and each point of the curve are small as well as the Riemannian distance between X and Y. In this case, the curve, the source X and the target Y can be considered as belonging to the same tangent space \(T_X\), and then, the whole curve can be simply translated in the tangent space (linear shift).
-
3.
The Riemannian distances between X and each point of the curve are large. In this case, the procedure of transporting a curve cannot be considered a PT and can be performed in different ways, depending on what one wants to obtain. A good procedure, from a geometrical point of view, should be unrolling (see [17, 20]) the whole curve on the tangent space \(T_X\), obtaining a curve in \(T_X\). Then, as for the previous cases, apply a PT toward \(T_Y\) and then re-rolling the transported curve on the manifold. An alternative method useful in cases of moderately large distances is the exp-parallelization proposed in [23].
Obviously the above classification depends on the considered Riemannian metric and then on the underlying manifold. Considering the Riemannian distances in the Kendall Size-and-Shape Space, the experiment on alien’s expressions could be classified in the first case: The Riemannian distances between the neutral human and all its deformations are small, while distances between the serious/neutral human and the four initial alien faces are not so small (see below). We note, on the other side, that for the Riemannian metric of the LDDMM, some of the analyzed deformations cannot be considered very small. For instance, opening/closing the mouth of an alien is very energetic in term of LDDMM. Nevertheless, in order to make a direct comparison, in the following, we consider the first case as an acceptable approximation for each method.
An example of NT in 2D. Left: two reference configurations \(X_B\) (black) and \(X_R\) (red). \(X_B\) is transformed by a non-affine transformation (defined in [49]) into the shape \(Y_B\) on the right. Using TPS, we find the deformed black grid, and the associated coefficients c, A, W. Then, using the NT as explained in the text, \(X_R\) is deformed using these TPS coefficients into \(Y_R\) on the right. Finally, a new TPS is calculated on the pair \(X_R\), \(Y_R\), and used to draw the deformed green grid on the right. As you may notice, those two grids do not overlap (Color figure online)
2.3.1 Linear Shift (LS)
Given a pair of configurations X, \(X'\), we want to estimate the deformation from X to \(X'\) and then use it to deform a third shape Y. The LS is based on the following steps:
This procedure is very easy to implement, and it does not require the computation of metrics or connections. It gives satisfactory results when all the involved forms \((X,X',Y)\) are very close to each other, according to the Procrustes distance.
2.3.2 Naïve Transport Method (NT)
The TPS can be naively used to transport a deformation as follows: At first, we compute the TPS parameters associated to a pair of configurations; then, we use these parameters to deform the entire ambient space, which includes our third shape.
With reference to Fig. 2, given the pair of configurations \((X,X')\), we calculate the TPS parameters \(c_X,A_X,W_X\) that interpolate the deformation between X and \(X'\):
Afterward, we use these TPS parameters to define a deformation for the configuration Y: The points \(y'_i\) of the new configuration \(Y'\) are given by
In short, we can write:
where
From (2.15) and (2.5), we observe that \(S_X=S(X,X)\). We note also that the NT, dubbed as an hybrid application of the TPS parameters to a different shape, is widely used in some biological fields such as physical anthropology where various types of developmental simulation have been performed using NT for the study of both extant and extinct hominoids [6]. Actually, the NT shows some limits: once \(Y'\) has been defined by (2.14), we can calculate a TPS between Y and \(Y'\), by obtaining
It easy to show that, in general
This means, in particular, that the affine part of the deformation which is transported, \(A_X\), differs from the actual one \(A_Y\). Moreover, it can be shown that the bending energy is not conserved by the NT, in fact:
Some consequences of the previous observations are:
-
The Cartesian grid is transformed differently by the TPS parameters \((c_Y, A_Y, W_Y)\) and \((c_X, A_X, W_X)\), see the deformed grids on Fig. 2, right.
-
The NT is not invertible along a straight path, that is going back and forth on the same path; we recall that invertibility is one of the requirement for defining a Riemannian PT [7].
We can conclude that we consider the NT as a method rather than a formal parallel transport.
2.3.3 Direct Transport (DT)
Within this section, we assume all the configurations to be centered, and represented by the Helmertized landmarks (see [10]); then, if no otherwise specified, each matrix is a \((k -1) \times m\) matrix. Furthermore, deformation vectors will have a subscript denoting the starting point, that is, the source configuration (for details see [49]).
Let X and Y be two source configurations, and \(V_X\), \(V_Y\) the two associated deformation vectors, given by:
We say that \(V_Y\) is the parallel transport of a given \(V_X\), that is, \(V_Y=\tau _{Y,X}(V_X)\), if and only if the uniform part of \(V_Y\) equals that of \(V_X\):
and the non-uniform part \(W_Y\) of \(V_Y\) solves the linear systems:
where the \((k-1)\times (k-1-m)\) principal warps matrix \(E_X\), collects all the principal warps of X, while \(Q_X\) is a suitable \((k-1-m)\times (k-1-m)\) orthogonal matrix (i.e., \(Q_X^TQ_X=I\)), defined on each configuration X, representing a rotation, or a reflection, of the principal warps. Once chosen a configuration P as a Pole for the space, \(Q_X\) is estimated minimizing the Euclidean distance \(\Vert E_X Q_X-E_P\Vert \) between the rotated principal warps of X, and the corresponding basis on the pole P.
The first equation of (2.18) constrains \(W_Y\) to be orthogonal to the affine part, while the second define the isometry in the subspace of the non-affine deformations. This last requirement implies the conservation of the total bending energy. The system (2.18) can be written as:
That can be re-written as:
where \(M_X=\begin{bmatrix} X^T \\ Q_X E_X^T \end{bmatrix}\) and \(M_Y=\begin{bmatrix} Y^T \\ Q_Y E_Y^T \end{bmatrix}\).
And so:
where \(\Gamma _{21X}\) and \(\Gamma _{11X}\) are calculated as:
Equation (2.19) characterizes \(V_Y\) as the parallel transport of \(V_X\).
2.3.4 Fanning Scheme (FS)
Under the LDDMM paradigm, the parallel transport along geodesics on the manifold of diffeomorphisms can be computed in an efficient way using a procedure described in [23]. A pseudo-code for the procedure is given below. This method converges linearly with the number of steps used in the discretization of the geodesic.

Using this Riemannian parallel transport, we propose to transport a deformation from X to \(X'\) onto a shape Y by parallel transporting the corresponding diffeomorphism along a registration from X to Y and to shoot the obtained deformation to obtain a prediction for \(Y'\). It is important to note here that [31] highlighted that in general a parallel transport within the LDDMM framework is not scale invariant. For this reason, to parallel transport deformations estimated via LDDMM, we used the FS on shapes scaled at unit centroid size; then, we multiplied the transported shapes by the original undeformed target sizes, times the ratio between neutral humans and the other human configurations.
2.4 Dataset
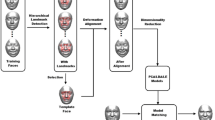
The primary material, used in this study, consists of seven triangular meshes (each identified by 240 homologous landmarks and 416 homologous triangles) of facial expressions. We used three 3D models of the same face, acquired using a real-time range camera, available on the Tosca database (http://tosca.cs.technion.ac.il) [3]. We built three Alien faces (Alien1, Alien2, Alien3) modifying the topology of the Face01, i.e., the serious-neutral human, (see Table 2; Fig. 3), using the software ZBrush (Pixologic; http://pixologic.com, version 4R7). The seventh 3D model was obtained cutting-out the mesh of the fictional character Yoda available on www.yobi3d.com online repository.
Being this face, quite different from a human one, we refine the meshes of all our seven surfaces (Fig. 3) up to approximately 25,000 vertices. The refinement is necessary in order to manually identify anatomically homologous points among the Yoda face and the other ones. Remeshing is done with the software Amira\(^{\textregistered }\), Visualization Sciences Group, 2013.
After this identification has been done, we down sample all the meshes again; on each face, we set 30 landmarks, 12 bi-lateral curves (140 points) and a surface patch of semilandmarks (100 bi-lateral points) (Fig. 4) for a total of 240 points that can be considered anatomically homologous (see below). The curves were sampled using the software Amira acquiring a surface path. The coordinates of the points composing each path were re-processed in R environment through the bezier and Arothron R packages [1, 39] to obtain a set of evenly-spaced points for each curve. Subsequently the points were projected on the corresponding surface using the Morpho R package [43].
The surface semilandmarks patch was built on the Face01 (reference) specimen and the coordinates of each of the 100 semilandmarks were placed on each item of the remaining surface sample (target specimens) through two steps: landmark-based aligning of the target specimen of the reference one; projection of the 100 semilandmarks on the target specimens. To guarantee homology for semilandmarks and curves, they were allowed to slide along the surface and the curves, respectively, minimizing bending energy toward the sample average [16] using the Morpho R package [43]. The sliding procedure establishes the geometric correspondence of the semilandmark sets among the sample by removing the effect of the arbitrary initial spacing [16]. After the sliding process, the landmarks, the surface semilandmarks patch and the semilandmarks along curves can be treated as homologous 3D coordinates in the subsequent statistical analysis. Finally, a mesh regularization has been applied following [44]; Figs. 3 and 4 show the final results.
2.5 The Experiment
Basing on the three human expressions \(X_N\) (neutral face), \(X_S\) (scared face) and \(X_H\) (happy face), we generated a sequence of different expressions \(X_i\), with \(i=1,\ldots ,20\), where \(X_1=X_N\), \(X_{10}=X_S\), and \(X_{20}=X_H\), by using a linear interpolation; (see Fig. 3 and Supplementary Information 1 where the complete animation is visualized).
Then, we evaluated 19 deformation maps \(\Phi _{X_1X_i}\), between the pair \(X_1\) and \(X_i\), using the TPS or the LDDMM method; eventually, we transported the deformations toward the alien faces, by using the four above mentioned transport methods. In particular, for each \(\Phi _{X_1X_i}\) we derived the deformation map \(\Phi _{Y_1Y_i}\), where \(Y_1\) is one of the four alien faces, as summarized in Fig. 5. Finally, we introduced some criteria to assess the performance of the different methods.
In our framework, although shapes are different, the underlying deformations are small enough to consider them belonging to the same tangent space (see Sect. 2.3). The Riemannian size and shape distances [10] for the human trajectory w.r.t. the neutral spans from 0.19 to 1.67, while those between the neutral human and the four undeformed aliens are 2.72, 1.96, 2.46, 10.68.
2.6 Criteria for Evaluating the Methods Performance
Here we introduce the notion of conservation of a deformation as a mean to evaluate the quality of the different transport methods. We present two different approaches to measure how a deformation is conserved; one is based on local measurements and gauges the deformation of each pair of homologous triangles, the other one considers the global shape.
2.6.1 Metrics for Local Deformation Evaluation
Given two different k-configurations X and Y, representing two different templates, each undergoing its own deformation, and describing these two deformations with the diffeomorphisms \(\Phi _{XX'}\) and \(\Phi _{YY'}\) (see Fig. 1), the key point is the ability to recognize whether or not they are experiencing the same deformation.
Naively, we could define two configurations being similarly deformed if the discrete displacement field is the same, i.e.,
However, this approach has several drawbacks, as reported in [49]. Here we assume a different point of view: Two templates undergo the same deformation if, for each corresponding point of the two templates, the following condition holds (see Fig. 1):
Such condition can be expressed also by means of the local metric properties: In other words, two configurations undergo the same deformation if the metric induced by the two diffeomorphisms, represented by the Right Cauchy–Green strain tensor \(\mathbf {C}\), is the same for each corresponding point, see for more details [30]. In the continuum mechanics formalism, the gradient tensor \(\nabla \Phi \) is generally denoted as \(\mathbf {F}\), and in the ensuing section it will be named as deformation tensor (the Jacobian).
In m dimensions, a tensor is represented by an \(m\times m\) matrix that encodes the entire information about the deformation. The strain tensor \(\mathbf {C}\) is defined as \(\mathbf {F}^T\,\mathbf {F}\); we note that \(\mathbf {F}\) can be represented as the composition of a rotation \(\mathbf {R}\) and a stretch \(\mathbf {U}\), called polar decomposition: \(\mathbf {F}=\mathbf {R}\,\mathbf {U}\). Then, by definition, \(\mathbf {C}=\mathbf {U}^2\); thus, the rigid part \(\mathbf {R}\) of the deformation \(\mathbf {F}\) is filtered out.
In the case of triangles in 3D, the symmetric \(3\times 3\) tensors \(\mathbf {F}\) and \(\mathbf {C}\) are singular as a triangle is a 2D shape, and they are projected along the normal to the triangle to obtain two symmetric \(2\times 2\) tensors \({\hat{\mathbf {F}}}\) and \({\hat{\mathbf {C}}}\) (see. [13, 14]). Performing an eigen decomposition on \({\hat{\mathbf {C}}}\) leads to find the directions and magnitudes of the transformation (see Fig. 6). To ease the notation, we define \(\mathbf {F}_{X_i}=\nabla \Phi _{X_1X_i}\), and \({\hat{\mathbf {F}}}_{X_i}\) as the 2D projection of \(\mathbf {F}_i\), analogously, we define \(\mathbf {F}_{Y_i}=\nabla \Phi _{Y_1Y_i}\), and \({\hat{\mathbf {F}}}_{Y_i}\).
It is worth noting that none of the four methods we contrast here is built in order to satisfy (2.23). Albeit this makes all the four methods somewhat inadequate, using this criterion as a diagnostic makes it neutral with respect to the various metrics involved in different parallel transports.
Here, we assess the quality of the deformation transport by checking that triangle-wise deformations are preserved; we note that each triangle can only have affine transformations. Given that each shape \(X_i\) or \(Y_i\) has a same number of homologous triangles, we denote with \(c_j\) the center of triangle j, with \(j=1,\ldots ,416\). We follow 4 steps:
-
1.
We measure the change in area of each triangle by evaluating \(\text {det}({\hat{\mathbf {F}}}_{X_i}(c_j))\), which measures the ratio between the area of the triangle j of the shape \(X_i\), and the area of the homologous triangle belonging to the source \(X_1\); this is done for each triangle j, and for each deformation \(\Phi _{X_1X_i}\), see Fig. 5.
-
2.
For all the four transport methods, we measure the same quantity also for the transported data, that is, we evaluate \(\text {det}({\hat{\mathbf {F}}}_{Y_i}(c_j))\). This is done for each alien face Y.
-
3.
For each i, we run the linear regression of \(\text {det}({\hat{\mathbf {F}}}_{Y_i}(c_j))\) versus \(\text {det}({\hat{\mathbf {F}}}_{X_i}(c_j))\), and we compute the regression coefficient \(\beta _i\). It turns out that we have 19 \(\beta _i\) regression coefficients for each of the four aliens, and for each method. These coefficients give a quantitative assessment of the average quality of the transport for all the triangles in a shape i: the closer \(\beta _i\) is to 1, the better is the area preserving features of the method; see Fig. 9, right.
-
4.
We then perform a nonparametric ANOVA using Wilcoxon test with pairwise comparisons among the 4 groups (i.e NT, DT, FS, LS), by using the \(\beta _i\) coefficients for each alien as dependent variable, see Table 5.
We use as measure the log of the area change, that is, the function \(\mathrm{log}\,[\mathrm{det}({{\hat{\mathbf {F}}}}_i)]\); a value of 0 means that no area change took place, a value\(>0\) means that the target experiences a local expansion, while a value \(<0\) indicates local contraction.
Apart from area change, we can also have a clue about shape change by evaluating the eigen-system of \({\hat{\mathbf {F}}}_i\); this information can be visualized by plotting unit circles at the center of each triangle of the source shapes \(X_1\), \(Y_1\); then, at the center of the homologous triangles belonging to the shapes \(X_i\), \(Y_i\), we plot the ellipses corresponding to the eigen-system of \({\hat{\mathbf {F}}}_i\), see Figs. 7 and 8.
Moreover, it is possible to define a distance between tensors; the choice of the proper distance formula is not trivial. Different formulas could look at different tensor properties. There is an entire field in image processing that deals with tensor analysis [21]. Reference [8] proposed a set of seven different formulas to analyze covariance matrices (strain tensors in our case) in the field of diffusion tensor imaging (see Table 3). We thus used these distances for a statistical comparison of the different methods, via nonparametric ANOVA (Wilcoxon test).
2.6.2 Metrics for Global Deformation Evaluation
As for the global measures of deformation, we use the mean strain energy density and the Procrustes distance. The mean strain energy \(\varphi _{X_i}\) associated to the deformation \({{\hat{\mathbf {F}}}}_{X_i}\) is defined as
where \(\hat{\mathbf {E}}_{X_i}=1/2 (\hat{\mathbf {C}}_{X_i}-\hat{\mathbf {I}})\), with \(\hat{\mathbf {C}}_{X_i}={{\hat{\mathbf {F}}}}_{X_i}^T\,{{\hat{\mathbf {F}}}}_{X_i}\), \(\hat{\mathbf {I}}\) is the 2D identity tensor, and \(\gamma \) is a coefficient representing the ratio between the volumetric and shear stiffness of the considered material [30]. Formula (2.24) can be also used to evaluate the mean energy triangle-wise, by integrating and averaging on each triangle \(\mathcal {B}_J\). An analogous formula is used for the mean strain energy \(\varphi _{Y_i}\) associated to the deformation \({{\hat{\mathbf {F}}}}_{Y_i}\).
We run a linear regression of \(\varphi _{Y_i}\) versus \(\varphi _{X_i}\), and we compute the regression coefficient \(\beta _\varphi \), for each method and for all the four alien faces, see Fig.11.
We run also a linear regression of the Procrustes distance \(\rho _{Y_i}=\rho (Y_i,Y_1)\) versus \(\rho _{X_i}=\rho (X_i,X_1)\), and we compute the regression coefficient \(\beta _\rho \), for each method and for all the four alien faces, see Fig. 12. For both cases, the lower the absolute deviation from 1 of the regression coefficients the better the performance of the method.
3 Results
Figures 7 and 8 show the visualization of deformed states of scared and happy emotions for the four aliens for the four methods using local tensors. Supplementary Information 2–5 shows the complete tensor animations for each method (NT, LS, DT, FS), respectively, from which Figs. 7 and 8 have been extracted as snapshots. In addition, Supplementary Information 6–9 shows the same with the triangulation structure instead of tensors.
Visualization of deformation using local tensors on the scared emotion. Undeformed states are shown using yellow circles having an arbitrary constant radius appropriately chosen for visualization. They are centered on the centroid of each triangle of the homologous triangulation. The deformed states show ellipses whose lengths of the axes are proportional to the square root of the eigenvalues of the \(2\times 2\) tensor \(\hat{\mathbf {C}}\) in Fig. 6. The color, instead, is proportional to the log(det(\({\hat{\mathbf {F}}}\))). White ellipses indicate log(det(\({\hat{\mathbf {F}}}\))) that exceed the chosen color-scale. For sake of visualization, shapes are not at their original size (Color figure online)
Visualization of deformation using local tensors on the happy emotion. Undeformed states are shown using yellow circles having an arbitrary constant radius appropriately chosen for visualization. They are centered on the centroid of each triangle of the homologous triangulation. The deformed states show ellipses whose axes lengths are proportional to the square root of the eigenvalues of the \(2\times 2\) tensor \(\hat{\mathbf {C}}\) in Fig. 6. The color, instead, is proportional to the log(det(\({\hat{\mathbf {F}}}\))). White ellipses indicate log(det(\({\hat{\mathbf {F}}}\))) that exceed the chosen color-scale. For sake of visualization, shapes are not at their original size (Color figure online)
Undeformed states are shown using yellow circles. The deformed states show ellipses whose axes are proportional to the square root of the eigenvalues of the \(2\times 2\) tensor \(\hat{\mathbf {C}}\) in Fig. 6. The color, instead, is proportional to the log(det(\({\hat{\mathbf {F}}}\))) . White ellipses indicate log(det(\({\hat{\mathbf {F}}}\))) that exceed the chosen color scale range. Pictorically, it appears evident that NT fails in recovering original deformation (e.g., the human on the leftmost column) mainly around the lips region: in the scary emotion (Fig. 7) the NT method applied to the first three aliens presents a nearly closed mouth with disproportionately enlarged lips, while Yoda clearly fails in opening mouth. This error should decrease starting from a wider open mouth, but here we are interested to check the robustness of the methods on a very challenging example. LS performs better than NT in opening Yoda’s mouth, while for alien 1 and 3 the opening seems too exaggerated in comparison to the other three methods. This could be explained by the fact that LS is very sensible to size differences as it transports, on the size and shape space, the entire difference vector as it is. This does not happen for DT and FS that appear the best methods in conserving the local deformation observed on the human. Looking at out-of-scale tensors, DT presents a smaller number of exaggerated tensors (in terms of axes of ellipses) in Yoda and more accurate tensors, in terms of log(det(\({\hat{\mathbf {F}}}\))) (i.e., the ellipses’ colors) when compared to human, in correspondence of the frontal and lips regions of the first three aliens. Qualitatively, similar results are shown in Fig. 8 for the happy emotion: There too the NT seems to be the worst method. Yoda, in fact, shows nearly undeformed circles, thus indicating that the corresponding tensors bear unfaithful deformations with respect to human. DT performs better than FS mainly for Yoda that, under FS, shows some exaggerated tensor.
Left panel: distributions, for the four aliens Y, of the \(\beta _i\) coefficients calculated at each deformational step, of the regressions computed between log(det(\({\hat{\mathbf {F}}}\))) of transported shapes, for the four methods, and those of the corresponding human benchmark. Significances of pairwise comparisons under nonparametric ANOVA are given in Table 5. Right panel: course of \(\beta _i\) coefficients for the four methods and the four aliens
Riemannian distance \(d_R\) according to Dryden et al. 2009 between human strain tensors and transported shapes for the four aliens for the four methods. We show 76 pairwise comparisons (19 steps for the 4 methods); each of the four plots shows the Riemannian distance between the human face and a given alien face, once it has been transported with the four transport methods (each method corresponds a to color, see legend). For each alien and for each method, we show the boxes of the \(50\%\) of the distribution for each of 19 deformation steps. The number in the top x-axis indicate the global ANOVA p-value. For the sake of visualization, we do not show here the labels of pairwise comparisons for each step while they can be appreciated in the supplementary information for this kind of distance as well as for the others (Color figure online)
Plot of the mean strain energy density \(\varphi _{Y_i}\) versus \(\varphi _{X_i}\), for the four aliens and the four methods. Solid line represents isometry; the value of the regression coefficient \(\beta _\varphi \) is shown in the title of each panel. It is worth noting the kinks that appear in some cases, as example, on line 2 in columns 2 and 4. Each point of the plot comes from data related to one deformation \(\Phi _{X_1X_i}\); the whole sequence of deformations is actually associated with two different sub-trajectories: \(i=1,\ldots ,10\) corresponds to \(X_N \rightarrow X_S\) (black dots), while \(i=11,\ldots ,20\) corresponds to \(X_N \rightarrow X_H\) (red dots) (Color figure online)
Plot of Procrustes distances \(\rho _{Y_i}\) versus \(\rho _{X_i}\), for the four aliens and the four methods. Solid line represents isometry; the value of the regression coefficient \(\beta _\rho \) is shown in the title of each panel. Each point of the plot comes from data related to one deformation \(\Phi _{X_1X_i}\); the whole sequence of deformations is actually associated with two different sub-trajectories: \(i=1,\ldots ,10\) corresponds to \(X_N \rightarrow X_S\) (black dots), while \(i=11,\ldots ,20\) corresponds to \(X_N \rightarrow X_H\) (red dots) (Color figure online)
What can be seen pictorially in Figs. 7 and 8 is returned quantitatively in Figs. 9 and 10 for local diagnostics and in Figs. 11 and 12 for synthetic diagnostics. In Fig. 9 (left panel), the maintenance of log(det(\({\hat{\mathbf {F}}}\))) with respect to human and quantified via regression analysis is evaluated for each of the 416 triangles for each of the 19 deformed states and the 19 \(\beta \) regressions for each method for each alien are contrasted via nonparamateric ANOVA (via pairwise Wilcoxon rank sum tests; significance level was set to 0.05) and illustrated via boxplot.
Table 4 shows means for the four methods for the four Aliens.
Pairwise comparisons under Wilcoxon test (Table 5) reveals that DT is always the best method. For alien 2, LS also presents a very good performance albeit it is not significantly different from DT. NT is always significantly the worst method. FS is always placed in the second place except for Yoda for which it places at the third place.
Figure 10 shows the Riemannian distance \(d_R\), according to [8], between human and different methods for the four alien for each deformational step. DT and LS are the methods that approach the most the 0-value. Supplementary Information 10 shows the same using other types of distances. Synthetic measures (i.e., mean strain energy density and Procrustes distances) of performance are shown in Figs. 11 and 12. According to the global strain energy density, the DT seems to be the best method in all aliens except for the first one that deserves special attention. There the NT seems to perform slightly better than DT while LS and FS are the less performant. All, however, seem to have too high \(\beta \) coefficients with respect to human. Actually, after a quality check performed on the entire set of triangles of the undeformed configuration of alien 1 we identified 30 triangles (on a total of 416) that are degenerate, i.e., with an area very close to 0. Their individual strain energy seriously bias the mean strain energy density. If removed the regression \(\beta \) coefficients are: NT = 10.02; LS = 3.78; DT = 1.63; FS = 0.7. It follows that, globally, DT can be considered the best method followed by FS, LS and NT, respectively. A similar behavior can be appreciated when looking at Fig. 12 where Procrustes distances of human and those of the four methods applied to the four aliens are contrasted.
4 Conclusions
The long-standing problem of the evaluation/estimation of the deformation and of its transport has been here faced using four different methods, NT, LS, DT and FS that are used in very distant fields and applications. To the best of our knowledge, this is the first study oriented at the comparison of these four approaches and at evaluating their performances quantified by different parameters. This has been done in the case of the transport of human emotions mapped on the surfaces of a face. This operation is commonly known as facial motion capture retargeting in the field of computer animation. The results obtained here are then referred to this particular case, while other applications should be of course re-evaluated using the same performance criteria used here and could yield anecdotally to slightly different conclusions. For example, one could face the problem of comparing not only neutral, scared and happy emotions but also a wider range of sentiments and in a wider range of initial face shapes; in this case, the high number of combinations of initial shape/type of emotion lead to a big rise of experimental complexity potentially very difficult to manage. As we anticipated in the previous sections, the maintenance of tensor distances and Jacobians are not the conservation criteria encoded on the contrasted methods. However, this neutrality was the sole way able to compare fairly different techniques. In fact, adopting the conservation criterion encoded on one particular method (some kind of energy, or shape distances, or displacement vector fields) inevitably would confer to that method an unjustified advantage in evaluating performance. On the other hand, the use of both local (i.e., tensor distances and Jacobian) and synthetic/global criteria (i.e., strain energy and Procrustes distance) can furnish, in our opinion, a complete picture of the actual ability of the four procedures in transporting the deformation trajectory. We observed that DT is very effective in doing that when looking at both the local and global criteria. FS and LS also perform rather well while NT does not seem properly equipped for doing what is asked by our experiment. Probably the goodness of DT could reside on the fact that it firstly separates affine and non-affine components of the deformation (not done by either FS or LS) and maintains them orthogonal w.r.t. each other. Moreover, both affine and non-affine parts are conserved during the construction of the Parallel Transport. The inability of NT in performing our experiment has been succintly explained in Sect. 2.3.1 where we have shown that NT performed on a pair (X, X\(^{\prime }\)), being an interpolant, is forced to become an extra-polant when demanded to deform the ambient space built around a third shape. We are of course aware that many more than only four methods exist in order to transport a deformation occurring between two shapes toward a third shape. In [49], it was shown that several methods have been developed and it could be desirable to compare them all albeit this is far beyond the scopes of the present paper. In other applications, the identification of homologous landmarks is not so easy to obtain. This can be seen, for example, in the case of brain CT-scan or other types of organs such the liver or spleen. In these cases, only a method equipped with a surface matching algorithm, such as LDDMM or similar approaches, can be applied as those methods requiring point correspondence cannot be used at all. We finally stress here that our comparison can be extended to other types of experimental/simulated examples as the transport of deformation is very often needed and applied to a variety of very distant scientific applications, and for this reason it always should be chosen the best approach for the specific experimental setting. We then encourage further investigation into our techniques using at least two possible courses: (1) analyzing the same dataset using different methods. In fact, as we stated in the Introduction, we did not exploited the potential of the full available number of methods for transporting the deformation; (2) applying the same four methods we explored here to different types of dataset not only in terms of human face emotions but also in terms of initial body that undergoes some kind of deformation such as an entire human body or an animal body, etc. For these reasons, we provide the following information:
-
The R scripts used in this paper for DT and LS are attached in Supplementary Information 11. For NT, we suggest the R package Morpho [42]. For FS, we suggest installing the software Deformetrica from https://www.deformetrica.org.
-
The whole dataset used in the present paper is attached in Supplementary Information 12.
-
The R scripts for the visualization and evaluation of the deformation are attached in the supplementary informations of [34],
-
For the calculation of the tensor distances, it is possible to use the R package shapes [9].
References
Aaron, O.: bezier: Bezier Curve and Spline Toolkit (2014). R package version 1.1
Bookstein, F.L.: Principal warps: thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell. 11(6), 567–585 (1989)
Bronstein, A.M., Bronstein, M.M., Kimmel, R.: Calculus of non-rigid surfaces for geometry and texture manipulation. In: IEEE Transactions on Visualization and Computer Graphics (2007)
Buckley, P.F., Dean, D., Bookstein, F.L., Friedman, L., Kwon, D., Lewin, J.S., Kamath, J., Lys, C.: Three-dimensional magnetic resonance-based morphometrics and ventricular dysmorphology in schizophrenia. Biol. Psychiat. 45(1), 62–67 (1999)
Campbell, K., Fletcher, P.: Efficient parallel transport in the group of diffeomorphisms via reduction to the lie algebra. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10551 LNCS, pp. 186–198 (2017)
Carlson, K.B., De Ruiter, D.J., Dewitt, T.J., Mcnulty, K.P., Carlson, K.J., Tafforeau, P., Berger, L.R.: Developmental simulation of the adult cranial morphology of australopithecus sediba. S. Afr. J. Sci. (2016). https://doi.org/10.17159/sajs.2016/20160012
do Carmo Valero, M.P.: Riemannian Geometry. Mathematics: Theory and Applications. Birkhäuser, London (1992)
Dryden, I., Koloydenko, A., Zhou, D.: Non-euclidean statistics for covariance matrices, with applications to diffusion tensor imaging. Ann. Appl. Stat. 3, 1102–1123 (2009)
Dryden, I.L.: Shapes: Statistical Shape Analysis (2019). R package version 1.2.5
Dryden, I.L., Mardia, K.V.: Statistical Shape Analysis, with Applications in R, 2nd edn. Wiley, Chichester (2016)
Durrleman, S., Pennec, X., Trouvé, A., Ayache, N., Braga, J.: Comparison of the endocranial ontogenies between chimpanzees and bonobos via temporal regression and spatiotemporal registration. J Hum Evol 62, 74–88 (2012)
Durrleman, S., Prastawa, M., Charon, N., Korenberg, J.R., Joshi, S., Gerig, G., Trouvé, A.: Morphometry of anatomical shape complexes with dense deformations and sparse parameters. NeuroImage 101, 35–49 (2014)
Evangelista, A., Gabriele, S., Nardinocchi, P., Piras, P., Puddu, P., Teresi, L., Torromeo, C., Varano, V.: Non-invasive assessment of functional strain lines in the real human left ventricle via speckle tracking echocardiography. J. Biomech. 48(3), 465–471 (2015)
Gabriele, S., Nardinocchi, P., Varano, V.: Evaluation of the strain-line patterns in a human left ventricle: a simulation study. Comput. Methods Biomech. Biomed. Eng. 18(7), 790–798 (2015)
Guigui, N., Jia, S., Sermesant, M., Pennec, X.: Symmetric algorithmic components for shape analysis with diffeomorphisms. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 11712 LNCS, pp. 759–768 (2019)
Gunz, P., Mitteroecker, P.: Semilandmarks: A method for quantifying curves and surfaces. Hystrix 24(1), (2013)
Le, H.: Unrolling shape curves. J. Lond. Math. Soc. 68, 511 (2003)
Huckemann, S., Hotz, T., Munk, A.: Intrinsic Manova for Riemannian manifolds with an application to Kendall’s space of planar shapes. IEEE Trans. Pattern Anal. Mach. Intell. 32(4), 593–603 (2010)
Joshi, S., Miller, M.: Landmark matching via large deformation diffeomorphisms. IEEE Trans. Image Process. 9(8), 1357–1370 (2000)
Kume, A., Dryden, I., Le, H.: Shape space smoothing splines for planar landmark data. Biometrika 94, 513–528 (2007)
Laidlaw, D.H., Weickert, J.: Visualization and Processing of Tensor Fields. Springer, Berlin (2009)
Lorenzi, M., Pennec, X.: Geodesics, parallel transport and one-parameter subgroups for diffeomorphic image registration. Int. J. Comput. Vis. 105, 111–127 (2013)
Louis, M., Bône, A., Charlier, B., Durrleman, S.: Parallel transport in shape analysis: a scalable numerical scheme. In International Conference on Geometric Science of Information, pp. 29–37. Springer, (2017)
Louis, M., Charlier, B., Jusselin, P., Pal, S., Durrleman, S.: A fanning scheme for the parallel transport along geodesics on Riemannian manifolds. SIAM J. Numer. Anal. 56(4), 2563–2584 (2018)
Madeo, A., Piras, P., Re, F., Gabriele, S., Nardinocchi, P., Teresi, L., Torromeo, C., Chialastri, C., Schiariti, M., Giura, G., Evangelista, A., Dominici, T., Varano, V., Zachara, E., Puddu, P.: A new 4d trajectory-based approach unveils abnormal lv revolution dynamics in hypertrophic cardiomyopathy. PLoS ONE 10(4), e0122376 (2015)
Miller, M., Trouvé, A., Younes, L.: Hamiltonian systems and optimal control in computational anatomy: 100 years since D’arcy Thompson. Annu. Rev. Biomed. Eng. 17, 447–509 (2015)
Miller, M.I., Qiu, A.: The emerging discipline of computational functional anatomy. Neuroimage 45(1), S16–S39 (2009)
Miller, M.I., Trouvé, A., Younes, L.: Geodesic shooting for computational anatomy. J. Math. Imaging Vis. 24(2), 209–228 (2006)
Miller, M.I., Younes, L., Trouvé, A.: Diffeomorphometry and geodesic positioning systems for human anatomy. Technology 2(01), 36–43 (2014)
Nardinocchi, P., Teresi, L., Varano, V.: The elastic metric: a review of elasticity with large distortions. Int. J. Non-Linear Mech. 56, 34–42 (2013)
Niethammer, M., Vialard, F.: Riemannian metrics for statistics on shapes: parallel transport and scale invariance. In:Proceedings of the 4th MICCAI workshop on Mathematical Foundations of Computational Anatomy (MFCA) (2013)
Piras, P., Evangelista, A., Gabriele, S., Nardinocchi, P., Teresi, L., Torromeo, C., Schiariti, M., Varano, V., Puddu, P.: 4d-analysis of left ventricular heart cycle using procrustes motion analysis. PLoS ONE 9(1), e86896 (2014)
Piras, P., Marcolini, F., Raia, P., Curcio, M., Kotsakis, T.: Testing evolutionary stasis and trends in first lower molar shape of extinct Italian populations of Terricola savii (arvicolidae, rodentia) by means of geometric morphometrics. J. Evolut. Biol. 22(1), 179–191 (2009)
Piras, P., Profico, A., Pandolfi, L., Raia, P., Di Vincenzo, F., Mondanaro, A., Castiglione, S., Varano, V.: Current options for visualization of local deformation in modern shape analysis applied to paleobiological case studies. Front. Earth Sci. 8, 66 (2020)
Piras, P., Sansalone, G., Teresi, L., Moscato, M., Profico, A., Eng, R., Cox, T., Loy, A., Colangelo, P., Kotsakis, T.: Digging adaptation in insectivorous subterranean eutherians. the enigma of mesoscalops montanensis unveiled by geometric morphometrics and finite element analysis. J. Morphol. 276(10), 1157–1171 (2015)
Piras, P., Torromeo, C., Evangelista, A., Gabriele, S., Esposito, G., Nardinocchi, P., Teresi, L., Madeo, A., Schiariti, M., Varano, V., Puddu, P.: Homeostatic left heart integration and disintegration links atrio-ventricular covariation’s dyshomeostasis in hypertrophic cardiomyopathy. Sci. Rep. 7(1), 6257 (2017)
Piras, P., Torromeo, C., Re, F., Evangelista, A., Gabriele, S., Esposito, G., Nardinocchi, P., Teresi, L., Madeo, A., Chialastri, C., Schiariti, M., Varano, V., Uguccioni, M., Puddu, P.: Left atrial trajectory impairment in hypertrophic cardiomyopathy disclosed by geometric morphometrics and parallel transport. Sci. Rep. 6, 34906 (2016)
Pokrass, J., Bronstein, A., Bronstein, M.: Partial shape matching without point-wise correspondence. Numer. Math. 6(1), 223–244 (2013)
Profico A.V.: Arothron: R Functions for Geometric Morphometrics Analyses (2015). R package
Qiu, A., Albert, M., Younes, L., Miller, M.: Time sequence diffeomorphic metric mapping and parallel transport track time-dependent shape changes. Neuroimage 45(1 Suppl), S51–60 (2009)
Raia, P., Piras, P., Kotsakis, T.: Detection of plio-quaternary large mammal communities of Italy. An integration of fossil faunas biochronology and similarity. Quatern. Sci. Rev. 25(7–8), 846–854 (2006)
Schlager, S.: Morpho and RVCG—shape analysis in R. In: Zheng, G., Li, S., Szekely, G. (eds). Statistical Shape and Deformation Analysis, pp. 217–256. Academic Press, London (2017)
Schlager, S.: Morpho and RVCG—Shape Analysis in R: R-Packages for Geometric Morphometrics, Shape Analysis and Surface Manipulations (2017)
Schlager, S., Profico, A., Di Vincenzo, F., Manzi, G.: Retrodeformation of fossil specimens based on 3d bilateral semi-landmarks: implementation in the r package “morpho”. PLoS ONE 13(3), e0194073 (2018)
Srivastava, A., Klassen, E., Joshi, S., Jermyn, I.: Shape analysis of elastic curves in Euclidean spaces. IEEE Trans. Pattern Anal. Mach. Intell. 33(7), 1415–1428 (2011)
Sundaramoorthi, G., Mennucci, A., Soatto, S., Yezzi, A.: A new geometric metric in the space of curves, and applications to tracking deforming objects by prediction and filtering. SIAM J. Imag. Sci. 4(1), 109–145 (2011)
Trouvé, A.: Diffeomorphisms groups and pattern matching in image analysis. Int. J. Comput. Vis. 28, 213–221 (1998)
Varano, V., Gabriele, S., Teresi, L., Dryden, I., Puddu, P., Torromeo, C., Piras, P.: Comparing shape trajectories of biological soft tissues in the size-and-shape space. In: Biomat 2014 International Symposium on Mathematical and Computational Biology, pp. 351–365 (2015)
Varano, V., Gabriele, S., Teresi, L., Dryden, I., Puddu, P., Torromeo, C., Piras, P.: The TPS direct transport: a new method for transporting deformations in the size-and-shape space. Int. J. Comput. Vis. 124(3), 384–408 (2017)
Xie, Q., Kurtek, S., Le, H., Srivastava, A.: Parallel transport of deformations in shape space of elastic surfaces. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 865–872 (2013)
Younes, L.: Shapes and Diffeomorphisms. Springer, Heidelberg (2010)
Acknowledgements
The work was supported by Sapienza Università di Roma through the Grant No. C26A15JZ7K. MIUR (Italian Minister for Education, Research, and University) and the PRIN 2017, Mathematics of active materials: From mechanobiology to smart devices, Project No. 2017KL4EF3. INdAM, National Group of Mathematical Physics (GNFM-INdAM), Italy.
Funding
Open access funding provided by Universitá degli Studi Roma Tre within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.









Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Piras, P., Varano, V., Louis, M. et al. Transporting Deformations of Face Emotions in the Shape Spaces: A Comparison of Different Approaches. J Math Imaging Vis 63, 875–893 (2021). https://doi.org/10.1007/s10851-021-01030-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-021-01030-6