Circular Laser/Camera-Based Attitude and Altitude Estimation: Minimal and Robust Solutions

Abstract

This paper proposes a basic structured light system for pose estimation. It consists of a circular laser pattern and a camera rigidly attached to the laser source. We develop a geometric modeling that allows to efficiently estimate the pose at scale of the system, relative to a reference plane onto which the pattern is projected. Three different robust estimation strategies, including two minimal solutions, are also presented with this geometric formulation. Synthetic and real experiments are performed for a complete evaluation, both quantitatively and qualitatively, according to different scenarios and environments. We also show that the system can be embedded for UAV experiments.

1 Introduction

Pose estimation is an essential step in many applications such as 3D reconstruction [1] or motion control [2]. Many solutions based on a single image have been proposed in past years. These systems use the image of a perceived object or surface in order to estimate the related rigid transformation [3].

When a monocular vision system and a known object are used, the problem is well known as PnP (Perspective-n-Points) [4,5,6,7]. In this case, the matching between known 3D points and their projection in the image allows to deduce the pose. For a calibrated stereovision sensor, the epipolar geometry and a direct triangulation between 2D matched points of stereoscopic images allow both to reconstruct the scene at scale and to estimate the pose of the camera. When the stereovision system is not calibrated and we do not have any knowledge about the 3D structure of the scene, the epipolar geometry can still be estimated, in the form of the fundamental matrix, but the final 3D reconstruction is only projective [3]. Finally, if we consider a single calibrated camera in motion, the essential matrix between two acquired images can be estimated from matched 2D points as well as the pose, but only up to scale [8].

All the previous methods are classified as passive because they only exploit images acquired under existing lighting conditions and without controlling the camera motion. They require the scene to be textured in order to extract discriminant features that can be matched easily. If the scene is globally homogeneous with very few remarkable features, the previous methods will mostly fail. Thus, when the scene is globally homogeneous, the best way to handle the problem without introducing assumptions about the material of the ground surface and about the lighting present in the scene is to employ active sensors that use the deformation of a projected known pattern in order to estimate the pose. These methods are also known as structured light [9], and one of the most popular sensors is undoubtedly the Kinect sensor [10].

The projected pattern can be obtained from a projector or a laser and different shapes and codings can be used [11]. Globally, patterns are based either on discernable points that have to be matched independently or on general shapes such as lines, grids, conics that have to be extracted in acquired images. The Kinect sensor is widely used in mobile robotics, but suffers from several downsides. First of all, its size and weight make it difficult to embed on a drone with a low payload. On the other hand, its field of view and its range of operation are limited: The field of view is around $57^{\circ }$ and the sensor runs from 0.6 to 4 m. It consequently has a close range blind spot that makes it unusable in a critical stage such as the landing of a drone. Moreover, since this type of sensor uses an infrared pattern, it is very sensitive to the material on which the pattern is projected, and is sensitive to the infrared light of the sun, which makes it unsuitable for outdoor applications.

In this paper, we propose a complete and simple laser–camera system for pose estimation based on a single image. The pattern consists in a simple laser circle, and no matching is required for the pose estimation. Using a circular pattern is very interesting because its projection onto a reference plane is a general conic; this has shown to be a strong mathematical tool for computational geometry [12]. Recently, in [13] the authors proposed a non-rigid system based on a conic laser pattern and an omnidirectional camera for a similar aim as ours. In their approach, rather than calibrating the complete system (laser–camera) they propose to detect simultaneously the laser emitter and the projected pattern in the image in order to estimate the pose.

In [14], an algebraic solution of our system was developed while a geometrical approach was given in [15]. This paper is an extension of the latter for which we propose different improvements. First, a complete dedicated calibration method is presented, giving improved results. Next, we propose a new robust algorithm that simultaneously estimates conic and pose parameters and that is particularly efficient and accurate. Finally, we present extensive simulations and experimental results with ground truth measures that allow comparison and quantitative evaluations of the approach in different environment settings.

The paper is organized as follows. The following section briefly describes notations and provides some basic material required in this paper. Section 3 describes our camera/laser setup and formulates the pose estimation problem. Section 4 gives a first solution to pose estimation. In Sect. 5, we then propose different robust approaches for the conic detection and the pose estimation. In Sect. 6, a new method to calibrate the system is presented. Finally, Sect. 7 presents the different simulation and experimental results, evaluations and comparisons. It is followed by a section with conclusions.

2 Basic Material and Notations

This section provides some mathematical materials required in this paper. Concerning notation: Matrices and vectors are denoted by bold symbols, scalars by regular ones. Geometric entities (planes, points, conics, projection matrices, etc.) are by default represented by vectors/matrices of homogeneous coordinates. Equality up to a scale factor, of such vectors/matrices, is denoted by the symbol $\sim$.

2.1 Representing Quadrics and Conics

A quadric is represented by a $4 \times 4$ matrix $\mathbf {Q}$ such that

$$\begin{aligned} \mathbf {X}^T \mathbf {Q}\mathbf {X} = 0 \end{aligned}$$

(1)

for all homogeneous 3D points $\mathbf {X}$ lying on the quadric.

Similarly, a conic is represented by a $3 \times 3$ matrix $\mathbf {c}$ such that

$$\begin{aligned} \mathbf {x}^T \mathbf {c}\mathbf {x} = 0 \end{aligned}$$

(2)

for all homogeneous 2D points $\mathbf {x}$ lying on the conic.

2.2 Representing a Pair of Planes

It is well known that a plane-pair can be considered as a degenerate quadric, actually a quadric of rank 2 [16]. Let $\mathbf {U}$ and $\mathbf {V}$ be 4-vectors of homogeneous coordinates, representing two planes. The quadric formed by the “union” of the two planes can then be represented by the following $4\times 4$ matrix:

$$\begin{aligned} \mathbf {Q} = \mathbf {V} \mathbf {U}^T + \mathbf {U} \mathbf {V}^T. \end{aligned}$$

(3)

This matrix is by construction of rank 2; hence, two of its eigenvalues are zero. As for the nonzero eigenvalues, it can be shown, see “Appendix A.1”, that they are always of opposite sign (unless $\mathbf {U} \sim \mathbf {V}$, i.e., unless the two planes are identical).

2.3 Back-Projecting a Conic

Let $\mathbf {P}$ be the $3\times 4$ projection matrix of a perspective camera, and let $\mathbf {c}$ be a symmetrix $3\times 3$ matrix representing a conic in the image plane. Back-projecting the conic into 3D gives rise by a cone (the cone spanned by the camera’s optical center and the conic in the image plane). It can be computed as

$$\begin{aligned} \mathbf {C} \sim \mathbf {P}^T \; \mathbf {c} \; \mathbf {P}. \end{aligned}$$

(4)

3 Problem Formulation

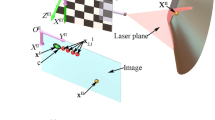
Figure 1 presents our system consisting of a camera and a laser source projecting a circular pattern. It can be mounted on a UAV to estimate its altitude and attitude (roll and pitch) relative to the ground plane on which the pattern is projected. The circular pattern from the laser projector defines a conic on the ground. The image of this conic in the camera is again a conic; extracting this conic allows to estimate the pose (altitude and attitude) of the laser/camera system. In the following, this is formulated mathematically.

Fig. 1

Geometric representation of the laser/camera setup

Let the camera coordinate frame be the reference (world) frame. Hence, the camera’s projection matrix can be written as

$$\begin{aligned} \mathbf {P}_\mathrm{cam} \sim \begin{bmatrix} \mathbf {K}&\mathbf {0} \end{bmatrix}_{3\times 4} \end{aligned}$$

(5)

where $\mathbf {K}$ is the $3\times 3$ matrix containing the camera’s intrinsic parameters.

As for the laser, we also describe the projection it carries out, in the form of a perspective camera. Let $\mathbf {P}_\mathrm{las}$ be the “projection matrix” of the laser, i.e.,

$$\begin{aligned} \mathbf {P}_\mathrm{las} = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \end{bmatrix} \begin{bmatrix} \mathbf {R}_\mathrm{las}&- \mathbf {R}_\mathrm{las} \mathbf {t}_\mathrm{las} \\ 0&1 \end{bmatrix} . \end{aligned}$$

(6)

Here, $\mathbf {R}_\mathrm{las}$ represents the orientation and $\mathbf {t}_\mathrm{las}$ the position of the laser, relative to the camera. They can be obtained by calibration as explained in Sect. 6

The circular laser pattern can be represented by a circle $\mathbf {d}$ in the laser’s “image plane” as

$$\begin{aligned} \mathbf {d} \sim \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-\tan ^2(\theta ) \end{bmatrix} \end{aligned}$$

(7)

where $\theta$ is the opening angle of the laser cone. The cone $\mathbf {D}$ is then obtained by back-projecting $\mathbf {d}$ to 3D (cf. Sect. 2):

$$\begin{aligned}&\mathbf {D} \sim \mathbf {P}^T_\mathrm{las} \; \mathbf {d} \; \mathbf {P}_\mathrm{las} \end{aligned}$$

(8)

$$\begin{aligned}&\mathbf {D} \sim \begin{bmatrix} \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las}&~&-\mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las} \mathbf {t}_\mathrm{las} \\ -\mathbf {t}_\mathrm{las}^T \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las}&~&\mathbf {t}_\mathrm{las}^T \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las} \mathbf {t}_\mathrm{las} \end{bmatrix}. \end{aligned}$$

(9)

As shown in Fig. 1, this cone cuts the ground plane in a conic, which is seen in the camera image again as a conic. Let the latter be represented by a symmetric $3\times 3$ matrix $\mathbf {c}$. The computation of $\mathbf {c}$ from edge points extracted in the image is described in Sect. 5.1.

The problem considered in this paper is then the estimation of the pose of the camera/laser system relative to the ground plane. Prior and fixed input is the knowledge of the laser pattern (circle $\mathbf {d}$, respectively, cone $\mathbf {D}$) and of the calibration of the camera/laser system (camera calibration $\mathbf {K}$ and relative camera/laser pose, represented by $\mathbf {R}_\mathrm{las}$ and $\mathbf {t}_\mathrm{las}$). Further input is then the image conic $\mathbf {c}$, extracted in the current camera image. This conic depends on the pose of the system relative to the ground plane.

Fig. 2

Two cones generated by the same conic intersect in general in a second conic

We can immediately observe that with this input, not all 6 degrees of freedom of the camera/laser system’s pose can be determined. As for the 3 translational degrees of freedom, translation of the system parallel to the ground plane does not affect any of the inputs, in particular the image conic $\mathbf {c}$ stays fixed in this case. The same holds true for rotations about the plane’s normal. As a consequence, we may determine 3 degrees of freedom of the pose: altitude above the plane and attitude relative to the plane (2 rotation angles—roll and pitch). Note that this is equivalent to determining the location of the ground plane relative to the camera/laser system. In the following sections, we thus describe methods to estimate the ground plane location.

4 A Geometric Solution for Altitude and Attitude Estimation

In the previous section, the cone $\mathbf {D}$ generated by the circular laser pattern was defined. Likewise, the back-projection of the image conic $\mathbf {c}$ into 3D gives rise to a cone $\mathbf {C}$ (cf. Fig. 1). It is computed as

$$\begin{aligned} \mathbf {C} \sim \mathbf {P}^T_\mathrm{cam} \; \mathbf {c} \; \mathbf {P}_\mathrm{cam}. \end{aligned}$$

(10)

In our scenario, these two cones, one from the laser projector and one from the camera, are “spanned” by the respective optical centers and the conic projected on the ground plane. To solve our pose estimation problem, one may proceed as follows. First, compute the intersection of the two cones. The intersection must contain the conic on the ground plane. Second, if that conic can be uniquely determined, it is then enough to compute the location of its support plane (the ground plane).

In the following, we present an analogous approach, but which does not require explicit intersection of the two cones. The approach is based on the study of the linear family of quadrics generated by the two cones, i.e., the family consisting of quadrics $\mathbf {Q}$ parameterized by a scalar x. $\mathbf {Q}$ is defined by

$$\begin{aligned} \mathbf {Q} = \mathbf {C} + x \mathbf {D}. \end{aligned}$$

(11)

We first study the properties of this family and then propose a pose estimation method based on this study.

4.1 Geometrical Study

In particular, we study the degenerate members of the above family of quadrics, i.e., quadrics with vanishing determinant: $\det (\mathbf {Q})=0$. The term $\det (\mathbf {Q})$ is in general a quartic polynomial in the parameter x. Among its up to four roots, we always have roots $x=0$ and $x \rightarrow \infty$, corresponding to the cones $\mathbf {C}$ and $\mathbf {D}$. As for the other two roots, they may be imaginary or real, depending on the cones $\mathbf {C}$ and $\mathbf {D}$ generating the family. In our setting, we know that these two cones intersect in at least one conic (the conic on the ground plane). In this case, it can be proved (see “Appendix A.2”) that the remaining two roots are real numbers and identical to one another. Further, the degenerate quadric associated with that root is of rank 2 and hence represents a pair of planes. Finally (cf. “Appendix A.2”), one of the planes is nothing else than the ground plane, whereas the second plane of the pair is a plane that separates the optical centers of the camera and of the laser, i.e., the two optical centers lie on opposite sides of the plane. This is illustrated in Fig. 2.

4.2 Pose Estimation Method

The properties outlined in the previous section are used here to devise a pose estimation method for our scenario. Concretely, we wish to compute the ground plane’s location relative to the camera.

Consider the linear family of quadrics generated by the two cones $\mathbf {C}$ and $\mathbf {D}$, i.e.,

$$\begin{aligned} \mathbf {Q} = \mathbf {C} + x \mathbf {D}. \end{aligned}$$

(12)

We first compute the roots of the polynomial $det(\mathbf {Q})$ and then consider the quadric $\mathbf {Q}$ associated with the only root that is different from 0 and $\infty$. This is a rank 2 quadric or a plane-pair. We now need to extract these two planes from $\mathbf {Q}$ and later to select the one corresponding to the ground plane.

Let $\mathbf {U}$ and $\mathbf {V}$ be the two planes we wish to “extract” from $\mathbf {Q}$. Let us remind, see Sect. 2.2, that the $4\times 4$ matrix representing the plane-pair, satisfies

$$\begin{aligned} \mathbf {Q} \sim \mathbf {V} \mathbf {U}^T + \mathbf {U} \mathbf {V}^T. \end{aligned}$$

(13)

The two planes can be extracted from $\mathbf {Q}$, for example, by applying an SVD (Singular Value Decomposition) on it. Since $\mathbf {Q}$ is of rank 2 and since the two nonzero eigenvalues are of opposite sign (see Sect. 2.2), its SVD must be of the following form:

$$\begin{aligned} \mathbf {Q} = \begin{bmatrix} \mathbf {A}&\mathbf {B}&\vdots&\vdots \end{bmatrix} \mathrm{diag}(\sigma _1, \sigma _2, 0, 0) \begin{bmatrix}\pm \mathbf {A}^T \\ \mp \mathbf {B}^T \\ \cdots \\ \cdots \end{bmatrix}. \end{aligned}$$

(14)

Hence, we can write

$$\begin{aligned} \mathbf {Q} = \pm (\sigma _1 \mathbf {A} \mathbf {A}^T - \sigma _2 \mathbf {B} \mathbf {B}^T). \end{aligned}$$

(15)

Thus, $\mathbf {U}$ and $\mathbf {V}$ satisfy

$$\begin{aligned} \mathbf {U} \mathbf {V}^T + \mathbf {V} \mathbf {U}^T \sim \sigma _1 \mathbf {A} \mathbf {A}^T - \sigma _2 \mathbf {B} \mathbf {B}^T. \end{aligned}$$

(16)

From (13), it is clear that $\mathbf {U}$ and $\mathbf {V}$ form a minimal basis for the row space of $\mathbf {Q}$ (and, $\mathbf {Q}$ being symmetric, of its column space too). From (14), $\mathbf {A}$ and $\mathbf {B}$ also form a minimal basis for this row space. Hence, the two planes $\mathbf {U}$ and $\mathbf {V}$ must be linear combinations of the singular vectors $\mathbf {A}$ and $\mathbf {B}$, i.e.,

$$\begin{aligned} \mathbf {U}= & {} u \mathbf {A} + \mathbf {B}, \end{aligned}$$

(17)

$$\begin{aligned} \mathbf {V}= & {} v \mathbf {A} + \mathbf {B}. \end{aligned}$$

(18)

We now need to determine u and v. By inserting (17) and (18) into Eq. (16), we get

$$\begin{aligned}&2 u v \mathbf {A} \mathbf {A}^T + 2 \mathbf {B} \mathbf {B}^T + (u+v) (\mathbf {A} \mathbf {B}^T + \mathbf {B} \mathbf {A}^T) \ldots \nonumber \\&\quad \ldots \sim \sigma _1 \mathbf {A} \mathbf {A}^T - \sigma _2 \mathbf {B} \mathbf {B}^T. \end{aligned}$$

(19)

Thus, we can conclude that $u+v=0$. Upon inserting $v = -u$ into Eq. (19), we get

$$\begin{aligned} -2 u^2 \mathbf {A} \mathbf {A}^T + 2 \mathbf {B} \mathbf {B}^T \sim \sigma _1 \mathbf {A} \mathbf {A}^T - \sigma _2 \mathbf {B} \mathbf {B}^T. \end{aligned}$$

(20)

This is satisfied for

$$\begin{aligned} u^2 = \frac{\sigma _1}{\sigma _2}. \end{aligned}$$

(21)

Finally, the two planes can now be computed to be

$$\begin{aligned} \mathbf {U}= & {} \sqrt{{\frac{\sigma _1}{\sigma _2}}} \mathbf {A} + \mathbf {B} \text {~and} \end{aligned}$$

(22)

$$\begin{aligned} \mathbf {V}= & {} -\sqrt{{\frac{\sigma _1}{\sigma _2}}} \mathbf {A} + \mathbf {B}. \end{aligned}$$

(23)

Note that since the singular values $\sigma _1$ and $\sigma _2$ are positive, the square root in these equations is well defined.

We still need to determine which one among these two planes is the ground plane. Obviously, the optical centers of camera and laser lie on the same side of the ground plane. From what is shown in “Appendix A.2”, the optical centers must lie on different sides of the second plane. It thus suffices to select the one plane among $\mathbf {U}$ and $\mathbf {V}$ relative to which the optical centers lie on the same side; this is the ground plane.

Let us scale the selected plane such that it can be written as $\mathbf {\Pi } = [n_x \, n_y \, n_z \, d]^T$, with $\sqrt{n_x^2 + n_y^2 + n_z^2} = 1$. Then, the altitude of our system is deduced by computing the orthogonal distance between the camera center and the plane, defined by

$$\begin{aligned} Altitude = |d| \end{aligned}$$

(24)

since the camera center is the origin of our reference frame.

We are now looking for the attitude of the system. We have the normal of the ground plane expressed in two frames: the world frame where it is $\begin{bmatrix} 0&0&1 \end{bmatrix}^T$ and in the camera frame where our estimation is $\begin{bmatrix} n_x&n_y&n_z \end{bmatrix}^T$. Recovering the attitude of the system is equivalent to finding the rotation matrix $\mathbf {R}$ from one frame to the other one, which satisfies

$$\begin{aligned} \begin{bmatrix} n_x \\ n_y \\ n_z \end{bmatrix} = \mathbf {R} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}. \end{aligned}$$

(25)

As mentioned earlier, rotation about the ground plane’s normal (yaw) cannot be recovered. We thus only consider pitch and roll angles. The Denavit–Hartenberg [17] parametrization of $\mathbf {R}$ with these two angles leads to

$$\begin{aligned} \begin{bmatrix} n_x \\ n_y \\ n_z \end{bmatrix} = \begin{bmatrix} \cos (\theta )&-\sin (\theta ) \cos (\alpha )&\sin (\theta ) \sin (\alpha ) \\ \sin (\theta )&\cos (\theta ) \cos (\alpha )&- \cos (\theta ) \sin (\alpha ) \\ 0&\sin (\alpha )&\cos (\alpha ) \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}. \end{aligned}$$

(26)

From (26), $\alpha$ (roll) and $\theta$ (pitch) can be easily recovered since

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha = \arccos (n_z) \\ \theta = \frac{\arcsin (n_x) }{\sqrt{1-\cos ^2(\alpha )}} \end{array}\right. }. \end{aligned}$$

(27)

They can be re-injected into (26) to compute the entire rotation matrix $\mathbf {R}$ that defines the attitude of the camera/laser system.

5 Robust Estimations

The methodology presented in Sect. 4 supposes that the cone associated with the projector (cone $\mathbf {D}$ in Fig. 1) is known without error. Well, not exactly, since calibration errors exist; but to compute the cone, we do not need to make any image processing. In contrast, the cone associated with the camera (cone $\mathbf {C}$ in Fig. 1) is computed by first extracting an ellipse $\mathbf {c}$ in the camera image. Note that our approach is valid for the case of $\mathbf {c}$ being a general conic; however, in our practical setting, it is always an ellipse, so we stick to this in the following. A potential problem is that outliers may affect the estimation of the ellipse. For instance, these outliers can appear when the laser projector intercepts a ground plane partially occluded by objects. To still work in this case, one can resort to a RANSAC scheme to compute the ellipse $\mathbf {c}$. In this section, we propose three robust estimations: one based on a 5-point RANSAC to estimate the ellipse in the image plane, one based on a 3-point RANSAC to estimate the ellipse by taking into account the epipolar geometry and one based on a 3-point RANSAC to directly estimate the ground plane (and consequently the altitude and attitude of our system), without estimating the ellipse.

The random sample consensus (RANSAC) scheme [18] consists in computing model hypotheses from minimal sets of randomly selected data, in our case image points. Each hypothesis is verified on the rest of the data points by computing a distance measure. The points within a threshold distance are considered as inliers and constitute the consensus set for the model hypothesis. This random selection is repeated a number of times, and the best model is the one with the higher consensus set. The number of iterations N needed to ensure with a probability p that at least one of the random samples is free from outliers can be computed by

$$\begin{aligned} N = \frac{ \log {(1-p)}}{\log {(1-(1-\epsilon )^s)}} \end{aligned}$$

(28)

where s is the minimal number of points necessary to compute the model and $\epsilon$ is the supposed fraction of outliers among the data points [3]. Usually, p is set to $p=0.99$ to ensure a high probability of success. As highlighted in Eq. (28), the number of iterations N is exponential with the size of the minimal subset so finding a minimal parameterization of the model is very advantageous for the computing time. For example, with $p=0.99$ and $\epsilon =0.5$ the 5-point method for ellipse fitting requires 146 iterations, whereas the two 3-point methods require only 35.

5.1 The Plane-Pair 5-Point (PP-5) Algorithm

The method for estimating altitude and attitude presented in Sect. 4 requires the computation of the ellipse $\mathbf {c}$. In this section, we explain how to estimate it with all points and then with 5 points using a RANSAC scheme. This robust estimation is denominated the Plane-Pair 5-point (PP-5) algorithm.

A point $\mathbf {x} = [x \quad y \quad z]^T$ (given in homogeneous coordinates) lies on $\mathbf {c}$ if $\mathbf {x}^T \; \mathbf {c} \; \mathbf {x} = 0$. Representing $\mathbf {c}$ as usual by a symmetric matrix

$$\begin{aligned} \mathbf {c} \sim \begin{bmatrix} a&b/2&d/2 \\ b/2&c&e/2 \\ d/2&e/2&f \end{bmatrix}, \end{aligned}$$

(29)

the above equation becomes

$$\begin{aligned} a x^2 + b x y + c y^2 + d x z + e y z + f z^2 = 0. \end{aligned}$$

(30)

The matrix representation of $\mathbf {c}$ has five degrees of freedom: The six elements of the matrix (29) minus one for the scale since multiplying Eq. (30) by a nonzero scalar does not affect this equation.

Suppose we have n points ($n\ge 5$) belonging to $\mathbf {c}$. Let $\mathbf {x}_i = [x_i \quad y_i \quad z_i]^T$ be the ith point. We can build the system of linear equations

$$\begin{aligned} \begin{bmatrix} x_1^2&x_1 y_1&y_1^2&x_1 z_1&y_1 z_1&z_1^2 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ x_n^2&x_n y_n&y_n^2&x_n z_n&y_n z_n&z_n^2 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = \mathbf {0}. \end{aligned}$$

(31)

The coefficients a, b, c, d, e and f can be obtained (up to scale) by a Singular Value Decomposition of the first matrix of Eq. (31).

Fig. 3

Epipolar geometry of the camera and the projector. The black lines are tangents to the cones relative to an epipolar plane. Their projection into the camera image gives epipolar lines (in cyan) which must be tangent to $\mathbf {c}$. The green curve is the second intersection curve of the two cones, besides the ellipse on the ground plane (see text). This figure can be explored in 3D at https://www.geogebra.org/m/x3x62vRQ

The points $\mathbf {x}_i$ are detected by an image processing step (e.g., thresholding and filtering) where outliers can appear. A direct estimation as presented in this section often leads to an erroneous result in the presence of outliers. To avoid this, the ellipse fitting algorithm is achieved in a RANSAC scheme to remove the potential outliers as described in Algorithm 1. Here, 5 points are the minimum required to solve the ellipse coefficients using Eq. (31).

5.2 The Plane-Pair 3-Point (PP-3) Algorithm

Three points are not enough in general to compute an ellipse, but in our case we have additional information, not used so far: We know the epipolar geometry between the camera and the projector. This epipolar geometry provides additional constraints since the two cones ($\mathbf {C}$ and $\mathbf {D}$) must be tangent to the same epipolar planes. Considering Fig. 3, for instance, both cones are tangent to the plane spanned by the two optical centers and the black lines on the cones. There is also a second epipolar plane that is tangent to both cones, behind them.

The analogous in 2D is as follows: Consider the circle in the projector image plane. There are two epipolar lines, i.e., lines that contain the epipole and that are tangent to that circle. The two corresponding epipolar lines in the camera image must be tangent to the ellipse we are looking for in the camera image. This is the epipolar constraint for images of conics [19].

As we know the pose of the laser with respect to the camera, we can directly compute the fundamental matrix given by

$$\begin{aligned} \mathbf {F} = \mathbf {K}^{-T} [\mathbf {t}_\mathrm{las}]_{\times } \mathbf {R}_\mathrm{las}. \end{aligned}$$

(32)

The epipoles can then be determined using the SVD of $\mathbf {F}$. The epipoles $\mathbf {e}$ in the laser image and $\mathbf {e}'$ in the camera image are the left and right null vectors of $\mathbf {F}$. It is now possible to compute the two tangent lines in the laser image since we know the epipole they are passing through and the equation of the circle in the laser image. As we also know the essential matrix, we can obtain the equation of these lines in the camera image.

Fig. 4

Our problem in two configurations: in the camera image and after applying the homography. The 3 points selected to estimate $\mathbf {c}$ are represented in green, the epipole in black, the two tangent lines in blue and the conic to be estimated in red. Note that on the right-hand side, obtained by applying the projective transformation $\mathbf {H}$, the conic may not be an ellipse. a The camera configuration and b the homography configuration

We thus have two constraints on the $\mathbf {c}$. They are not trivial to use though. We propose the following formulation. Let $\mathbf {u}$ and $\mathbf {v}$ be the two epipolar lines that must be tangent to the ellipse $\mathbf {c}$. In other words, the two lines must be on the conic that is dual to $\mathbf {c}$, which can be written as

$$\begin{aligned} \mathbf {u}^T \; \mathbf {c}^{-1} \; \mathbf {u}= & {} 0 \, \text {~ and} \end{aligned}$$

(33)

$$\begin{aligned} \mathbf {v}^T \; \mathbf {c}^{-1} \; \mathbf {v}= & {} 0 . \end{aligned}$$

(34)

On the other hand, any point $\mathbf {x}$ that lies on $\mathbf {c}$, gives a constraint

$$\begin{aligned} \mathbf {x}^T \; \mathbf {c} \; \mathbf {x} = 0. \end{aligned}$$

(35)

If we consider 3 points, we thus have 3 linear constraints on $\mathbf {c}$ and 2 linear constraints on its inverse. The resolution of such a system of equations is not trivial. To simplify expressions, we first apply an homography to the image plane that leads to simple coordinates for the considered points. Let $\mathbf {x}_i, i=1,2,3$ be the three points lying on the ellipse and $\mathbf {x}_4$ the intersection point of the two tangent lines $\mathbf {u}$ and $\mathbf {v}$, i.e., the epipole $\mathbf {e}'$ in the camera image. Let us compute an homography $\mathbf {H}$ which maps these four points to

$$\begin{aligned} \mathbf {x}'_1 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, \mathbf {x}'_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \mathbf {x}'_3 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} \text {~and} \mathbf {x}'_4 = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}. \end{aligned}$$

(36)

This homography is computed from the linear equations of type $(\mathbf {H} \mathbf {x}_i) \times \mathbf {x}'_i = \mathbf {0}$. For each of the four pairs of points $\mathbf {x}_i = \begin{bmatrix} x_i&y_i&z_i \end{bmatrix}^T$ and $\mathbf {x}'_i = \begin{bmatrix} x'_i&y'_i&z'_i \end{bmatrix}^T$, we can build the following system of equations and solve it by SVD:

$$\begin{aligned} \begin{bmatrix} \mathbf {0}^T&z'_i \mathbf {x}^T_i&- y'_i \mathbf {x}^T_i \\ -z'_i \mathbf {x}^T_i&\mathbf {0}^T&- x'_i \mathbf {x}^T_i \\ y'_i \mathbf {x}^T_i&-x'_i \mathbf {x}^T_i&\mathbf {0}^T \end{bmatrix} \begin{bmatrix} \mathbf {h}_1 \\ \mathbf {h}_2 \\ \mathbf {h}_3 \end{bmatrix} = \mathbf {0}. \end{aligned}$$

(37)

Here, $\mathbf {h}_i$ are rows of $\mathbf {H}$. After computing $\mathbf {H}$, we use it to map the two tangent lines as follows

$$\begin{aligned} \mathbf {u}' = \mathbf {H}^{-T} \mathbf {u} \end{aligned}$$

(38)

$$\begin{aligned} \mathbf {v}' = \mathbf {H}^{-T} \mathbf {v} . \end{aligned}$$

(39)

This mapping is illustrated in Fig. 4.

$\mathbf {u}'$ and $\mathbf {v}'$ contain the point $[1,1,0]^T$ and hence must be of the form

$$\begin{aligned}&\mathbf {u}' \sim \begin{bmatrix} 1 \\ -1 \\ r \end{bmatrix} \, \text {~and} \end{aligned}$$

(40)

$$\begin{aligned}&\mathbf {v}' \sim \begin{bmatrix} 1 \\ -1 \\ s \end{bmatrix} \end{aligned}$$

(41)

where r and s can be extracted from equations (38) and (39).

We now turn to the actual estimation of the conic $\mathbf {c}'$. First, since it contains $\mathbf {x}'_i, i=1,2,3$, with the particular coordinates as given in Eq. (36), it must be of the special form

$$\begin{aligned} \mathbf {c}' \sim \begin{pmatrix} 2 v &{} u &{} -v \\ u &{} 2 t &{} -t \\ -v &{} -t &{} 0 \end{pmatrix}. \end{aligned}$$

(42)

Without loss of generality, we may fix the homogeneous scale factor for $\mathbf {c}'$ by setting $v=1$ (the only case where this is not allowed would be if $v=0$, but in that case, $\mathbf {c}'$ is degenerate; this case can be safely excluded in our application, where in practice we will always observe a non-degenerate ellipse in the camera image). Hence, we set

$$\begin{aligned} \mathbf {c}' = \begin{pmatrix} 2 &{} u &{} -1 \\ u &{} 2 t &{} -t \\ -1 &{} -t &{} 0 \end{pmatrix}. \end{aligned}$$

(43)

The inverse of $\mathbf {c}'$ is, up to scale, equal to

$$\begin{aligned} \mathbf {c}'^{-1} \sim \begin{pmatrix} -t^2 &{} t &{} -t (u-2) \\ t &{} -1 &{} 2 t - u \\ -t (u-2) &{} 2 t - u &{} 4 t - u^2 \end{pmatrix}. \end{aligned}$$

(44)

To determine the two unknowns t and u, we use

$$\begin{aligned} \mathbf {u}'^T \; \mathbf {c}'^{-1} \; \mathbf {u}'= & {} 0 \, \text {~and} \end{aligned}$$

(45)

$$\begin{aligned} \mathbf {v}'^T \; \mathbf {c}'^{-1} \; \mathbf {v}'= & {} 0 . \end{aligned}$$

(46)

Making these equations explicit gives two quadratic equations in t and u:

$$\begin{aligned} -(t+1)^2 + 2 r u (1 - t) + r^2 (4 t - u^2)= & {} 0 , \end{aligned}$$

(47)

$$\begin{aligned} -(t+1)^2 + 2 s u (1 - t) + s^2 (4 t - u^2)= & {} 0 . \end{aligned}$$

(48)

We may subtract the two equations from one another to get

$$\begin{aligned} 0= & {} 2 r u (1 - t) + r^2 (4 t - u^2) - 2 s u (1 - t) - s^2 (4 t - u^2), \end{aligned}$$

(49)

$$\begin{aligned} 0= & {} 2 u (1 - t) (r - s) + (4 t - u^2) (r^2 - s^2), \end{aligned}$$

(50)

$$\begin{aligned} 0= & {} t \left( 2 u (s - r) + 4 (r^2 - s^2)\right) + \left( 2 u (r - s) + u^2 (s^2 - r^2)\right) . \end{aligned}$$

(51)

This equation is linear in t, and we may solve for t as follows:

$$\begin{aligned} t = \frac{2 u (s - r) + u^2 (r^2 - s^2)}{2 u (s - r) + 4 (r^2 - s^2)}. \end{aligned}$$

(52)

Plugging this into either (47) or (48), and extracting the numerator, gives the following quartic equation in u:

$$\begin{aligned}&(r-s)^2 u^4 + 8(r+s)(r s-1) u^3 + 8(r^2+4 r s+s^2+2) u^2 \nonumber \\&\quad - 32 (r+s)(r s+1) u + 16 (r+s)^2 = 0. \end{aligned}$$

(53)

Solving Eq. (53) leads up to four real solutions for u. For each solution, we can then compute t from Eq. (52) and thus a potential solution for $\mathbf {c}'$ from Eq. (44). We now only need to map each such solution back to the original image plane with

$$\begin{aligned} \mathbf {c} = \mathbf {H}^T \; \mathbf {c}' \; \mathbf {H}. \end{aligned}$$

(54)

It may be possible to rule out spurious solutions for $\mathbf {c}$, by eliminating conics that are not ellipses. To check for an ellipse: If and only if the eigenvalues of the upper left $2\times 2$ sub-matrix of $\mathbf {c}$ are both nonzero and have the same sign, then $\mathbf {c}$ is an ellipse. Nevertheless, we may obtain several solutions which are ellipses. To get a unique solution, at least one more point is necessary. Let $\mathbf {x}_5$ be this point; the right solution is the one where

$$\begin{aligned} \mathbf {x}^T_5 \; \mathbf {c} \; \mathbf {x}_5 = 0. \end{aligned}$$

(55)

Since the 3-point estimation method explained above is in practice embedded in a RANSAC scheme, selecting such a fourth point is not necessary. We can simply evaluate all obtained solutions for $\mathbf {c}$ that are ellipses, using all the other image points, in the consensus step of RANSAC, see Algorithm 2.

5.3 A Minimal Solution: The Ground Plane 3-Point (GP-3) Algorithm

The fitting of the ellipse from 3 points is feasible, as shown in Sect. 5.2, but not quite simple. It turns out that it is simpler to directly solve the problem we are interested in: the estimation of the ground plane. The intersection of the two cones in 3D gives, as shown in Figs. 2 and 3, two conics in 3D. One of them is the trace of the projected circle on the ground plane and the support plane of that conic is hence the ground plane, expressed in the reference system in which the cones are represented (the camera frame in our case).

Let us consider now 3 points in the camera image that are assumed to lie on the ellipse $\mathbf {c}$. What we can now do is to actually back-project these 3 points to 3D, i.e., to compute their lines of sight. We then intersect the laser cone $\mathbf {D}$ with each of these lines, giving in general two intersection points each. There are thus $2^3=8$ possible combinations of 3D points associated with our 3 image points, and one of them must correspond to points lying on the ground plane. Selecting this correct solution can be done by embedding this scheme into a RANSAC, as explained below.

Let us now provide details on these operations. Let $\mathbf {x}$ be an image point, supposed to lie on $\mathbf {c}$. Its back-projection gives a line in 3D, consisting of points parameterized by a scalar $\lambda$. With the camera projection matrix as given in Eq. (5), the back-projection gives

$$\begin{aligned} \mathbf {X}(\lambda ) = \begin{bmatrix} \lambda \mathbf {K}^{-1} \mathbf {x} \\ 1 \end{bmatrix}. \end{aligned}$$

(56)

To find the intersection points with this line and the laser cone, we must solve the following equation for $\lambda$:

$$\begin{aligned} \mathbf {X}(\lambda )^T \; \mathbf {D} \; \mathbf {X}(\lambda ) = 0 \end{aligned}$$

where $\mathbf {D}$ is the cone, as defined in equation (9). In detail, this is the following quadratic equation:

$$\begin{aligned}&\lambda ^2 \underbrace{\mathbf {x}^T \mathbf {K}^{-T} \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las} \mathbf {K}^{-1} \mathbf {x}}_{c_2}\nonumber \\&\quad ~~~ - 2 \lambda \underbrace{\mathbf {x}^T \mathbf {K}^{-T} \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las} \mathbf {t}_\mathrm{las}}_{c_1}\nonumber \\&\quad ~~~~~~ + \underbrace{\mathbf {t}_\mathrm{las}^T \mathbf {R}_\mathrm{las}^T \mathbf {d} \; \mathbf {R}_\mathrm{las} \mathbf {t}_\mathrm{las}}_{c_0} = 0 . \end{aligned}$$

(57)

Let $\Delta = c_1^2 - c_0 c_2$. Then,

• if $\Delta <0$, there is no real solution and consequently no real intersection between the cone and the ray,

• if $\Delta = 0$, there is only one real solution ($\lambda = \frac{c_1}{c_2}$), corresponding to a line tangent to the cone,

• if $\Delta >0$, there are two intersections: $\lambda =\frac{ c_1 \pm \sqrt{\Delta }}{c_2}$.

As mentioned above, the up to two intersection points per back-projected image point, give up to 8 triplets of 3D points, among which one triplet is lying on the ground plane. To determine this, one may use geometric constraints (as already used above, the optical centers of the camera and laser must lie on the same side of the ground plane) and additional image points. The latter possibility is described in the RANSAC scheme embodied in Algorithm 3.

The advantages of this 3-point RANSAC method are multiple:

• Lower computational cost than the general 5-point fitting method (many fewer RANSAC samples need to be considered as shown in Sect. 5).

• Higher robustness as shown in Sect. 7.

• The solution computed from 3 points satisfies all geometric constraints (the epipolar constraints actually); this means that the intersection of cones will be exact. On the contrary, if one first estimates a general ellipse in the camera image and then intersects its cone with the cone from the projector: That problem is over-constrained and the solution will not be an exact intersection of the cones. The numerical solution obtained with such a 5-point method may be worse than the 3-point method.

Fig. 5

Our calibration method uses a planar surface with a known texture. The source image a is treated to extract the pattern and the equation of the conic (b). a One of the images used for the calibration and b detection of the conic and of the pattern

6 Calibration

Calibration is a necessary step to run our algorithms on real data. In our system, we have three elements to calibrate: the projector, the camera and the relative pose between the camera and the laser.

Regarding the projector, we suppose that we know the opening angle of the laser cone since it is given by the manufacturer or it can easily be measured.

The camera is calibrated by a conventional method, using a checkerboard pattern [20].

The main problem thus lies in the estimation of the relative pose between the laser and the camera. Pose consists normally of three translation/position parameters and three rotation parameters. Since the laser cone is circular, rotation about its axis is irrelevant in our application; hence, only two rotation parameters need and can be determined.

Our method uses a planar surface with a known texture, e.g., a calibration pattern. In that case, the pose of the planar surface relative to the camera can be computed [7].

It is theoretically possible to perform the calibration from one image. Nevertheless, for best results, one should combine all available images, in a bundle adjustment fashion.

One way of doing this is as follows. We have to optimize the pose of the laser cone relative to the camera and for this, we need to define a cost function. One possibility is to sample points of the ground plane ellipses and to minimize the sum of squared distances between the sampled points and the ellipses that are generated by cutting the cone with the ground plane, where the cone is a function of the pose parameters to be optimized. Minimizing this sum of squared distances allows to optimize the cone parameters. Such a point-based cost function is more costly to optimize than, for instance, a cost function that compares ellipses as such (e.g., that compares the symmetric $3\times 3$ matrices representing ellipses), but should be better suited.

The optimization of the proposed cost function can be done in several different ways; here we describe a solution analogous to one proposed for fitting conics to points in [21]. It requires to optimize, besides the cone parameters, one parameter per point that expresses the position of each point on the cone.

The formulation is as follows. Consider first a cone in canonical position, with vertex at the origin and with the Z-axis as axis of revolution. Directions of lines on the cone can be parameterized by an angle $\gamma _i$ as

$$\begin{aligned} \mathbf {D}_i = \begin{bmatrix} \cos \gamma _i&-\sin \gamma _i&0 \\ \sin \gamma _i&\cos \gamma _i&0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} \sin \frac{\Theta }{2} \\ 0 \\ \cos \frac{\Theta }{2} \end{bmatrix}. \end{aligned}$$

(58)

The unknowns of the pose estimation problem are the orientation and the position of the cone relative to the camera. The orientation is given up to a rotation about the Z-axis, i.e., can be represented by a rotation about Y, followed by one about X. The position can be represented simply as the position of the vertex, given by a vector $\mathbf {v}=[v_x ~ v_y ~v_z]^T$.

Fig. 6

Form of the Jacobian matrix for our calibration formulation consisting of 5 relative pose parameters and n points. Zero entries in the matrix are shown in gray

Fig. 7

Evaluation of the proposed algorithms under varying image noise. a Altitude, b pitch, c roll

As for the orientation, the direction $\mathbf {D}_i$ is mapped to a direction $\mathbf {D}'_i$ in the camera coordinate system by

$$\begin{aligned} \mathbf {D}'_i= & {} \mathbf {R}_{las,X} \mathbf {R}_{las,Y} \mathbf {D}_i \nonumber \\ ~= & {} \begin{bmatrix} 1&0&0 \\ 0&\cos \alpha&-\sin \alpha \\ 0&\sin \alpha&\cos \alpha \end{bmatrix} \begin{bmatrix} \cos \beta&0&\sin \beta \\ 0&1&0 \\ -\sin \beta&0&\cos \beta \end{bmatrix} \mathbf {D}_i. \end{aligned}$$

(59)

Finally, for a frame j, let the camera pose relative to the calibration grid on the ground plane be given by a rotation matrix $\mathbf {S}_j$ and a vector $\mathbf {t}_j$ such that points in the camera coordinate system are mapped to the calibration grid coordinate system by

$$\begin{aligned} \mathbf {Q}^g = \mathbf {S}_j \mathbf {Q}^c + \mathbf {t}_j. \end{aligned}$$

(60)

Now, in the grid’s coordinate system, the direction is given as

$$\begin{aligned} \mathbf {D}^g_{ij} = \mathbf {S}_j \mathbf {D}'_i \end{aligned}$$

(61)

and the cone’s vertex as

$$\begin{aligned} \mathbf {t}^g_j = \mathbf {S}_j \mathbf {v} + \mathbf {t}_j. \end{aligned}$$

(62)

We need to find the intersection of the line given by the vertex and the direction, with the ground plane (set to the plane $Z=0$ for the calibration process). This is simply given by the point

$$\begin{aligned} \mathbf {S}_j \mathbf {v} + \mathbf {t}_j + \lambda _{ij} \mathbf {S}_j \mathbf {D}'_i \end{aligned}$$

(63)

such that

$$\begin{aligned} \lambda _{ij} = -\frac{(\mathbf {S}_j \mathbf {v} + \mathbf {t}_j)_3}{(\mathbf {S}_j \mathbf {D}'_i)_3}. \end{aligned}$$

(64)

The XY-coordinates of that point are given as

$$\begin{aligned} X_{ij}= & {} (\mathbf {S}_j \mathbf {v} + \mathbf {t}_j)_1 - \frac{(\mathbf {S}_j \mathbf {v} + \mathbf {t}_j)_3}{(\mathbf {S}_j \mathbf {D}'_i)_3} (\mathbf {S}_j \mathbf {D}'_i)_1 \text {~and}\nonumber \\ Y_{ij}= & {} (\mathbf {S}_j \mathbf {v} + \mathbf {t}_j)_2 - \frac{(\mathbf {S}_j \mathbf {v} + \mathbf {t}_j)_3}{(\mathbf {S}_j \mathbf {D}'_i)_3} (\mathbf {S}_j \mathbf {D}'_i)_2. \end{aligned}$$

(65)

The cost function is the sum of squared differences between these predicted XY-coordinates, and the ones measured (for the sampled points mentioned above). To optimize it, we use the Levenberg–Marquardt algorithm [22] which requires to compute its partial derivatives in the unknowns, which are: $\alpha , \beta , \mathbf {v}$ and the $\gamma _i$, as shown in Fig. 6.

Fig. 8

Estimated conic using the PP-5 (a) and the PP-3 (b) algorithms. Outlier ratio$\,=\,75\%$, number of RANSAC iterations$\,=\,100$, RANSAC threshold$\,=\,0.01$

Fig. 9

Evaluation of the proposed algorithms under varying intrinsic parameters noise. a Altitude, b pitch, c roll

To ensure the convergence of the algorithm, the optimization is achieved in two steps: We firstly optimize only the $\gamma _i$ before the re-estimation of all the parameters ($\alpha , \beta , \mathbf {v}, \gamma _i$).

7 Experiments

To verify the validity of the proposed methods, we perform experiments using both simulated data and real images. The latter have been acquired with a camera–laser system and a motion capture system as ground truth for quantitative comparisons.

7.1 Synthetic Evaluation

In these first experiments, we generate a set of laser points on the ground floor, given the intrinsic parameters of the camera and of the laser as well as their relative pose. We then introduced different noises in the simulated data such as image noise, outliers, noise on intrinsic and extrinsic parameters. The performances of the three proposed algorithms are evaluated by comparing the mean error of the respective estimated altitude, roll and pitch angles over a thousand trials.

7.1.1 Evaluation Under Image Noise

In order to evaluate the robustness of the three algorithms in presence of image noise, we have added different levels of noise to the pixel coordinates of the image points lying on the image of the laser beam’s intersection with the ground plane. We then propose to compare the mean error of the estimated altitude, roll and pitch angles obtained from the three methods over a thousand trials. Results are shown in Fig. 7.

The GP-3 algorithm gives the best results for the altitude estimation while for the attitude estimation (roll and pitch) the PP-3 and GP-3 have similar performances. We believe that the 5-point is the most sensitive since less constraints than the two other approaches are used.

7.1.2 Evaluation Under Varying Outlier Ratios

In this second experiment, we generate a given proportion of outliers in the whole camera image. The comparison is not based on error curves since the estimation leads to an exact solution (no noise is added to the inlier points). The results are summarized in Table 1 where the proportions of outliers that cause the algorithms to fail are given. Both PP-3 and GP-3 algorithms seem to have a similar robustness to the outliers.

Table 1 Proportion of outliers from which algorithms fail

Fig. 10

Evaluation of the proposed algorithms under varying baseline noise. a Altitude, b pitch, c roll

Examples of ellipse estimation, respectively, based on the PP-5 and the PP-3 are shown in Fig. 8. This kind of result is not proposed for the GP-3 algorithm since it does not estimate an ellipse, but directly the ground plane. The main advantage of our PP-3 algorithm is that it takes into account the geometric constraints (the epipolar geometry of our system) to estimate the ellipse. The introduction of these additional constraints increases the robustness of this algorithm when the number of outliers becomes very large. As shown in Fig. 8, in the same conditions of iteration number and threshold, the PP-3 algorithm provides a good ellipse estimation, whereas the conventional PP-5 algorithm fails.

Fig. 11

Evaluation of the proposed algorithms under varying ground plane noise. a Altitude, b pitch, c roll

Fig. 12

Hand-held system used for the Vicon experiment

Fig. 13

Results of the three stages of the calibration process. a Estimated projection (in red) and real points (in green) of the conic on the ground plane with the values used for initialization, b estimated projection (in red) and real points (in green) of the conic on the ground plane after the $\gamma _i$ convergence and c estimated projection (in red) and real points (in green) of the conic on the ground plane after the convergence of all parameters (points and relative pose) (Color figure online)

7.1.3 Evaluation Under Varying Calibration Noise (Intrinsic Parameters)

For this experiment, we introduced noise in the intrinsic parameters. Results are given in Fig. 9. As illustrated in this figure, the PP-3 and GP-3 algorithms give better results for the altitude estimation than the PP-5. For the attitude estimation, the three algorithms provide similar results.

Fig. 14

Real experiment. a Trajectory realized in the real experiment and b an example of image grabbed by the camera

Fig. 15

Results of the real experiments. a Estimated altitude, b estimated pitch, c estimated roll

7.1.4 Evaluation Under Varying Calibration Noise (Extrinsic Parameters)

In this case, we introduced noise on the extent of the baseline between camera and laser. Results are given in Fig. 10. As illustrated in this figure, the baseline has a stronger influence on the altitude estimation than on the attitude. All the proposed algorithms seem to react in the same way for the altitude estimation. The PP-3 and GP-3 algorithms give better results for the attitude estimation than the PP-5.

7.1.5 Evaluation under Varying Ground Plane Noise

Complementary to the outliers previously treated, we also introduced noise in the ground plane points coordinates. The aim is to simulate what would happen with a non-uniform ground (presence of gravel or grass). Results are given in Fig. 11. As illustrated in this figure, the non-uniform plane has a strong influence on the altitude and attitude estimations. The PP-3 and GP-3 algorithms give the best results, in particular for the altitude estimation.

7.2 Experiments on Real Data with Vicon-Based Ground Truth

In order to have a practical evaluation of our algorithms, a dataset has been collected with a reliable ground truth obtained by a motion capture system. The experiments have been conducted in a room equipped with a Vicon motion capture system composed of 20 Vicon T40S cameras. With such a system, we can assure a 6 DoF (Degrees of Freedom) localization of our system with a sub-millimetric accuracy as demonstrated in [23] and a high framerate (500fps).

Table 2 Altitude, pitch and roll errors of the real experiment

Fig. 16

UAV experiment (see [15] for more details). a Our system mounted on a Pelican UAV and b the Pelican UAV in the VICON area. The flying area available is $15\times 10\times 5\mathrm{m}^3$ equipped with twenty T40S Vicon cameras

The camera used in the experiments is a uEye color camera from IDS with an image resolution of $1600\times 1200$ pixels and a 60fps framerate. The color helps the laser segmentation in the image since the laser produces a red light. The laser is a Z5M18B-F-635-c34 from Z-Laser which provides a red light (635 nm) with a power of 5 mW. It is equipped with a circle optic with an opening angle of 34$^{\circ }$.

For the evaluation of the accuracy of our algorithms, we used a hand-held system as shown in Fig. 12. The camera and the laser are mounted on a trihedron to facilitate the positioning of the markers of the motion capture system.

Due to the low power of the laser and the dark color of the floor, the experiments are conducted in a dark environment as in our previous works [14, 15]. The lights are nevertheless not totally turned off since the camera has to observe a calibration pattern. The processing pipeline to detect the conic points in the image is simple. The color image is firstly converted from the RGB space into the HSV one. Then, a fixed threshold is applied only on the H-channel since it contains the colorimetric information and we are looking for the red light of the laser. There is no additional processing; the outliers are directly removed by using the three proposed algorithms.

A first dataset is acquired for the calibration of the system as explained in Sect. 6. This dataset is composed of 16 images where the laser projection and a calibration pattern are visible as shown in Fig. 5. The relative pose of the laser with respect to the camera is initialized by measuring it roughly. This first estimation is represented in Fig. 13a. An intermediate and the final estimations after the algorithm convergence are shown, respectively, in Fig. 13b, c. The average error after calibration is less than 1.6 mm per point.

A second dataset composed of 106 images has then been acquired without the calibration pattern. The trajectory of this second dataset is represented in Fig. 14. The ground truth is given by the Vicon system. The results of our algorithms are given in Fig. 15 and in Table 2.

As we can see, the three algorithms provide a reliable estimate of the altitude and attitude of our system. PP-3 and GP-3 algorithms have a similar performance, and they provide a better accuracy than the PP-5 algorithm.

As previously shown in [15], our system can also be mounted on a UAV vehicle with a similar baseline to the hand-held experiment. This experiment aimed to demonstrate the feasibility of a UAV positioning application as shown in Fig. 16.

8 Conclusion

This paper proposes different approaches to estimate the altitude and attitude of a mobile system equipped with a circular laser and a camera. We propose a geometric formulation and three robust methods for estimating the pose from 5 or 3 points. The results of the synthetic and real experiments show that the two 3-point approaches are the most robust because they use additional constraints for solving the problem. A new calibration approach, based on a bundle adjustment with one parameter per point, is also proposed to estimate the relative pose between the camera and the laser. As future work, we could study if the projection of the cone axis on the ground plane brings additional constraints since this point is visible on the images, or even what would be the advantage of using several concentric circles instead of a single one. The addition of geometric constraints could provide a better accuracy as demonstrated in [24].

A Proofs

1.1 A.1 Eigenvalues of a Plane-Pair Quadric

We prove here the statement made in Sect. 2.2 that a quadric representing a pair of planes has two zero eigenvalues and two nonzero eigenvalues of opposite sign. Let the quadric be given as in Sect. 2.2, i.e.,

$$\begin{aligned} \mathbf {Q} = \mathbf {V} \mathbf {U}^T + \mathbf {U} \mathbf {V}^T. \end{aligned}$$

Its eigenvalues can be easily computed to be

$$\begin{aligned} 0, 0, \mathbf {U}^T \mathbf {V} \pm \sqrt{\sum _{i=1}^4 \sum _{j=1}^4 U_i^2 V_j^2}. \end{aligned}$$

We need to show that the nonzero eigenvalues have opposite sign. This is exactly the case if

$$\begin{aligned} \sqrt{\sum _{i=1}^4 \sum _{j=1}^4 U_i^2 V_j^2} > \mathbf {U}^T \mathbf {V} \end{aligned}$$

or, if

$$\begin{aligned} \sum _{i=1}^4 \sum _{j=1}^4 U_i^2 V_j^2 > \left( \mathbf {U}^T \mathbf {V}\right) ^2. \end{aligned}$$

(66)

Let u and v be scalars such that $\bar{\mathbf {U}}=\mathbf {U}/u$ and $\bar{\mathbf {V}}=\mathbf {V}/v$ have unit norm. Equation (66) can then be written as

$$\begin{aligned} u^2 v^2 \sum _{i=1}^4 \sum _{j=1}^4 \bar{U}_i^2 \bar{V}_j^2 > u^2 v^2 \left( \bar{\mathbf {U}}^T \bar{\mathbf {V}}\right) ^2. \end{aligned}$$

This is true exactly if

$$\begin{aligned} \sum _{i=1}^4 \sum _{j=1}^4 \bar{U}_i^2 \bar{V}_j^2 > \left( \bar{\mathbf {U}}^T \bar{\mathbf {V}}\right) ^2. \end{aligned}$$

Since $\bar{\mathbf {U}}$ and $\bar{\mathbf {V}}$ have unit norm, the left-hand side is equal to 1 and the condition becomes

$$\begin{aligned} 1 > \left( \bar{\mathbf {U}}^T \bar{\mathbf {V}}\right) ^2. \end{aligned}$$

As for the right-hand side: The absolute value of the dot product of two unit vectors is always less or equal to 1. Equality occurs exactly if $\bar{\mathbf {U}} = \pm \bar{\mathbf {V}}$, which is the case exactly if the original (not normalized) plane coordinate vectors are equal up to scale: $\mathbf {U} \sim \mathbf {V}$.

Overall, this means that unless the two planes are identical, the quadric representing the plane-pair has nonzero eigenvalues of opposite sign, as stated. (If the planes are identical, the quadric is actually of rank 1 only and has three zero eigenvalues.)

1.2 A.2 Quadric Family Generated by Cones

We prove here the statements made in Sect. 4.1, concerning the degenerate members of a family of quadric generated by two cones $\mathbf {G}_1$ and $\mathbf {G}_2$:

$$\begin{aligned} \mathbf {Q} = \mathbf {G}_1 + x \mathbf {G}_2. \end{aligned}$$

(67)

In particular, we consider the case where the cones are known to intersect in a conic. Without loss of generality (supposing that the conic’s support plane is not the plane at infinity), let us suppose that this conic lies on the plane $Z=0$ and that in this plane it is represented by the symmetric $3\times 3$ matrix $\mathbf {M}$. Let the two cones be spanned by this conic and vertices

$$\begin{aligned} \mathbf {H}_i = \begin{bmatrix} X_i \\ Y_i \\ Z_i \\ 1 \end{bmatrix} \end{aligned}$$

for $i=1,2$ and with $Z_i \ne 0$.

The two cones are then given by

$$\begin{aligned} \mathbf {G}_i= & {} \begin{bmatrix} M_{11} Z_i^2&M_{12} Z_i^2&-g_i Z_i&M_{13} Z_i^2 \\ M_{21} Z_i^2&M_{22} Z_i^2&-h_i Z_i&M_{23} Z_i^2 \\ -g_i Z_i&-h_i Z_i&m_i&-k_i Z_i \\ M_{31} Z_i^2&M_{32} Z_i^2&-k_i Z_i&M_{33} Z_i^2 \end{bmatrix} \\ \text {with} \qquad g_i= & {} M_{11} X_i + M_{12} Y_i + M_{13} \\ h_i= & {} M_{21} X_i + M_{22} Y_i + M_{23} \\ k_i= & {} M_{31} X_i + M_{32} Y_i + M_{33} \\ m_i= & {} g_i X_i + h_i Y_i + k_i. \end{aligned}$$

That this represents these cones can be checked as follows. First, the intersection of these quadrics with the plane $Z=0$ is obtained by striking out the third row and third column of the matrices $\mathbf {G}_i$ (the row/column corresponding to the Z-coordinate). This gives the matrix

$$\begin{aligned} \begin{bmatrix} M_{11} Z_i^2&M_{12} Z_i^2&M_{13} Z_i^2 \\ M_{21} Z_i^2&M_{22} Z_i^2&M_{23} Z_i^2 \\ M_{31} Z_i^2&M_{32} Z_i^2&M_{33} Z_i^2 \end{bmatrix} \sim \mathbf {M} \end{aligned}$$

which is equal to the conic $\mathbf {M}$. Second, it is easy to check that $\mathbf {H}_i$ is a null vector of $\mathbf {G}_i$. Hence, $\mathbf {G}_i$ is indeed the cone spanned by the vertex $\mathbf {H}_i$ and the conic $\mathbf {M}$ in plane $Z=0$.

Let us now develop the determinant of $\mathbf {Q}$, defined in Eq. (67) as a member of the family generated by cones $\mathbf {G}_1$ and $\mathbf {G}_2$. Elementary computations give

$$\begin{aligned} \det (\mathbf {Q}) = W x (Z_2^2 x + Z_1^2)^2 \end{aligned}$$

where W does not depend on x, only on coefficients of $\mathbf {M}, \mathbf {H}_1$ and $\mathbf {H}_2$. Hence, $\det (\mathbf {Q}) = 0$ for $x=0$ and $x = -Z_1^2/Z_2^2$, the latter being a double root. The case $x=0$ corresponds to the cone $\mathbf {G}_1$, which is obviously a degenerate quadric. The second cone, $\mathbf {G}_2$, corresponds to a root $x \rightarrow \infty$.

Let us now study the double root $x = -Z_1^2/Z_2^2$ and the associated degenerate quadric

$$\begin{aligned} \mathbf {Q}= & {} \mathbf {G}_1 - \frac{Z_1^2}{Z_2^2} \mathbf {G}_2 \\= & {} \begin{bmatrix} 0&0&g_2 \frac{Z_1^2}{Z_2} - g_1 Z_1&0 \\ 0&0&h_2 \frac{Z_1^2}{Z_2} - h_1 Z_1&0 \\ g_2 \frac{Z_1^2}{Z_2} - g_1 Z_1&h_2 \frac{Z_1^2}{Z_2} - h_1 Z_1&m_1 - m_2 \frac{Z_1^2}{Z_2^2}&k_2 \frac{Z_1^2}{Z_2} - k_1 Z_1 \\ 0&0&k_2 \frac{Z_1^2}{Z_2} - k_1 Z_1&0 \end{bmatrix}. \end{aligned}$$

This matrix is of rank 2 at most and thus represents a plane-pair quadric. From Sect. 2.2, we deduce that the two planes represented by $\mathbf {Q}$ are

$$\begin{aligned}&\mathbf {U} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \\&\quad \mathbf {V} = \begin{bmatrix} g_2 \frac{Z_1^2}{Z_2} - g_1 Z_1 \\ h_2 \frac{Z_1^2}{Z_2} - h_1 Z_1 \\ \frac{m_1 - m_2 \frac{Z_1^2}{Z_2^2}}{2} \\ k_2 \frac{Z_1^2}{Z_2} - k_1 Z_1 \end{bmatrix} \sim \begin{bmatrix} Z_1 Z_2 (g_2 Z_1 - g_1 Z_2) \\ Z_1 Z_2 (h_2 Z_1 - h_1 Z_2) \\ \frac{m_1 Z_2^2 - m_2 Z_1^2}{2} \\ Z_1 Z_2 (k_2 Z_1 - k_1 Z_2) \end{bmatrix} \end{aligned}$$

with $g_i, h_i, k_i, m_i$ defined as above. The first one is the plane $Z=0$, as expected (the support plane of the conic known to be contained in both cones). The second plane also carries a conic in which the two cones intersect (see also Fig. 2 for an illustration). Its location depends on the cones; it is of no particular interest in this paper.

We prove now one additional property of our scenario. Namely that for one of the two planes, the cone’s vertices lie both on the same side of the plane, whereas they lie on opposite sides of the other plane. This property is useful in finding a unique solution to pose estimation in this paper. To prove this, one should study the signs of the dot products of the planes with the cone’s vertices (two points are on the same side of a plane, if the respective dot products have the same sign). In particular, it can be shown by elementary computations (details omitted) that

$$\begin{aligned} \left( \mathbf {H}^T_1 \mathbf {U} \right) \left( \mathbf {H}^T_2 \mathbf {U} \right) \left( \mathbf {H}^T_1 \mathbf {V} \right) \left( \mathbf {H}^T_2 \mathbf {V} \right) < 0. \end{aligned}$$

This implies that one of the two planes “splits” the two vertices, whereas for the other one, they lie on the same side of it (this can be easily proved by contradiction).