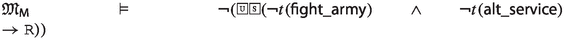Abstract
Centered around the analysis of the prescriptive portion of the Vedas, the Sanskrit philosophical school of Mīmāṃsā provides a treasure trove of normative investigations. We focus on the leading Mīmāṃsā authors Prabhākara, Kumārila and Maṇḍana, and discuss three modal logics that formalize their deontic theories. In the first part of this paper, we use logic to analyze, compare and clarify the various solutions to the śyena controversy, a two-thousand-year-old problem arising from seemingly conflicting commands in the Vedas. In the second part, the formalized Mīmāṃsā theories are analyzed and employed to provide alternative perspectives on well-known paradoxes from the contemporary field of deontic logic. Thus, we go from logic to Mīmāṃsā and back again.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Deontic logic is the branch of logic dealing with obligations and related notions. Since the introduction of standard deontic logic (SDL) by von Wright (1951) in the 1950s, an incredible amount of different systems have been proposed and there is no consensus on the “best” deontic logic formalisms, see, e.g., Benzmüller et al. (2018). By contrast, Mīmāṃsā –one of the most important schools of Indian philosophy– was active and influential for over two millennia, shaping the field of deontics and, through it, many related areas in the Sanskrit cosmopolis. It focuses on the exegesis and systematization of the commands found in the Vedas, the sacred texts of what is now called Hinduism, considered by Mīmāṃsā to be without any human or divine author. Consequently, Mīmāṃsā authors invested much intellectual effort in rationally interpreting Vedic commands and explaining “what has to be done” in presence of seeminglyFootnote 1 conflicting commands. For this purpose, they developed metarules (nyāya in Sanskrit), which are so systematic that they have been applied in many other fields, and are still used in Indian jurisprudence.
Mīmāṃsā doctrines have influenced Sanskrit philosophy, theology and law more than any other system of thought.Footnote 2 However, despite their undeniable importance, most of their specificities have remained unexplored or misunderstood. The use of symbolic logic enables a deeper understanding of the source texts. Moreover, given that the nyāyas are generally not clearly outlined but just implemented by Mīmāṃsā authors, a rigorous mathematical formalization greatly enhances the understanding of their purpose and scope.
Like all other Sanskrit schools, Mīmāṃsā does not use logic formulae. Nonetheless, their method lends itself to a formalization, insofar as it is based on the nyāya-metarules and on the general acceptance of the rules of valid inferences. However, as most of the Mīmāṃsā texts are still untranslated, they are accessible only through teaming up with Sanskritists. As will become evident in this article, the results of our interdisciplinary collaboration can benefit the various involved fields.
In this paper, we formalize the deontic theories of the three main Mīmāṃsā authors: Prabhākara, Kumārila (both ca. 7th c. CE) and Maṇḍana (ca. 8th c. CE) giving rise to different interpretations of Vedic commands, and provide three distinct modal logics \({\mathsf {LPr^{+}}}\), \({\mathsf {LKu^{+}}}\) and \({\mathsf {LMa^{-}}}\). Prabhākara’s and Kumārila’s logic are non-normal modal logics that take deontic operators as primitive notions (\({\mathsf {LKu^{+}}}\) has an additional operator in the language), while Maṇḍana’s logic is an action logic reducing deontic concepts to notions of instrumentality.
Since the faithfulness to the philosophical ideas of the authors is crucial for our enterprise, \({\mathsf {LPr^{+}}}\), \({\mathsf {LKu^{+}}}\) and \({\mathsf {LMa^{-}}}\) are defined by “extracting” Hilbert axioms from translated and parsed Mīmāṃsā nyāyas and further textual passages by the three authors; special care is taken not to impose any external property and assumption. The introduced logics are used here to compare the deontic theories of Prabhākara, Kumārila and Maṇḍana, and their different solution to the controversial sentences in the Vedas about śyena, a key debate which remains surprisingly understudied in contemporary literature about Sanskrit philosophy (a notable exception is the recent paper by Guhe (Guhe 2021)). The śyena is a ritual in which the Soma beverage is offered. Its putative result is the death of the sacrificer’s enemy. The controversy is due to the fact that the śyena appears to be prescribed in the Vedas (through the command “The one who desires to kill their enemy should sacrifice bewitching with the śyena”), that also prohibits to harm (“One should not harm any living being”). The śyena controversy can be seen as a millennia-old counterpart of deontic dilemmas (so-called paradoxes), which are used to drive developments in modern deontic logic.
To analyze the behaviour of our Mīmāṃsā logics, we use as benchmarks some of the standard paradoxes from the deontic logic literature (see, e.g., Carmo and Jones (2002)): Chisholm (Chisholm 1963), Gentle Murder (Forrester 1984), Considerate Assassin (Prakken and Sergot 1996), Ross (Ross 1944), Good Samaritan (Prior 1958), and Alternative Service (Horty 1994). Prabhākara’s logic \({\mathsf {LPr^{+}}}\) and Kumārila’s logic \({\mathsf {LKu^{+}}}\) solve most of these paradoxes, while Maṇḍana’s logic \({\mathsf {LMa^{-}}}\) solves all of them, when formalizing the sentences in the spirit of the Mīmāṃsā authors. The solution strategy of our logics resembles the two best known strategies in modern deontic logics: weakening the logic (\({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\)) or adopting a logic of actions (\({\mathsf {LMa^{-}}}\)). These encouraging results may be due to the depth of the deontic theories of Prabhākara, Kumārila and Maṇḍana behind them. Our logics come indeed with millenary full-fledged philosophical and juridical motivation.
The paper is organized as follows: The next section presents a gentle introduction to Mīmāṃsā. Section 3 describes the deontic theories of Prabhākara, Kumārila and Maṇḍana, and their corresponding logics. Section 4 puts the introduced logics to work, by formalizing the three different solutions of the śyena controversy, and discusses (Sect. 4.3) other solutions to the controversy from further Sanskrit philosophers or schools. Section 5 evaluates the introduced logics on a set of deontic benchmark paradoxes. The last section offers concluding remarks.
This paper is an extension of the work presented in van Berkel et al. (2021). The logics for Prabhākara, Kumārila and Maṇḍana are refined and extended here with a recently identified nyāya which leads to a form of restricted aggregation. Moreover, the analysis of the introduced logics using benchmark paradoxes (i.e., the “back”direction) is new, as well as the discussion of further solutions to the śyena controversy in Sanskrit philosophy.
2 Mīmāṃsā in a Nutshell
Mīmāṃsā is one of the main schools of Sanskrit philosophy, and the only one focusing on the analysis of norms. Thriving for over two millennia, from the last centuries BCE to the 20th c., Mīmāṃsā focuses on the exegesis of the prescriptive portions of the Vedic sacred texts.
Mīmāṃsā authors devised a system of rules called nyāyas, meant to be applicable to any deontic text. The nyāyas are used to understand the Vedas independentlyFootnote 3 of any (super)human authority or mediation. Mīmāṃsā authors agree that the Veda is a consistent corpus of rules, and that what might look like a conflict can be explained away by applying the correct nyāyas.
Different Mīmāṃsā authors adopt different views, and interpret the Vedic commands in different ways, still they all recognise the authority of Jaimini’s Mīmāṃsā Sūtra (or Pūrva Mīmāṃsā Sūtra, henceforth PMS, approximately 250 BCE) and Śabara’s Bhāsya ‘commentary’ thereon (henceforth ŚBh, approx. 5th c. CE), which we will refer to as “common Mīmāṃsā”.Footnote 4 Of particular importance are the following authors, who originated different orientations within the school:
-
Kumārila (7 CE?); considered to be the founder of the Bhāṭṭa subschool.
-
Prabhākara (7 CE?); a younger contemporary of Kumārila, considered to be the founder of the Prābhākara subschool.
-
Maṇḍana (8 CE); authored independent treatises on various issues (especially on the nature of prescriptions) and innovated the Bhāṭṭa school.
Common Mīmāṃsā classifies the commands encountered in the Vedas into prescriptions and prohibitions. Prescriptions are distinguished on the basis of the duty they enjoin: nitya-karman ‘fixed sacrifices’, to be performed every single day; naimittika-karman ‘occasional sacrifices’, to be performed only on given occasions, e.g., the sacrifice to be performed on the birth of a son; kāmya-karman ‘elective sacrifices’, to be performed only if one wishes to obtain their result. These duties may have varying deontic strength: one cannot omit the performance of fixed and occasional sacrifices (various authors provide different reasons for this), whereas the performance of elective sacrifices can be omitted without any adverse consequence, apart from not getting the intended result. Furthermore, prescriptions are understood in relation to eligibility conditions (adhikāra). These include one’s belonging to a certain class of living beings, one’s being able to perform the prescribed action, and also one’s desire for the action’s result.
Prohibitions form their own category and Mīmāṃsā authors distinguish between prohibitions ‘regarding the person’ (puruṣārtha), i.e., applying to the person throughout their life, and those ‘regarding the sacrifice’ (kratvartha), i.e., applying only to the specific situation of the sacrifice. An easy parallel would be represented by the command ‘don’t kill’ (which applies to one’s entire life) and ‘don’t dress informally’ (which applies only in certain settings). Furthermore, obeying an obligation gives positive results (if no desire is expressed, a standard desire for happiness is postulated), and violating it implies the absence of these results. Accordingly, prescriptions presuppose one’s desire for the output of the prescribed action. Conversely, the observance of a prohibition gives no result and the violation of it leads to a sanction, typically the accumulation of bad karma. Consequently, prohibitions cannot be defined in terms of obligations (i.e., as a negative obligation) because the observance and transgression of these two types of commands have different consequences. The difference between negative obligations and prohibitions is amply discussed by Mīmāṃsā authors, who state that prohibitions, if observed, only lead to the absence of a sanction. By contrast, negative obligations, if fulfilled, lead to results. For instance, suppose that there are two simultaneous commands, namely, a prohibition to lie and a negative obligation not to tell lies. The effect of both may seem the same, but in the case of the negative obligation an additional mental act (mānasakarman) is involved, namely the resolve not to lie. And this mental act is what leads to a result.
3 Mīmāṃsā Deontic Logics
The Mīmāṃsā school provides a treasure trove of normative investigations. Logic is an adequate tool for accessing such treasures. Its use is justified by the rigorousness of Mīmāṃsā’s theory of inference and the attention paid to possible violations of it. For instance, Kumārila emphasises the fact that a text is not epistemically reliable if the whole chain of transmission is reliable but not its beginning, comparing it to “a chain of truthful blind people transmitting information concerning colours” (Tantravārttika on PMS 1.3.27). Also noteworthy in this connection is the Mīmāṃsā focus on general rules (nyāyas) which must be applied independently of the interpreter (see Sect. 2).
Thus, the main question is, which logic(s) should be used to formalize Mīmāṃsā reasoning? Since we do not want to impose ready-made reasoning principles, and aim instead at faithfully reproducing the reasoning of Mīmāṃsā, we extract the principles on which the logics are based directly from Mīmāṃsā texts. No Sanskrit philosophical school used mathematical formalization, which implies that a certain degree of abstraction is needed. The Mīmāṃsā school makes this task easier because of its insistence on using general rules of reasoning (nyāyas). As a consequence, we can build our logics solely on principles explicitly discussed or applied in Mīmāṃsā texts.
From a methodological point of view, this implies patient team work, since those rules and principles first need to be identified in source texts that are in general not translated from Sanskrit into English and only then can they be interpreted and analyzed. Furthermore, Mīmāṃsā authors do not discuss nyāyas explicitly in any introductory chapter, and these have rather to be carefully distilled from their concrete applications within Mīmāṃsā texts. Sanskrit philosophical texts usually take the form of a staged discussion among the upholders of different points of view (vaguely resembling a Platonic dialogue). Hence, nyāyas are typically found within a discussion among several authors who invoke different rules to solve a given problem. At this point, one needs to translate them and isolate the key reasoning behind them, which is often hidden behind a vivid phrase, such as “The prescription takes care of its fulfilment, like a master of their servants”. As an example, from the literal translation of the nyāya adhikaṃ vānyārthatvāt (see PMS 10.4.14) “Alternatively, [the new cloth to be used in the mahāvrata ritual] is additional, because it has a different purpose” we extracted a restricted version of aggregation stating that aggregation is only possible when the two commands in question serve different purposes (principle P4 in Sect. 3.1).
Prabhākara, Kumārila and Maṇḍana provide different interpretations of their common Mīmāṃsā inheritance. Hence three distinct logics are needed to formalise their thought. A first step to transform Mīmāṃsā reasoning into a logic was taken in Ciabattoni et al. (2015) with the introduction of “basic Mīmāṃsā Deontic Logic” (\(\textsf{bMDL}\)). Although entirely based on Mīmāṃsā principles, the necessity-free fragment of this logic is in fact identical to the dyadic version of the non-normal deontic logic MD Chellas (1980) (see Freschi et al. (2019) and Lellmann et al. (2021)). The logic \(\textsf{bMDL}\) captures the concept of obligation in common Mīmāṃsā –encompassing both fixed and occasional duties– but adopted obligation as its only deontic operator. The logics formalizing the deontic theories of Prabhākara and Kumārila, called \(\textsf{LPr}\) and \(\textsf{LKu}\) respectively, were introduced in van Berkel et al. (2021) (see also Lellmann et al. (2021)). The two logics adopt (a variant of) \(\textsf{bMDL}\) as their core, and extend it with a prohibition operator and, in case of Kumārila, also with an operator for elective duties. In the sections below, we refine and extend these logics with an additional property recently identified in Mīmāṃsā texts. The property captures the aforementioned restricted form of aggregation. We name the resulting logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\), respectively.
Maṇḍana’s deontic theory is completely different from those of the previous two authors and, consequently, so is the logic formalizing it. Maṇḍana proposed a unifying theory for normative reasoning that reduces all command types to instrumentality statements about actions leading to results. We call it Maṇḍana’s deontic reduction. A first version of Maṇḍana’s logic was introduced in van Berkel et al. (2021) under the name \(\textsf{LMa}\). In Sect. 3.3, we refine this logic and its deontic reduction. We call the resulting logic \({\mathsf {LMa^{-}}}\). The newly acquired aggregation property, which led to an extension of the logics for Prabhākara and Kumārila, is addressed through formally defining instrumentality in \({\mathsf {LMa^{-}}}\).
Remark 1
The three logics discussed below are developed for reasoning about commands as interpreted by Mīmāṃsā authors. Mīmāṃsā authors consider Vedic commands to be self-contained and immutable, which means that they cannot be modified or updated. Hence, no new Vedic commands can be derived through logic. Accordingly, our logics deal with commands on the derived level.
3.1 The Logic of Prabhākara
Prabhākara’s system is eminently deontic: agents follow commands because they are enjoined, and they recognise that they have been enjoined because the Vedic command identifies them through their desires. For instance, “if one desires rain, one should sacrifice with the Kārīri” identifies the one who desires rain as the enjoined person upon whom the duty to sacrifice with the Kārīri becomes incumbent. For Prabhākara, unlike in common Mīmāṃsā, the desires for specific worldly results represent only the eligibility conditions (adhikāra) for performing elective rituals (rituals which other Mīmāṃsā authors consider as not strictly speaking obligatory). The distinction between sacrifices classified as elective and fixed/occasional depends on the eligibility conditions and not on a difference in deontic strength. In Prabhākara’s theory, once the eligibility conditions are met, the sacrifice must be performed. Hence for Prabhākara the two types of obligations –namely, fixed/occasional and elective– can be represented by a single deontic operator: \(\mathcal {O}(\varphi /\psi )\), to be read as “\(\varphi \) is obligatory under the condition \(\psi \)”. In case of fixed duties, the condition \(\psi \) can be taken to represent the mere fact of being alive, denoted with \(\top \). In case of occasional and elective duties, \(\psi \) contains only states of affairs, respectively desires.
The logic \({\mathsf {LPr^{+}}}\) for Prabhākara is obtained in a modular way by extending a base logic with a necessity modality  and two dyadic deontic operators \(\mathcal {O}(./.)\) and \(\mathcal {F}(./.)\) for obligation and prohibition, respectively. We use as the base logic classical propositional logic. Indeed, when it comes to deontic logic reasoning the two main alternatives as underlying system are classical and intuitionistic logic. The use of classical logic (instead of intuitionistic logic as employed, e.g., in Abraham et al. (2011)) is motivated by various examples found in Mīmāṃsā texts which implicitly assume the legitimacy of excluded middle and reductio ad absurdum. For instance, consider the nyāya (contained in Jayanta’s book Nyāyamañjarī, see Ciabattoni et al. (2015)): “When there is a contradiction, at the denial of one [alternative], the other is known [to be true]”.
and two dyadic deontic operators \(\mathcal {O}(./.)\) and \(\mathcal {F}(./.)\) for obligation and prohibition, respectively. We use as the base logic classical propositional logic. Indeed, when it comes to deontic logic reasoning the two main alternatives as underlying system are classical and intuitionistic logic. The use of classical logic (instead of intuitionistic logic as employed, e.g., in Abraham et al. (2011)) is motivated by various examples found in Mīmāṃsā texts which implicitly assume the legitimacy of excluded middle and reductio ad absurdum. For instance, consider the nyāya (contained in Jayanta’s book Nyāyamañjarī, see Ciabattoni et al. (2015)): “When there is a contradiction, at the denial of one [alternative], the other is known [to be true]”.
Technically, Prabhākara’s logic \({\mathsf {LPr^{+}}}\) extends \(\textsf{bMDL}\) in Ciabattoni et al. (2015) with (i) an explicit operator \(\mathcal {F}(\cdot /\cdot )\) for prohibitions, (ii) an additional property for the obligation operator \(\mathcal {O}(./.)\), and following van Berkel et al. (2021), (iii) an \(\textsf{S5}\) characterization of necessity (instead of \(\textsf{S4}\) as in \(\textsf{bMDL}\)). Concerning (i), as discussed in Sect. 2, prohibitions in Mīmāṃsā cannot be written in terms of negative obligations and must therefore be taken as primitive. Concerning (ii), we have extended van Berkel et al. (2021) with a property corresponding to nyāyas expressing the accumulation of fixed obligations that are not in conflict. Concerning (iii), although Mīmāṃsā authors (and Sanskrit philosophers in general) appeal to notions of possibility and necessity, they do not explicitly define them. The necessity operator is used in our logics to better formalize the deontic operators. In Ciabattoni et al. (2015), we employed \(\textsf{S4}\) for necessity due to its simpler proof theory (compared to \(\textsf{S5}\)). Following van Berkel et al. (2021), here we use necessary statements as global assumptions, i.e., assertions commonly recognised as describing facts which holds in all possible situations, thus motivating the use of  as an \(\textsf{S5}\) modality.
as an \(\textsf{S5}\) modality.
Axiomatization
The language \({\mathcal {L}_{\textsf{P}}}\) for Prabhākara’s logic is defined via the following BNF grammer:

with \(p\in \textsf{Atom}\). We take \(\textsf{Atom}\) as the set of atomic propositions, \(\lnot \) and \(\vee \) are primitive connectives, and we define the other connectives as usual. Furthermore, \(\top \) is an abbreviation for \(p\vee \lnot p\) and we define \(\bot \) as its dual. The modality  reads “it is universally necessary that \(\varphi \)” and its dual
reads “it is universally necessary that \(\varphi \)” and its dual  is defined as usual. The operators \(\mathcal {O}(\varphi /\psi )\) and \(\mathcal {F}(\varphi /\psi )\), read as “\(\varphi \) is obligatory/forbidden, given \(\psi \)”.
is defined as usual. The operators \(\mathcal {O}(\varphi /\psi )\) and \(\mathcal {F}(\varphi /\psi )\), read as “\(\varphi \) is obligatory/forbidden, given \(\psi \)”.
Although in common Mīmāṃsā the content of a command is always an action and the eligibility conditions are often state of affairs, the logics developed for Prabhākara and Kumārila do not employ an explicit language of actions (this contrasts with Maṇḍana’s logic which will be introduced in Sect. 3.3). The reason is that for the former two authors the logical features of action do not play a distinctive role in characterizing commands. Consequently, the two resulting logics allow us to speak about state of affairs only. To illustrate, we do not take an atomic proposition \(\texttt {harm}\) to refer to the general action of ‘harming’, but instead we interpret it as a state of affairs that is a witness of the fact that “harm has been done”. As a consequence, the negated \(\lnot \texttt {harm}\) expresses that “it is not the case that harm has been done”.
The properties of the deontic operators are extracted from Mīmāṃsā texts and transformed into the axioms in Definition 1. The correspondence between axioms and nyāyas is summarized below, see also Ciabattoni et al. (2015); Freschi et al. (2017); Lellmann et al. (2021); van Berkel et al. (2021) for a discussion.
Definition 1
Prabhākara’s logic \({\mathsf {LPr^{+}}}\) extends the logic \(\textsf{S5}\) for  with:
with:
- \(\textsf{A}_{\textsf{P}}1\):
-
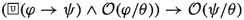
- \(\textsf{A}_{\textsf{P}}2\):
-
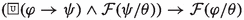
- \(\textsf{A}_{\textsf{P}}3\):
-
\(\lnot ( \mathcal {X}(\varphi /\theta ) \wedge \mathcal {X}(\lnot \varphi /\theta ))\) for \(\mathcal {X}\in \{\mathcal {O,F}\}\)
- \(\textsf{A}_{\textsf{P}}4\):
-
\(\lnot ( \mathcal {O}(\varphi /\theta )\wedge \mathcal {F}(\varphi /\theta ))\)
- \(\textsf{A}_{\textsf{P}}5\):
-
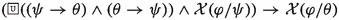 for \(\mathcal {X}\in \{\mathcal {O,F}\}\)
for \(\mathcal {X}\in \{\mathcal {O,F}\}\) - \(\textsf{A}_{\textsf{P}}6\):
-
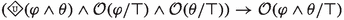
A derivation of \(\varphi \in {\mathcal {L}_{\textsf{P}}}\) in \({\mathsf {LPr^{+}}}\) from a set \(\Sigma \subseteq {\mathcal {L}_{\textsf{P}}}\) (written \(\Sigma \vdash _{{\mathsf {LPr^{+}}}}\varphi \)) is defined as usual Blackburn et al. (2004). If \(\Sigma =\emptyset \), we say that \(\varphi \) is an \({\mathsf {LPr^{+}}}\)-theorem.
Remark 2
\({\mathsf {LPr^{+}}}\) extends \(\textsf{LPr}\) in van Berkel et al. (2021) with (\(\textsf{A}_{\textsf{P}}6\)). In Definition 1 we use alternative axioms (\(\textsf{A}_{\textsf{P}}3\)) and (\(\textsf{A}_{\textsf{P}}4\)), which are \({\mathsf {LPr^{+}}}\)-equivalent to those in van Berkel et al. (2021).Footnote 5
The above axioms of Prabhākara’s logic are based on variations of the following (translated and generalized) Mīmāṃsā principles in van Berkel et al. (2021):
- (P1):
-
If the accomplishment of an action presupposes the accomplishment of another connected but different action, the obligation to perform the first action prescribes also the second one. Conversely, if an action necessarily implies a prohibited action, it will also be prohibited.
- (P2):
-
Two actions that exclude each other can neither be prescribed nor prohibited simultaneously to the same group of eligible people under the same conditions.
- (P3):
-
If two sets of conditions always identify the same group of eligible agents, then a command valid under the conditions in one of those sets is also enforceable under the conditions in the other set.
To the above, we add a principle only recently identified:
- (P4):
-
If two fixed duties are prescribed and compatible, their conjunction is obligatory as well.
Principle (P1), on which axioms (\(\textsf{A}_{\textsf{P}}1\)) and (\(\textsf{A}_{\textsf{P}}2\)) are based, constitutes the abstraction and reformulation of various nyāyas; among them, a nyāya present in the Tantrarahasya (IV.4.3.3) composed by the Mīmāṃsā author Rāmānujācārya (possibly 15th c. CE).Footnote 6 Formally, the principle corresponds to the properties of upwards monotonicity in the first argument of the dyadic operator for obligations, i.e., \(\mathcal {O}(\varphi \wedge \psi /\theta )\rightarrow \mathcal {O}(\varphi /\theta )\), and of downwards monotonicity in the first argument of the prohibition operator, i.e., \(\mathcal {F}(\varphi \vee \psi /\theta )\rightarrow \mathcal {F}(\varphi /\theta )\)). This implies that if an obligatory act consists of sub-actions, these constitutive actions are obligatory as well (e.g., \(\varphi \wedge \psi \) presupposes the accomplishment of both \(\varphi \) and \(\psi \)). Conversely, if an action is forbidden, all the composed rituals which include that action are forbidden too. For instance, given a prohibition to cross the ocean, working in a place across the ocean would also be prohibited since it would necessarily imply crossing the ocean first. Since the involvement of sub-actions and -rituals is an intrinsic property of ritual acts, monotonicity in the first argument is a natural property of deontic operators in Mīmāṃsā logics (we come back to this when we deal with Maṇḍana’s deontic theory).
Principle (P2) is the base for axioms (\(\textsf{A}_{\textsf{P}}3\)) and (\(\textsf{A}_{\textsf{P}}4\)) and constitutes the abstract formulation of the so-called principle of the half-hen, which is for instance applied in Kumārila’s Tantravārtika ad 1.3.3, see Śubbaśāstrī 1934 (also see Freschi et al. (2017)). In its general form, this principle says that the collection of all Vedic commands is consistent, i.e., the performance (non-performance) of an action which is obligatory (forbidden) according to the Vedas, cannot lead to violating another Vedic command. Note that (\(\textsf{A}_{\textsf{P}}3\)) and (\(\textsf{A}_{\textsf{P}}4\)) represent a variation of the \(\textsf{D}\)-axiom for obligations and prohibitions as found in deontic logic, since they guarantee that if some action is obligatory (forbidden), then neither is that action prohibited (obligatory) nor is its opposite obligatory (forbidden).
Moreover, principle (P2) means that prohibitions cannot forbid what is logically impossible and is based on the metarule according to which nothing impossible can be commanded (see Āpadeva’s Mīmāṃsānyāyaprakāśa 171, Edgerton (1929)). As pointed out above, one must think of conflicting commands such as \(\mathcal {F}(\varphi /\theta )\) and \(\mathcal {F}(\lnot \varphi /\theta )\) not as involving actions, but as prohibiting two logically incompatible states of affairs. That is, their contents exhaust the complete sphere of possibilities: ‘one may neither be in a state where \(\varphi \) has been performed nor in any other state’.
Principle (P3), arising from a discussion on the eligibility to perform sacrifices (in ŚBh on PMS 6.1.25), is formalized by axiom (\(\textsf{A}_{\textsf{P}}5\)) and expresses the generality of prescriptions with respect to logically equivalent conditions (see Freschi et al. (2017)). This principle represents a natural property of conditions: its absence would make a formalised prescription dependent upon the particular form of a formulae, e.g., \(\mathcal {O}(\varphi /\psi )\) would not be equivalent to \(\mathcal {O}(\varphi /\psi \wedge \psi )\). Note that principle (P3) is weaker than (downwards) monotonicity in the second argument of a deontic operator. It implies that if a ritual is obligatory for all bachelors, then it is obligatory for all unmarried men, but it does not imply that the ritual is obligatory for all unmarried blonde men.
The new principle (P4), on which axiom (\(\textsf{A}_{\textsf{P}}6\)) is based, corresponds to a restricted form of the logical property known as aggregation. In common Mīmāṃsā, cases of different fixed obligations to be performed in the same context are handled as follows: 1. If the two actions are compatible and are functional towards different intermediate results, (e.g., brush your teeth and floss them, achieving different intermediate results even though both having the overall purpose of having healthy teeth), one performs them both (this is called ‘accumulation’, samuccaya in Sanskrit). 2. Otherwise, only one of the two will be performed, chosen according to various criteria (with as a last resort vikalpa, the act of choosing randomly). Hence, samuccaya is a restricted form of aggregation (see Parent and van der Torre (2018) for a discussion on aggregation and restricted forms). The samuccaya principle does not apply to elective sacrifices because even if the two were compatible, they would have the same purpose and, therefore, it is enough to only perform one of the two.Footnote 7 Since samuccaya is defined in relation to prescriptions and their results, it does not apply to prohibitions.
Lemma 1
The following formulas are derivable in \({\mathsf {LPr^{+}}}\):
-
1
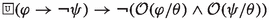
-
2
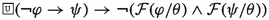
-
3
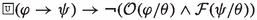
Proof
1. Follows by (\(\textsf{A}_{\textsf{P}}3\)) for \(\mathcal {O}(\cdot /\cdot )\) and (\(\textsf{A}_{\textsf{P}}1\)). 2. Follows by (\(\textsf{A}_{\textsf{P}}3\)) for \(\mathcal {F}(\cdot /\cdot )\) and (\(\textsf{A}_{\textsf{P}}2\)), and 3. follows by (\(\textsf{A}_{\textsf{P}}4\)), (\(\textsf{A}_{\textsf{P}}1\)) and (\(\textsf{A}_{\textsf{P}}2\)). \(\square \)
Semantics
The semantic characterization of \({\mathsf {LPr^{+}}}\) is similar to that of \(\textsf{bMDL}\) in Ciabattoni et al. (2015). The universal necessity operator  represents the idea that any world is accessible from all the worlds in the model. The modality captures global necessity of truths and is evaluated as usual, see Blackburn et al. (2004) (in this sense, the entire set of worlds can be seen as an equivalence class). The additional modalities are captured using neighbourhood semantics (Chellas (1980)). Intuitively, the neighbourhood function for obligations identifies, for a set of worlds defined by some eligibility condition, a set of “deontically best” sets of worlds. In terms of logical formulae, this means that, if a pair (X, Y) of sets of worlds is in world w’s obligation-neighbourhood, at w it is true that the worlds in X represent worlds of compliance “from the point of view of” the ones in Y. This is the case because w is in the truth set of a formula \(\mathcal {O}(\varphi /\psi )\) such that X is a subset of the truth set of \(\varphi \) and Y corresponds to the truth set of \(\psi \). Symmetrically, if (X, Y) is in w’s prohibition-neighbourhood, it means that at w it is true that, “from the point of view of” the worlds in Y (where the conditions of the prohibition are verified) the worlds belonging to X are worlds of violation, as X contains worlds where a forbidden act has been carried out.
represents the idea that any world is accessible from all the worlds in the model. The modality captures global necessity of truths and is evaluated as usual, see Blackburn et al. (2004) (in this sense, the entire set of worlds can be seen as an equivalence class). The additional modalities are captured using neighbourhood semantics (Chellas (1980)). Intuitively, the neighbourhood function for obligations identifies, for a set of worlds defined by some eligibility condition, a set of “deontically best” sets of worlds. In terms of logical formulae, this means that, if a pair (X, Y) of sets of worlds is in world w’s obligation-neighbourhood, at w it is true that the worlds in X represent worlds of compliance “from the point of view of” the ones in Y. This is the case because w is in the truth set of a formula \(\mathcal {O}(\varphi /\psi )\) such that X is a subset of the truth set of \(\varphi \) and Y corresponds to the truth set of \(\psi \). Symmetrically, if (X, Y) is in w’s prohibition-neighbourhood, it means that at w it is true that, “from the point of view of” the worlds in Y (where the conditions of the prohibition are verified) the worlds belonging to X are worlds of violation, as X contains worlds where a forbidden act has been carried out.
Definition 2
An \({\mathsf {LPr^{+}}}\)-frame \({\mathfrak {F}_{\textsf{P}}}=\langle W, \mathcal {N}_{\mathcal {O}}, \mathcal {N}_{\mathcal {F}} \rangle \) is a tuple where \(W\ne \emptyset \) is a set of worlds \(w,v,u,\ldots \), and \(\mathcal {N}_{\mathcal {X}}: W \mapsto \mathcal {P}{(\mathcal {P}{(W)}\times \mathcal {P}{(W)})}\) is a neighbourhood function for \(\mathcal {X}\in \{\mathcal {O},\mathcal {F}\}\). Let \(X,Y,Z\subseteq W\), \({\mathfrak {F}_{\textsf{P}}}\) satisfies the following:
-
i.
if \((X,Z) \in \mathcal {N}_{\mathcal {O}}(w)\) and \(X \subseteq Y \), then \((Y,Z) \in \mathcal {N}_{\mathcal {O}}(w)\);
-
ii.
if \((X,Z) \in \mathcal {N}_{\mathcal {F}}(w)\) and \(Y \subseteq X \), then \((Y,Z) \in \mathcal {N}_{\mathcal {F}}(w)\);
-
iii.
if \((X,Y) \in \mathcal {N}_{\mathcal {X}}(w)\), then \((\overline{X} ,Y) \notin \mathcal {N}_{\mathcal {X}}(w)\) for \(\mathcal {X}\in \{\mathcal {O,F}\}\);
-
iv.
if \((X,Z) \in \mathcal {N}_{\mathcal {O}}(w)\) then \((X,Z) \not \in \mathcal {N}_{\mathcal {F}}(w)\).
-
v.
if \(X\bigcap Y \ne \emptyset \) and \((X,W), (Y, W) \in \mathcal {N}_{\mathcal {O}}(w)\), then \((X\bigcap Y,W) \in \mathcal {N}_{\mathcal {O}}(w)\)
An \({\mathsf {LPr^{+}}}\)-model is a tuple \({\mathfrak {M}_{\textsf{P}}}=\langle {\mathfrak {F}_{\textsf{P}}},V\rangle \) where \({\mathfrak {F}_{\textsf{P}}}\) is an \({\mathsf {LPr^{+}}}\)-frame and V is a valuation function mapping atomic propositions from \(\textsf{Atom}\) to sets of worlds.
Note that properties (i) and (ii) correspond to axioms (\(\textsf{A}_{\textsf{P}}1\)) and (\(\textsf{A}_{\textsf{P}}2\)) (principle (P1)), expressing the property of monotonicity in the first argument of the deontic operators, (iii) and (iv) correspond to axioms (\(\textsf{A}_{\textsf{P}}3\)) and (\(\textsf{A}_{\textsf{P}}4\)) (principle (P2)), and (v) is the semantic equivalent of axiom (\(\textsf{A}_{\textsf{P}}6\)) (and principle (P4)). Axiom (\(\textsf{A}_{\textsf{P}}5\)) (principle (P3)) does not correspond to any additional condition on \({\mathfrak {F}_{\textsf{P}}}\)-frames but is a minimal property of neighborhood frames in general since equivalent formulae have identical sets of worlds satisfying them, i.e., if \((X,Z) \in \mathcal {N}_{\mathcal {X}}(w)\) (with \(\mathcal {X}\in \{\mathcal {O,F}\}\)) and \(Z= Y\), then \((X,Y) \in \mathcal {N}_{\mathcal {X}}(w)\), see Chellas (1980).
Definition 3
Consider the \({\mathsf {LPr^{+}}}\)-model \({\mathfrak {M}_{\textsf{P}}}\) and let \(\vert \!\vert \varphi \vert \!\vert \) be the truth set \(\{ w\in W\;\vert \; {\mathfrak {M}_{\textsf{P}}}, w\models \varphi \}\) of the formula \(\varphi \in {\mathcal {L}_{\textsf{P}}}\). We define the satisfaction of a formula \(\varphi \in {\mathcal {L}_{\textsf{P}}}\) at any w of \({\mathfrak {M}_{\textsf{P}}}\) as follows:
\({\mathfrak {M}_{\textsf{P}}}, w\vDash p\) iff \(w\in V (p)\), for \(p\in \textsf{Atom}\)
\({\mathfrak {M}_{\textsf{P}}}, w\vDash \lnot \varphi \) iff \({\mathfrak {M}_{\textsf{P}}}, w\nvDash \varphi \)
\({\mathfrak {M}_{\textsf{P}}}, w\vDash \varphi \vee \psi \) iff \({\mathfrak {M}_{\textsf{P}}}, w\vDash \varphi \) or \({\mathfrak {M}_{\textsf{P}}}, w\vDash \psi \)
 iff for all \(w_i\in W\), \({\mathfrak {M}_{\textsf{P}}}, w_i\vDash \varphi \)
iff for all \(w_i\in W\), \({\mathfrak {M}_{\textsf{P}}}, w_i\vDash \varphi \)
\({\mathfrak {M}_{\textsf{P}}}, w\vDash \mathcal {X}(\varphi /\psi )\) iff \((\vert \!\vert \varphi \vert \!\vert ,\vert \!\vert \psi \vert \!\vert ) \in \mathcal {N}_{\mathcal {X}}(w)\) for \(\mathcal {X} \in \{\mathcal {O},\mathcal {F}\}\)
Global truth and validity are defined as usual, see Blackburn et al. (2004).
Theorem 2
(Soundness and Completeness) A formula is a theorem of \({\mathsf {LPr^{+}}}\) if and only if it is valid on all \({\mathsf {LPr^{+}}}\)-models
Since \({\mathsf {LPr^{+}}}\) is a fragment of Kumārila’s logic \({\mathsf {LKu^{+}}}\), the theorem’s proof for the former is a straightforward adaptation of the proof for \({\mathsf {LKu^{+}}}\), which is presented in Appendix A.
3.2 The Logic of Kumārila
Kumārila’s deontic theory differs from the one of Prabhākara on the interpretation of those Vedic statements concerning elective sacrifices (kāmya-karman). Kumārila interprets the injunctions prescribing them as not properly binding, insofar as their performance can be omitted at no risk. Elective duties only give a guaranteed way to bring about a desired result. By contrast, fixed and occasional sacrifices can never be omitted. In fact, a rational agent can choose to ignore the specific results of elective rituals, but not the results of fixed and occasional ones, since the latter lead to happiness, an aspiration characterizing every human being. Hence, Kumārila’s logic \({\mathsf {LKu^{+}}}\) requires an additional operator for elective sacrifices.
Axiomatization
The language \({\mathcal {L}_{\textsf{K}}}\) for Kumārila’s logic \({\mathsf {LKu^{+}}}\) extends \({\mathcal {L}_{\textsf{P}}}\) with the additional operator \(\mathcal {E}(\varphi /\psi )\) to be read as “\(\varphi \) is enjoined by an injunction prescribing an elective sacrifice, given \(\psi \)”. This operator is characterized by weaker properties with respect to the other deontic operators, expressing the fact that its content is somewhat different from that of a fixed/occasional duty. The operator \(\mathcal {E}(\cdot /\cdot )\) does not interact with \(\mathcal {O}(\cdot /\cdot )\) or \(\mathcal {F}(\cdot /\cdot )\). Since being an elective ritual is intrinsically different from being obligatory, in general \(\mathcal {O}(\varphi /\psi )\) does not imply \(\mathcal {E}(\varphi /\psi )\).
Definition 4
Kumārila’s logic \({\mathsf {LKu^{+}}}\) extends the logic \({\mathsf {LPr^{+}}}\) Definition 1, with the axiom (\(\textsf{A}_{\textsf{P}}5\)) extending to the operator \(\mathcal {E}(\cdot /\cdot )\), together with:
- \(\textsf{A}_{\textsf{K}}7\):
-
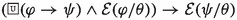
- \(\textsf{A}_{\textsf{K}}8\):
-
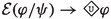
Axiom (\(\textsf{A}_{\textsf{K}}7\)) represents the property (P1) concerning upwards monotonicity in the first argument of the operator \(\mathcal {E}(\cdot /\cdot )\). Property (P3) representing congruence in the second argument is expressed by (\(\textsf{A}_{\textsf{P}}5\)) extended to \(\mathcal {E}(\cdot /\cdot )\): i.e.,  for \(\mathcal {X}\in \{\mathcal {O,F, E}\}\). Finally, note that, as elective sacrifices do not represent proper duties for Kumārila, they are not subject to Mīmāṃsā property (P2); instead, the only requirement imposed is self-consistency, expressed by axiom (\(\textsf{A}_{\textsf{K}}8\)) and capturing the idea that that something logically impossible cannot be prescribed.
for \(\mathcal {X}\in \{\mathcal {O,F, E}\}\). Finally, note that, as elective sacrifices do not represent proper duties for Kumārila, they are not subject to Mīmāṃsā property (P2); instead, the only requirement imposed is self-consistency, expressed by axiom (\(\textsf{A}_{\textsf{K}}8\)) and capturing the idea that that something logically impossible cannot be prescribed.
Semantics
We introduce a semantic characterization of Kumārila’s logic, allowing us to identify and describe worlds at which different kinds of commands are obeyed or violated. The models for Kumārila’s logic extend those for Prabhākara’s with additional conditions for the \(\mathcal {E}(\cdot /\cdot )\) operator.
Definition 5
An \({\mathsf {LKu^{+}}}\)-frame \({\mathfrak {F}_{\textsf{K}}}=\langle W, \mathcal {N}_{\mathcal {O}}, \mathcal {N}_{\mathcal {F}}, \mathcal {N}_{\mathcal {E}} \rangle \) extends an \({\mathsf {LPr^{+}}}\)-frame with a neighbourhood function \(\mathcal {N}_{\mathcal {E}}: W \mapsto \mathcal {P}{(\mathcal {P}{(W)}\times \mathcal {P}{(W)})}\) such that:
-
vi.
if \((X,Z) \in \mathcal {N}_{\mathcal {E}}(w)\) and \(X \subseteq Y \), then \((Y,Z) \in \mathcal {N}_{\mathcal {E}}(w)\);
-
vii.
if \((X,Y) \in \mathcal {N}_{\mathcal {E}}(w)\), then \(X \ne \emptyset \).
An \({\mathsf {LKu^{+}}}\)-model \({\mathfrak {M}_{\textsf{K}}}=\langle {\mathfrak {F}_{\textsf{K}}}, V \rangle \) is an \({\mathsf {LKu^{+}}}\)-frame with a valuation function V.
Also in this case the properties of neighbourhood functions correspond to the \({\mathsf {LKu^{+}}}\) axioms: (vi) matches the axiom (\(\textsf{A}_{\textsf{K}}7\)) and clause (vii) corresponds to the axiom (\(\textsf{A}_{\textsf{K}}8\)). Recall that axiom (\(\textsf{A}_{\textsf{P}}5\)) extended to \(\mathcal {E}(\cdot /\cdot )\) corresponds to a minimal property of neighborhood models in general.
Definition 6
Let \({\mathfrak {M}_{\textsf{K}}}\) be an \({\mathsf {LKu^{+}}}\)-model and \(\vert \!\vert \varphi \vert \!\vert = \{ w\in W\ \vert {\mathfrak {M}_{\textsf{K}}},w\vDash \varphi \}\). The satisfaction of a formula \(\varphi \in {\mathcal {L}_{\textsf{K}}}\) at any w of \({\mathfrak {M}_{\textsf{K}}}\) is defined as for \({\mathsf {LPr^{+}}}\), with the addition of the following clause

Theorem 3
(Soundness and Completeness) A formula is a theorem of \({\mathsf {LKu^{+}}}\) if and only if it is valid on all \({\mathsf {LKu^{+}}}\)-models.
Proof
See Appendix A. \(\square \)
3.3 The Logic of Maṇḍana
Maṇḍana’s account of deontic reasoning breaks with the Mīmāṃsā tradition. According to Maṇḍana, fixed and occasional duties, elective duties, and prohibitions can be expressed solely in terms of desire, outcome and instruments. Maṇḍana’s approach is, so to say, a deontic reduction: a reduction of all Vedic commands to purely descriptive statements of instrumentality. To illustrate this, consider the prescriptive statement “If one desires rain, one should perform the Kārīri ritual”. On Maṇḍana’s account, this command is reduced to the descriptive statement “the Kārīri is an instrument for attaining rain”. One of the central features of this reduction is that different commands are reduced to the singular notion of instrument. In short, an instrumentality relation means a relation between an action and a result, that is, the action is regarded as the instrument leading to the intended result. The result is a state of affairs (i.e., a partial description of the world). Another common way to think about instrumentality is as means-end relations.
The uniform language employed in the reduction may suggest that different commands are reduced to have the same ‘normative’ status. However, to maintain the desired distinction between fixed/occasional duties, elective duties and prohibitions, Maṇḍana adopts two additional constraints. These constraints involve accumulation and reduction of bad karma (pāpa in Sanskrit). First, fixed and occasional duties describe those actions that are instrumental to the universally desired reduction of bad karma. To distinguish those duties from other types of instruments that fulfil desires, Maṇḍana argues at length that the desire for the reduction of bad karma is a unique desire shared by every rational being. Second, to ensure that prohibitions retain their prohibitive strength, Maṇḍana argues that prohibitions refer to actions as instruments leading to strongly undesirable outcomes. In particular, prohibited actions are instrumental to outcomes whose undesirability is incommensurably greater than any desirable result, including the desire to reduce bad karma. For Maṇḍana, this universally undesirable result is the accumulation of bad karma. Additionally, elective duties are taken to describe instrumentality relations between actions and results, for those actions that neither lead to the reduction nor to the accumulation of bad karma directly. Since obligations and elective duties lead to something desirable, they are grouped together under the term iṣṭasādhana, i.e., “instrument to something desirable” (with the reduction of bad karma being universally desirable). Prohibitions are actions instrumental to something strictly undesirable, and are for that reason called aniṣṭasādhana, i.e., “instrument to something undesirable” (with ‘an-’ being the Sanskrit equivalent to the English prefix ‘un-’).
Due to Maṇḍana’s alternative deontic theory, a language such as employed for Prabhākara and Kumārila would be inadequate. Instead of deontic operators, we take instrumentality as the basic idea, and use it to define the different deontic concepts. Additionally, as Maṇḍana’s deontic reduction depends on the distinction between actions as instruments and states of affairs as results, we adopt an action language that enables us to differentiate between the two. Hence, the language \({\mathcal {L}_{\textsf{M}}}\) for Maṇḍana’s logic \({\mathsf {LMa^{-}}}\) combines a language of action with a modal language.
Let \(\textsf{Act}\) be a set of atomic actions \(\delta \) (such as ‘threshing the rice’). The action language \(\mathcal {L}_{\textsf{Act}}\) is given through the following BNF grammar:

with \(\delta \in \textsf{Act}\). We leave agents implicit due to the fact that Mīmāṃsā philosophers in general, and Maṇḍana in particular do not deal with multi-agent interaction. One can see the action language \(\mathcal {L}_{\textsf{Act}}\) as a single-agent action language. The operator − indicated by a line over an action formula denotes the complement of an action, and \(\cup \) is taken to define a disjunction of actions. We use uppercase Greek letters \(\Delta , \Gamma \ldots \) to refer to arbitrary actions. Additionally one can define alternative action operators such as \(\Delta \cap \Gamma =\overline{\overline{\Delta }\cup \overline{\Gamma }}\) which represents the conjunctive (i.e., joint) performance of actions. In what follows, we use \(\lnot \Delta \) and \(\overline{\Delta }\) interchangeably when denoting the negation of an action \(\Delta \).
The language \({\mathcal {L}_{\textsf{M}}}\) for \({\mathsf {LMa^{-}}}\) is defined via the following BNF grammar:

with \(p\in \textsf{Atom}\) and \(\texttt {d}_{\delta }\in \mathsf {Wit_{\textsf{Act}}}\). We take \(\textsf{Atom}\) as the set of atomic propositions p, and \(\mathsf {Wit_{\textsf{Act}}}\) as the set of atomic constants called ‘action-witnesses’ \(\texttt {d}_{\delta }\), where \(\texttt {d}_{\delta }\) signifies that ‘the action \(\delta \) has just been successfully performed’. (Below we find a mapping between actions from the action language and action witnesses from the logical language.) The other connectives, as well as \(\top \) and \(\bot \), are defined as usual. Furthermore, the constants \(\texttt {P}\) and \(\texttt {R}\) witness ‘bad karma is accumulated’ and ‘bad karma is reduced’, respectively. Last, we take the unary modalities  and
and  to refer to ‘in all succeeding worlds it holds that’, and to ‘it is universally necessary that’, respectively. Their duals
to refer to ‘in all succeeding worlds it holds that’, and to ‘it is universally necessary that’, respectively. Their duals  and
and  are defined as usual.
are defined as usual.
We define a translation between \(\mathcal {L}_{\textsf{Act}}\) and \({\mathcal {L}_{\textsf{M}}}\):
-
For all \(\delta \in \textsf{Act}\), \(t(\delta )=\texttt {d}_{\delta }\)
-
For all \(\Delta \in \mathcal {L}_{\textsf{Act}}\), \(t(\overline{\Delta })=\lnot t(\Delta )\)
-
For all \(\Delta ,\Gamma \in \mathcal {L}_{\textsf{Act}}\), \(t(\Delta \cup \Gamma )=t(\Delta )\vee t(\Gamma )\)
The translation between the two languages –which will be useful for defining deontic modalities in terms of instruments– enables reasoning with actions on the object language level.
As an example of a formula from the language \({\mathcal {L}_{\textsf{M}}}\), consider  which reads “at every successor world witnessing the successful performance of action \(\Delta \), the state of affairs \(\varphi \) holds”. Note that when used in combination with actions, the modality
which reads “at every successor world witnessing the successful performance of action \(\Delta \), the state of affairs \(\varphi \) holds”. Note that when used in combination with actions, the modality  may be taken as an indeterministic execution operator in the spirit of Propositional Dynamic Logic (PDL) from Fischer and Ladner (1979): “every successful execution of \(\Delta \), guarantees \(\varphi \)”. See van Berkel and Pascucci (2018) for a more extensive discussion.
may be taken as an indeterministic execution operator in the spirit of Propositional Dynamic Logic (PDL) from Fischer and Ladner (1979): “every successful execution of \(\Delta \), guarantees \(\varphi \)”. See van Berkel and Pascucci (2018) for a more extensive discussion.
Axiomatization
The logic \({\mathsf {LMa^{-}}}\) is a normal modal logic defined as follows:
Definition 7
Maṇḍana’s logic \({\mathsf {LMa^{-}}}\) extends the logic \(\textsf{S5}\) for  with:
with:
- \(\textsf{A}_{\textsf{M}}1\):
-
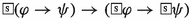
- \(\textsf{A}_{\textsf{M}}2\):
-

- \(\textsf{A}_{\textsf{M}}3\):
-
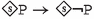
- \(\textsf{A}_{\textsf{M}}4\):
-
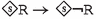
A derivation of \(\varphi \in \mathcal {L}\) in \({\mathsf {LMa^{-}}}\) from a set \(\Sigma \subseteq \mathcal {L}\) (written \(\Sigma \vdash _{{\mathsf {LMa^{-}}}}\varphi \)) is defined as usual, see Blackburn et al. (2004). If \(\Sigma =\emptyset \), we say that \(\varphi \) is an \({\mathsf {LMa^{-}}}\)-theorem.
The axiomatization is rather minimal as all axioms not related to the normality of the logic can be traced back to nyāyas from common Mīmāṃsā, and, as seen below, the deontic reduction is solely based on Maṇḍana’s theory. \(\textsf{A}_{\textsf{M}}2\) is a bridge axiom, expressing that what holds universally must also hold at any successor world. \(\textsf{A}_{\textsf{M}}3\) conveys the Mīmāṃsā principle stating that whenever bad karma is attainable, it is also avoidable. \(\textsf{A}_{\textsf{M}}4\) captures the same property for the reduction of bad karma. Both principles are based on the nyāya requiring that all commands must be non-trivial, see Freschi (2018).
Remark 3
The logic \({\mathsf {LMa^{-}}}\) in Definition 7 differs from the logic \(\textsf{LMa}\) in van Berkel et al. (2021) because of the absence of axiom (\(\textsf{A}_{\textsf{M} } 5\))  in the former. This modification has been triggered by the formalization of the newly discovered principle P4, which we will discuss at the end of this section. Axiom (\(\textsf{A}_{\textsf{M} } 5\)) was supposed to formalize the Mīmāṃsā principle endorsed by Maṇḍana: “an action \(\Delta \) cannot be an instrument for both the reduction and the increase of bad karma” (Viraraghavacharya (1971) on PMS 1.1.2). However, (\(\textsf{A}_{\textsf{M} } 5\)) forces this property on any possible action, including compound actions: e.g., if the action of shooting someone is prohibited, and the action of giving water to a person who needs it is obligatory, this axiom excludes any world where the combined action of shooting-someone-with-the-right-hand-and-giving-water-with-the-left could happen. The withdrawal of (\(\textsf{A}_{\textsf{M} } 5\)) is accompanied by a change in the notions of obligation and prohibition (see Definition 10), allowing for restricted aggregation of obligations and prohibitions in terms of instruments.
in the former. This modification has been triggered by the formalization of the newly discovered principle P4, which we will discuss at the end of this section. Axiom (\(\textsf{A}_{\textsf{M} } 5\)) was supposed to formalize the Mīmāṃsā principle endorsed by Maṇḍana: “an action \(\Delta \) cannot be an instrument for both the reduction and the increase of bad karma” (Viraraghavacharya (1971) on PMS 1.1.2). However, (\(\textsf{A}_{\textsf{M} } 5\)) forces this property on any possible action, including compound actions: e.g., if the action of shooting someone is prohibited, and the action of giving water to a person who needs it is obligatory, this axiom excludes any world where the combined action of shooting-someone-with-the-right-hand-and-giving-water-with-the-left could happen. The withdrawal of (\(\textsf{A}_{\textsf{M} } 5\)) is accompanied by a change in the notions of obligation and prohibition (see Definition 10), allowing for restricted aggregation of obligations and prohibitions in terms of instruments.
Semantics
Since \({\mathsf {LMa^{-}}}\) is a normal modal logic (cf. Definition 7), we provide a semantic characterization using the simpler relational semantics (w.r.t. the neighbourhood semantics). An additional reason for employing relational semantics is that the directed graphs of relational semantics explain better Maṇḍana’s theory of how actions (seen as transitions between states) may lead to different outcomes, which may or may not be deontically desirable.
Definition 8
An \({\mathsf {LMa^{-}}}\)-frame  is a tuple with \(W\ne \emptyset \) a set of worlds \(w,v,u,\ldots \). For every \(\texttt {d}_{\delta }\in \mathsf {Wit_{\textsf{Act}}}\) (with \(\texttt {d}_{\delta }=t(\delta )\)) let \(W_\delta \subseteq W\) be the set of worlds witnessing the successful performance of \(\delta \). \(W_{\texttt {P}}\subseteq W\) and \(W_{\texttt {R}}\subseteq W\) are sets of worlds witnessing the accumulation, respectively reduction of bad karma. Let
is a tuple with \(W\ne \emptyset \) a set of worlds \(w,v,u,\ldots \). For every \(\texttt {d}_{\delta }\in \mathsf {Wit_{\textsf{Act}}}\) (with \(\texttt {d}_{\delta }=t(\delta )\)) let \(W_\delta \subseteq W\) be the set of worlds witnessing the successful performance of \(\delta \). \(W_{\texttt {P}}\subseteq W\) and \(W_{\texttt {R}}\subseteq W\) are sets of worlds witnessing the accumulation, respectively reduction of bad karma. Let  such that the following holds:
such that the following holds:
-
i.
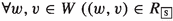 and \( v\in W_{\texttt {P}})\) implies
and \( v\in W_{\texttt {P}})\) implies 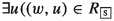 and \( u \not \in W_{\texttt {P}} )\);
and \( u \not \in W_{\texttt {P}} )\); -
ii.
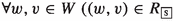 and \( v\in W_{\texttt {R}}) \) implies
and \( v\in W_{\texttt {R}}) \) implies 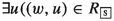 and \( u \not \in W_{\texttt {R}})\).
and \( u \not \in W_{\texttt {R}})\).
An \({\mathsf {LMa^{-}}}\)-model is a tuple \({\mathfrak {M}_{\textsf{M}}}=\langle {\mathfrak {F}_{\textsf{M}}},V\rangle \) where \({\mathfrak {F}_{\textsf{M}}}\) is an \({\mathsf {LMa^{-}}}\)-frame and V is a valuation function mapping atomic propositional symbols from \(\textsf{Atom}\cup \mathsf {Wit_{\textsf{Act}}}\cup \{\texttt {P}\}\cup \{\texttt {R}\}\) to sets of worlds, which satisfies:
-
\(V(\texttt {d}_{\delta })=W_{\delta }\) for every \(\texttt {d}_{\delta }\in \mathsf {Wit_{\textsf{Act}}}\), \(V(\texttt {P})=W_{\texttt {P}}\), and \(V(\texttt {R})=W_{\texttt {R}}\).
Some observations concerning Definition 8: The  -modality represents the universal modality and is therefore characterized through an equivalence relation whose equivalence class is the set W, i.e., the set of all worlds (cf. the logics of Prabhākara and Kumārila). The bridge axiom 2 is therefore guaranteed by the fact that
-modality represents the universal modality and is therefore characterized through an equivalence relation whose equivalence class is the set W, i.e., the set of all worlds (cf. the logics of Prabhākara and Kumārila). The bridge axiom 2 is therefore guaranteed by the fact that  . Moreover we point out that the valuation function V is such that the constants \(\texttt {P}\), \(\texttt {R}\) and those from \(\mathsf {Wit_{\textsf{Act}}}\) have a fixed evaluation over frames (which allows us to impose the desired frame properties involving such constants). Finally, notice the correspondence between the frame properties (i)-(ii) in Definition 8 and the axioms (\(\textsf{A}_{\textsf{M}}3\)) and (\(\textsf{A}_{\textsf{M}}4\)).
. Moreover we point out that the valuation function V is such that the constants \(\texttt {P}\), \(\texttt {R}\) and those from \(\mathsf {Wit_{\textsf{Act}}}\) have a fixed evaluation over frames (which allows us to impose the desired frame properties involving such constants). Finally, notice the correspondence between the frame properties (i)-(ii) in Definition 8 and the axioms (\(\textsf{A}_{\textsf{M}}3\)) and (\(\textsf{A}_{\textsf{M}}4\)).
Semantic evaluation of formulae is defined as usual:
Definition 9
Let \({\mathfrak {M}_{\textsf{M}}}\) be an \({\mathsf {LMa^{-}}}\)-model and \(w\in W\) of \({\mathfrak {M}_{\textsf{M}}}\). We define the satisfaction of a formula \(\varphi \in {\mathcal {L}_{\textsf{M}}}\) in \({\mathfrak {M}_{\textsf{M}}}\) at w as follows:
\({\mathfrak {M}_{\textsf{M}}}, w\vDash \chi \) iff \(w\in V(\chi )\), for any \(\chi \in \textsf{Atom}\cup \mathsf {Wit_{\textsf{Act}}}\cup \{\texttt {P}\}\cup \{\texttt {R}\}\)
\({\mathfrak {M}_{\textsf{M}}},w\vDash \lnot \varphi \) iff \({\mathfrak {M}_{\textsf{M}}}, w\nvDash \varphi \)
\({\mathfrak {M}_{\textsf{M}}}, w\vDash \varphi \vee \psi \) iff \({\mathfrak {M}_{\textsf{M}}}, w\vDash \varphi \) or \({\mathfrak {M}_{\textsf{M}}}, w\vDash \psi \)
 iff for all \(v\in W\), \({\mathfrak {M}_{\textsf{M}}},v\vDash \varphi \)
iff for all \(v\in W\), \({\mathfrak {M}_{\textsf{M}}},v\vDash \varphi \)
 iff for all \(v\in W\) s.t.
iff for all \(v\in W\) s.t.  , \({\mathfrak {M}_{\textsf{M}}},v\vDash \varphi \)
, \({\mathfrak {M}_{\textsf{M}}},v\vDash \varphi \)
Global truth, validity and semantic entailment are defined as usual, see Blackburn et al. (2004).
The logic \({\mathsf {LMa^{-}}}\) is sound and complete with respect to the relational semantics defined in Definition 8.
Theorem 4
(Soundness and Completeness) A formula is a theorem of \({\mathsf {LMa^{-}}}\) if and only if it is valid on all \({\mathsf {LMa^{-}}}\)-models.
Proof
See Appendix B. \(\square \)
Before we turn to the formal analysis of instruments, we point out that it suffices to adopt a general notion of the immediate successor relation  , with the idea of imposing as few as possible additional properties on this relation. Notice that such an immediate successor relation may be refined through imposing intransitivity and asymmetry as additional properties. However, as there is no Mīmāṃsā characterization of time available to justify such properties, and Maṇḍana’s analysis does not depend on inherent properties of time, we omit such refinements here.
, with the idea of imposing as few as possible additional properties on this relation. Notice that such an immediate successor relation may be refined through imposing intransitivity and asymmetry as additional properties. However, as there is no Mīmāṃsā characterization of time available to justify such properties, and Maṇḍana’s analysis does not depend on inherent properties of time, we omit such refinements here.
Instruments and Maṇḍana’s deontic reduction
At the heart of Maṇḍana’s deontic theory lies the reduction of all deontic modalities to a uniform notion of instrumentality. Following Maṇḍana, our formal definition of instrumentality must satisfy the following criteria: (i) The instrument relation contains three components: an action \(\Delta \), serving as the instrument; a state of affairs \(\varphi \), representing the outcome of \(\Delta \); and a state of affairs \(\chi \) defining the circumstances in which \(\Delta \) functions as an instrument for bringing about \(\varphi \). (ii) The circumstances \(\chi \) must be meaningful which in Mīmāṃsā terms means that \(\chi \) must be possible in the broadest sense (i.e., not inconsistent). Moreover, the agent in question must have a proper choice to execute action \(\Delta \) when the appropriate circumstances \(\chi \) occur. We split choice into a positive and negative component: (iii) \(\Delta \) can be performed by the agent and (iv) the agent can refrain from performing \(\Delta \). For a motivation of i–iv, see Śabara on PMS 6.1 in Śubbaśāstrī (1934). Hence, we take the defined instrumentality operator \(\mathcal {I}(\Delta /\varphi /\chi )\) to read:
“\(\Delta \) is an instrument for guaranteeing \(\varphi \) in circumstances \(\chi \)” iff
“(i) If circumstance \(\chi \) holds, performance of \(\Delta \) guarantees \(\varphi \), (ii) \(\chi \) is possible, and if \(\chi \) holds, both (iii) \(\Delta \) is possible and (iv) \(\overline{\Delta }\) is possible.”
The corresponding formal definition, based on (i)-(iv), is given in Definition 10.
On the basis of the above, we can define Maṇḍana’s reduction of the various command types to statements of instrumentality: prohibited and obligatory actions are defined in terms of those actions being instrumental to the outcome of bad karma (denoted by \(\texttt {P}\)), and the reduction of bad karma (denoted by \(\texttt {R}\)), respectively. Elective commands are actions instrumental to outcomes that are neither \(\texttt {P}\) nor \(\texttt {R}\). Additionally, we need to ensure that the following Maṇḍana principle, which applies to obligations and prohibitions, is satisfied: “an action \(\Delta \) cannot be an instrument for both the reduction \(\texttt {R}\) and the increase \(\texttt {P}\) of bad karma” (cf. Remark 3). This is done by introducing an additional clause requiring that the action in question is not simultaneously instrumental to the accumulation, respectively reduction, of bad karma. We thus have that an action is obligatory (prohibited) if and only if it is an instrument for reducing (accumulating) bad karma and at the same time the action is not an instrument for accumulating (reducing) bad karma.
Definition 10
Maṇḍana’s notion of instruments in \({\mathsf {LMa^{-}}}\) is defined as:
\(\mathcal {I}(\Delta /\varphi /\chi )\) \(:=\) (i)  \(\wedge \)
\(\wedge \)
(ii)  \(\wedge \)
\(\wedge \)
(iii)  \(\wedge \)
\(\wedge \)
(iv) 
Maṇḍana’s reduction of obligations, prohibitions and elective duties in \({\mathsf {LMa^{-}}}\):
\(\mathcal {O}(\Delta /\chi )\) \(:=\) \(\mathcal {I}(\Delta /\texttt {R}/\chi ) \wedge \lnot \mathcal {I}(\Delta /\texttt {P}/\chi )\)
\(\mathcal {F}(\Delta /\chi )\) \(:=\) \(\mathcal {I}(\Delta /\texttt {P}/\chi )\wedge \lnot \mathcal {I}(\Delta /\texttt {R}/\chi )\)
\(\mathcal {E}(\Delta /\varphi /\chi )\) \(:=\) \(\mathcal {I}(\Delta /\varphi /\chi )\) with \(\varphi \not \vdash _{{\mathsf {LMa^{-}}}} \texttt {P}\) and \(\varphi \not \vdash _{{\mathsf {LMa^{-}}}}\texttt {R}\)
The side condition on \(\mathcal {E}(././.)\) in Definition 10 ensures that results explicitly described by the command do not directly entail the accumulation or reduction of bad karma. However, indirectly this is allowed. We will see this when analyzing the śyena controversy in Sect. 4. Last, we point out that obligations \(\mathcal {O}(\Delta /\chi )\) could be equivalently defined as  ) due to the overlapping clauses (ii)-(iv) of the definition of instruments in \(\mathcal {I}(\Delta /\texttt {R}/\chi )\) and \(\mathcal {I}(\Delta /\texttt {P}/\chi )\). This is similar for prohibitions. The above definitions for the three command types ensure that Vedic actions can never be instrumental to both the reduction and the accumulation of bad karma (with electives leading to neither).
) due to the overlapping clauses (ii)-(iv) of the definition of instruments in \(\mathcal {I}(\Delta /\texttt {R}/\chi )\) and \(\mathcal {I}(\Delta /\texttt {P}/\chi )\). This is similar for prohibitions. The above definitions for the three command types ensure that Vedic actions can never be instrumental to both the reduction and the accumulation of bad karma (with electives leading to neither).
Remark 4
In \({\mathsf {LMa^{-}}}\), we define commands as having a state of affairs as their condition. In addition, due to the translation t from the action language to the object level language \({\mathcal {L}_{\textsf{M}}}\), we can express prescriptions as “offer to Agni once you have offered to Soma”, having as a condition an action that temporally precedes the prescribed action. This sentence corresponds to \(\mathcal {O}(\textsf{Agni}/t(\textsf{Soma}))\), where \(t(\textsf{Soma})\) is actually the state of affairs of witnessing that “the Soma offering has just been performed”.
In what follows, we show that important Mīmāṃsā properties hold for the derived deontic operators and that the Mīmāṃsā principles adopted by Maṇḍana are \({\mathsf {LMa^{-}}}\)-theorems.
Irreducibility
Recall that for Mīmāṃsā authors, obligations, prohibitions and electives are reciprocally irreducible, see Lellmann et al. (2021) and Freschi and Pascucci (2021). Maṇḍana also adopts this view by limiting the type of results of the instruments corresponding to the three command types. We can easily see that Definition 10 preserves this property. In addition, in Maṇḍana’s account the elective operator \(\mathcal {E}\) receives an additional argument as compared to the operators employed in the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\). The reason for it is the expressivity of the language \({\mathcal {L}_{\textsf{M}}}\); indeed, as a consequence of the employed action language we can distinguish between variables representing the eligibility condition of the command (i.e., the desire or particular circumstances) and variables representing the purpose served by the instrument (i.e., the object of the desire).
Contingency
For Mīmāṃsā, actions occurring in Vedic commands must be meaningful (cf. ŚBh on PMS 6.1, Śubbaśāstrī 1934). An action is meaningful when an agent can perform the action as well as refrain from performing it. The property of meaningfulness of actions is expressed via the following \({\mathsf {LMa^{-}}}\)-valid formula, which is a consequence of clauses (iii) and (iv) of Definition 10:

where either \(\varphi \in \{\texttt {P},\texttt {R}\}\) or \((\varphi \not \vdash \texttt {P}\) and \( \varphi \not \vdash \texttt {R})\). That is, the above holds for all three command types. In deontic logic this property is known as the contingency principle, see Anderson and Moore (1957) and von Wright (1951).
For obligations and prohibitions the property is also implied by axioms (\(\textsf{A}_{\textsf{M}}3\)) and (\(\textsf{A}_{\textsf{M}}4\)), ensuring that the accumulation, respectively reduction, of bad karma can always be avoided. That is, in the light of these axioms, condition (iv) of instruments (Definition 10) is admissible for obligations and prohibitions, but remains necessary for ensuring meaningfulness of actions involved in elective duties. See van Berkel et al. (2021) for a discussion.
No impossible commands
Although the logic \({\mathsf {LMa^{-}}}\) does not contain a D-axiom for deontic consistency, the following formula is in fact \({\mathsf {LMa^{-}}}\)-valid:
This valid formula corresponds to the Mīmāṃsā principle: “It is impossible that the Vedas tell you that you’ll fall (i.e., be reborn in hell) both if you do something and if you don’t do it” (Viraraghavacharya 1971, p. 32). The quote illustrates the impossibility of the Vedas to give contradictory commands. The formula is valid due to the definition of instrumentality together with axiom (\(\textsf{A}_{\textsf{M}}3\)). We obtain a similar \({\mathsf {LMa^{-}}}\)-valid formula expressing this property for obligations:
As desired, the property does not hold for elective duties; this follows from the fact that these duties lead to worldly results on which no additional property is imposed (see Definitions 7 and 10).
Furthermore, the logic \({\mathsf {LMa^{-}}}\) satisfies the Mīmāṃsā principle that obligations and prohibitions are mutually exclusive, namely, no action \(\Delta \) can be both obligatory and prohibited (cf. the principle of ‘half-hen’ mentioned in Sect. 3.1). This is expressed by the following formula which is valid in \({\mathsf {LMa^{-}}}\):
The property is guaranteed by Definition 10. The way in which obligations and prohibitions are defined implies that, in Maṇḍana’s language, \(\Delta \) cannot at the same time be an instrument for the reduction and for the accumulation of bad karma. Still, from a semantic perspective, \({\mathsf {LMa^{-}}}\) allows for situations where we end up at a world at which both \(\texttt {P}\) and \(\texttt {R}\) hold after the execution of some action \(\Delta \) (cf. Remark 3). However, in those cases Definition 10 ensures that this action \(\Delta \) is neither obligatory nor prohibited.
Mīmāṃsā principles
The logics of Prabhākara and Kumārila are built upon four principles (P1)-(P4). Since Maṇḍana conceptually deviates from the Mīmāṃsā tradition, we investigate whether those principles are preserved in his deontic reduction. To address this question, we first reformulate those principles in the language of \({\mathsf {LMa^{-}}}\), starting with (P1)-(P3). Observe that the Mīmāṃsā principles we are interested in are postulated for commands only. Hence, we rewrite them in terms of instruments for the three command types:
- p1:
-
 such that (\(\star \)) holds
such that (\(\star \)) holds - p2:
-
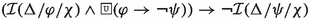 such that (\(\star \)) holds
such that (\(\star \)) holds - p3:
-
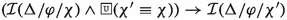 such that (\(\star \)) holds with (\(\star \)) imposing that either \(\varphi \in \{\texttt {P},\texttt {R}\}\) or (\(\varphi \not \vdash _{{\mathsf {LMa^{-}}}} \texttt {P}\) and \(\varphi \not \vdash _{{\mathsf {LMa^{-}}}} \texttt {R}\))
such that (\(\star \)) holds with (\(\star \)) imposing that either \(\varphi \in \{\texttt {P},\texttt {R}\}\) or (\(\varphi \not \vdash _{{\mathsf {LMa^{-}}}} \texttt {P}\) and \(\varphi \not \vdash _{{\mathsf {LMa^{-}}}} \texttt {R}\))
The condition \((\star )\) ensures that the three properties are defined for obligations, prohibitions and elective duties. Principle (p1) is not an \({\mathsf {LMa^{-}}}\)-valid formula (it is straightforward to construct a counter-model) as it should be: instrumentality is a notion of sufficient means, not of necessary means (as expressed in (P1)). Maṇḍana seems to be aware of this consequence. To preserve the property expressed by (P1), Maṇḍana explains the role of necessary preconditions independent of instrumentality. Namely, Maṇḍana’s account of the universally desired reduction of bad karma explains that, from a rational point of view, no agent would be willing to omit the actions \(\Gamma \) serving as necessary preconditions for other obligatory actions \(\Delta \), even though the necessary conditions \(\Gamma \) themselves are not sufficient (hence instruments) for reducing bad karma. Principle (p2) is an \({\mathsf {LMa^{-}}}\)-valid formula and follows from the Maṇḍana property that instrumental actions must be meaningful (thus leading to meaningful outcomes). Last, principle (p3) is \({\mathsf {LMa^{-}}}\)-valid, due to the fact that the universal necessity modality  is a normal modal operator. The additional principle (P4), not present in the logics defined in van Berkel et al. (2021), expresses a restricted form of aggregation: (P4) ‘If two fixed duties are prescribed and compatible, their conjunction is obligatory as well’. Recall that the logics of Prabhākara and Kumārila needed to be extended in order to satisfy (P4). To formalize (P4) in \({\mathsf {LMa^{-}}}\) we are confronted with a choice: do we take ‘compatible’ as a global notion (referring to
is a normal modal operator. The additional principle (P4), not present in the logics defined in van Berkel et al. (2021), expresses a restricted form of aggregation: (P4) ‘If two fixed duties are prescribed and compatible, their conjunction is obligatory as well’. Recall that the logics of Prabhākara and Kumārila needed to be extended in order to satisfy (P4). To formalize (P4) in \({\mathsf {LMa^{-}}}\) we are confronted with a choice: do we take ‘compatible’ as a global notion (referring to  ) or a local notion (referring to
) or a local notion (referring to  )? Observe that the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) are not expressive enough to make this distinction, i.e., they only allow for a global notion. In \({\mathsf {LMa^{-}}}\) we then obtain two formalizations of (P4):
)? Observe that the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) are not expressive enough to make this distinction, i.e., they only allow for a global notion. In \({\mathsf {LMa^{-}}}\) we then obtain two formalizations of (P4):
- p4a:
-
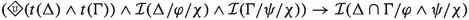
- p4b:
-
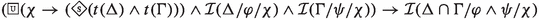
(p4a) states that the two actions are not contradictory, whereas (p4b) expresses the stronger reading of compatibility stating that whenever the circumstances \(\chi \) hold the two actions are compatible. Formalization (p4a) is not an \({\mathsf {LMa^{-}}}\)-valid formula. The local interpretation of P4, expressed by (p4b), is instead valid in \({\mathsf {LMa^{-}}}\). An intuitive explanation for this is: since \(\varphi \), respectively \(\psi \), is propagated at all worlds that witness performances of \(\Delta \), respectively \(\Gamma \), both \(\varphi \) and \(\psi \) are also propagated at those worlds witnessing \(\Delta \cap \Gamma \). The fact that \(\Delta \cap \Gamma \) is possible, together with the fact that  implies
implies  , ensures that
, ensures that  holds, which is a necessary condition for instrumentality (cf. the meaningfulness requirement and the notion of ‘refraining from’). Property (p4b) holds for instruments in general, and thus also for commands defined in terms of them. For instance, we obtain the following \({\mathsf {LMa^{-}}}\)-valid formulae for obligations, with
holds, which is a necessary condition for instrumentality (cf. the meaningfulness requirement and the notion of ‘refraining from’). Property (p4b) holds for instruments in general, and thus also for commands defined in terms of them. For instance, we obtain the following \({\mathsf {LMa^{-}}}\)-valid formulae for obligations, with  :
:
This property also holds for prohibitions, i.e., the formula \( (\theta \wedge \mathcal {F}(\Delta /\chi )\wedge \mathcal {F}(\Gamma /\chi ))\rightarrow \mathcal {F}(\Delta \cap \Gamma /\chi )\) is \({\mathsf {LMa^{-}}}\)-valid. Recall that in Mīmāṃsā, principle (P4) is only adopted for obligations, and therefore likewise in the logics for Prabhākara and Kumārila. The reason why there is no such distinction in Maṇḍana’s logic, is that the principle is approached from the perspective of instruments instead of commands. Namely, in Maṇḍana’s reduction the three command types are just instruments, whose possible joint performance gives rise to another instrument. On this general level, there is no difference between aggregating consistent obligations or prohibitions.
Related logics
The logics in this article are tailored to the deontic theories of the respective Mīmāṃsā authors. This also holds for Maṇḍana, for whom we introduced a logic which reflects his theory; below we point out similarities and differences between \({\mathsf {LMa^{-}}}\) and related existing logics.
Since Maṇḍana’s elementary concepts are actions and outcomes, we adopted a PDL-like language (Fischer and Ladner (1979); Meyer (1988)). For our purposes, a minimal action-language suffices using negation, disjunction, and conjunction. We have therefore followed the approach in van Berkel and Pascucci (2018) –dealing with Von Wright’s concept of instrumentality– which introduces this minimal language reducing action-modalities to action constants. Despite its simplicity and in contrast with PDL, this language allows for notions of instruments that, for instance, take actions as preconditions. In van Berkel et al. (2020) a similar approach was adopted for a deontic setting. There, instruments were used, not as a means for reducing deontic operators, but as a refinement for talking about instruments that are obligatory or forbidden. An alternative approach is that of BDI (Belief-Desire-Intention) logic see Meyer et al. (2015) due to its connection to means-end reasoning (see also Hughes et al. (2007)). However, such logics do not fully accommodate the required distinction between actions and outcomes as in van Berkel and Pascucci (2018).
To reason about bad karma, we adopted an Andersonean reduction to deontic logic (Anderson and Moore 1957): “\(\varphi \) is obligatory iff \(\lnot \varphi \) necessarily implies a sanction”. To avoid problems, Castañeda (1972) proposed to use violations instead of sanctions. An Andersonean reduction was adapted by Meyer (1988) in a PDL-like setting: “an action is obligatory iff all performances of its complement lead to a violation”. Similarly, Maṇḍana can be seen as a reductionist of deontic reasoning: every Vedic command is an instrumentality statement about actions leading to states of affairs, sanctions and rewards. Kanger (1971) defined obligations using positive constants: “\(\varphi \) is obligatory iff in the good world \(\varphi \) holds”. A major difference between Kanger’s approach and Maṇḍana’s, is that the former takes \(\varphi \) as a necessary condition for the ‘good world’ whereas for Maṇḍana \(\varphi \) is a sufficient condition for ‘reducing bad karma’.
The Action Deontic Logic (Giordani and Canavotto (2016)), used in Guhe (2021) to formalize Gaṅgeśa’s solution to the śyena controversy (see Sect. 4.3), shares certain similarities with \({\mathsf {LMa^{-}}}\). This modal logic distinguishes actions from results, employs a universal necessity modality, as well as a successor modality. The logic also adopts an Andersonean reduction. Although there is the potential of defining Maṇḍana’s conception of instruments, this logic has a more complex action language and axiomatization that would be an overkill compared to the relatively simple logic needed for Maṇḍana, baring the risk of imposing unwanted conditions. Furthermore, it misses some desired notions such as a “badness” constant.
4 There: Solutions to the śyena Controversy
The introduced logics enable us to highlight the underlying structure of the reasoning about duty in the three main authors of the Mīmāṃsā school. Here we apply them to the famous śyena controversy, which proved to be a challenge for many Mīmāṃsā scholars, in order to reconstruct and formally verify the different solutions provided by Prabhākara, Kumārila and Maṇḍana.
The śyena is a one-day long ritual in which the Soma beverage is offered. Its putative result is the death of the sacrificer’s enemy. The controversy is due to the fact that the śyena appears to be prescribed in the Vedas, that also prohibits to harm any living being (note the similarity with the paradoxes in Sect. 5.1). The śyena controversy in a nutshellFootnote 8:
-
(A) The one who desires to kill their enemy should sacrifice with the śyena
-
(B) One should not harm any living being
-
(C) Performing śyena implies causing someone’s death
-
(D) Causing someone’s death implies harming
We use \({\mathsf {LKu^{+}}}\), \({\mathsf {LPr^{+}}}\) and \({\mathsf {LMa^{-}}}\) to show the consistency of the solutions to the controversy for Prabhākara, Kumārila, and Maṇḍana and clarify their explanations. All the authors agree that the śyena should not be performed, but they disagree on the reasons underlying it. Drawn from the mathematical models satisfying the formal representation of the controversy, the explanations turn out to be faithful to those found in Mīmāṃsā texts.
Before discussing the various solutions we note that Mīmāṃsā authors agree on the fact that śyena is an elective sacrifice (A) and that the command to not harm any living being (B) should be interpreted as a prohibition.
Models \(\mathfrak {M}_{P}\) and \(\mathfrak {M}_{K}\) satisfying the śyena controversy. Worlds \(w_i\in |\!|\texttt {harm}|\!|\), where (B) is violated, are coloured grey, and for \((|\!|\acute{\texttt{S}}{} \texttt {y}|\!|,|\!|\texttt {des\_kill}|\!|)\in \mathcal {N}_{\mathcal {E}}^K(w_{i}) = \mathcal {N}_{\mathcal {O}}^P(w_{i})\) (expressing A\(_P\) and A\(_K\), resp.) the elements are indicated by arrows from each \(w_i\in |\!|\texttt {des\_kill}|\!|\) to each \(w_j\in |\!|\acute{\texttt {S}}{} \texttt {y}|\!|\).
4.1 Prabhākara’s and Kumārila‘s view
We discuss the solutions of Prabhākara and Kumārila together, the logic \({\mathsf {LPr^{+}}}\) being a subset of \({\mathsf {LKu^{+}}}\). Sentences (A)-(D) of the controversy are formalized in \({\mathsf {LPr^{+}}}\) as follows:
(A\(_P\)) \(\mathcal {O}(\acute{\texttt {S}}{} \texttt {y}/\texttt {des\_kill})\)
(C) 
(B) \(\mathcal {F}(\texttt {harm}/\top )\)
(D) 
while the formalization of the sentences (B)-(D) in \({\mathsf {LKu^{+}}}\) is the same, the conditional obligation (A\(_P\)) is replaced in Kumārila’s logic by the following:
The models \(\mathfrak {M}_{P}\) and \(\mathfrak {M}_{K}\) demonstrating the mutual satisfiability of the (formalization of the) sentences (A\(_P\)), (B), (C), (D) in \({\mathsf {LPr^{+}}}\) and (A\(_K\)), (B), (C), (D) in \({\mathsf {LKu^{+}}}\), respectively, are depicted in Fig. 1. They are defined as follows: \(W^P\) \(=W^K{=}\lbrace w_{i} \mid 1 \le i \le 8\rbrace \) s.t. \(\vert \!\vert \texttt {harm}\vert \!\vert =V(\texttt {harm}){=} \{w_{2},w_{3},w_{4},w_{6},w_{7},w_{8}\}\), \(\vert \!\vert \texttt {death}\vert \!\vert =V(\texttt {death})=\{w_{3},w_{4},w_{7},w_{8}\}\), \(\vert \!\vert \acute{\texttt {S}}{} \texttt {y}\vert \!\vert = V(\acute{\texttt {S}}{} \texttt {y})= \{w_{4},w_{8}\}\), \(\vert \!\vert \texttt {des\_kill}\vert \!\vert =V(\texttt {des\_kill})= \{w_{5},w_{6},w_{7},w_{8}\}\) (with \(V^P=V^K=V\)), \(\mathcal {N}^P_{\mathcal {F}}(w_{i}) =\mathcal {N}^K_{\mathcal {F}}(w_{i})=\{ (X,Y) \;\vert \; X\subseteq \{w_{2},w_{3},w_{4},w_{6},w_{7},w_{8}\},Y=W\}\), \(\mathcal {N}_{\mathcal {O}}^P(w_{i}) = \mathcal {N}^K_{\mathcal {E}}(w_{i}) = \{ (V,Z) \;\vert \; \{w_{2},w_{6}\}\subseteq V, Z = \{w_{5},w_{6},w_{7},w_{8}\} \}\) and \(\mathcal {N}^K_{\mathcal {O}}(w_{i})=\emptyset \).
In these models there is always at least one world in which no command is not followed, i.e., violated (we say that a command \(\mathcal {O}(\varphi /\psi )\) or a weak injunction \(\mathcal {E}(\varphi /\psi )\) is not followed if \(\psi \) is satisfied, but \(\varphi \) is not and that \(\mathcal {F}(\varphi /\psi )\) is not followed when both \(\varphi \) and \(\psi \) are satisfied). For Prabhākara this world is \(w_1\), whereas for Kumārila these are \(w_1\) and \(w_5\) since (A\(_K\)) has no deontic force. The model formally shows how the statements, that appear to be conflicting in natural language, do not give rise to inconsistencies for any of the two authors.
Although the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) are similar, they lead to different solutions to the śyena controversy. Kumārila’s solution relies on the distinction between obligations and statements prescribing elective sacrifices, which are mutually independent: in case of conflict with a prohibition, elective sacrifices can be omitted without risk, thus avoiding the violation of the prohibition.
In contrast, in Prabhākara’s logic the two neighbourhoods associated with (A\(_P\)) and (B) are not independent: i.e., condition (iv) of Definition 2 excludes the possibility that the same neighbourhood of a world represents both a prohibition and an obligation. However, since the eligibility conditions of the two commands do not coincide, we have that at world \(w_1\)—where one does not desire to kill one’s enemy—no command is violated. Since desires are interpreted by Prabhākara as irreversible decisions—i.e., for Prabhākara the desire to kill amounts to a decision to kill—his solution is a case of contrary-to-duty (CTD) reasoning: namely, the injunction to perform the śyena represents an obligation taking effect when a violation (the decision to cause a death) has occurred. Prabhakara indeed explains that the obligation to perform śyena only applies to people who are in the sub-ideal eligibility condition of wishing the death of their enemy. Thus, in ideal eligibility conditions, no one would wish the death of their enemy and would therefore not be eligible to perform the śyena. By contrast, if one is in the relevant sub-ideal eligibility condition, then the duty to perform the śyena becomes incumbent upon one.
Remark 5
Although (B) was interpreted in Ciabattoni et al. (2015) as a negative obligation, the resulting model of the śyena controversy is very similar to \(\mathfrak {M}_P\). It also explains Prabhākara’s claim that “the Vedas do not impel one to perform the malevolent sacrifice śyena, they only say that it is obligatory”. This claim, which implies that a Vedic obligation does not necessarily impel, was wrongly considered meaningless, e.g., in Stcherbatsky (1926).
4.2 Maṇḍana’s View
In what follows, we use this font to denote propositional atoms, whereas we use this font to single out actions. The śyena controversy can be formalized in \({\mathsf {LMa^{-}}}\) as follows:
(A\(_M\)) 
(B\(_M\)) 
(C\(_M\)) 
(D\(_M\)) 
The following model \({\mathfrak {M}_{\textsf{M}}}\) shows the consistency of (A\(_M\))-(D\(_M\)) in \({\mathsf {LMa^{-}}}\): \({\mathfrak {M}_{\textsf{M}}}=\langle {\mathfrak {F}_{\textsf{M}}}, V\rangle \), with \(W=\{w_1,w_2,w_3\}, W_{\mathsf {{S}y}}=W_{\textsf{harm}}=W_\texttt {P}=\{w_2\}\), \(W_\texttt {R}=\emptyset \), \(V(\mathtt {des\_kill})=\{w_1\}\) and \(V(\texttt{death})=\{w_2\}\), and  . Figure 2 represents this model graphically. It is the case that
. Figure 2 represents this model graphically. It is the case that  , and
, and  . Furthermore, we have
. Furthermore, we have  and also
and also  . So all the conditions defining instruments (cf. Definition 10) are satisfied, and thus we have that
. So all the conditions defining instruments (cf. Definition 10) are satisfied, and thus we have that  (sentence (A\(_M\))). Similarly, it can be verified that indeed \({\mathfrak {M}_{\textsf{M}}}\) also satisfies sentences (B\(_M\)), (C\(_M\)) and (D\(_M\)).
(sentence (A\(_M\))). Similarly, it can be verified that indeed \({\mathfrak {M}_{\textsf{M}}}\) also satisfies sentences (B\(_M\)), (C\(_M\)) and (D\(_M\)).
What is more, the assumptions (A\(_M\)), (C\(_M\)) and (D\(_M\)) entail that, in fact, the śyena is prohibited; indeed these sentences imply that  . A\(_M\) implies that
. A\(_M\) implies that  ,
,  , and also
, and also  . Furthermore,
. Furthermore,  , because \(W_{\texttt {R}}=\emptyset \). Hence, all conditions of instrumentality in the definition of prohibition are satisfied and we have that
, because \(W_{\texttt {R}}=\emptyset \). Hence, all conditions of instrumentality in the definition of prohibition are satisfied and we have that  .Footnote 9
.Footnote 9
For Maṇḍana then, there is a dilemma; it is true that “if you desire to kill your enemy, you ought to sacrifice with the śyena”, but also “if you desire to kill your enemy, you are prohibited from performing the śyena”. He solves this dilemma not on a normative level, but by appealing to the agent’s rationality. Maṇḍana argues that the śyena should not be performed, because even though it provides the worldly reward of the death of one’s enemy, this reward is not appealing enough compared to the accumulation of bad karma which always necessarily accompanies the śyena.
As illustrated by the śyena controversy, Maṇḍana distinguishes between two kinds of desires: worldly desires (such as desiring the death of one’s enemy) and karma-desires (the desire to diminish one’s accumulated bad karma and the desire not to accumulate bad karma). According to Maṇḍana the last kind of desire is necessarily present for any rational being, and hence does not need to be explicitly stated. Whereas Maṇḍana does not make a distinction between types of worldly desires (which are either present or absent), he does make a distinction between worldly desires and karma-desires. Our formalization mirrors this, as P and R define obligation and prohibition, and worldly desires define elective duties. Additionally, Maṇḍana distinguishes between the strength of worldly desires and karma-desires. This is made apparent in the informal discussion of the śyena controversy above, where Maṇḍana looks at the distinction in strength of these two types of desires only for the purpose of resolving the apparent decision dilemma of the śyena controversy: no rational agent would prefer worldly desires over karma-desires in case of conflict.
4.3 Other Perspectives on śyena
The debate around the śyena controversy is not limited to the three authors that we have analyzed. The topic has indeed been thoroughly investigated in Sanskrit philosophy for more than two millennia, and many more (different) solutions have been provided; some of the most important ones are briefly discussed below, in an informal way. The reader may recognise that much work is still needed to be done unearth the logical background for each of these authors/schools, whose positions are recalled below, in chronological order.
Position of the Sāṅkhya school
The Sāṅkhya school is mentioned as an opponent in Mīmāṃsā texts. According to Sāṅkhya, the śyena should not be performed, because not all the Vedic commands should be fulfilled, in particular the ones clashing with prohibitions should not be fulfilled. In a logic formalizing this position, prohibitions should have a stronger deontic value than prescriptions; the latter should only be followed in the absence of clashes. The specific properties of these deontic operators remain to be investigated on the basis of relevant Sanskrit texts.
Śabara’s position
Śabara (around 5th c.CE) is the author of a fundamental text of Mīmāṃsā, accepted by Kumārila, Prabhākara and Maṇḍana. According to him, the śyena should not be performed, because it is in conflict with the overall purpose of the Veda (anartha). Thus, the Veda appears to prescribe mainly things which conduce to the fulfilment of human purposes in harmony with the overall purpose of the Veda, but occasionally also things that clash with the Vedic purpose. The latter should be disregarded. As in common Mīmāṃsā, Śabara assumes that the Veda is overall consistent, and that seeming conflicts are due to an error in one’s interpretation and can therefore be explained away through an accurate interpretation. Note that for Śabara the śyena should not be performed, because it clashes with the overall purpose of the Veda (e.g., avoiding violence), whereas for Kumārila only its result does. A logic formalizing Śabara’s reasoning in the case of conflicting commands should filter out those which clash with the overall purpose of the Veda. The latter concept seems hard to formalize, since it is not directly spelt out. In turn, it is identifiable as the purpose conveyed by Vedic prescriptions once one has eliminated localised cases of conflict.
Veṅkaṭanātha’s position
Veṅkaṭanātha’s traditional dates are 1269–1370. He reconfigured the school of Viśiṣṭādvaita Vedānta as a unitary school of Vedānta and Mīmāṃsā. Accordingly, he wrote a Mīmāṃsā treatise in which he disagrees with the interpretations of Śabara and of all the authors following him and reinterprets Mīmāṃsā in a theistic way. According to him, the śyena should be performed if one is already in the controversial position of desiring to kill one’s enemy, because the śyena will cause less suffering to the enemy about to be killed and less karmic penalty to oneself. Moreover, in case a person is about to cause major damages, performing the śyena will even be obligatory. Thus, like in Maṇḍana one is invited to consider costs and benefits attached to the performance of the śyena, but this is seen as the best solution if one really needs to kill an enemy, for instance if one needs to stop someone who is about to perpetrate a murder. Underlying principles: The whole Veda is here interpreted as God’s will. Hence, it cannot contain any part to be just disregarded (as in Śabara) or not-to-be performed (as in Kumārila, Maṇḍana and Prabhākara). Rather, some parts of it may come to use only in extremely exceptional situations, as the less evil solution. A logic formalizing Veṅkaṭanātha should have features of both Maṇḍana’s logic (the cost benefit approach) and Prabhākara’s (the handling of contrary-to-duties commands).
Gaṅgeśa’s solution
Gaṅgeśa is generally credited with the foundation of the Navya Nyāya school of philosophy, which implements a metalanguage to describe and represent the relations among the terms of a syllogism according to the school of Nyāya. This metalanguage and the Navya Nyāya approach in general has been very influential in the methodology of Sanskrit philosophy after the 13th c. Following Maṇḍana, Gaṅgeśa recognises a prescription as communicating three elements, namely: 1. the action prescribed is the means to a desired end (as in Maṇḍana); 2. the action prescribed is realisable by oneself (as in Maṇḍana); 3. the action prescribed will lead to more benefits than disadvantages (only implicit in Maṇḍana). The performance of śyena should be avoided, because it satisfies 1 and 2, but it violates 3. Gaṅgeśa’s position was formally analyzed in Guhe (2021) using Action Deontic Logic (Giordani and Canavotto (2016)). Note that in contrast with our approach that attempts to formalize the various authors by extracting logics from the original texts, Guhe adapted a ready-made logic and applied it to Navya Nyāya discussions of the śyena controversy.
Later solutions
More recent and contemporary authors, like the 20th c. U.T. Vīrarāghavācārya, discuss the śyena in a new context, namely that of preventing acts of violence. They explain that the śyena is justified in case an enemy is ātatāyin, i.e., ready to attack. This point of view would also solve the seeming problem of the Vedas prescribing a sacrifice that should not be performed, by explaining that its performance is restricted to specific cases of self-defence or defence of others. This position is not discussed by the earlier authors presented in the preceding sections.
5 Back: Deontic Paradoxes in Mīmāṃsā Logics
In deontic logic, paradoxes are the driving force for defining new systems, and serve as sanity checks for existing ones. The paradoxes allow to identify and underline what (intuitively) should or should not hold in a logic. They usually consist of (un)derivable formulas which are counterintuitive in a common-sense reading. The word “paradox” might be too strong, and arguably many of the considered problems are not paradoxes per se. Although in the literature denoted as such, the reader is encouraged to view them as dilemmas or puzzles.
This section analyses how the logics developed for the three Mīmāṃsā authors deal with well known deontic paradoxes. We consider standard paradoxes which relate to actions rather than only states of affairs (an example of the latter are the cottage regulations in Prakken and Sergot (1996)). For a structured analysis of the paradoxes we group them into paradoxes of conditionals, by which we mean puzzles related to issues arising from conditional norms, such as Contrary-To-Duties (CTDs) and exceptions, and paradoxes of logical properties, which arise from properties of the deontic systems themselves, such as axioms or inference rules.
We start by pointing out some characteristics of our logics: (i) for Mīmāṃsā, negative obligations and prohibitions are two distinct concepts (contrary to common approaches in deontic logic) and (ii) duties are either obligations or electives, the distinctive fact of the latter being the presence of a desire.
Note that in our systems, having both obligation and prohibition as primitives allows us to re-think the paradoxes, and to analyse them in multiple ways, each with its own outcome; this contrasts with the usualFootnote 10 approach to deontic logic in which obligations and prohibitions are interdefinable.
Recall that Kumārila’s logic \({\mathsf {LKu^{+}}}\) is a proper extension of Prabhākara’s logic \({\mathsf {LPr^{+}}}\) and the perspectives of the two authors only differ on the interpretation of elective sacrifices. As the additional operator \(\mathcal {E}(\cdot /\cdot )\) of Kumārila’s logic is not applicable to the analysed paradoxes (none of them are conditional on desires), we discuss Kumārila’s and Prabhākara’s possible interpretations of the paradoxes as a single point of view.
5.1 Paradoxes of Conditionals
Paradox 1
(Chisholm) Consider the following four sentences:
-
1
You ought to go to the assistance of your neighbours
-
2
If you go to the assistance of your neighbours, you ought to let them know that you are coming
-
3
If you do not go to the assistance of your neighbours, you ought to not tell them that you are coming
-
4
You are not going to the assistance of your neighbours
In SDL these sentences are either mutually inconsistent, or not mutually independent. Discussed by Chisholm (1963), this paradox represents the turning point in deontic logic from monadic to dyadic operators. It is indeed traditionally solved by introducing a dyadic obligation operator. This results in CTD reasoning, where obligations have different grades. First, the primary obligation is in effect (sentence 1), and then the secondary obligation comes into effect when in a world of violation (sentence 3).
Paradox 2
(Gentle Murder (GMP)) In many deontic logic systems, the following four sentences allow to derive the obligation to kill:
-
1
You ought not kill
-
2
If you kill, you ought to kill gently
-
3
Killing gently is killing
-
4
You do kill
The GMP (also called Forrester’s Paradox) was originally introduced as a stronger variant of the Good Samaritan Paradox in Forrester (1984) (which we will discuss in Sect. 5.2), but later seen as a classic case of CTD reasoning. This paradox shows that not all CTD reasoning can be resolved by introducing temporal distinctions (as it would be the case of Chisholm’s Paradox). Killing and killing gently should indeed occur simultaneously.
Paradox 3
(Considerate Assassin Paradox (CAP)) The paradox consists of the following sentences:
-
1
You should not kill the witness
-
2
If you kill the witness, you should offer him a cigarette
-
3
You should not offer cigarettes
-
4
Killing without offering a cigarette and vice versa are possible
-
5
You kill the witness
where 1 and 2 come from the same normative code (mafia rules), whereas 1 and 3 come from a different code (moral).
The above paradox was introduced by Prakken and Sergot (1996). In contrast with the previous paradoxes, it combines two normative sources. We thus get that 2 is a CTD to 1, and also 2 is in conflict with 3. The authors claim that this is precisely what we want: a system which makes 2 and 3 inconsistent, as they are unrelated obligations. Alternatively, if we regard 2 as an exception to 3, we need some nonmonotonicity to adequately deal with this scenario. So this paradox allows us to do a double-sanity-check. First, we can verify if sentences 1,2,4,5 are consistent in our logics, and in a second step we can see if adding 3, the exception sentence, makes them inconsistent.
Prabhākara and Kumārila
From their perspectives, all dilemmas related to representing conditionals are similar to the case of śyena (cf. Sect. 4). For the GMP, this similarity is extended even to the content of the sentences, with the difference between śyena and GMP being the fact that the condition of killing someone is not a desire, and the lack of statement 4 in the śyena case. Hence we consider in detail only the statements of Chisholm’s Paradox and informally discuss the CAP. The sentences involved in Chisholm’s paradox can be formalized as:
-
1
\(\mathcal {O}(\texttt{go}/\top )\) or \(\mathcal {F}(\lnot \texttt{go}/\top )\)
-
2
\(\mathcal {O}(\texttt{tell}/\texttt{go})\) or \(\mathcal {F}(\lnot \texttt{tell}/\texttt{go})\)
-
3
\(\mathcal {O}(\lnot \texttt{tell}/\lnot \texttt{go})\) or \(\mathcal {F}(\texttt{tell}/\lnot \texttt{go})\)
-
4
We observe that, by axioms (\(\textsf{A}_{\textsf{P}}3\)), and (\(\textsf{A}_{\textsf{P}}4\)), formalizing sentences 1, 2, 3 as either obligations or prohibitions does not generate different outcomes in terms of conflicts between commands. Therefore, we use the most natural interpretation of the sentences, as “positive” commands, i.e., obligations.
Unlike in the śyena controversy, we have the additional assumption that a violation has necessarily already occurred ( ). The use of
). The use of  represents the fact that worlds free of violations, where the conditions for the CTD obligation (\(\mathcal {O}(\lnot \texttt{tell}/\lnot \texttt{go})\)) do not hold, are not taken into account. Still, statements 1–4 are not mutually inconsistent.
represents the fact that worlds free of violations, where the conditions for the CTD obligation (\(\mathcal {O}(\lnot \texttt{tell}/\lnot \texttt{go})\)) do not hold, are not taken into account. Still, statements 1–4 are not mutually inconsistent.
Remark 6
Having in the logics the rule of Deontic Detachment (DD) and Factual Detachment (FD) would lead to contradictions in CTD scenarios; these rules, in case of dyadic deontic operators, can be formalized as follows:
Indeed, using DD we can derive \(\mathcal {O}(\texttt{tell}/\top )\) from \(\mathcal {O}(\texttt{tell}/\texttt{go})\) and \(\mathcal {O}(\texttt{go}/\top )\), whereas FD allows us to derive \(\mathcal {O}(\lnot \texttt{tell}/\top )\) from \(\mathcal {O}(\lnot \texttt{tell}/\lnot \texttt{go})\) and  .
.
DD and FD are not included in \({\mathsf {LPr^{+}}}\) or \({\mathsf {LKu^{+}}}\) on purpose. The main reason for rejecting the former is the fact that Mīmāṃsā authors consider the duties to perform a sacrifice to be conditional only on states of affairs that cannot be prescribed, such as basic desires or external events whose occurrence cannot be enjoined to the agent, like a solar eclipse. The DD principle is also not applicable to the specific duties within a sacrifice, which could be conditioned on actions, because it would lead to the unwanted consequence of altering the sequence of enjoined duties (e.g., “Offer to Agni once you have offered to Soma”, “Offer to Soma after having milked the cow”).
As for FD, although a restricted form allowing to derive \(\mathcal {O}(\varphi /\top )\) from \(\mathcal {O}(\varphi /\psi )\) and  would not give rise to inconsistencies in \({\mathsf {LPr^{+}}}\) or \({\mathsf {LKu^{+}}}\), there are good reasons for not detaching the content of a command from its conditions in Mīmāṃsā logics. As a standard example, given the command “If one desires to kill their enemy, they should sacrifice bewitching with the śyena” and one’s desire to kill one’s enemy, Prabhākara and Kumārila do not conclude that one is obliged to perform the śyena, see Sect. 4. This interpretation is consistent with the already mentioned observation in Prabhākara “A prescription regards what has to be done; but it does not say that it has to be done” (see Remark 5) and corresponds to the approach to CTD obligations of traditional dyadic deontic logics, already outlined in von Wright (1956).
would not give rise to inconsistencies in \({\mathsf {LPr^{+}}}\) or \({\mathsf {LKu^{+}}}\), there are good reasons for not detaching the content of a command from its conditions in Mīmāṃsā logics. As a standard example, given the command “If one desires to kill their enemy, they should sacrifice bewitching with the śyena” and one’s desire to kill one’s enemy, Prabhākara and Kumārila do not conclude that one is obliged to perform the śyena, see Sect. 4. This interpretation is consistent with the already mentioned observation in Prabhākara “A prescription regards what has to be done; but it does not say that it has to be done” (see Remark 5) and corresponds to the approach to CTD obligations of traditional dyadic deontic logics, already outlined in von Wright (1956).
The CAP includes slightly different aspects, w.r.t. the previous paradoxes. Indeed, statement 2 (“if you kill the witness, you should offer him a cigarette”) does not only apply when command 1 (“you should not kill the witness”) is violated, but it explicitly violates a different unrelated command (3 “you should not offer cigarettes”). If 2 is formalized as an obligation, then the worlds where the act of offering cigarettes has been performed should be worlds of violation from the point of view of any world in the model, but also worlds of obedience from the perspective of the ones where the witness is killed. Surprisingly enough, none of the possible interpretations of sentences involved in the paradox is inconsistent. This happens because of the lack of monotonicity in the second arguments of the deontic operators: since we cannot obtain “even if you kill the witness, you should not offer cigarettes” from command 3, we do not derive any conflict between 2 and another injunction. In this sense, the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) are so weak, that only commands with conflicting contents and exactly equivalent conditions can give rise to contradictions.
Maṇḍana
We are faced with an additional challenge when formalizing the paradoxes in Maṇḍana’s logic. The deontic operators in Definition 10 are conditional on states of affairs, while the three paradoxes considered in this section are conditional on actions. Sentences such as “if you kill, you ought to kill gently” are fundamentally different than the ones discussed in Remark 4, where the condition and the prescribed action happen sequentially, while killing and gentle-killing are taking place at the same time. Below, we propose alternative interpretations of the conditional obligations and prohibitions occurring in the three deontic paradoxes of this section. We do this in order to adjust the paradoxes to Maṇḍana’s vocabulary, i.e., rewriting the involved commands in terms of instruments. The first attempt to translate to instruments an obligation \(\mathcal {O}(\Delta /\Gamma )\), where \(\Delta ,\Gamma \) are actions, is to keep the same format as before: \(\mathcal {I}(\Delta /\texttt {R}/t(\Gamma ))\). As a reminder, \(t(\Gamma )\) means that \(\Gamma \) has just been performed. However, sentences such as (from Chisholm’s paradox) “if you go to the assistance of your neighbours, you ought to let them know that you are coming”, will create problems. To illustrate this, consider the following. If we encode \(\mathcal {O}(\textsf{tell}/\textsf{go})\) as above, we obtain \(\mathcal {I}(\textsf{tell}/\texttt {R}/t(\textsf{go} ))\wedge \lnot \mathcal {I}(\textsf{tell}/\texttt {P}/t(\textsf{go} ))\). Since \(t(\textsf{go} )\) receives a temporal interpretation, meaning the action has just been performed, the formula would roughly mean “if you have just gone to the assistance of your neighbours, you ought to tell them you are coming”, which is not chronological and clearly not the intended meaning. Hence, we propose to think of the sentences with regard to the meaning that Maṇḍana assigns to something being obligatory or prohibited, namely referring to the reward or the penalty. What is expressed by a conditional obligation such as \(\mathcal {O}(\textsf{tell} /\textsf{go} )\), is that going-and-telling is instrumental to a reward. Similarly, if we expressed it as a prohibition \(\mathcal {F}(\lnot {\textsf{tell}}/\textsf{go} )\), then going-and-not-telling is instrumental to a sanction. Given the above, we formalize the conditional commands of the paradoxes in terms of instruments (Definition 10), as follows:
This definition has as effect the loss of symmetry between the treatment of obligations as prohibitions, which will be discussed in Remark 7.
Two remarks on the new commands. First, \(\mathcal {O^*}(\Delta /\Gamma )\) is different from \(\mathcal {O}(\Delta /t(\Gamma ))\), the former taking \(\Delta \) and \(\Gamma \) to be performed jointly in order to guarantee \(\texttt {R}\) and the latter introducing a temporal order (\(t(\Gamma )\) denotes that the action has already been performed). Second, in the above definition \(\mathcal {O^*}(\Delta /\Gamma )\) is equivalent to \(\mathcal {O^*}(\Gamma /\Delta )\). However, this is unproblematic, as it captures the idea that it is the joint performance of \(\Delta \) and \(\Gamma \) leading to \(\texttt {R}\).
Let us turn our attention to the individual paradoxes now. Paradox 1 can be formalized in the following way:
-
1
\(\mathcal {O}(\textsf{go}/\top )\) or \(\mathcal {F}(\lnot {\textsf{go}}/\top )\)
-
2
\(\mathcal {O^*}(\textsf{tell}/\textsf{go})\) or \(\mathcal {F}^*(\lnot {\textsf{tell}}/\textsf{go})\)
-
3
\(\mathcal {O^*}(\lnot {\textsf{tell}}/\lnot {\textsf{go}})\) or \(\mathcal {F}^*(\textsf{tell}/\lnot {\textsf{go}})\)
-
4
\(t(\lnot {\textsf{go}})\)
Unlike Prabhākara and Kumārila, we formalise sentence 4 without the box modality. This is because we use a temporal-like structure, and thus having  would be counter-intuitive.Footnote 11 Furthermore, if an instrument is true in a model, then the instrumentality relation is true at every world in the model, so for proving consistency we require a model of 1–4 such that 1–3 are true in the model, and that 4 holds in at least one world. Table 1 shows the different possibilities of formalizing sentences 1–3, and their consistency status. Out of the eight possible formalizations, four are consistent in \({\mathsf {LMa^{-}}}\). As an example, we provide a model for the formalization #3 in Table 1. The following \({\mathsf {LMa^{-}}}\)-model \({\mathfrak {M}_{\textsf{M}}}=\langle {\mathfrak {F}_{\textsf{M}}}, V\rangle \) satisfies \(\mathcal {F}(\lnot {\textsf{go}}/\top )\wedge \mathcal {O^*}(\textsf{tell}/\textsf{go})\wedge \mathcal {F}^*(\textsf{tell}/\lnot \textsf{go})\wedge \lnot t(\textsf{go})\) at world w: with \(W=\{w,v\}\), \(W_{\textsf{go}}=\{v\}\), \(W_{\textsf{tell}}=\{w,v\}\), \(W_{\texttt {P}}=\{w\}\), \(W_{\texttt {R}}=\{v\}\).
would be counter-intuitive.Footnote 11 Furthermore, if an instrument is true in a model, then the instrumentality relation is true at every world in the model, so for proving consistency we require a model of 1–4 such that 1–3 are true in the model, and that 4 holds in at least one world. Table 1 shows the different possibilities of formalizing sentences 1–3, and their consistency status. Out of the eight possible formalizations, four are consistent in \({\mathsf {LMa^{-}}}\). As an example, we provide a model for the formalization #3 in Table 1. The following \({\mathsf {LMa^{-}}}\)-model \({\mathfrak {M}_{\textsf{M}}}=\langle {\mathfrak {F}_{\textsf{M}}}, V\rangle \) satisfies \(\mathcal {F}(\lnot {\textsf{go}}/\top )\wedge \mathcal {O^*}(\textsf{tell}/\textsf{go})\wedge \mathcal {F}^*(\textsf{tell}/\lnot \textsf{go})\wedge \lnot t(\textsf{go})\) at world w: with \(W=\{w,v\}\), \(W_{\textsf{go}}=\{v\}\), \(W_{\textsf{tell}}=\{w,v\}\), \(W_{\texttt {P}}=\{w\}\), \(W_{\texttt {R}}=\{v\}\).  and V such as defined in Definition 8 (note that we only use action atoms).
and V such as defined in Definition 8 (note that we only use action atoms).
Inconsistencies arise in the following situation: Let \(\mathcal {X}(\Delta /\top )\) be the primary command and \(\mathcal {Y^*}(\Gamma /\Gamma ')\) another command, with \(\mathcal {X,Y}\in \{\mathcal {O},\mathcal {F}\}\). If \(\mathcal {X}\ne \mathcal {Y}\) and \(t(\Gamma )\wedge t(\Gamma ')\rightarrow t(\Delta )\), then the action \(\Gamma \cap \Gamma '\) necessarily leads to both the reduction and the accumulation of bad karma (which is not allowed by Definition 10). Indeed, by assumption \(\Gamma \cap \Gamma '\) is an instrument for \(\texttt {P}\) (or \(\texttt {R}\)), while \(\Delta \) is an instrument for \(\texttt {R}\) (or \(\texttt {P}\)), yet \(\Gamma \cap \Gamma '\) is never performed without \(\Delta \). Note that in general an action may trigger \(\texttt {P}\wedge \texttt {R}\) (cf. Remark 3), however that action can neither be obligatory nor prohibited, as excluded by Definition 10. As an example, consider the formalization #5 in Table 1: we have \(\lnot t({\textsf{tell}})\wedge \lnot t({\textsf{go}})\rightarrow \lnot t({\textsf{go}})\) and \(\mathcal {F}(\lnot {\textsf{go}}/\top )\) as primary command (\(\mathcal {X}\)); it means that performing the action \(\lnot {\textsf{tell}}\cap \lnot {\textsf{go}}\) leads to \(\texttt {P}\), while \(\mathcal {O^*}(\lnot {\textsf{tell}}/\lnot {\textsf{go}})\) as CTD (\(\mathcal {Y}\)) implies that action \(\lnot {\textsf{tell}}\cap \lnot {\textsf{go}}\) leads to \(\texttt {R}\) at the same time, hence by definition \(\lnot \mathcal {O^*}(\lnot {\textsf{tell}}/\lnot {\textsf{go}})\), contradiction. Clearly, for Mīmāṃsā, non-meaningfulness of the prescribed actions is not allowed and hence the inconsistent formalizations are dismissed.
It is easy to see that in Table 1 all the sentences in each formalization are mutually independent. Notice that obligations and prohibitions are mutually irreducible due to their definition in terms of instruments (Definition 10).
The GMP is handled similarly to Chisholm’s paradox, with only two commands, bringing the number of formalization possibilities down to four:
-
1
\(\mathcal {O}(\lnot \textsf{kill}/\top )\) or \(\mathcal {F}(\textsf{kill}/\top )\)
-
2
\(\mathcal {O^*}(\mathsf {kill\_gently}/\textsf{kill})\) or \(\mathcal {F}^*(\lnot \mathsf {kill\_gently}/\textsf{kill})\)
-
3
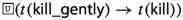
-
4
\(t(\textsf{kill})\)
Three of them are consistent. The only inconsistent option is having the primary prohibition \(\mathcal {F}(\textsf{kill}/\top )\) and the secondary obligation \(\mathcal {O^*}(\mathsf {kill\_gently}/\textsf{kill})\), for the same reason as in Chisholm’s Paradox (Paradox 1). (We do have an additional constrains  , but this does not change the pattern.) It is interesting to note how, in Maṇḍana’s formalization, the GMP is actually quite different from the śyena controversy. The GMP’s CTD is conditional on the action of killing, whereas in the śyena case the prescription is conditional on the state of affairs of desiring the death of one’s enemy, which makes their respective formalizations different in a logic differentiating between actions and results, such as \({\mathsf {LMa^{-}}}\). Furthermore, we have formalized the śyena as having a primary prohibition and a CTD obligation, which is precisely the case that is excluded for the GMP. If we want to insist on formalizing the “you ought not kill” as a prohibition (in the Mīmāṃsā fashion, since killing necessarily has ethical and/or legal bad consequences), then we have to formalize the CTD prescription as a prohibition as well, in order to preserve consistency.
, but this does not change the pattern.) It is interesting to note how, in Maṇḍana’s formalization, the GMP is actually quite different from the śyena controversy. The GMP’s CTD is conditional on the action of killing, whereas in the śyena case the prescription is conditional on the state of affairs of desiring the death of one’s enemy, which makes their respective formalizations different in a logic differentiating between actions and results, such as \({\mathsf {LMa^{-}}}\). Furthermore, we have formalized the śyena as having a primary prohibition and a CTD obligation, which is precisely the case that is excluded for the GMP. If we want to insist on formalizing the “you ought not kill” as a prohibition (in the Mīmāṃsā fashion, since killing necessarily has ethical and/or legal bad consequences), then we have to formalize the CTD prescription as a prohibition as well, in order to preserve consistency.
Lastly, let us discuss the peculiar CAP. Here we have at the same time a CTD and an exception, that share similar structures but require different treatment. In \({\mathsf {LMa^{-}}}\), we can formalize the paradox the following way:
-
1
\(\mathcal {O}(\lnot \textsf{kill}/\top )\) or \(\mathcal {F}(\textsf{kill}/\top )\)
-
2
\(\mathcal {O^*}(\textsf{cigarette}/\textsf{kill})\) or \(\mathcal {F}^*(\lnot \textsf{cigarette}/\textsf{kill})\)
-
3
\(\mathcal {O}(\lnot \textsf{cigarette}/\top )\) or \(\mathcal {F}(\textsf{cigarette}/\top )\)
-
4
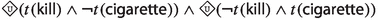
-
5
\(t(\textsf{kill})\)
As mentioned, Prakken and Sergot (1996) argue that in CAP, sentences 1 and 2 should not create any conflicts, while sentences 2 and 3 should. Hence, we first look at sentences 1,2,4,5 in all possible interpretations, and see which models are consistent. Then, for the consistent models, we add sentence 3 in both possible interpretations, and see whether this makes the model inconsistent. The results are the following. For the first step, we are in a very similar situation as for the GMP, and here we also have that three of the four possibilities are consistent, with one inconsistent (primary prohibition, CTD obligation). Building the second part on top of the three consistent possibilities, we get in the end six possibilities, five of which are inconsistent (the only consistent one is when the commands are all formalized as prohibitions). In particular, formalising all three commands as obligations, as done in Prakken and Sergot (1996), is inconsistent, as the authors claim it should be.
Remark 7
In the deontic logic literature, there is often a symmetry between obligation and prohibition. Indeed prohibition is typically defined using obligation and negation, i.e., \(\mathcal {F}\beta =_{def} \mathcal {O}\alpha \) with \(\beta =\lnot \alpha \). As seen in the formalizations of GMP and CAP, by adopting a Maṇḍana interpretation of the conditionals occurring in those paradoxes, we lose this symmetry on the instrumentality level. To illustrate that, first consider an action \(\Delta \) and a state of affairs \(\varphi \) in the sentence “you ought not do \(\Delta \) given \(\varphi \)”. We can interpret the sentence as either
-
\(\mathcal {O^*}(\lnot \Delta /\varphi ) =\mathcal {I}(\lnot \Delta /\texttt {R}/\varphi )\wedge \lnot \mathcal {I}(\lnot \Delta /\texttt {P}/\varphi )\), or
-
\(\mathcal {F}^*(\Delta /\varphi ) =\mathcal {I}( \Delta /\texttt {P}/\varphi )\wedge \lnot \mathcal {I}( \Delta /\texttt {R}/\varphi )\)
In this case, we find the above symmetry preserved (with the addition of exchanging \(\texttt {R}\) for \(\texttt {P}\), and vice versa). Now, consider two actions \(\Delta \) and \(\Gamma \) and the sentence “you ought not to do \(\Delta \) given \(\Gamma \)”. As argued in our discussion of Chisholm’s paradox, in the context of Maṇḍana the sentence can be formalised as either
-
\(\mathcal {O^*}(\lnot \Delta /\Gamma ) =\mathcal {I}(\lnot \Delta \cap \Gamma /\texttt {R}/\top )\wedge \lnot \mathcal {I}(\lnot \Delta \cap \Gamma /\texttt {P}/\top )\), or
-
\(\mathcal {F}^*(\Delta /\Gamma ) =\mathcal {I}( \Delta \cap \Gamma /\texttt {P}/\top )\wedge \lnot \mathcal {I}( \Delta \cap \Gamma /\texttt {R}/\top )\)
The complex action in the first argument of the two instruments defining the obligation is \(\alpha =\lnot \Delta \cap \Gamma \), and in the case of the prohibition it is \(\beta =\Delta \cap \Gamma \). In this case, we cannot obtain anymore a prohibition from an obligation by changing the modal operators and negating the involved action as \(\lnot \alpha \not \equiv \beta \). This is in line with Mīmāṃsā deontic theory for which there is no symmetry between obligation and prohibition (see Sect. 2). The reason for this break in symmetry lies in the way obligations and prohibitions conditional on actions are defined: we interpret the action \(\Delta \) (cf. \(\textsf{tell}\)) and \(\Gamma \) (cf. \(\textsf{go}\)) as occurring simultaneously. In fact, in Prakken and Sergot (1996) it was argued that many contrary-to-duty scenarios (cf. Chisholm’s paradox) do not have a temporal reading, and the involved actions must be considered as occurring simultaneously.
5.2 Paradoxes of Logical Properties
Paradox 4
[Ross] The paradox consists in the derivation of
-
You should mail the letter or burn it
from the sentence
-
You should mail the letter
This paradox was introduced in Ross (1944), and has been a discussion topic ever since. It arises from the following formula, expressing (upwards) monotonicity of the obligation operator, which is valid in many deontic logics:
One can easily explain the paradox away, since mailing the letter automatically satisfies mailing-or-burning it. However, it does not suffice to burn the letter, since one also has the second obligation to mail it. Hence, mailing is sufficient for both obligations, and burning only for one.
Paradox 5
(Good Samaritan (GSP)) The paradox consists in deriving
-
A person ought to be robbed
from the sentence
-
You ought to help a robbed person
In SDL, this paradox arises from the fact that helping a robbed person together with formula (1) above implies that there is a robbed person. In its original form (Prior 1958), this paradox was introduced in terms of prohibitions, where the sentence “You are prohibited to help a robbed person” can be derived from “A person should not be robbed”with (downward) monotonicity of the deontic operator in (1):
Paradox 6
(Alternative Service) Given the following two sentences,
-
1
You should (fight in the army or perform alternative service)
-
2
You should not fight in the army
we would like to derive that you should perform alternative service.
This paradox was first discussed in Horty (1994), arguing that obligations like these may arise from different normative codes; the first one plausibly can be given by a legal code, and the second by a religious or moral one. Given the obligations above, one intuitively would like to derive the obligation of performing alternative service, a solution that would satisfy both initial obligations. In many systems, however, such derivation cannot be made.
Prabhākara and Kumārila
Let us first consider the logical form of the statements involved in Ross paradox, which might also be considered as a base case of the Good Samaritan Paradox (i.e., Paradox 5).
-
(i)
“you ought to mail the letter” \(\mathcal {O}(\texttt{mail}/\top )\)
-
(ii)
\(\vdash _{{\mathsf {LPr^{+}}}} \texttt{mail}\rightarrow (\texttt{mail}\vee \texttt{burn})\)
-
(iii)
“you ought to mail or burn the letter” \(\mathcal {O}(\texttt{mail}\vee \texttt{burn}/\top )\)
As all “paradoxes” determined by the monotonicity in the first argument of the deontic operators, Ross paradox cannot be avoided in \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\). However it may be argued that this paradox is intrinsic to the use of material implication and, though strange, the phenomenon does not give rise to contradictions, nor to normative problems.
In principle, the GSP is not dissimilar from the previous case; however the dyadic setting changes its status. The most natural interpretation of the first statement “You ought to help a robbed person” in \({\mathsf {LPr^{+}}}\) appears to be \(\mathcal {O}(\texttt{help}/\texttt{robbed})\) (“you ought to help a person if this person is being robbed”), from which the second statement “A person ought to be robbed” cannot be derived. Hence, though it remains derivable that “helping a person who is being robbed implies that a person is being robbed” ( ), we do not obtain that “it ought to be the case that a person is being robbed”, because the theft was never among the states of affairs to be achieved. The analysis does not change if we interpret the main command as the prohibition “it is forbidden not to help a robbed person” \(\mathcal {F}(\lnot \texttt{help}/\texttt{robbed})\). As in the case of obligations, the counterintuitive command cannot be derived.
), we do not obtain that “it ought to be the case that a person is being robbed”, because the theft was never among the states of affairs to be achieved. The analysis does not change if we interpret the main command as the prohibition “it is forbidden not to help a robbed person” \(\mathcal {F}(\lnot \texttt{help}/\texttt{robbed})\). As in the case of obligations, the counterintuitive command cannot be derived.
The Alternative Service Paradox presents some peculiarities, as it does not depend on the monotonicity of deontic operators. Let us consider the following possible formal interpretations of the paradox:
-
i
\(\mathcal {O}(\mathtt {fight\_army}\vee \mathtt {alt\_service}/\top )\) and \(\mathcal {O}(\lnot \mathtt {fight\_army}/\top )\)
-
ii.
\(\mathcal {O}(\mathtt {fight\_army}\vee \mathtt {alt\_service}/\top )\) and \(\mathcal {F}(\mathtt {fight\_army}/\top )\)
-
iii.
\(\mathcal {F}(\lnot \mathtt {fight\_army}\wedge \lnot \mathtt {alt\_service}/\top )\) and \(\mathcal {O}(\lnot \mathtt {fight\_army}/\top )\)
-
iv.
\(\mathcal {F}(\lnot \mathtt {fight\_army}\wedge \lnot \mathtt {alt\_service}/\top )\) and \(\mathcal {F}(\mathtt {fight\_army}/\top )\)
From the point of view of a Mīmāṃsā-inspired logic, the second command seems more properly formalized as a prohibition, as no reward appears to be attached to its fulfilment. Only if we were to attach a reward to the fulfilment of the command —interpreting it as moral duty or a social norm compensated by heaven or public approval— it would be possible to formalize it as the negative obligation “one ought to perform the action of refraining from fighting”: under this interpretation, the paradox can be analysed in terms of obligations. Although no interpretation gives rise to inconsistencies, the use of the obligation operator for both the sentences involved in the paradox is the only one which solves it. The reason for this is that, as discussed in Sect. 3.1 with reference to the principle (P4), unconditional obligations are the only commands to which the aggregation principle (expressed by axiom (\(\textsf{A}_{\textsf{P}}6\))) is applicable; hence (i) is the only case which allows us to derive the obligation to perform alternative service.
Maṇḍana
Ross Paradox does not hold in \({\mathsf {LMa^{-}}}\). Indeed the sentence “you should mail the letter” can be written in \({\mathsf {LMa^{-}}}\) either as \(\mathcal {O}(\textsf{mail}/\top )\) or as \(\mathcal {F}(\lnot \textsf{mail}/\top )\). A model of \({\mathsf {LMa^{-}}}\) such that it is obligatory to mail the letter holds, without it being obligatory to mail-or-burn the letter is as follows: \(\mathfrak {M}_\textsf{M}=\langle \mathfrak {F}_\textsf{M}, V\rangle \), with \(W=\{w,v\}\), \(W_\textsf{mail}=\{w\}\), \(W_\textsf{burn}=\{v\}\), \(W_\texttt {P}= \emptyset \), \(W_\texttt {R}= \{w\}\),  , and V as defined in Definition 8. Then it is the case that \({\mathfrak {M}_{\textsf{M}}}\vDash O(\textsf{mail}/\top )\) but \({\mathfrak {M}_{\textsf{M}}}\not \vDash O(\textsf{mail}\cup \textsf{burn}/\top )\) (condition (i) of Definition 10 is not satisfied). A model in which it holds that \(\mathcal {F}(\lnot \textsf{mail}/\top )\) but without having \(\mathcal {F}(\lnot (\textsf{mail}\cup \textsf{burn})/\top )\) can be defined in a similar way. Note indeed that the formula (1), which gives rise to the paradox, is not \({\mathsf {LMa^{-}}}\)-valid. Here we go back to the discussion of principle (p1) in Sect. 3.3. Instrumentality is a notion of sufficient cause, not of necessary cause. So even if
, and V as defined in Definition 8. Then it is the case that \({\mathfrak {M}_{\textsf{M}}}\vDash O(\textsf{mail}/\top )\) but \({\mathfrak {M}_{\textsf{M}}}\not \vDash O(\textsf{mail}\cup \textsf{burn}/\top )\) (condition (i) of Definition 10 is not satisfied). A model in which it holds that \(\mathcal {F}(\lnot \textsf{mail}/\top )\) but without having \(\mathcal {F}(\lnot (\textsf{mail}\cup \textsf{burn})/\top )\) can be defined in a similar way. Note indeed that the formula (1), which gives rise to the paradox, is not \({\mathsf {LMa^{-}}}\)-valid. Here we go back to the discussion of principle (p1) in Sect. 3.3. Instrumentality is a notion of sufficient cause, not of necessary cause. So even if  , \(\Delta \) being an instrument for \(\varphi \) does not imply that \(\Gamma \) is also an instrument for \(\varphi \). Although we know that \(\Delta \) is always accompanied by \(\Gamma \), we have no information on whether \(\Gamma \) is sufficient for achieving \(\varphi \) (\(\Gamma \) could be independent of \(\varphi \) in a non-\(\Delta \) context).
, \(\Delta \) being an instrument for \(\varphi \) does not imply that \(\Gamma \) is also an instrument for \(\varphi \). Although we know that \(\Delta \) is always accompanied by \(\Gamma \), we have no information on whether \(\Gamma \) is sufficient for achieving \(\varphi \) (\(\Gamma \) could be independent of \(\varphi \) in a non-\(\Delta \) context).
With respect to GSP (i.e., Paradox 5), “you ought to help a robbed person” and “a person should not be robbed” can be formalised as \(\mathcal {O^*}(\textsf{help}/\textsf{robbed})\) and \(\mathcal {F}(\textsf{robbed}/\top )\). It is easy to construct a model such that the above obligation, resp. prohibition holds, without having \(\mathcal {O}(\textsf{robbed}/\top )\), resp. \(\mathcal {F}^*(\textsf{help}/\textsf{robbed})\). Although similar to Ross’s paradox, this paradox disappears in a dyadic representation.
Last, let us consider the Alternative Service paradox. We have the following formalization choices:
-
1
\(\mathcal {O}(\mathsf {fight\_army}\cup \mathsf {alt\_service}/\top )\) or \(\mathcal {F}(\lnot \mathsf {fight\_army} \cap \lnot \mathsf {alt\_service}/\top )\)
-
2
\(\mathcal {O}(\lnot \mathsf {fight\_army}/\top )\) or \(\mathcal {F}(\mathsf {fight\_army}/\top )\)
Out of the four possible combinations, three are inconsistent:
-
(a)
\(\mathcal {O}(\mathsf {fight\_army}\cup \mathsf {\mathsf {alt\_service}}/\top )\wedge \mathcal {O}(\lnot \mathsf {fight\_army}/\top )\) is inconsistent: any such model cannot have a \(\lnot \texttt {R}\) world, since both \(\mathsf {fight\_army}\) as well as \(\lnot \mathsf {fight\_army}\) necessarily lead to \(\texttt {R}\). Thus contradicting axiom \(\textsf{A}_{\textsf{M}}4\).
-
(b)
\(\mathcal {O}(\mathsf {fight\_army} \cup \mathsf {alt\_service} /\top )\wedge \mathcal {F}(\mathsf {fight\_army} /\top )\) is inconsistent: any such model has to satisfy
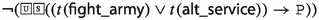 because of the obligation, and
because of the obligation, and 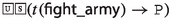 because of the prohibition.
because of the prohibition. -
(c)
\(\mathcal {F}(\lnot \mathsf {fight\_army} \cap \lnot \mathsf {alt\_service}/\top )\wedge \mathcal {O}(\lnot \mathsf {fight\_army}/\top )\) is inconsistent for the same reason as the previous one.
-
(d)
\(\mathcal {F}(\lnot \mathsf {fight\_army} \cap \lnot \mathsf {alt\_service}/\top )\wedge \mathcal {F}(\mathsf {fight\_army} /\top )\) is consistent: consider the model: \({\mathfrak {M}_{\textsf{M}}}=\langle {\mathfrak {F}_{\textsf{M}}}, V\rangle \) with \(W=\{w,v,u\}\), \(W_{\mathsf {fight\_army}}=\{w\}\), \(W_{\mathsf {alt\_service}}=\{w,u\}\), \(W_{\texttt {R}}=\emptyset \), \(W_{\texttt {P}}=\{w,v\}\),
 and V as in Definition 8.
and V as in Definition 8.
Furthermore, the following claim holds (the proof is in “Appendix C”):
Claim 1
Let \({\mathfrak {M}_{\textsf{M}}}\) be an \({\mathsf {LMa^{-}}}\)-model. If \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \cap \lnot \mathsf {alt\_service}/\top )\) and \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\mathsf {fight\_army}/\top )\), then also \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {alt\_service}/\top )\)
Note that we cannot apply the restricted aggregation principle discussed in Sect. 3.3, since the actions \(\lnot \mathsf {fight\_army} \cap \lnot \mathsf {alt\_service}\) and \(\mathsf {fight\_army}\) cannot be performed at the same time. The prohibition of both, however, can be complied with by performing \(\mathsf {alt\_service}\cap \lnot \mathsf {fight\_army}\).
To summarize, we have a single possibility of formalizing the Alternative Service Paradox for Maṇḍana, and this formalization gives in fact the desired result. In natural language these norms are expressed as obligations rather than prohibitions, so is our formalization “correct”? Here, it is important to recall the Mīmāṃsā idea that transgressing an obligation has no effect, and obeying it has a positive effect, while transgressing a prohibition has a negative effect and obeying a prohibition has no effect. Looking back at the initial sentences, it makes sense to formalize “you should fight in the army or perform alternative service” as a prohibition, since in many countries violating this command results in a sanction. Furthermore, the second sentence “you should not fight in the army”, can reasonably be seen as a prohibition as well: transgressing it might result in an ethical sanction. We thus claim that the fourth formalization is the correct one (in the spirit of the Mīmāṃsā authors), and that \({\mathsf {LMa^{-}}}\) solves the paradox in the desired manner.
6 Conclusions
The philosophical school of Mīmāṃsā provides a treasure trove of more than two millennia of deontic investigations. This paper analyses them through an interdisciplinary collaboration between scholars of logic, computer science and Sanskrit philosophy. Within it, (i) we have introduced logics formalizing the deontic theories of the leading Mīmāṃsā authors: Prabhākara, Kumārila and Maṇḍana. We obtained these logics by “extracting” Hilbert axioms out of translated and parsed Mīmāṃsā nyāyas (and additional passages by the three authors), and (ii) we have used them to formally reconstruct the different solutions of Prabhākara, Kumārila and Maṇḍana to the millennia-old śyena controversy. The obtained formal solutions, which clarify the positions of the three authors, turned out to be faithful to the explanations found in Mīmāṃsā texts themselves.
Furthermore, we analyzed the introduced logics and their behaviour (thus addressing the “back”direction). We used an established method in the deontic logic literature: confronting them with some of the most famous deontic paradoxes, which we grouped into “paradoxes of conditionals” (Chisholm’s Paradox, the Gentle Murder Paradox (GMP), and the Considerate Assassin Paradox (CAP)), and “paradoxes of logical properties” (Ross’s Paradox, the Good Samaritan Paradox (GSP) and the Alternative Service Paradox).
The śyena controversy is based on real prescriptions found in the Vedas. Yet, it is very close to some of the above paradoxes, with certain differences for the various authors:
For Prabhākara, the śyena is a clear case of Contrary-to-Duty (CTD) reasoning, with the primary prohibition to perform violence, and the secondary obligation to perform the śyena, which becomes active only when the prohibition is violated (i.e., when someone desires to kill their enemy). Content- and structure-wise the śyena is close to the GMP.
Kumārila interprets instead the prescription to perform the śyena as an elective duty, which for him has no deontic force. Accordingly, Kumārila’s logic simply discredits the controversy as such, and does not consider it to be a paradox. One could compare Kumārila’s solution to approaches on priority orderings or hierarchies among deontic modalities (e.g., Boella and van der Torre (2008); Hansen (2008)), assigning the lowest rank to elective duties.
In contrast with the other two authors, Maṇḍana endorses the view that there is an actual dilemma, as we have the elective duty to perform the śyena, as well as the prohibition which tells us to refrain from performing it, the two are incompatible instruments that hold in the same context. The presence of the dilemma makes Maṇḍana’s interpretation of the śyena closest to the GSP. Maṇḍana’s solution appeals to the rationality of the agent, who would never perform the śyena, as the bad result associated with it (the accumulation of bad karma), outweighs any worldly result such as the death of one’s enemy.
Deontic paradoxes have been successfully used in the deontic literature as benchmarks, and to motivate the introduction of new logical systems. The logics \({\mathsf {LPr^{+}}}\), \({\mathsf {LKu^{+}}}\) and \({\mathsf {LMa^{-}}}\) behave well with respect to the considered paradoxes, which were selected among the best known paradoxes referring to actions. \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) solve indeed most of the paradoxes, and \({\mathsf {LMa^{-}}}\) solves all of them, when formalizing the sentences in the spirit of these three Mīmāṃsā author. These encouraging results may be due to the depth of the deontic theories of Prabhākara, Kumārila and Maṇḍana at the base of their logics.
More precisely, due to the deliberate absence of deontic and factual detachment, the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) can represent CTDs. Their weakness, however, does not allow to detect the desired inconsistency in the CAP. Maṇḍana’s case is slightly different. Some of the various formalization possibilities for the paradoxes were inconsistent, but many others represented CTD reasoning consistently. In particular, using the same deontic operator to formalize the commands in a CTD “conflict” results in a consistent formalization. The presence of exceptions, such as in the CAP, most often results in inconsistencies, as required.
Among the “paradoxes of logical properties”, Ross’s paradox cannot be avoided in Prabhākara’s and Kumārila’s logics, due to the monotonicity in the first argument of the deontic operators, while it is solved in Maṇḍana’s logic which deals with instruments. The GSP case disappears when formalised in a dyadic setting for all considered logics. Last, the logics of Prabhākara and Kumārila solve the Alternative Service Paradox only when the sentences are formalized as obligations, due to the Mīmāṃsā peculiarity of only letting obligations aggregate, while for Maṇḍana we found a single formalization that preserved consistency and that derives the desired result; this representation coincides with the Mīmāṃsā reading, as we represent all commands involved as prohibitions, each associated with a negative result.
In summary, the logics formalizing Prabhākara’s, Kumārila’s and Maṇḍana’s deontic theories solve the paradoxes in accordance with two main solution strategies also adopted in modern deontic logics: weaken the logic à la Chellas (see, e.g., Carmo and Jones (2002)), or change completely the method and adopt instead a logic of actions as, e.g., in Bartha (1993), Castañeda (1981), Giordani and Canavotto (2016), and Meyer et al. (1994). This is a surprising convergence for a philosophical approach whose foundations lie millennia back.
The present results only scratch the surface of the research opportunities offered by formal approaches to the study of Mīmāṃsā deontic reasoning.
We believe that Mīmāṃsā can offer new stimuli for the deontic logic community and challenge commonly accepted design choices, such as the inter-definability of obligations and prohibitions or the presence or absence of certain deontic principles.
Change history
21 January 2023
Missing Open Access funding information has been added in the Funding Note.
Notes
The Vedic commands are assumed to be consistent. Thus, Mīmāṃsā authors focused on finding the correct interpretation to make their consistency appear as such.
In this sense, Mīmāṃsā authors differed from other thinkers offering systematic interpretations of sacred texts, like the authors of the Talmud, since the latter aim at “not a logical solution but a practical one” Abraham et al. (2011). In other words, Talmudic deontic reasoning depends on the mediation of a rabbi who applies it, Mīmāṃsā deontic reasoning does not.
The PMS is divided into books, chapters and aphorisms. We will therefore refer to it, as is common in scholarship about Sanskrit philosophy, indicating the number of book, chapter and section: e.g., PMS 1.1.1 will indicate the first aphorism of the first chapter of the first book. Since the standard form of philosophy in the Sanskrit cosmopolis was writing a commentary on an earlier text, readers will find references to, e.g., Śabara’s or Kumārila’s commentaries on the PMS.
The literal translation of this nyāya is “When the various [requirements of a given duty], beginning with the origination [of a new duty], are not established by other distinct prescriptions, then [the only prescription available] itself creates the other four prescriptions that are related to it.”
tayor ekārthatvāt samuccayo na sambhavati (ŚBh 8.1.15.26),“Since the two [actions] have the same purpose, aggregation (samuccaya) is impossible”.
(A) and (B) are direct translations from Sanskrit, whereas (C) and (D) are derived from Mīmāṃsā arguments about the śyena.
Note that the conclusion
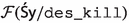 is not a Vedic prohibition; there is no such statement in the sacred texts. On a derived level, it is possible for Maṇḍana to have electives and prohibitions of the same actions, without having inconsistency. See Remark 1.
is not a Vedic prohibition; there is no such statement in the sacred texts. On a derived level, it is possible for Maṇḍana to have electives and prohibitions of the same actions, without having inconsistency. See Remark 1.A notable exception is Talmudic logic, see Abraham et al. (2011).
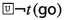 would mean that at every world in the model it is the case that one did not go to the assistance of one’s neighbours. Such an expression would make sentence number 2 not meaningful (recall, for a command the context must be possible in at least one world in order to not be devoid of meaning).
would mean that at every world in the model it is the case that one did not go to the assistance of one’s neighbours. Such an expression would make sentence number 2 not meaningful (recall, for a command the context must be possible in at least one world in order to not be devoid of meaning).
References
Abraham, M., Gabbay, D. M., & Schild, U. (2011). Obligations and prohibitions in Talmudic deontic logic. Artificial Intelligence and Law, 19(2–3), 117–148. https://doi.org/10.1007/s10506-011-9109-0.
Anderson, A. R., & Moore, O. K. (1957). The formal analysis of normative concepts. American Sociological Review, 22(1), 9–17. https://doi.org/10.2307/2088759.
Bartha, P. (1993). Conditional obligation, deontic paradoxes, and the logic of agency. Annals of Mathematics and Artificial Intelligence, 9, 1–23. https://doi.org/10.1007/BF01531259.
Benzmüller, C., Parent, X., & van der Torre, L. W. N. (2018). A deontic logic reasoning infrastructure. In F. Manea, R.G. Miller, & D. Nowotka (Eds.), Conference on Computability in Europe, CiE 2018 (Vol 10936 of Lecture Notes in Computer Science, pp. 60–69). Springer. 10.1007/978-3-319-94418-0_6.
van Berkel, K., & Pascucci, M. (2018). Notions of instrumentality in agency logic. In T. Miller, N. Oren, Y. Sakurai, I. Noda, B. T. R. Savarimuthu, & T. CaoSon (Eds.), PRIMA 2018: Principles and practice of multi-agent systems (pp. 403–419). Springer. https://doi.org/10.1007/978-3-030-03098-8_25.
van Berkel, K., Ciabattoni, A., Freschi, E., Gulisano, F., & Olszewski, M. (2021). The gentle murder paradox in sanskrit philosophy. In F. Liu, A. Marra, P. Portner, & F. V. D. Putte (Eds.), 15th international conference on deontic logic and normative systems, DEON 2020/2021. College Publications.
van Berkel, K., Lyon, T., & Olivieri, F. (2020). A decidable multi-agent logic for reasoning about actions, instruments, and norms, In M. Dastani, H. Dong, & L. van der Torre (Eds.), International conference on logic and argumentation (pp. 219–241). Springer. https://doi.org/10.1007/978-3-030-44638-3_14
Blackburn, P., de Rijke, M., & Venema, Y. (2004). Modal logic. Number 53 in Cambridge tracts in theoretical computer science. Cambridge University Press.
Boella, G., & van der Torre, L. (2008). Institutions with a hierarchy of authorities in distributed dynamic environments. Artificial Intelligence and Law, 16(1), 53–71. https://doi.org/10.1007/s10506-007-9059-8.
Carmo, J., & Jones, A. J. (2002). Deontic logic and contrary-to-duties. Handbook of Philosophical Logic, 8, 265–345. https://doi.org/10.1007/978-94-010-0387-2_4.
Castañeda, H. N. (1972). On the semantics of the ought-to-do. In D. Davidson & G. Harman (Eds.), Semantics of natural language, Volume 40 of Synthese Library (pp. 675–694). Springer. https://doi.org/10.1007/978-94-010-2557-7_21.
Castañeda, H. N. (1981). The paradoxes of deontic logic: The simplest solution to all of them in one fell swoop. In R. Hilpinen (Ed.), New Studies in Deontic Logic: Norms, Actions, and the Foundations of Ethics (pp. 37–85). Springer. https://doi.org/10.1007/978-94-009-8484-4_2.
Chellas, B. F. (1980). Modal logic. Cambridge University Press.
Chisholm, R. M. (1963). Contrary-to-duty imperatives and deontic logic. Analysis, 24(2), 33–36. https://doi.org/10.1093/analys/24.2.33.
Ciabattoni, A., Freschi, E., Genco, F. A., & Lellmann, B. (2015). Mīmāṃsā deontic logic: Proof theory and applications. In H. De Nivelle (Ed.), Automated reasoning with analytic tableaux and related methods (pp. 323–338). Springer. https://doi.org/10.1007/978-3-319-24312-2_22.
Edgerton, F. (Ed.). (1929). Mīmāṃsānyāyaprakāśa of Āpadeva. Yale University Press.
Fischer, M. J., & Ladner, R. E. (1979). Propositional dynamic logic of regular programs. Journal of Computer and System Sciences, 18(2), 194–211. https://doi.org/10.1016/0022-0000(79)90046-1.
Forrester, J. (1984). Gentle murder, or the adverbial samaritan. Journal of Philosophy, 81(4), 193–197. https://doi.org/10.2307/2026120.
Freschi, E. (2018). The role of paribhāṣās in Mīmāṃsā: Rational rules of textual exegesis. Asiatische Studien/Études Asiatiques, 72(2), 567–595. https://doi.org/10.1515/asia-2018-0018.
Freschi, E., Ciabattoni, A., Genco, F. A., & Lellmann, B. (2017). Understanding prescriptive texts: Rules and logic as elaborated by the Mīmāṃsā school. Journal of World Philosophies, 2(1), 47–66. https://doi.org/10.2979/jourworlphil.2.1.05.
Freschi, E., Ollett, A., & Pascucci, M. (2019). Duty and sacrifice: A logical analysis of the theory of Vedic injunctions. History and Philosophy of Logic, 40(4), 323–354. https://doi.org/10.1080/01445340.2019.1615366.
Freschi, E., & Pascucci, M. (2021). Deontic concepts and their clash in Mīmāṃsā: Towards an interpretation. Theoria, 87(3), 659–703. https://doi.org/10.1111/theo.12307.
Giordani, A., & Canavotto, I. (2016). Basic action deontic logic. In O. Roy, A. M. Tamminga, & M. Willer (Eds.), 13th International Conference on Deontic logic and normative systems, DEON 2016 (pp. 80–92). College Publications.
Guhe, E. (2021). Killing gently by means of the śyena: The Navya-Nyāya analysis of Vedic and secular injunctions (vidhi) and prohibitions (niṣedha) from the perspective of dynamic deontic logic. Journal of Indian Philosophy, 49, 421–449. https://doi.org/10.1007/s10781-021-09465-2.
Hansen, J. (2008). Prioritized conditional imperatives: Problems and a new proposal. Autonomous Agents and Multi-Agent Systems, 17(1), 11–35. https://doi.org/10.1007/s10458-007-9016-7.
Horty, J. F. (1994). Moral dilemmas and nonmonotonic logic. Journal of Philosophical Logic, 23(1), 35–65. https://doi.org/10.1007/BF01417957.
Hughes, J., Kroes, P., & Zwart, S. (2007). A semantics for means-end relations. Synthese, 158(2), 207–231. https://doi.org/10.1007/s11229-006-9036-x.
Kanger, S. (1971). New foundations for ethical theory, Deontic logic: Introductory and systematic readings (pp. 36–58). Springer. https://doi.org/10.1007/978-94-010-3146-2_2
Lellmann, B., Gulisano, F., & Ciabattoni, A. (2021). Mīmāṃsā deontic reasoning using specificity: a proof theoretic approach. Artificial Intelligence and Law, 29, 351–394. https://doi.org/10.1007/s10506-020-09278-w.
McCrea, L. & Rao, A. eds. (forthcoming). The Age of Vedānta.
McCrea, L. (2008). The Teleology of Poetics in Medieval Kashmir. Cambridge (Mass.): Department of Sanskrit and Indian Studies, Harvard University.
McCrea, L. (2010). Hindu jurisprudence and scriptural hermeneutics. In T. Lubin, J. Davis, R. Donald, & J. K. Krishnan (Eds.), Hinduism and Law: An Introduction (Vol. 7, pp. 123–136). Cambridge University Press. https://doi.org/10.1017/CBO9780511781674.012.
Meyer, J. J. C., Broersen, J. M., & Herzig, A. (2015). BDI logics. In H. van Ditmarsch, J. Y. Halpern, W. van der Hoek, & B. Kooi (Eds.), Handbook of logics of knowledge and belief (pp. 453–498). College Publications.
Meyer, J., Dignum, F., & Wieringa, R. (1994). The paradoxes of deontic logic revisited: A computer science perspective (or: Should computer scientists be bothered by the concerns of philosophers?). Technical Report UU-CS-1994-38, Department of Computer Sciences, Utrecht University.
Meyer, J. J. C. (1988). A different approach to deontic logic: Deontic logic viewed as a variant of dynamic logic. Notre Dame J. Formal Log., 29(1), 109–136. https://doi.org/10.1305/ndjfl/1093637776.
Parent, X., & van der Torre, L. W. N. (2018). I/O logics with a consistency check. In J. M. Broersen, C. Condoravdi, N. Shyam, & G. Pigozzi (Eds.), 14th International Conference on Deontic logic and normative systems, DEON 2018 (pp. 285–299). College Publications.
Prakken, H., & Sergot, M. (1996). Contrary-to-duty obligations. Studia Logica, 57(1), 91–115. https://doi.org/10.1007/BF00370671.
Prior, A. N. (1958). Escapism: The logical basis of ethics. In A. Melden (Ed.), Essays in moral philosophy. University of Washington Press. https://doi.org/10.2307/2271385.
Ross, A. (1944). Imperatives and logic. Philosophy of Science, 11(1), 30–46. https://doi.org/10.1086/286823.
Stcherbatsky, T. I. (1926). Über die Nyāyakaṇikā des Vācaspatimiśra und die indische Lehre des kategorischen Imperativ, In Beiträge zur Literaturwissenschaft und Geistesgeschichte Indiens. Festgabe Hermann Jacobi zum 75. Geburtstag, ed. Kirfel, W., 369–380. Bonn: Kommissionsverlag F. Klopp.
Śubbaśāstrī ed. 1929-1934. Śrīmajjaiminipraṇītaṃ, mīmāṃsādarśanam Poona:Anandasramamudarnalaya.
Viraraghavacharya, U. T. ed. (1971). Seśvaramīmāṃsā-mīmāṃsāpāduke, Seswara mimamsa and paduka [by Ve\(\dot{\rm n}\)katanātha]. Ubhaya Vedanta Granthamala.
von Wright, G. H. (1951). Deontic logic. Mind, 60(237), 1–15. https://doi.org/10.1093/mind/LX.237.1.
von Wright, G. H. (1956). A note on deontic logic and derived obligation. Mind, 65(1), 507–509. https://doi.org/10.1093/mind/65.1.507.
Acknowledgements
Work supported by WWTF (Vienna Science and Technology Fund) and FWF (Austrian Science Fund) projects MA16-028 and W1255-N23.
Funding
Open access funding provided by Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Prabhākara and Kumārila
We demonstrate soundness and completeness for the logics \({\mathsf {LPr^{+}}}\) and \({\mathsf {LKu^{+}}}\) as presented in Theorems 2 and 3 of Sect. 3.1 and 3.2, respectively. The proof of Theorem 2 is a straightforward adaptation of the one of Theorem 3.
Theorem 3
(Soundness and Completeness) A formula is a theorem of \({\mathsf {LKu^{+}}}\) if and only if it is valid on all \({\mathsf {LKu^{+}}}\)-models.
Proof
The soundness follows by showing that all axiom-schemata of \({\mathsf {LKu^{+}}}\) are valid in \({\mathsf {LKu^{+}}}\)-models and that the rules of Necessitation and Modus Ponens preserve validity. The proof is straightforward.
The completeness proof uses the method of canonical models, see Chellas (1980). Namely, the universal modality  is axiomatized as an \(\textsf{S5}\) modality, which is canonical for the equivalence relation
is axiomatized as an \(\textsf{S5}\) modality, which is canonical for the equivalence relation  . This guarantees that in the canonical model
. This guarantees that in the canonical model  , but not that
, but not that  . This is however unproblematic: we generate a submodel of the canonical model which is in fact an \({\mathsf {LKu^{+}}}\)-model characterizing the universal modality.
. This is however unproblematic: we generate a submodel of the canonical model which is in fact an \({\mathsf {LKu^{+}}}\)-model characterizing the universal modality.
First, we define a canonical model for the logic \({\mathsf {LKu^{+}}}\) in the standard way, see Chellas (1980). Let the canonical model of \({\mathsf {LKu^{+}}}\) be:  . Let \({\textsf{W}^c}\) be the set of all \({\mathsf {LKu^{+}}}\)-maximally consistent sets. Let \((Y,Z)\in \mathcal {N}_{\mathcal {X}}^{c}(w)\) iff there is a formula \(\mathcal {X}(\varphi /\psi ) \in w\) such that \(\{w_j\in {\textsf{W}^c}\vert \varphi \in w_j\} \subseteq Y\) and \(\{w_j\in {\textsf{W}^c}\vert \psi \in w_j\} = Z\) for \(\mathcal {X} \in \{\mathcal {O}, \mathcal {E}\}\) (cf. upward monotonicity). Furthermore, let \((Y,Z)\in \mathcal {N}_{\mathcal {F}}^{c}(w)\) iff there is a formula \(\mathcal {F}(\varphi /\psi ) \in w\) such that \(Y\subseteq \{w_j\in {\textsf{W}^c}\vert \varphi \in w_j\}\) and \(\{w_j\in {\textsf{W}^c}\vert \psi \in w_j\} = Z\) (cf. downward monotonicity). Since the canonical model is closed under non-proof sets (cf. upward and downward monotonicity above), we prove that \({\textsf{M}^c}\) actually is a canonical model for the logic \({\mathsf {LKu^{+}}}\). It suffices to show that, for each \(w_i\in {\textsf{W}^c}\) and \(\varphi \in {\mathcal {L}_{\textsf{K}}}\), \({\textsf{M}^c}, w_i \models \varphi \) iff \(\varphi \in w_i\). The proof is by a straightforward induction on the complexity of \(\varphi \) (Chellas 1980).
. Let \({\textsf{W}^c}\) be the set of all \({\mathsf {LKu^{+}}}\)-maximally consistent sets. Let \((Y,Z)\in \mathcal {N}_{\mathcal {X}}^{c}(w)\) iff there is a formula \(\mathcal {X}(\varphi /\psi ) \in w\) such that \(\{w_j\in {\textsf{W}^c}\vert \varphi \in w_j\} \subseteq Y\) and \(\{w_j\in {\textsf{W}^c}\vert \psi \in w_j\} = Z\) for \(\mathcal {X} \in \{\mathcal {O}, \mathcal {E}\}\) (cf. upward monotonicity). Furthermore, let \((Y,Z)\in \mathcal {N}_{\mathcal {F}}^{c}(w)\) iff there is a formula \(\mathcal {F}(\varphi /\psi ) \in w\) such that \(Y\subseteq \{w_j\in {\textsf{W}^c}\vert \varphi \in w_j\}\) and \(\{w_j\in {\textsf{W}^c}\vert \psi \in w_j\} = Z\) (cf. downward monotonicity). Since the canonical model is closed under non-proof sets (cf. upward and downward monotonicity above), we prove that \({\textsf{M}^c}\) actually is a canonical model for the logic \({\mathsf {LKu^{+}}}\). It suffices to show that, for each \(w_i\in {\textsf{W}^c}\) and \(\varphi \in {\mathcal {L}_{\textsf{K}}}\), \({\textsf{M}^c}, w_i \models \varphi \) iff \(\varphi \in w_i\). The proof is by a straightforward induction on the complexity of \(\varphi \) (Chellas 1980).
As observed above, \({\textsf{M}^c}\) is not necessarily an \({\mathsf {LKu^{+}}}\)-model since it is not guaranteed that  . Nevertheless, it can be easily shown that \({\textsf{M}^c}\) satisfies all properties (i)-(vii) of Definition 5. For the sake of illustration, we present the case of (vii): Assume \((X,Y) \in {\mathcal {N}_{\mathcal {E}}^{c}}(w)\). By definition of the canonical model this implies that there is a formula \(\varphi \) s.t. \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\}\subseteq X\) and there is a \(\psi \) s.t. \(\{w_i\in {\textsf{W}^c}\vert \psi \in w_i\}=Y\) and \((\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\},Y)\in {\mathcal {N}_{\mathcal {E}}^{c}}(w)\). By construction of the canonical model, this gives us \(\mathcal {E}(\varphi /\psi )\in w\). Since all worlds are maximally consistent sets of formulae, by axiom (\(\textsf{A}_{\textsf{K}}8\)), w also contains the formula
. Nevertheless, it can be easily shown that \({\textsf{M}^c}\) satisfies all properties (i)-(vii) of Definition 5. For the sake of illustration, we present the case of (vii): Assume \((X,Y) \in {\mathcal {N}_{\mathcal {E}}^{c}}(w)\). By definition of the canonical model this implies that there is a formula \(\varphi \) s.t. \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\}\subseteq X\) and there is a \(\psi \) s.t. \(\{w_i\in {\textsf{W}^c}\vert \psi \in w_i\}=Y\) and \((\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\},Y)\in {\mathcal {N}_{\mathcal {E}}^{c}}(w)\). By construction of the canonical model, this gives us \(\mathcal {E}(\varphi /\psi )\in w\). Since all worlds are maximally consistent sets of formulae, by axiom (\(\textsf{A}_{\textsf{K}}8\)), w also contains the formula  . Hence, there is at least one world which contains the formula \(\varphi \), i.e., \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\} \ne \emptyset \). Since \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\}\subseteq X\), this also means \(X \ne \emptyset \) (in fact,
. Hence, there is at least one world which contains the formula \(\varphi \), i.e., \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\} \ne \emptyset \). Since \(\{w_i\in {\textsf{W}^c}\vert \varphi \in w_i\}\subseteq X\), this also means \(X \ne \emptyset \) (in fact,  ).
).
In order to obtain the desired model it suffices to define a generated submodel  of the canonical model \({\textsf{M}^c}\). \({\textsf{M}^{*}}\) is defined relative to a single equivalence class generated by a given \({\mathsf {LKu^{+}}}\)-maximally consistent set. Such a model \({\textsf{M}^{*}}\) satisfies
of the canonical model \({\textsf{M}^c}\). \({\textsf{M}^{*}}\) is defined relative to a single equivalence class generated by a given \({\mathsf {LKu^{+}}}\)-maximally consistent set. Such a model \({\textsf{M}^{*}}\) satisfies  . One subsequently shows that all properties (i)-(vii) are preserved from \({\textsf{M}^c}\) to \({\textsf{M}^{*}}\), and thus the generated submodel \({\textsf{M}^{*}}\) is an \({\mathsf {LKu^{+}}}\)-model. Last, by showing that for each \(w\in {\textsf{W}^{*}}\) and \(\varphi \in {\mathcal {L}_{\textsf{K}}}\), \({\textsf{M}^c},w \models \varphi \) iff \({\textsf{M}^{*}},w\models \varphi \), we obtain the desired result. We omit details here. \(\square \)
. One subsequently shows that all properties (i)-(vii) are preserved from \({\textsf{M}^c}\) to \({\textsf{M}^{*}}\), and thus the generated submodel \({\textsf{M}^{*}}\) is an \({\mathsf {LKu^{+}}}\)-model. Last, by showing that for each \(w\in {\textsf{W}^{*}}\) and \(\varphi \in {\mathcal {L}_{\textsf{K}}}\), \({\textsf{M}^c},w \models \varphi \) iff \({\textsf{M}^{*}},w\models \varphi \), we obtain the desired result. We omit details here. \(\square \)
Appendix B: Maṇḍana
We demonstrate soundness and completeness for the logic \({\mathsf {LMa^{-}}}\) as presented in Theorem 4 of Sect. 3.3.
Theorem 4
(Soundness and Completeness) A formula is a theorem of \({\mathsf {LMa^{-}}}\) if and only if it is valid on all \({\mathsf {LMa^{-}}}\)-models.
Proof
Directly from Theorem 5 and Theorem 7. \(\square \)
Theorem 5
(Soundness) If a formula is a theorem of \({\mathsf {LMa^{-}}}\), then it is valid on all \({\mathsf {LMa^{-}}}\)-models
Proof
Soundness is proven as usual, see Blackburn et al. (2004). We show the case of axiom \(\textsf{A}_{\textsf{M}}3\), explaining the use of constants:
-
\(\textsf{A}_{\textsf{M}}3\). Let \({\mathfrak {M}_{\textsf{M}}}\) be an \({\mathsf {LMa^{-}}}\)-model with
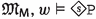 . Then \(\exists v\in W\) such that
. Then \(\exists v\in W\) such that 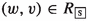 with \({\mathfrak {M}_{\textsf{M}}},v\vDash \texttt {P}\), so \(v\in W_\texttt {P}\). By (i) of Definition 8, \(\exists u\in W\) such that
with \({\mathfrak {M}_{\textsf{M}}},v\vDash \texttt {P}\), so \(v\in W_\texttt {P}\). By (i) of Definition 8, \(\exists u\in W\) such that 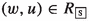 and \(u\not \in W_{\texttt {P}}\). So \({\mathfrak {M}_{\textsf{M}}},u\not \vDash \texttt {P}\) and therefore
and \(u\not \in W_{\texttt {P}}\). So \({\mathfrak {M}_{\textsf{M}}},u\not \vDash \texttt {P}\) and therefore 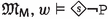 .
.
\(\square \)
Completeness is proven via canonical model construction, adjusted to the inclusion of constants. \({\mathsf {LMa^{-}}}\)-maximally consistent sets (MCS) are defined as usual, enjoying the usual properties, see Blackburn et al. (2004). Lindenbaum’s Lemma tells us that for every \({\mathsf {LMa^{-}}}\)-consistent set \(\Sigma ^{-}\) there exists an \({\mathsf {LMa^{-}}}\)-MCS \(\Sigma \) s.t. \(\Sigma ^{-}\subseteq \Sigma \). Since we reserved \(\Delta \) for arbitrary action types, we use \(\Sigma ,\Gamma ,\Theta \) to refer to \({\mathsf {LMa^{-}}}\)-MCSs. The canonical model is defined as usual.
Definition 11
Let  be a canonical model, where \({\textsf{W}^c}\) is the set of all \({\mathsf {LMa^{-}}}\)-MCSs and:
be a canonical model, where \({\textsf{W}^c}\) is the set of all \({\mathsf {LMa^{-}}}\)-MCSs and:
-
For all \(\texttt {d}_{\delta }\in \mathsf {Wit_{\textsf{Act}}}\) and \(\Sigma \in {\textsf{W}^c}\), \(\Sigma \in {\textsf{W}^c_{\texttt {d}_{\delta }}}\) iff \(\texttt {d}_{\delta }\in \Sigma \)
-
For \(\alpha \in \{\texttt {P},\texttt {R}\}\), and all \(\Sigma \in {\textsf{W}^c}\), \(\Sigma \in {\textsf{W}^c}_{\alpha }\) iff \(\alpha \in \Sigma \)
-
For
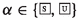 , and all \(\Sigma ,\Gamma \in {\textsf{W}^c}\), \((\Sigma ,\Gamma )\in \textsf{R}^{c}_{\alpha }\) iff \(\{\varphi \vert \ [\alpha ]\varphi \in \Sigma \}\subseteq \Gamma \)
, and all \(\Sigma ,\Gamma \in {\textsf{W}^c}\), \((\Sigma ,\Gamma )\in \textsf{R}^{c}_{\alpha }\) iff \(\{\varphi \vert \ [\alpha ]\varphi \in \Sigma \}\subseteq \Gamma \) -
For all \(\chi \in \textsf{Atom}\cup \mathsf {Wit_{\textsf{Act}}}\cup \{\texttt {P}\}\cup \{\texttt {R}\}\), \({\textsf{V}^c}(\chi )=\{\Sigma \in {\textsf{W}^c}\vert \chi \in \Sigma \}\)
The existence lemma and truth lemma are proven in Blackburn et al. 2004, Sect. 4.2 (nb. \({\mathsf {LMa^{-}}}\) is a normal modal logic). We first show that \({\textsf{M}^c}\) satisfies the relevant properties (i) and (ii) of Definition 8.
Theorem 6
\({\textsf{M}^c}\) satisfies properties (i) and (ii) of Definition 8.
Proof
We only prove the case for (i), since (ii) is similar:
-
(i) For all \(\Sigma , \Gamma \in {\textsf{W}^c}\), if
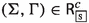 and \(\Gamma \in {\textsf{W}^c_{\texttt {P}}}\), then there exists a \(\Theta \in {\textsf{W}^c}\) s.t.
and \(\Gamma \in {\textsf{W}^c_{\texttt {P}}}\), then there exists a \(\Theta \in {\textsf{W}^c}\) s.t. 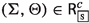 and \(\Theta \not \in {\textsf{W}^c_{\texttt {P}}}\). Assume the antecedent, we construct the set \(\Theta \). Let
and \(\Theta \not \in {\textsf{W}^c_{\texttt {P}}}\). Assume the antecedent, we construct the set \(\Theta \). Let 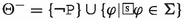 . Suppose \(\Theta ^{-}\) is not \({\mathsf {LMa^{-}}}\)-consistent. Hence for some \(\varphi _1,..,\varphi _n\in \Theta ^{-}\), we have \(\vdash _{{\mathsf {LMa^{-}}}}\varphi \wedge \ldots \wedge \varphi _n\rightarrow \texttt {P}\). By \({\mathsf {LMa^{-}}}\) we have
. Suppose \(\Theta ^{-}\) is not \({\mathsf {LMa^{-}}}\)-consistent. Hence for some \(\varphi _1,..,\varphi _n\in \Theta ^{-}\), we have \(\vdash _{{\mathsf {LMa^{-}}}}\varphi \wedge \ldots \wedge \varphi _n\rightarrow \texttt {P}\). By \({\mathsf {LMa^{-}}}\) we have 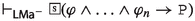 , which implies
, which implies 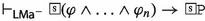 , and so
, and so 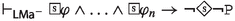 . By monotonicity of \({\mathsf {LMa^{-}}}\),
. By monotonicity of \({\mathsf {LMa^{-}}}\),  . By assumption
. By assumption 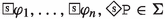 and MCS properties, we have
and MCS properties, we have 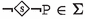 . However, since \(\Sigma \) is a \({\mathsf {LMa^{-}}}\)-MCS we have
. However, since \(\Sigma \) is a \({\mathsf {LMa^{-}}}\)-MCS we have 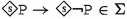 , and thus
, and thus 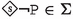 . Contradiction. Hence, \(\Theta ^{-}\) is \({\mathsf {LMa^{-}}}\)-consistent. Let \(\Theta \) be the \({\mathsf {LMa^{-}}}\)-MCS extending \(\Theta ^{-}\) (Lindenbaum’s lemma). By construction of \({\textsf{M}^c}\) we obtain
. Contradiction. Hence, \(\Theta ^{-}\) is \({\mathsf {LMa^{-}}}\)-consistent. Let \(\Theta \) be the \({\mathsf {LMa^{-}}}\)-MCS extending \(\Theta ^{-}\) (Lindenbaum’s lemma). By construction of \({\textsf{M}^c}\) we obtain 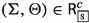 and since \(\lnot \texttt {P}\in \Theta ^{-}\subseteq \Theta \) we have \(\Theta \not \in {\textsf{W}^c_{\texttt {P}}}\). \(\square \)
and since \(\lnot \texttt {P}\in \Theta ^{-}\subseteq \Theta \) we have \(\Theta \not \in {\textsf{W}^c_{\texttt {P}}}\). \(\square \)
Theorem 7
For any \(\varphi \in {\mathcal {L}_{\textsf{M}}}\) and \(\Sigma \subseteq {\mathcal {L}_{\textsf{M}}}\), if \(\Sigma \vDash _{{\mathsf {LMa^{-}}}} \varphi \), then \(\Sigma \vdash _{{\mathsf {LMa^{-}}}}\varphi \).
Proof
The proof follows by general results from Blackburn et al. (2004). We sketch the proof here. Suppose that \(\varphi \) is not \({\mathsf {LMa^{-}}}\)-derivable from \(\Sigma \). This means \(\Sigma \cup \{\lnot \varphi \}\) is \({\mathsf {LMa^{-}}}\)-consistent. Let \(\Sigma ^{*}\) be the \({\mathsf {LMa^{-}}}\)-MCS extending \(\Sigma \cup \{\lnot \varphi \}\).
Recall that the universal modality  is axiomatized as \(\textsf{S5}\), which is canonical for the equivalence relation
is axiomatized as \(\textsf{S5}\), which is canonical for the equivalence relation  (Blackburn et al. 2004, Ch.4). Using the standard canonical model construction this only guarantees that
(Blackburn et al. 2004, Ch.4). Using the standard canonical model construction this only guarantees that  in \({\textsf{M}^c}\) but not that
in \({\textsf{M}^c}\) but not that  . The solution is straightforward: we use generated submodels of the canonical model \({\textsf{M}^c}\) which are in fact \({\mathsf {LMa^{-}}}\)-models, using the general definition of generated submodels in Blackburn et al. (2004), Def. 2.5. We define this submodel relative to the \({\mathsf {LMa^{-}}}\)-MCS \(\Sigma ^{*}\).
. The solution is straightforward: we use generated submodels of the canonical model \({\textsf{M}^c}\) which are in fact \({\mathsf {LMa^{-}}}\)-models, using the general definition of generated submodels in Blackburn et al. (2004), Def. 2.5. We define this submodel relative to the \({\mathsf {LMa^{-}}}\)-MCS \(\Sigma ^{*}\).
Let  be a generated submodel with respect to \(\Sigma ^{*}\). It is straightforwardly shown that
be a generated submodel with respect to \(\Sigma ^{*}\). It is straightforwardly shown that  . Because of axiom (\(\textsf{A}_{\textsf{M}}2\)),
. Because of axiom (\(\textsf{A}_{\textsf{M}}2\)),  is guaranteed and so \({\textsf{M}^{*}}\) is also a generated submodel for
is guaranteed and so \({\textsf{M}^{*}}\) is also a generated submodel for  . Since modal satisfaction is invariant under generated submodels (Blackburn et al. 2004, Prop. 2.6), we know \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \Sigma ^{*}\). Hence, \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \Sigma \) and \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \lnot \varphi \). By Theorem 6 and the fact that \({\textsf{M}^{*}}\) is a generated submodel of \({\textsf{M}^c}\), we know that \({\textsf{M}^{*}}\) is an \({\mathsf {LMa^{-}}}\)-model. \(\square \)
. Since modal satisfaction is invariant under generated submodels (Blackburn et al. 2004, Prop. 2.6), we know \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \Sigma ^{*}\). Hence, \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \Sigma \) and \({\textsf{M}^{*}}, \Sigma ^{*}\vDash \lnot \varphi \). By Theorem 6 and the fact that \({\textsf{M}^{*}}\) is a generated submodel of \({\textsf{M}^c}\), we know that \({\textsf{M}^{*}}\) is an \({\mathsf {LMa^{-}}}\)-model. \(\square \)
Appendix C: Paradoxes
Claim 1 Let \({\mathfrak {M}_{\textsf{M}}}\) be an \({\mathsf {LMa^{-}}}\)-model. If \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\) and \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\mathsf {fight\_army}/\top )\), then also \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {alt\_service}/\top )\)
Proof
Let \({\mathfrak {M}_{\textsf{M}}}\) be an \({\mathsf {LMa^{-}}}\)-model with \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\) and \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\mathsf {fight\_army}/\top )\). To show that \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {alt\_service}/\top )\), we will show that \({\mathfrak {M}_{\textsf{M}}}\) satisfies all four conditions of an instrument (see Definition 10) for \(\mathcal {I}(\lnot \mathsf {alt\_service}/\texttt {P}/\top )\), as well as  .
.
-
(i)
By \(\mathcal {I}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\texttt {P}/\top )\) we have that
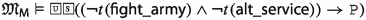 . By \(\mathcal {I}(\mathsf {fight\_army}/\texttt {P}/\top )\) we have that
. By \(\mathcal {I}(\mathsf {fight\_army}/\texttt {P}/\top )\) we have that 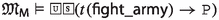 , so in particular
, so in particular 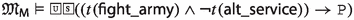 . This gives
. This gives 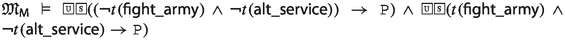 , so
, so 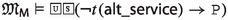 .
. -
(ii)
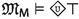 holds because of \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\) and \(\mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\rightarrow \mathcal {I}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\texttt {P}/\top )\) (condition (ii) of instrumentality).
holds because of \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\) and \(\mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\rightarrow \mathcal {I}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\texttt {P}/\top )\) (condition (ii) of instrumentality). -
(iii)
Since \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\) and \(\mathcal {F}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\top )\rightarrow \mathcal {I}(\lnot \mathsf {fight\_army} \wedge \lnot \mathsf {alt\_service}/\texttt {P}/\top )\), we have, by condition (iii) of instrumentality that
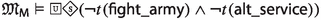 , so in particular
, so in particular 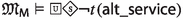 .
. -
(iv)
-
1
\({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot t(\mathsf {fight\_army})\wedge \lnot t(\mathsf {alt\_service})/\top )\)(assumption)
-
2
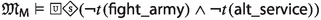 (from 1, condition (iii) of instruments)
(from 1, condition (iii) of instruments) -
3
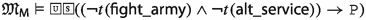 (from 1, condition (i) of instruments)
(from 1, condition (i) of instruments) -
4
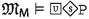 (from 2,3)
(from 2,3) -
5
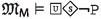 (from 4, axiom (\(\textsf{A}_{\textsf{M}}3\)))
(from 4, axiom (\(\textsf{A}_{\textsf{M}}3\))) -
6
\({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(a/\top )\)(assumption)
-
7
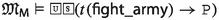 (from 6, condition (i) of instruments)
(from 6, condition (i) of instruments) -
8
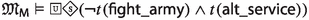 (from 3,5,7)
(from 3,5,7) -
9
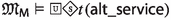 (from 8)
(from 8)
-
1
-
(v)
 is trivially true, since \(\mathcal {F}(\lnot \mathsf {fight\_army}\cap \lnot \mathsf {alt\_service}/\top )\) gives us that
is trivially true, since \(\mathcal {F}(\lnot \mathsf {fight\_army}\cap \lnot \mathsf {alt\_service}/\top )\) gives us that 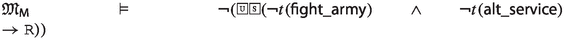
Hence \({\mathfrak {M}_{\textsf{M}}}\vDash \mathcal {F}(\lnot \mathsf {alt\_service}/\top )\) \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van Berkel, K., Ciabattoni, A., Freschi, E. et al. Deontic Paradoxes in Mīmāṃsā Logics: There and Back Again. J of Log Lang and Inf 32, 19–62 (2023). https://doi.org/10.1007/s10849-022-09375-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-022-09375-w





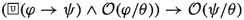
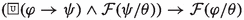
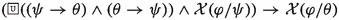 for
for 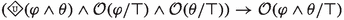
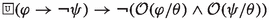
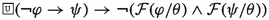
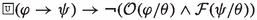
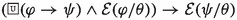
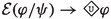
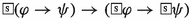

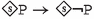
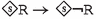
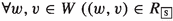 and
and 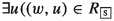 and
and 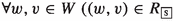 and
and 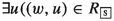 and
and  such that (
such that (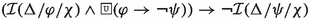 such that (
such that (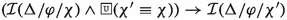 such that (
such that (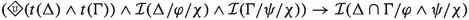
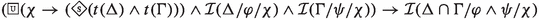


 and
and  .
.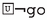
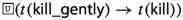
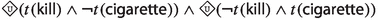
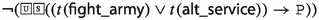 because of the obligation, and
because of the obligation, and 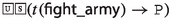 because of the prohibition.
because of the prohibition. and V as in Definition
and V as in Definition 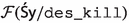 is not a Vedic prohibition; there is no such statement in the sacred texts. On a derived level, it is possible for Maṇḍana to have electives and prohibitions of the same actions, without having inconsistency. See Remark 1.
is not a Vedic prohibition; there is no such statement in the sacred texts. On a derived level, it is possible for Maṇḍana to have electives and prohibitions of the same actions, without having inconsistency. See Remark 1.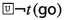 would mean that at every world in the model it is the case that one did not go to the assistance of one’s neighbours. Such an expression would make sentence number 2 not meaningful (recall, for a command the context must be possible in at least one world in order to not be devoid of meaning).
would mean that at every world in the model it is the case that one did not go to the assistance of one’s neighbours. Such an expression would make sentence number 2 not meaningful (recall, for a command the context must be possible in at least one world in order to not be devoid of meaning).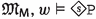 . Then
. Then 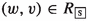 with
with 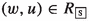 and
and 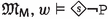 .
.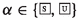 , and all
, and all 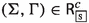 and
and 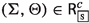 and
and 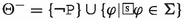 . Suppose
. Suppose 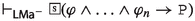 , which implies
, which implies 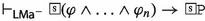 , and so
, and so 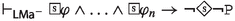 . By monotonicity of
. By monotonicity of  . By assumption
. By assumption 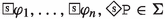 and MCS properties, we have
and MCS properties, we have 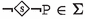 . However, since
. However, since 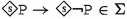 , and thus
, and thus 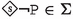 . Contradiction. Hence,
. Contradiction. Hence, 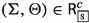 and since
and since 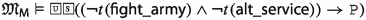 . By
. By 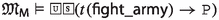 , so in particular
, so in particular 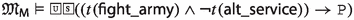 . This gives
. This gives 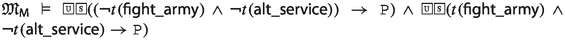 , so
, so 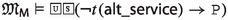 .
.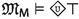 holds because of
holds because of 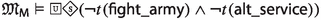 , so in particular
, so in particular 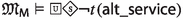 .
.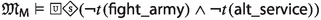 (from 1, condition (iii) of instruments)
(from 1, condition (iii) of instruments)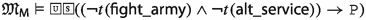 (from 1, condition (i) of instruments)
(from 1, condition (i) of instruments)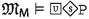 (from 2,3)
(from 2,3)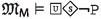 (from 4, axiom (
(from 4, axiom (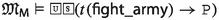 (from 6, condition (i) of instruments)
(from 6, condition (i) of instruments)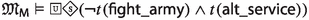 (from 3,5,7)
(from 3,5,7)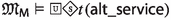 (from 8)
(from 8) is trivially true, since
is trivially true, since