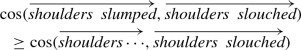Abstract
Despite the incremental nature of Dynamic Syntax (DS), the semantic grounding of it remains that of predicate logic, itself grounded in set theory, so is poorly suited to expressing the rampantly context-relative nature of word meaning, and related phenomena such as incremental judgements of similarity needed for the modelling of disambiguation. Here, we show how DS can be assigned a compositional distributional semantics which enables such judgements and makes it possible to incrementally disambiguate language constructs using vector space semantics. Building on a proposal in our previous work, we implement and evaluate our model on real data, showing that it outperforms a commonly used additive baseline. In conclusion, we argue that these results set the ground for an account of the non-determinism of lexical content, in which the nature of word meaning is its dependence on surrounding context for its construal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
At the core of Dynamic Syntax (DS) as a grammar formalism has been the claim that the traditional concept of syntax—principles underpinning a set of structures inhabited by strings—should be replaced by a dynamic perspective in which syntax is a set of procedures for incrementally building up representations of content relative to context. Central to this claim has been the concept of underspecification and update, with partial content-representations being progressively built up on a word-by-word basis, allowing the emergence of progressively established content.
Being a grammar formalism, DS underpins both speaker actions and hearer actions, with the immediate consequence of being able to characterise directly the to-and-fro dynamic of conversational dialogue. In informal conversations, people fluently switch between speaking and listening in virtue of each agent constructing incrementally evolving representations as driven by the words uttered and the procedures they induce. As a result, any one of them is able to adopt the lead role in this process at any stage. This was one of many confirmations of the general stance of incorporating within the grammar formalism a reflection of time incrementality (Kempson et al. 2016, inter alia).
Within this framework, words have been defined as inducing procedures for developing tree-theoretic representations of content (Cann et al. 2005; Kempson et al. 2001, 2011). However throughout much of the DS development there has been one major conservatism. The concept of semantic representation was taken, along broadly Fodorian lines, as involving a simple word-concept mapping. This was defined by Kempson et al. (2001) as a mapping onto expressions of the epsilon calculus, with its set-theoretically defined semantics (an epsilon term being defined as denoting a witness for the constructed arbitrary name manipulated in natural deduction systems of predicate calculus), a stance adopted as commensurate with the broadly proof-theoretic perspective of DS, and additionally motivated by the character of epsilon terms under development as displaying a growing reflection of the context within which they are constructed. Though attractive in matching the characteristic entity-typing of noun phrases, such a concept of word meaning is both too narrow in reflecting only what is expressible within predicate logic terms, and yet too strong in defining fixed extensions as content of the individual expressions, a move which provides no vehicle for addressing how content words display considerable context-dependence. In effect, the problem of explaining what meaning can be associated with a word as the systematic contribution it makes to sentence meaning without positing a veritable Pandora’s box of ambiguities was not addressed. The same is true in many other frameworks: formal semanticists have by and large remained content with defining ambiguities whenever denotational considerations seemed to warrant them; and Partee (2018) cites the context-dependence of lexical semantics as a hurdle for which such a methodology does not appear to offer any natural means of addressing. And even within pragmatics, with its dedicated remit of explicating context-particular effects external to a standard competence model of grammar, and recent work on polysemy probing what this amounts to (Recanati 2017; Carston 2019), there nevertheless remains a tendency to invoke ambiguity involving discrete token-identical forms in the face of multiple interpretation potential, thereby leaving the phenomenon of natural language plasticity unexplained (Fretheim 2019). For DS as defined in (Kempson et al. 2001; Cann et al. 2005; Kempson et al. 2011), polysemy would thus also seem to remain a hurdle despite accounts of anaphora and ellipsis (see Kempson et al. 2015).
The challenge is this: words of natural language (NL) can have extraordinarily variable interpretations (even setting the problem of metaphor aside). A ‘fire’ in a grate is a warm welcome upon entering a house while a ‘fire’ in surrounding countryside causes widespread alarm. A ‘burning’ of a scone denotes a quite different process leading to quite different effects than ‘burning’ of a frying pan, or indeed ‘burning’ of a forest. The substance of the way in which such NL tokens are understood is deeply embedded within the contingent and culture-specific variability of perspectives which individual members of that community bring to bear in interaction with each other based on both supposedly shared knowledge of that language and their own practical and emotional experience. And such variation can occur when, within a single exchange, even a single speaker is able to shift construal for a single word, fragment by fragment as the participants finesse what they are talking. This is shown by the potential surface ungrammaticality of shared utterances (or compound contributions, Howes et al. 2011) which is in fact perfectly grammatical across speakers:
-
(1)
A: I’ve almost completely burned the kitchen. B: Did you burn..? A: (interrupting) Myself? No, fortunately not. Well, only my hair
Yet, as long as the assumption that knowledge of language has to be modelled in some sense as prior to, hence independent of, any model of how that knowledge is put to use, this endemic context-relativity of even the basic units of language remains deeply intransigent; and the assumptions underpinning the long-held competence performance distinction have until very recently only been subject to minor modification amongst formal semanticists, despite the advocacy of need for more radical change from conversation analysts such as Schegloff (1984), psycholinguists such as Clark (1996) and Healey et al. (2018), and increasingly within cognitive neuroscience (e.g. Anderson 2014).
Though DS purports to provide a general framework for modelling NL grammar in incremental terms, it was not until Purver et al. (2011) combined DS with Type Theory with Records (DS-TTR) that it became able to fully capture the incremental compositionality of semantic representation required to explain, for example, how people interactively co-construct shared utterances (see Purver et al. 2014). Even then, however, the challenge of modelling rampant lexical ambiguity was not addressed, and the attendant process of disambiguation also remained an open issue.
In previous work (Sadrzadeh et al. 2017, 2018a, b) we showed how in principle one can address these problems within the DS framework via the use of distributional or vector space semantics (VSS). By representing word meanings as vectors within a continuous space, VSS approaches can provide not only quantitative tools for measuring graded relations between words such as relatedness and similarities of meaning, but also a natural way to express the non-determinism of a word’s construal from a denotational perspective, even relative to context (see e.g. Coecke 2019, for initial work on how such an approach can model the change of meaning through discourse). Moreover, we believe that the combination of a vector-space rendition of word meaning with the DS process-oriented characterisation of NL syntax is timely and of cross-disciplinary significance, as it promises to fill a niche within cognitive neuroscience where the emphasis is increasingly one of defining cognitive abilities in processual rather than representational terms – see discussion in Sect. 6.
In that earlier work, we outlined a theoretical approach to incorporating VSS within DS (Sadrzadeh et al. 2017, 2018b); we then demonstrated with toy examples how this approach might work to capture incremental measures of plausibility, and suggested that it might also be applied to word sense disambiguation (Sadrzadeh et al. 2018a). In this paper, we first review that approach (Sects. 2 and 3), and then continue to explore this research program by extending that work: in Sect. 4 we show in detail how the proposed model can be applied to a word sense disambiguation task, and in Sect. 5 we implement the theoretical model using real data, and evaluate it on existing datasets for word sense disambiguation. Our approach addresses the polysemy problem directly by adopting the presumption that even relatively unorthodox cases of putative ambiguity such as the verbs slump, tap, and dribble can be analysed from a unitary processual base (these cases are where Vector Space Semantics, since its early days, has been known to apply most successfully; see e.g. the original work of Schütze , 1998). We take the corpus-based approach to word meaning with vector spaces deducible from possible containing contexts within large scale corpora as a formal analogue to the contingent and highly culture-specific variability of word meanings and usages. We provide evidence from the corpora on degrees of similarities between variations of finished and unfinished utterances, present accuracy results, and explore the effect of incrementality on an existing disambiguation dataset. In conclusion, we reflect on how VSS combined with DS assumptions opens up the possibility of modelling the general non-determinism of NL meaning in the light of this incremental interactive perspective with its shift away from direct pairings of string and denotational content to a more dynamic and non-deterministic stance.
2 Background
2.1 Dynamic Syntax and Incremental Semantic Parsing
Dynamic Syntax (DS) provides a strictly incremental formalism relating word sequences to semantic representations. Conventionally, these are seen as trees decorated with semantic formulae that are terms in a typed lambda calculus (Kempson et al. 2001, chapter 9):

This permits analyses of the semantic output of the word-by-word parsing process in terms of partial semantic trees, in which nodes are labelled with types Ty and semantic formulae Fo, or with requirements for future development (e.g. ?Ty, ?Fo), and with a pointer \(\diamondsuit \) indicating the node currently under development. This is shown in Fig. 1 for the simple sentence Mary likes John. Phenomena such as conjunction, apposition and relative clauses are analysed via Linked trees (corresponding to semantic conjunction). For reasons of space we do not present an original DS tree for these here (see Sect. 2.5 of the introduction to this volume); an example of a non-restrictive relative clause linked tree labelled with vectors is presented later in Sect. 3.
The property of strict word-by-word incrementality inherent in all versions of DS makes it a good candidate for modelling language in natural human interaction. Speakers and hearers in dialogue can swap roles during sentences, without holding to notions of traditional syntactic or semantic constituency (see Howes et al. (2011) and example (1)). Speakers often produce incomplete output, and hearers manage to understand the meaning conveyed so far. In order to perform these ordinary feats, a suitable parsing and generation model must deal in incremental representations which capture the semantic content built at any point, and reflect grammatical constraints appropriately, and this is something DS does well (Cann et al. 2007). Accordingly, DS analyses of many dialogue phenomena have been produced: for example, shared utterances (Purver et al. 2014), self-repair (Hough and Purver 2012), and backchannelling (Eshghi et al. 2015).
Much recent work in dialogue understanding takes a purely machine-learning approach, learning how to encode input utterances into representations which can be decoded into appropriate follow-ups, without requiring prior knowledge of dialogue phenomena or structure (see e.g. Vinyals and Le 2015). However, while these models can show good accuracy in terms of understanding speaker intentions and generating suitable output, their representations are suitable only for the task and domain for which they are learned, and do not learn meaningful information about important linguistic phenomena like self-repair (Hupkes et al. 2018). Structured grammar-based approaches like DS can therefore contribute more general, informative models, from which robust versions can be learned (Eshghi et al. 2017).
2.2 DS and Semantic Representation
As presented above, however, and in its original form, DS assumes semantic formulae expressed in a standard symbolic predicate logic, and therefore not well suited to the problems of non-determinism, (dis)similarity and shift in word meanings discussed in Sect. 1. But the DS formalism is in fact considerably more general. To continue the quotation above:
\([\ldots ]\) it is important to keep in mind that the choice of the actual representation language is not central to the parsing model developed here. \([\ldots ]\) For instance, we may take \(X_1, X_2, X_3\) to be feature structures and the operation \(\mathbf {O}\) to be unification, or \(X_1, X_2, X_3\) to be lambda terms and \(\mathbf {O}\) Application, or \(X_1, X_2, X_3\) to be labelled categorial expressions and \(\mathbf {O}\) Application: Modus Ponens, or \(X_1, X_2, X_3\) to be DRSs and \(\mathbf {O}\) Merging.
This generality has been exploited in more recent work: Purver et al. (2010, 2011) outlined a version in which the formulae are record types in Type Theory with Records (TTR, Cooper 2005) in DS-TTR; and Hough and Purver (2012) show how this can confer an extra advantage – the incremental decoration of the root node, even for partial trees, with a maximally specific formula via type inference, using the TTR merge operation  as the composition function. In the latter account, underspecified record types decorate requirement nodes, containing a type judgement with the relevant type (e.g.
as the composition function. In the latter account, underspecified record types decorate requirement nodes, containing a type judgement with the relevant type (e.g.  at type ?Ty(e) nodes)– see Fig. 2 for a DS-TTR parse of “Mary likes John”. Hough and Purver (2017) show that this underspecification can be given a precise semantics through record type lattices: the dual operation of merge, the minimum common super type (or join)
at type ?Ty(e) nodes)– see Fig. 2 for a DS-TTR parse of “Mary likes John”. Hough and Purver (2017) show that this underspecification can be given a precise semantics through record type lattices: the dual operation of merge, the minimum common super type (or join)  is required to define a (probabilistic) distributive record type lattice bound by
is required to define a (probabilistic) distributive record type lattice bound by  and
and  . The interpretation process, including reference resolution, then takes the incrementally built top-level formula and checks it against a type system (corresponding to a world model) defined by a record type lattice. Implicitly, the record type on each node in a DS-TTR tree can be seen to correspond to a potential set of type judgements as sub-lattices of this lattice, with the appropriate underspecified record type (e.g.
. The interpretation process, including reference resolution, then takes the incrementally built top-level formula and checks it against a type system (corresponding to a world model) defined by a record type lattice. Implicitly, the record type on each node in a DS-TTR tree can be seen to correspond to a potential set of type judgements as sub-lattices of this lattice, with the appropriate underspecified record type (e.g.  ) as their top element, with a probability value for each element in the probabilistic TTR version. Building on this, Sadrzadeh et al. (2018b) took the first steps in showing how equivalent underspecification, and narrowing down of meaning over time can be defined for vector space representations with analogous operations to
) as their top element, with a probability value for each element in the probabilistic TTR version. Building on this, Sadrzadeh et al. (2018b) took the first steps in showing how equivalent underspecification, and narrowing down of meaning over time can be defined for vector space representations with analogous operations to  and
and  —this gives the additional advantages inherent in vector space models such as established techniques for computing similarity judgements between word, phrase and sentence representations.
—this gives the additional advantages inherent in vector space models such as established techniques for computing similarity judgements between word, phrase and sentence representations.
3 Compositional Vector Space Semantics for DS
Vector space semantics are commonly instantiated via lexical co-occurrence, based on the distributional hypothesis that meanings of words are represented by the distributions of the words around them; this is often described by Firth’s claim that ‘you shall know a word by the company it keeps’ (Firth 1957). More specifically, the methodology of distributional semantics has involved taking very large corpus collections as the data source and defining the content of a word as a function of the number of times it occurs in relation to other relevant expressions in that collection, as determined by factors such as similarity and dependency relations with such expressions. This can be implemented by creating a co-occurrence matrix (Rubenstein and Goodenough 1965), in which the columns are labelled by context words and the rows by target words; the entry of the matrix at the intersection of a context word c and a target word t is a function (such as TF-IDF or PPMI) of the number of times t occurred in the context of c (as defined via e.g. a lexical neighbourhood window, a dependency relation, etc.). The meaning of each target word is represented by its corresponding row of the matrix. These rows are embedded in a vector space, where the distances between the vectors represent degrees of semantic similarity between words (Schütze 1998; Lin 1998; Curran 2004). Alternatively, rather than instantiating these vectors directly from co-occurrence statistics, the vectors can be learned (usually via a neural network) in order to predict co-occurrence observations and thus encode meaning in a similar way (see e.g. Baroni et al. 2014b, for a comparison of these methods).
Distributional semantics has been extended from word level to sentence level, where compositional operations act on the vectors of the words to produce a vector for the sentence. Existing models vary from using simple additive and multiplicative compositional operations (Mitchell and Lapata 2010) to operators based on fully fledged categorial grammar derivations, e.g. pregroup grammars (Coecke et al. 2010; Clark 2013), the Lambek Calculus (Coecke et al. 2013), Combinatory Categorial Grammar (CCG) (Krishnamurthy and Mitchell 2013; Baroni et al. 2014a; Maillard et al. 2014) and related formalisms, such as multimodal Lambek Calculi (Moortgat and Wijnholds 2017). However, most work done on distributional semantics has not been directly compatible with incremental processing, although first steps were taken in Sadrzadeh et al. (2017) to develop such an incremental semantics, using a framework based on a categorial grammar as opposed to in the DS formalism, i.e. one in which a full categorial analysis of the phrase/sentence was the obligatory starting point.
Compositional vector space semantic models have a complementary property to DS. Whereas DS is agnostic to its choice of semantics, compositional vector space models are agnostic to the choice of the syntactic system. Coecke et al. (2010) show how they provide semantics for sentences based on the grammatical structures given by Lambek’s pregroup grammars (Lambek 1997); Coecke et al. (2013) show how this semantics also works starting from the parse trees of Lambek’s Syntactic Calculus (Lambek 1958); Wijnholds (2017) shows how the same semantics can be extended to the Lambek-Grishin Calculus; and (Krishnamurthy and Mitchell 2013; Baroni et al. 2014a; Maillard et al. 2014) show how it works for CCG trees. These semantic models homomorphically map the concatenation and slashes of categorial grammars to tensors and their evaluation/application/composition operations, as shown by (Maillard et al. 2014), all of which can be reduced to tensor contraction.
In DS terms, structures \(X_1, X_2, X_3\) are mapped to general higher order tensors, e.g. as follows:
Each \(T_{i_1i_2 \cdots i_n}\) abbreviates the linear expansion of a tensor, which is normally written as follows:
for \({e}_i\) a basis of \(V_i\) and \(C_{i_1i_2 \cdots i_n}\) its corresponding scalar value. The \(\mathbf {O}\) operations are mapped to contractions between these tensors, formed as follows:
In their most general form presented above, these formulae are large and the index notation becomes difficult to read. In special cases, however, it is often enough to work with spaces of rank around 3. For instance, the application of a transitive verb to its object is mapped to the following contraction:
This is the contraction between a cube \(T_{i_1 i_2 i_3 }\) in \(X_1 \otimes X_2 \otimes X_3\) and a vector \(T_{i_3}\) in \(X_3\), resulting in a matrix in \(T_{i_1i_2}\) in \( X_{1} \otimes X_2\).
We take the DS propositional type Ty(t) to correspond to a sentence space S, and the entity type Ty(e) to a word space W. Given vectors \(T_i^{mary}, T_k^{john}\) in W and the (cube) tensor \(T_{ijk}^{like}\) in \(W \otimes S \otimes W\), the tensor semantic trees of the DS parsing process of “\(Mary \ likes \ John\)” become as in Fig. 3.Footnote 1
A very similar procedure is applicable to the linked structures, where conjunction can be interpreted by the \(\mu \) map of a Frobenius algebra over a vector space, e.g. as in (Kartsaklis 2015), or as composition of the interpretations of its two conjuncts, as in (Muskens and Sadrzadeh 2016). The \(\mu \) map has also been used to model relative clauses (Clark et al. 2013; Sadrzadeh et al. 2013, 2014). It combines the information of the two vector spaces into one. Figure 2 shows how it combines the information of two contracted tensors \(T_i^{mary}T_{ij}^{sleep}\) and \(T_i^{mary}T_{ij}^{snore}\).
DS requirements can now be treated as requirements for tensors of a particular order (e.g. ?W, \(?W \otimes S\) as above). If we can give these suitable vector-space representations, we can then provide a procedure analogous to that of Hough and Purver (2012)’s incremental type inference procedure, allowing us to compile a partial tree to specify its overall semantic representation (at its root node). One alternative would be to interpret them as picking out an element which is neutral with regards to composition: the unit vector/tensor of the space they annotate. A more informative alternative would be to interpret them as enumerating all the possibilities for further development. This can be derived from all the word vectors and phrase tensors of the space under question—i.e. all the words and phrases whose vectors and tensors live in W and in \(W \otimes S\) in this case — by taking either the sum \(T^{+}\) or the direct sum \(T^{\oplus }\) of these vectors/tensors. Summing will give us one vector/tensor, accumulating the information encoded in the vectors/tensors of each word/phrase; direct summing will give us a tuple, keeping this information separate from each other. This gives us the equivalent of a sub-lattice of the record type lattices described in (Hough and Purver 2017), with the appropriate underspecified record type as the top element, and the attendant advantages for incremental probabilistic interpretation (Fig. 4).
These alternatives all provide the desired compositionality, but differ in the semantic information they contribute. The use of the identity provides no extra semantic information beyond that contributed by the words so far; the sum gives information about the “average” vector/tensor expected on the basis of what is known about the language and its use in context (encoded in the vector space model); the direct sum enumerates/lists the possibilities. In each case, more semantic information can arrive later as more words are parsed. The best alternative will depend on task and implementation. In the experiments below, we implement and compare all these three methods.
4 Incremental Disambiguation
In this section, we show how our model can be applied to a common task in compositional distributional semantics: disambiguation of verb meanings.
4.1 A Disambiguation Task
Verbs can have more than one meaning and their contexts, e.g. their subjects, objects and other elements, can help disambiguate them. In compositional distributional semantics, this has been modelled by comparing different hypothesized paraphrases for a sentence, one for each of the meanings of the verb, and then measuring the degree of semantic similarity between the vectors for these hypothesized paraphrased sentences and the original sentence (the one containing the ambiguous verb). The sentence that is closer to the original sentence will then be returned as the one containing the disambiguated meaning of the verb. For instance, consider the verb slump; it can mean ‘slouch’ in the context of an utterance with “shoulders” as its subject, or it can mean ‘decline’ in the context of an utterance with “sales” as its subject. This procedure is implemented in compositional distributional semantics by building vectors for the following sentences:
“Shoulders slumped”, “Shoulders slouched”, “Shoulders declined”.
“Sales slumped”, ‘Sales slouched”, “Sales declined”
The semantic distances, e.g. the cosine distance, between these vectors are employed to see which ones of these sentences are closer to each other. If “x slumped” is closest to “x slouched”, then it is concluded that an utterance of “slump” means ‘slouch’ in the context of “x”. This idea was used by Mitchell and Lapata (2010) to disambiguate intransitive verbs using their subjects as context. They showed that the compositional distributional methods work better than simple distributional methods: comparing distances between composed sentence representations gives more accurate paraphrase disambiguation than simply comparing the vectors of the individual verbs.
To test this, they used a dataset of sentences arranged in pairs:
Sentence1 | Sentence2 | Landmark |
|---|---|---|
Shoulders slumped | Shoulders declined | Low |
Shoulders slumped | Shoulders slouched | High |
Sales slumped | Sales declined | High |
Sales slumped | Sales slouched | Low |
Each entry of the dataset consists of a pair of sentences and a similarity landmark (LOW, HIGH). Each sentence in the pair is created by replacing the verb of the first sentence with each of its two most orthogonal meanings. The meanings and the degrees of their orthogonality are drawn from WordNet and the synsets of the original verbs.
This dataset has been extended to transitive verbs, first by Grefenstette and Sadrzadeh (2011), using a set of frequent verbs from the British National Corpus (BNC, Burnard 2000) and two of their meanings which are furthest apart using WordNet distances; and then by Kartsaklis and Sadrzadeh (2013) using a set of genuinely ambiguous verbs and their two eminent meanings introduced in (Pickering and Frisson 2001) using eye tracking. Examples of the verbs of these are as follows:
Sentence1 | Sentence2 | Landmark |
|---|---|---|
Fingers tap table | Fingers knock table | High |
Fingers tap table | Fingers intercept table | Low |
Police tap telephone | Police knock telephone | Low |
Police tap telephone | Police intercept telephone | High |
Babies dribble milk | Babies drip milk | High |
Babies dribble milk | Babies control milk | Low |
Footballers dribble ball | Footballers control ball | High |
Footballers dribble ball | Footballers drip ball | Low |
In compositional distributional semantics, one can build vectors for the words of these sentences and add or pointwise multiply them to obtain a vector for the whole sentence (Mitchell and Lapata 2008). Alternatively, one can build vectors for nouns and tensors for adjectives and verbs (and all other words with functional types) and use tensor contraction to build a vector for the sentence (Grefenstette and Sadrzadeh 2015; Kartsaklis and Sadrzadeh 2013). It has been shown that some of the tensor-based models improve on the results of the additive model, when considering the whole sentence (Grefenstette and Sadrzadeh 2015; Kartsaklis and Sadrzadeh 2013; Wijnholds and Sadrzadeh 2019); here, we focus on incremental composition as described above to investigate how the disambiguation process works word-by-word.
In the intransitive sentence datasets (Mitchell and Lapata 2008), the disambiguation context only consists of the subject and verb, and the incremental process is fairly trivial (the ambiguity is only introduced when the verb is processed, and at that point the sentence is complete). We use intransitive examples to explain the principle first, but thereafter work with the transitive sentence datasets and their different variants.
4.2 An Incremental Disambiguation Procedure
In a nutshell, the disambiguation procedure is as follows: when we hear the word “shoulders” uttered, we can build a vectorial interpretation for the as-yet incomplete utterance, using the compositional distributional semantics of Dynamic Syntax as explained in Sect. 3 (and using either neutral identity information, or (direct) sum information about all the intransitive verbs and verb phrases that can follow). After we hear the verb “slump”, our uttered sentence is complete and we form a vector for it, again by using the compositional distributional semantics of DS (or the more traditional methods; the two should result in the same semantics for complete utterances). We can check the incremental behaviour of this process by one or more of the following steps:
-
1.
The semantic vector of the unfinished utterance “shoulders \(\cdots \)” should be closer to the semantic vector of the sentence with the correct meaning of “slump” (i.e. to “Shoulders slouched”) than to the vector of the sentence with the incorrect meaning of “slump” (i.e. to “Shoulders declined”). Formally, using the cosine similarity measure of distributional semantics, the following should be the case:
$$\begin{aligned}&\cos (\overrightarrow{{\textit{shoulders}} \cdots },\overrightarrow{{\textit{shoulders \ slouched}}})\\&\quad \ge \cos (\overrightarrow{{\textit{shoulders}} \cdots },\overrightarrow{{\textit{shoulders \ declined}}}) \end{aligned}$$Of course, the complete utterance “shoulders slumped” should also be closer to “shoulders slouched”. This is not incremental and has been verified in previous work (Mitchell and Lapata 2008). We do not experiment with this case here, although, we might also expect, and could check, that it is closer to the full correct paraphrase than is the partial sentence:
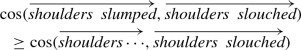
-
2.
Conversely, for an example in which the other verb paraphrase is appropriate: the semantic vector of the unfinished utterance sales \(\cdots \) should be closer to the vector of the sentence sales declined than to that for sales slouched, and a full sentence be closer than an incomplete one:
$$\begin{aligned}&\cos (\overrightarrow{{\textit{sales}} \cdots },\overrightarrow{{\textit{sales \ declined}}})\ge \cos (\overrightarrow{{\textit{sales}} \cdots },\overrightarrow{{\textit{sales \ slouched}}})\\&\cos (\overrightarrow{{\textit{sales \ slumped}}},\overrightarrow{{\textit{sales \ declined}}})\ge \cos (\overrightarrow{{\textit{sales}} \cdots },\overrightarrow{{\textit{sales \ declined}}}) \end{aligned}$$ -
3.
We can also compare between the examples: the semantic vector of the unfinished utterance shoulders \(\cdots \) should also be closer to the vector of the full sentence shoulders slouched than the vector of the unfinished utterance “sales \(\cdots \)” is to that of the complete sentence “sales slouched”:
$$\begin{aligned} \cos (\overrightarrow{{\textit{shoulders}} \cdots },\overrightarrow{{\textit{shoulders \ slouched}}})\ge \cos (\overrightarrow{{\textit{sales}} \cdots },\overrightarrow{{\textit{sales \ slouched}}}) \end{aligned}$$And the other way around should also hold, that is, the vector of the unfinished utterance sales \(\cdots \) should be closer to the vector of the uttered sentence sales declined than the vector of shoulders \(\cdots \) is to shoulders declined.
$$\begin{aligned} \cos (\overrightarrow{{s\textit{ales}} \cdots },\overrightarrow{{\textit{sales \ declined}}})\ge \cos (\overrightarrow{{\textit{shoulders}} \cdots },\overrightarrow{{\textit{shoulders \ declined}}}) \end{aligned}$$
A symbolic generalisation of the above procedure for the Sbj Vrb Obj cases, which is the case we will experiment with, is presented below. In Sect. 5, we then provide evidence from real data, first giving a worked example for each of these cases, and then a large scale experimental evaluation.
Consider a verb Vrb that is ambiguous between two meanings Vrb1 and Vrb2; suppose further that a subject Sbj makes more sense with the first meaning of the verb, that is with Vrb1, rather than with its second meaning, that is with Vrb2. This is because Sbj has more associations with Vrb1, e.g. since it has occurred more with Vrb1 (or with verbs with similar tensors to Vrb1) than with Vrb2 in a corpus. These correlations are interpreted in our setting as follows:
We can extend this when we incrementally proceed and parse the verb Vrb. Now we can check the following:
Here, we are incrementally disambiguating the unfinished utterance Sbj Vrb using the vector semantics of its subject Sbj, the tensor meaning of its verb Vrb, and the contraction (read composition) of the two. As we add more context and finish the incremental parsing of the utterances, similar regularities to the above are observed and we expect the corresponding degrees of semantic similarity to become more sharply distinguished as the object meaning Obj is added:
The fronted object cases, Obj Sbj Vrb, such as in the sentence The milk the baby dribbled can also be dealt with, but are left to future work.
5 Evidence from Real Data
Of course, the real test is whether similarities calculated this way reflect those we would intuitively expect. In this section, we test this with some selected example sentences, using vectors and tensors calculated from real corpus data.
Our noun vectors are produced using word2vec, a commonly used neural network model for learning word vector representations (Mikolov et al. 2013): we use 300-dimensional vectors learned from the Google News corpus.Footnote 2 Our verb tensors are derived using the method of Grefenstette and Sadrzadeh (2011): the tensor \(\overrightarrow{V}\) is the sum of \(\overrightarrow{S} \otimes \overrightarrow{O}\) over the subject noun vectors \(\overrightarrow{S}\) and object noun vectors \(\overrightarrow{O}\) observed to co-occur with the verb in question in a large parsed corpus. Here we take the verb-subject/verb-object occurrences from the dependency-parsed version of UKWaC (Baroni et al. 2009), and use the same word2vec noun vectors; our verb tensors are therefore 300x300-dimensional matrices. To compose a sentence representation \(\overrightarrow{A}\), we again follow Grefenstette and Sadrzadeh (2011), using point-wise multiplication of the verb tensor with the Kronecker product of the subject and object vectors (other methods are possible, and we explore these in the next section):
We start with an example from the dataset of Kartsaklis et al. (2013b): the ambiguous verb dribble has a different sense in the sentence Footballers dribble balls than in the sentence Babies dribble milk. If we take these senses to be roughly paraphrased as ‘control’ and ‘drip’, respectively, we can examine not only whether the full sentence representations are more similar to the appropriate paraphrases (as in the experiments of Kartsaklis et al. , 2013b), but also whether this disambiguation is exhibited incrementally. Here, we take the option described above of representing unsatisfied requirements with the identity tensor I; we express similarities using the cosine similarity measure:
First, we note that the expected pattern is observable between completed utterances (as expected, given the results of Mitchell and Lapata (2008) and Kartsaklis et al. (2013b)), with the representation for the complete sentence being more similar to the correct paraphrase (following Kartsaklis et al. (2013b) we simplify here by ignoring inflections such as plural suffixes and use the vectors and tensors for noun and verb root forms):
We can check the incremental behaviour by calculating and comparing similarities at incremental stages. First, after parsing only the subject, we see that “Footballers \(\cdots \)” has a closer semantic similarity with “Footballers control \(\cdots \)” than with “Footballers drip \(\cdots \)”: that as you add to your unfinished utterances, its semantics builds up in a coherent way:
Next, after parsing the subject and verb, we again see the expected effect:
Similarly we can examine similarities with possible complete utterances, giving us a notion of incremental expectation in parsing; again we see an effect in the expected direction – the unfinished utterance “Footballers \(\cdots \)” is semantically closer to “Footballers dribble balls” than to “Footballers dribble milk”, which is of course what semantically makes sense:
And this also holds when the verb is parsed, i.e. as we carry on finishing the utterance, we get higher more reasonable similarity degrees:
Similarly, for the unfinished utterance “Babies \(\cdots \)” we obtain the following desirable results that agree with semantic incrementality:
However, this is not always the case; for the same utterance, the similarities calculated after parsing only the subject point in the opposite direction to that expected:
It seems, therefore, that it must be the verb dribble and then even more strongly, the combination with the object milk that provides much of the disambiguating information in this case – perhaps babies alone are no more likely to drip than to control.
We have a similar situation for the ambiguous verb tap, its two meanings ‘knock’ and ‘intercept’, and the subject “finger” which disambiguates “tap” to its ‘knock’ meaning:
For the case when “tap” is disambiguated to its ‘intercept’ meaning, we do not yield the expected cosine correlations. For instance, “police \(\dots \)” is not semantically closer to “police intercept \(\dots \)” than to “police knock \(\dots \)”, as one would expect. This might be since policemen knock many objects, such as tables and doors, and also since tap is too strongly associated with its knocking meaning than with its intercepting meaning.
Because of these individual mismatches, we require a larger scale evaluation to get a more general picture, which we perform in the following section.
5.1 Larger-Scale Evaluation
We apply this method for incremental disambiguation in the full versions of the above mentioned datasets to see how well it scales up. Previous work on compositional distributional semantics provides three preliminary datasets suitable for this task: in each, sets of transitive S-V-O sentences in which the verb V is ambiguous are paired with human judgements of similarity between each given sentence and two possible paraphrases (e.g. for the sentence “footballer dribbles ball”, the possible paraphrases ‘footballer carries ball’ and ‘footballer drips ball’). Grefenstette and Sadrzadeh (2011) provide a dataset with 32 paraphrase examples (hereafter GS2011); Grefenstette and Sadrzadeh (2015) a modification and extension of this to 97 paraphrase examples (GS2012); and Kartsaklis et al. (2013a) a further 97 examples on a different verb set (KSP2013).Footnote 3
The GS2011 dataset is small, and contains judgements from only 12 annotators per example; the authors found it not to show significant differences between additive baselines and more complex compositional methods. The extended GS2012 version provides a larger set of 97 examples, each with 50 annotators’ judgements; we expect it to provide a more reliable test. KSP2013 is then the same size, but selects the verbs using a different method. While Grefenstette and Sadrzadeh (2015) chose verbs which spanned multiple senses in WordNet (Fellbaum 1998), taking the paraphrases as two of their most distant senses, Kartsaklis et al. (2013a) chose verbs specifically for their ambiguity, based on psycholinguistic evidence collected by eye tracking and human evaluation by Pickering and Frisson (2001). We therefore expect the KSP2013 dataset to provide an evaluation which is not only robust but a more direct test of the task of disambiguation in natural dialogue.
Again, we use the same 300-dimensional word2vec vectors and 300x300-dimensional verb tensors derived from them. For sentence composition, we now compare the method used in the previous section, from (Grefenstette and Sadrzadeh 2011), which we term “G&S” below; with alternatives proposed by Kartsaklis et al. (2013b) termed “copy-subj” and “copy-obj”. Here, \(\odot \) denotes pointwise multiplication and \(\otimes \) the Kronecker product as before, and \(\times \) denotes matrix multiplication:
The latter alternatives have been shown to perform better in some compositional tasks (see e.g. Kartsaklis et al. 2013b; Milajevs et al. 2014). We also compare the use of the identity I and sum \(T^{+}\) to represent nodes with unsatisfied requirements; given our disambiguation task setting here, the natural way to use the direct sum \(T^{\oplus }\) is to average the resulting distances over its output tuples, thus making it effectively equivalent to using the sum in this case. We compare these options to a simple, but often surprisingly effective, additive baseline (Mitchell and Lapata 2008): summing the vectors for the words in the sentence. In this case, verbs are represented by their word2vec vectors, just as nouns (or any other words) are, viz. without taking their grammatical role into account; and incremental results are simply the sum of the words seen so far.
Mean disambiguation accuracy over the GS2011 dataset (Grefenstette and Sadrzadeh 2011), as incremental parsing proceeds left-to-right through “S V O” sentences. Note that the sum/G&S and identity/G&S methods give identical average accuracy on this dataset, and thus share a line on the graph
Mean disambiguation accuracy over the GS2012 dataset (Grefenstette and Sadrzadeh 2015), as incremental parsing proceeds left-to-right through “S V O” sentences. Note that the sum/G&S and identity/G&S methods give identical average accuracy on this dataset, as do the sum/copy-subj and identity/copy-subj methods, and thus those pairs share lines on the graph
Mean disambiguation accuracy over the KSP2013 dataset (Kartsaklis et al. 2013a), as incremental parsing proceeds left-to-right through “S V O” sentences. Note that the sum/copy-obj and identity/copy-obj methods give identical average accuracy on this dataset, and thus share a line on the graph
We evaluate the accuracy of these approaches by comparing to the human judgements in terms of the direction of preference indicated for the two possible paraphrases.Footnote 4 As several human judges were used for each sentence, we compare to the mean judgement for each sentence-paraphrase pair. Accuracy can therefore be calculated directly in terms of the percentage of sentences for which the most similar paraphrase is correctly identified. Given our incremental setting, we can make this comparison at three points in each S-V-O sentence (after parsing the subject S only; after parsing S and V; and after parsing the full S-V-O), at each point comparing the similarity between the (partial) sentence and each of the (partial) paraphrase sentences. Note though that after parsing S only, all methods are equivalent: the only information available is the vector representing the subject noun, the ambiguous verb has not even been observed, and disambiguation is therefore a random choice with 50% accuracy; the performance then diverges at S-V and S-V-O points.
Results Results for the small Grefenstette and Sadrzadeh (2011) dataset are shown in Fig. 5; while none of our compositional approaches beat the additive baseline, it appears that the incremental performance after S-V may be reasonable compared to the full-sentence performance S-V-O. However, none of the differences are statistically significant (a \(\chi ^2\) test shows \(\chi ^2_{(1)}=1.56, p=0.21\) for the largest difference, identity/G&S vs. add at the S-V point), given the small size of the dataset, and conclusions are therefore hard to draw. One thing that, however, stands out, is that disambiguation accuracy increases from S-V to S-V-O for the relational G&S model and the copy-subject model. The additive model stays almost the same after adding the verb and after adding the object, while the copy-object method gets worse; these may be undesirable properties in terms of providing a good model of incrementality.
For the larger datasets, results are shown in Tables 1 and 2 and depicted in Figs. 6 and 7. For GS2012, all methods do significantly better than chance (taking \(p<0.05\) for significance, \(\chi ^2_{(1)}=5.08, p=0.024\) for the worst method, add); the compositional methods outperform the additive baseline, and although the improvement is not statistically significant at the \(p<0.05\) level it suggests an effect (\(p<0.15\), with \(\chi ^2_{(1)}=2.51, p=0.11\) for the best method, identity/copy-obj at the V-O point).The copy-object method seems to do best, outperforming copy-subject and the G&S method, and particularly to perform well incrementally at the mid-sentence S-V point (76% accuracy, with 72% after S-V-O). Again, similar to GS2011, and despite the fact that copy-object does best on the overall accuracy, the identity/G&S and identity/copy-subj models seem to do best in terms of incremental accuracy development; their accuracies increase more when going from S-V to S-V-O, and seem to increase more smoothly through the sentence, whereas the copy-obj models increase to S-V and then decrease.
For KSP2013, the task seems harder: here, the additive baseline performs almost at chance level with about 52%, but all the tensor-based compositional methods do better; the best improvement being significant at \(p<0.1\), although not at \(p<0.05\) (\(\chi ^2_{(1)}=2.77, p=0.096\) for identity/copy-obj at S-V-O). Again, the copy-object composition method seems to perform best, giving good accuracy at S-V and S-V-O points (62% accuracy); the G&S method does better this time, particularly at the mid-sentence point; but copy-subject does well for the full sentence but not incrementally. Copy-object with identity, the model that provides the best accuracy, also shows a steady increase in accuracy through the sentence, although copy-subject with identity still shows the steepest increase from S-V to S-V-O. This latter method shows the steepest increase in all the datasets.
Accuracy comparisons between the identity and sum/direct sum methods show little difference. As we see in Tables 1 and 2, whenever there is a difference in results among the different requirement representations, the identity approach gives slightly higher accuracy. An explanation of this is that the identity is only used as a mechanism to be able to compute a sentence representation in a compositional way, but without contributing information by itself. On the contrary, the sum and direct sum methods introduce averages of vectors found in the corpus, which is akin to adding noisy information to the sentence representation; remember that the datasets we use here (from which we must take our information about the possible continuations that we average over) are very small compared to the large corpora used to build standard word vectors. It is encouraging that all methods perform well; it may be that in larger datasets the sum methods will improve, given more information about the possible distributions over continuations, and in other tasks which depend on more than just average sentence distances, the sum and direct sum methods will diverge.
Discussion and comparison The main point of interest here, of course, is the intermediate point after processing S-V (but before seeing the object O): here the additive baseline does approximately as well as with full sentences, suggesting that most disambiguating information comes from the verb vector in these datasets. The compositional tensor-based methods on the other hand, particularly copy-object, seem able to use information from the combination of S-V to improve on that, and then to incorporate further information from O to improve again (at least with KSP2013). Composition therefore allows useful information from all arguments to be included; and it seems that our method allows that to be captured incrementally as the sentence proceeds.
An error analysis showed that in the majority of cases our overall best performing models (sum/copy-obj, identity/copy-obj) either correctly disambiguated both the S-V and the S-V-O pairs, or got it wrong in both cases; in other words, the incremental accuracy was as good (or bad) as that for complete sentences. In a minority of cases, though, the incremental behaviour diverged (either S-V was disambiguated correctly, while S-V-O was not, or vice versa). These are the cases of interest here (for discussion of the behaviour of different compositional models for full sentences, see Kartsaklis et al. , 2013b).
Interestingly, a prominent erratic ambiguous verb was to file, where in some cases, the smooth meaning was expected but the model wrongly computed it to be the register meaning, and in the other cases, the register meaning was expected whereas the model wrongly computed it to be the smooth meaning. Examples of the data set entries were (all words in stem form):
-
(1)
woman file nail
englishman file steel
-
(2)
state file declaration
union file lawsuit
where the smooth meaning is expected in (1) and register in (2). For (1) examples, the copy-obj models predicted correctly at the S-V point, and then incorrectly at the S-V-O point. These seem to be examples where most disambiguating information intuitively comes in the object. We therefore suspect that although the S-V subject and verb tensor combination itself contains sufficient information about the kind of object in these cases (see Kartsaklis et al. 2013b for discussion of how the copy-obj method encodes more object information), these particular objects did not occur frequently enough in the corpus with this verb meaning, but had more occurrences in the context of other verbs. In the case of file nail, for instance, the noun nail may occur more with verbs such as to hammer or to sell, or to cut, rather than the verb to file. The copy-subj models performed the opposite way, predicting incorrectly at S-V and then correctly with the full S-V-O sentence: here, the S-V composition themselves encode less information about the disambiguating object (hence incorrectness at S-V), and this can be supplied later on S-V-O composition, while giving the object less weight than with the copy-obj method.
We observed the same pattern for our most smoothly incremental models: copy-subject with sum and identity. In the majority of cases, these models either got the meaning of the verb correctly for both S-V and S-V-O, or got it wrong, again for both S-V and S-V-O. Their mistakes, i.e. cases where S-V was correctly disambiguated, but S-V-O was not, were more varied, apart from the verb to file, they also had instances of to cast, to tap and to lace, in the following contexts:
-
(3)
company file account
boat cast net
palace cast net
monitor tap conversation
child lace shoe
In all of these cases, the object provided in the data set has occurred more frequently with contexts of other verbs, e.g. account in the first sentence above has occurred more in the context of verbs such as funded or issued; net in the second and third examples is itself ambiguous and occurred much more frequently in its financial sense (where it contrasts with gross) in the very large naturally occurring dataset taken as base. Similarly for conversation and shoe, which occurred more with had and wore respectively, than tapped and laced.
Differences between the sum and identity methods are smaller and thus harder to investigate in a conclusive manner. Some verbs, such as dribble, show interesting differences: for woman dribble wine, identity seems to give better accuracy at the S-V stage than at S-V-O; for player dribble ball it is the opposite.
Overall, following the Kartsaklis et al. (2013b) demonstration that copy-obj outperforms others for full-sentence disambiguation in virtue of encoding more information about the object, the results here, which incorporate in addition an incrementality factor, also indicate that copy-obj does better overall, and for similar reasons, though here based on probability rather than encoding. However, with some verbs getting disambiguated with their objects better than with their subject and some verbs the other way round, it is hard to evaluate which model’s performance is really most desirable. In future work we would hope to investigate comparisons with human ratings of disambiguation at the S-V stage, but this raises complex questions about datasets and about bias in the vector/tensor corpora which are beyond the scope of this paper.
6 Discussion
Although the theoretical predictions of the model have only been verified on S-V-O triples, they are immediately applicable to sentences of greater complexity. Of importance here, however, are utterances arising within natural dialogue, and of those, particularly unfinished and interrupted instances. These kinds of utterance have not been dealt with in the commonly used type-logical vector space approaches so far, as those rely on a sentential level of grammaticality. As our simple experiment shows, our setting does not rely on sentential grammaticality: we have theoretically prescribed how to build vector representations for any DS tree; on the practical side, we have applied these prescriptions to subject-only, subject-verb, and subject-verb-object strings. This is the first time it has been shown that disambiguation of unfinished utterances can be computed incrementally in vector space semantics, not only opening the practical possibilities of real-time distributional semantic processing for spoken Natural Language Understanding tasks, but also allowing for a more realistic simulation of human processing than previously possible. The match that our setting provides for human disambiguation judgements is being derived solely on the basis of observed co-occurrences between words and syntactic roles in a corpus, without any specification of content intrinsic to the word itself. Further experiments will be needed to extend this approach to larger datasets and to dialogue data and examine its effectiveness, perhaps using the work extending DS grammars to dialogue (Eshghi et al. 2017), and possibly evaluating on the similarity dataset of Wijnholds and Sadrzadeh (2019) that extends the transitive sentence datasets used in this paper to a verb phrase elliptical setting.
Our assumption from the outset of this work was that distributions across a sufficiently large corpus can be taken to provide an analogue and basis for formal modelling of the observation that interpretation of words depends on contingent, contextual and encyclopaedic facts associated with objects. To place these results and the adopted methodology in a psychological perspective, the way in which these statistical methods show that discrete facets of meaning of an individual word are progressively distinguishable in an incremental way provides at least partial confirmation that the meaning that words have is recoverable from affordances made available in the contingent contexts in which they occur, these being anticipations routinely associated with the word in question over many uses that they come to constitute, including the actions triggered by the word.Footnote 5 Moreover, the underlying concept of a context of affordances has the cross-temporal, cross-spatial attributes shared by “big-data” corpora.
We thus take the results as provisionally confirming a thin concept of meaning, not associated with some intrinsically fixed encoded content, but merely a non-deterministic set of associations which the word triggers for the individual agent(s). We also expect to be able to deal with cases when an interpretation shifts during the incremental process (say, when uttering “The footballer dribbled beer down his chin”), when the incoming input acts as a filter over-riding an otherwise accumulating default. This is exactly what one would expect of an account with a basis in non-deterministic meanings, the underpinnings allowing variability as the interpretation gradually consolidates, directly in line with a range of Radical Embodied Cognition perspectives (Clark 2016; Bruineberg and Rietveld 2014; Kempson and Gregoromichelaki 2019). It also gives us hope that such an approach (although we currently have no direct model of this) should extend to modelling the more general shifts in understanding that occur within the ubiquitous coordinating to-and-fro between interlocutors in dialogue (Healey et al. 2018). In the mean time, we hope these provisional results make a contribution towards grounding the claim that languages are defined as procedures for inducing growth of specifications of content in real time, with plasticity of such constituent parts playing an irreducible role.
Notes
There has been much discussion about whether sentence and word spaces should be the same or separate. In previous work, we have worked with both cases, i.e. when \(W \ne S\) and when \(W = S\).
Taken from: https://code.google.com/archive/p/word2vec/
Note that despite the date of the associated publication (Grefenstette and Sadrzadeh 2015), the GS2012 dataset was created in 2012 and came second in the series. All datasets are publicly available; we provide information on how to download them, together with the software used here for our experiments, for replication purposes at https://osf.io/hby4e/.
We do not attempt to evaluate whether the magnitude of the preference matches the magnitude of human preferences, but only whether the direction is correct: in other words, we treat this as a classification rather than a regression task.
The original Gibsonian concept of affordance, ‘perceivable relations between an organism’s abilities and the properties of the environment’ (Anderson 2014), was restricted to that of affordances for motor activity made available by the environment to the individual in question, but following Bruineberg and Rietveld inter alia we take affordances to be all types of possibility relevant to an agent for action within the environment provided (Clark 2016; Bruineberg and Rietveld 2014; Rietveld et al. 2018), including words and the grammar.
References
Anderson, M. L. (2014). After phrenology: Neural reuse and the interactive brain. Cambridge, MA: MIT Press.
Baroni, M., Bernardi, R. & Zamparelli, R. (2014a). Frege in space: A program of compositional distributional semantics. Linguistic Issues in Language Technology, 9.
Baroni, M., Bernardini, S., Ferraresi, A., & Zanchetta, E. (2009). The WaCky wide web: A collection of very large linguistically processed web-crawled corpora. Language Resources and Evaluation, 43(3), 209–226.
Baroni, M., Dinu, G. & Kruszewski, G. (2014b). Don’t count, predict! A systematic comparison of context-counting versus context-predicting semantic vectors. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, pages 238–247, Baltimore, Maryland. Association for Computational Linguistics.
Bruineberg, J., & Rietveld, E. (2014). Self-organization, free energy minimization, and optimal grip on a field of affordances. Directions in Human Neuroscience, 8(599).
Burnard, L. (2000). Reference guide for the British national corpus (World ed.). Oxford, UK: Oxford University Computing Services.
Cann, R., Kempson, R., & Marten, L. (2005). The dynamics of language: An introduction. Syntax and semantics (Vol. 35). San Diego, CA: Academic Press.
Cann, R., Kempson, R., & Purver, M. (2007). Context and well-formedness: The dynamics of ellipsis. Research on Language and Computation, 5(3), 333–358.
Carston, R. (2019). Ad-hoc concepts, polysemy and the lexicon. Relevance, pragmatics and interpretation (pp. 150–162). Cambridge University Press.
Clark, A. (2016). Surfing uncertainty: Prediction. Action and the embodied mind. Oxford University Press.
Clark, H. H. (1996). Using language. Cambridge, UK: Cambridge University Press.
Clark, S. (2013). Vector space models of lexical meaning. In Heunen, C., Sadrzadeh, M., and Grefenstette, E., editors, Quantum physics and linguistics: A compositional, diagrammatic discourse, 1st edition, pages 359–377. Oxford University Press.
Clark, S., Coecke, B. & Sadrzadeh, M. (2013). The Frobenius anatomy of relative pronouns. In 13th Meeting on Mathematics of Language (MoL), pages 41–51, Stroudsburg, PA. Association for Computational Linguistics.
Coecke, B. (2019). The mathematics of text structure. Computing Research Repository (CoRR), arXiv:abs/1904.03478.
Coecke, B., Grefenstette, E., & Sadrzadeh, M. (2013). Lambek vs Lambek: Functorial vector space semantics and string diagrams for Lambek calculus. Annals of Pure and Applied Logic, 164(11), 1079–1100.
Coecke, B., Sadrzadeh, M., & Clark, S. (2010). Mathematical foundations for a compositional distributional model of meaning. Linguistic Analysis, 36, 345–384.
Cooper, R. (2005). Records and record types in semantic theory. Journal of Logic and Computation, 15(2), 99–112.
Curran, J. (2004). From Distributional to Semantic Similarity. PhD thesis, School of Informatics, University of Edinburgh.
Eshghi, A., Howes, C., Gregoromichelaki, E., Hough, J. & Purver, M. (2015). Feedback in conversation as incremental semantic update. In Proceedings of the 11th International Conference on Computational Semantics, pages 261–271, London, UK. Association for Computational Linguistics.
Eshghi, A., Shalyminov, I. & Lemon, O. (2017). Bootstrapping incremental dialogue systems from minimal data: The generalisation power of dialogue grammars. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pages 2220–2230, Copenhagen, Denmark. Association for Computational Linguistics.
Fellbaum, C. (Ed.). (1998). WordNet: An electronic lexical database. Cambridge, MA: MIT Press.
Firth, J. (1957). A synopsis of linguistic theory 1930–1955. Studies in linguistic analysis. Oxford.
Fretheim, T. (2019). The polysemy of a Norwegian modal adverb. Relevance, pragmatics and interpretation (pp. 163–173). Cambridge University Press.
Grefenstette, E. & Sadrzadeh, M. (2011). Experimental support for a categorical compositional distributional model of meaning. In Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, pages 1394–1404, Edinburgh, Scotland, UK. Association for Computational Linguistics.
Grefenstette, E., & Sadrzadeh, M. (2015). Concrete models and empirical evaluations for the categorical compositional distributional model of meaning. Computational Linguistics, 41(1), 71–118.
Healey, P. G., Mills, G. J., Eshghi, A., & Howes, C. (2018). Running repairs: Coordinating meaning in dialogue. Topics in Cognitive Science, 10(2), 367–388.
Hough, J. & Purver, M. (2012). Processing self-repairs in an incremental type-theoretic dialogue system. In Proceedings of the 16th SemDial Workshop on the Semantics and Pragmatics of Dialogue (SeineDial), pages 136–144, Paris, France.
Hough, J., & Purver, M. (2017). Probabilistic record type lattices for incremental reference processing. In S. Chatzikyriakidis & Z. Luo (Eds.), Modern Perspectives in Type-Theoretical Semantics (pp. 189–222). Basel, Switzerland: Springer.
Howes, C., Purver, M., Healey, P. G. T., Mills, G. J., & Gregoromichelaki, E. (2011). On incrementality in dialogue: Evidence from compound contributions. Dialogue and Discourse, 2(1), 279–311.
Hupkes, D., Bouwmeester, S. & Fernández, R. (2018). Analysing the potential of seq-to-seq models for incremental interpretation in task-oriented dialogue. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, pages 165–174, Brussels, Belgium. Association for Computational Linguistics.
Kartsaklis, D. (2015). Compositional Distributional Semantics with Compact Closed Categories and Frobenius Algebras. PhD thesis, Department of Computer Science, University of Oxford.
Kartsaklis, D. & Sadrzadeh, M. (2013). Prior disambiguation of word tensors for constructing sentence vectors. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, pages 1590–1601.
Kartsaklis, D., Sadrzadeh, M. & Pulman, S. (2013a). Separating disambiguation from composition in distributional semantics. In Proceedings of the Seventeenth Conference on Computational Natural Language Learning (CoNLL), pages 114–123, Sofia, Bulgaria.
Kartsaklis, D., Sadrzadeh, M., Pulman, S. & Coecke, B. (2013b). Reasoning about meaning in natural language with compact closed categories and Frobenius algebras. In Logic and Algebraic Structures in Quantum Computing and Information. Cambridge University Press.
Kempson, R., Cann, R., Gregoromichelaki, E., & Chatzikyriakidis, S. (2016). Language as mechanisms for interaction. Theoretical linguistics, 42(3–4), 203–276.
Kempson, R., Cann, R., Gregoromichelaki, E. & Purver, M. (2015). Ellipsis. In Handbook of contemporary semantic theory, 2nd edition, pages 156–194. Blackwell.
Kempson, R., & Gregoromichelaki, E. (2019). Procedural syntax. Relevance, pragmatics and interpretation (pp. 187–202). Cambridge University Press.
Kempson, R., Gregoromichelaki, E., & Howes, C. (Eds.). (2011). The dynamics of lexical interfaces. CSLI.
Kempson, R., Meyer-Viol, W., & Gabbay, D. (2001). Dynamic syntax: The flow of language understanding. Oxford, UK: Blackwell.
Krishnamurthy, J. & Mitchell, T. M. (2013). Vector space semantic parsing: A framework for compositional vector space models. In Proceedings of the ACL Workshop on Continuous VSMs and their Compositionality.
Lambek, J. (1958). The mathematics of sentence structure. American Mathematics Monthly, 65, 154–170.
Lambek, J. (1997). Type grammars revisited. In Proceedings of the 2nd International Conference on Logical Aspects of Computational Linguistics (LACL). Springer.
Lin, D. (1998). Automatic retrieval and clustering of similar words. In Proceedings of the 17th International Conference on Computational Linguistics (COLING), pages 768–774. Association for Computational Linguistics.
Maillard, J., Clark, S. & Grefenstette, E. (2014). A type-driven tensor-based semantics for CCG. In Proceedings of the Type Theory and Natural Language Semantics Workshop, EACL 2014.
Mikolov, T., Yih, W.-t. & Zweig, G. (2013). Linguistic regularities in continuous space word representations. In Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT), pages 746–751.
Milajevs, D., Kartsaklis, D., Sadrzadeh, M. & Purver, M. (2014). Evaluating neural word representations in tensor-based compositional settings. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 708–719, Doha, Qatar. Association for Computational Linguistics.
Mitchell, J. & Lapata, M. (2008). Vector-based models of semantic composition. In Proceedings of the 46th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies (ACL-HLT), pages 236–244.
Mitchell, J., & Lapata, M. (2010). Composition in distributional models of semantics. Cognitive Science, 34, 1388–1439.
Moortgat, M. & Wijnholds, G. (2017). Lexical and derivational meaning in vector-based models of relativisation. In Proceedings of the 21st Amsterdam Colloquium.
Muskens, R. & Sadrzadeh, M. (2016). Context update for lambdas and vectors. In LNCS Proceedings of the 9th International Conference on Logical Aspects of Computational Linguistics, Nancy. Springer.
Partee, B. (2018). Changing notions in the history of linguistic competence. The science of meaning: Essays on the metatheory of natural language semantics (pp. 172–186). Oxford University Press.
Pickering, M., & Frisson, S. (2001). Processing ambiguous verbs: Evidence from eye movements. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27, 556–573.
Purver, M., Eshghi, A. & Hough, J. (2011). Incremental semantic construction in a dialogue system. In Proceedings of the 9th International Conference on Computational Semantics, IWCS ’11, pages 365–369, Stroudsburg, PA, USA. Association for Computational Linguistics.
Purver, M., Gregoromichelaki, E., Meyer-Viol, W. & Cann, R. (2010). Splitting the ‘I’s and crossing the ‘You’s: Context, speech acts and grammar. In Proceedings of the 14th SemDial Workshop on the Semantics and Pragmatics of Dialogue, pages 43–50.
Purver, M., Hough, J., & Gregoromichelaki, E. (2014). Dialogue and compound contributions. In A. Stent & S. Bangalore (Eds.), Natural language generation in interactive systems (pp. 63–92). Cambridge, UK: Cambridge University Press.
Recanati, F. (2017). Contextualism and polysemy. Dialectica, 71(3), 379–397.
Rietveld, E., Denys, D., & van Westen, M. (2018). Ecological-enactive cognition as engaging with a field of relevant affordances: The skilled intentionality framework (SIF). In A. Newen, L. de Bruin, & S. Gallagher (Eds.), The Oxford handbook of 4E cognition (pp. 156–194). Oxford, UK: Oxford University Press.
Rubenstein, H., & Goodenough, J. (1965). Contextual correlates of synonymy. Communications of the ACM, 8(10), 627–633.
Sadrzadeh, M., Clark, S., & Coecke, B. (2013). Frobenius anatomy of word meanings I: Subject and object relative pronouns. Journal of Logic and Computation, 23, 1293–1317.
Sadrzadeh, M., Clark, S., & Coecke, B. (2014). Frobenius anatomy of word meanings II: possessive relative pronouns. Journal of Logic and Computation, 26, 785–815.
Sadrzadeh, M., Purver, M., Hough, J. & Kempson, R. (2018a). Exploring semantic incrementality with dynamic syntax and vector space semantics. In Proceedings of the 22nd SemDial Workshop on the Semantics and Pragmatics of Dialogue (AixDial), pages 122–131, Aix-en-Provence.
Sadrzadeh, M., Purver, M. & Kempson, R. (2017). Incremental distributional semantics for dynamic syntax. In Proceedings of the 1st Dynamic Syntax Conference, London, UK.
Sadrzadeh, M., Purver, M. & Kempson, R. (2018b). A tensor-based vector space semantics for dynamic syntax. In Proceedings of the 2nd Dynamic Syntax Conference, Edinburgh, UK.
Schegloff, E. (1984). On some questions and ambiguities in conversation. Structures of Social Action: Studies in Conversation Analysis (pp. 28–52). Cambridge, UK: Cambridge University Press.
Schütze, H. (1998). Automatic word sense discrimination. Computational Linguistics, 24(1), 97–123.
Vinyals, O. & Le, Q. (2015). A neural conversational model. In Proceedings of the 31st International Conference on Machine Learning (ICML) Deep Learning Workshop.
Wijnholds, G. & Sadrzadeh, M. (2019). Evaluating composition models for verb phrase elliptical sentence embeddings. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers). Association for Computational Linguistics.
Wijnholds, G. J. (2017). Coherent diagrammatic reasoning in compositional distributional semantics. In Proceedings of the 24th Workshop on Logic, Language, Information and Computation (WoLLIC), pages 371–386.
Acknowledgements
The contributions of this paper reflect joint work with a number of people over a considerable period. In particular we thank Arash Eshghi for extensive illuminating discussions during the writing of this paper and of other related work in this line of research, and Eleni Gregoromichelaki for ongoing insights into the relevance of the issues raised for the larger cognitive perspective. Special thanks go to the anonymous reviewers of this paper, and the editors, for helpful comments which led to substantial improvements. Purver is partially supported by the EPSRC under grant EP/S033564/1, and by the European Union’s Horizon 2020 program under grant agreements 769661 (SAAM, Supporting Active Ageing through Multimodal coaching) and 825153 (EMBEDDIA, Cross-Lingual Embeddings for Less- Represented Languages in European News Media). The results of this publication reflect only the authors’ views and the Commission is not responsible for any use that may be made of the information it contains.
This is a post-peer-review, pre-copyedit version of an article published in the Journal of Logic, Language and Information. The final authenticated version will be available online at: http://dx.doi.org/TBD.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is a post-peer-review, pre-copyedit version of an article published in the Journal of Logic, Language and Information. The final authenticated version will be available online at: http://dx.doi.org/TBD
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Purver, M., Sadrzadeh, M., Kempson, R. et al. Incremental Composition in Distributional Semantics. J of Log Lang and Inf 30, 379–406 (2021). https://doi.org/10.1007/s10849-021-09337-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-021-09337-8