Abstract
Epistemic logic is usually employed to model two aspects of a situation: the factual and the epistemic aspects. Truth, however, is not always attainable, and in many cases we are forced to reason only with whatever information is available to us. In this paper, we will explore a four-valued epistemic logic designed to deal with these situations, where agents have only knowledge about the available information (or evidence), which can be incomplete or conflicting, but not explicitly about facts. This layer of available information or evidence, which is the object of the agents’ knowledge, can be seen as a database. By adopting this sceptical posture in our semantics, we prepare the ground for logics where the notion of knowledge—or more appropriately, belief—is entirely based on evidence. The technical results include a set of reduction axioms for public announcements, correspondence proofs, and a complete tableau system. In summary, our contributions are twofold: on the one hand we present an intuition and possible application for many-valued modal logics, and on the other hand we develop a logic that models the dynamics of evidence in a simple and intuitively clear fashion.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Epistemic logic usually features a set of propositions about the world, and models a group of agents and their knowledge (or beliefs) about these propositions. Despite being very useful, this simple model leaves out of the discussion an important factor in the formation of beliefs: evidence.
Belnap (1977) gave an interpretation to first degree entailment (\({{\mathbf {\mathsf{{FDE}}}}}\)) (Dunn 1976; Priest 2008), a four-valued logic, centered on the idea of evidence. In that logic, a proposition p can be, besides true or false, both (true and false) or neither (true nor false). He interpreted these truth-values as the status of information possibly coming from several sources. For example, if both is the value assigned to p, then this means that some source supports the truth and another the falsity of p. The value none means that no information is available about p. In this way, the valuation already has an epistemic (not ontic) character.
Later, modal extensions of \({{\mathbf {\mathsf{{FDE}}}}}\) have been developed, such as \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) (Priest 2008) and \({{\mathbf {\mathsf{{BK}}}}}\) (Odintsov and Wansing 2010). As remarked by Fitting in the conclusion of Fitting (1991), very little has been said about intuitions underlying many-valued modal logics, a situation which seems to persist in the current literature. One of our main objectives in this paper is to extend the Belnapian epistemic interpretation of \({{\mathbf {\mathsf{{FDE}}}}}\) to a modal setting. By doing this, we simultaneously achieve two goals: (i) we design a four-valued modal logic suited to model situations where there is a publicly available body of potentially conflicting or incomplete evidence, and a group of agents that might be uncertain about what evidence is actually there and about what others know about this evidence; and (ii) we provide an epistemic intuition to many-valued logics, contributing to their practical applicability.
\({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\), in fact, is exactly a modal extension of \({{\mathbf {\mathsf{{FDE}}}}}\). The logic studied here, however, can express much more within the class of situations described in (i) due to the addition of the connective  and (to a lesser extent) public announcements. Nevertheless, much of the intuition presented here (item (ii)) can be transferred to \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) and \({{\mathbf {\mathsf{{BK}}}}}\).
and (to a lesser extent) public announcements. Nevertheless, much of the intuition presented here (item (ii)) can be transferred to \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) and \({{\mathbf {\mathsf{{BK}}}}}\).
The difficulty in extending the Belnapian interpretation lies in the fact that the valuation already has an epistemic character. The addition of a modal operator—which also has an epistemic nature—to this logic will, then, create two separate epistemic “layers”. Look at the classical epistemic model of Fig. 1 (left). It represents a situation wherein an agent cannot distinguish between the truth and falsity of proposition p, or, equivalently, wherein the agent does not know whether p.
Now, compare this situation with the four-valued model of Fig. 1 (right), where \(\{1\}\), \(\{0\}\), \(\{0,1\}\) and \(\emptyset \) mean, respectively, true, false, both and none. What is a plausible interpretation for this model? Here, the agent not only cannot distinguish between worlds where p is true or false, but also between worlds where it is neither true nor false, or both. If we adopt an epistemic interpretation of the valuations, what kind of interpretation is left for the operator \(\Box \)? As mentioned before, we should think of the (four-valued) valuation function as representing evidence or information, while the accessibility relations account for the uncertainty of the agents about which evidential state is the correct one.
For example, we can regard the valuation as representing the information about some propositions stored in a database. The database only registers the information it receives, so it is well possible that at first it receives the information that p is true, but subsequently it receives (possibly from another source) the information that p is false. In this case the database contains contradictory information about p. The accessibility relations may symbolise, in this case, the knowledge of a user of this database. The user may be in a state like the one in Fig. 1 (right), where she considers it possible that the database is in any of the four possible states regarding p. That is the natural extension of the Belnapian interpretation to a modal setting: models depicting agents that are uncertain about evidential states. Notice that those agents do not possess knowledge about facts, but only a superficial knowledge about evidence itself.Footnote 1
Another example not involving databases can be given. Suppose that Anne lives in Groningen, and that she usually informs herself of the weather by watching the local television’s newscast. Let proposition G mean that It will rain in Groningen tonight. Now, imagine the situation in which Anne heard that G in the newscast of Channel 1, but \(\lnot G\) in the newscast of Channel 2. The status of G for Anne is now contradictory. In this logic, however, we are not going to talk about ontic literals such as G and \(\lnot G\), but only about epistemic literals g and \(\lnot g\), meaning there is evidence for G and there is evidence against G, respectively. The confusion of Anne about G is denoted by assigning value both to g. Moreover, assuming that Anne is always up to date with the weather news from Channels 1 and 2, she will always know what is the four-valued status of g. So, in a state where G was announced to be both true and false, Anne is aware of that. She does not consider a world to be possible where only \(\lnot G\) was announced, for she already knows this is not the case. Bart, who lives in Rotterdam, on the other hand, does not have access to Groningen weather information in his local newscast, so he considers all of the four values to be possible for g. Now we can have a formula like \(\Box _a(g\wedge \lnot g)\), meaning that Anne knows that there is information supporting both the truth and the falsity of g.
The rest of this paper will explore in detail this logic of evidence, which we will simply call four-valued epistemic logic (FVEL, in short). In Sect. 2 we define the syntax and semantics of the logic, and present some of its basic properties. The formalism is a variant of the logic \({{\mathbf {\mathsf{{BK}}}}}\) (Odintsov and Wansing 2010). In Sect. 3 we present a sound and complete tableau system. In Sect. 4 we show some correspondence results concerning classical epistemic logic axioms. As a fundamental part of modern dynamic epistemic logics, public announcements are added to FVEL in Sect. 5, and are shown not to increase expressivity. We also extend the tableau system with rules for public announcements, and prove completeness. In the interpretation proposed here, public announcements will only have the effect of changing agents’ knowledge about evidence, but not the evidence itself.Footnote 2 This clearly leaves open the possibility for other kinds of dynamics, but they are not explored here. In Sect. 6 we comment on related work. This paper is placed among a rapidly growing body of literature on the topic of logics of evidence, some of which are discussed in Sect. 6.1. Conclusions and possibilities for future work are found in Sect. 7.
A preliminary version of this study appears in Santos (2018). This extended version was re-organised for a clearer presentation, and contains improved explanations, motivation and pointers to related literature. This version also includes some new results and comments on decidability, fragments and conservative extensions, equivalence, equi-satisfiability, validity and designated values. The section on tableaux was completely reformulated, as well as the tableau system itself. More complete comparisons with similar works in the literature are also included. All the proofs are not only included but also revised.
2 Four-Valued Epistemic Logic
In this section, we will define the syntax and the semantics of the logical language being examined.
2.1 Syntax
Let P be a countable set of atomic propositions and A a finite set of agents.Footnote 3 A well-formed formula \(\varphi \) in our language \(\mathcal {L}\) is inductively defined as follows:

with \(p\in P\) and \(i\in A\). The following abbreviations will be employed throughout the text: \((\varphi \vee \psi ) {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}\lnot (\lnot \varphi \wedge \lnot \psi )\); \((\varphi \rightarrow \psi ) {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}(\lnot \varphi \vee \psi )\); \((\varphi \leftrightarrow \psi ) {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}((\varphi \rightarrow \psi )\wedge (\psi \rightarrow \varphi ))\);  ;
;  ; \(\varphi \tilde{\leftrightarrow }\psi {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}(\varphi \tilde{\rightarrow }\psi )\wedge (\psi \tilde{\rightarrow }\varphi )\); \(\Diamond _i\varphi {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}\lnot \Box _i\lnot \varphi \). Parentheses will be omitted when there is no room for ambiguity.
; \(\varphi \tilde{\leftrightarrow }\psi {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}(\varphi \tilde{\rightarrow }\psi )\wedge (\psi \tilde{\rightarrow }\varphi )\); \(\Diamond _i\varphi {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}\lnot \Box _i\lnot \varphi \). Parentheses will be omitted when there is no room for ambiguity.
Later, we will refer to several fragments of the language \(\mathcal {L}\):
Definition 1
Consider the following fragments of \(\mathcal {L}\):
-
1.
Propositional Fragment the subset of \(\mathcal {L}\) not containing formulas with symbols \(\Box _i\), for any \(i\in A\).
-
2.
FDE Fragment the subset of the Propositional Fragment above not containing formulas with the symbol
 .
. -
3.
KFDE Fragment the subset of \(\mathcal {L}\) not containing formulas with
 .
. -
4.
K Fragment the subset of \(\mathcal {L}\) not containing formulas with the symbol \(\lnot \).
2.2 Semantics
Given the non-empty finite set \(A=\{1, 2, \ldots , n\}\) of agents, an interpretation is a tuple \(M=\langle S,R,V\rangle \), where S is a non-empty set of states, \(R=\langle R_1, R_2, \ldots , R_n\rangle \) is an n-tuple of binary relations on S and \(V:P\times S\rightarrow 2^{\{0,1\}}\) is a valuation function that assigns to each proposition one of four truth values: \(\{0\}\) is false (f), \(\{1\}\) is true (t), \(\emptyset \) is none (n) and \(\{0,1\}\) is both (b). Although we work with arbitrary accessibility relations throughout most of this paper for generality, Sect. 4 presents some results that illustrate the effects of restricting R. With \(p\in P\), \(s\in S\), \(i\in A\) and \(\varphi ,\psi \in \mathcal {L}\), the satisfaction relation \(\models \) is inductively defined as follows:

Below we derive the truth conditions for \(\vee \),\(\rightarrow \),\(\leftrightarrow \) and \(\Diamond \):Footnote 4
Now, we can talk not only about 4-valued atoms but also about 4-valued formulas in general. We define the extended valuation function \(\overline{V}:\mathcal {L}\times S\rightarrow 2^{\{0,1\}}\) as follows:
Using the above definition, we say that a formula \(\varphi \) has value both at s, for example, if and only if \(\overline{V}(\varphi ,s)=\{0,1\}\), which is the case when both \(M,s\models \varphi \) and \(M,s\models \lnot \varphi \). Truth and falsity of formulas are evaluated independently, and for that reason we define semantic conditions for each negated formula separately. Even though the semantics of \(\lnot \) above is defined case by case,Footnote 5 the connective is still truth-functional, as we will see in Sect. 2.5.1.
2.3 Intended Readings of Formulas
Since the semantics of FVEL is non-compositional, the readings of its formulas will be non-compositional as well. The four values combined with a modality plus an additional negation also create further complications, which are clarified below.
The intended readings of purely propositional formulas follow the Belnapian view of \({{\mathbf {\mathsf{{FDE}}}}}\) as talking about evidence: non-modal formulas \(\varphi \) and \(\lnot \varphi \) are read as there is evidence for \(\varphi \) and there is evidence against \(\varphi \), respectively. The second negation ( ) is classical:
) is classical:  means that it is not the case that \(\varphi \). We can see the propositional fragment of FVEL (Definition 1.1) as a logic that preserves evidence, a concept mentioned in a recent paper by Carnielli and Rodrigues (2019).
means that it is not the case that \(\varphi \). We can see the propositional fragment of FVEL (Definition 1.1) as a logic that preserves evidence, a concept mentioned in a recent paper by Carnielli and Rodrigues (2019).
The \(\Box \) operator inherits its natural reading from epistemic logic, but we have to remember that propositional formulas are read as statements about evidence. So, for example, \(\Box _i\varphi \) and \(\Box _i\lnot \varphi \) will have the intended meaning of agent i knows that there is evidence for \(\varphi \) and agent i knows that there is evidence against \(\varphi \), respectively.
Nested \(\Box \) formulas are read in the expected way: \(\Box _i\Box _j\varphi \) just means that agent i knows that j knows that \(\varphi \) (again, the same remark about the reading of a propositional \(\varphi \) applies here).
It is worth noting that all formulas of FVEL are four-valued according to our semantics, not only the propositional ones. What does it mean, then, to say that \(\Box _i\varphi \) has value both or none? With the intuitions provided so far (for instance, the database example), it certainly does not make sense to say that an agent knows and doesn’t know \(\varphi \) at the same time. Breaking down the semantics, however, we can see that a statement such as \(\overline{V}(\Box _i\varphi ,s)=\{0,1\}\) means, in fact, that \(M,s\models \Box _i\varphi \) and \(M,s\models \lnot \Box _i\varphi \), which is equivalent to \(M,s\models \Box _i\varphi \wedge \Diamond _i\lnot \varphi \) (recall the definition of \(\Diamond _i\)), that is, agent i knows that there is evidence for \(\varphi \) but considers possible that there is evidence against it as well. Likewise, we find that \(\overline{V}(\Box _i\varphi ,s)=\emptyset \) means that agent i considers it possible that there is no evidence for \(\varphi \) and she knows that there is no evidence against it.
Finally, we have to remark that no formula with a \(\lnot \) in front of a \(\Box \), such as \(\lnot \Box _i p\), has a straightforward reading. Nevertheless, one can always convert such formulas into equivalent ones where \(\lnot \) is restricted to propositional subformulas, allowing for an intuitive reading. One can devise a recursive translation \(\varphi ^N\), the negation normal form of \(\varphi \), that maps any formula \(\varphi \) into an equivalent one, in the language of \(\mathcal {L}\) plus the abbreviations \(\vee \) and \(\Diamond \), where all occurrences of \(\lnot \) are in front of atoms, in the same vein as Fitting (2017, Def. 7.3). A proof that \(\varphi ^N\) is equivalent to \(\varphi \) can be done by induction in the complexity of \(\varphi \) (in each translation rule the formula under \(\lnot \) is mapped to subformulas of it). That \(\varphi ^N\) is equivalent to \(\varphi \) can be shown by proving that each translation rule generates an equivalent formula. (Equivalence is defined in Sect. 2.5.3.) For example, \(\lnot \Box _i p\) is equivalent to \(\Diamond _i\lnot p\), so it is simply read as agent i considers possible that there is evidence against p.
2.4 Validity and Entailment
We say that \(M\models \varphi \) if and only if \(M,s\models \varphi \) for all \(s\in S\), where \(M=\langle S,R,V\rangle \). A formula \(\varphi \) is valid (\(\models \varphi \)) if and only if \(M\models \varphi \) for all models M. A frame is a pair \(\mathcal {F}=\langle S,R\rangle \). We say a formula \(\varphi \) is valid in a frame \(\mathcal {F}=\langle S,R\rangle \), that is, \(\mathcal {F}\models \varphi \), if and only if, for all valuations V, it holds that \(M\models \varphi \), where \(M=\langle S,R,V\rangle \) (and we say M is based on frame \(\mathcal {F}\)). If for all models M and all states s it is the case that \(M,s\models \psi \) for all \(\psi \in \Sigma \) implies \(M,s\models \varphi \), we say that \(\Sigma \models \varphi \) (\(\varphi \) is a logical consequence of \(\Sigma \)). If \(\Sigma \models \varphi \) holds, we say it is a valid entailment or a valid inference.
Logical consequence in classical logics preserves truth. Many-valued logics generalise this idea, with their logical consequence preserving designated values. Following Priest (2008) and others, we define \(\{1\}\) and \(\{0,1\}\) as designated values, and \(\emptyset \) and \(\{0\}\) as non-designated values. Notice that statements of the form \(M,s\models \varphi \), which can be translated to \(1\in \overline{V}(\varphi ,s)\), really are just saying that \(\varphi \) is designated. A formula is called designated (non-designated) with respect to a model M and state s if it has a designated (non-designated) value at M, s, i.e. \(\overline{V}(\varphi ,s)\) is designated (non-designated). If one wants to check whether a formula \(\varphi \) has precisely the value true (or whatever other value) one just has to check two satisfaction statements: \(M,s\models \varphi \) and \(M,s\models \lnot \varphi \).
2.5 Basic Properties of FVEL
2.5.1 Connectives and Notable Fragments
Now we build the truth tables for the truth-functional connectives according to the truth definitions given above (Tables 1, 2, 3, 4, 5). The ones for \(\wedge \), \(\lnot \) and \(\vee \) turn out to be identical to the ones in Priest (2008, p. 146).

Example for Table 1 (\(\lnot \)b\(=\)b): \(\overline{V}(\varphi ,s)=\{0,1\}\) iff \(0\in \overline{V}(\varphi ,s)\) and \(1\in \overline{V}(\varphi ,s)\) iff \(M,s\models \lnot \varphi \) and \(M,s\models \varphi \) iff \(M,s\models \lnot \varphi \) and \(M,s\models \lnot \lnot \varphi \) iff \(1\in \overline{V}(\lnot \varphi ,s)\) and \(0\in \overline{V}(\lnot \varphi ,s)\) iff \(\overline{V}(\lnot \varphi ,s)=\{0,1\}\).
Example for Table 4 (n\(\vee \)b\(=\)t):Footnote 6 Recall that disjunction is defined in terms of conjunction and negation. \(M,s\models \lnot (\lnot \varphi \wedge \lnot \psi )\) iff \(M,s\models \lnot \lnot \varphi \) or \(M,s\models \lnot \lnot \psi \) iff \(M,s\models \varphi \) or \(M,s\models \psi \) iff \(1\in \overline{V}(\varphi ,s)\) or \(1\in \overline{V}(\psi ,s)\), which is true, for \(\overline{V}(\psi ,s)=\{0,1\}\). \(M,s\models \lnot \lnot (\lnot \varphi \wedge \lnot \psi )\) iff \(M,s\models \lnot \varphi \wedge \lnot \psi \) iff \(M,s\models \lnot \varphi \) and \(M,s\models \lnot \psi \) iff \(0\in \overline{V}(\varphi ,s)\) and \(0\in \overline{V}(\psi ,s)\), which is false, for \(\overline{V}(\varphi ,s)=\emptyset \). Therefore \(M,s\models \varphi \vee \psi \) holds, but \(M,s\models \lnot (\varphi \vee \psi )\) does not, thus \(1\in \overline{V}(\varphi \vee \psi )\) and \(0\notin \overline{V}(\varphi \vee \psi )\), hence \(\overline{V}(\varphi \vee \psi )=\{1\}\).
The next observation follows from the truth tables and the semantics of \(\Box \):
Observation 1
For all models M, if for all states s and \(p\in P\) it holds that \(V(p,s)\notin \{\emptyset ,\{0,1\}\}\), then for all states t and \(\varphi \in \mathcal {L}\) it holds that \(\overline{V}(\varphi ,t)\notin \{\emptyset ,\{0,1\}\}\).
If we leave \(\lnot \) out (fragment of Definition 1.4), we are left with (the validities of) classical modal logic, with designated values behaving as true, and non-designated values behaving as false.
Moreover, observing these truth tables, we notice that the fragment resulting from leaving  and \(\Box \) out (Definition 1.2) behaves exactly as \({{\mathbf {\mathsf{{FDE}}}}}\) (Dunn 1976; Priest 2008).Footnote 7 Conjunction and disjunction are given by the meet and join, respectively, of the values in the lattice depicted in Fig. 2, called L4 in Belnap (1977). Now, adding the modal operator \(\Box \) to \({{\mathbf {\mathsf{{FDE}}}}}\) we obtain \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) (our fragment of Definition 1.3), a logic which Priest has studied (Priest 2008). He provides a complete tableau system for this logic. Moreover, he shows that this logic contains no validities, as is the case for \({{\mathbf {\mathsf{{FDE}}}}}\) itself. In the class of four-valued Kripke models, FVEL is strictly more expressive than \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\): formulas such as
and \(\Box \) out (Definition 1.2) behaves exactly as \({{\mathbf {\mathsf{{FDE}}}}}\) (Dunn 1976; Priest 2008).Footnote 7 Conjunction and disjunction are given by the meet and join, respectively, of the values in the lattice depicted in Fig. 2, called L4 in Belnap (1977). Now, adding the modal operator \(\Box \) to \({{\mathbf {\mathsf{{FDE}}}}}\) we obtain \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) (our fragment of Definition 1.3), a logic which Priest has studied (Priest 2008). He provides a complete tableau system for this logic. Moreover, he shows that this logic contains no validities, as is the case for \({{\mathbf {\mathsf{{FDE}}}}}\) itself. In the class of four-valued Kripke models, FVEL is strictly more expressive than \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\): formulas such as  can only be expressed in the former.
can only be expressed in the former.
We can also build the truth tables for \(\tilde{\vee }\) and \(\tilde{\rightarrow }\) (Tables 6 and 7). Despite these connectives being binary functions accepting two four-valued parameters, they behave analogously to their classical (Boolean) counterparts. They can be viewed as a composition of a function that compresses designated values into true and non-designated values into false (just like a double application of the operator  ) with the corresponding Boolean function. In other words, if or is classical disjunction and imp is classical implication,
) with the corresponding Boolean function. In other words, if or is classical disjunction and imp is classical implication,  and
and  . It is also relevant to remark that when the operands take on only classical values, both pairs of operators (\(\vee \),\(\rightarrow \) and \(\tilde{\vee }\),\(\tilde{\rightarrow }\)) behave exactly alike.
. It is also relevant to remark that when the operands take on only classical values, both pairs of operators (\(\vee \),\(\rightarrow \) and \(\tilde{\vee }\),\(\tilde{\rightarrow }\)) behave exactly alike.
The propositional part of FVEL (Definition 1.1) can be considered a fragment of the bilattice logic in Arieli and Avron (1996), and the latter is strictly more expressive than the former. Moreover, our modal and public announcement extensions have many similarities with BPAL (Rivieccio 2014b) (more on these comparisons in Sect. 6.2).
2.5.2 Validities
We can define \(\top \), a validity, as  . While \({{\mathbf {\mathsf{{FDE}}}}}\) has no validities, FVEL has an infinity of them, including \(\top \). Moreover, all propositional tautologies (built with
. While \({{\mathbf {\mathsf{{FDE}}}}}\) has no validities, FVEL has an infinity of them, including \(\top \). Moreover, all propositional tautologies (built with  ) are still validities in FVEL, as expected, but there are other valid formulas with both
) are still validities in FVEL, as expected, but there are other valid formulas with both  and \(\lnot \), such as
and \(\lnot \), such as  . All validities in FVEL have the connective
. All validities in FVEL have the connective  or one of its derivative connectives (\(\tilde{\vee }\) and \(\tilde{\rightarrow }\)). Some standard modal validities are also valid in FVEL when built using \(\tilde{\leftrightarrow }\), e.g. \(\Box (\varphi \wedge \psi )\tilde{\leftrightarrow }(\Box \varphi \wedge \Box \psi )\) and \(\Diamond (\varphi \vee \psi )\tilde{\leftrightarrow }(\Diamond \varphi \vee \Diamond \psi )\).
or one of its derivative connectives (\(\tilde{\vee }\) and \(\tilde{\rightarrow }\)). Some standard modal validities are also valid in FVEL when built using \(\tilde{\leftrightarrow }\), e.g. \(\Box (\varphi \wedge \psi )\tilde{\leftrightarrow }(\Box \varphi \wedge \Box \psi )\) and \(\Diamond (\varphi \vee \psi )\tilde{\leftrightarrow }(\Diamond \varphi \vee \Diamond \psi )\).
A logic \(L'\) is a conservative extension of a logic L iff the language of \(L'\) contains the language of L and all validities of L are also validities of \(L'\). Building on the observations of Sect. 2.5.1, we can establish the following. \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) is a conservative extension of \({{\mathbf {\mathsf{{FDE}}}}}\), and FVEL is a conservative extension of \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\). FVEL is also a conservative extension of classical modal logic (taking  as classical negation), which is the fragment of Definition 1.4. Bilattice logic (Arieli and Avron 1996) is a conservative extension of the propositional fragment of FVEL (Definition 1.1).
as classical negation), which is the fragment of Definition 1.4. Bilattice logic (Arieli and Avron 1996) is a conservative extension of the propositional fragment of FVEL (Definition 1.1).
2.5.3 Equivalence
Logical equivalence (sameness in truth value) cannot be expressed by \(\varphi \leftrightarrow \psi \) in FVEL. Look at Table 8. The diagonal should be designated, and the rest non-designated. In fact, in this case even the biconditional connective (\(\tilde{\leftrightarrow }\)) derived using  instead of \(\lnot \) does not give a truth table which is designated in the diagonal and non-designated everywhere else, for it treats \(\{1\}\) and \(\{0,1\}\) as equals (and the same goes for \(\emptyset \) and \(\{0\}\)), resulting in a weaker type of equivalence (see Table 9).
instead of \(\lnot \) does not give a truth table which is designated in the diagonal and non-designated everywhere else, for it treats \(\{1\}\) and \(\{0,1\}\) as equals (and the same goes for \(\emptyset \) and \(\{0\}\)), resulting in a weaker type of equivalence (see Table 9).
The reason for adding the classical negation ( ) to a language which already has a negation operator (\(\lnot \)) is that this increases the expressivity of the language.Footnote 8 For instance, we can now define formulas discriminating which of the four truth values a formula \(\varphi \) has:
) to a language which already has a negation operator (\(\lnot \)) is that this increases the expressivity of the language.Footnote 8 For instance, we can now define formulas discriminating which of the four truth values a formula \(\varphi \) has:  ;
;  ;
;  ;
;  . As can be seen in Table 10, \(\varphi ^i\) is true if and only if \(\varphi \) has truth value i, for \(i\in \{n, f, t, b\}\), and false otherwise. Now we can read \(\Box _a\varphi ^i\) as Agent a knows that the status of evidence for \(\varphi \) is i (where \(i\in \{t,f,b,n\}\)). Using these connectives, it is easy to see that a stronger notion of logical equivalence can be expressed in FVEL:
. As can be seen in Table 10, \(\varphi ^i\) is true if and only if \(\varphi \) has truth value i, for \(i\in \{n, f, t, b\}\), and false otherwise. Now we can read \(\Box _a\varphi ^i\) as Agent a knows that the status of evidence for \(\varphi \) is i (where \(i\in \{t,f,b,n\}\)). Using these connectives, it is easy to see that a stronger notion of logical equivalence can be expressed in FVEL:
Since this formula is complex and difficult to evaluate, we will often favor the use of metalanguage as follows:
The formula \(\varphi \,\dot{\leftrightarrow }\,\psi \) is true if \(\varphi \) and \(\psi \) have the same truth value and false otherwise (as shown in Table 11).
Proposition 1
\(\varphi \equiv \psi \) iff \(\,\models \varphi \,\dot{\leftrightarrow }\,\psi \).
Proof
Suppose \(\varphi \equiv \psi \). Then, by the definition of \(\equiv \), for all models M and states s, \(M,s\models \varphi \) iff \(M,s\models \psi \) and \(M,s\models \lnot \varphi \) iff \(M,s\models \lnot \psi \), and therefore \(\varphi \) and \(\psi \) have the same truth value (in all states of all models), i.e. for all models M and states s: \(\overline{V}(\varphi ,s)=\overline{V}(\psi ,s)\). This implies (by Table 10) that for any model M and state s, either \(M,s\models \varphi ^n\wedge \psi ^n\) or \(M,s\models \varphi ^f\wedge \psi ^f\) or \(M,s\models \varphi ^t\wedge \psi ^t\) or \(M,s\models \varphi ^b\wedge \psi ^b\). By the definition of \(\varphi \,\dot{\leftrightarrow }\,\psi \), it follows that, for all models M and states s, \(M,s\models \varphi \,\dot{\leftrightarrow }\,\psi \).
Now for the other direction. Suppose \(\models \varphi \,\dot{\leftrightarrow }\,\psi \). Then for every M and s, \(M,s\models \varphi \,\dot{\leftrightarrow }\,\psi \), which by definition means that either \(M,s\models \varphi ^n\wedge \psi ^n\) or \(M,s\models \varphi ^f\wedge \psi ^f\) or \(M,s\models \varphi ^t\wedge \psi ^t\) or \(M,s\models \varphi ^b\wedge \psi ^b\). But, by Table 10, \(M,s\models \chi ^i\) iff \(\overline{V}(\chi ,s)=i\), for \(i\in \{n,f,t,b\}\). Therefore, if any of the statements of the form \(M,s\models \varphi ^i\wedge \psi ^i\) mentioned before hold, then \(\overline{V}(\varphi ,s)=\overline{V}(\psi ,s)\) (for any model M and state s), and thus, by the definition of \(\overline{V}\), \(\varphi \equiv \psi \) holds. \(\square \)
Equi-satisfiability and equivalence coincide in classical logics, but here they differ. One has to keep this in mind when analysing statements such as  (which appears, for example, when checking Rivieccio (2014b)’s axiom
(which appears, for example, when checking Rivieccio (2014b)’s axiom  and our validity for public announcements (An\(\lnot \)An)). One might be tempted to replace
and our validity for public announcements (An\(\lnot \)An)). One might be tempted to replace  by \(\psi \) (as they are equi-satisfiable) and obtain \(M,s\models \lnot \psi \). Although for all models M and states s we have that
by \(\psi \) (as they are equi-satisfiable) and obtain \(M,s\models \lnot \psi \). Although for all models M and states s we have that  iff \(M,s\models \psi \), it holds that
iff \(M,s\models \psi \), it holds that  . So the only simplification for
. So the only simplification for  is by using the semantic clause for formulas of the form
is by using the semantic clause for formulas of the form  , which gives us
, which gives us  . We prove later (Proposition 11) that if \(\varphi \) is a subformula of \(\chi \) and \(\varphi \equiv \psi \), then substitution of \(\psi \) for \(\varphi \) in \(\chi \) yields a formula that is logically equivalent to \(\chi \).
. We prove later (Proposition 11) that if \(\varphi \) is a subformula of \(\chi \) and \(\varphi \equiv \psi \), then substitution of \(\psi \) for \(\varphi \) in \(\chi \) yields a formula that is logically equivalent to \(\chi \).
2.6 A Simple Example
Now we describe the situation depicted in Fig. 3. John (j) knows that there are studies regarding health benefits of coffee consumption, for he often sees headlines about the subject. However, he never cared enough to read those articles, so he is sure that there is evidence for or against (or even both for and against) coffee being beneficial for health (p), but he does not know exactly what is the status of the evidence about p, he only knows that there is some information. Looking at Fig. 3, one can easily see that  , which is equivalent to \(\Box _j(p\vee \lnot p)\), holds in the actual world (\(s_3\)).
, which is equivalent to \(\Box _j(p\vee \lnot p)\), holds in the actual world (\(s_3\)).
Kate (k), on the other hand, is a researcher on the effects of coffee on health, and for this reason she knows exactly what evidence is available (notice that her relation \(R_k\) has only reflexive arrows). We can see that \(M,s_3\models \Box _k(p\wedge \lnot p)\), that is, in this state, Kate actually knows that there is evidence both for and against the benefits of coffee. Moreover, John knows Kate and her job, so he also knows that she knows about p, whatever its status is (using abbreviations defined in Sect. 2.5.1: \(\Box _j(\Box _k p^f \vee \Box _k p^t\vee \Box _k p^b)\)). Likewise, Kate knows that John simply knows that there is some information about p ( ).
).
3 Tableaux
A tableau is a structure used to check derivability and theoremhood. In this section we will show how to build a tableau to verify whether \(\Sigma \vdash \varphi \) (\(\varphi \) is derivable from \(\Sigma \) in FVEL), where \(\Sigma \cup \{\varphi \}\in \mathcal {L}\) and \(\Sigma \) is finite.Footnote 9
Our tableau system is inspired by the one for \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) given in Priest (2008, p. 28). A tableau is a tree, that is, an irreflexive partially-ordered set (N, E), where N is a (possibly infinite) set of nodes and \(E\subseteq N\times N\), with a unique maximum element \(r\in N\), the root. A minimum element of N w.r.t. E is called a leaf. A (possibly infinite) sequence of nodes where each element is related to the next by E is called a path, and a maximal path is called a branch. All nodes are of the form \((\psi ,+i)\), \((\psi ,-i)\) or \((ir_mj)\), where \(\psi \in \mathcal {L}\), \(m\in A\) and \(i,j\in \mathbb {N}\). A branch is closed if it contains nodes \((\psi ,+i)\) and \((\psi ,-i)\), for some \(\psi \in \mathcal {L}\) and \(i\in \mathbb {N}\). Otherwise, the branch is open.
Let \(\Sigma =\{\sigma _1,\ldots ,\sigma _n\}\), \(n\in \mathbb {N}\). A tableau for \(\Sigma \vdash \varphi \) starts with the so-called initial list for \(\Sigma \vdash \varphi \), defined as follows:
Notice that the initial list is a sequence of nodes forming a single branch (edges omitted above).
The construction of the tableau for \(\Sigma \vdash \varphi \) proceeds by way of applying rules of the tableau calculus for FVEL (R1-R14 below).Footnote 10 On the top of a rule we find the rule’s pre-conditions: a set of schematic nodes. If we can find a set of nodes in a branch of the tableau - the target nodes - that are instances of the pre-conditions, we say that that instance of the rule is applicable to those nodes of that branch. The process of applying a rule, thus, consists in verifying that it is applicable to a set of target nodes of a branch, and then appending nodes to the leaf of the target branch according to the rule: for rules R5–R7 and R10–R14 one node is appended to the leaf; for rules R1, R4 and R8–R9 two nodes are appended in sequence; and for rules R2–R3 two nodes are appended forming separate branches. If all rules that are applicable to any set of target nodes in a branch have been applied, the branch is complete. If all open branches are complete, we say the tableau is complete.
We say that \(\Sigma \vdash \varphi \) iff there is a tableau for \(\Sigma \vdash \varphi \) where all branches are closed. Otherwise we write \(\Sigma \nvdash \varphi \). If \(\emptyset \vdash \varphi \) (short: \(\vdash \varphi \)), we say \(\varphi \) is an FVEL theorem.
Whenever \(\Sigma \nvdash \varphi \), we can read off a countermodel for \(\Sigma \vdash \varphi \) from any complete open branch of a tableau for \(\Sigma \vdash \varphi \), which we dub a model induced by that branch (following Priest 2008):
Definition 2
Let b be a complete open branch of a tableau. We say an FVEL model \(M=\langle S,R,V\rangle \) is induced by b iff M is such that:
-
\(s_i\in S\) iff \((\psi ,+i)\), \((\psi ,-i)\), \((ir_mj)\) or \((jr_mi)\) appears in b;
-
\(s_iR_ms_j\) iff \((ir_mj)\) appears in b;
-
\(1\in V(p,s_i)\) if \((p,+i)\) appears in b;
-
\(1\notin V(p,s_i)\) if \((p,-i)\) appears in b;
-
\(0\in V(p,s_i)\) if \((\lnot p,+i)\) appears in b;
-
\(0\notin V(p,s_i)\) if \((\lnot p,-i)\) appears in b.
For future proofs, we also need the following definition (adapted from Priest 2008):
Definition 3
An FVEL model \(M=\langle S,R,V\rangle \) is faithful to a branch b of a tableau iff there are functions \(f:\mathbb {N}\rightarrow W\) and \(g:\mathbb {N}\rightarrow A\) such that for all \(i\in \mathbb {N}\), \(\varphi \in \mathcal {L}\) and \(m\in A\):
-
if \((\varphi ,+i)\) is on b, then \(1\in \overline{V}(\varphi ,f(i))\);
-
if \((\varphi ,-i)\) is on b, then \(1\notin \overline{V}(\varphi ,f(i))\);
-
if \((ir_mj)\) is on b, then \(f(i)R_{g(m)}f(j)\).
Clearly, a model induced by a branch is faithful to it.
The rules R1–R2 and R5–R8 below are directly taken from the tableau system for \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\) (Priest 2008, p. 248). We then modify the rules for negated conjunctions and boxes, rules R3–R4 and R9-R10, respectively, since in our language \(\vee \) and \(\Diamond \) are only abbreviations. Then, we add four more rules for classical negation (R11–R14). This tableau system will be further augmented in Sect. 4 to prove some correspondence results between the tableau system and classes of frames and in Sect. 5 to cope with public announcements.

Figures 4 and 5 show two examples of proofs using the tableau system. In the first example, one of the branches closes, but no rule is applicable to any nodes in the other branch, which is left open, showing therefore that the derivation \(\{\lnot (p\wedge \lnot q),p\}\vdash q\) (which is equivalent to \(\{p\rightarrow q,p\}\vdash q\)) does not hold. The second example proves the theorem  .
.
Before proving soundness, we need to show that the following Soundness Lemma (adapted from Priest 2008, Lemma 11a.9.3) holds:
Lemma 1
Footnote 11 Let b be any branch of a tableau and M an FVEL model. If M is faithful to b, and a tableau rule is applied to b, then it produces at least one extension \(b'\) such that M is faithful to \(b'\).
Similarly, we need the following Completeness Lemma (adapted from Priest 2008, Lemma 11a.9.6):
Lemma 2
Let b be a complete open branch of a tableau, and let \(M=\langle S,R,V\rangle \) be an FVEL model induced by b. Then:
-
If \((\varphi ,+i)\) is on b, then \(1\in \overline{V}(\varphi ,s_i)\);
-
If \((\varphi ,-i)\) is on b, then \(1\notin \overline{V}(\varphi ,s_i)\);
-
If \((\lnot \varphi ,+i)\) is on b, then \(0\in \overline{V}(\varphi ,s_i)\);
-
If \((\lnot \varphi ,-i)\) is on b, then \(0\notin \overline{V}(\varphi ,s_i)\).
Now we can prove soundness and completeness of this enhanced tableau system with respect to FVEL.
Theorem 1
For any finite set of formulas \(\Sigma \cup \{\varphi \}\), \(\Sigma \vdash \varphi \text { iff }\Sigma \models \varphi \).
Proof
This proof is an extension of the proofs in Priest (2008), for \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\).
For soundness, we adapt Priest (2008, Definition 11a.9.2, Lemma 11a.9.3 and Theorem 11a.9.4, pp. 255–256). The proof for the theorem is found in Priest (2008, Theorem 2.9.4, p. 32). Our only addition here is to the Soundness Lemma (Priest 2008, Lemma 11a.9.3), which we proved in Lemma 1.
For completeness, the situation is very similar. We adapt Priest (2008, Definition 11a.9.5, Completeness Lemma 11a.9.6 and Theorem 11a.9.7, p. 256–257). Again, the only additions (besides minor adaptations of notation) concern the lemma, which we proved in Lemma 2. The proof of Priest (2008), [Completeness Theorem 11a.9.7] is identical to that of Priest (2008, Theorem 2.9.7, p. 33). \(\square \)
4 Correspondence Results
Now we will take a look at standard axioms and inference rules from modal logics. Consider the following inference/rule schemes:
Proposition 2
MP does not preserve validity in FVEL.Footnote 12
Proof
Counterexample:  ,
,  .
.
p | \(\varphi \) | \(\varphi \rightarrow \psi \) | \(\psi \) |
|---|---|---|---|
n | t | t | t |
f | t | t | t |
t | t | t | t |
b | b | b | f |
\(\square \)
Proposition 3
The rule NEC preserves validity in FVEL.
Proof
Suppose an arbitrary \(\varphi \) is provable in FVEL. So we have a closed tableau with root \((\varphi ,-0)\). Now, we can build a tableau for \(\Box \varphi \) with the following procedure. First, relabel each number in the tableau for \(\varphi \) with its successor (ignoring the sign). Notice that uniformly changing the labels does not affect the validity of the formula being tested. Then, append the two lines below immediately above the root, obtaining the following closed tableau for \(\Box \varphi \):
\(\square \)
Now consider the following typical modal logical axioms, and their versions built with \(\tilde{\vee }\) and \(\tilde{\rightarrow }\) (agent indices removed for readability):

Axiom K is not a theorem of FVEL, but \(\tilde{K}\) is. None of the other axioms above are theorems; this is expected, for recall that we are dealing with arbitrary accessibility relations. Whether these or any other formulas are theorems can be easily checked using the tableau method.
Proposition 4
\(\mathcal {F}\models \tilde{K}\), for all frames \(\mathcal {F}=\langle S,R\rangle \).
Proof
The only part needing explanation regards the semantics of \(\tilde{\rightarrow }\): for any formulas \(\varphi \) and \(\psi \), \(M,s\models \varphi \tilde{\rightarrow }\psi \) iff  iff
iff  iff
iff  iff
iff  iff \(M,s\not \models \varphi \) or
iff \(M,s\not \models \varphi \) or  iff \(M,s\not \models \varphi \) or \(M,s\models \psi \) iff \(M,s\models \varphi \) implies \(M,s\models \psi \).
iff \(M,s\not \models \varphi \) or \(M,s\models \psi \) iff \(M,s\models \varphi \) implies \(M,s\models \psi \).
The rest amounts to proving that \(M,s\models \Box (\varphi \tilde{\rightarrow }\psi )\tilde{\rightarrow }(\Box \varphi \tilde{\rightarrow }\Box \psi )\), for arbitrary \(M=\langle S,R,V\rangle \) and \(s\in S\). That formula is satisfied in a state s of a model M iff at least one of the following holds: (a) there is a t such that sRt and \(M,t\models \varphi \) and \(M,t\not \models \psi \), (b) there is a t such that sRt and \(M,t\not \models \varphi \), or (c) for all t such that sRt, it holds that \(M,t\models \psi \). If condition (c) holds, we are done, so let us assume that (c) does not hold. This implies that there is a state t such that \(M,t\not \models \psi \). If \(M,t\models \varphi \), then condition (a) holds, otherwise, condition (b) holds. Either way, \(\tilde{K}\) is satisfied at s. \(\square \)
Not surprisingly, the correspondences between some properties of frames and validity of formulas still hold, as shown by the propositions below. For the next proofs, let \(\mathcal {F}=\langle S,R\rangle \), and consider the following frame properties:
Proposition 5
\(\mathcal {F}\models \tilde{T}\) iff \(\mathcal {F}\) is reflexive.
Proof
\(\tilde{T}\) is given by  . By the semantics, \(\tilde{T}\) is satisfied in a state s iff at least one of the following holds: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) \(1\in \overline{V}(\varphi ,s)\).
. By the semantics, \(\tilde{T}\) is satisfied in a state s iff at least one of the following holds: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) \(1\in \overline{V}(\varphi ,s)\).
\(\Leftarrow \): Consider a reflexive \(\mathcal {F}\). For all valuations, for each state s either \(1\in \overline{V}(\varphi ,s)\) or \(1\notin \overline{V}(\varphi ,s)\). In the first case, the axiom is satisfied by condition (b). In the second case, since sRs and \(1\notin \overline{V}(\varphi ,s)\), condition (a) holds.
\(\Rightarrow \): Let us suppose that the frame \(\mathcal {F}\) is not reflexive. Consider a state s for which sRs does not hold. We need to show that there is a valuation for which \(\tilde{T}\) does not hold in s. If we take a valuation V where \(1\notin V(p,s)\), but \(1\in V(p,t)\) for all t such that sRt, we will have  at s.\(\square \)
at s.\(\square \)
Proposition 6
\(\mathcal {F}\models \tilde{4}\) iff \(\mathcal {F}\) is transitive.
Proof
Axiom \(\tilde{4}\) is given by  . \(\tilde{4}\) is satisfied in a state s iff this state satisfies at least one of the following conditions: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) for all t and r such that sRt and tRr it is the case that \(1\in \overline{V}(\varphi ,r)\).
. \(\tilde{4}\) is satisfied in a state s iff this state satisfies at least one of the following conditions: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) for all t and r such that sRt and tRr it is the case that \(1\in \overline{V}(\varphi ,r)\).
\(\Leftarrow \): Consider a transitive frame. If condition (b) does not hold for some formula \(\varphi \), then there are states s, t, r such that sRt and tRr and \(1\notin \overline{V}(\varphi ,r)\). But since the frame is transitive, we have sRr and thus condition (a) is satisfied.
\(\Rightarrow \): Consider a non-transitive frame. Hence, there are states s, t, r such that sRt and tRr but not sRr. Consider a valuation V where \(1\in V(p,x)\) for all x such that sRx, and \(1\notin V(p,r)\). In that case,  . \(\square \)
. \(\square \)
Proposition 7
\(\mathcal {F}\models \tilde{B}\) iff \(\mathcal {F}\) is symmetric.
Proof
Axiom \(\tilde{B}\) ( ) is satisfied in a state s iff: (a) \(1\notin \overline{V}(\varphi ,s)\) or (b) for all t there is an r such that sRt, tRr and \(1\in \overline{V}(\varphi ,r)\).
) is satisfied in a state s iff: (a) \(1\notin \overline{V}(\varphi ,s)\) or (b) for all t there is an r such that sRt, tRr and \(1\in \overline{V}(\varphi ,r)\).
\(\Leftarrow \): Either \(1\notin \overline{V}(\varphi ,s)\) or \(1\in \overline{V}(\varphi ,s)\). In the first case, (a) is satisfied. In the second case, if \(\mathcal {F}\) is symmetric, then for any t such that sRt it is also the case that tRs, therefore condition (b) is satisfied.
\(\Rightarrow \): Suppose \(\mathcal {F}\) is not symmetric, that is, there are states s, t such that sRt but not tRs. Consider the instance  and a valuation where \(1\in V(p,s)\)—which violates condition (a)—and \(1\notin V(p,r)\) for all \(r\ne s\). Since \((t,s)\notin R\), there is no state r such that tRr and \(1\in V(p,r)\), and therefore (b) is violated in s. \(\square \)
and a valuation where \(1\in V(p,s)\)—which violates condition (a)—and \(1\notin V(p,r)\) for all \(r\ne s\). Since \((t,s)\notin R\), there is no state r such that tRr and \(1\in V(p,r)\), and therefore (b) is violated in s. \(\square \)
Proposition 8
\(\mathcal {F}\models \tilde{D}\) iff \(\mathcal {F}\) is serial.
Proof
Axiom \(\tilde{D}\) ( ) is satisfied in a state s iff: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) there is a t such that sRt and \(1\in \overline{V}(\varphi ,t)\). Condition (a) or (b) is satisfied iff: (c) there is a t such that sRt.
) is satisfied in a state s iff: (a) there is a t such that sRt and \(1\notin \overline{V}(\varphi ,t)\), or (b) there is a t such that sRt and \(1\in \overline{V}(\varphi ,t)\). Condition (a) or (b) is satisfied iff: (c) there is a t such that sRt.
\(\Leftarrow \): Suppose \(\mathcal {F}\) is serial. Then for any state s there is a t such that sRt, and therefore condition (c) is satisfied in s.
\(\Rightarrow \): Suppose \(\mathcal {F}\) is not serial. Then there is a state s such that there is no t with sRt. So s violates condition (c), and therefore s does not satisfy \(\tilde{D}\). \(\square \)
Proposition 9
\(\mathcal {F}\models \tilde{5}\) iff \(\mathcal {F}\) is Euclidean
Proof
Axiom \(\tilde{5}\) ( ) is satisfied in a state s iff: (a) for all t such that sRt it is the case that \(0\notin \overline{V}(\varphi ,t)\), or (b) for all t such that sRt there is an r with tRr and \(0\in \overline{V}(\varphi ,r)\).
) is satisfied in a state s iff: (a) for all t such that sRt it is the case that \(0\notin \overline{V}(\varphi ,t)\), or (b) for all t such that sRt there is an r with tRr and \(0\in \overline{V}(\varphi ,r)\).
\(\Leftarrow \): Suppose \(\mathcal {F}\) is Euclidean. For any state s, condition (a) is either satisfied or not. If it is, \(\tilde{5}\) is satisfied. Now suppose (a) is violated at s, that is, there is a state r such that sRr and \(0\in \overline{V}(\varphi ,r)\). Since \(\mathcal {F}\) is Euclidean, sRt implies tRr for any t, and then condition (b) is satisfied for s. Therefore \(\tilde{5}\) is satisfied in either case.
\(\Rightarrow \): Suppose \(\mathcal {F}\) is not Euclidean, that is, there are states s, t, r such that sRt, sRr but tRr does not hold. Let V be the valuation such that \(0\in V(p,r)\)—which violates condition (a) for formula \(\varphi =p\)—but \(0\notin V(p,w)\) for all \(w\ne r\), which violates condition (b) at s (because sRt but there is no z such that tRz and \(0\in V(p,z)\)). Therefore, \(\langle S,R,V\rangle ,s\not \models \tilde{5}\). \(\square \)
Now, we can augment the tableau system with any combination of the rules below and show that it is complete with respect to the corresponding class of models.Footnote 13

Let \(\star \subseteq \{\rho ,\tau ,\sigma ,\eta ,\epsilon \}\). We use the symbol \(\vdash _\star \) for the provability relation of the tableau system augmented with rules R\(\circ \), for each \(\circ \in \star \), and \(\models _\star \) to represent satisfiability restricted only to models satisfying properties in \(\star \).
Theorem 2
For all finite sets of formulas \(\Sigma \cup \{\varphi \}\), and \(\star \subseteq \{\rho ,\tau ,\sigma ,\eta ,\epsilon \}\), the following statement holds: \(\Sigma \vdash _\star \varphi \) iff \(\Sigma \models _\star \varphi \).
Proof
This proof is similar to the proof of Theorem 1, the only difference is that now we consider particular classes of models, and augment the tableau system with its corresponding rule(s).
We will again build upon Priest’s proofs (Priest 2008). Again, the main modifications are in the soundness and completeness lemmas (Lemmas 11a.9.3 and 11a.9.6 of Priest 2008, respectively). The soundness and completeness theorems remain unchanged (Theorems 11a.9.4 and 11a.9.7 of Priest 2008, respectively, whose actual proofs are found in Theorems 1.11.3 and 2.9.7, respectively).
Reflexive models Now we will prove soundness and completeness of the tableau system augmented with the rule R\(\rho \) w.r.t. reflexive models. Let us first analyse soundness. In this case, the model M mentioned in the soundness lemma (Lemma 1) should be restricted to be a reflexive model. We only have to check the new rule R\(\rho \), because for all the other rules it was already shown that there will be at least one faithful extension (our restriction of M to reflexive models is still covered by the lemma, which says “any model”). Suppose b is faithful to M, which is reflexive, and that \(b'\) is generated from b by the application of R\(\rho \). If the added node is \((ir_mi)\), then i has occurred in b, but since M is reflexive, \(f(i)R_mf(i)\) is in M.
For completeness, since the new rule R\(\rho \) does not involve any formula, the only thing we need to show is that the induced model will always be reflexive. Suppose the label i occurs on the branch. Then, since the branch is complete, at some point the rule R\(\rho \) should be applied, generating the node \(ir_mi\). By the definition of induced model, we conclude it is indeed reflexive. This finishes the proof of the first statement.
Transitive models The second statement concerns transitive models and the tableau with R\(\tau \). For soundness, the lemma should be rephrased again to consider only transitive models. Now we have to check whether the application of the rule R\(\tau \) to b will produce a faithful extension \(b'\). Suppose b is faithful to M, and contains nodes \((ir_mj)\) and \((jr_mk)\). By applying R\(\tau \) we get \((ir_mk)\). But since b is faithful to M, \(f(i)R_mf(j)\) and \(f(j)R_mf(k)\) are in M, and since M is transitive, \(f(i)R_mf(k)\) is also in M, and therefore \(b'\) is faithful to M.
For completeness we need to ensure that the induced model is transitive. Suppose the nodes \((ir_mj)\) and \((jr_mk)\) occur on the complete branch. Then at some point the rule R\(\tau \) had to be applied, with \((ir_mk)\) as outcome. By the definition of induced model, we conclude it is transitive.
Symmetric and Euclidean models The proofs for symmetric and Euclidean models are analogous to the previous ones.
Serial models Soundness: we need to check if the application of R\(\eta \) to b will generate at least one faithful branch \(b'\). Suppose that label i occurs in b and that we apply R\(\eta \), generating only one new node: \((ir_mj)\). Since b is faithful to M, which is serial, \(f(i)R_mf(j)\) is in M, for some f, and thus \(b'\) is faithful to M.
Completeness We will show that the induced model M is serial. Suppose i occurs on the complete open branch. Then at some point R\(\eta \) must be applied and thus \((ir_mj)\) will be on the branch as well. Now the same happens with the new label j, and so on, ad infinitum. So this infinitely long branch will contain, for all labels i that occur on it, some node \((ir_mj)\), and therefore, by the definition of induced models, M is serial. (Notice that the issue of infinitely long branches does not prevent completeness—it might affect decidability, but we are not concerned with it in this proof.) \(\square \)
Decidability of tableau provability for these systems can be shown using the proofs for standard modal logics (like those in Halpern and Moses 1992, Sec. 6.3 and Fitting 1983, Chap. 8, Sec. 7), and making minor adaptations. The four-valuedness of FVEL does not change anything with respect to decidability, since what may cause infinite branches is always the modal part, in particular when transitivity is involved. This problem is usually solved in the literature by detecting and preventing creation of new labels (worlds) if the formulas associated with them are identical to the ones associated with some previous label in the branch.
5 Public Announcements
In this section, we extend the language with public announcements, provide a set of reduction validitiesFootnote 14 and prove completeness for this extended language. The first time an axiomatisation was given to a four-valued modal logic with public announcements can be credited to Rivieccio (2014a, b), with Bilattice Public Announcement Logic (BPAL). The reduction axioms for BPAL are all valid in FVEL if our language is extended with the missing connectives (more on the comparison between FVEL and BPAL in Sect. 6.2).
Let us name the extension of FVEL with public announcements FVPAL. In terms of syntax, FVPAL extends the BNF grammar of Sect. 2.1 with the following clause: \([\varphi ]\varphi \). A formula of the type \([\varphi ]\psi \) is read as after the announcement of \(\varphi \), \(\psi \) holds. The semantics for the new operator are defined as shown below. Differently from Plaza (1989), Plaza (2007); van Ditmarsch et al. (2007), we define a separate clause for the negated announcement, in line with the rest of our semantics:
where \(M=\langle S,R,V\rangle \) and \(M|_{\varphi }=\langle S',R',V'\rangle \), with \(S'=\{s\in S\mid M,s\models \varphi \}\), \(R'=R\cap (S'\times S')\) and \(V'=V|_{P\times S'}\).
The model of Fig. 1 (right), upon the public announcement of \(\lnot p\), would be transformed according to Fig. 6.
Notice that, for propositional atoms, the announcement of p does not delete worlds where \(\lnot p\) holds, but only worlds where p does not hold, that is, worlds where  holds. To delete worlds where \(\lnot p\) holds we would have to announce
holds. To delete worlds where \(\lnot p\) holds we would have to announce  , so that only worlds s with
, so that only worlds s with  (which is equivalent to \(M,s\not \models \lnot p\)) would survive.
(which is equivalent to \(M,s\not \models \lnot p\)) would survive.
As explained earlier, public announcements in FVPAL do not change the evidence itself (that would require a valuation-changing operation), just what agents know about it. This is not to say that only the accessibility relations are altered: what actually happens is that evidential states not conforming to the announcement, which is a truthful description of the actual evidential situation, are removed. So, for example, if the formula \(\varphi ^b\) is announced, any state where \(\varphi \) does not have value both (that is, where there is not evidence both for and against \(\varphi \)) will be removed. Note also that this kind of announcement which specifies one out of the four truth values would not be possible in a logic such as \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\), which lacks  .
.
5.1 An Example
Consider again the example from Sect. 2.6. Now suppose the actual world is \(s_2\), and so p (coffee is beneficial for health) is true, i.e., there is only positive evidence for p (and Kate knows that). Suppose also that Kate announces that a paper was published in a very respectable journal reassessing all the main studies that concluded that coffee was not beneficial for health, and that the new paper concluded that those studies were not reliable due to sloppy methodology. Now this is equivalent to an announcement of  (Kate knows that there is no evidence for the falsity of p). This announcement results in the removal of worlds where evidence for the falsity of p is present, namely \(s_1\) and \(s_3\). The resulting model is the one in Fig. 7, where John knows the status of p too. The formula
(Kate knows that there is no evidence for the falsity of p). This announcement results in the removal of worlds where evidence for the falsity of p is present, namely \(s_1\) and \(s_3\). The resulting model is the one in Fig. 7, where John knows the status of p too. The formula  , which is satisfied in \(s_2\) before the announcement, reflects the fact that John does not know the status of p, but after Kate’s announcement he learns that p is true.
, which is satisfied in \(s_2\) before the announcement, reflects the fact that John does not know the status of p, but after Kate’s announcement he learns that p is true.
These examples show the dynamics of the agents’ knowledge about available information/evidence. It might be puzzling, however, to notice that these models actually do not say much about factual knowledge. Nevertheless, it is based on information and evidence that one can form knowledge and beliefs. This observation calls for an extension of FVEL in which knowledge about evidence could be converted into factual knowledge or belief. This endeavor is left for future work.
5.2 Reduction Validities
As is the case for Public Announcement Logic (Plaza 1989, 2007; Gerbrandy and Groeneveld 1997), public announcements in FVEL do not increase expressivity. Any formula with public announcements in FVPAL can be rewritten as an FVEL formula, through the use of the following reduction validities.

Proposition 10
All formulas above for public announcements in FVPAL are valid.
Before proving that any formula of FVPAL can be rewritten as an equivalent formula of FVEL, we need the next proposition (proof in the “Appendix”).
Proposition 11
(Substitution of Equivalents) For all formulas \(\varphi ,\psi ,\chi \) of FVPAL, \(\varphi \equiv \psi \) implies \(\chi \equiv \chi [\psi /\varphi ]\). (\(\chi [\psi /\varphi ]\) is the formula that results from \(\chi \) after substitution of all occurrences of \(\varphi \) by \(\psi \).)
The result above might not seem surprising, but it is important to ensure that it holds for FVPAL, since some other intuitive properties do not hold for this logic. For example, even when \(M,s\models \varphi \) iff \(M,s\models \psi \) for all models M and states s, we might have that \(\varphi \not \equiv \psi \). Now we can prove the following:
Proposition 12
For any formula \(\varphi \) of FVPAL, a formula \(\varphi '\) of FVEL can be found such that \(\varphi \equiv \varphi '\).
Proof
This proof performs a simple inside-out reduction of announcements in a formula \(\varphi \) in FVPAL, finitely many times, until all announcements are eliminated.
Call \(\chi \) an innermost announcement subformula (IAS) of \(\varphi \) a subformula of \(\varphi \) such that \(\chi =[\delta ]\gamma \) and \(\gamma \) is an FVEL formula (and therefore has no announcements). Call this \(\gamma \) the formula under the announcement \([\delta ]\).
Consider all IAS of a formula \(\varphi \). Assume the largest formula under the announcements of these IAS has n symbols. Now, consider the formula \(\varphi '\) resulting from replacing all IAS in \(\varphi \) by their reductions, i.e. the subformula in the right-hand side of the reduction validity that matches the IAS. Thanks to Propositions 1 and 11, we know that \(\varphi \equiv \varphi '\). Moreover, since the reduction validities cover all syntactical cases of formulas under the announcements (on the left-hand side), and due to the format of the reduction validities, we know that the largest subformula under an the announcement of an IAS in \(\varphi '\) has \(k<n\) symbols. If we repeat this procedure at most k times, we will eventually obtain a formula in FVEL, i.e. a formula without announcements. \(\square \)
We remark that, in the presence of Proposition 11, validities (AnAn) and (An\(\lnot \)An) are redundant: we can make a complete reduction of any formula without using them (via Proposition 12). Alternatively, we can use all of the reduction validities presented before, including (AnAn) and (An\(\lnot \)An), and obtain an outside-in reduction as in Plaza (1989, 2007), without making use of Proposition 11.Footnote 15
5.3 Tableaux
To account for public announcements, the tableau system can be extended with the following rule schemas (each of which actually represent eight rules):

where \(\psi \,\dot{\leftrightarrow }\,\chi \) or \(\chi \,\dot{\leftrightarrow }\,\psi \) is one of the reduction validities above (except for (AnAn) and (An\(\lnot \)An)).Footnote 16 Finally we can prove completeness of the extended tableau system with respect to FVPAL.
Theorem 3
For any finite set of formulas \(\Sigma \cup \{\varphi \}\) of FVPAL, \(\Sigma \vdash \varphi \) iff \(\Sigma \models \varphi \).
Proof
The proof system being considered here is the tableau calculus for FVEL (rules R1-R14) augmented with rules RPA1 and RPA2. Soundness is already proven (soundness for the tableau for FVEL is proven in Theorem 1, soundness of public announcements’ reduction validities is proven in Proposition 10 and soundness of the substitution rules RPA1 and RPA2 follows from that and Proposition 11).
For completeness, suppose \(\Sigma \models \varphi \). When building a tableau for \(\Sigma \vdash \varphi \), right after the initial list we just need to apply rules RPA1 and RPA2 until we get equivalent versions without announcements for all formulas in \(\Sigma \cup \{\varphi \}\) (which are guaranteed to exist by Proposition 12). Let us denote the announcement-free version of \(\Sigma \) by \(\Sigma '\), and of \(\varphi \) by \(\varphi '\). First, \(\Sigma \models \varphi \) implies \(\Sigma '\models \varphi '\). Since the tableau without public announcements is complete, if \(\Sigma '\models \varphi '\), then \(\Sigma '\vdash \varphi '\). This means there is a closed tableau for \(\Sigma '\vdash \varphi '\). But by applying the substitution rules we just obtained a tableau with a single branch that contains all the nodes in the initial list of the tableau for \(\Sigma '\vdash \varphi '\). (Notice that adding nodes to the initial list of a tableau does not make it any harder for a tableau to close: these nodes can simply be ignored.) \(\square \)
6 Related Work
First we will discuss works that have a similar goal to ours, then we will comment on approaches that are comparable to ours from a technical viewpoint.
6.1 Logics of Evidence
The logic developed here can be compared to other epistemic logics in the literature that also deal with evidence (Renne 2009; van Benthem and Pacuit 2011; Baltag et al. 2012, 2014; Carnielli and Rodrigues 2019; Fitting 2017).
The closest works to ours have been developed roughly in parallel with it (see Santos 2018), and come in two very recent papers (Carnielli and Rodrigues 2019; Fitting 2017). First, Carnielli and Rodrigues (2019) develop the basic logic of evidence (BLE), which is a propositional logic similar to \({{\mathbf {\mathsf{{FDE}}}}}\) and whose philosophical motivations are closely related to FVEL’s. As mentioned in Sect. 2.3, their logic is concerned with preservation of evidence, instead of truth preservation. Then, Fitting (2017) comes even closer to our work by developing a modal logic inspired by BLE. Fitting’s logic KX4, however, is different from FVEL. It consists of a classical (two-valued) propositional base, extended with a modality which denotes existence of evidence. The behaviour of BLE, which is somewhat reflected in FVEL’s propositional part, appears embedded in KX4 via the modal operator (with its propositional fragment being classical, i.e. representing ontic facts). One can claim that Fitting’s approach is more intuitive than ours, but FVEL is, nevertheless, a natural modal extension of a popular many-valued logic (\({{\mathbf {\mathsf{{FDE}}}}}\)).
Baltag et al. (2014) study a justification logic with an evidence function that resembles awareness functions (Fagin and Halpern 1987): for each state, it gives a set of justification terms (“good”/correct evidence) that the agent possesses. Differently from Fagin and Halpern (1987), the evidence sets in Baltag et al. (2014) must abide by certain closure conditions. The first obvious difference between that paper and ours is that the only type of evidence being considered is “good” (true) evidence, whereas one of our main goals is to model agents having conflicting evidence.
Nevertheless, in a previous paper by the same authors Baltag et al. (2012), contradictory evidence is allowed. Both papers by Baltag et al., however, deal with evidence in a very different way than we do in this paper. First, they use evidence as justifications for formulas, which are then used to grant explicit status to otherwise implicit beliefs/knowledge. That is, the role of evidence is to make implicit beliefs explicit, although implicit beliefs (and even implicit knowledge) are entirely independent from evidence. For this reason, what is called evidence in Baltag et al. (2012, 2014) is conceptually closer to the idea of awareness (as studied in Fagin and Halpern 1987) than to that of evidence as we intuitively conceive it. We have not talked about factual beliefs in this paper, but, in future work, the concept of belief can be defined in a way such that it will be semantically dependent on the valuation, which here intuitively represents evidence.
In van Benthem and Pacuit (2011), neighborhood semantics are employed to model evidence and its dynamics. In their logic, lacking and conflicting evidence is allowed, as well as contradictory beliefs, without implying a trivial epistemic state. One of the highlights of their paper is how they make use of the additional evidence structure to enable interesting dynamics: removal, addition, modification and combination of pieces of evidence. As we plan to do in future work with FVEL, the concept of belief depends entirely on evidence in their semantics (although neither does existence of evidence imply belief, nor vice-versa). That formalism largely differs from ours in a number of aspects. Van Benthem and Pacuit’s semantics for \(\Box \varphi \) and \(B\varphi \) (“the agent has evidence that implies \(\varphi \)” and “the agent belives that \(\varphi \)”, respectively) is rather involved. In comparison, FVEL comprises a simpler semantics, especially with respect to what constitutes possession of evidence. In future work, we can devise a definition of belief for FVEL that depends on the agents’ knowledge of evidence, that is, on statements such as \(M,s\models \Box _i\varphi ^t\) (agent i knows that there is only positive evidence for \(\varphi \)). Thereby, realistic rules for belief formation might be obtained, such as agent i believes \(\varphi \) iff she knows that there is only positive evidence for \(\varphi \), for example.Footnote 17 Moreover, the “logic of combining evidence” in FVEL differs from that of Van Benthem and Pacuit’s logic. For example, whereas in FVEL (i) \(M,s\models \Box _i\varphi \) and \(M,s\models \Box _i\psi \) together imply \(M,s\models \Box _i(\varphi \wedge \psi )\), and at the same time it is possible to have (ii) \(M,s\not \models \Box _i(p\vee \lnot p)\), which makes agents in FVEL less (classically) logically omniscient (Hintikka 1979); in their logic (i) does not hold, which allows for more fine-grained evidence, and (ii) is not possible. Whether these are good or bad properties is open for debate.
6.2 Other Many-Valued Modal Logics
Many authors have studied the subject of many-valued modal logics (Segerberg 1967; Thomason 1978; Ostermann 1988; Morgan 1979; Schotch et al. 1978; Morikawa 1988; Fitting 1991; Odintsov and Wansing 2010; Rivieccio 2014a). Of these, the most closely related to ours are Odintsov and Wansing (2010) and Rivieccio (2014a). Both papers explore some kind of four-valued epistemic logics. We will now discuss the differences between these and our approach.
Logic \({{\mathbf {\mathsf{{BK}}}}}\) Odintsov and Wansing (2010) describe a logic called \({{\mathbf {\mathsf{{BK}}}}}\) (a Belnapian variant of \({{\mathbf {\mathsf{{K}}}}}\)), which is closely related to FVEL. They also provide a tableau system similar to ours, but their paper does not cover public announcements, nor the correspondence results presented here. There are other small differences between the two formalisms. The logic \({{\mathbf {\mathsf{{BK}}}}}\) uses two entailment symbols, namely support for truth (\(\models ^+\)) and support for falsity (\(\models ^-\)), whereas we opted for an additional negation. While this small change still results in equi-expressive logics, FVEL can express statements like \(M,s\models \lnot p\wedge \lnot q\) directly, whereas \({{\mathbf {\mathsf{{BK}}}}}\) always places the “negation” in front of the formula: \(M,s\models ^- p\vee q\). The latter has a more natural equivalent in our logic: \(\lnot (p\vee q)\). Moreover, this choice allows us to announce a formula like \(\lnot p\), which in \({{\mathbf {\mathsf{{BK}}}}}\) is only expressible w.r.t. a state of a model (\(M,s\models ^- p\)).
Bilattice Public Announcement LogicArieli and Avron (1996) present a four-valued propositional logic based on bilattices (recall Fig. 2). This logic has been extended to a modal setting by Jung and Rivieccio (2013), and then augmented with public announcements by Rivieccio (2014a, b), who called it Bilattice Public Announcement Logic (BPAL).Footnote 18 Despite being a very different formalism, BPAL has many similarities with FVPAL. First, for the propositional part, the connectives  are identical in both logics. BPAL’s \(\supset \) can be defined in FVPAL by
are identical in both logics. BPAL’s \(\supset \) can be defined in FVPAL by  . BPAL defines constants for all truth values. While we can define
. BPAL defines constants for all truth values. While we can define  and
and  , the connectives \(\bot \) (always evaluated to none) and \(\top \) (always both) are not definable in FVPAL, due to Observation 1 (which implies that for any frame, there is a valuation such that no formula has value both nor none).
, the connectives \(\bot \) (always evaluated to none) and \(\top \) (always both) are not definable in FVPAL, due to Observation 1 (which implies that for any frame, there is a valuation such that no formula has value both nor none).
Moreover, adding one of them is not enough to define the other, so in order to define all connectives of Arieli and Avron’s logic in FVPAL we need to add both. With these two new constants, we can also define Arieli and Avron’s \(\oplus \) and \(\otimes \) in FVPAL, and consequently all other connectives used in BPAL. In summary, adding \(\bot \) and \(\top \) to FVPAL makes its propositional part equi-expressive with BPAL’s.
Now, for the modal part, BPAL uses a four-valued relation. The definition of \(\Box \) comes from Jung and Rivieccio (2013), and is motivated by the definition of \(\Box \) in the standard translation of modal logic to first order logic: \(v(\Box \varphi ,w)=\bigwedge \{R(w,w')\rightarrow v(\varphi ,w'): w'\in W\}\), where v is their valuation function, which maps pairs of formulas and worlds to one of the four truth values. The implication used in the definition is their connective \(\rightarrow \), which gives a \(\Box \) that is strictly more expressive than the one defined with \(\supset \). FVPAL’s \(\Box \) also aligns smoothly with the standard translation:
Even if we restrict BPAL’s four-valued relation to a binary one (as in FVPAL), boxed formulas will be evaluated differently. In BPAL, \(\Box \varphi \) is true in state s whenever there is no accessible state; otherwise, we take the truth values of \(\varphi \) in all the accessible states, replacing both by false, and take their meet as the truth value of \(\Box \varphi \). We can see immediately that in a model where there is only one state s with a reflexive arrow and with \(V(p,s)=\{0,1\}\), \(\Box p\) will be both in FVPAL, but false in BPAL. In BPAL, \(\Box \varphi \) can actually only assume truth values other than both. Moreover, as shown in Proposition 3, NEC preserves validity in FVPAL, but it does not in BPAL. Despite these differences, the three additional axioms for the modal part given in Jung and Rivieccio (2013) are valid in FVPAL (as long as we add the constant \(\bot \)). For the public announcements part, if we define \(\langle \varphi \rangle \psi {\mathop {=}\limits ^{{{{\mathrm{def}}}}}}\lnot [\varphi ]\lnot \psi \) (plus \(\bot ,\top \)) in FVPAL, all the axioms for public announcements listed in Rivieccio (2014b, Sec. 4) are also valid here.
To summarise the differences: BPAL has two extra constants, which if added to FVPAL make their propositional parts equi-expressive. The modal operator has different behaviour in each logic, NEC preserves validity only in FVPAL, but the axioms for BPAL are all valid in FVPAL. Another main difference between these works is that we present a tableau calculus, whereas Rivieccio (2014b) has a Hilbert-style axiomatic system.
Levesque’s Logic of Implicit and Explicit Beliefs Also worth mentioning is Levesque’s Logic of Implicit and Explicit Belief (Levesque 1984). Although he is not concerned with the idea of evidence, his framework features a four-valued propositional part and two belief modalities: one implicit and one explicit. Validities are assessed according to standard possible worlds, so all classical tautologies are still valid, but beliefs take into account non-standard “situations”, allowing for non-omniscient agents (at least w.r.t. explicit beliefs).
7 Conclusions and Future Work
In this paper, we presented a multi-agent four-valued logic that can model evidence and what a group of agents know about this evidence. In this way it is possible to model realistic scenarios where agents have access to an inconsistent or incomplete base of information. Some examples are the database scenario described in the introduction, or a robot that collects data through several sensors, which may result in inconsistent data due to sensors’ inaccuracy.
First degree entailment was used as the propositional basis for the logic, with its four-valued atoms playing the role of evidence, where a proposition could be both true and false or have no value at all. A modal layer was built on top of that. The accessibility relation, then, defines the knowledge of the agents about the possibly contradictory or incomplete evidence. Moreover, classical negation was added to the language, increasing its expressivity. That addition allowed us to define an equivalence operator and reduction validities for public announcements, besides having a natural interpretation in the logic as well. A tableau calculus and some correspondence results were provided.
While on the technical side there are similarities among our approach and others, new results have been presented. Furthermore, the type of situations we model with this many-valued modal logic is different from the ones modelled by other logics of evidence. With this paper, we aim to contribute to the study of many-valued modal logics by providing an intuitive reading (with potential practical applicability) to these formal tools.
There are several possible directions for further work. First, other update actions (along the lines of van Benthem et al. 2006) could be studied, such as the actions mentioned in the introduction, which change the informational layer instead of only changing the knowledge about it. These actions, instead of removing states, could just add or remove truth (or falsity) from the value of a proposition in all worlds.
Our logic does not take into account the amount of evidence for and against propositions (as well as other aspects of evidence, such as reliability, source, etc.). FVEL could be modified to include this feature if we define the valuation to be a function \(V:P\times S\rightarrow \mathbb {N}\times \mathbb {N}\), where the first element of the pair, \(V(p,s)^+\), denotes the amount of evidence for p and the second element, \(V(p,s)^-\), denotes the amount of evidence against p. A belief modality could be introduced along the lines of \(M,s\models B_i p\) iff for all t such that \(sR_i t\), \(V(p,t)^+>V(p,t)^-\).Footnote 19 As stated in the end of Sect. 5.1, another obvious avenue for improvements is the study of methods for extracting factual knowledge/belief from these evidence models (as done in Santos 2019). Agents possessing an inconsistent or incomplete body of evidence could process this information to obtain a consistent epistemic state (along the lines of belief revision, in particular Tamminga 2001). Finally, we note that other interpretations for FVEL can be explored: for example, if we consider each state as the epistemic state of a particular agent, then these states would represent agents, and the accessibility relation would represent relations between them. This opens the possibility for new dynamics, where the knowledge of one agent is influenced by its social network (see Baltag et al. 2016, 2019; Christoff and Hansen 2015).
Notes
Usually there is a link between evidence and reality, but in this formalism, once evidence is allowed to be misleading, these concepts have to be fully independent.
An evidence-changing operation would entail modification in the valuation function.
Note that
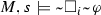 iff \(M,s\models \lnot \Box _i\lnot \varphi \), but
iff \(M,s\models \lnot \Box _i\lnot \varphi \), but  iff for all t such that \(sR_it\), it holds that
iff for all t such that \(sR_it\), it holds that 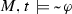 , whereas \(M,s\models \lnot \lnot \Box _i\lnot \varphi \) iff for all t such that \(sR_it\), it holds that \(M,t\models \lnot \varphi \).
, whereas \(M,s\models \lnot \lnot \Box _i\lnot \varphi \) iff for all t such that \(sR_it\), it holds that \(M,t\models \lnot \varphi \).What \(n\vee b=t\) is saying is that if we have propositions \(\varphi \) and \(\psi \) such that we have no evidence about the first but we do have evidence both for and against the second, then we have only evidence for (and not against) \(\varphi \vee \psi \). Does this make sense? Indeed, evidence against this disjunction would require evidence against both its disjuncts, but we have no evidence whatsoever about \(\varphi \).
Sometimes we omit the agent index from the \(\Box \) operator, for simplicity. Everything that is said here is generalisable to a language with multiple boxes.
Interestingly, Girard and Tanaka (2016) show that the standard definition of \(p\rightarrow q\) as \(\lnot p\vee q\) does not suffice to prove reduction axioms for public announcements when working with an epistemic extension of Priest’s three-valued Logic of Paradox. To circumvent that, they introduce an alternative implication. Our classical negation has a similar role with respect to our reduction axioms of Sect. 5.
The representation of tableau rules here is similar to that in Priest (2008).
The proof of this lemma and some other proofs are in the “Appendix”.
The notation used for these rules follows the frame property names defined previously, which in turn are taken from Priest (2008, Sec. 3.2.3.)
The term “reduction axioms” is commonly used in the literature, but here we are working with validities, not axioms.
We thank an anonymous reviewer for pointing this out. We show both possibilities, however, because the substitution result of Proposition 11 is an essential tool when dealing with FVEL and FVPAL.
These rules for belief formation are in line with some discussions in epistemology. Feldman and Conee (1985), for example, argue that a rational belief is one that fits the evidence.
During revision of this paper we also became aware of an extension of Modal Bilattice Logic with epistemic actions (see Bakhtiari et al. 2019).
References
Arieli, O., & Avron, A. (1996). Reasoning with logical bilattices. Journal of Logic, Language and Information, 5(1), 25–63.
Bakhtiari, Z., van Ditmarsch, H., & Rivieccio, U. (2019). Bilattice logic of epistemic actions and knowledge. Annals of Pure and Applied Logic (in press).
Balbiani, P., van Ditmarsch, H., Herzig, A., & de Lima, T. (2010). Tableaux for public announcement logic. Journal of Logic and Computation, 20(1), 55.
Baltag, A., Christoff, Z., Rendsvig, R., & Smets, S. (2016). Dynamic epistemic logics of diffusion and prediction in social networks. In Proceedings of the 12th conference on logic and the foundations of game and decision theory.
Baltag, A., Christoff, Z., Rendsvig, R., & Smets, S. (2019). Dynamic epistemic logics of diffusion and prediction in social networks. Studia Logica, 107(3), 489–531.
Baltag, A., Renne, B., & Smets, S. (2012). The logic of justified belief change, soft evidence and defeasible knowledge. WoLLIC (Vol. 7456, pp. 168–190). Springer.
Baltag, A., Renne, B., & Smets, S. (2014). The logic of justified belief, explicit knowledge, and conclusive evidence. Annals of Pure and Applied Logic, 165(1), 49–81.
Belnap, N. (1977). A useful four-valued logic. In J. M. Dunn & G. Epstein (Eds.), Modern uses of multiple-valued logic (pp. 5–37). Berlin: Springer.
Carnielli, W., & Rodrigues, A. (2019). An epistemic approach to paraconsistency: A logic of evidence and truth. Synthese, 196(9), 3789–3813.
Christoff, Z., & Hansen, J. U. (2015). A logic for diffusion in social networks. Journal of Applied Logic, 13(1), 48–77.
Dunn, J. (1976). Intuitive semantics for first-degree entailments and ‘coupled trees’. Philosophical Studies, 29(3), 149–168.
Fagin, R., & Halpern, J. Y. (1987). Belief, awareness, and limited reasoning. Artificial Intelligence, 34(1), 39–76.
Fagin, R., Halpern, J. Y., Moses, Y., & Vardi, M. (2004). Reasoning about knowledge. Cambridge: MIT Press.
Feldman, R., & Conee, E. (1985). Evidentialism. Philosophical Studies, 48(1), 15–34.
Fitting, M. (1983). Proof methods for modal and intuitionistic logics (Vol. 169). Berlin: Springer.
Fitting, M. (1991). Many-valued modal logics. Fundamenta Informaticae, 15(3–4), 235–254.
Fitting, M. (2017). Paraconsistent logic, evidence and justification. Studia Logica, 105(6), 1149–1166.
Gerbrandy, J., & Groeneveld, W. (1997). Reasoning about information change. Journal of Logic, Language, and Information, 6(2), 147–169.
Ghosh, S., & de Jongh, D. (2013). Comparing strengths of beliefs explicitly. Logic Journal of the IGPL, 21(3), 488–514.
Girard, P., & Tanaka, K. (2016). Paraconsistent dynamics. Synthese, 193(1), 1–14.
Halpern, J. Y., & Moses, Y. (1992). A guide to completeness and complexity for modal logics of knowledge and belief. Artificial Intelligence, 54(3), 319–379.
Hansen, J. (2010). Terminating tableaux for dynamic epistemic logics. Electronic Notes in Theoretical Computer Science, 262, 141–156.
Hintikka J (1979) Impossible possible worlds vindicated. In Game-theoretical semantics (pp. 367–379). Springer.
Jung, A., & Rivieccio, U. (2013). Kripke semantics for modal bilattice logic. In Proceedings of the 2013 28th annual ACM/IEEE symposium on logic in computer science (pp. 438–447). IEEE Computer Society.
Levesque, H. (1984). A logic of implicit and explicit belief. In AAAI (pp. 198–202).
Meyer, J. J. C., & Van Der Hoek, W. (2004). Epistemic logic for AI and computer science (Vol. 41). Cambridge: Cambridge University Press.
Morgan, C. (1979). Local and global operators and many-valued modal logics. Notre Dame Journal of Formal Logic, 20(2), 401–411.
Morikawa, O. (1988). Some modal logics based on a three-valued logic. Notre Dame Journal of Formal Logic, 30(1), 130–137.
Odintsov, S., & Wansing, H. (2010). Modal logics with Belnapian truth values. Journal of Applied Non-Classical Logics, 20(3), 279–301.
Ostermann, P. (1988). Many-valued modal propositional calculi. Mathematical Logic Quarterly, 34(4), 343–354.
Pacuit, E., & Salame, S. (2004). Majority logic. In D. Dubois, C. Welty, & M. A. Williams (Eds.), Principles of knowledge representation and reasoning (Vol. 4, pp. 598–605). Stanford: AAAI Press.
Plaza, J. (1989). Logics of public communications. In M. L. Emrich, M. S. Pfeifer, M. Hadzikadic, & Z. W. Ras (Eds.), Proceedings of the 4th international symposium on methodologies for intelligent systems (ISMIS 1989): Poster session program, Charlotte, NC (pp. 201–216). Oak Ridge National Laboratory ORNL/DSRD-24.
Plaza, J. (2007). Logics of public communications. Synthese, 158(2), 165–179.
Priest, G. (2008). An introduction to non-classical logic: From if to is (2nd ed.). Cambridge: Cambridge University Press.
Renne, B. (2009). Evidence elimination in multi-agent justification logic. In Proceedings of the 12th conference on theoretical aspects of rationality and knowledge, ACM (pp. 227–236).
Rivieccio, U. (2014a). Algebraic semantics for bilattice public announcement logic. In Studia Logica, proceedings of trends in logic XIII. Springer.
Rivieccio, U. (2014b). Bilattice public announcement logic. In R. Goré, B. Kooi, & A. Kurucz (Eds.), Advances in modal logic (Vol. 10, pp. 459–477). College Publications.
Santos, Y. D. (2018). A dynamic informational-epistemic logic. In A. Madeira & M. Benevides (Eds.), Dynamic logic. New trends and applications, Lecture Notes in Computer Science (Vol. 10669, pp. 64–81). Berlin: Springer.
Santos, Y. D. (2019). Consolidation of belief in two logics of evidence. International workshop on logic. Rationality and interaction (LORI) (pp. 57–70). Springer.
Schotch, P., Jensen, J., Larsen, P., & MacLellan, E. (1978). A note on three-valued modal logic. Notre Dame Journal of Formal Logic, 19(1), 63–68.
Segerberg, K. (1967). Some modal logics based on a three-valued logic. Theoria, 33(1), 53–71.
Tamminga, A. (2001). Belief dynamics: (Epistemo)logical investigations. Ph.D. thesis, ILLC.
Thomason, S. (1978). Possible worlds and many truth values. Studia Logica, 37(2), 195–204.
van Benthem, J., & Pacuit, E. (2011). Dynamic logics of evidence-based beliefs. Studia Logica, 99(1), 61–92.
van Benthem, J., van Eijck, J., & Kooi, B. (2006). Logics of communication and change. Information and Computation, 204(11), 1620–1662.
van Ditmarsch, H., van der Hoek, W., & Kooi, B. (2007). Dynamic epistemic logic (Vol. 337). Berlin: Springer.
Acknowledgements
Special thanks to Rineke Verbrugge, Barteld Kooi and Allard Tamminga for comments that greatly improved this work. I am very grateful to the anonymous reviewers as well, who gave me very detailed and useful feedback. I would also like to thank my colleagues from the RUG who participated in a discussion of a preliminary version of this paper, and all those present at the LIRa seminar in the ILLC/UvA who gave me very relevant suggestions. Research supported by Ammodo KNAW project “Rational Dynamics and Reasoning”.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof (Lemma 1)
This proof is just a modification of the proof for the Soundness Lemma for \({{\mathbf {\mathsf{{K}}}}}_{{{\mathbf {\mathsf{{{FDE}}}}}}}\), in Priest (2008, Lemma 11a.9.3).
Suppose as induction hypothesis that functions \(f:\mathbb {N}\rightarrow W\) and \(g:\mathbb {N}\rightarrow A\) show M to be faithful to a branch b containing at least the initial list and the premises of the rule in question. The cases for rules R1–R2 and R5–R8 are already covered there, we need to prove the lemma for the remaining rules; We will use Definition 3 instead of the definition of faithful interpretation in Priest (2008, Def. 11a.9.2) (this adaptation only concerns notation).
For rule R3, since M is faithful to b, we have \(1\in \overline{V}(\lnot (\varphi \wedge \psi ),f(i))\). For M to be faithful to one of the extensions of b (according to Definition 3), either \(1\in \overline{V}(\lnot \varphi ,f(i))\) or \(1\in \overline{V}(\lnot \psi ,f(i))\) has to hold. But, by our semantics, this is precisely what is implied by \(1\in \overline{V}(\lnot (\varphi \wedge \psi ),f(i))\).
The case for rule R4 is similar. Since M is faithful to b, \(1\notin \overline{V}(\lnot (\varphi \wedge \psi ),f(i))\). This happens exactly when \(1\notin \overline{V}(\lnot \varphi ,f(i))\) and \(1\notin \overline{V}(\lnot \psi ,f(i))\), which are the new conditions in the extended branch.
For rule R9, since M is faithful to b, we have \(1\in \overline{V}(\lnot \Box _m\varphi ,f(i))\). By our semantics, there has to be an s such that \(f(i)R_ms\) and \(M,s\models \lnot \varphi \). After applying R9, nodes \(ir_mj\) (with j fresh in b) and \(\lnot \varphi ,+j\) are appended to b. Then, take \(f'\) identical to f except that \(f'(j)=s\). Also, if there was no previous mention of \(r_m\) in b, take \(g'\) identical to g except that \(g'(m)=m\); otherwise just take \(g'=g\). Thus, \(f'(i)R_{g'(m)}f'(j)\) and \(1\in \overline{V}(\lnot \varphi ,f'(j))\), and therefore M is faithful to the extension of b.
For rule R10, we have \(1\notin \overline{V}(\lnot \Box _m\varphi ,f(i))\) and \(f(i)R_{g(m)}f(j)\). From our semantics, we get that for all t such that \(f(i)R_{g(m)}t\), we have \(1\notin \overline{V}(\lnot \varphi ,t)\). In particular, we have \(1\notin \overline{V}(\lnot \varphi ,f(j))\), which is what we needed to show.
For rule R11, we want to prove that \(1\notin \overline{V}(\varphi ,f(i))\). Since M is faithful,  . But then
. But then  , which implies \(M,f(i)\not \models \varphi \) and we are done. The case for R12 is analogous.
, which implies \(M,f(i)\not \models \varphi \) and we are done. The case for R12 is analogous.
For rule R13, we need to prove that \(1\in \overline{V}(\varphi ,f(i))\). But by hypothesis our interpretation M is faithful to the branch, so  . The result follows:
. The result follows:  , then \(M,f(i)\models \varphi \), and we are done. The case for rule R14 is analogous. \(\square \)
, then \(M,f(i)\models \varphi \), and we are done. The case for rule R14 is analogous. \(\square \)
Proof (Lemma 2)
This is also an adaptation of the proof of Priest (2008, Lemma 11a.9.6). The proof is by induction on the length of \(\varphi \). The base case where \(\varphi =p\) is covered by Definition 2. I.H.: the lemma holds for all \(\varphi '\) with length smaller than n, where n is the length of \(\varphi \). The step will be shown by cases. Consider a formula \(\varphi \) of length n. The case where \(\varphi =\lnot p\) for some atom p is also covered by Definition 2.
First, \(\varphi =(\psi \wedge \chi )\). The cases when \((\psi \wedge \chi ,\pm i)\) are on b were already covered by Priest (2008, Lemma 11a.9.6).
\((\lnot (\psi \wedge \chi ),+i)\) is on b: We need to show \(0\in \overline{V}(\psi \wedge \chi ,s_i)\). But since b is complete, rule R3 has been applied to the node, which means that \((\lnot \psi ,+i)\) or \((\lnot \chi ,+i)\) is on b. But then (by the I.H.) \(0\in \overline{V}(\psi ,s_i)\) or \(0\in \overline{V}(\chi ,s_i)\), which means that \(0\in \overline{V}(\psi \wedge \chi ,s_i)\) by our semantics.
\((\lnot (\psi \wedge \chi ),-i)\) is on b: We need to show \(0\notin \overline{V}(\psi \wedge \chi ,s_i)\). Since b is complete, R4 has been applied, so \((\lnot \psi ,-i)\) and \((\lnot \chi ,-i)\) are on b. By I.H. we have \(0\notin \overline{V}(\psi ,s_i)\) and \(0\notin \overline{V}(\chi ,s_i)\), which implies the desired result by the semantics.
Now, \(\varphi =\Box _m\psi \). The non-negated cases were shown by Priest (2008, Lemma 11a.9.6). Let us cover the remaining ones:
\((\lnot \Box _m\psi ,+i)\) is on b: We have to show that \(0\in \overline{V}(\Box _m\psi ,s_i)\). Since b is complete, R9 has been applied, so \((ir_mj)\) and \((\lnot \psi ,+j)\) are on b, for some j. By Definition 2, \(s_iR_ms_j\), and by I.H. \(0\in \overline{V}(\psi ,s_j)\). By our semantics, \(0\in \overline{V}(\Box _m\psi ,s_i)\).
\((\lnot \Box _m\psi ,-i)\) is on b: We have to show that \(0\notin \overline{V}(\Box _m\psi ,s_i)\). There are two cases. If there is no j such that \((ir_mj)\) is in b, then by Definition 2 there is no j such that \(s_iR_ms_j\). Then by semantics \(M,s\not \models \lnot \Box _m\psi \), so \(0\notin \overline{V}(\Box _m\psi ,s_i)\). Now, if there are \((ir_mj)\) nodes on b, since b is complete, R10 has been applied for all such j to obtain nodes \((\lnot \psi ,s_j)\). By Definition 2, for all such j, \(s_iR_ms_j\). By I.H. this implies that for all such j, \(0\notin \overline{V}(\psi ,s_j)\), so there is no t such that \(s_iR_mt\) and \(M,t\models \lnot \psi \), and therefore \(M,s_i\not \models \lnot \Box _m\psi \), which gives us the desired result.
Now the cases where  .
.
 is on b: Then, since the branch is complete, \((\psi ,-i)\) is on b. By the I.H., \(1\notin \overline{V}(\psi ,s_i)\). Then \(M,s_i\not \models \psi \), so
is on b: Then, since the branch is complete, \((\psi ,-i)\) is on b. By the I.H., \(1\notin \overline{V}(\psi ,s_i)\). Then \(M,s_i\not \models \psi \), so  and finally
and finally  . The case when
. The case when  is on b is analogous.
is on b is analogous.
 is on b: then, since b is complete, rule R13 has been applied and \((\psi ,+i)\) is on b. Then by I.H. \(1\in \overline{V}(\psi ,s_i)\), so \(M,s_i\models \psi \), which implies \(M,s_i\models \lnot \lnot \psi \), and therefore \(1\in \overline{V}(\lnot \lnot \psi ,s_i)\). Also, notice that since \(M,s_i\models \lnot (\lnot \psi )\), we have that \(0\in \overline{V}(\lnot \psi ,s_i)\), as desired. \(\square \)
is on b: then, since b is complete, rule R13 has been applied and \((\psi ,+i)\) is on b. Then by I.H. \(1\in \overline{V}(\psi ,s_i)\), so \(M,s_i\models \psi \), which implies \(M,s_i\models \lnot \lnot \psi \), and therefore \(1\in \overline{V}(\lnot \lnot \psi ,s_i)\). Also, notice that since \(M,s_i\models \lnot (\lnot \psi )\), we have that \(0\in \overline{V}(\lnot \psi ,s_i)\), as desired. \(\square \)
Proof (Proposition 10)
For each validity \(\varphi \,\dot{\leftrightarrow }\,\psi \), we will prove the equivalent \(\varphi \equiv \psi \) instead of \(\models \varphi \,\dot{\leftrightarrow }\,\psi \) (relying on Proposition 1). To verify that a validity of the form \(\varphi \equiv \psi \) is correct, one just has to check that the semantic conditions for \(M,s\models \varphi \) are equivalent to the conditions for \(M,s\models \psi \), and do the same for \(M,s\models \lnot \varphi \) and \(M,s\models \lnot \psi \) (with arbitrary M and s).
(AnAt):  :
:
We will check the truth conditions for each side of the validity and make sure they are equivalent.
\(M,s\models [\varphi ]p\)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models p\)
iff  or \(M|_\varphi ,s\models p\)
or \(M|_\varphi ,s\models p\)
But since \(M|_\varphi =\langle S',R',V'\rangle \) with \(V'(p,s)=V(p,s)\) for all atoms p and \(s\in S'\), we have \(M,s\models p\) iff \(M|_\varphi ,s\models p\), and therefore \(M,s\models [\varphi ]p\) iff  . Now we have to check the truth conditions for the negations of each side of the validity, and see if they are equivalent. This will guarantee that the formulas on each side of the equivalence always take on the same truth value.
. Now we have to check the truth conditions for the negations of each side of the validity, and see if they are equivalent. This will guarantee that the formulas on each side of the equivalence always take on the same truth value.
\(M,s\models \lnot [\varphi ]p\)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot p\)
And:

iff [by the definition of \(\vee \)]

iff 
iff \(M,s\models \varphi \wedge \lnot p\)
iff \(M,s\models \varphi \) and \(M,s\models \lnot p\)
It turns out that those conditions are exactly the same, for (again) \(M=\langle S,R,V\rangle \) and \(M|_\varphi =\langle S',R',V'\rangle \) with \(V'(p,s)=V(p,s)\) for all atoms p and \(s\in S'\). Therefore validity (AnAt) holds.
(An\(\lnot \)):  :
:
\(M,s\models [\varphi ]\lnot p\)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \lnot p\)
iff \(M,s\not \models \varphi \) or \(0\in V(p,s)\)
iff \(M,s\not \models \varphi \) or \(M,s\models \lnot p\)
iff 
And for the negated formulas:
\(M,s\models \lnot [\varphi ]\lnot p\)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot \lnot p\)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models p\)
And:

iff 
iff 
iff \(M,s\models \varphi \) and \(M,s\models p\)
Since \(M|_\varphi \)’s valuation is only a restriction of M’s valuation, both truth conditions are the same.
(An\(\wedge \)): \([\varphi ](\psi \wedge \chi ) \equiv [\varphi ]\psi \wedge [\varphi ]\chi \):
The proof for this and the following validitities will follow the same structure as the previous one. We will just show the truth conditions.
\(M,s\models [\varphi ](\psi \wedge \chi )\)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \wedge \chi \)
iff \(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and \(M|_\varphi ,s\models \chi \))
And:
\(M,s\models [\varphi ]\psi \wedge [\varphi ]\chi \)
iff \(M,s\models [\varphi ]\psi \) and \(M,s\models [\varphi ]\chi \)
iff (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \)) and (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \chi \))
iff \(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and \(M|_\varphi ,s\models \chi \))
Now for the conditions for the negated formulas.
\(M,s\models \lnot [\varphi ](\psi \wedge \chi )\)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot (\psi \wedge \chi )\)
iff \(M,s\models \varphi \) and (\(M|_\varphi ,s\models \lnot \psi \) or \(M|_\varphi ,s\models \lnot \chi \))
And:
\(M,s\models \lnot ([\varphi ]\psi \wedge [\varphi ]\chi )\)
iff \(M,s\models \lnot [\varphi ]\psi \) or \(M,s\models \lnot [\varphi ]\chi \)
iff (\(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot \psi \)) or (\(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot \chi \))
iff \(M,s\models \varphi \) and (\(M|_\varphi ,s\models \lnot \psi \) or \(M|_\varphi ,s\models \lnot \chi \))
(An\(\lnot \wedge \)): \([\varphi ]\lnot (\psi \wedge \chi ) \equiv [\varphi ]\lnot \psi \vee [\varphi ]\lnot \chi \):
\(M,s\models [\varphi ]\lnot (\psi \wedge \chi )\)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \lnot (\psi \wedge \chi )\)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \lnot \psi \) or \(M|_\varphi ,s\models \lnot \chi \)
iff \(M,s\models [\varphi ]\lnot \psi \) or \(M,s\models [\varphi ]\lnot \chi \)
iff \(M,s\models [\varphi ]\lnot \psi \vee [\varphi ]\lnot \chi \)
For the negated formulas:
\(M,s\models \lnot [\varphi ]\lnot (\psi \wedge \chi )\)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \wedge \chi \)
And:
\(M,s\models \lnot ([\varphi ]\lnot \psi \vee [\varphi ]\lnot \chi )\)
iff \(M,s\models \lnot [\varphi ]\lnot \psi \) and \(M,s\models \lnot [\varphi ]\lnot \chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \) and \(M|_\varphi ,s\models \chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \wedge \chi \)
(An\(\Box \)):  :
:
\(M,s\models [\varphi ]\Box \psi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \Box \psi \)
iff \(M,s\not \models \varphi \) or for all \(t\in S'\) s.t. \(sR't(M|_\varphi ,t\models \psi )\)
And:

iff \(M,s\not \models \varphi \) or for all \(t\in S\) s.t. \(sRt(M,t\models [\varphi ]\psi )\)
iff \(M,s\not \models \varphi \) or for all \(t\in S\) s.t. \(sRt(M,t\not \models \varphi \) or \(M|_\varphi ,t\models \psi )\)
iff [by classical logic]
\(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and for all \(t\in S\) s.t. \(sRt(M,t\not \models \varphi \) or \((M,t\models \varphi \) and \(M|_\varphi ,t\models \psi )\))
iff [by set theory: \(S=(S\setminus S')\cup S'\)]
\(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and
for all \(t\in S\setminus S'\) s.t. \(sRt(M,t\not \models \varphi \) or \((M,t\models \varphi \) and \(M|_\varphi ,t\models \psi )\) and
for all \(t\in S'\) s.t. \(sRt(M,t\not \models \varphi \) or \((M,t\models \varphi \) and \(M|_\varphi ,t\models \psi )\))
iff [by: \(M,s\models \varphi \) for all \(s\in S'\), and \(M,s\not \models \varphi \) for all \(s\in S\setminus S'\)]
\(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and
for all \(t\in S\setminus S'\) s.t. sRt (true or (\(M,t\models \varphi \) and \(M|_\varphi ,t\models \psi \))) and
for all \(t\in S'\) s.t. sRt(false or (true and \(M|_\varphi ,t\models \psi \))))
iff [by classical logic]
\(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and for all \(t\in S'\) s.t. \(sRt(M|_\varphi ,t\models \psi )\))
iff [by: \(s\in S\) and \(M,s\models \varphi \) iff \(s\in S'\); sRt and \(s,t\in S'\) iff \(sR't\)]
\(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and for all \(t\in S'\) s.t. \(sR't(M|_\varphi ,t\models \psi )\))
iff [by classical logic]
\(M,s\not \models \varphi \) or for all \(t\in S'\) s.t. \(sR't(M|_\varphi ,t\models \psi )\)
For the negated formulas:
\(M,s\models \lnot [\varphi ]\Box \psi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot \Box \psi \)
iff \(M,s\models \varphi \) and there is a \(t\in S'(sR't\) and \(M|_\varphi ,t\models \lnot \psi )\)
And:

iff 
iff \(M,s\models \varphi \wedge \lnot \Box [\varphi ]\psi \)
iff \(M,s\models \varphi \) and \(M,s\models \lnot \Box [\varphi ]\psi \)
iff \(M,s\models \varphi \) and there is a \(t\in S(sRt\) and \(M,t\models \lnot [\varphi ]\psi )\)
iff \(M,s\models \varphi \) and there is a \(t\in S(sRt\) and \((M,t\models \varphi \) and \(M|_\varphi ,t\models \lnot \psi ))\)
But, since \(M,t\models \varphi \) in the latest condition, \(t\in S'\).
(An\(\lnot \Box \)):  :
:
\(M,s\models [\varphi ]\lnot \Box \psi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \lnot \Box \psi \)
iff \(M,s\not \models \varphi \) or there is a \(t\in S'(sR't\) and \(M|_\varphi ,t\models \lnot \psi )\)
And:

iff \(M,s\not \models \varphi \) or \(M,s\models \lnot \Box [\varphi ]\psi \)
iff \(M,s\not \models \varphi \) or there is a \(t\in S(sRt\) and \(M,t\models \lnot [\varphi ]\psi )\)
iff \(M,s\not \models \varphi \) or there is a \(t\in S(sRt\) and \(M,t\models \varphi \) and \(M|_\varphi ,t\models \lnot \psi )\)
Notice that the final conditions for the satisfaction of both formulas are equivalent, for the states \(t\in S\) such that \(M,t\models \varphi \) are exactly the states \(t\in S'\); additionally, notice that in the existential condition we can consider that \(M,s\models \varphi \). Now for the negated formulas:
\(M,s\models \lnot [\varphi ]\lnot \Box \psi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot \lnot \Box \psi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \Box \psi \)
iff \(M,s\models \varphi \) and for all \(t\in S'\) s.t. \(sR't\) (\(M|_\varphi ,t\models \psi \))
And:

iff  and \(M,s\models \lnot \lnot \Box [\varphi ]\psi \)
and \(M,s\models \lnot \lnot \Box [\varphi ]\psi \)
iff \(M,s\models \varphi \) and \(M,s\models \Box [\varphi ]\psi \)
iff \(M,s\models \varphi \) and for all \(t\in S\) s.t. \(sRt(M,t\models [\varphi ]\psi )\)
iff \(M,s\models \varphi \) and for all \(t\in S\) s.t. \(sRt(M,t\not \models \varphi \) or \(M|_\varphi ,t\models \psi )\)
(An ):
):  :
:

iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\not \models \psi \)
And:

iff \(M,s\not \models \varphi \) or \(M,s\not \models [\varphi ]\psi \)
iff \(M,s\not \models \varphi \) or not (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \))
iff \(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and \(M|_\varphi ,s\not \models \psi \))
For the negated formulas:

iff \(M,s\models \varphi \) and 
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \)
And

iff 
iff \(M,s\models \varphi \wedge [\varphi ]\psi \)
iff \(M,s\models \varphi \) and (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \))
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \)
(An ):
):  :
:

iff \(M,s\not \models \varphi \) or 
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \)
And:

iff  or \(M,s\models [\varphi ]\psi \)
or \(M,s\models [\varphi ]\psi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \)
And for the negated formulas:

iff \(M,s\models \varphi \) and 
iff \(M,s\models \varphi \) and 
And:

iff  and
and 
iff \(M,s\models \varphi \) and 
iff \(M,s\models \varphi \) and not (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \))
iff \(M,s\models \varphi \) and (\(M,s\models \varphi \) and  )
)
iff \(M,s\models \varphi \) and 
(AnAn): \([\varphi ][\psi ]\chi \equiv [\varphi \wedge [\varphi ]\psi ]\chi \):
\(M,s\models [\varphi ][\psi ]\chi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models [\psi ]\chi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\not \models \psi \) or \((M|_\varphi )|_\psi ,s\models \chi \)
And:
\(M,s\models [\varphi \wedge [\varphi ]\psi ]\chi \)
iff \(M,s\not \models \varphi \wedge [\varphi ]\psi \) or \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \)
iff \(M,s\not \models \varphi \) or \(M,s\not \models [\varphi ]\psi \) or \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \)
iff \(M,s\not \models \varphi \) or not (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \)) or \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \)
iff \(M,s\not \models \varphi \) or (\(M,s\models \varphi \) and \(M|_\varphi ,s\not \models \psi \)) or \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\not \models \psi \) or \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \)
Now the question is: are \((M|_\varphi )|_\psi ,s\models \chi \) and \(M|_{\varphi \wedge [\varphi ]\psi },s\models \chi \) equivalent? We will just show that the domains \(S_{\varphi |\psi }\) and \(S_{\varphi \wedge [\varphi ]\psi }\) (of \((M|_\varphi )|_\psi \) and \(M|_{\varphi \wedge [\varphi ]\psi }\), respectively) are the same, which is a sufficient condition.
We have \(S_{\varphi |\psi }=\{s\in S_\varphi \mid M|_\varphi ,s\models \psi \}= \{s\in S\mid M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \}\), where S and \(S_\varphi \) are the domains from M and \(M|_\varphi \), respectively. Moreover, \(S_{\varphi \wedge [\varphi ]\psi }= \{s\in S\mid M,s\models \varphi \wedge [\varphi ]\psi \}\), but \(M,s\models \varphi \wedge [\varphi ]\psi \) iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \). Therefore, \(S_{\varphi \wedge [\varphi ]\psi }= \{s\in S\mid M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \}\).
Now for the negated formulas:
\(M,s\models \lnot [\varphi ][\psi ]\chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \lnot [\psi ]\chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \) and \((M|_\varphi )|_\psi ,s\models \lnot \chi \)
And:
\(M,s\models \lnot [\varphi \wedge [\varphi ]\psi ]\chi \)
iff \(M,s\models \varphi \wedge [\varphi ]\psi \) and \(M|_{\varphi \wedge [\varphi ]\psi },s\models \lnot \chi \)
iff \(M,s\models \varphi \) and (\(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \psi \)) and \(M|_{\varphi \wedge [\varphi ]\psi },s\models \lnot \chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models \psi \) and \(M|_{\varphi \wedge [\varphi ]\psi },s\models \lnot \chi \)
(An\(\lnot \)An):  :
:
\(M,s\models [\varphi ]\lnot [\psi ]\chi \)
iff \(M,s\not \models \varphi \) or \(M|_\varphi ,s\models \lnot [\psi ]\chi \)
iff \(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and \((M|_\varphi )|_\psi ,s\models \lnot \chi \))
iff [by classical logic]
\(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and (\(M|_\varphi ,s\not \models \psi \) or \((M|_\varphi )|_\psi ,s\models \lnot \chi \)))
And:

iff \(M,s\not \models \varphi \) or 
iff \(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and \(M|_\varphi ,s\models [\psi ]\lnot \chi \))
iff \(M,s\not \models \varphi \) or (\(M|_\varphi ,s\models \psi \) and (\(M|_\varphi ,s\not \models \psi \) or \((M|_\varphi )|_\psi ,s\models \lnot \chi \)))
And for the negated formulas:
\(M,s\models \lnot [\varphi ]\lnot [\psi ]\chi \)
iff \(M,s\models \varphi \) and \(M|_\varphi ,s\models [\psi ]\chi \)
iff \(M,s\models \varphi \) and (\(M|_\varphi ,s\not \models \psi \) or \((M|_\varphi )|_\psi ,s\models \chi \))
iff [by classical logic]
\(M,s\models \varphi \) and (\(M|_\varphi ,s\not \models \psi \) or (\(M|_\varphi ,s\models \psi \) and \((M|_\varphi )|_\psi ,s\models \chi \)))
And:

iff \(M,s\models \varphi \) and 
iff \(M,s\models \varphi \) and ( or \(M|_\varphi ,s\models \lnot [\psi ]\lnot \chi \))
or \(M|_\varphi ,s\models \lnot [\psi ]\lnot \chi \))
iff \(M,s\models \varphi \) and (\(M|_\varphi ,s\not \models \psi \) or (\(M|_\varphi ,s\models \psi \) and \((M|_\varphi )|_\psi ,s\models \chi \))) \(\square \)
Proof (Proposition 11)
This is a quite straightforward proof by structural induction on \(\chi \).
I.H.: If \(\chi '\) is a proper subformula of \(\chi \) and \(\psi \equiv \varphi \), then \(\chi '\equiv \chi '[\psi /\varphi ]\).
Base case: \(\chi =p\). Assume \(\varphi \equiv \psi \). Then, if \(\varphi =p\), we have that \(\chi \equiv p\equiv \varphi \equiv \psi \equiv \chi [\psi /\varphi ]\).
Now, for all cases (including the base case) there are two trivial possibilities: \(\varphi \) is not a subformula of \(\chi \), and \(\chi =\varphi \). In this cases the result is evident, so in the step we will cover the other cases. Now we look at each case based on the structure of \(\chi \) (\(\psi \equiv \varphi \) is always assumed):
\(\chi =\delta \wedge \gamma \). For all models M and states s, \(M,s\models \delta \wedge \gamma \) iff \(M,s\models \delta \) and \(M,s\models \gamma \) iff (by I.H., \(\delta \equiv \delta [\psi /\varphi ]\) and \(\gamma \equiv \gamma [\psi /\varphi ]\)) \(M,s\models \delta [\psi /\varphi ]\) and \(M,s\models \gamma [\psi /\varphi ]\) iff \(M,s\models \delta [\psi /\varphi ]\wedge \gamma [\psi /\varphi ]\) iff \(M,s\models (\delta \wedge \gamma )[\psi /\varphi ]\). So, \(M,s\models \chi \) iff \(M,s\models \chi [\psi /\varphi ]\). By analogous reasoning we obtain \(M,s\models \lnot \chi \) iff \(M,s\models \lnot \chi [\psi /\varphi ]\), and therefore \(\chi \equiv \chi [\psi /\varphi ]\).
\(\chi =[\delta ]\gamma \). Since \(\varphi \equiv \psi \), and by I.H. \(\delta \equiv \delta [\psi /\varphi ]\) and \(\gamma \equiv \gamma [\psi /\varphi ]\), we have that for all models M and states s, \(M,s\models \delta \) iff \(M,s\models \delta [\psi /\varphi ]\) and \(M,s\models \gamma \) iff \(M,s\models \gamma [\psi /\varphi ]\). Now \(M,s\models [\delta ]\gamma \) iff \(M,s\not \models \delta \) or \(M|_\delta ,s\models \gamma \). Since \(\delta \equiv \delta [\psi /\varphi ]\) and \(\gamma \equiv \gamma [\psi /\varphi ]\), we get that \(M,s\not \models \delta \) or \(M|_\delta ,s\models \gamma \) iff \(M,s\not \models \delta [\psi /\varphi ]\) or \(M|_{\delta [\psi /\varphi ]},s\models \gamma [\psi /\varphi ]\) iff \(M,s\models [\delta [\psi /\varphi ]]\gamma [\psi /\varphi ]\) iff \(M,s\models ([\delta ]\gamma )[\psi /\varphi ]\). And \(M,s\models \lnot [\delta ]\gamma \) iff \(M,s\models \delta \) and \(M_\delta ,s\models \lnot \gamma \) iff \(M,s\models \delta [\psi /\varphi ]\) and \(M|_{\delta [\psi /\varphi ]},s\models \lnot \gamma [\psi /\varphi ]\) iff \(M,s\models (\lnot [\delta ]\gamma )[\psi /\varphi ]\). So \(\chi \equiv \chi [\psi /\varphi ]\). (Note that the reduction validities of Proposition 10 are not used to prove this result.)
The cases for \(\chi =\lnot \delta \),  and \(\chi =\Box _i\delta \) are also quite straightforward, so we skip them. \(\square \)
and \(\chi =\Box _i\delta \) are also quite straightforward, so we skip them. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Santos, Y.D. A Four-Valued Dynamic Epistemic Logic. J of Log Lang and Inf 29, 451–489 (2020). https://doi.org/10.1007/s10849-020-09313-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-020-09313-8






 .
. .
.



 :
: 

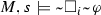 iff
iff  iff for all t such that
iff for all t such that 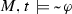 , whereas
, whereas