Abstract
We provide a computational model of semantic alignment among communicating agents constrained by social and cognitive pressures. We use our model to analyze the effects of social stratification and a local transmission bottleneck on the coordination of meaning in isolated dyads. The analysis suggests that the traditional approach to learning—understood as inferring prescribed meaning from observations—can be viewed as a special case of semantic alignment, manifesting itself in the behaviour of socially imbalanced dyads put under mild pressure of a local transmission bottleneck. Other parametrizations of the model yield different long-term effects, including lack of convergence or convergence on simple meanings only.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inconsistencies are commonplace in linguistic interactions. Participants can disagree about the truth-value of a sentence, or about the reference of an expression in a given context. Such inconsistencies can be rooted in pragmatics, lack of common ground, perceptual differences, or other non-semantic factors. However, certain misalignments are clearly of a semantic nature.
Discrepancies in meaning naturally occur throughout the process of language acquisition and in second-language learning. Their treatment is also crucial when considering language origins and language evolution. However, variation in meaning is often present among adults speaking the same language (e.g., when they are forced to collaboratively solve a problem for which they have few or no precedents; see Garrod and Anderson 1987; Garrod and Doherty 1994; Mills and Healey 2008 for evidence in experimental psychology of dialogue). The preexisting individuated meanings, however, are also subjected to variation, even in the case of allegedly primitive and frequently used expressions (Brown et al. 2016; Schober 2004).
Inconsistencies occurring in linguistic interaction are sometimes bearable or even desirable, depending on the goal of the communicative encounter (Fusaroli et al. 2014). However, in many contexts it is beneficial to share semantics: when there is pressure for efficient communication (Garrod and Anderson 1987) or willingness to be identified as a member of a group (Labov 2001). Whatever the reasons, experiments show that participants are capable of reliable and efficient removal of inconsistencies whenever required (Garrod and Anderson 1987; Garrod and Doherty 1994). To explain this behaviour, a fully fleshed-out model of interactive semantic alignment is in order (Pickering and Garrod 2004).
Building upon our earlier work (Kalociński et al. 2015; Kalociński 2016), in this paper we propose a model of semantic alignment in a population of communicating agents. Each agent is assumed to assign a meaning to a given expression. Through the process of semantic alignment, triggered by disagreements in communication, agents autonomously adjust their individual meanings to fit those of other participants. As a case study, we choose to focus on semantic constructions corresponding to quantifier expressions. Mathematical, linguistic, and even psychological aspects of quantifiers are well studied and relatively easy to capture in a computational model.
In the next section, we describe our model in more detail against the background of existing approaches to language learning and language evolution. In Sect. 3, we present the interactive semantic alignment model in its generic form. In Sect. 4, we focus on modelling semantic coordination in isolated dyads. We choose a particular space of meanings, simplicity ordering and stimuli which occur during interactions. We also discuss two main parameters: social influence and a local transmission bottleneck. In Sect. 5, we test the model by investigating how various settings of parameters affect plausibility and effectiveness of semantic coordination of quantifiers. We conclude in Sect. 6 and outline some future directions in Sect. 7.
2 Related Work
In modelling language acquisition it is often assumed that the semantic system of adults is fixed and the burden of alignment falls on children (Piantadosi et al. 2012; Frank et al. 2007). A similar assumption is also at the heart of many formal approaches to learning semantics, not necessarily concerned with acquisition (Gierasimczuk 2007; Clark 2010). On this view, the teacher determines the standard form-meaning associations which are gradually unveiled to the learner through language use. The learner probes incoming linguistic input, usually consisting of expression-referent pairs, and induces a system of general rules for capturing the prescribed associations. Under this classical view, it is assumed that the teacher does not change their language throughout learning. Moreover, a successful learner is conceived as the one who is able to eventually infer the target language. We shall use the term learning by recognizing to refer to such models.
The assumptions of learning by recognizing do not always translate straightforwardly to other scenarios, for example, to the case of the communication between two competent speakers, where the roles are not clearly dichotomized into that of the leader and that of the follower. Even though in such cases keeping or abandoning one’s own semantics is harder, as long as alignment is valuable to participants, we should expect that both parties will attempt to align their meanings. The lack of social dichotomy may also invalidate another assumption usually implicitly inscribed in modelling: the unalterability of the standard form-meaning associations (with the notable exception of optimality-theoretic semantics Hendriks and Hoop 2001). Semantic representations of interacting agents may change in parallel, as a result of simultaneous alignment (Garrod and Anderson 1987).
The traditional approach to learning is less common in research on language evolution. For example, in collaborative models of semantic alignment, agents’ linguistic representations are subject to change in local language games (Steels and Belpaeme 2005; Puglisi et al. 2008; Pauw and Hilferty 2012). A language game can ‘fail’ in many different ways, and such ‘failures’ usually trigger various repair mechanisms which have potential to alter agents’ cognitive states. Simulations reveal that after a sufficient number of linguistic interactions, agents’ idiosyncratic languages align (Steels 2011). Another difference with learning by recognizing is that collaborative models usually treat agents as equal. Sociolinguistic factors have been investigated in studies of non-semantic levels of linguistic representation. One of the first models in this vein explains how an initially unpopular linguistic expression may eventually become dominant within a population (Nettle 1999). The utterance selection model describes the mechanisms of grammatical change and explicitly introduces modulation of grammatical alignment by social influence (Baxter et al. 2006). A similar model has been used to explain the emergence of dialects (Blythe et al. 2016). A recent Bayesian model treats learning simple grammatical distinctions, contrasting extreme cases of social impact where an agent learns equally from everyone in the population or learns preferentially from one individual (Smith et al. 2017). Various social hierarchies have been investigated in grammatical alignment (Gong 2009). On a more abstract level, social networks have been proven to bootstrap learning in cooperative games (Kosterman and Gierasimczuk 2015).
Certain semi-formal models of semantic alignment have been proposed to account for patterns observed in experimental dialogues. For example, the output-input coordination model (Garrod and Anderson 1987) puts forward that a participant will try to match their linguistic representations, including semantics, to those used most recently by their partner. Another influential approach is the interactive alignment model where coordination of linguistic representations proceeds through a largely automatic priming mechanism (Pickering and Garrod 2004). Interestingly, Garrod and Anderson hint at a possible sociolinguistic phenomenon allowing interlocutors in dialogue to switch between different semantic representations. According to their view, one way of achieving this is through adopting asymmetrical roles of leader and follower. The research on non-verbal communication systems evolved by coordination within the Tacit Communication Game is also worth mentioning here (Blokpoel et al. 2012).
Another line in language evolution research is iterated learning—an individualistic model of cultural transmission across generations (Kirby and Hurford 2002; Kirby et al. 2014). Here, a variant of social influence is more evident. In its basic form, language evolution is modelled as a chain of multiple teacher-learner scenarios. At any given link of the chain, the follower acquires language by observing their partner, and becomes the teacher for the next individual, and so on. Clearly, iterated learning inherits an important assumption from the learning by recognizing paradigm—the dichotomy between the leader and the follower. Because iterated learning is primarily designed to model cultural transmission and thus each link in the chain represents a single acquisition episode, this assumption seems to be justified. Crucially, though, unlike learning by recognizing, iterated learning does not require that the learner adopts precisely the same language as the teacher. Quite the opposite—learning is imperfect due to transmission bottleneck and cognitive biases of learners. The importance of these factors, though manifesting at a different time-scale, resonates in our model.
Finally, let us mention one aspect in which our model is restrictive when compared to the work in language evolution. Unlike in the case of signalling games (Lewis 1969; Skyrms 2010), where a whole system of signals is coordinated, here we consider the alignment of a single meaning at a time. The optimality of the signal in our case does not depend on other signals, but rather on various agent-based assumptions. This significantly simplifies the analysis and allows to look closer at the isolated phenomena related to the social and cognitive aspects.
Our model steers away from learning by recognizing in the sense that social stratification is one of the model parameters. This allows us to obtain the standard teacher/learner dichotomy, as well as other social structures. Moreover, semantic coordination, instead of being performed unilaterally, is a universal strategy employed autonomously by all agents. None of the agents are privileged to keep their semantic representations constant, and this brings our approach closer to the collaborative models of language evolution. Another common point with collaborative models and with iterated learning, is the incorporation of a local variant of the transmission bottleneck. The bottleneck is realized by narrowing agents’ perception to the current interaction, which allows them to test their semantic representations against a small portion of the environment only. This constraint seems to play an important role in shaping our language by promoting simplicity and ease of processing (Christiansen and Chater 2016).
Crucially, the exact workings of alignment are modulated by the perceived social ranks of the interlocutors and by the input collected during interaction. As such, the alignment mechanism is generic in the sense that it should be universal over different social structures and interaction topologies, thus allowing to implement, for example, diffusion chains or random pairwise interactions. In this paper, we focus on dyadic interactions and the influence of social stratification and local transmission bottleneck on semantic alignment in the case of quantifiers.
3 Semantic Alignment Model
In what follows, a population is a finite set denoted by A. To reflect the relative social standing of agents, we assume that each \(a \in A\) is equipped with an authority function \(w_a: A \rightarrow {\mathbb {R}}\). Given two agents, \(a, b \in A\), the intuitive sense of \(w_a(b)\) is that a perceives b as having the authority equal to \(w_a(b)\), whereas \(w_a(a)\) reflects how much weight agent a assigns to its own opinion. This framework allows us to analyze various configurations of authority and their influence on alignment.
We use the notion of authority rather loosely. We treat it as a technical term which may stand for various real-world variables. For example, in some circumstances, social impact can be measured by age, affiliation, social status, to mention just a few. A seminal work exploring the role of social factors in language is Labov (2001).
We use H to denote the set of meanings from which agents may choose their current hypotheses. At this level of abstraction, we do not specify what those meanings are. However, to ascertain that they carry a semantic content, we posit that there is a set C of (all possible) external stimuli and that each \(h \in H\) is a mapping \(h: C \rightarrow \{0,1\}\). Under this general assumption, each hypothesis classifies stimuli to examples and non-examples. To link this with linguistic reality, one may think about each hypothesis \(h \in H\) as one of possible meanings of a sentence that makes it either true or false in a given situation \(c \in C\).
To introduce cognitive bias towards simple meanings, we assume that H is ordered: for \(x,y \in H\), \(x \preceq y\) means that x is simpler than or as simple as y. We posit the same simplicity ordering for all agents. This is justified as long as agents are equipped with similar cognitive capacities. For a more fine-grained discussion on the abstract notion of simplicity, relevant in the context of language learning, see, for example, (Baltag et al. 2011, 2015).
A typical cognitive structure for representing semantics is an associative map between expressions and meanings (see, e.g., Steels and Belpaeme 2005). Each connected pair is assigned a weight designating the strength of the coupling. We approach this in a more simplistic way. In our case, at any given stage t, each agent has one preferred meaning which it effectively uses while communicating with others.
At the population level, this is described by a function \(s_t: A \rightarrow H\). We refer to \(s_t\) as a synchronic description at stage t. Using this notation, \(s_t(a)\) is the meaning that agent a uses at stage t. We assume that each agent is acquainted only with its own semantics, not the semantics of others and has no metalinguistic abilities for explicit meaning negotiation. There are experimental data suggesting that explicit negotiation in spontaneous interaction is rare and does not give rise to stable conventions (Garrod and Anderson 1987).
Evolution of meaning proceeds in discrete steps \(t =0,1,2,\ldots \), each comprising two stages: interaction and alignment. First comes the interaction stage where several interactions are realized. A single interaction is represented by (a, b, n, v), where a, b, n are speaker, hearer and a shared stimulus, respectively, whereas v is the response of a for stimulus n according to a’s current hypothesis, namely \(v = s_t(a)(n)\).
During alignment, each agent uses an input comprising exactly those interactions in which it plays the role of the hearer. Moreover, only the most recent interaction stage is taken into consideration. This is how the local transmission bottleneck enters the model (Christiansen and Chater 2016).
We represent the input by providing separate lists of stimuli \(r_1, r_2, \ldots , r_m \in C\) and speakers’ responses \(v_1, v_2, \ldots , v_m \in \{0,1\}\). Instead of giving the list of the speakers, we provide their corresponding authorities \(w_1, w_2, \ldots , w_m\). For example, given that interactions \((a,b,n_1,v_1),(a,b,n_2,v_2), (b,a,n_1,v_3)\) have been realized at the interaction stage and assuming that b perceives a as having authority w (i.e., \(w_b(a) = w)\), the input for agent b comprises three lists: stimuli \(n_1,n_2\), responses \(v_1,v_2\) and authorities w, w. Supposing that \(w_a(b)= w'\), the input for agent a is: \(n_1\) (stimulus), \(v_3\) (response) and \(w'\) (authority).
Crucially, apart from external inputs, an aligning agent relies on its own characteristics which include self-authority \(w_0\) and current hypothesis \(h_0\). Intuitively, self-authority is to reflect the agent’s resistance to external influences. In practice, self-authority can make an agent keep to its current hypothesis \(h_0\), provided that external influences are not too high when compared to \(w_0\).
An important idea behind alignment is the concept of the reward associated with a given hypothesis. Intuitively, given an aligning agent, the value of the reward function for a hypothesis h is to measure how successful the agent would be if it adopted h during the most recent interaction stage.
Suppose \(r_1,\ldots ,r_m\), \(v_1,\ldots , v_m\) and \(w_1,\ldots ,w_m\) is the input for an agent with self-authority \(w_0\) and current hypothesis \(h_0\). Given an arbitrary \(h \in H\), let \({\overline{z}} = z_1,z_2, \ldots , z_m\) be a binary sequence such that \(z_j = 1\) iff \(h(r_j) = v_j\), for \(j=1,2,\ldots ,m\). The value of \(z_j\) indicates whether there is agreement between the response given by the speaker for stimulus \(r_j\) and the output of h for the same stimulus. If we add all \(z_j\), we obtain the number of interactions in which the aligning agent would be successful, provided it used h as its current hypothesis. Such a cumulative reward is a measure of fitness of h to a particular set of interactions. However, mere summing does not rely on social factors modelled by \(w_1,\ldots ,w_m\). Hence, we rather take a weighted cumulative reward (henceforth, reward), modulated additionally by self-authority and current hypothesis:

Observe that if all agents have authority 1, the reward of h is simply the number of successful interactions that a would participate in as the hearer, provided it used h. Additionally, if h is equal to the current hypothesis of a, the reward is increased by the value \(w_0\) to reflect the fact that a is to some extent independent from external social influences.
Full details of the alignment operator are presented in Algorithm 1. The intuitive idea behind alignment is as follows: an agent chooses the simplest hypothesis that would guarantee them maximal reward in interactions from the interaction stage.

Let us briefly go through the alignment operator. The aligning agent computes the reward for every \(h \in H\) (lines 1–6). This amounts to computing, for each h, which interactions would be successful, if it used h in the interactions given by the input (lines 2–4) and assigning a reward to h (line 5). Next, the aligning agent considers only those hypotheses that have the highest value of the reward function (line 7). The agent rejects excessively complicated hypotheses (line 8) and, finally, changes its current semantics to a random hypothesis from what is left (line 9). We assume that the probability of drawing an element from M such that \(|M| = k\) equals \(\frac{1}{k}\).
At the macro-level, the evolution of semantics may be represented as a sequence of synchronic descriptions \(s_0,s_1,s_2, s_3, \ldots \). During the interaction stage at timestep \(t=0,1,2,\ldots \), agents use their current hypotheses, given by \(s_t\), and then each of them aligns (Algorithm 1) using its own input. This yields synchronic description \(s_{t+1}\).
4 Modelling Dyadic Interactions
In the present work, we focus on the most fundamental and simple interactions performed within dyads. Dyads are assumed to be static in the sense that agents are not replaced during learning. Restriction to dyads allows us to observe whether the model works as expected in the basic communicative setting. Moreover, this section gives all the details which were left unspecified in Sect. 3, namely hypotheses and simplicity ordering. We also comment on crucial parameters (i.e., social impact and local transmission bottleneck).
It would be convenient to keep in mind a simple scenario. Imagine two agents interacting with each other. Upon interaction, several balls are drawn from an urn containing black and white balls. Agents look at the balls and announce that Blarg balls are white or It is not the case that blarg balls are white. It is assumed that the meaning of blarg is the only source of problematic understanding. Misalignment manifests itself when agents assert different statements against the same set of balls (one thinks that Blarg balls are white whereas the other that It is not the case that blarg balls are white). After announcement, agents update their understanding of what blarg means based on what they hear. In the next sections, we gradually formalize this scenario and analyze how dyads align for different sets of parameters.
4.1 Meanings
To keep our considerations simple and close to linguistic reality, we choose a small subset of proportional quantifiers as meanings. The prominent example of everyday language quantifier interpretable in this way is the English most. However, some and all can also be interpreted in this way.
Let us pinpoint the concept of proportional quantifiers in a precise way. Consider a 1-place predicate R(x) saying x is white. Now, a finite structure (D, R) corresponds to a particular set of balls \(D \ne \emptyset \) drawn from an urn with \(R \subseteq D\) indicating which of the balls in D are white. In model-theoretic semantics, it is common to identify quantifiers with classes of models which are mathematical abstractions of reality. This idea leads to the notion of a generalized quantifier (Mostowski 1957; Lindström 1966). For our current purposes, we can think of a generalized quantifier as an isomorphism-closed class of finite structures (D, R).Footnote 1
Definition 1
A generalized quantifier \({\mathcal {Q}}\) is proportional if there is a rational number \(h \in [0,1]\) and a relation \(\star \in \{<,\le , >, \ge \}\) such that for every structure (D, R):
Let us see how this definition works for most, some and all. One of the conventionalized meanings of most corresponds to \(h = \frac{1}{2}\) and \(\star = \,>\). Suppose that d balls have been drawn from an urn with \(r \le d\) balls being white. This situation is described by a structure (D, R) with \(|D| = d\) and \(|R| = r\). Now, \((D,R) \in most\) (i.e., most balls are white) iff \(\frac{r}{d} > \frac{1}{2}\). Similarly, some corresponds to \(h = 0\) and \(\star = \,>\): \((D,R) \in some\) iff \(\frac{r}{d} > 0\). Finally, all corresponds to \(h = 1\) and \(\star = \, \ge \): \((D,R) \in all\) iff \(\frac{r}{d} \ge 1\).
In our analysis, we largely stick to the three quantifiers described above. For notational simplicity we refer to such a space of meanings by \(H = \{0,\frac{1}{2},1\}\), leaving out the information about \(\star \)—one should only bear in mind that 0, \(\frac{1}{2}\) and 1 correspond to some, most and all, respectively.
4.2 Cognitive Simplicity
So far, we have treated meanings purely extensionally. Extension divides situations into two kinds: examples and non-examples. For instance, the meaning of a sentence divides situations into those in which the sentence is true and those in which it is false. However, this approach is not free from caveats, particularly when viewed from the cognitive perspective. Therefore, we adopt a refined view on semantics according to which the meaning of an expression may be identified with an algorithm for computing its extension (Tichý 1969) (for a broader discussion, see also Szymanik 2016). To see how this view applies to our case, consider verification of the quantifier most against finite situations. We say an algorithm computes most if for every structure (D, R), the computation of the algorithm on input (D, R) outputs the correct answer to the query \(\frac{|R|}{|D|} > \frac{1}{2}\).
The algorithmic approach to meaning proved to give quite robust predictions concerning cognitive difficulty of verification and reasoning with natural language constructions, including quantifiers (Mostowski and Wojtyniak 2004; Gierasimczuk and Szymanik 2009; Gierasimczuk et al. 2012; Szymanik 2016). For example, experiments show that the most quantifier engages working memory, as predicted by the computational model (Szymanik and Zajenkowski 2010). On the contrary, some and all do not require additional memory resources, which is explained by the fact that those quantifiers are recognized by finite automata (Benthem 1986), computational devices without additional memory.
The above considerations allow us to formulate the simplicity ordering which we use throughout the paper. We assume that some and all are equally simple and that they both are strictly simpler than most. Thus, using \(0, \frac{1}{2}, 1\) for the quantifiers and \(\preceq \) for the simplicity ordering, we have: \(0 \preceq 1\), \(1 \preceq 0\), \(0 \preceq \frac{1}{2}\), \(\frac{1}{2} \not \preceq 0\), \(1 \preceq \frac{1}{2}\), \(\frac{1}{2} \not \preceq 1\).
The restriction to some, most and all is a major one used in this paper. Crucial comparisons of different parametrizations of the semantic alignment model developed in Sect. 5 are based on this restriction. However, one may envisage a more comprehensive sets of hypotheses. For example, consider a set of proportional quantifiers corresponding to so-called Farey fractions belonging to the Farey sequence of order k, denoted by \(F_k\). \(F_k\), for \(k > 0\), is defined as the set of completely reduced fractions from [0, 1] with denominators not exceeding k. For instance, \(F_3 = \{0,\frac{1}{3},\frac{1}{2},\frac{2}{3},1\}\). When considering \(F_k\) as sets of hypotheses, we will take \(\star = \,>\) in Definition 1 for \(h < 1\) and \(\star = \, \ge \) for \(h = 1\). Consequently, we will be able to identify H with a particular Farey sequence \(F_k\).
When considering a more comprehensive set of hypotheses \(H = F_k\), we posit that the simplicity ordering is defined as follows: \(\frac{a}{b} \preceq \frac{c}{d} \Leftrightarrow b \le d\), for all completely reduced fractions \(\frac{a}{b}, \frac{c}{d} \in F_k\). This ordering contains the already assumed ordering for \(H = F_2 = \{0,\frac{1}{2},1\}\) and matches the cognitive reality to the extent that 0 and 1 are still minimal. However, the assumed ordering predicts that the denominator has a major influence on the cognitive difficulty of verification of a proportional quantifier. We treat it only as a tentative assumption. To the authors’ knowledge, no empirical account of quantifier comprehension has investigated relative difficulty of verification between various proportional quantifiers.Footnote 2
4.3 Stimuli
The result of drawing several black and white balls from an urn is easily represented by a finite structure (D, R), where D is the set of the drawn balls and \(R \subseteq D\) indicates which of them are white. Note, however, that using (D, R) is superfluous. All we need to verify a proportional quantifier against (D, R) is the proportion \(\frac{|R|}{|D|}\). Hence, we represent the set of the drawn balls by a fraction from [0, 1]. Clearly, this can be done without loss of generality because a single proportional quantifier cannot tell the difference between two structures (D, R) and \((D',R')\) satisfying \(\frac{|R|}{|D|} =\frac{|R'|}{|D'|}\).
On many occasions, contexts we encounter during interactions are unpredictable. Hence, we envisage stimuli as random deviates of a fixed random variable X assuming values in [0, 1]. Discrete random variables are sufficient for our purposes (in general, one may consider continuous random variables supported on [0, 1]). In what follows, when a particular choice of a random variable is needed, we take \(X \sim B(10,0.5)\), which means that each stimulus obtained from X is the result of ten Bernoulli trials with the probability of success (say, drawing a white ball) equal to 0.5 (see, e.g., Feller 1968). Choosing Bernoulli distribution is not entirely arbitrary because it is approximated by normal distribution which describes behaviour of many natural properties.
4.4 Social Impact
In the present account, we investigate positive authority functions. Additionally, we require that for every \(a,b,c \in A\), \(w_a(c) = w_b(c)\). Hence, we may assume that there is only one authority function \(w: A \rightarrow {\mathbb {R}}_+\) which specifies social impact for each agent in the population. Another implicit assumption is that w does not change during interaction.
Taking just one objective authority function corresponds to a situation where interacting agents perceive their social ranks in a similar way. This choice is not overly restrictive for our purposes because it allows to introduce equality as well as dichotomy between agents. This is enough to check in what ways (if at all) teacher-learner and peer-to-peer interactions differ, provided that social influence is stable and does not change during interaction.
4.5 Interaction and Local Transmission Bottleneck
We keep faithful to our original example of a dyad using blarg and assume that both interlocutors respond to any stimulus occurring during interaction (symmetry assumption). We envisage that interlocutors can share a number of stimuli before alignment begins. The overall number of shared stimuli per interaction stage is denoted by n and constitutes one of the model parameters. Observe that by the symmetry assumption, if \(r_1,r_2,\ldots ,r_n\) are shared stimuli then there are 2n interactions because each \(r_i\) occurs in two interactions, namely \((a,b,r_i,v_i)\) and \((b,a,r_i,v_{i}{'})\). We shall refer to n as the local transmission bottleneck.
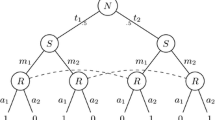
How many stimuli and responses should be directly accessible at the interaction stage before alignment? In principle, one could allow agents to monitor all past experience and give them access to all stimuli and responses they have encountered through their lifetimes. However, this does not sound like a realistic option, particularly in the presence of the “now-or-never” bottleneck: data occurring in a typical linguistic interaction are quickly obliterated by new incoming material and only a small portion of it can be effectively stored and used for processing (Christiansen and Chater 2016). Hence, we take a minimalistic approach and assume that just a few stimuli and responses occur during the interaction stage prior to alignment (Fig. 1, illustrates the case for n = 1).
5 Testing the Model
We set out to test the semantic alignment model (Sect. 3). One of the crucial questions is whether the model encompasses traditional individualistic learning as its special case. We approach this question by looking for appropriate values of model parameters to obtain the desired behaviour. Differentiation of agents’ authorities and the size of the local transmission bottleneck will be of particular importance. We also check whether other parametrizations of the model yield different results and if so in what ways they are different. This should generate predictions of the model for the communicative scenarios which are unlike traditional learning. Specifically, we consider two conditions.
- Authority Condition :
-
interacting agents are dichotomized as in the traditional teacher-learner scenario. This is operationalized by setting the authority function to make agents differ significantly with respect to social impact (\(w_1 > w_2\)).Footnote 3 In absence of this condition, agents assume similar authorities (\(w_1 = w_2\)).
- Bottleneck Condition :
-
agents interact having direct access to a minimal number of stimuli per interaction (\(n=1\)). In the absence of this condition, local transmission bottleneck assumes greater values (\(n=2\)).Footnote 4
Before we proceed to modelling different conditions, let us put all pieces of the model together. In what follows, we assume that \(A = \{ 1,2 \}\) and \(H=\{0,\frac{1}{2},1\}\) (occasionally, a more general space of meanings is used, namely \(H = F_k\)) where 0, \(\frac{1}{2}\) and 1 correspond to some, most, and all, respectively. The simplicity ordering is given in Sect. 4.2. Given n, we have 2n interactions before alignment begins (see Sect. 4.5).
5.1 Semantic Alignment as a Markov Chain
At this point, it is not obvious how the semantics evolve according to our model and how they are affected by various parameters. We approach this problem by providing a Markov chain representation.Footnote 5
Recall that at a given timestep t, agents interact with each other using their current hypotheses which are collectively represented by the synchronic description \(s_t: A \rightarrow H\). Then, each agent takes the data from the current interaction stage as input and updates its hypothesis by running the alignment operator (Algorithm 1). This results in a new synchronic description \(s_{t+1}: A \rightarrow H\). Observe that \(s_{t+1}\) depends only on \(s_t\) and the data obtained by the agents during the most recent interaction stage. Hence, the evolution of meaning implied by our model is a memoryless process—the past is irrelevant for the current behaviour of the system. Discrete-time Markov chains are well suited to describe this kind of process (Feller 1968) (see, also, Kemeny and Snell 1960).
One way of defining a Markov chain is to specify a set S of all possible states of the system and a stochastic matrix \([p_{ss'}]_{s,s' \in S}\) of transition probabilities.Footnote 6 A stochastic matrix is a square matrix of non-negative reals such that each row sums up to 1. The transition probability \(p_{ss'}\) is to measure the likelihood that the state of the system changes from s to \(s'\) in one step. We give an example of such a system in Fig. 2, which illustrates a three-state Markov chain of a very simple model describing the probabilities of weather conditions given the weather for the preceding day.
We posit that the set of states S is the set of all synchronic descriptions, namely all functions from A to H or, equivalently, all |A|-tuples assuming values in H. Given \(s,s' \in S\), the value \(p_{ss'}\) designates the probability that the synchronic description changes from s to \(s'\) in one step (i.e., after a single interaction stage followed by alignment).
Before we proceed further, let us fix some notation. We write s(1)s(2) to designate the state \(s \in S\). For example, the state s such that \(s(1) = 0\) and \(s(2) = \frac{1}{2}\) is designated by \(0 \frac{1}{2}\). The transition probability from s to \(s'\), normally denoted by \(p_{ss'}\), is written as \(p_{s(1)s(2) \rightarrow s'(1)s'(2)}\). For example, the transition probability from the state s such that \(s(1) = 0\) and \(s(2) = \frac{1}{2}\) to the state \(s'\) such that \(s'(1) = 1\) and \(s'(1) = 1\) is designated by \(p_{0 \frac{1}{2}\rightarrow 1 1}\). Let \(x x'\), \(y y'\), \(z z'\) be states. If \(p_{x x' \rightarrow y y'} = p_{x x' \rightarrow z z'} = p\), we write \(p_{xx'\rightarrow yy' | zz'} = p\) to denote the conjunction of \(p_{xx'\rightarrow yy'} = p\) and \(p_{xx' \rightarrow zz'}=p\).
In what follows, we analyze various conditions thoroughly by providing Markov chains that completely and accurately describe how such systems evolve. A more detailed explanation of proofs is contained in a separate technical appendix (Kalociński 2018b).
5.2 Bottleneck-only Condition
Under the Bottleneck-only Condition, the Bottleneck Condition holds but the Authority Condition is absent. This is operationalized by setting \(w_1=w_2 > 0\) and \(n=1\).
Theorem 1
Let \(A = \{1,2\}\), \(H = F_k\), for \(k \ge 1\), \(w_1=w_2 > 0\) and \(n=1\). Let X be a random variable assuming values in [0, 1] with a probability function P. Then, the model is represented by the Markov chain on \(S = H^2\) induced by the following probabilities:
Proof
A careful determination of all probabilities is a lengthy process which we describe in a separate document (Kalociński 2018b). Here, we show in detail how to calculate transitions for \(u=0\) and \(v=1\).
Let \(uv \in H^2\) be a synchronic description. Let us denote by \(M^{uv}_{a,r \in E}\) the set of hypotheses for which the value of the reward function computed relative to agent \(a\in \{1,2\}\), the state \(uv \in H^2\), and the stimulus \(r \in E \subseteq [0,1]\), is maximal. Let us consider all possible arrangements of the stimulus r that may affect the value of the reward function. These arrangements are: (i) \(r=0\), (ii) \(0< r < 1\) and (iii) \(r =1\).
We need to carefully work through the alignment operator (Algorithm 1).
Let us compute \(M^{01}_{1,r \in (0,1)}\). The situation is visualized in Fig. 3.
The horizontal line is [0, 1]. We have a stimulus \(r \in (0,1)\). The semantics of agent 1 is \(s(1)=0\) and that of agent 2 is \(s(2)=1\). Rewards for hypotheses \(h \in H \subset [0,1]\) (relative to agent 1) are described above the horizontal line. Below we show that in this situation, the reward equals (i) w for \(h = 0\), (ii) 0 for \(0< h < r\), and (iii) w for \(h \ge r\), where \(w = w_1=w_2\).
Case (i) Suppose agent 1 used \(h=0\). It would not agree with agent 2, whose answer is negative (because it is not the case that \(r \ge s(2)=1\)), whereas the answer of agent 1 would be positive (because \(r > h = 0\)). According to Algorithm 1, the reward relative to an agent for a given hypothesis is not increased by the interlocutor’s authority when they disagree. However, \(h=0\) is the current hypothesis of agent 1, so the reward for h is promoted by the authority of agent 1, namely \(w_1\), as indicated in Fig. 3.
Case (ii) Suppose that agent 1 used h such that \(0< h < r\). Agent 1 would not agree with agent 2 for the same reason as in the case (i). Hence, the reward for h is not incremented by the authority of its interlocutor. The value of h is not promoted by the authority of agent 1 either, since \(h \ne s(1) = 0\). Therefore, the reward for h is 0.
Case (iii) Suppose that agent 1 used \(r \le h \le 1\). Agent 1 would agree with agent 2, since the answer of agent 1 would be negative (because it is not the case that \(r > h\)). So the reward for h is increased by the authority of agent 2, namely \(w_2\). Since \(h \ne s(1) = 0\), the reward for h is not further promoted by the authority of agent 1. Hence, the reward for h is \(w_2\).
We have just proven that \(M^{01}_{1,r \in (0,1)} = \{0\}\cup \{h \in H: h\ge r\}\). In a similar way, we prove that \(M^{01}_{1,r=0} = \{0\}\), \(M^{01}_{2,r=0} = \{1\}\), \(M^{01}_{2,r \in (0,1)} = \{h \in H: h < r\}\cup \{1\}\), \(M^{01}_{1,r=1} = \{0\}\) and \(M^{01}_{2,r=1} = \{1\}\).
Observe that under the condition that a random variate is \(r=0\) (or \(r=1\)), agent 1 chooses 0 from \(M^{01}_{1,r=0}\) (or \(M^{01}_{1,r=1}\)) with probability 1 and agent 2 chooses 1 from \(M^{01}_{2,r=0}\) (or \(M^{01}_{2,r=1}\)) with probability 1. Under the condition that a random variate is \(0< r < 1\), agent 1 chooses either 0 or 1 as its new meaning, each alternative being equally probable. Similarly, under the same condition, agent 2 chooses randomly either 0 or 1. Observe that the events \(X=0\), \(0< X < 1\) and \(X=1\) form a finite partition of a sample space. Hence, by the law of total probability, \(p_{01 \rightarrow 01} = P(X = 0) + P(0< X < 1)/4 + P(X=1)\) and \(p_{01 \rightarrow 00 | 11 | 10} = \frac{1}{4}P(0< X < 1)\). \(\square \)
5.2.1 Comments on the Bottleneck-only Condition
By Theorem 1, agents never change to more complicated semantics. They either retain their hypotheses or change to simpler ones. What is more, the actual change to a simpler hypothesis leads always to 0 (some) or 1 (all), which are minimal under the assumed simplicity ordering. Dyads interacting under this condition cannot stabilize on semantics other than 0 or 1, unless the initial synchronic description is a constant function \(s : A \rightarrow \{u\}\), for some u such that \(0< u < 1\). This property is also readily visible in Table 1, which summarizes certain properties of the Markov chain presented in Fig. 4. Clearly, the absorption probabilities of the state \(\frac{1}{2} \frac{1}{2}\) (most-most) are all equal to 0. In linguistic terms, only some or all may emerge through alignment under this condition, whereas most is not achievable in such a model, unless most was common to every agent from the start.
Observe that the evolution of meaning in interaction may proceed in subsequent rounds in the following way: \(01,10,01,10,\ldots \). Interestingly, a similar behaviour can be observed in many everyday coordinative scenarios (not necessarily pertaining to linguistic interaction). For example, two people approaching each other from opposite directions often switch between two incorrect solutions while trying to avoid collision.
The above property of the model is reminiscent of the Lewis’ idea that conventionalized language is a solution to a coordination problem having multiple equally good alternatives (Lewis 1969). Here, (full) coordination (or a fully conventionalized language), means that both agents endorse the same meaning of a signal. When this happens, the language has already settled down and does not pose any problem to interlocutors (see next paragraph). However, if the meanings of participants are not aligned, the postulated mechanism of alignment automatically strives to achieve coordination. Although the mechanism is targeted precisely at achieving this goal, in some circumstances it fails to give satisfying results, leading agents to switch their hypotheses between two simple alternatives which at the time of alignment seem to be among the best options to choose from. The coordination problem is thus readily visible as the dynamics of the system unfolds, occasionally resulting in a series of uncoordinated behaviours.
Figure 4 presents a Markov chain for \(H = F_2\) and \(X \sim B(10,0.5)\). An interesting aspect to observe is that the resulting Markov chain is absorbing (Kemeny and Snell 1960). This means that the chain contains some absorbing states (i.e., the states that cannot be left once entered) and that there is a path from each state of the chain to some absorbing state. Hence, it is in principle possible that, finally, a dyad will attain mutual-intelligibility, no matter which state is the initial one. Therefore, in a sense, alignment under the Bottleneck-only Condition may be viewed as a variant of learning. However, it cannot be viewed as traditional learning because both agents may change their hypotheses across trials.
Looking at transition and absorption probabilities alone is not sufficient to assess the efficiency of alignment. Hence, we have calculated two additional properties of the model from Fig. 4: the expected number of steps before being absorbed, denoted by E, and associated standard deviation (Table 1). It turns out that E is relatively low because it oscillates between 2 and 3.7. Moreover, associated dispersion is equally small because SD ranges from 1.4 to 2.5. This suggests that attaining coordinated behaviour under the Bottleneck-only Condition remains within practical limits—a few problematic exchanges seem to fit time constraints of an interaction and does not require too much collaborative effort on the part of participants.
5.3 Authority-and-Bottleneck Condition
We proceed to analyse what happens if both Authority and Bottleneck Conditions hold. We set \(w_1> w_2 > 0\) and \(n=1\). The only difference from the Bottleneck-only Condition lies in making agents unequal in terms of social influence.
Theorem 2
Let \(A = \{1,2\}\), \(H = F_k\), for \(k \ge 1\), \(w_1> w_2 > 0\) and \(n=1\). Let X be a random variable assuming values in [0, 1] with a probability function P. Then, the model is represented by the Markov chain on \(S = H^2\) induced by the following probabilities:
5.3.1 Comments on Authority-and-Bottleneck Condition
Social imbalance revamps alignment in a crucial way. An important aspect to notice is that the most influential agent, unlike its partner, never changes its mind. This observation suggests that social impact affects alignment as expected. Henceforth, we use the terms leader and follower to refer to the more and the less influential agent, respectively.
Observe that, unlike in the Bottleneck-only Condition, cycles of the form \(01,10,01,10,\ldots \) are not possible. This follows from our initial observation that the leader does not change their mind. However, a different kind of cycle can appear. When the leader uses u such that \(0< u < 1\), the follower cannot catch up with them. This is readily visible in Fig. 5. Indeed, the states where the leader keeps to the more difficult meaning form a cycle. Crucially, though, these states constitute a closed class of states from which there is no escape. Hence, unlike in the Bottleneck-only Condition, the resulting Markov chain is not absorbing: if the leader uses difficult meaning, the follower can never adapt—the semantics of interlocutors diverge forever.
The above effect is partially due to the cognitive bias that pushes agents towards simple hypotheses. Observe that if agents differ in meaning and disagree on a given stimulus, then their maximum-reward hypotheses include either 0 or 1. However, these hypotheses are cognitively least effortful and thus are finally selected by the alignment operator. As we shall see in a different condition, this effect may be compromised by loosening the local transmission bottleneck.
Still though, some amount of mutual understanding is achievable. If the leader uses 0 or 1, then, eventually, the follower will adapt, accordingly. This property is readily visible in Table 2: absorption probabilities are set to one for the absorbing states matching the meaning of the leader.
Another point of interest is that convergence, if possible, seems to occur more quickly on average than in the Bottleneck-only Condition (Table 2). Moreover, the expected number of steps before being absorbed drops by 1 (Table 1). The associated dispersion diminishes as well. This suggests that social imbalance may have a positive effect on the efficiency of alignment.
5.4 Null Condition
The Null Condition corresponds to dyadic interactions where both Authority and Bottleneck Conditions are absent. This is operationalized by setting \(w_1=w_2 > 0\) and \(n=2\). We omit the representation theorem. Instead, we give a Markov chain for \(H = F_2\) and \(X \sim B(10,0.5)\) (Fig. 6).
An important point to note is that the structure of the resulting Markov chain resembles the one already observed in Fig. 4. Note, however, that certain phenomena that were present in the Bottleneck-only Condition, now are amplified. For example, cycles \(01,10,01,\ldots \) are almost certain and, consequently, escaping them is almost impossible. This conclusion receives further support when considering the expected number of steps before absorption (Table 1). Indeed, E assumes values ranging from 121 to 513 which renders alignment under the Null Condition as largely impractical. However, the associated dispersion is equally large, which suggests that some number of interactions lead to absorption after a relatively small number of steps.
It is interesting to see what happens if the local transmission bottleneck becomes less and less tight. It turns out that for \(n > 2\), the switching behaviour is also present between \(0\frac{1}{2}\), \(\frac{1}{2}0\) and \(1\frac{1}{2}\), \(\frac{1}{2}1\) and becomes stronger and stronger as n becomes larger. Moreover, the expected number of steps before absorption and associated dispersion become progressively larger for bigger n. An example of the Markov chain for \(n=5\) is given in Fig. 7.
5.5 Authority-only Condition
We proceed to analyse dyadic interactions satisfying the Authority Condition and lacking the Bottleneck Condition. This is operationalized by setting \(w_1> w_2 > 0\) and \(n=2\).
We restrict our attention to \(H = F_2\). The resulting Markov chain is simple enough to perform precise calculations and rich enough to observe some interesting features, such as complex semantics formation. In this case, complex semantics is \(\frac{1}{2}\), corresponding to the most quantifier.
Theorem 3
Let \(A = \{1,2\}\), \(H = F_2\), \(w_1> w_2 + w_2 > 0\) and \(n=2\). Let X be a random variable assuming values in [0, 1] with a probability function P. Then, the model is represented by the Markov chain on \(S = H^2\) induced by the following probabilities:
5.5.1 Comments on Authority-only Condition
We have three types of authority functions that lead to different Markov chains: (a) \(w_1 > w_2 + w_2\), (b) \(w_1 = w_2 + w_2\), and (c) \(w_1 < w_2 + w_2\). Theorem 3 relies on (a). The difference between (a–c) is a direct consequence of how rewards of hypotheses are computed and translates into the degree to which the follower adapts to the leader. The imbalance introduced by (a) is the most severe one among the three options and prevents the leader from mind-changes, provided that the bottleneck is set to \(n \le 2\). However, if the bottleneck was set to \(n>2\), the leader could sometimes be persuaded to change their mind. In fact, this is an interesting consequence of the model: relative difference in social influence is intertwined with the size of bottleneck. For certain authority functions and sizes of the bottleneck, we would obtain a mixture of phenomena we have observed so far and those which are observed in the present condition.
Apart from the conservativeness of the leader, the Authority-only Condition is similar to the Authority-and-Bottleneck Condition in the sense that if the leader uses 0 or 1 then the follower can catch up with them. However, there is an important difference. Unlike under any of the previous conditions, agents can change their semantics to more complex hypotheses. Crucially, the follower can align with the leader on \(\frac{1}{2}\) (see Eq. 5j, 5m). Moreover, for a typical random variable such as \(X \sim B(10,0.5)\), the resulting Markov chain is absorbing (Fig. 8). After a closer look at absorption probabilities (Table 2), one can see the true leadership effect—interaction inevitably steers towards the hypothesis of the most influential agent. Hence, no matter which state is the initial one, the dyad can eventually achieve mutual understanding convergent with the leader’s hypothesis. Therefore, dyads aligning in the Authority-only Condition form a replica of the traditional teacher-learner scenario.
As far as effectiveness of alignment is concerned, the Authority-only Condition outperforms previous parameter settings (Table 1). The expected number of steps before being absorbed ranges from 1 to 2.1 with standard deviation oscillating between 0.002 and 1.56. In particular, convergence on most requires roughly 1-3 steps on average. This suggests that attaining coordinated behaviour under the Authority-only Condition fits time constraints of ordinary interaction.
Finally, note that the behaviour observed under the Authority-only Condition requires both social imbalance and less severe transmission bottleneck. This conclusion follows from our previous considerations: we have combined Authority and Bottleneck Condition in all other configurations and we have not witnessed any behaviour that would count as learning by recognizing.
6 Conclusions
The semantic alignment model specifies a generic agent-based mechanism for updating the meaning of an expression based on recent input data collected during situated interactions with other agents. The model steers away from individualistic learning in the sense that all agents continually adapt their semantic representations. Alignment is modulated by three realistic constraints: social influence, cognitive bias, and local transmission bottleneck. Meanings—here identified with procedures for computing extensions—come with a natural notion of simplicity understood in terms of a relevant complexity measure of corresponding computational problems. Assuming a hypothesis space of basic proportional quantifiers and by independently controlling two parameters, social influence and the size of the local transmission bottleneck, we are able to assess how their values affect alignment in the basic communicative setting of interacting dyads.
-
1.
Agents that are equal with respect to social influence try to follow in each other’s footsteps and eagerly change their mind whenever they see an opportunity to imitate their conversational partner. This behaviour hinders semantic alignment in two ways. First, an interacting dyad cannot converge on complex meanings. Second, alignment on simple meanings is possible, but rather inefficient. This is reminiscent of the idea that attempts of communication lead to the problem of coordination of linguistic representations of participants. Our model shows how a local convention may emerge in isolated dyads across several interaction-alignment episodes and that this process is not always efficient or effective.
-
2.
High social imbalance (relative to the size of transmission bottleneck) alters agents’ behaviour in a significant way. The more authoritative agent becomes a conservative leader who does not change their mind during interaction. The less authoritative agent becomes a follower who tries to catch up with their partner. This property of the model resonates well with the hypothesis that an aligning dyad can improve its effectiveness through imposing local social division between two complementary roles of leader and follower (Garrod and Anderson 1987).
-
3.
A socially imbalanced dyad interacting through a narrow transmission bottleneck can align on simple meanings only. The follower cannot adapt if the leader uses complex meanings. This may be seen as a consequence of the “now-or-never” bottleneck (Christiansen and Chater 2016). The model presented here thus provides a formal justification for the claim that the local bottleneck might result in a major simplification of language during interaction.
-
4.
Significant social imbalance and loose transmission bottleneck allows agents to efficiently align on complex meanings as well. Efficiency is even stronger as the bottleneck becomes less tight. Thus, under this condition, we have thus been able to replicate learning by recognizing: the follower can align on the same meaning as the leader. Modulo minor changes in the model, replication of main characteristics of diffusion chains known from the iterated learning (Kirby et al. 2014) should also be possible within the present framework.Footnote 7
The above remarks suggest that an individualistic approach to learning semantics, understood as inferring (perhaps not accurately) the prescribed meaning from observations, constitutes a special case of a broader phenomenon of semantic alignment. However, semantic alignment operating in other conditions can still show some signs of what we may call learning: agents are capable of developing mutual-intelligibility, although this (i) happens mostly for simple meanings, (ii) is rather less efficient and (iii) can make both parties revamp their semantic representations. This suggests a more encompassing notion of learning understood as an interactive process of reducing between-agent misalignment.
7 Perspectives
The semantic alignment model presented in this paper investigates a few natural constraints that can influence agents’ linguistic behaviour: social impact, cognitive bias, and local transmission bottleneck. However, there are other pressures that can play a significant role in semantic alignment, expressiveness probably being the most important one (Christiansen and Chater 2008). Although we have used the meaning space that includes more and less expressive meanings, the pressure towards expressiveness is not included in the present account and thus interaction does not provide agents with any reason, apart from a combination of social pressures and mutual conformity, to abide or give up their current hypotheses.
It is not unusual to implement the pressure for expressiveness in collaborative or individualistic models of language evolution (Kirby and Hurford 2002; Steels and Belpaeme 2005; Pauw and Hilferty 2012; Kirby et al. 2015). However, expressiveness has been mainly addressed in relation to language as a whole. Crucially, though, this notion is also meaningful for individual constructions. In model-theoretic semantics and its applications to linguistics, it is customary to investigate expressiveness of individual linguistic forms (Peters and Westerståhl 2006). An important point here is that higher expressiveness usually translates into higher computational complexity (for a more concrete analysis in the case of quantifiers see Mostowski and Szymanik 2012). Hence, the two pressures are likely to compromise each other in language learning, use and semantic alignment. The question is whether this trade-off might have some deeper bearing on language (see, for example, Kalociński and Godziszewski 2018).
A related research question concerns the relationship between the structure of the lexicon of a given community and the structure of environment in which this community is immersed and communicates about. As far as spatial descriptions are concerned, it has been observed that languages relying on an absolute frame of reference are more common for rural or open-terrain societies, whereas relative frame of reference tends to be found in densely forested and urban environments (Levinson 1996, 2003; Majid et al. 2004). Moreover, it has been suggested that regional daylight characteristics might influence the structure of color categories of local communities (Lindsey and Brown 2002; Plewczyński et al. 2014). It seems natural to ask a similar question in the context of quantification and determine whether distributional characteristics of the properties that agents communicate about (probability distributions on stimuli) influence the structure of the emerging quantifier lexicons. Apart from the research on quantification in the multi-agent context (Gierasimczuk and Szymanik 2011; Pauw and Hilferty 2012), it has recently been argued that certain properties of the environment can have a significant influence on the evolution of scalar terms, and in particular, of quantifiers (Kalociński 2018a). Finally, the relationship between the structure of the environment and the structure of the lexicon has been studied extensively in the signalling games paradigm, in the context of Voronoi languages (Jäger et al. 2011), vagueness (O’Connor 2014), or compositionality (Steinert-Threlkeld 2016).
7.1 Alignment in Dialogue
Our analysis of dyadic interactions might raise the question of the model’s applicability to semantic coordination in dialogue. Having this in mind, we point to main advantages and disadvantages of the proposed approach.
Let us start with the good news. First, observe that alignment proceeds through simple priming—an agent, instead of modelling mental states of its partner, consistently adapts its own hypothesis relying on the most recent input obtained from its interlocutor (Pickering and Garrod 2004). Second, negotiation of meaning is not explicit—it proceeds through tacit modifications based on observed examples of language use. This property of alignment matches findings known from the experimental psychology of dialogue (Garrod and Anderson 1987; Garrod and Doherty 1994). Third, alignment is mainly driven by miscommunication—agents change their hypotheses on encountering problematic usage. This aspect of the model also resonates well with experimental research (Healey 2008). Fourth, alignment can operate on input gathered from a number of discussants and thus extends naturally to multi-party dialogues. Last but not least, alignment is vulnerable to social influence. The latter property fits with the proposal according to which social influence might be exploited by participants to facilitate alignment (Garrod and Anderson 1987). Indeed, we have seen that social imbalance has a largely positive impact on the effectiveness of alignment.
Time for the bad news. The present account does not distinguish between separate turns. Turn-taking is a defining feature of dialogue and should be incorporated into modelling (Levinson 2016). The question is what would change if we divided a single interaction-alignment episode into two separate turns with the roles of the speaker and the hearer exchanged. It seems that socially balanced dyads would be more effective, provided that only one agent (presumably, the hearer) aligns per turn. We hypothesise, however, that this would not completely reduce the threat of misalignment, as long as the aligning agent has several equally good alternatives to choose from.
Another crucial assumption involved in the present account is that authority functions are positive and remain constant throughout interaction. This seems to be adequate for certain communicative scenarios—for example, when changing the relative social standing of agents is difficult or mutually recognized as inappropriate. However, abandoning these assumptions naturally extends the model to competitive scenarios. Moreover, allowing authority functions to vary across trials leads to an interesting theme of modelling social coordination. All these modifications taken together seem to provide an interesting challenge, particularly in connection to semantic alignment.
Notes
For more details on applications of a generalized quantifier theory in natural language see Peters and Westerståhl (2006).
Research dealing with the cognitive difficulty of verification of proportional quantifiers is confined to most, more than half or less then half (and to some and all, if they are viewed as proportional). This gives us enough justification for the assumed simplicity ordering over 0 (some), \(\frac{1}{2}\) (most) and 1 (all). However, we lack a similar justification for the assumption that, for example, more than half is easier than more than a quarter (\(\frac{1}{2} \prec \frac{1}{4}\)).
This means that agent 1 is more influential than agent 2. We could instead assume that \(w_2 > w_1\); the only thing that matters is that one agent is more influential than another.
The difference between 1 and 2 might seem negligible but—as we will see—it affects alignment in a significant way.
To obtain a complete description, we need initial probabilities \(p_i\), for every \(i \in S\). However, \(p_i\)’s are not important for our purposes.
For example, at a given learning episode between two agents, one is ranked highly and thus becomes a conservative leader. Their follower, after having learnt some meaning from the leader, becomes a new highly ranked agent and leads the way in the subsequent learning episode with another agent, and so on. Since alignment is modulated by the cognitive biases of learners and transmission bottleneck, we should expect that the meaning evolving across generations will become simpler, provided no other pressures apply.
References
Baltag, A., Gierasimczuk, N., & Smets, S. (2011). Belief revision as a truth-tracking process. In K. Apt (Ed.), TARK’11: Proceedings of the 13th conference on theoretical aspects of rationality and knowledge, Groningen, The Netherlands, July 12–14, 2011 (pp. 187–190). Groningen, Netherlands: ACM. https://doi.org/10.1145/2000378.2000400.
Baltag, A., Gierasimczuk, N., & Smets, S. (2015). On the solvability of inductive problems: A study in epistemic topology. In R. Ramanujam (Ed.), Proceedings of the 15th conference on theoretical aspects of rationality and knowledge (TARK).
Baxter, G. J., Blythe, R. A., Croft, W., & McKane, A. J. (2006). Utterance selection model of language change. Physical Review E, 73(4), 046–118.
Blokpoel, M., van Kesteren, M., Stolk, A., Haselager, P., Toni, I., & Rooij, I. (2012). Recipient design in human communication: Simple heuristics or perspective taking? Frontiers in Human Neuroscience, 6, 253.
Blythe, R. A., Jones, A. H., & Renton, J. (2016). Spontaneous dialect formation in a population of locally aligning agents. In: S. G. Roberts, C. Cuskley, L. McCrohon, L. Barceló-Coblijn, O. Fehér, & T. Verhoef (Eds.), The evolution of language: proceedings of the 11th international conference (EVOLANGX11). Online at: http://evolang.org/neworleans/papers/19.html.
Brown, A. M., Isse, A., & Lindsey, D. T. (2016). The color lexicon of the Somali language. Journal of Vision, 16(5), 14. https://doi.org/10.1167/16.5.14.
Christiansen, M. H., & Chater, N. (2008). Language as shaped by the brain. Behavioral and Brain Sciences, 31(05), 489–509.
Christiansen, M. H., & Chater, N. (2016). The now-or-never bottleneck: A fundamental constraint on language. Behavioral and Brain Sciences, 39, e62.
Clark, R. (2010). On the learnability of quantifiers. In J. van Benthem & A. ter Meulen (Eds.), Handbook of logic and language (2nd ed., pp. 909–922). Amsterdam: Elsevier.
Feller, W. (1968). An introduction to probability theory and its applications (3rd ed., Vol. 1). London: Wiley.
Frank, M. C., Goodman, N. D., & Tenenbaum, J. B. (2007). A Bayesian framework for cross-situational word-learning. In Proceedings of the 20th international conference on neural information processing systems, NIPS’07 (pp. 457–464). Curran Associates Inc., USA. http://dl.acm.org/citation.cfm?id=2981562.2981620.
Fusaroli, R., Rączaszek-Leonardi, J., & Tylén, K. (2014). Dialog as interpersonal synergy. New Ideas in Psychology, 32, 147–157.
Garrod, S., & Anderson, A. (1987). Saying what you mean in dialogue: A study in conceptual and semantic co-ordination. Cognition, 27(2), 181–218.
Garrod, S., & Doherty, G. (1994). Conversation, co-ordination and convention: An empirical investigation of how groups establish linguistic conventions. Cognition, 53(3), 181–215.
Gierasimczuk, N. (2007). The problem of learning the semantics of quantifiers. In TBiLLC’05: 6th international Tbilisi symposium on logic, language, and computation. revised selected papers, lecture notes in artificial intelligence (Vol. 4363, pp. 117–126). Springer.
Gierasimczuk, N., Maas, H. v. d., & Raijmakers, M. (2012). Logical and psychological analysis of deductive mastermind. In J. Szymanik, & R. Verbrugge (Eds.), Proceedings of the logic & cognition workshop at ESSLLI 2012, Opole, Poland, 13–17 August, 2012, CEUR workshop proceedings (Vol. 883, pp. 1–13). CEUR-WS.org.
Gierasimczuk, N., & Szymanik, J. (2009). Branching quantification v. two-way quantification. Journal of Semantics, 26(4), 367–392.
Gierasimczuk, N., & Szymanik, J. (2011). Invariance properties of quantifiers and multiagent information exchange. In M. Kanazawa, A. Kornai, M. Kracht, & H. Seki (Eds.), The mathematics of language—12th biennial conference, MOL 12, Nara, Japan, September 6–8, 2011. Proceedings, lecture notes in computer science (Vol. 6878, pp. 72–89). Springer.
Gong, T. (2009). Computational simulation in evolutionary linguistics: A study on language emergence. Taipei: Institute of Linguistics, Academia Sinica Taipei.
Healey, P. (2008). Interactive misalignment: The role of repair in the development of group sub-languages. In R. Cooper & R. Kempson (Eds.), Language in flux (Vol. 212, pp. 13–39). Basingstoke: Palgrave-McMillan.
Hendriks, P., & de Hoop, H. (2001). Optimality theoretic semantics. Linguistics and Philosophy, 24(1), 1–32. https://doi.org/10.1023/A:1005607111810.
Jäger, G., Metzger, L. P., & Riedel, F. (2011). Voronoi languages: Equilibria in cheap-talk games with high-dimensional types and few signals. Games and Economic Behavior, 73(2), 517–537. https://doi.org/10.1016/j.geb.2011.03.008.
Kalociński, D. (2016). Learning the semantics of natural language quantifiers, Ph.D. thesis. http://depotuw.ceon.pl/bitstream/handle/item/1661/3501-DR-FF-67104.pdf?sequence=1.
Kalociński, D. (2018a). Environmental constraints in the evolution of scalar concepts: Road to ‘most’. In C. Cuskley, M. Flaherty, H. Little, L. McCrohon, A. Ravignani, & T. Verhoef (Eds.), The evolution of language: Proceedings of the 12th international conference (EVOLANGXII). Online at: http://evolang.org/torun/proceedings/papertemplate.html?p=185.
Kalociński, D. (2018b). Interactive semantic alignment model: Social influence and local transmission bottleneck (technical appendix) http://semanticsarchive.net/~semant60/Archive/DIyNGFhO/interactive-semantic-alignment-model-technical-appendix.pdf.
Kalociński, D., & Godziszewski, M. T. (2018). Semantics of the Barwise sentence: Insights from expressiveness, complexity and inference. Linguistics and Philosophy. https://doi.org/10.1007/s10988-018-9231-5.
Kalociński, D., Gierasimczuk, N., & Mostowski, M. (2015). Quantifier learning: An agent-based coordination model. In Proceedings of the 2015 international conference on autonomous agents and multiagent systems, AAMAS ’15 (pp. 1853–1854). International Foundation for Autonomous Agents and Multiagent Systems, Richland, SC. http://dl.acm.org/citation.cfm?id=2772879.2773470.
Kemeny, J. G., & Snell, J. L. (1960). Finite markov chains (Vol. 356) van Nostrand Princeton, NJ. http://tocs.ulb.tu-darmstadt.de/12997448X.pdf.
Kirby, S., Griffiths, T., & Smith, K. (2014). Iterated learning and the evolution of language. Current Opinion in Neurobiology, 28, 108–114.
Kirby, S., & Hurford, J. R. (2002). The emergence of linguistic structure: An overview of the iterated learning model. In A. Cangelosi & D. Parisi (Eds.), Simulating the evolution of language (pp. 121–147). Springer.
Kirby, S., Tamariz, M., Cornish, H., & Smith, K. (2015). Compression and communication in the cultural evolution of linguistic structure. Cognition, 141, 87–102.
Kosterman, S., & Gierasimczuk, N. (2015). Collective learning in games through social networks. In Proceedings of the 1st international conference on social influence analysis—Volume 1398, SocInf’15 (pp. 35–41). CEUR-WS.org, Aachen, Germany, Germany. http://dl.acm.org/citation.cfm?id=2907168.2907176.
Labov, W. (2001). Principles of linguistic change, II: Social factors. Oxford: Blackwell.
Levinson, S. C. (1996). Language and space. Annual Review of Anthropology, 25(1), 353–382. https://doi.org/10.1146/annurev.anthro.25.1.353.
Levinson, S. C. (2003). Space in language and cognition: Explorations in cognitive diversity (Vol. 5). Cambridge: Cambridge University Press.
Levinson, S. C. (2016). Turn-taking in human communication—Origins and implications for language processing. Trends in Cognitive Sciences, 20(1), 6–14.
Lewis, D. (1969). Convention. Cambridge: Harvard University Press.
Lindsey, D. T., & Brown, A. M. (2002). Color naming and the phototoxic effects of sunlight on the eye. Psychological Science, 13(6), 506–512. https://doi.org/10.1111/1467-9280.00489.
Lindström, P. (1966). First order predicate logic with generalized quantifiers. Theoria, 32, 186–195.
Majid, A., Bowerman, M., Kita, S., Haun, D. B., & Levinson, S. C. (2004). Can language restructure cognition? The case for space. Trends in Cognitive Sciences, 8(3), 108–114. https://doi.org/10.1016/j.tics.2004.01.003.
Mills, G. J., & Healey, P. G. (2008). Semantic negotiation in dialogue: the mechanisms of alignment. In Proceedings of the 9th SIGdial workshop on discourse and dialogue (pp. 46–53). Association for Computational Linguistics.
Mostowski, A. (1957). On a generalization of quantifiers. Fundamenta Mathematicae, 44, 12–36.
Mostowski, M., & Szymanik, J. (2012). Semantic bounds for everyday language. Semiotica, 2012(188), 323–332. https://doi.org/10.1515/sem-2012-0022.
Mostowski, M., & Wojtyniak, D. (2004). Computational complexity of the semantics of some natural language constructions. Annals of Pure and Applied Logic, 127(1–3), 219–227.
Nettle, D. (1999). Using social impact theory to simulate language change. Lingua, 108(2), 95–117.
O’Connor, C. (2014). The evolution of vagueness. Erkenntnis, 79(4), 707–727. https://doi.org/10.1007/s10670-013-9463-2.
Pauw, S., & Hilferty, J. (2012). The emergence of quantifiers. In L. Steels (Ed.), Experiments in cultural language evolution (Vol. 3, pp. 277–304). John Benjamins Publishing.
Peters, S., & Westerståhl, D. (2006). Quantifiers in language and logic. Oxford: Oxford University Press.
Piantadosi, S. T., Tenenbaum, J. B., & Goodman, N. D. (2012). Bootstrapping in a language of thought: A formal model of numerical concept learning. Cognition, 123(2), 199–217.
Pickering, M. J., & Garrod, S. (2004). Toward a mechanistic psychology of dialogue. Behavioral and Brain Sciences, 27(02), 169–190.
Plewczyński, D., Łukasik, M., Kurdej, K., Zubek, J., Rakowski, F., & Rączaszek-Leonardi, J. (2014). Generic framework for simulation of cognitive systems: A case study of color category boundaries. In A. Gruca, T. Czachórski, & S. Kozielski (Eds.), Man-machine interactions 3 (pp. 385–393). Springer.
Puglisi, A., Baronchelli, A., & Loreto, V. (2008). Cultural route to the emergence of linguistic categories. Proceedings of the National Academy of Sciences, 105(23), 7936–7940.
Schober, M. F. (2004). Just how aligned are interlocutors’ representations? Behavioral and Brain Sciences, 27(02), 209–210.
Skyrms, B. (2010). Signals: Evolution, learning, and information. Oxford: Oxford University Press.
Smith, K., Perfors, A., Fehér, O., Samara, A., Swoboda, K., & Wonnacott, E. (2017). Language learning, language use and the evolution of linguistic variation. Philosophical Transactions of the Royal Society B, 372(1711), 20160051.
Steels, L. (2011). Modeling the cultural evolution of language. Physics of Life Reviews, 8(4), 339–356. https://doi.org/10.1016/j.plrev.2011.10.014.
Steels, L., & Belpaeme, T. (2005). Coordinating perceptually grounded categories through language: A case study for colour. Behavioral and Brain Sciences, 28(4), 469–489.
Steinert-Threlkeld, S. (2016). Compositional signaling in a complex world. Journal of Logic, Language and Information, 25(3), 379–397. https://doi.org/10.1007/s10849-016-9236-9.
Szymanik, J. (2016). Quantifiers and cognition: logical and computational perspectives, No. 96 in studies in linguistics and philosophy (1st ed.). Berlin: Springer.
Szymanik, J., & Zajenkowski, M. (2010). Comprehension of simple quantifiers. Empirical evaluation of a computational model. Cognitive Science: A Multidisciplinary Journal, 34(3), 521–532. https://doi.org/10.1111/j.1551-6709.2009.01078.x.
Tichý, P. (1969). Intension in terms of Turing machines. Studia Logica, 24(1), 7–21. https://doi.org/10.1007/BF02134290.
van Benthem, J. (1986). Essays in logical semantics. Dordrecht: D. Reidel.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dariusz Kalociński is supported by the Polish National Science Centre Grant 2014/13/N/HS1/02048. Nina Gierasimczuk is funded by the Polish National Science Centre Grant 2015/19/B/HS1/03292 and by the Netherlands Organisation for Scientic Research (NWO), an Innovational Research Incentives Scheme Veni Grant No. 275-20-043.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kalociński, D., Mostowski, M. & Gierasimczuk, N. Interactive Semantic Alignment Model: Social Influence and Local Transmission Bottleneck. J of Log Lang and Inf 27, 225–253 (2018). https://doi.org/10.1007/s10849-018-9267-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-018-9267-5