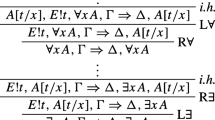A Sequent Calculus for Urn Logic

Abstract

Approximately speaking, an urn model for first-order logic is a model where the domain of quantification changes depending on the values of variables which have been bound by quantifiers previously. In this paper we introduce a model-changing semantics for urn-models, and then give a sequent calculus for urn logic by introducing formulas which can be read as saying that “after the individuals $a_{1}, \ldots , a_{n}$ have been drawn, $A$ is the case”.

1 Introduction

Urn logic is a generalisation of first-order logic introduced in Rantala (1975). The idea behind urn logic is to think of the domain of quantification in a way reminiscent of the eponymous urns of balls used in probability theory. The metaphor here is to think of quantifying over objects in a domain as being analogous to drawing balls from an urn. Typically in first-order logic what we are doing is always quantifying over the same objects—our domain stays fixed every time we ‘draw’ from the domain. But, just as we can alter the contents of the urn based upon what we’ve drawn from it (for example, by simply not replacing it, or by putting more objects back into the urn of a kind based on what we’ve drawn out), we can also think about models for the quantifiers where the domain of quantification changes in the course of evaluating a formula.

Hintikka (1975) argues that urn models can be used to give a satisfactory model theoretic account of impossible worlds (and thus deal with issues of logical omniscience). Hintikka’s idea is, when giving our first-order epistemic logic, to have two kinds of worlds—invariant, and almost-invariant worlds—the invariant ones being those which are used for determining logical truths, and all worlds (invariant and almost-invariant alike) being used in the interpretation of the epistemic operators. These almost-invariant worlds are envisaged as being urn models where the domain from which we can ‘draw’ is constant up until we have made $n$ draws, the $n$ being determined by the agent’s cognitive capacities. We will dwell no further on this potential application, outlined by Hintikka, of the notion of an urn model. Instead our focus will be largely technical (although we will mention another potential application at the end of the next section).

Relatively little work has been done on urn logic—notable exceptions being Cresswell (1982) and Olin (1978). In Cresswell (1982) a ‘classical analogue’ of Rantala’s urn logic is investigated, using a modification of the standard Tarskian semantics for first-order logic as opposed to the game-theoretic semantics used by Rantala. Using these semantics Cresswell gives a Henkin-style completeness proof for a range of urn logics with various constraints placed upon how we can draw individuals from the domain. Olin (1978), also using a classical version of urn Logic, has investigated the model-theory of urn models, with particular attention to issues concerning satisfiability and categoricity.

Our plan here is as follows. In Sect. 2 we will describe the (standard/Tarskian) semantics for urn logic which we will be using, and comparing it to the semantic treatments given by Rantala, Cresswell and Olin. We will then proceed in Sect. 3 to give a sequent calculus for urn logic obtained by ‘decorating’ formulas so as to give us a way to keep track of changes in the domain. We then prove this sequent calculus to be sound and complete w.r.t. the semantics described in Sect. 2 before going on to show how to extend our sequent calculus in Sect. 5 so that it is sound and complete w.r.t. the class of urn models which Rantala is concerned with.

2 Semantics for Urn Logic

The language of urn logic is just the standard language of first-order logic without identity or individual constants. The restriction to first-order languages without individual constants is (aside from some minor complications discussed in Sect. 5.2) entirely for expository ease—unless noted all results here will hold for languages which contain individual constants. We will think of our models for urn logic in a similar vein to Cresswell, taking our models to be triples $\langle U, D, V\rangle$ where $U$ is a non-empty set (the initial domain), $V$ is a standard first-order interpretation, and $D$ is a function from sequences of objects from $U$ to subsets of $U$. We do this mostly so that we can talk about domains in the standard way: the value of $D$ on a sequence $\langle a_{1}, \ldots , a_{n}\rangle$ being the effective domain for the next quantification after $\langle a_{1}, \ldots , a_{n}\rangle$ have been ‘drawn’. In order for a structure $\langle U, D, V\rangle$ to be an urn model we will also require that it satisfies the following condition.

$$\begin{aligned} (Draw){:}\quad D\left( \langle a_{1}, \ldots , a_{n}\rangle \right) \not = \emptyset \Rightarrow a_{n}\in D\left( \langle a_{1}, \ldots , a_{n-1}\rangle \right) . \end{aligned}$$

So our official definition of an urn model here will be that a structure $\langle U, D, V\rangle$ is an urn model iff $U$ is a non-empty set, $V$ is a function which assigns subsets of $U^{n}$ to $n$-place primitive predicates, and $D$ is a function from sequences of objects for $U$ to subset of $U$ which satisfies the condition $(Draw)$ above. In his discussion, Rantala places two further constraints upon the class of models $\langle U, D, V\rangle$ he is concerned with, which we will discuss further in Sect. 5.

The semantic discussion of urn logic in Rantala (1975) is a modification of the game-theoretic semantics for first-order logic from Hintikka (1979). Rather than working within the framework of game-theoretic semantics, though, we will instead work within a more familiar looking semantic framework, somewhat reminiscent of that used in Cresswell (1982) and Olin (1978). Rantala’s reasons (Rantala 1975, p. 351) for using the game-theoretic semantics is so that we can have a ‘model-changing’ semantics in the sense discussed in Sect. 4 of Humberstone (2008), the semantics for urn logic not requiring any of the independent-choice style phenomena which game-theoretic semantics is particularly amenable to.

In the semantics for urn logic which we will be using, we will keep our model fixed, but evaluate formulas for truth relative, not just to a variable assignment as with standard Tarskian treatments of first-order logic, but also relative to a draw.

Definition 1

Given an urn model ${\mathcal {M}} = \langle U, D, V\rangle$ a sequence $\langle s_{1}, \ldots , s_{n}\rangle$ of objects from $U$ is a draw from ${\mathcal {M}}$ iff (1) $s_{1}\in D(\emptyset )$ and (2) $s_{i+1} \in D(\langle s_{1},\ldots , s_{i}\rangle )$ for all $1\le i \le n-1$.

One of the effects of the condition $(Draw)$ is that whenever the domain determined by a sequence $\underline{s}$ is non-empty, then $\underline{s}$ is automatically a draw.

Definition 2

An assignment $\nu$ is an $x$ -variant of $\mu$ iff $\nu (y) = \mu (y)$ for all variables $y$ except (possibly) $x$.

Our fundamental notion, then, will be truth of a formula $\varphi$ in an urn model ${\mathcal {M}} = \langle U, D, V\rangle$ relative to an assignment $\mu$ and a draw $\underline{s}$, which we will write as ${\mathcal {M}}, \underline{s}\models \varphi [\mu ]$. Throughout we will use $\underline{s}\cdot t$ to denote the concatenation of $\underline{s}$ with $t$.

$$\begin{aligned}&{\mathcal {M}}, \underline{s} \models Fx_{1}\ldots x_{n}\ [\mu ] \iff \langle \mu (x_1), \ldots \mu (x_{n})\rangle \in V(F).\\&{\mathcal {M}}, \underline{s} \models \lnot \varphi \ [\mu ] \iff {\mathcal {M}}, \underline{s}\not \models \varphi \ [\mu ].\\&{\mathcal {M}}, \underline{s} \models \varphi \wedge \psi \ [\mu ] \iff {\mathcal {M}}, \underline{s} \models \varphi \ [\mu ] \text { and } {\mathcal {M}}, \underline{s} \models \psi \ [\mu ].\\&{\mathcal {M}}, \underline{s} \models \forall x \varphi \ [\mu ] \iff {\mathcal {M}}, \underline{s}\cdot \nu (x) \models \varphi [\nu ]\\&\qquad \text {for all}\,x\text {-variants}\,\nu \,\hbox {of} \,\mu \hbox { s.t. }\\&\qquad \nu (x) \in D(\underline{s}). \end{aligned}$$

To give the reader an example of the way in which the urn semantics for first-order logic differs from the standard semantics for the quantifiers, consider the following classically valid formula:

$$\begin{aligned} (\forall y)\big ((\forall x)Fx \rightarrow Fy\big ). \end{aligned}$$

This formula is not valid in the semantics outlined above—where we take a sentence to be valid whenever it is true in a model w.r.t. the empty sequence of draws. To see this consider the following simple urn model $\langle U, D, V\rangle$.

• $U = \{a, b\}$.

• $D(\emptyset ) = \{a, b\}$, $D(a) = \{b\}$, $D(b) = \{a\}$, and $D(\underline{s}) = U$ for all sequences of length 2 or more.

• $V(F) = \{a\}$.

Now to see that the above formula is false in this urn model note that we can assign $b$ to $y$, forcing us to consider whether ${\mathcal {M}}, \langle b\rangle \models \forall x Fx \rightarrow Fy [\mu ]$, but we know that ${\mathcal {M}},\langle b\rangle \not \models Fy [\mu ]$, as $\mu (y) = b$, so in order for the above formula to be true we must have ${\mathcal {M}},\langle b\rangle \not \models \forall x Fx[\mu ]$. But as $D(b) = \{a\}$, and $a\in V(F)$ it follows that ${\mathcal {M}},\langle b\rangle \models \forall x Fx[\mu ]$, and thus the above formula is invalid.

The above example also shows how our semantics differs from that of Cresswell and Olin. According to our semantics the truth of a quantified formula like $\exists x\varphi$ in a model is evaluated relative to a sequence of ‘draws’ from the domain which, when we are considering sentences, will be determined by the values which have been assigned to variables which do not occur in the formula under consideration. By contrast, (again considering sentences) Cresswell and Olin evaluate formulas relative to the effect which such assigning has had upon the formula being evaluated, having the relevant domain of quantification be determined by the values assigned to the free variables in the formula in question. In the above case, for example, Cresswell and Olin would evaluate $\forall xFx$ relative to $D(\emptyset )$ (and consequently judge the above formula as valid).

2.1 Globally and Locally Determined Domains

This difference between the approach we are taking here, and that taken by Cresswell and Olin corresponds quite neatly to the distinction between the strongly and weakly exclusive interpretation of the quantifiers discussed in (Hintikka 1956, p. 230) and given a proof-theoretic treatment in Wehmeier (2004, 2009). The following terminology is more suggestive, though: call any semantics for the quantifiers where the domain quantified over is a non-constant function of the formula under investigation one with locally determined domains. Similarly, we will call any semantics for the quantifiers in which the domain quantified over is a non-constant function of the broader sentential-context in which the quantified expression occurs one with globally determined domains.¹ So the strongly-exclusive interpretation of the quantifiers (discussed in Wehmeier (2009)) is one where we have globally determined domains, and the weakly-exclusive interpretation (discussed in Wehmeier (2004)) one where we have locally determined domains. In the case of the semantics for urn logic discussed above, the semantics used by Cresswell and Olin is one with local domain determination, and that used by Rantala and myself one with global domain determination.

One issue which globally determined domains allows us to get clearer on is the status of what is called the ‘Binding Assumption’ in Stanley (2000). Approximately speaking, this is the assumption that if a part $\alpha$ of a clause semantically binds another part $\beta$ of that clause, then this binding must show up in the logical form of the two clauses with a variable being bound in $\alpha$ which is a constituent of $\beta$. For example, consider the following sentences (both of which are variants of sentences from Stanley (2000)).

• $(\star )$   In all of John’s classes he fails three students.

• $(\star ^{\prime })$    Whatever office you go to, the supervisor is always unavailable.

The most straightforward reading of $(\star )$ is one where in each of John’s classes $x$ he fails three students in $x$, but the logical form which most closely mirrors its surface form is something like the following (where ‘$\exists ^{\not =}$’ is an abbreviation for ‘there exist distinct...’).

$$\begin{aligned} \forall x (\mathsf{John{\hbox {-}}Class}(x) \rightarrow \exists ^{\not =} tuv(&\mathsf{Student}(t)\wedge \mathsf{Student}(u)\wedge \mathsf{Student}(v)\\&\wedge \mathsf{Fail}(t)\wedge \mathsf{Fail}(u)\wedge \mathsf{Fail}(v))). \end{aligned}$$

Similarly, the most forward reading of $(\star ^{\prime })$ is that where for every office $x$ which you go to, the supervisor of $x$ is always unavailable, but the straightforward logical form of this sentence similarly does not exhibit the required kind of syntactic binding. Concerning cases like these Stanley says the following.

In each of the cases we have discussed, the domain of the second quantified expression varies with the values introduced by the initial quantifier expression. Therefore, given what we have been assuming about the relation between semantic binding and syntactic binding outlined above [i.e. the Binding Assumption], it follows that there are bindable variables in the logical form of sentences containing quantifier expressions whose values are quantifier domains. (Stanley 2000, p. 421)

What this argument tells us, then, is that due to the fact that in order for sentences like $(\star )$ and $(\star ^{\prime })$ to be given the straightforward truth conditions mentioned above the outer quantified expression must semantically bind the inner quantified expression. According to Stanley’s Binding Assumption this can only be so if the outer quantified expression binds variables which are otherwise free in the inner quantified expression, and thus the true logical form of sentences like $(\star )$ and $(\star ^{\prime })$ must contain such bound variables, unlike the surface form given above.

Quantifiers with globally determined domains, like the urn quantifiers we will be investigating here, give us the technical machinery to undermine part of the plausibility of the Binding Assumption. If our quantifiers are to work just like standard Tarskian quantifiers then the only way for there to be semantic binding of quantifier expressions is, as the Binding Assumption tells us, by having free-variables in the semantically bound expression being syntactically bound by the expression which is doing the binding. If the only treatment of quantifiers we are countenancing is the Tarskian one then the Binding Assumption seems warranted, but in the presence of alternative ways of registering semantic binding without having syntactic binding this warrant is at least somewhat weakened.

To see that we can do without the Binding Assumption, note that if we were to use quantifiers with globally determined domains then we could get the correct interpretation for $(\star )$ using its surface logical form. For example, we will end up with the semantically bound reading of $(\star )$ whenever, for all $a \in D(\emptyset )\cap ||\mathsf{John\hbox {-}Class}||$ we have $D(a)\cap ||\mathsf{Student}|| = ||\mathsf{InClass}(a)||$, where $||F||$ is the extension of the predicate $F$. Here the predicate $\mathsf{InClass}$, which is implicit in the standard interpretation of $(\star )$, is used implicitly the semantically restrict our domain of quantification. We might think of the process of domain determination on this picture as being a top-down pragmatic process, based on an assessment of speaker intent and features of the conversational context.

This kind of semantic (as opposed to syntactic) binding also has the additional advantage of allowing us to accommodate deviant interpretations of $(\star )$ in a relatively straightforward manner. For example, suppose John finds teaching so stressful that for each class he teaches he finds that the only way he can unwind is by failing three students, and that he is thoroughly unconcerned which classes the students are in. In such a situation we can imagine an (understandably) confused interlocutor engaging with someone who has just uttered $(\star )$ querying whether John fails three students from each class he teaches and being told “No, John just gets very stressed and can only get relief by failing students. He’s not overly concerned which class they’re in!”. Inappropriate behaviour for a teacher, perhaps, but a perfectly legitimate reading of $(\star )$ all the same.

Our aim is not to necessarily endorse such a view here, but mostly to illustrate how being clearer about the various options we have for interpreting the quantifiers provides us with greater flexibility in giving the semantics of natural language without having to postulate additional bindable variables or hidden constituents.

3 A Sequent Calculus for Urn Logic

In this section we will provide a sequent calculus which is sound and complete w.r.t. the class of all urn models. To do this we will find it useful to modify the standard language of first-order logic as follows. Suppose that $L$ is the set of wffs for a first-order language without identity. Then the wffs of $L^{U}$ are all the formulas of $L$, as well as any formula of the form

$$\begin{aligned} \langle t_{1},\ldots , t_{n}\rangle {:} A \end{aligned}$$

where $\langle t_{1},\ldots , t_{n}\rangle$ is a sequence of terms from $L$, and $A$ is a wff from $L$. The idea behind this change to our object language is to read formulas like that inset above as saying that “after the objects denoted by $t_{1}, \ldots , t_{n}$ are drawn, $A$”, to modify Rantala’s turn of phrase.

3.1 The System UC

Let us define the following sequent calculus, which we will call UC (mnemonic for ‘Urn Calculus’). Formally speaking our sequents are pairs of multisets of $L^{U}$-formulas $\langle \varGamma , \varDelta \rangle$, which we will write as $\varGamma {>\!\!\!-}\varDelta$. Throughout we will use $\underline{s}$ and $\underline{u}$ as variables over sequences of terms, $A$ and $B$ as $L$-formulas. We will also occasionally find it useful to use $\alpha$ and $\beta$ as schematic letters for $L^{U}$-formulas. Throughout $t$ and $u$ be schematic for terms, and $a$ be schematic for free-variables (variously, in both cases, with and without subscripts). Where $\underline{s}$ is the sequence $\langle s_{1}, \ldots , s_{n}\rangle$ we will write $\underline{s}\cdot t$ to denote the sequence $\langle s_{1}, \ldots , s_{n}, t\rangle$.

Axioms: All of the axiomatic sequents for UC are of the following form:

$$\begin{aligned} \varGamma , \underline{s}: Ft_1\ldots t_n {>\!\!\!-}\underline{s^{\prime }}{:} Ft_1\ldots t_n,\varDelta \end{aligned}$$

where $\underline{s}$ and $\underline{s^{\prime }}$ are sequences of terms from $L$, and $t_1, \ldots , t_n$ are terms, and $F$ is an $n$-ary atomic predicate of $L$.

Operational Rules: UC has the following operational rules for the connectives $\lnot$, $\wedge$ and $\forall$.

where for some $B$ and some (possibly empty) term sequence $\underline{s^{\prime }}$ we have $\underline{s}\cdot t\cdot \underline{s^{\prime }}:B\in \varGamma \cup \varDelta$ in $(\forall L)$, and $a$ does not appear in $\varGamma \cup \varDelta \cup \{\underline{s}:\forall x A(x)\}$ in $(\forall R)$.

Structural Rules: The system UC has the following standard structural rules.

It also have the following variation on the standard $(Cut)$ rule:

provided that for some formula $B\in L$ and some term sequence $\underline{s^{\prime }}$ we have $\underline{s}\cdot \underline{s^{\prime }}:B\in \varGamma \cup \varDelta$.

Urn-Rules: Let $\varphi$ be a quantifier-free formula.

Consider the following example of a sequent derivation in this system.

3.2 Soundness

Let us abbreviate the claim that $\underline{s}$ is a draw from ${\mathcal {M}}$ by writing $draw^{{\mathcal {M}}}(\underline{s})$. Furthermore we will occasionally write $\mu (\underline{s})$ where $\mu$ is a variable assignment and $\underline{s}$ is a sequence of terms from $L$, understanding that as being the result of applying the variable assignment to each member of the sequence in turn (e.g. $\mu (\langle a, b\rangle ) = \langle \mu (a), \mu (b)\rangle$).

Definition 3

Let $\langle s_{1}, \ldots , s_{n}\rangle :A$ be a formula from $L^{U}$. Then we will say that ${\mathcal {M}}\Vdash ^{+} \langle s_{1}, \ldots , s_{n}\rangle :A[\mu ]$ whenever:

$$ \begin{aligned} draw^{{\mathcal {M}}}(\langle \mu (s_{1}), \ldots , \mu (s_{n})\rangle )\ \& \ {\mathcal {M}}, \langle \mu (s_{1}), \ldots , \mu (s_{n})\rangle \models A [\mu ]. \end{aligned}$$

Let us say that ${\mathcal {M}}\Vdash ^{-} \langle s_{1}, \ldots , s_{n}\rangle :A[\mu ]$ whenever:

$$ \begin{aligned} draw^{{\mathcal {M}}}(\langle \mu (s_{1}), \ldots , \mu (s_{n})\rangle )\ \& \ {\mathcal {M}}, \langle \mu (s_{1}), \ldots , \mu (s_{n})\rangle \not \models A [\mu ]. \end{aligned}$$

Definition 4

Say that a sequent $\varGamma {>\!\!\!-}\varDelta$ fails in an Urn-Model ${\mathcal {M}}$ on an assignment $\mu$ whenever for all $\alpha \in \varGamma$ we have ${\mathcal {M}}\Vdash ^{+} \alpha [\mu ]$ and for all $\beta \in \varDelta$ we have ${\mathcal {M}}\Vdash ^{-} \beta [\mu ]$. Otherwise we will say that it holds in ${\mathcal {M}}$ on $\mu$ and write ${\mathcal {M}}\models \varGamma {>\!\!\!-}\varDelta [\mu ]$.

We will often find it convenient to write ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$ (or ${\mathcal {M}}\Vdash ^{-}\varGamma [\mu ]$) for some set of formulas $\varGamma$, which should be understood as meaning that ${\mathcal {M}}\Vdash ^{+}\alpha [\mu ]$ (resp. ${\mathcal {M}}\Vdash ^{-}\alpha [\mu ]$) for all formulas $\alpha \in \varGamma$, in which case the above definition tells us that a sequent fails in a model ${\mathcal {M}}$ on an assignment $\mu$ whenever we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$.

We will occasionally find the following lemma useful to appeal to in what follows.

Lemma 1

For all quantifier-free formulas $\varphi$, all models ${\mathcal {M}} = \langle U, D, V\rangle$, variable assignments $\mu$, and all draws $\underline{s}$, and $\underline{u}$ from ${\mathcal {M}}$ we have the following:

$$\begin{aligned} {\mathcal {M}}, \underline{s}\models \varphi [\mu ] \quad \textit{if and only if }{\mathcal {M}}, \underline{u}\models \varphi [\mu ] \end{aligned}$$

Proposition 1

(Soundness) If $\varGamma {>\!\!\!-}\varDelta$ is derivable in UC then, for all models ${\mathcal {M}}$ and assignments $\mu$, we have ${\mathcal {M}}\models \varGamma {>\!\!\!-}\varDelta [\mu ]$.

Proof

What we want to show is that if a sequent $\varGamma {>\!\!\!-}\varDelta$ is derivable in UC then, for all models ${\mathcal {M}}$ and all assignments $mu$ we have either it is not the case that ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$ or it is not the case that ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$—i.e. that a sequent is derivable if it holds in all models. Put more explicitly, the consequent of this conditional means that, for all models ${\mathcal {M}}$ and all assignments $\mu$ that either we have ${\mathcal {M}}\not \Vdash ^{+}\alpha$ for some $\alpha \in \varGamma$ or ${\mathcal {M}}\not \Vdash ^{-}\beta$ for some $\beta \in \varDelta$.

To prove this we will show that the axioms hold in all models, and show that each of the rules preserve the property of holding in a model (in particular by showing that if the conclusion of a rule fails in a model on an assignment, then (one of its) premise sequents also fails in a model on an assignment. Thus, given that the axioms hold in all models, and the rules preserve the property of holding in a model it follows by a simple induction on the length of derivations that if a sequent is derivable then it holds in all models, as desired.

Axiom Case: Suppose that $\varGamma {>\!\!\!-}\varDelta$ is an axiom. Then we have some formula $Ft_1\ldots t_n$ and some term sequences $\underline{s}$ and $\underline{s^{\prime }}$ s.t. $\underline{s}:Ft_1\ldots t_n\in \varGamma$ and $\underline{s^{\prime }}:Ft_1\ldots t_n\in \varDelta$. If we have either $\underline{s}$ or $\underline{s^{\prime }}$ fail to be a draw then we’re done, as this will mean that either ${\mathcal {M}}\not \Vdash ^{+}\underline{s}:Ft_1\ldots t_n[\mu ]$ or ${\mathcal {M}}\not \Vdash ^{-}\underline{s^{\prime }}:Ft_1\ldots t_n[\mu ]$. So suppose that we have both $draw^{{\mathcal {M}}}(\underline{s})$ and $draw^{{\mathcal {M}}}(\underline{s^{\prime }})$. It follows now that either (1)${\mathcal {M}}, \underline{s}\models Ft_1\ldots t_n[\mu ]$ or (2)${\mathcal {M}}, \underline{s}\not \models Ft_1\ldots t_n[\mu ]$. If (1) then we have ${\mathcal {M}}, \underline{s^{\prime }}\models Ft_1\ldots t_n[\mu ]$ by Lemma 1, and so ${\mathcal {M}}\not \Vdash ^{-}\underline{s^{\prime }}:Ft_1\ldots t_n[\mu ]$. The case for (2) follows similarly.

We now cover some representative cases of the rules.

$\lnot$ -cases: For $(\lnot L)$ suppose that we have $\varGamma , \underline{s}:\lnot A{>\!\!\!-}\varDelta$ failing in some model ${\mathcal {M}}$ on an assignment $\mu$. That is we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{+} \underline{s}:\lnot A[\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$. As we have ${\mathcal {M}}\Vdash ^{+} \underline{s}:\lnot A[\mu ]$ it follows that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and ${\mathcal {M}},\mu (\underline{s})\models \lnot A$, and hence that ${\mathcal {M}}, \mu (\underline{s})\not \models A$, from which it follows that ${\mathcal {M}}\Vdash ^{-} \underline{s}:A[\mu ]$, resulting in $\varGamma {>\!\!\!-}\underline{s}:A, \varDelta$ failing in ${\mathcal {M}}$ on $\mu$ as desired. For $(\lnot R)$ suppose that we have $\varGamma {>\!\!\!-}\varDelta , \underline{s}:\lnot A$ failing in some model ${\mathcal {M}}$ on an assignment $\mu$. That is, we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{-} \underline{s}:\lnot A[\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$. From ${\mathcal {M}}\Vdash ^{-} \underline{s}:\lnot A[\mu ]$ it follows that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and ${\mathcal {M}},\mu (\underline{s})\not \models \lnot A[\mu ]$, and hence that ${\mathcal {M}},\mu (\underline{s})\models A[\mu ]$ from which it follows that ${\mathcal {M}}\Vdash ^{+}\underline{s} A[\mu ]$, resulting in $\varGamma , \underline{s}:A{>\!\!\!-}\varDelta$ failing in ${\mathcal {M}}$ on $\mu$ as desired.

$\forall$ -cases: For $(\forall \hbox {L})$ suppose that we have $\varGamma , \underline{s}:\forall x A(x){>\!\!\!-}\varDelta$ failing in a model ${\mathcal {M}}$ on an assignment $\mu$. That is to say, we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{+} \underline{s}:\forall x A(x)[\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$. As we have ${\mathcal {M}}\Vdash ^{+} \underline{s}:\forall x A(x)[\mu ]$ it follows that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and ${\mathcal {M}},\mu (\underline{s})\models \forall x A(x)[\mu ]$. So for all $e \in D(\underline{s})$ we have ${\mathcal {M}}, \mu (\underline{s})\cdot e\models A(x)[\mu ^{\prime }]$ where $\mu ^{\prime }$ is an $x$-variant of $\mu$ for which $\mu (x) = e$. Now by the side condition for the rule we know that for some formula $B$ and (possibly empty) term sequence $\underline{s^{\prime }}$ we have $\underline{s}\cdot t\cdot \underline{s^{\prime }}: B\in \varGamma \cup \varDelta$ from which it follows that $draw^{{\mathcal {M}}}(\mu (\underline{s}\cdot t\cdot \underline{s^{\prime }}))$, and thus that $draw^{{\mathcal {M}}}(\mu (\underline{s}\cdot t))$ by the (Draw) condition. Thus, letting $\mu ^{\prime }(x)=\mu (t)$ it follows that ${\mathcal {M}}, \mu (\underline{s}\cdot x)\models A(x)[\mu ^{\prime }]$. As $\mu ^{\prime }$ is an $x$-variant of $\mu$ it follows that ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ^{\prime }]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ^{\prime }]$. Further, as $\mu ^{\prime }(x)=\mu ^{\prime }(t)$ we have ${\mathcal {M}}\Vdash ^{+}\underline{s}\cdot t:A(t)[\mu ^{\prime }]$, from which we have $\varGamma , \underline{s}\cdot t:A(t){>\!\!\!-}\varDelta$ failing in ${\mathcal {M}}$ on $\mu ^{\prime }$ as desired.

For $(\forall R)$ suppose that we have $\varGamma {>\!\!\!-}\varDelta , \underline{s}:\forall x A(x)$ failing in some model ${\mathcal {M}}$ on an assignment $\mu$. That is to say, we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{-} \underline{s}:\forall x A(x)[\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$. It follows, then, that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and that there is an object $e \in D(\mu (\underline{s}))$ s.t. ${\mathcal {M}},\mu (\underline{s})\cdot e\not \models A(x)[\mu ^{\prime }]$ where $\mu ^{\prime }$ is an $x$-variant of $\mu$ for which $\mu (x) = e$. Given that, by the side condition on $(\forall R)$, the term $a$ does not occur in $\varGamma$, $\varDelta$ or $\underline{s}:\forall x A(x)$ we can simply let our variable assignment assign $e$ to $a$ in which case we have ${\mathcal {M}}, \mu ^{\prime }(\underline{s})\cdot a \not \models A(a)[\mu ^{\prime }]$–which given $draw^{{\mathcal {M}}}(\mu (\underline{s}\cdot a))$ gives us ${\mathcal {M}}\Vdash ^{-}\underline{s}\cdot a: A(a)[\mu ^{\prime }]$. Further, as $\mu ^{\prime }$ is an $x$-variant of $\mu$ it follows that ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ^{\prime }]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ^{\prime }]$ from which it follows that $\varGamma {>\!\!\!-}\varDelta ,\underline{s}\cdot a:A(a)$ fails in ${\mathcal {M}}$ on $\mu ^{\prime }$ as desired.

$(Draw)$ -cases: For the case of $(Draw\hbox {-}L)$ suppose that $\varGamma , \underline{s}\cdot t:\varphi {>\!\!\!-}\varDelta$ fails in some model ${\mathcal {M}}$ on an assignment $\mu$, that is to say that we have ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{+} \underline{s}\cdot t: \varphi [\mu ]$ and ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$. It follows directly that $draw^{{\mathcal {M}}}(\underline{s}\cdot t)$ and hence that $draw^{{\mathcal {M}}}(\underline{s})$ by the (Draw) condition, and that ${\mathcal {M}}, \underline{s}\cdot t\models \varphi [\mu ]$. Thus applying Lemma 1 it follows that ${\mathcal {M}}, \underline{s}\models \varphi [\mu ]$, and so ${\mathcal {M}}\Vdash ^{+}\underline{s}:\varphi [\mu ]$ as desired. The case for $(Draw\hbox {-}R)$ follows similarly.

$(dCut)$ -case: For the case of the rule of $(dCut)$ suppose that the sequent $\varGamma {>\!\!\!-}\varDelta$ fails in the model ${\mathcal {M}}$ on an assignment $\mu$—i.e. that ${\mathcal {M}}\Vdash ^{+}\varGamma [\mu ]$, ${\mathcal {M}}\Vdash ^{-}\varDelta [\mu ]$, and further that for some formula $B$ and term sequent $\underline{s^{\prime }}$ we have $\underline{s}\cdot \underline{s^{\prime }}: B\in \varGamma \cup \varDelta$. From the above it follows by the (Draw) condition that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and so either ${\mathcal {M}}, \mu (\underline{s})\models A[\mu ]$ or ${\mathcal {M}}, \mu (\underline{s})\not \models A[\mu ]$—i.e. that either ${\mathcal {M}}\Vdash ^{+}\underline{s}:A[\mu ]$ or ${\mathcal {M}}\Vdash ^{-}\underline{s}:A[\mu ]$, meaning that one of the sequents $\varGamma {>\!\!\!-}\varDelta , \underline{s}:A$ or $\varGamma , \underline{s}:A{>\!\!\!-}\varDelta$ must fail in ${\mathcal {M}}$ on the variable assignment $\mu$, as desired. $\square$

4 Completeness

What we are going to do here is to construct a reduction tree. We will use reduction trees a few times in what is to follow so we will define the procedure in general terms here so that we can use it in the completeness proofs below. Our presentation below is largely a generalisation of that given in Takeuti (1987).

4.1 Reduction Rules

The first concept we will need is that of a reduction rule, which is a rule which tells us how we can extend our reduction tree. For example, the reduction rule for $(\lnot R)$ has the following form.

We apply this rule to a formula $\underline{s}:\lnot A$ appearing on the RHS of the sequent turnstile by extending our reduction tree by the addition of the node (or in the case of multi-premise rules, nodes) above.

Unlike the reduction rules which one might commonly see in completeness proofs for the classical sequent calculus (like that in Takeuti (1987)), some of our reduction rules can only be applied under certain circumstances. For example, the reduction rule for $(\forall L)$ is of the following form.

where for some $B$ and some $\underline{s^{\prime }}$ we have $\underline{s}\cdot t\cdot \underline{s^{\prime }}:B\in \varGamma \cup \varDelta$

What this means is that in order for us to apply this rule to a formula $\underline{s}:\forall x A(x)$ appearing on the LHS of the sequent turnstile we require that there be some formula of the appropriate form appearing somewhere in the sequent. If the side conditions to a reduction rule are not met, then we do not extend the branch.

We will now explain how we can use reduction rules to construct a reduction tree. This is a tree, each node of which is a sequent. If the tip of a branch in the reduction tree is an axiom then we will say that that branch is closed, otherwise it is open.

Definition 5

Given a sequent ${\mathcal {S}} = \varGamma {>\!\!\!-}\varDelta$, and a set ${\mathbb {R}}$ of reduction rules the ${\mathbb {R}}$ -reduction tree of ${\mathcal {S}}$ is the tree formed by the following iterative procedure.

• Stage 0 At stage 0 we begin with $\varGamma {>\!\!\!-}\varDelta$ as the root node of the tree.

• Stage $n+1$ At stage $n+1$ we apply all of the reduction procedures in ${\mathbb {R}}$ in the order given as many times as possible to every formula introduced at an earlier stage which occurs in the tip of an open branch.

The tree which results of applying this procedure $\omega$-many times is the ${\mathbb {R}}$ -reduction tree of ${\mathcal {S}}$.

Theorem 1

(Completeness) Let ${\mathcal {S}} = \varGamma {>\!\!\!-}\varDelta$ be a sequent. Then either there is a $(dCut)$-free proof of ${\mathcal {S}}$, or there is an urn model in which ${\mathcal {S}}$ fails.

Proof

Given a sequent ${\mathcal {S}}$ let $R_{{\mathcal {S}}}$ be the ${\mathbb {UC}}$-reduction tree of ${\mathcal {S}}$ (Table 1). By the construction of the reduction tree either the tip of every branch in the tree is an axiom (in which case it is trivial work to convert the reduction tree into a proof of ${\mathcal {S}}$) or the tree has a (potentially infinite) open branch. Letting $\varGamma _{0}{>\!\!\!-}\varDelta _{0}$ be ${\mathcal {S}}$ we can think of this branch as being of the form

$$\begin{aligned} \varGamma _{0}{>\!\!\!-}\varDelta _{0}, \varGamma _{1}{>\!\!\!-}\varDelta _{1}, \ldots , \varGamma _{n}{>\!\!\!-}\varDelta _{n}, \ldots \end{aligned}$$

and let ${\varvec{\Gamma }} = \cup \varGamma _{i}$ and ${\varvec{\Delta }} = \cup \varDelta _{i}$. We will now use ${\varvec{\Gamma }}$ and ${\varvec{\Delta }}$ to construct an urn model in which our sequent ${\mathcal {S}}$ fails. Let us define the model ${\mathcal {M}}^{{\mathcal {S}}} = \langle U^{{\mathcal {S}}}, D^{{\mathcal {S}}}, V^{{\mathcal {S}}}\rangle$ as follows.

• $U^{{\mathcal {S}}}$ is the set of all terms from $L^{U}$.

  Table 1 The ${\mathbb {UC}}$-reduction rules

• $D^{{\mathcal {S}}}(\emptyset ) = \{t | \text { for some}\, L\text {-formula}\,A\text { and term sequence}\,\underline{s}, t\cdot \underline{s}{:}A\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}\}$

• $D^{{\mathcal {S}}}(\underline{s}) = \{t | \text { for some}\, L\text {-formula}\,A\text { and term sequence}\,\underline{s^{\prime }}, \underline{s}\cdot t\cdot \underline{s^{\prime }}{:}A\in {\varvec{\Gamma }} \cup {\varvec{\Delta }}\}$

• $V^{{\mathcal {S}}}(F) = \{\langle t_1,\ldots , t_n\rangle | \text {for some sequence of terms}\,s_1, \ldots , s_n,\langle s_1,\ldots , s_n\rangle {:} Ft_1\ldots t_n\in {\varvec{\Gamma }}\}$

All that remains to be done is to show that ${\mathcal {M}}^{{\mathcal {S}}}$ is an urn model, and that ${\mathcal {S}}$ fails in ${\mathcal {M}}^{{\mathcal {S}}}$.

${\mathcal {M}}^{{\mathcal {S}}}$ is an urn model: It is easy to verify that ${\mathcal {M}}^{{\mathcal {S}}}$ satisfies the condition $(Draw)$ and thus is an urn model. Suppose that $D^{{\mathcal {S}}}(\underline{s}\cdot s_{n}) \not = \emptyset$. Then there is some $b$ and some (possibly empty) term sequence $\underline{s^{\prime }}$ s.t. for some formula $A$ we have $\underline{s}\cdot s_{n}\cdot b\cdot \underline{s^{\prime }}:A\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$. But this also means that there is some term sequence $\underline{u}$ s.t. $\underline{s}\cdot s_{n}\cdot \underline{u}:A\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$, and so $s_{n}\in D^{{\mathcal {S}}}(\underline{s})$, as desired.

${\mathcal {M}}^{{\mathcal {S}}}$ is a counter-model to ${\mathcal {S}}$: What we need to show here is that:

$$ \begin{aligned} {\mathcal {M}}^{{\mathcal {S}}}\Vdash ^{+} {\varvec{\Gamma }}[i]\qquad \& \qquad {\mathcal {M}}^{{\mathcal {S}}}\Vdash ^{-}{\varvec{\Delta }}[i], \end{aligned}$$

where $i$ is the variable assignment s.t. $i(x) = x$ for all variables $x$.

We proceed by induction on the complexity of formulas, the basis case following from the definition of $V^{{\mathcal {S}}}$, the cases for the boolean connectives are standard, the only case of interest being that of the quantifiers. We begin by noting that, by the construction of $D^{S}$ that for every $L$-formula $B$ and term sequence $\underline{s}$, if $\underline{s}:B\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$ then $draw^{{\mathcal {M}}^{{\mathcal {S}}}}(i(\underline{s}))$.

Suppose, then, that $\underline{s}:\forall x A(x)\in {\varvec{\Gamma }}$. Then by the $(\forall L\hbox {-}\mathbf{Red})$ reduction step it follows that we have

$$\begin{aligned} \underline{s}\cdot t{:} A(t)\in {\varvec{\Gamma }} \end{aligned}$$

for every term $t$ s.t. for some formula $B$ and term sequence $\underline{s^{\prime }}$ we have $\underline{s}\cdot t \cdot \underline{s^{\prime }}:B\in {\varvec{\Gamma }}$. By the construction of ${\mathcal {M}}^{S}$ these are precisely the terms which are in $D^{{\mathcal {S}}}(i(\underline{s}))$. So by the induction hypothesis it follows that ${\mathcal {M}}^{S}\Vdash ^{+} \underline{s}\cdot t: A(t)[i]$ for all $t \in D^{{\mathcal {S}}}(i(\underline{s}))$, and thus ${\mathcal {M}}^{{\mathcal {S}}}, i(\underline{s}\cdot t)\models A(t)[i]$. From which it follows that ${\mathcal {M}}^{{\mathcal {S}}}\Vdash ^{+} \underline{s}:\forall x A(x)[i]$ as desired.

Suppose, now, that $\underline{s}:\forall x A(x)\in {\varvec{\Delta }}$. Then by the $(\forall R\hbox {-}\mathbf{Red})$ reduction step it follows that we have

$$\begin{aligned} \underline{s}\cdot a: A(a)\in {\varvec{\Delta }}. \end{aligned}$$

So by the induction hypothesis it follows that ${\mathcal {M}}^{{\mathcal {S}}}\Vdash ^{-}i(\underline{s})\cdot a:A(a)[i]$, and thus that ${\mathcal {M}}^{{\mathcal {S}}}, i(\underline{s}\cdot a)\not \models A(a)[i]$, from which it follows that ${\mathcal {M}}^{{\mathcal {S}}}, i(\underline{s})\not \models \forall x A(x)[i]$, giving us ${\mathcal {M}}^{{\mathcal {S}}}\Vdash ^{-}\underline{s}:\forall x A(x)[i]$, as desired. $\square$

This gives us the following corollary.

Corollary 1

The rule of $(dCut)$ is eliminable from UC.

5 Rantala’s Conditions

The system described in the previous section is sound and complete relative to the class of all urn models, as we have defined them above. As noted above, though, this is not quite the class of urn models which Rantala is concerned with, his models also satisfying the conditions $(Ran1)$ and $(Ran2)$ below.

$$\begin{aligned} (Ran1)&: D({\emptyset }) = U\\ (Ran2)&: D(\langle a_{1}, \ldots , a_{n}\rangle )\not = \emptyset \quad \textit{if and only if } a_{n} \in D(\langle a_{1}, \ldots , a_{n-1}\rangle ). \end{aligned}$$

What we will do in this section is to look at extensions of the sequent calculus UC which are sound and complete w.r.t. models which satisfy the above conditions (or in the case of $(Ran1)$ a near neighbour thereof). We begin by looking at the sequent calculus for models which satisfy $(Ran2)$.

5.1 The Condition $(Ran2)$

In order to capture the logic of Urn models which satisfy $(Ran2)$ we need to extend our system by the following three rules—two structural, and one additional $(\forall L)$-rule.

where in all three rules $a$ is an eigenvariable (i.e. $a$ does not occur in the lower sequent in any of these three reduction rules), and $\varphi$ is a quantifier free formula. Call the extension of UC by the above rules UCR2.

These three rules force every draw to always be extendable. To see this first note that all three rules are sound in urn models which satisfy $(Ran2)$.

Proposition 2

UCR2 is sound for the class of all urn models which satisfy $(Ran2)$.

Proof

For $(\forall L)\hbox {-}{Ran2}$ suppose that we have ${\mathcal {M}}\Vdash ^{+}\underline{s}: \forall x A(x)[\mu ]$— i.e. that $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ and ${\mathcal {M}}, \mu (\underline{s})\models \forall x A(x)[\mu ]$. From $draw^{{\mathcal {M}}}(\mu (\underline{s}))$ we get that there must be some object $e\in D(\mu (\underline{s}))$ by $(Ran2)$. So we can simply let $\mu (a) = e$ and thus we have ${\mathcal {M}}, \mu (\underline{s}\cdot a)\models A(a)[\mu ]$ as desired.

For the $(Ran2L)$ case suppose that we have ${\mathcal {M}}\Vdash ^{+}\underline{s}:\varphi [\mu ]$. Then we have that $\mu (\underline{s})$ is a draw from ${\mathcal {M}}$ and thus, by $(Ran2)$ that there is some object $\mu (\underline{s})\cdot b$ is also a draw. Given that we also have ${\mathcal {M}}, \mu (\underline{s})\models \varphi [\mu ]$ it follows by Lemma 1 that ${\mathcal {M}}, \mu (\underline{s}\cdot a)\models \varphi [\mu ]$ where $\mu (a) = e$, yielding ${\mathcal {M}}\Vdash ^{+}\underline{s}\cdot a: \varphi [\mu ]$ as desired. The case of $(Ran2R)$ follows similarly. $\square$

Lemma 2

Suppose that ${\mathcal {S}}$ is a UCR2-unprovable sequent and that $R$ is a reduction tree for ${\mathcal {S}}$ for which the ${\mathbb {UCR}}2$ (and hence ${\mathbb {UC}}$) reduction rules have been applied, and that

$$\begin{aligned} \varGamma _{0}{>\!\!\!-}\varDelta _{0}, \ldots , \varGamma _{n}{>\!\!\!-}\varDelta _{n}, \ldots \end{aligned}$$

is an open branch in $R$ (there is guaranteed to be such a branch as the sequent is unprovable). Then for all $i$, if $\underline{s}:A \in \varGamma _{i}\cup \varDelta _{i}$ then for some $j$, there is a quantifier-free formula $\varphi _{A}$ and a sequence of terms $\underline{s^{\prime }}$ s.t. $\underline{s}\underline{s^{\prime }}:\varphi _{A}\in \varGamma _{j}\cup \varDelta _{j}$.

Proof

We prove something stronger, namely that for every formula $A$ there is some such atomic formula (or formulas) $\varphi _{A}$ s.t. for some sequence of terms $\underline{s^{\prime }}$ we have $\underline{s}\underline{s^{\prime }}:\varphi _{A}\in \varGamma _{j}\cup \varDelta _{j}$.

To prove this we show that for every formula $\underline{s}:A\in \varGamma _{k}\cup \varDelta _{k}$, there is a formula $B$ of lower complexity such that, for some sequence of terms $\underline{s^{\prime }}$, $\underline{s}\underline{s^{\prime }}:B\in \varGamma _{k}\cup \varDelta _{k}$.To see this note that the reduction steps for ${\mathbb {UC}}$ guarantee that at each stage we can produce a formula of the required kind whenever the main connective of $A$ is not a quantifier. In the case where the main connective of $A$ is $\forall$ either we can produce the appropriate formula using $(\forall R\hbox {-}\mathbf{Red})$, or using $(\forall L\hbox {-}\mathbf{Red})$ (if the conditions are met), or (and here is where we require ${\mathbb {UCR}}2$) we can produce it using $(\forall L\hbox {-}Ran2\hbox {-}\mathbf{Red})$. $\square$

Proposition 3

UCR2 is complete for the class of all urn models which satisfy $(Ran2)$.

Proof

The proof is just like that of Theorem 1, except that we now create a ${\mathbb {UCR}}2$ reduction tree for our sequent ${\mathcal {S}}$ (Table 2). To verify that this results in a countermodel to ${\mathcal {S}}$ which satisfies condition $(Ran2)$ suppose that $s_{n+1} \in D^{{\mathcal {S}}}(\langle s_1, \ldots , s_n\rangle )$. Then by the construction of ${\mathcal {M}}^{{\mathcal {S}}}$ there must be some formula of the form $\langle s_1, \ldots , s_{n+1}\rangle \cdot \underline{s^{\prime }}: B\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$. If any such formula has a non-empty sequence $\underline{s^{\prime }}$ then we are done, so suppose that all such formulas are of the form $\langle s_1, \ldots , s_{n+1}\rangle : B$. Such a formula must have been in the tree at some stage $k$, and so we know by Lemma 2 that there is some later stage at which we have some sequence of terms $\underline{s^{\prime \prime }}$ and some quantifier-free formula $\varphi$ s.t. $\langle s_1, \ldots , s_{n+1}\rangle \cdot \underline{s^{\prime \prime }}: \varphi \in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$. Again, if $\underline{s^{\prime \prime }}$ is non-empty then we are done, so suppose it is empty. Then by (depending on whether it is in ${\varvec{\Gamma }}$ or ${\varvec{\Delta }}$) either the $(Ran2\hbox {-}L\hbox {-}\mathbf{Red})$ or $(Ran2\hbox {-}R\hbox {-}\mathbf{Red})$ reductions we know that, for some term $a$ that $\langle s_1, \ldots , s_{n+1}\rangle \cdot a:\varphi \in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$, and so by construction of ${\mathcal {M}}^{{\mathcal {S}}}$ we have that for some term $a$, $a\in D^{{\mathcal {S}}}(\langle s_1, \ldots , s_{n+1}\rangle )$, as desired. $\square$

5.2 $(Ran1)$ and Almost-Rantala Models

What we will do in this section is to describe a system, which we will call UCRant- which agrees with the system described by Rantala when every formula which occurs in a sequent is a sentence.² In fact, UCRant- is a slightly stronger system, being sound and complete w.r.t. the class of all urn models which satisfy both $(Ran2)$ as well as the following condition:

$$\begin{aligned} \left( Ran1^{\prime }\right) {:}\qquad t\in D(\underline{s})\Rightarrow t\in D(\emptyset ). \end{aligned}$$

This condition makes each $D(\underline{s})$ be a subset of $D(\emptyset )$. Let us call urn models which satisfy $(Ran1^{\prime })$ and $(Ran2)$ almost-Rantala models, and those which satisfy $(Ran1)$ and $(Ran2)$ Rantala models. It is relatively simple to see that any almost-Rantala model ${\mathcal {M}} = \langle U, D, V\rangle$ can be transformed into a Rantala model ${\mathcal {M}}^{r} =\langle U^{r}, D, V^{r}\rangle$ where $U^{r}$ is the union of all $D(\underline{s})$, where $\underline{s}$ is a sequence of objects from $D(\emptyset )$, and where $V^{r}$ is just $V$ restricted to $U^{r}$ in the obvious way. These two models are equivalent in the sense that for all $L^{U}$-formulas $\alpha$ (recalling that these formulas do not contain individual constants) and all assignments $\mu$ which are restricted to $U^{r}$ we have ${\mathcal {M}}\models \alpha [\mu ]$ iff ${\mathcal {M}}^{r}\models \alpha [\mu ]$. In particular this means that for all $L^{U}$-formulas of the form $\emptyset : A$ where $A$ is a sentence we have ${\mathcal {M}}\models \emptyset : A[\mu ]$ iff ${\mathcal {M}}^{r}\models \emptyset : A[\mu ]$ for all assignments $\mu$, and so almost-Rantala and Rantala models agree on all sentences when our language does not contain individual constants.

Table 2 The ${\mathbb {UCR}}2$-reduction rules

Let UCRant- be the result of adding the following rules to UCR2.

What we will now show is that the system UCRant- is sound and complete w.r.t. the class of all almost-Rantala models. Note that our proofs below do not show that the result of adding the above rules to UC forces it to satisfy $(Ran1')$, as our proofs make heavy use of Lemma 2.

Proposition 4

UCRant- is sound for the class of all urn models which satisfy both $(Ran1')$ and $(Ran2)$.

Proof

What needs to be shown is that $(Ran1'\hbox {-}L)$ and $(Ran1'\hbox {-}R)$ are sound in models which satisfy $(Ran1')$. We treat just the cases of the left rule here (the right rule following similarly).

Suppose that a conclusion of an application of $(Ran1'\hbox {-}L)$ were to fail in a model ${\mathcal {M}}$ on an assignment $\mu$. Then in particular we would have that ${\mathcal {M}}\Vdash ^{+}\underline{s}\cdot t\cdot \underline{u}:\varphi [\mu ]$, and so $draw^{{\mathcal {M}}}(\mu (\underline{s}\cdot t\cdot \underline{u}))$. and ${\mathcal {M}}, \mu (\underline{s}\cdot t\cdot \underline{u})\models \varphi [\mu ]$. By $(Draw)$ it follows that $\mu (t)\in D(\underline{s})$ and so by $(Ran1')$ that $\mu (t)\in D(\emptyset )$, and thus that $\mu (t)$ is a draw from ${\mathcal {M}}$. Then by Lemma 1 it follows that ${\mathcal {M}}, \mu (t)\models \varphi [\mu ]$ and thus ${\mathcal {M}}\Vdash ^{+}t:\varphi [\mu ]$ as desired. $\square$

Proposition 5

UCRant- is complete for the class of all urn models which satisfy $(Ran1^{\prime })$ and $(Ran2)$.

Proof

The proof is just like that of Theorem 1, except that we now create a ${\mathbb {UCRANT}}-$ reduction tree for our sequent ${\mathcal {S}}$ (Table 3). That this results in a countermodel to ${\mathcal {S}}$ which satisfies condition $(Ran2)$ follows as in Proposition 3. All that remains to be shown is that the resulting countermodel satisfies $(Ran1^{\prime })$.

Table 3 The ${\mathbb {UCRANT}}-$-reduction rules

Suppose, then, that $t\in D^{{\mathcal {S}}}(\underline{s})$ for some sequence $\underline{s}$. Then by the construction of ${\mathcal {M}}^{{\mathcal {S}}}$ it follows that for some formula $B$ and sequence of terms $\underline{s^{\prime }}$ we have $\underline{s}\cdot t\cdot \underline{s^{\prime }}:B\in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$. Then by Lemma 2 there is some sequence of terms $\underline{u}$ and variable free formula $\varphi$ s.t. $\underline{s}\cdot t\cdot \underline{s^{\prime }} \cdot \underline{u}:\varphi \in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$. So by either ${(Ran1^{\prime }\hbox {-}L)\hbox {-}\mathbf{Red}}$ or ${(Ran1^{\prime }\hbox {-}R)\hbox {-}\mathbf{Red}}$ it follows that $t:\varphi \in {\varvec{\Gamma }}\cup {\varvec{\Delta }}$, and so by the construction of $D^{{\mathcal {S}}}$ that $t\in D^{{\mathcal {S}}}(\emptyset )$ as desired. $\square$

6 Conclusion

One of the things which we have endeavoured to do here in our proof theoretic investigation of urn logic is to provide the first steps towards a more general framework for thinking about the quantifiers more generally. In particular the alterations to the language we made in Sect. 3 were made specifically in order to induce extra structure into our formulas (and thus into our sequents) which we could adjust without altering the operational rules for our quantifiers in order to validate further inferences. Our approach here has been directed specifically at the goal of giving a proof theoretic characterisation of urn logic, rather than a general investigation of this approach to the proof theory of the quantifiers, the more general study having to wait until another occasion.