Introduction

The grade of structural steel is a fundamental building material in today’s construction and manufacturing sectors, owing to its unique advantages. Over time, these materials may be deformed due to usage or surface defects. Corrosion or cracks on the steel’s surface can degrade its structure, eventually rendering it unusable. For instance, in the manufacturing sector, cracks and scratches can occur on the surfaces of rolling mill rolls during hot and cold rolling processes. These rolls are crucial, and any deformation directly damages both the roll itself and the products it produces. This adverse impact is not limited to the final product but also extends to undesirable influences on process times. Steel used in industry is subjected to various factors such as compression, tension, pressure, friction, and heat. The structural integrity of steel, when exposed to these conditions, is of paramount importance for its strength, performance, and safety. Structures requiring robust and long-lasting materials, such as missile barrels, ship hulls, steel bridges, high voltage poles, wave breakers, and underwater gas pipes, underscore the significance of material science in construction and production stages (Li & Chen, 2023; Jiang et al., 2023; Liang et al., 2022; Huang et al., 2020). Analyzing the mechanical properties of metallic materials through mechanical testing, metallography, chemical analysis, corrosion testing, dimensional measurement, and non-destructive testing allows for an evaluation of product quality (Singh, 2020).

As material deformation increases, the performance of the material decreases, and its service life is shortened. Several factors influence the life of a material (Dieter & Bacon, 1976). Environmental factors, usage conditions, and exposure directly affect material longevity. While some deformations are visible, many are not. In instances where deformation is not visible, materials can be assessed using both destructive and nondestructive testing methods. The microstructure of a material provides critical information to experts in materials science. By examining the phase compositions, grain sizes, and grain boundary characteristics, experts can make preliminary assessments about a material’s condition, including hardness, strength, heat treatment history, and inclusions. Observing a material’s microstructure allows for the identification of deformation effects. Recent studies in materials science have introduced methods for detecting early stages of deformation in steel microstructures. Gathering information about the grain structure of the alloys forming the material and the shape of the grains plays a crucial role in predicting the deformation rate (Bulzak et al., 2022; Chaboche, 1988, 1981). However, such investigations are time-consuming and subjective, as they rely on physical observations, making it challenging to obtain reliable information.

Materials can be used for extended periods, with a few precautions taken before the completion of their service life. For instance, high-cost industrial products, such as rolling mill rolls, can be inspected for minor damage and repaired using various methods before serious defects such as fracture and disintegration manifest, allowing for their reutilization. This proactive approach permits reutilization, as evidenced in the study by Gorbatyuk and Kochanov (2012). The use of railways in the transportation sector is a remarkable example. While the lifetime of rails on straight roads is known to be twenty to twenty-five years, this period decreases to two to three years on narrow winding roads. Defects in rails are detected in advance and repaired at a low cost. Thus, the service life of the material was extended. As explained by Zhou (2021), these expensive and difficult-to-manufacture products can be repaired in time and continue to be used for a long time. Considering the global challenges related to the availability issue of raw materials, the effective and long-term utilization of materials through restoration is of vital importance. The material used in this study, S235-JR structural steel, which is widely used in the aforementioned fields, is primarily composed of iron and carbon, as indicated in Table 1.

Understanding material fatigue and fracture mechanisms plays a crucial role in predicting and preventing potential future failures. This way, unexpected failures caused by material deformation and the economic losses they may lead to can be avoided. For example, damages or breakages in high-speed train tracks can lead to irreparable consequences. The detection of damages and defects in the inner and outer surfaces of high-pressure boilers is of vital importance. Such materials pose significant risks to both human health and the environment. Similarly, steel buildings and bridges can be cited as examples. The importance of material deformation analyses cannot be overlooked or disregarded. When conducting deformation analysis, obtaining reliable results is an indisputable necessity. S235-JR structural steel, as exemplified in the above-mentioned areas, is widely used in various other sectors such as construction, automotive, and machinery manufacturing.

Table 1 Chemical composition of the S235-JR steel used in the study (İrsel, 2022)
Full size table

In the field of metallurgy, the structural integrity of steel components is compromised over time due to environmental conditions. The exertion of mechanical loads or stress factors induces the development of weak structural areas within the internal and surface microstructures of these materials (Yu et al., 2009).

Literature studies have demonstrated that microstructural characterization of materials can reveal physical properties such as damage extent, weld integrity, durability, flexibility, and strength through the analysis of phase structures (Huang et al., 2020; Bostanabad et al., 2018; Iren et al., 2021; Cameron & Tasan, 2022; Shen et al., 2021). The advent of computer-aided systems has significantly facilitated the work of researchers, while the rapid advancements in artificial intelligence, particularly over the past decade, have revolutionized the scope of research in materials science. The application of AI-supported software for processing or analyzing microstructure images markedly enhances the quality and volume of derived information (Iacoviello et al., 2017; Warmuzek et al., 2021; Tsutsui et al., 2022, 2019). Notably, in tasks such as classification, segmentation, and labeling, AI has enabled the identification of features in images that are imperceptible to the human eye, yielding impressive results (Iacoviello et al., 2017; DeCost & Holm, 2015; Panda et al., 2019; Gola et al., 2019; Liu et al., 2023; Zhu et al., 2022; Motyl & Madej, 2022).

Currently, the field of machine learning (ML), which is an integral part of the broader artificial intelligence spectrum, is advancing at a notable pace. Sarkar and his team (2021) present a fuzzy combination approach for microstructure image classification. In their study, they utilized an ultra-high carbon steel dataset, comprising images of three microstructural classes: Martensite, pearlite, and spheroidite. Feature extraction was performed using the rotational local tetra pattern feature descriptor. The extracted features were then fed into three different classifiers: support vector machine (SVM), random forest (RF), and K-nearest neighbors (kNN). Unlike traditional classifier combination methods, the proposed approach nonlinearly combines the relative importance of different classifiers through subjective evaluations and fuzzy membership functions. This approach provides higher classification accuracy compared to other standard classifier combination methods. The microstructure images were classified with a success rate of over 96%.

ML algorithms necessitate the manual extraction of features from images (Holm et al., 2020). Gola et al. (2018) acquired microstructure images of steel plates featuring martensite, pearlite, and bainite phases through LOM and Scanning Electron Microscopy (SEM), and conducted phase classification using SVM. They demonstrated that the classification success rate for the three phases was 84.80%. Although the incorporation of computer support and, by extension, artificial intelligence into this field eases the workload of researchers, the reliance on expert knowledge for these studies, compared to current DL algorithms, and the requirement for manual feature extraction in images can be seen as a reflection of the nascent stage of artificial intelligence at the time of the aforementioned research.

Considering that artificial intelligence encompasses all of these processes, it’s accurate to position ML and DL algorithms as foundational elements within this broader framework. DL, in particular, excels in the analysis, classification, and segmentation of microstructure images. Techniques like transfer learning within the DL domain have proven to be more sophisticated and effective than traditional ML approaches (Muñoz-Rodenas et al., 2023). DL algorithms are capable of autonomously extracting features from images, facilitating the detection and prediction of surface defects, stress-crack areas, and classifications of materials’ microstructures using DL methods (Zhu et al., 2022; Tsopanidis et al., 2020; Ding et al., 2023; Chen et al., 2023). Furthermore, the examination of a material’s microstructure can yield valuable insights into its chemical composition and processing history (Farizhandi & Mamivand, 2022; Farizhandi et al., 2022).

Muñoz-Rodenas et al. (2023), conducted a study utilizing ML and DL for the microstructure analysis and classification of low carbon steels, based on different heat treatments. Samples of low carbon steel, subjected to various heat treatments, were examined with optical microscopy, yielding microstructure images of these controlled deformed steels. From these images, a dataset was created and labeled according to processes such as annealing, quenching, and quenching-tempering. The application of DL algorithms, particularly GoogLeNet and residual neural network (ResNet), resulted in a high success rate of 99% accuracy. This highlights the superiority of DL techniques over traditional ML algorithms like RF, SVM, and simple linear iterative clustering, which demonstrated lower accuracy rates. This research illustrates the enhanced effectiveness of DL in classifying the microstructures of low carbon steels, thereby contributing significantly to the advancement of microstructure recognition research.

Predicting fatigue damage plays a pivotal role in material engineering and durability analysis. Akhil Thomas and his colleagues investigated the application of graph neural networks in identifying fatigue damage within ferritic steels and in forecasting the orientation of such damages. The specimens underwent fatigue testing, and their microstructures were visualized through electron backscatter diffraction (EBSD). A unique dataset was compiled from these microstructure images (Durmaz & Thomas, 2023; Durmaz et al., 2022). During the analysis of microstructure images, grain structures and dislocations within these grains were pinpointed to assess deformations. The emergence of “slip markings” and potential cracks within the grains was noted. Interestingly, areas adjacent to the grain boundaries where deformation was identified exhibited less or no deformation. The efficacy of various ML algorithms was evaluated against the graph convolutional network with principal component analysis (GCN-PCA) model. The findings suggest that graph-based models, conceptualizing data as networks with nodes and edges, are more adept at capturing the intricate relationships and dependencies inherent in the data (Thomas et al., 2023).

In another study, Khurjekar et al. (2023) examined the applicability of DL methods for classifying microstructures in materials science. Experiments conducted on the microstructure data of alumina monoliths obtained through EBSD were used to test the classification success of the DL algorithms. Specifically, the convolutional neural network (CNN) algorithm achieved an accuracy rate exceeding 90% in classifying nontextured and textured microstructures. This high success rate demonstrates the potential of DL algorithms for microstructure classification. Consequently, this study highlights the significance of employing DL methods in the classification of microstructures in materials science, indicating that they can make substantial contributions to the material discovery process. It is anticipated that increasing the amount of data used in this study will also increase the success rate.

Mohammadzadeh and Lejeune (2022) developed a CNN-based DL model specifically designed to predict crack paths in materials, utilizing a dataset known as Mechanical MNIST Lejeune (2020). This model, trained on the Mechanical MNIST dataset, demonstrated its capability to predict the mechanical behavior of new datasets with remarkable accuracy. Impressively, it achieved an accuracy rate of up to 98.5% on the Mechanical MNIST fashion dataset. Moreover, when applied to the Mechanical MNIST crack-path dataset, the same model secured an accuracy rate of up to 96.5%.

A study was conducted by Satterlee et al. (2023) on the automatic detection of pores within the binder jetting process, a technique employed in the fabrication of metal parts. DL methods, notably the Faster R-CNN and YOLOv5 algorithms, were evaluated in their study. Through the utilization of data augmentation techniques, a modest dataset of 67 images was expanded into a more substantial dataset comprising 3966 images. Despite the dataset’s limited size, an 88% success rate was achieved using the YOLOv5 model, whereas the success rate of the Faster R-CNN model was limited to 75%. Additionally, the YOLOv5 model’s training concluded within a few hours, contrasting with the several weeks required for the Faster R-CNN model. It is posited that the success rate can be further enhanced through an increase in data volume and the employment of masking and polygon-outlining algorithms.

Warmuzek et al. (2021) compiled a dataset of iron and aluminium alloys to evaluate DL architectures for phase detection from microstructure images. Although the dataset was unbalanced and modest in size, phase detection, including twigg, petal, polyhedron, sphere, dendrite, needle, and chinese script phases, was accomplished with an accuracy exceeding 91.2% using the DenseNet201 architecture.

Azimi et al. (2018) introduce a novel DL approach for the microstructural classification of low carbon steels, focusing on the identification of phases such as martensite, tempered martensite, bainite, and pearlite. The dataset employed encompasses images of steel microstructures obtained via SEM and LOM. Utilizing Fully Convolutional Neural Networks (FCNNs), a pixel-wise microstructural classification method was applied, achieving an impressive accuracy of 93.94%. The study underscores the potential of DL approaches in microstructural classification, demonstrating these methods as an objective and reliable alternative for steel quality assessment. However, the research notes that the classification of certain microstructural classes, like bainite, may lead to misclassifications due to their smaller size and appearance variability. Additionally, the limited size and scope of the dataset might affect the model’s generalizability across various steel types and microstructures.

Tsutsui et al. (2022) subjected low-carbon steel of identical composition to eight different heat treatments and generated two distinct datasets from SEM images using different emission methods (field emission and tungsten). These datasets were trained using the ResNet50 architecture after being combined equally. It was observed that mixing both sources yielded an average accuracy that exceeded 98%. Training ResNet50 with only one of the datasets resulted in a 64% accuracy rate. A study demonstrated that the acquisition method for microstructure images significantly influences the outcomes.

Although these studies on microstructure images considerably advance the field of materials science, they fail to provide insights into the deformation rate of materials. Nonetheless, the impact of deformation on the structural phases of materials, changes in the grain structure, and other aspects have been explored using contemporary DL techniques. The findings from these limited studies hold particular value for product quality in industrial production (Wang et al., 2022, 2023).

The temperature significantly affects material aging. The study by Vejdannik and Sadr (2016) on the changes in the microstructures of Nb-based alloys at high temperatures and the classification of these changes is noteworthy in this field. The Nb-based alloys were subjected to thermal aging at \(650^\circ \text {C}\) and \(950^\circ \text {C}\) for durations of 10, 100, and 200 hour, and the changes were observed using ultrasonic signals. During this process, alterations in the alloy microstructure were examined through the analysis of the reflected ultrasonic signals and characterized using classification algorithms. This approach enabled the determination of the alloy condition during the thermal aging process and provided insights into the potential maintenance requirements. For the classification task, the probabilistic neural network (PNN) algorithm Azizi (2018), which is a DL algorithm, was employed. The success rates of the PNN algorithm in these studies were reported to be 97.0% at \(650^\circ \text {C}\) and 83.5% at \(950^\circ \text {C}\).

Medghalchi et al. (2020) focused on a study examining damage analysis in the microstructure of steel materials. Microstructural images were obtained by deforming the prepared tensile specimens through uniaxial to biaxial straining tensile tests. Using data augmentation techniques, 6000 images with dimensions of \(250 \times 250\) were generated. Researchers have developed a method using a CNN model to automatically classify damage in the microstructure of steel materials, known as inclusion, martensite crack, notch effect, interface decohesion, and shadowing. This method has been particularly utilized for analyzing the damage that occurs during the shaping of steel materials. Details such as the layers of the employed CNN model and hyper-parameters were not provided. It is feasible to conduct segmentation studies with algorithms such as YOLO, in addition to classification studies with popular DL models such as EfficientNet, Visual Geometry Group (VGG), and ResNet, which would increase the success rate of classification work.

Wang et al. (2022) studied the segregation of the \(\delta \) phase by looking at the SEM microstructure images of Inconel 718 alloy. The detection of the \(\delta \) phase along the grain boundaries is also important as it affects the mechanical properties of the material. The 718 alloy was subjected to a compression test at different strain rates: no strain, strain=0.1 (which means the material elongated to 10% of its original length), strain=0.3, and strain=0.5, resulting in 3072 microstructure images obtained. In all images of this dataset, the \(\delta \) phase at the grain boundaries was manually marked. Then, they detected the \(\delta \) phase with a using a CNN-based hybrid regression model and compared their results with ResNet18, ResNet50, ResNet152, VGG16, VGG19 DL-based networks.

Wang et al. (2023) in their other study, they deformed Inconel 718 alloy by subjecting it to tensile test and obtained 560 microstructure images with \(256 \times 256\) pixels by SEM. With these images, they trained a DL network called predictive recurrent neural network (PredRNN). The model examined the first 10 microstructures based on temporal deformation and successfully predicted subsequent deformation effects. They predicted that success would be further improved by increasing the number of images.

When the literature is examined, it is possible to access a large amount of data on the material by examining its microstructure. In the aforementioned studies, it was observed that deformation detection is performed through microstructures using advanced computer vision techniques, such as DL, but the extent of deformation and deformation classification has not been studied. This study aims to fill this gap in literature.

Recent research has elucidated that the microstructure of a material critically influences its mechanical, physical, and chemical properties, further indicating that changes within the microstructure can ascertain the rate of deformation. This study investigated the correlation between microstructure images and the lifespan of structural steel S235-JR through the application of artificial intelligence techniques. Integrating artificial intelligence techniques, including ML and DL algorithms, into materials science has yielded significant advancements, offering sophisticated tools for analyzing and characterizing material microstructures. As underscored in the literature review, the use of DL architectures for classifying microstructure images has proven to be effective in autonomously detecting intricate patterns and attributes.

Building on this foundation, our work specifically focuses on the use of state-of-the-art algorithms in this field, such as VGG and ResNet, to correlate the microstructure images of S235-JR structural steel with its mechanical deformation. By using the original dataset and transfer learning methods, we aim to expand the existing body of knowledge and improve the accuracy of microstructure classification. The promising results from our classification process highlight the potential of DL in unraveling the complex relationship between the microstructure and material deformation, leading to advances in materials science and engineering. Furthermore, the new five-class dataset generated in this study will contribute to the expanding range of labeled images available for future research.

Another objective of this study is to propose a methodology enabling material manufacturers and testing centers to perform deformation analysis of structural steels quickly and reliably. In conclusion, our research aims to fill a gap in material deformation detection and material life determination through advances in materials science and the application of DL techniques. In doing so, we aim to explore how artificial intelligence and DL techniques can be used to analyze material deformation and overcome traditional methods in materials science. In addition, this study presents a new approach to material deformation analysis by combining advances in materials science and artificial intelligence applications.

Materials and methods

Each step of the proposed methodology is discussed here, from the material deformation stages, obtaining data from deformed material at different rates, to the classification of these data using artificial intelligence techniques. The proposed methodology includes preprocessing steps, dimensioning, segmentation of the image into training, validation and testing, fine tuning of CNN models, training of models, extraction of feature vectors of CNN and classification. The general procedure of the proposed methodology is shown in Fig. 1.

Fig. 1
figure 1

Classification of deformation rate via DL network

Full size image

Dataset

In this study, we analyzed S235-JR structural steel, the chemical constituents of which are detailed in Table 2 and the appearance shown in Fig. 2. The steel was subjected to deformation at different rates and divided into five classes, resulting in a unique dataset comprising 10000 microstructural images.

Fig. 2
figure 2

Dimensional drawing of S235-JR structural steel tensile specimen

Full size image

The specimen size was set to 100 mm, which is widely accepted in the literature (Fig. 2). The specimens were numbered consecutively from 1 to 10, at equal intervals. Tensile tests were performed on the prepared specimens in the laboratory in accordance with the TS EN ISO 4136 standard using an INSTON model tensile testing machine with a capacity of 100 kN at a speed of 1 mm/min.

Table 2 Technical properties of S235-JR construction steel
Full size table

Knowing the mechanical properties of materials is directly related to their field of application. Properties such as strength, hardness, brittleness, and fatigue are among the most significant mechanical properties. In this study, we focused on strength and fatigue, which are crucial for determining the lifespan of materials. The stress-strain diagrams of the specimens subjected to tensile tests are shown in Fig. 3. It is observed that the deformation process can be divided into three stages: the elastic deformation zone, the uniform plastic deformation zone, and the non-uniform plastic deformation zone.

In the elastic deformation zone, the material deforms under the applied stress but returns to its original shape once the stress is removed. The uniform plastic deformation zone is characterized by permanent plastic deformation, where the material slightly alters its shape. The non-uniform plastic deformation zone is marked by significant plastic deformation, leading to considerable changes in the material’s shape. Because this study focuses on the life analysis of the material, the damage in the plastic deformation region was investigated.

As shown in Fig. 3, sample number 5 has fractured. Taking into consideration the yield strength, necking, and fracture points of the fractured sample, certain areas stand out. These are: the 7 mm point, where the yield strength threshold is exceeded and a clear deterioration in the material structure can be observed; the 14 mm point, which represents the maximum stress value (ultimate tensile strength); and the 21 mm points, indicating the specimen’s stable state just before fracturing. The fact that these points are almost equidistant from each other in terms of deformation ratio is particularly noteworthy. The selection of deformation categories in this study is based on these observations.

Fig. 3
figure 3

S235-JR Structurel steel stress-strain diagram

Full size image

When the catalog information of the S235-JR structural steel was examined, it was found that the total elongation amount was 26% (Table 2). In measuring the fractured specimen, the total elongation was observed to be approximately 26 mm. This confirms the consistency of the specimen with the catalog information. In addition to the fractured specimens, the other specimens were subjected to deformations of 7, 14, and 21 mm in the tensile tests. The as-received specimens were included in this examination. The properties of the five classes with different deformation rates are provided below.

* As-received specimen category: This category comprised undeformed and unused specimens.

* Specimen elongation category of 7 mm: The specimens in this category were subjected to a tensile test, which resulted in an elongation of 7 mm. The rationale for selecting this category is to surpass the elastic deformation zone, where deformation occurs effectively.

* Specimen elongation category of 14 mm: The specimens in this category underwent a tensile test, resulting in an elongation of 14 mm. This category was selected because the material reaches its maximum stress value (ultimate tensile strength).

* Specimen elongation category of 21 mm: The specimens in this category underwent a tensile test, resulting in an elongation of 21 mm. This category was selected because it is close to the fracture point and is the most pronounced point within the uniform plastic deformation zone.

* Fractured specimen category: The specimens in this category were subjected to tensile tests to determine their tensile strength until the point of fracture.

Following the tensile tests and categorization described above, the average elasticity modulus (\(E\)) of the S235-JR structural steel specimens was calculated using Eq. (1)

$$\begin{aligned} E = \frac{1}{n} \sum _{i=1}^{n} \frac{\Delta \sigma _i}{\Delta \varepsilon _i} \end{aligned}$$
(1)

Here, \(E\) represents the average elasticity modulus, \(\Delta \sigma _i\) denotes the measured stress increase on the i-th test specimen, and \(\Delta \varepsilon _i\) signifies the measured strain increase on the same test specimen. The summation \(\sum _{i=1}^{n}\) is performed across all test specimens, and \(n\) denotes the total number of measurements.

The average elasticity modulus obtained reflects the material’s capacity for deformation under stress, thereby offering significant insights into its mechanical properties. Classifying specimens according to distinct deformation rates enhances the comprehensive understanding of the steel’s performance under various loading conditions.

The as-received specimen was sectioned at the midpoint, from which a segment was extracted. For other categories, the area exhibiting the most significant deformation was precisely measured with calipers to identify the region of maximal elongation (indicated by the minimal cross-sectional area). This specific region was then excised from the main specimen. Classical metallographic techniques were utilized to obtain microstructure images from segments taken from deformed specimens. As described in the literature, these techniques sequentially include mounting, coarse and fine grinding, polishing, and etching with a 2% nital solution. Microstructure images were acquired using LOM. A schematic overview of these processes is presented in Fig. 4.

Fig. 4
figure 4

Summary of the dataset creation method

Full size image

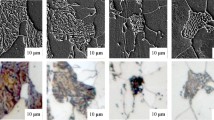
As a result of the conducted procedures, five distinct classes characterized by varying degrees of deformation were established. Each class comprises 2000 microstructure images with a resolution of \(256 \times 256\) pixels, contributing a total of 10000 images to the scientific community. Representative data examples from each class are illustrated in Fig. 5, while the specific properties of the classes are detailed in Table 3.

Table 3 Categories and number of microstructure images of the original dataset created
Full size table

The model

VGG network proposed by Simonyan and Zisserman (2014) is a CNN model trained on the ImageNet ILSVRC dataset. The VGG takes images of dimensions \(224 \times 224 \times 3\) at its input layer and utilizes \(3 \times 3\) filters across all its layers. There are two main variations of VGG: VGG16 and VGG19, comprising 16 and 19 layers (convolutional and fully connected layers) respectively. Both architectures employ the Softmax layer for classification purposes and the ReLU activation function in convolutional layers.

The layer details of the VGG16 and VGG19 architectures used in this study are shown in Figs. 6 and 7, respectively, while the characteristics of the layers are provided in Table 4 and Table 5.

The ResNet, which is a pivotal component in the evolution of DL, is a popular choice in various studies owing to its remarkable effectiveness (He et al., 2016). Compared with VGG networks, ResNet exhibits reduced filter counts and lower complexity. Although it is theoretically expected that the accuracy should increase with an increase in the number of layers and depth, real-world results may not align with this expectation. In general, as deep networks are trained on datasets, network performance tends to decrease. However, ResNet addresses this problem by implementing a structure known as a “skip connection”. This structural innovation enables certain layers within the network to be bypassed, thereby establishing direct connections to subsequent layers of equal dimensions. ResNet architectures with various depth variations are available, including ResNet50, ResNet101, and ResNet152, encompassing 50, 101, and 152 layers, respectively. The ResNet architectural model is shown in Fig. 8, and the layer details are presented in Table 6.

Fig. 5
figure 5

Categories of datasets consisting of specimens deformed by tensile testing

Full size image
Fig. 6
figure 6

VGG16 architecture DL network

Full size image
Fig. 7
figure 7

VGG19 architecture DL network

Full size image
Table 4 VGG16 architectures layer details
Full size table
Table 5 VGG19 architectures layer details
Full size table
Table 6 ResNet architectures layer details
Full size table
Fig. 8
figure 8

ResNet50, ResNet101 and ResNet152 architectures DL network

Full size image

Training a neural network with random initial values can be both time-consuming and demanding in terms of system resources, including CPU and GPU, depending on the size of the data. Using models trained on large datasets, such as ImageNet (comprising millions of data), on new and specialized datasets enables the model to adapt to new tasks more quickly and efficiently. This approach, known as transfer learning, reduces the time and resources required for the artificial intelligence model to learn the general features of the data it encounters, thus allowing for effective results even with less data (Ross et al., 2023).

Comparison of ResNet with VGG models

ResNet and VGG architectures, as DL models previously trained on the ImageNet dataset, are utilized for transfer learning on new datasets. Although both models are effective in visual recognition tasks, they demonstrate significant differences in architectural design and computational costs.

The ResNet architecture offers an innovative solution to the vanishing gradient problem in deep networks through the use of “skip connection”. These connections enable the ResNet model to be effectively trained and learn faster even with deeper configurations. Specifically, the ResNet50 model offers computational efficiency with 3.8 billion Floating Point Operations (FLOPs), ResNet101 with 7.6 billion FLOPs, and ResNet152 with 11.3 billion FLOPs, whereas the VGG19 model has a higher computational cost with 19.6 billion FLOPs, and VGG16 with 15.3 billion FLOPs.

VGG architecture, with its simple and repetitive structure, has been widely used in the field of visual recognition. However, the large number of parameters and the need for high computational power slow down the application process, particularly with large-scale datasets (Mai et al., 2020; Chandrapu et al., 2022).

In conclusion, in terms of depth and computational efficiency, the ResNet architecture provides similar or better performance with fewer parameters and lower computational costs than VGG. Therefore, ResNet is generally the preferred option for feature transfer.

Model train

To evaluate the performance of the models objectively, data preprocessing followed a predefined methodology. This process involved shuffling the dataset based on classes and splitting it into three distinct partitions: training, validation, and testing. During the model training phase, 8000 images were employed with 1600 randomly selected images from each class. Of these, 6000 images were designated for training, while the remaining 2000 were set aside for validation.

To mitigate the risk of overfitting and address the data-partitioning uncertainty at each stage of the training process, the dataset was subdivided into four distinct subsets using the K-Fold cross-validation method (k=4). Performance metrics such as accuracy and error were used to gauge the model performance and were computed as the average of these metrics across the four subsets. When determining the k value, it varies according to the amount of data and number of categories. In classification studies, the trial-and-error method is preferred for determining the optimal k value. In this study, three different k values (k = 3, 4, and 5) were used, and the best results were obtained when k=4 was selected. The training time increased with k.

Upon completion of the training process, the neural networks was subjected to a testing phase, where it encountered 2000 microstructure images that it had not seen previously. The testing stage was conducted to assess the generalizability of the model and its response to real-world data.

In this study, the epoch values were set to 20 and 50, and the batch size was set to 20 to train the models. High success was achieved with the SGD and RMSprop algorithms in the model optimization process Table 7. The weights of the best model based on the minimum loss value were recorded during the training process using the Keras “callback” function. As loss function for multiclass problems we used “categorical cross entropy” (Chollet et al., 2015a, b). As mentioned earlier, softmax activation was used in all DL models for probability estimation in the classification. Softmax normalizes all values in the range 0 to 1 and the sum of these values is always equal to 1. If the probability of one of the classes changes, it affects the probability values of the other classes such that the sum of the probabilities is equal to 1.

$$\begin{aligned} \text {Softmax}(z_i) = \frac{\exp (z_i)}{\sum _{j=1}^N \exp (z_j)} \end{aligned}$$
(2)

The mathematical expression of the softmax function is described by Eq. (2), where \(z_i\) is the i-th element of the input vector of the softmax layer. Exp() is a nonlinear exponential function applied to each value of \(z_i\), which makes the scores positive and comparable. The lower part of Eq. (2) represents the sum of the exponential functions of all elements in the input vector. This step takes the sum of the scores of all the classes and normalizes them. Consequently, the Softmax function normalizes the score of a given class as the ratio of its contribution to the scores of all classes. Thus, output can be interpreted as a probability distribution. That is, it shows the extent to which each class contributes to the probability.

The DL architectures utilized in this study were pre-trained models, and as such, transfer learning was employed during neural network training. The computational efforts reported in this study were conducted at the TUBITAK ULAKBIM High Performance and Grid Computing Center (TRUBA Resources). The models were trained on hardware consisting of a Xeon E5-2690 v3 2.60GHz processor with 16 cores and 32 threads, 256 GB of RAM, and an Nvidia M2090 graphics card. The coding was implemented in the Python programming language, utilizing TensorFlow and Keras APIs as the backend and frontend, respectively.

Hyper-parameters settings

The hyper-parameters, including batch size, optimizer, learning rate, epochs, and loss function, were empirically tuned to determine the most effective combinations for training the model and achieving the desired results. This provides appropriate optimization for multiclass classification problems. The evaluation of the performance of a classification system is based on metrics such as overall accuracy, precision, recall, or agreement between the model and ground truth for different class values. For the dataset used in this study, which contains five different deformation rates, categorical cross entropy was chosen as the loss function. ResNet50, ResNet101, and ResNet152 architectures, and the VGG16 and VGG19 architectures were trained and evaluated using experimental and hyper-parameter settings. Table 7 summarizes the optimized values of all the hyper-parameters used throughout the experiments.

Table 7 List of hyper-parameters of ResNet and VGG Architectures and their respective values
Full size table

Performance evaluation metrics

The performance of the model was assessed using a confusion matrix, which presents the predicted and actual values in a convenient table format. There are four categories in the confusion matrix.

a) True Positive (TP) for class “as-received specimen”  This refers to images that belong to the “as-received specimen” class and are correctly predicted by the model as “as-received specimen”. In other words, the model correctly identified the images belonging to the “as-received specimen” class.

b) True Negative (TN) for class “as-received specimen”: TN for class “as-received specimen” represents samples that are not actually from the class “as-received specimen” and are correctly predicted by the model to be not from the class “as-received specimen”.

c) False Positive (FP) for class “as-received specimen”: Classification of “non-as-received specimen” as “as-received specimen”

d) False Negative (FN) for class “as-received specimen”: Classifies an image that is a “as-received specimen” not as “as-received specimen” but as another category. In other words, it missed or overlooked the “as-received specimen” images.

The percentage of correctly predicted data out of all data in the training result gives “accuracy”, as shown in Eq. 3.

$$\begin{aligned} \textit{Accuracy}_{\_\textit{as-rs}} = \frac{T\!P_{\textit{as-rs}} + T\!N_{\textit{as-rs}}}{T\!P_{\textit{as-rs}} + F\!P_{\textit{as-rs}} + T\!N_{\textit{as-rs}} + F\!N_{\textit{as-rs}}} \end{aligned}$$
(3)

where as-rs is the “as-received specimen” class

The data used in the classification, estimation, and segmentation processes may be underdistributed in some cases and unevenly distributed across the categories. In this case, artificial intelligence models may favor the data in the category group where there are more data. Therefore, using “accuracy” as a performance measure in a dataset with unbalanced data distribution may not reflect the actual results.

Precision indicates that the proportion of the estimated deformation rate is the correct estimate. This is expressed mathematically in Eq. 4.

$$\begin{aligned} \textit{Precision}_{\_\textit{as-rs}}=\dfrac{T\!P_{\textit{as-rs}}}{T\!P_{\textit{as-rs}}+F\!P_{\textit{as-rs}}} \end{aligned}$$
(4)

The sensitive (recall) is the number of TNs divided by the sum of the TNs and FNs. Recall indicates the number of true instances of a class that we correctly detected. This is expressed mathematically, as shown in Eq. 5.

$$\begin{aligned} \textit{Sensitivity (Recall)}_{\_\textit{as-rs}}=\dfrac{T\!P_{\textit{as-rs}}}{T\!P_{\textit{as-rs}}+F\!N_{\textit{as-rs}}} \end{aligned}$$
(5)

In modern classification research, the F-measure or F1-score is a widely used metric for assessing the performance. This measurement represents the harmonic mean of precision and recall and provides a comprehensive evaluation of the model effectiveness. The F1-score involves a balance between precision and recall, showcasing a trade-off between the two. The mathematical formula used to compute the F1-score can be found in Eq. 6.

$$\begin{aligned} \textit{F1-score}_{\_\textit{as-rs}} = 2 \left( \dfrac{\textit{Precision}_{\_\textit{as-rs}} * \textit{Recall}_{\_\textit{as-rs}}}{\textit{Precision}_{\_\textit{as-rs}}+\textit{Recall}_{\_\textit{as-rs}}} \right) \end{aligned}$$
(6)

The false negative rate (FNR) measures how often a classification model incorrectly classifies samples labeled as positive as negative. A low FNR value indicates that the model is successful in detecting the positive class and that important positive cases are not overlooked. Eq. 7 provides the formula for calculating the FNR for the category “as-received specimen”.

$$\begin{aligned} \textit{FNR}_{\_\textit{as-rs}} =\dfrac{F\!N_{\textit{as-rs}}}{F\!N_{\textit{as-rs}}+T\!P_{\textit{as-rs}}} \end{aligned}$$
(7)

Results and discussion

ResNet50, ResNet101, ResNet152, VGG16 and VGG19 DL architectures were applied to classify the deformation rate of S235-JR structural steels. These architectures were trained with epoch values of 20 and 50, respectively. As shown in Table 8, the highest precision, recall and F1-score values were obtained in the ResNet50 architecture model at epoch=20. This result is shown in Fig. 9 in the confusion matrix.

According to the results of the evaluation of the models with the test data, the highest success rate of ResNet101 was 98% accuracy at 50 epochs. The results obtained using the ResNet101 model are shown in the confusion matrix in Fig. 10. Similarly, the ResNet152 results are shown in Fig. 11, the VGG16 results are shown in Fig. 12 and the VGG19 results are shown in Fig. 13. Furthermore, it was observed that the ResNet152 architecture required training with more epochs than the other architectures. Because it was observed that the success rate decreased in the experiments with values higher than 50 epochs in all models, they were not added to the table.

Table 8 Comparison of DL networks
Full size table

Following the completion of training, the classification success of images belonging to the five categories was evaluated for each cross-validation model. Table 9 presents the precision, recall, and F1-score values for each category, and the cross-validation fold of the ResNet50 model. The average TP, FN, FP, precision, recall, and F1-score values for classifying the test data are provided in Table 10. The classification performance of the ResNet50 architecture is further illustrated by a confusion matrix, as depicted in Fig. 9. Notably, the highest FNR was observed in samples subjected to the 21 mm tensile test, whereas the lowest FNR was found in the images of the raw and Specimen elongated 7 mm. Additionally, the highest precision, recall, and F1-score values were achieved for images of undeformed specimens and specimens subjected to a 7 mm tensile test.

When the confusion matrices are examined, it is seen that the DL models used make very good discrimination in the raw and 7 mm elongated samples, but the microstructure images of the 14 mm, 21 mm elongated and fractured samples are very similar to each other, and the DL models have difficulty in discriminating. Table 11 lists the FNR values of the different DL models for each category. In general, the FNR values were quite low, proving that the models mostly made correct positive predictions. However, there were significant differences between the architectures and classes. For example, the ResNet50 and ResNet101 architectures have low FNR values in most classes, indicating that these architectures are well-adapted to this problem. On the other hand, the VGG19 architecture stands out with high FNR values, especially in the “Fractured specimen” class. This indicates that the VGG19 architecture is more prone to classifying this particular class as a FN.

Furthermore, the “Specimen elongated 21 mm” and “Fractured specimen” classes generally have higher FNR values than the other classes. This indicates that these classes are more difficult to classify than the others, and DL models are more likely to classify these classes as FNs.

The confusion matrix of the ResNet50 DL model shows the classification results of 400 test samples for each category Fig. 9. Upon examining the model’s performance for the “Specimen elongated 21 mm” category, it is observed that 385 images were correctly classified (TP = 385), while 1 image was misclassified as “As-received specimen”, 5 images as “Specimen elongated 14 mm”, and 9 images as “Fractured specimen”. Therefore, the FN for the “Specimen elongated 21 mm” category is 15 (FN = 1 + 5 + 9 = 15). Additionally, 11 “Fractured specimen” images and 5 “Specimen elongated 14 mm” images were incorrectly classified as “Specimen elongated 21 mm”, resulting in a FP count of 16 (FP = 11 + 5 = 16) for the “Specimen elongated 21 mm” category.

The classification performance of the ResNet50 DL model for the “Specimen elongated 21 mm” can be summarized as follows:

- TP: 385 (the number of images correctly classified as “Specimen elongated 21 mm”)

- FN: 15 (the number of images that should have been classified as “Specimen elongated 21 mm” but were assigned to another category)

- FP: 16 (the number of images incorrectly classified as “Specimen elongated 21 mm” but actually belonging to another category)

Table 9 Class-wise average of metrics obtained from K-Fold cross-validation (k=4) results for ResNet50 architecture (epoch=20)
Full size table
Table 10 Class-wise results of metrics obtained on the test data of ResNet50 (epoch=20) DL architecture
Full size table
Fig. 9
figure 9

Confusion matrix for ResNet50 architecture (epoch=20)

Full size image
Table 11 Class-wise FNR metric for different DL architectures
Full size table
Fig. 10
figure 10

Confusion matrix for ResNet101 architecture (epoch=50)

Full size image
Fig. 11
figure 11

Confusion matrix for ResNet152 architecture (epoch=20)

Full size image
Fig. 12
figure 12

Confusion matrix for VGG16 architecture (epoch=20)

Full size image

The main contributions and highlights of this study are summarized below.

* S235-JR non-alloy structural steels were prepared as five different tensile test specimens. The first of these prepared specimens was left as a raw specimen. The other specimens were subjected to tensile tests at 7, 14, and 21 mm. The final specimen fractured during tensile testing. Consequently, materials with five distinct deformation rates were produced. The microstructural images of each specimen were captured and recorded at dimensions \(256 \times 256\) pixels. A dataset consisting of 10000 images, with 2000 images per category, was created.

* This study is the first to identify the deformation rate and determine life by applying a DL algorithm to material microstructure images.

The detection of deformation in steel materials and its rate have been realized using popular DL architectures based on material microstructure images. In addition, the life expectancy of the material can be predicted.

Table 12 Current studies on deformation analysis from microstructure images
Full size table

Looking at the deformation analysis studies in Table 12, it can be seen that most research detects surface defects (cracks, scratches, etc.) by looking at microstructure images, mostly using DL algorithms. Microstructural analysis studies have been conducted in areas such as phase detection, grain boundary detection, and segmentation. However, these studies did not provide information on the deformation rate. This study is the first to demonstrate that deformation detection and life prediction can be achieved from microstructural images of materials using DL.

As there are no other similar studies in the literature that compare the results, this study aims to achieve the highest success rate by using and comparing different DL algorithms. A success rate of over 98% proves that the introduced model is acceptable for deformation-rate detection.

Fig. 13
figure 13

Confusion matrix for VGG19 architecture (epoch=20)

Full size image

Muñoz-Rodenas et al. (2023) have conducted a three-class microstructure image classification study using DL networks and ML algorithms, based on a dataset of 19200 images. In their study, classification extended up to 600 epochs. A high number of epochs indicates a significant computational cost in terms of time and energy for the DL and ML networks. However, in our study, the highest success in DL networks was achieved with only 20 epochs.

In the study conducted by Khurjekar et al. (2023) using a CNN model, it has been demonstrated that an accuracy rate exceeding 90% was achieved in the two-category classification of textured and non-textured microstructures. However, in our study, the classification category was expanded to include five different deformation rates. Despite the increase in the number of classification categories, our study achieved a high success rate of 98.45%.

In research conducted by Zhu et al. (2022), the success of ML and DL networks in microstructure classification was measured. In this study, the VGG16 networks were found to be more successful than the FCNN, RF, SVM, and kNN algorithms. The study examined changes in microstructure features resulting from the hot stamping process and classified microstructure phases with 98% accuracy using 2400 SEM images. In our study, however, the focus was on the deformation rate, and a classification success of 98.45% was achieved in the classification study.

Medghalchi et al. (2020) in their research on the classification of dual-phase steel microstructures, utilized a CNN model and successfully identified five different types of damage with a 97% accuracy rate. Our study, on the other hand, not only uses the most current DL model to determine the damage rate by focusing on the material lifespan, but also applies the K-Fold cross-validation method to achieve a reliable and higher success rate.

Conclusion

This study focuses on the automatic detection of physical issues such as material deformation, deterioration, and damage through microstructure analysis. DL networks, which are a sub-branch of artificial intelligence, are recommended for the detection of such problems. DL is quite successful in microstructure segmentation and classification processes. The method presented in this article analyzes the material lifespan related to deformation using DL. Whether the material is deformed has reached the breaking point or the degree of deformation can be determined through microstructural images. Samples made of S235-JR structural steel were subjected to tensile tests at various rates in the laboratory, causing deformation, and 10000 microstructural images of these samples were recorded. These images were processed using DL models.

The results show that all the algorithms tested had a success rate of over 90%. Although the VGG16 algorithm produced a success rate of approximately 96.6% with fewer parameters and training time, the highest rate was achieved by the ResNet50 algorithm at 98.45% with 29.5 million parameters in 3.1 training hours.

Future studies are planned to be conducted with the aim of improving the accuracy of the models. This can be achieved by applying various image processing techniques such as segmentation of microstructural images, clarification of grain boundaries, and coloring of grains in images. Additionally, the deformation rates and damage analyses of the S235-JR structural steel examined in this article will be carried out using non-destructive testing methods, and the results will be compared with those from destructive tests.

A perfect deformation rate determination can be achieved by conducting improvement studies to reduce the high FNR values of the 14 mm, 21 mm elongated, and fractured specimen classes in the classification categories. In this way, deformation rates that are close to each other will be easily detected.

It is known that the compression and tensile forces causing material deformation are simulated using various software, such as ANSYS Mechanical, Abaqus, and LS-DYNA, and the effects of these simulations on the material are investigated. The data obtained in this study are anticipated to be used in future simulation-based studies.

The methods and techniques proposed here will enable material manufacturers and testing centers to quickly and reliably perform life span determination and deformation analysis of steels. This microstructural study, specifically conducted on S235-JR structural steel, is recommended for materials used in nearly every field, including metals and alloys, ceramics, polymers, composite materials, and biomaterials.

Limitations

In materials science, it is difficult and costly to collect and analyze sufficient data to understand a given phenomenon. Therefore, it may be necessary to consider a combination of mechanical, chemical, and other properties. It is not possible to address all of these factors using a single characterization method. The resulting datasets can be affected by high epistemic uncertainty. In the field of materials science, epistemic uncertainty can arise when certain material properties or behaviors are not fully understood. Epistemic uncertainty can arise if all factors required for a full understanding of a complex phenomenon, such as material fatigue, which is addressed in this study, are unknown or incomplete. This uncertainty emphasizes the need for further research and data collection by material engineers to better understand material properties and improve the performance of materials.

In this study, the deformation process was conducted using a uniaxial tensile test. In future studies, depending on the application area of the materials, different deformation tests (compression, bending, torsion, impact, hardness, and fatigue tests) could be performed to generate various datasets for a comprehensive evaluation.

One of the limitations in performing microstructure analysis using DL algorithms is the amount of data. Sufficient and diverse data are crucial for the success of image classification studies using artificial intelligence algorithms because they ensure the model’s ability to generalize across new, unseen images. It is not clear how many microstructure images should be used to identify these phenomena (Yi et al., 2023). A small number of microstructure images may cause artificial intelligence to fail in training. Excessive amounts of data may lead to an unnecessary prolongation of the learning time and memorization of the machine, and the results may be misleading. The amount of data obtained was revealed by the experimental results of this study.