Synthetic data generation using finite element method to pre-train an image segmentation model for defect detection using infrared thermography

Abstract

The vision of a deep learning-empowered non-destructive evaluation technique aligns perfectly with the goal of zero-defect manufacturing, enabling manufacturers to detect and repair defects actively. However, the dearth of data in manufacturing is one of the biggest obstacles to realizing an intelligent defect detection system. This work presents a framework for bridging the data gap in manufacturing using the potential of synthetic datasets generated using the finite element method-based digital twin. The non-destructive technique under consideration is pulse infrared thermography. A large number of synthetic thermographic measurements were generated using 2D axisymmetric transient thermal simulations. The representativeness of synthetic data was thoroughly investigated at various steps of the framework, and the image segmentation model was trained separately on experimental and synthetic datasets. The study results reveal that when carefully rendered, synthetic datasets represent the experimental data well. When evaluated on real-world experimental samples, the segmentation model pre-trained on synthetic datasets generalizes well to the experimental samples. Furthermore, another advantage of synthetic datasets is the ease of labelling a large amount of data. Finally, the robustness assessment of the model was done on two new datasets: one where the complete experimental setup was changed, and the other was an open-source infrared thermography dataset

Introduction

Under the paradigm of Industry 4.0, digital and automated manufacturing has gained traction recently. However, as one might anticipate, the current increment in competitive manufacturing capabilities also leads to increased waste of materials, time and energy in the form of defective samples. Quality management for sustainable manufacturing on both financial and environmental fronts is the need of the hour. In a recent publication, V. Azamfirei et al. (2023) presented an adapted framework for zero-defect manufacturing (ZDM), which focuses on waste minimization using data-driven technologies for enhancing the quality of manufacturing by getting things right in the first try. Although a varying degree of automation is found in the current production lines, this largely depends on the product and the processes involved in manufacturing. Tasks such as handling the materials and product fabrication are mainly automated; however, human involvement still plays an essential role in assessing the production line’s reproducibility, reliability and quality via quality tests at regular intervals based on the results from the suitable inspection tool. The drawback of manual inspection is its dependency on humans; the interpretation of the defects is subjective to the skill and understanding of the person; long production hours also bring in the factor of human fatigue affecting the interpretation capabilities of the human, the constant need for human supervision around the clock and lack of complete automation makes the process slow and expensive. A more sustainable and reliable approach would be to work towards automated inline checks for traceability and immediate rectification at the source. The automated inline inspection approach does not aim to replace the human expert responsible for the inspection. Instead, it aims to increase efficiency and bring a standardized approach to the process, thus striking a balance between automation and human involvement for optimizing the production line.

Non-destructive testing (NDT) (Shull 2002) helps evaluate the sample quality and integrity in a non-destructive manner such that its functionality for further applications is not altered or affected. Thus, NDT techniques perfectly align with the vision of ZDM. This work uses pulse thermography (PT) as a NDT. However, the spatiotemporal data obtained from the PT measurement needs post-processing to maximize the sub-surface defect information spread across the dataset, and the understanding of obtained post-processing results relies on expert interpretation.

The quest to automate defect detection in PT measurement has led researchers to tap into the potential of machine learning (ML) algorithms, be it a conventional fully connected neural network (FCN) or current state-of-the-art deep learning (DL) algorithm such as convolutional neural networks (CNN). Thus, on the one hand, applying defect detection models for automated defect detection has brought advancements in the field; on the other hand, it has introduced a new severe problem of dependency on data for training the models. Thus, the method has only been used in research labs so far.

The model’s performance depends on the quantity and quality of the data. However, there is always a dearth of data in the manufacturing. The reason behind the lack of data is manifold. To begin with, consider a case when a respectable amount of data is available from the production line; the problem, in this case, will be an imbalanced dataset as a majority of the inspected samples will be non-defective, and few of them will be defective, thus making the model ineffective in learning from the dataset. Purposely manufacturing large amounts of samples with defects alone will be inefficient and unsustainable in terms of precious manufacturing time, money and material, also not to forget the difficulty in surgically inducing defects encompassing a wide variety of scenarios. The requirement for special scientific equipment further aggravates the problem; for example, well-controllable and durable excitation sources such as lasers, high-energy flash lamps and state-of-the-art infrared cameras for PT experiments. Even if all the mentioned hurdles are passed, labelling such a specialized dataset is challenging.

As the governing equations for the underlying physical process of heat transfer in PT experiments are well understood, it is possible to create synthetic data using the finite element method (FEM) (Strang and Fix 2008). The use of simulated data not necessarily from FEM can be seen in works related to automated defect detection using PT and neural networks (NNs) (Trétout et al. 1995; Maldague et al. 1998; Saintey and Almond 1997; Manduchi et al. 1997; Darabi and Maldague 2002; Benitez et al. 2006; Benitez et al. 2007; Saeed et al. 2018; Duan et al. 2019) or state-of-the-art DL algorithms (Fang and Maldague 2020; Fang et al. 2021). However, there is scope for considerable improvement in understanding the generation of large amounts of synthetic data, their application to bridge the data gap and their role in automated defect detection using PT and DL algorithms.

To the best of our knowledge, there is a gap in the literature that provides and systematically examines the complete end-to-end framework (from the generation of large amounts of synthetic data using FEM to the inference of pre-trained model on third-party PT dataset) of automated defect detection using image segmentation models pre-trained on synthetic data. This research aims to fill this gap in the knowledge. The main contribution of this work is as follows:

• 1. Generation of hundreds of synthetic PT measurement data using FEM, based on the previously introduced (Pareek et al. 2022) concept of defect signatures, thus addressing and providing a solution for computation time for transient thermal simulation.

• 2. Evaluating the representativeness of the synthetic PT measurements by comparing it with the experiments and improving the representativeness of the synthetic PT measurements by a novel noise addition method, thus, illustrating the legitimacy of the synthetic dataset.

• 3. Training and validating an image segmentation model (U-Net) on principal component thermography images of synthetic PT measurements with and without added noise and comparing their inference on the experimental dataset, thus highlighting the advantage of training the model on a representative and non-redundant synthetic dataset.

• 4. Evaluating the usability of the models trained and validated on the synthetic datasets (with and without noise) when the same samples are tested on a completely different experimental setup and a third-party open-source dataset with a different material and experimental setup, thus, showcasing the viability of the pre-training the model on the synthetic datasets.

The paper is divided into five parts. Section “Theory and literature review” provides the necessary theoretical background for a better understanding of the methodology and a detailed literature review of the advancements in automated defect detection over the years. Section “Methodology” explains the adopted methodology, i.e. sample preparation and experimental setup, synthetic data validation, data pre-processing, the addition of noise, and the image segmentation algorithm. In Sect. “Segmentation performance on different datasets: results, discussion and comparison”, the results are explored and the feasibility of the model is evaluated on new datasets. The final section discusses the conclusions drawn and the outlook of the work.

Theory and literature review

Introduction to infrared thermography

Infrared thermography (IRT) is a non-destructive evaluation technique for defect detection based on temperature and heat flow measurement; it relies on thermal contrast between the defect and defect-free (sound) regions of the sample for detecting any possible sub-surface defects in the sample. Usually, the sample is in thermal equilibrium, i.e. no thermal contrast exists between the defect and the sound region. However, the thermal equilibrium can be disturbed with the help of an external thermal source which induces thermal waves in the sample for the desired thermal contrast for detecting sub-surface defects in the sample. This approach of actively stimulating the sample with the help of an external thermal excitation to induce a thermal contrast is called active thermography (Shepard 1997) and is always transient in character.

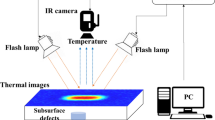
Pulse thermography is one of the most widely used active thermography approaches for sub-surface defect detection in samples. In PT, one side of the specimen is subjected to a short-duration heat impulse from the thermal source; the thermal source usually consists of single or multiple flash lamps. The optimal pulse duration ranges from a few ms to several seconds, depending on the material properties of the sample and the depth of the sub-surface defects. The resulting transient response of the sample to the applied excitation is recorded with the help of an infrared camera. Due to the pulse heating of the sample surface, the heat front propagates into the material; as time advances, the surface temperature of the sample starts decreasing. In an ideal condition (homogeneous and defect-free sample), the surface temperature will uniformly decrease until it reaches the steady state temperature (ambient temperature), leading to no thermal contrasts on the sample surface. However, in the case of samples with defects (voids, delamination), the defect region obstructs the heat flow resulting in higher surface temperatures above the defect region in contrast to the sound region; the infrared camera captures this resulting thermal contrast on the sample surface. Figure 1a shows a typical PT setup.

Fig. 1

a Principle and experimental arrangement of pulse thermography: 1. Heat source, 2. specimen with sub-surface defects, 3. IR camera, 4. signal and image processing system, b recorded image sequence from an IR camera as a 3D matrix of shape $N_Y \times N_X \times N_T$

The temperature response of the sample to the heat pulse can be described using the 1D solution of the Fourier Equation for a Dirac delta function in a semi-infinite isotropic solid, which is given as (Carslaw and Jaeger 1986):

$$\begin{aligned} T(z, t) = T_0 + \frac{Q}{e\sqrt{\pi t}}\exp \left( \frac{-z^2}{4\alpha t}\right) , \end{aligned}$$

(1)

where Q is the energy absorbed by the surface [$\hbox {J/m}^{2}$]; $T_0$ is the initial temperature [K]; $\alpha$ is the thermal diffusivity [$\hbox {m}^{2}/\hbox {s}$], and e is the thermal effusivity (the square root of the product of density, heat capacity and thermal conductivity). At the surface of the specimen ($z=0$), Eq. (1) can be written as

$$\begin{aligned} T(0, t) = T_0 + \frac{Q}{e\sqrt{\pi t}}. \end{aligned}$$

(2)

Thus, ideally, the temperature evolution of the surface temperature to the applied impulse excitation is inversely proportional to the square root of time ($T \propto t^{-1/2}$). However, in the case of a sub-surface defect, the surface temperature above the defect area will diverge from this expected behaviour depending on the material’s thermal properties, which gives the required thermal contrast detected for identifying the sub-surface defects. The acquired temperature data is a 3D matrix (Fig. 1b). The i-j dimensions of the matrix are the spatial temperature values of the surface at a given time, and the k-dimension corresponds to the temporal evolution of the surface pixels.

Like in many other data acquisition systems, noise is also an essential concern in a PT setup. The excitation source introduces noise in the form of uneven heating of the sample, i.e. the sample is not uniformly heated, leading to unwanted temperature gradients on the sample’s surface, which leads to uncertainty in defect detection due to falsely induced thermal contrasts. Furthermore, the resulting radiation for the applied excitation from the sample is attenuated via absorption or scattering while travelling through the atmosphere, the camera window or the optics (Vollmer and Möllmann 2017). The components of the infrared camera further degrade the thermal signal by adding electromagnetic and electronic noise. Thus, each element shown in Fig. 1a degrades the thermal signature from the sample under investigation. The weak and noisy signal from the infrared camera needs to be processed to reduce noise, enhance the image contrast and retrieve valuable information from the measurement. Also, a typical PT measurement consists of tens or hundreds of infrared images, making it challenging to find the image (or images) with the most optimum information about the sample’s sub-surface defects. Post-processing of the PT measurement also helps find images with valuable information about the sample defects relatively efficiently. Some of the prominent post-processing techniques for PT measurements are pulse phase thermography (PPT), thermographic signal reconstruction (TSR), principal component thermography (PCT), slope and correlation coefficient. PPT (Maldague and Marinetti 1996; Ibarra-Castanedo and Maldague 2004; Ibarra-Castanedo et al. 2004; Castanedo 2005) is a technique based on the Fourier transforms (FT); here, an FT is calculated for the temporal evolution of each pixel, and the resulting amplitude and phase plots provide the sub-surface defect information of the sample. TSR (Shepard 2001; Shepard et al. 2002, 2003) is based on reconstructing the measurement data using an $N^{th}$ order polynomial fit and taking the first and second-order derivative of fitted data, the reconstructed images have less noise compared to the raw measurement data; thus, aiding in defect detection. As shown in Eq. (2), a defect-free region will have a slope of $-0.5$ for $\ln (\Delta T)$ vs $\ln (t)$; any deviation from this ideal slope will help to identify the underlying anomalies in the sample. The deviation in slope can be measured with the help of the square of the correlation coefficient $R^2$, which quantifies the degree of linear correlation between the observed and expected values. Thus, the defect can be detected using two new parameters, slope and $R^2$ (Palumbo and Galietti 2016). PCT (Rajic 2002a; b; Marinetti et al. 2004; Parvataneni 2009; Brunton and Kutz 2019; Kaur et al. 2020; Milovanović et al. 2020) uses the singular value decomposition algorithm; here, the infrared dataset is decomposed into empirical orthogonal functions, which help decode underlying defect information more clearly. Thus, different post-processing techniques are available, each with advantages and disadvantages, and a comparison between them is provided in (D’Accardi et al. 2018). The ease of finding the best image with the objective of their application in deep learning algorithm is provided in (Pareek et al. 2022).

Application of neural networks for defect detection in infrared thermography

The application of NNs for defect detection in IRT requires a holistic approach that focuses on the correct experimental setup for data acquisition, tailoring the spatiotemporal data for input to the NNs and the architecture of the NNs.

Preliminary processing of the input data affects the NNs performance (Trétout et al. 1995; Chulkov et al. 2019). Initially, the input for NNs was either the temperature evolution of the pixels over time (Prabhu and Winfree 1993) or pixel-wise thermal contrast curves, i.e. the subtraction of temperature evolution of the sound region from that of the defect region. The information associated with the thermal contrast curves was further enriched by either supplementing the contrast curves with some measurable values from the contrast curves, for example, maximum contrast value and the time of maximum contrast (Bison et al. 1994; Saintey and Almond 1997) or in the form of normalized thermal contrast curves (Manduchi et al. 1997), thermal running-contrast curves (Darabi and Maldague 2002). However, the drawback of using thermal contrast curves is their dependency on the selection of sound region for the contrast calculation, which is difficult due to the uneven heating of the samples. The dependency of thermal contrast curves on the sound region selection was circumvented by changing the input data to PPT phase data (Maldague et al. 1998), modified differential absolute contrast (DAC) (Benitez et al. 2008; Benitez et al. 2006) and TSR coefficients (Benitez et al. 2006; Duan et al. 2019).

In terms of the NNs architecture, many initial studies used multilayer perceptron (MLP) to automate defect detection and characterization. The studies showed that the lack of data is one of the most critical limiting factors when it comes to the training of the NNs, and the NNs fail to generalize when there is a change of material and experimental setup (Trétout et al. 1995; Manduchi et al. 1997; Benitez et al. 2008). The use of synthetic data was proposed to address the dearth of data, and thermal models were used to generate synthetic temperature curves. Furthermore, it was demonstrated that the representativeness of the synthetic data to the actual test conditions plays an essential role in the classification accuracy of the network (Darabi and Maldague 2002). The application of modern-day neural network architecture for defect detection in IRT has been researched intensively by Q. Fang et al. Considering the time series continuity of the acquired thermal sequence, Q. Fang et al. (2020) quantified defects using gated recurrent units (GRU). The network was only trained on thermal contrast curves from simulated data (FEM). Q. Fang et al. (2020) evaluated different deep-learning algorithms for defect detection in infrared thermography. The images were sampled from the experiments without post-processing for training different networks. The study concluded that Mask-RCNN, an instance segmentation approach, was the most promising. Also, a pixel-based marking is better when compared to the bounding box approach as it extracts non-defect areas along with defective ones, possibly introducing multiple errors. Addressing the lack of data availability, Q. Fang et al. (2021) adopted a data augmentation strategy based on synthetic images from FEM. Here, a Mask-RCNN network was trained on filtered raw IRT images. The network performed better on the validation data set when trained on synthetic and experimental images than on experiments alone.

A common theme in the presented research is the lack of data in manufacturing which hinders the development of an intelligent defect detection system based on state-of-the-art deep learning algorithms. Although there were some efforts towards using synthetic data to make up for the lack of data, the actions lacked a concrete approach or a framework to tackle the problem. For example, in most of the studies which used simulated data, the training and testing of the NNs were done on the synthetic datasets alone, thus lacking performance evaluation on actual measurement data; in a few studies, when the network trained on the synthetic data was evaluated on the actual measurement dataset, the network failed to detect defects in the new distribution. Also, a comparative analysis of the representativeness of the generated synthetic data is lacking. Furthermore, only a handful of simulations are done, insufficient to bridge the data gap. Likewise, the choice of input data to the NN is not consistent, with each method either having some selection parameters or is affected by uneven heating; for example, the thermal contrast curve requires the selection of sound regions whose selection is affected by uneven heating, modified DAC has its dependency on the selection of time $t'$, changes in the temperature curves due to uneven heating affects the TSR coefficients. Training the network on raw thermal images sampled at regular intervals from the raw data set would be inefficient as the information about the defects would be spread throughout the dataset, and manually inspecting a large number of frames from the measurement dataset and annotating them would be tedious.

This work aims to address these shortcomings by proposing an end-to-end framework to bridge the data gap. Hundreds of synthetic PT measurements are generated using 2D axisymmetric transient thermal simulations, which helps reduce the simulation’s computation time. As the success of generated synthetic dataset in bridging the data gap depends on its fidelity towards the actual measurement data, the representativeness of the generated synthetic data is audited in detail at each step of the proposed framework. A novel noise addition technique further improves the representativeness of the synthetic data. The segmentation model is trained on orthogonal images obtained from PCT, which helps condense the important information in the measurement dataset into a few images. The ability of segmentation models pre-trained on the synthetic dataset to generalize on actual measurement data is showcased, and the model’s viability is checked beyond the experimental setup it was trained on and on an open-source dataset.

Methodology

The proposed development pipeline can be divided into the following subsections:

• 1. Sample preparation and experimental setup

• 2. Validating the FEM against IRT experimental setup

• 3. Synthetic data generation and data pre-processing

• 4. Experimental noise approximation and addition to synthetic data

• 5. Dataset labelling and segregation

• 6. Training and evaluation of image segmentation model (U-Net)

This section will explain the mentioned subsections in detail.

Samples and experimental setup

The samples are made up of resin-bonded cellulose laminate with artificially induced defects in the form of flat bottom holes (Fig. 2a). The material properties of the sample are shown in Table 1. The low thermal conductivity, even surface emissivity and ease of machinability make it a suitable choice for experiments and fundamental research. Flat bottom holes as defects provide precision and control while artificially inducing defects of different sizes at different depths. The sample dimensions are $50\,\hbox {mm} \times 50\,\hbox {mm} \times 3.9\,\hbox {mm}$. The diameter of the flat bottom hole varies from 1 mm to 7 mm, and the depth varies from 0.1 mm to 0.5 mm. A total of 20 such samples were manufactured.

Fig. 2

a Rear side of a sample with four defects (Top) along with its CAD diagram (Bottom), b the experimental setup

Table 1 Material properties of the sample

The experimental setup (Fig. 2b) consists of an InfraTec ImageIR 8300^® infrared camera with an detector resolution of $640 \times 512$ IR pixels and a thermal resolution of 20 mK, two flash lamps with a total energy of 2.4 kJ synchronised using the same power source. As the material has low thermal conductivity, thermal changes occur slowly but over an extended period. Thus, a relatively moderate frame rate of 62.5 Hz and a sufficiently long acquisition period of 16 s was chosen. The acquired thermographic data was flattened to a 2D matrix (Fig. 3) for optimal post-processing of the acquired measurements; here, the columns represent the flattened image at a given time t and the rows represent the temperature evolution of the pixels over time.

Fig. 3

Reshaping the 3D matrix of shape $(N_Y, N_X, N_T)$ to a 2D matrix of shape $(N_YN_X, N_T)$. The numbers in the images represent the pixel position

Finite element modelling: model creation, boundary condition estimation and validation

A detailed description of the finite element model creation, boundary condition extraction and validation of the results has been provided had been provided by Pareek et al. (2022). This section provides a brief overview of the key points of this paper.

In the paper, the authors aim to model a digital twin of the experimental setup for the samples under consideration. The sample description is the same as in Sect. “Samples and experimental setup”. The objective of the digital twin is to determine how the surface temperature of the sample under given boundary conditions varies over time, thus, aiding in generating synthetic PT measurements for a wide variety of synthetic samples. The paper implements the digital twin using transient thermal simulations in ANSYS (Ansys 2022) and PyAnsys (Kaszynski et al. 2021). A Digital twin implemented using transient thermal finite element simulations helps determine the sample’s cooling behaviour after being excited by the flash source. The resulting data obtained from the FEM simulation is similar to that obtained by the experimental setup. In the paper, the FEM simulation provides 1000 images of the sample top surface temperature as it would be seen by the IR camera (frame rate of 62.5 Hz with an acquisition time of 16 s) used in the experimental setup.

For transient thermal analysis, there is discretisation of both the temporal and the spatial domain, which makes the simulations resource-intensive in terms of time and computational requirements. In order to reduce the computation time and resources, the paper introduces the concept of defect signatures. A defect signature is the characteristic temperature evolution of a defect of radius $r_D$ [mm] at depth $z_D$ [mm] in the sample. The 2D axisymmetric simulations are used to create defect signatures of different radii at different depths and surrounding sound (defect-free) regions. Simplifying the 3D simulations of the samples to 2D axisymmetric simulations of the defects reduces the number of nodes in the FEM model and, thus, improves the computational efficiency.

Fig. 4

Generation of a 2D PT image from axisymmetric FEM data: a nodal temperatures along the top surface of the axisymmetric model, b polar mesh centred at the origin, c rectangular grid representing the sample and d polar mesh interpolated on the rectangular grid (Pareek et al. 2022)

For a given time t, a 2D PT image can be generated from a 2D axisymmetric FEM data in five steps; in the first step, the temperature data of the top surface from the 2D axisymmetric FE model is extracted, the second step consists of the creation of a polar mesh centred at the origin, the polar mesh represents the defect signature data, for the third step an empty rectangular grid that represents the sample is created, the number of points in the rectangular grid depends on the resolution of the IR camera, in the fourth step the polar mesh (representing the defect) is moved to its cartesian coordinate on the rectangular grid (representing the sample), the polar mesh temperature data is interpolated onto the empty rectangular grid, finally in the fifth step rest of the defects are placed and interpolated onto the rectangular grid. The paper comprehensively explains the complete procedure of generating 2D PT images from the 2D axisymmetric simulation.

Fig. 5

Schematic representation of a an axisymmetric FE model and b the applied boundary conditions for a defect signature with defect radius $r_D$ [mm] at depth $z_D$ [mm] from the sample’s top surface where the heat flux $q''(t)$ [$\hbox {W/m}^{2}$] is applied, $r_S$ [mm] represents the radius of the axisymmetric model, and $z_S$ [mm] represents the sample width. Nodal temperatures are read from the top surface between the points T1(t) and T2(t) (Pareek et al. 2022)

Achieving promising results from a FEM model requires a fair estimation of the boundary conditions. Boundary conditions for the FEM model of a PT experiment comprise of thermal properties of the material, parameters describing heat exchange with the surroundings, and knowledge of the heat flux imparted from the excitation source to the surface of the sample. The authors use the material properties from the data sheet for the sample and temperature-dependent material properties for the air underneath the flat bottom holes. The authors estimate the heat flux from the temperature evolution of the sound region of the sample. The heat flux is obtained by a non-linear least square fit of the analytical equation defining the surface temperature for a rectangular pulsed surface heating of a semi-infinite solid (Jaeger 1953) onto the sound region.

Fig. 6

Flowchart explaining the procedure of development of the FEM model

Finally, the FEM model is validated against the experimental results based on the temperature evolution of the sound and the defect regions, the thermal contrast, and the obtained surface temperature distribution of the surface images. Figure 7 and Fig. 8 show a few of the validation results from the study. The validation results from the paper are promising for the objective placed by the authors in the beginning, i.e. to generate the data for the training of an image segmentation algorithm.

Fig. 7

a Experiment and b simulated PT measurement at time $t =$ 8.06 s (Pareek et al. 2022)

Fig. 8

Comparison of temperature curves between experiments (Exp) and simulations (FEM) for a sound region and b defect of diameter 3 mm at a depth of 0.5 mm (Pareek et al. 2022)

Synthetic data: generation and pre-processing

Based on the FEM model described in the previous Sect. “Finite element modelling: model creation, boundary condition estimation and validation”, 2D axisymmetric simulations were done to generate defect signatures. The range of defect diameters described in Sect. “Samples and experimental setup” was discretized into steps of 0.5 mm (1 mm, 1.5 mm, ..., 6.5 mm, 7 mm) and defect depth into steps of 0.05 mm (0.1 mm, 0.15 mm, ..., 0.45 mm, 0.5 mm). All the possible combinations of defect signatures were simulated, i.e. defects with thirteen different diameters at nine varied depths leading to a total of 117 2D axisymmetric simulations.

The next step is to generate synthetic samples for which synthetic PT measurements need to be done. Layouts for synthetic samples are generated with different numbers of defects. A layout consists of information about the defect, i.e. the defect of radius $r_D$ [mm] at depth $z_D$ [mm] has its centre located at position (x mm, y mm). A synthetic sample may consist of varying defects (from one to five) placed randomly on the grid. A python script was used to generate the layouts; the script generates layouts by randomly selecting n defects (where n = 1, 2, 3, 4, 5) from the 117 generated defect signatures and placing them randomly on the synthetic sample at a given coordinate. A total of 517 layouts were created. Table 2 summarises the synthetic samples with the different numbers of defects. Later, synthetic PT measurements were created for the generated synthetic samples using the sample’s layout information and placing the associated defect signature on the grid as described in Sect. “Finite element modelling: model creation, boundary condition estimation and validation”.

Table 2 Synthetic samples numerics

Thus, for 517 synthetic samples, there are 517 synthetic PT measurements. Each PT measurement has 1000 images with the sample’s top surface temperature information. To find the needed defect information from the 1000 images of a given measurement, PCT was performed. The philosophy behind the PCT can be understood by looking at the PT measurement data set as a space-time dataset, i.e. the measurement images are the time series (temperature evolution) collected at spatial locations (pixels of the image), consider Fig. 3; here, the columns represent the temperature value at different spatial locations, i.e., pixels values of the image at a given time t, and the rows represent the time series, i.e., temperature evolution of the pixel over time. Even though each time series, in principle, represents the cooling behaviour of the sample after external excitation, the cooling behaviour between the time series may vary, i.e., the cooling curve of a defect region will be different from that of a sound region, defects with different aspect ratios will have varying cooling curves. However, there is some dependency between these different time series, i.e., they carry some replicated information. PCT helps to find the relationship in the spatial domain that shares the same temporal variability by combining them into spatial patterns sharing the common temporal variability.

PCT is an eigenvector analysis tool that helps decompose the PT measurement dataset into natural spatial patterns or empirical orthogonal functions (EOFs) - functions with no standard mathematical representation (Martinson 2018) present in the PT measurement dataset. Each identified EOF (the spatial patterns) has associated temporal variation, which shows how the particular EOF change over time; this temporal series is called principal component (PC). The EOF and its PC are called a mode. This decomposition of the data matrix into EOFs and the associated PCs is done using singular value decomposition SVD, which decomposes a matrix $\textbf{X}$ of shape $m \times n$ ($m > n$) as:

$$\begin{aligned} \mathbf {X_{mn}} = \mathbf {U_{mm}}\mathbf {S_{mn}}\mathbf {V^T_{nn}}, \end{aligned}$$

(3)

where $\textbf{U}$, $\mathbf {V^T}$ are orthogonal and $\textbf{S}$ is a diagonal matrix.

(4)

The columns of $\textbf{U}$ represent the EOFs, and the rows of $\mathbf {V^T}$ represent the corresponding PCs and diagonal values of $\textbf{S}$ are the singular values of the $\textbf{X}$ arranged in descending order.

$$\begin{aligned} \begin{aligned} \textbf{X}&= \sigma _1\mathbf {u_1 v^T_1} + \sigma _2 \mathbf {u_2 v^T_2} + \cdots + \sigma _r\mathbf {u_r v^T_r}, \\&= \sigma _1 \mathbf {(mode_1)} + \sigma _2\mathbf {(mode_2)} + \cdots + \sigma _r \mathbf {(mode_r)}. \end{aligned} \end{aligned}$$

(5)

Thus, the original data matrix $\textbf{X}$ can be reconstructed as the sum of the r rank one matrices or modes weighted by the singular values. For the PT measurement, the steps for calculating the PCT are as follows:

• 1. Wrap the acquired 3D data matrix into a 2D raster-like matrix (Fig. 3).

• 2. Discard the cold frames (frames before the trigger of the flash) as they contain no defect information and flash frames (frames during the flash region) due to saturation or non-linear effects during the flash. This step ensures that only the cooling curves are considered for the computation.

• 3. Normalise the images by the first image (after discarding frames in step 2) to reduce the effects of the possible uneven heating patterns.

• 4. Subtract the mean image, i.e. mean column, from other columns.

• 5. Take the SVD of the matrix. In this work, SVD was computed using NumPy (Harris et al. 2020).

Fig. 9

From left to right, the first four PCs (top row) and their corresponding EOFs (bottom row) for a sample with three defects. PCs are weighted by their respective singular values, i.e. $\sigma _1 \mathbf {v^T_1}$, $\sigma _2 \mathbf {v^T_2}$, $\sigma _3 \mathbf {v^T_3}$ and $\sigma _4 \mathbf {v^T_4}$

Figure 9 shows the first four EOFs and their corresponding PCs multiplied by their singular values for an experimental sample with three defects of varying diameters at varying depths. For each time step, $EOF_i$ is multiplied by $PC_i$ for that time step to give the contribution of $mode_i$ for that time step. The obtained EOFs and PCs can correlate to the sample’s physical cooling phenomena after external excitation. For example, consider $EOF_1$ and the corresponding $PC_1$. The $EOF_1$ has negative values, with values for the defects being lower than the sound region. Also, shallower defects have higher values compared to deeper defects. $PC_1$ resembles an inverted cooling curve with zero crossing at around t = 4 s. Thus, $mode_1$ gives information about the mean temperature decay of the sample, i.e., the temperature of the sample being above the mean initially and then decaying to temperatures below the mean. Also, $mode_1$ is the dominant mode or the significant contributor to the sum in the Eq. (5). In the case of higher EOFs, the sound region has values near zero compared to the defects; thus, higher modes focus more on the defect’s characteristics. The PCs are similar to the thermal contrast. Also, it can be seen that the $PC_4$ has higher noise compared to its predecessors. Thus, higher modes describe noise in the dataset.

Fig. 10

a Singular values and b percentage variance retained

The percentage of variance retained by the first k singular values for a rank r matrix is given as:

$$\begin{aligned} Variance \ retained = \frac{\sum _{i=1}^k \sigma _i}{\sum _{i=1}^r \sigma _i} \times 100. \end{aligned}$$

(6)

Figure 10 shows the first 20 singular values and the percentage of variance they retained. As can be seen, significant variance is retained by the first four singular values. After the fourth singular value, the increment in the percentage of variance retained by the inclusion of successive singular values is incremental as the singular values become smaller and smaller. Thus, each PT measurement was reduced from 1000 images to a set of the first four EOF images (each EOF reshaped into a 2D array), which were used to train the U-Net convolutional neural network.

When extending the proposed methodology of using PCT to extract the most relevant information from the original PT dataset in actual application, a prior variance study, as shown in Fig. 10, helps determine the relevant number of EOFs for model predictions. An elbow point cutoff (in this example at EOF 4), after which the singular values tend to level out, helps identify EOFs that explain the most variance. Thus, the final defect detection results are on these selected EOFs, and the corresponding predictions are displayed to the end users.

Noise: analysis, extraction and addition

The synthetic PT measurement data generated using transient thermal simulations lacks noise which is present in the IRT experimental setup. Adding a well-approximated experimental noise to the synthetic PT measurements helps capture more nuances of the experimental measurements and, thus, helps create a robust synthetic measurement dataset which is a better representation of the experimental dataset and can be used as a substitute for the training of the neural network.

In the case of the IRT setup, the noise source can be briefly categorised into two parts: high-frequency noise in the cooling curve due to the nonlinearity of the camera or background radiation and noise due to the uneven heating of the sample. Thus, the aim is to construct a noise matrix which approximates the experimental noise profile for each pixel at all the time steps and add the resulting noise matrix to the synthetic PT measurement. For this purpose, the IRT measurement of a defect-free sample is examined and analysed for noise extraction. A pristine defect-free sample helps understand the uneven heating in the experimental setup, as the surface temperature field is not disturbed due to a sub-surface defect. It also helps understand high-frequency noise in the recorded surface cooling curves.

The high-frequency noise from the measurement dataset can be extracted using the polynomial fitting similar to that in TSR (Shepard 2001; Shepard et al. 2002, 2003). TSR is based on the assumption of one-dimensional heat flow. As a result, the one-dimensional heat diffusion equation (Eq. (2)) can be used to accurately describe the response of a defect-free sample to the pulse excitation. Equation (2) can be rewritten as:

$$\begin{aligned} \Delta T = \frac{Q}{e\sqrt{\pi t}}, \end{aligned}$$

(7)

where $\Delta T = T - T_0$. Taking natural logarithms on both sides helps separate the input energy Q and the thermal diffusivity e from the time dependency t.

$$\begin{aligned} \ln (\Delta T) = \ln \left( \frac{Q}{e} \right) - \frac{1}{2}\ln (\pi t). \end{aligned}$$

(8)

Thus, from Eq. (8), it can be seen that a defect-free pixel should follow a straight line in a logarithmic scale with a slope of $-$0.5. This logarithmic time dependency of the pixel can be approximated with the help of a low-order polynomial function as:

$$\begin{aligned} \ln (\Delta T) = \sum _{n=0}^{N} a_n[ln(t)]^n, \end{aligned}$$

(9)

where $a_n$ is the $n^{th}$ coefficient of the polynomial fit to the measurement data. Typically, the order of the polynomial fit is between 5 and 7, as higher-order polynomial fit leads to overfitting and adding noise in the measurement data. Finally, the denoised pixel can be reconstructed from the polynomial fit as:

$$\begin{aligned} \Delta T = \exp \left( \sum _{n=0}^{N} a_n[\ln (t)]^n\right) . \end{aligned}$$

(10)

Fig. 11

a Raw (Data) and the reconstructed sequence (Fit) using a $7^{th}$ order polynomial for a single pixel in the IRT measurement, b extracted noise from the sequence and c its associated histogram along with normal distribution fit

Now, the associated noise can be extracted for the corresponding pixel by subtracting the polynomial fit of each pixel from the measurement thermographic data of the pixel.

Figure 11b shows the extracted high-frequency noise from a representative pixel. It was observed that the extracted high-frequency noise for each pixel had a zero mean ($\mu$), and the standard deviation ($\sigma$) varied between 0.025 and 0.065. Furthermore, a histogram analysis of the noise shows the underlying normal distribution (Fig. 11c). Thus, the high-frequency noise discussed can be modelled as random samples drawn from a normal distribution of $\mu = 0$ and $\sigma$ within a specific range (0.025 and 0.065).

Let $\textbf{X}$ represent the flattened 2D measurement data matrix of shape $N_YN_X \times N_T$, then the denoised measurement data matrix (polynomial fit matrix) $\mathbf {X_F}$ is given as

$$\begin{aligned} \mathbf {X_F} = \begin{bmatrix} - &{}f(\mathbf {X[1, :]})&{} - \\ - &{}f(\mathbf {X[2, :]})&{} - \\ &{}\vdots &{} \\ - &{}f(\mathbf {X[N_YN_X, :]})&{} - \end{bmatrix}, \end{aligned}$$

(11)

where $\mathbf {X[i,:]}$ is the $i^{th}$ row of matrix $\textbf{X}$, and $f(\mathbf {X[i,:]})$ represents the denoised temperature response using the polynomial fit function applied to that row (Eq. (10)). Finally, the associated Gaussian noise matrix $\mathbf {N_{GN}}$ is calculated as:

$$\begin{aligned} \mathbf {N_{GN} = X - X_F}. \end{aligned}$$

(12)

The reconstructed denoised measurement matrix $\mathbf {X_F}$ from Eq. (11) can be further used for studying the uneven heating of the sample. Ideally, each pixel should have an identical cooling curve for a defect-free sample, provided the heating was uniform. However, in reality, this is not the case. Depending on the lamp’s position in the experimental setup, the sample has non-uniform heating, i.e. different pixels have different cooling curves. In the given experimental setup, the effect of uneven heating is more prominent on the edges of the sample due to the flash position, leading to relatively higher temperatures for the edge pixels when compared to pixels away from the edge (Fig. 12a).

Fig. 12

a Example of uneven heating of the sample; (Top) Px_1 is a pixel near the edge of the sample, and Px_2 is a pixel near the centre of the sample; the difference in the temperature is shown at the bottom. b Comparison of experiment and simulation for temperature evolution of defect-free sample averaged over the sample surface

In order to approximately quantify the effect of uneven heating, the mean cooling curve (the mean temporal profile) is subtracted from the temperature evolution of each pixel. As shown in Fig. 12b, the mean cooling curve is a good approximation of the FEM model with uniform heating. The discrepancies in the temperature values in the initial time steps immediately after the flash are due to the saturation region resulting from the flash pulse application, which causes inaccurate measurements in this region. Thus, in this case, the mean cooling curve of a defect-free sample is a good approximation of the temperature response of the defect-free sample if the pulse excitation had been uniform, and subtracting it from the temperature evolution of individual pixels gives a measure of how much the pixel deviated from this assumed ideal cooling curve. The measured difference can then be added to the noise matrix, thus completing the noise extraction process.

If $\mathbf {x_{F_{mean}}}$ is the $1 \times N_T$ row vector which is the mean cooling curve of the $\mathbf {X_{F}}$, $\textbf{e}$ is a $N_YN_X \times 1$ column vector of all ones, then the uneven heating matrix $\mathbf {N_{UEH}}$ captures the deviation of each pixel sequence from the mean cooling curve as:

$$\begin{aligned} \mathbf {N_{UEH} = X_{F} - ex_{F_{mean}}}, \end{aligned}$$

(13)

and the final noise matrix $\textbf{N}$ is calculated as:

$$\begin{aligned} \mathbf {N = N_{GN} + N_{UEH}}. \end{aligned}$$

(14)

The calculated noise matrix is added to the synthetic PT measurements to create a synthetic measurement dataset that includes noise similar to the experimental setup.

Network architecture

The U-Net convolutional neural network was introduced by Ronneberger et al. (2015) in their paper titled “U-Net: Convolutional Network for Biomedical Image Segmentation”. Unlike typical CNNs, where a single label is assigned to a whole image, U-Net provides a more localized approach where each pixel in the image is provided with a class label. The context or the “what?” of the input is captured by the contracting path of the U-Net architecture, and the location or the “where?” is enabled by the symmetric expanding path of the architecture. U-Net strongly relies on data augmentation techniques which helps it to utilize the available annotated samples more efficiently, thus, overcoming the problem of a traditional deep neural network where a large amount of annotated samples are required for the successful training of the network.

A layer in the contracting path follows the typical architecture of a CNN, i.e., convolution followed by activation function and max pooling for downsampling. Each max-pooling reduces the spatial dimension of the image and increases the number of channels.

The spatial information lost in the contracting path is recovered by supplementing the contracting path with an expansive path. A layer in the expansive path consists of up-convolution, which upsamples the feature map and reduces the number of channels, thus opposite of downsampling in the contraction path; furthermore, the upsampled feature map is concatenated with the corresponding feature map from the contraction path, which is followed by convolution and activation function. The concatenation of the feature maps from the corresponding layer in the contraction path helps to propagate the context information to the higher-resolution feature maps in the expansive path. There are no fully connected layers in the network.

Fig. 13

U-Net architecture, as proposed by Ronneberger et al. (2015)

Here, the conventional CNN architecture in the contracting path is replaced with a ResNet34 architecture (He et al. 2016) initialized by the ImageNet pre-trained weights.The ImageNet dataset (Russakovsky et al. 2015) consists of millions of labelled images from several categories, thus using a model pre-trained on such a large dataset helps leverage better feature extraction from new samples by transferring the model’s learning onto the new task; also, it provides a good base model which can be fine-tuned for the segmentation task at hand. The loss function used in this work combines binary cross entropy ($L_{BCE}$) and Jaccard loss ($L_{JL}$). The binary cross entropy measures the pixel-wise difference between the predicted mask and the ground truth. It is expressed as:

$$\begin{aligned} L_{BCE} = \frac{-1}{N}\sum _{i=1}^{i=N}y_{true}^{(i)}\log (y_{pred}^{(i)}) + (1-y_{true}^{(i)})\log (1-y_{pred}^{(i)}), \end{aligned}$$

(15)

where N represents the total number of pixels in the segmentation mask, $y_{truth}$ represents the ground truth for the pixel, with 0 representing the sound region and 1 representing the defect region, $y_{pred}$ is the predicted probability that the pixel belongs to the defect region. On the other hand, the Jaccard loss evaluates the overlap between the predicted and ground truth mask. It is calculated as:

$$\begin{aligned} L_{JL} = 1 - \text {IoU}, \end{aligned}$$

(16)

where IoU is the Intersection over Union between the predicted and the ground truth mask, calculated as:

$$\begin{aligned} \text {IoU} = \frac{{\text {{Intersection}}}}{{\text {{Union}}}} = \frac{\sum _{i=1}^{N} y_{true}^{(i)} \wedge y_{pred}^{(i)}}{\sum _{i=1}^{N} y_{true}^{(i)} \vee y_{pred}^{(i)}}, \end{aligned}$$

(17)

where $\wedge$ denotes “logical and” operation between the pixel’s ground truth and prediction and $\vee$ denotes “logical or” operation. Thus, the final loss function (L) is

$$\begin{aligned} L = L_{BCE} + L_{JL}. \end{aligned}$$

(18)

Combining these two loss functions helps improve pixel-level predictions and better align the predicted and true mask. The evaluation metric used is IoU, and the average IoU is calculated for the validation samples. Table 3 provides all the details related to the model implementation.

Table 3 Detailed summary of all the parameters related to the DL model

Datasets

As discussed in the previous section, the data for training and evaluating the model stem from FEM and experiments. The dataset consists of EOFs and their corresponding masks. A dataset sourcing from synthetic PT measurement comprises 2068 synthetic EOF images, i.e., the first four EOFs from each of the 517 synthetic PT measurements and their corresponding masks. A dataset sourcing from PT experiments comprises 80 measurement EOF images, i.e. first four EOFs from each of the 20 samples and their corresponding mask.

In the case of the synthetic EOFs, as the location and size of the defects are known, the annotation process was automated using Python code, thus, providing precise and reliable labels for the synthetic EOFs (Fig. 14b). The ease of generating precise labels for large amounts of images is one of the most significant advantages of synthetic PT measurements. The measurement EOFs were labelled manually (Fig. 14a) using the image annotation software “Labelme: Image Polygonal Annotation with Python” (Wada 2018). As the number of defects in a sample and their locations are known, the manually generated labels can be considered reliable regarding the defect being present at a marked location. However, the lateral heat diffusion in the measurements makes it difficult to precisely label the defect boundaries, i.e., the actual diameter of the defect.

Fig. 14

From left to right: EOF image, the mask for the image, and overlay of the mask on the original image to show the labelled defects. The masks are for the third EOFs from a the PT measurement of a sample with three defects and b its corresponding FEM simulations without added noise

Three different datasets are created: measurement dataset (total size of 80 EOFs from experiments), synthetic dataset w/o noise (total size of 2068 EOFs from synthetic PT measurements without noise) and synthetic dataset with noise (total size of 2068 EOFs from synthetic PT measurements with noise). Three U-Net models with the same implementation details as in Sect. “Network architecture" were trained on three different configurations of these datasets. Model 1 was trained and evaluated on the measurement dataset alone, with the measurement EOFs randomly divided into a training set (56 EOFs) and a validation set (24 EOFs). For model 2, the EOFs in the synthetic dataset w/o noise were randomly divided into a training set (1758 EOFs) and a validation set (310 EOFs; referred to as “val syn w/o noise”). Model 2 was also validated after each epoch on the measurement EOFs (“val exp”). Lastly, for model 3, the synthetic dataset with noise was randomly divided into a training set (1758 EOFs) and a validation set (310 EOFs; referred to as “val syn with noise”). Model 3 was also validated after each epoch on the measurement EOFs (“val exp”). Model 1 was trained for a total of 200 epochs, and models 2 and 3 were trained for a total of 100 epochs each. Validating models 2 and 3 on the measurement dataset helps monitor and understand how well the models trained on synthetic datasets perform on the actual samples. Finally, to increase the diversity of the training dataset in all three models, traditional data augmentation techniques were also applied; this includes random transformations in the form of flipping, rotation, translation and cropping. Later, a global threshold of 0.8 was applied to the predicted segmentation masks, i.e. if the predicted value of a pixel was greater than or equal to 0.8, it was classified as a defect pixel (value of 1) or else as a sound pixel (value of 0) to convert it into a binary mask.

Table 4 Summary of the dataset source and the distribution for the three models

Segmentation performance on different datasets: results, discussion and comparison

Comparative analysis of the data

As discussed in the previous sections, the goal of the synthetic dataset is to bridge the data gap that plagues real-world applications. The representativeness of the synthetic data to the actual data is critical to the model’s success. This section compares a sample from the measurement samples with three defects to its corresponding simulated synthetic version without and with noise (referred to in this section as synthetic w/o noise and synthetic with noise).

Figure 16 shows the raw unprocessed measurement image from all three cases. The synthetic PT measurement image (Fig. 16b) shows the same temperature distribution as the experiment (Fig. 16a) but lacks noise as in the experimental images. However, with the addition of noise (Fig. 16c), it is a better representation of the experimental image, i.e., uneven heating can be observed on the sample surface, especially the edges and the defect signal blurring.

As the deep learning model will be trained on the EOFs obtained from the PCT, the measurement and the synthetic EOFs and PCs were analyzed.

Fig. 15

Summary of the suggested methodology framework

Fig. 16

PT images for the sample with three defects at time $t =$ 8.06 s for a experiment, b synthetic w/o noise and c synthetic with noise

Fig. 17

Comparison of the EOFs and PCs from the PCT for a measurement sample with three defects with the corresponding simulations results (with and without noise). Row description from top to bottom: a first PC and EOF, b second PC and EOF, c third PC and EOF and lastly, d fourth PC and EOF. Column description from left to right: PCs for all three cases weighed by their respective singular values ($\sigma _i\mathbf {v_i^T}$), EOFs for the experiment, synthetic w/o noise and the last column is synthetic with noise

Figure 17 compares the first four PCs and EOFs for the measurement and the synthetic versions. Consider the comparison of the first EOF and PC (Fig. 17a); the first EOF for all three cases has negative values with the value of defects being lower than the sound region, first EOF when looked at in conjunction with its corresponding PC also reveals that all three cases have a similar dominant mode of cooling and the time of zero crossing is identical.

While comparing the second EOF and PC (Fig. 17b), one can notice how, in contrast to the first EOF, the sound region has the lowest value in the second EOF, and the defect has the highest value in all three cases. The second EOF focuses on the characteristics of the defects. The second EOF for the synthetic w/o noise shows the idealized case of the sound region being ideally zero, which is not the case for the other two cases due to noise. Also, the second PC for all three versions shows a similar trend for the temporal evolution of the second EOF.

In the case of the third and the fourth PCs and EOFs (Fig. 17c and 17d), the sound region has values near zero, and the defect marks and radially outwards heat dispersion around the defect are visible. The variation range of PCs reduces, and the EOFs are noisier when compared to the first and second EOFs. Thus, in higher EOFs and PCs, the effect of noise is seen more prominently (compare synthetic w/o noise with measurement and synthetic with noise). An interesting observation is in the case of the fourth PC and EOF (Fig. 17d) for the case of synthetic with noise where an inversion in defect values for the EOF can be observed when compared to the fourth EOF for experiment and synthetic w/o noise. This inversion in the fourth EOF value has been compensated by the corresponding inversion of the fourth PC for synthetic with noise compared to the fourth PC for experiment and synthetic w/o noise; as a result, $mode_4$, i.e. the matrix $\sigma _4 \mathbf {u_4v_4^T}$ has similar contribution in all three cases.

The singular values for all three cases are shown in Fig. 18. The first four singular values for all three cases are similar. In the case of synthetic w/o noise, all the information is retained in the first 18 singular values; i.e., the matrix $\textbf{X}$ in Eq. (5) can be reconstructed entirely with the first 18 modes. However, this is not the case for the actual measurement, where each singular value adds incremental value to the whole sum. This discrepancy between the singular values is due to the absence of noise in the synthetic measurement generated via FEM. As a result, when the noise matrix is added to the synthetic measurements, the obtained singular values are similar to the measurement singular values.

The above-discussed points show that the FEM-generated synthetic data (synthetic w/o noise) can be representative of the actual measurement. However, in the higher EOFs and PCs of the measurement, the effects of noise present can be noticed. The representativeness of the synthetic data can be improved by adding the extracted system noise, as explained in Sect. "Noise: analysis, extraction and addition". With the addition of noise (synthetic with noise), more nuances of the measurement setup can be captured, thus making the synthetic dataset even more robust and encompassing more details of the measurement dataset.

Segmentation results

This section discusses the segmentation results of the U-Net model trained on three different datasets (Table 4) for the set of hyperparameters shown in Table 3.

Fig. 18

Comparison of the first 20 singular values obtained from the PCT on the experiment and the corresponding simulated PT measurements. For synthetic w/o noise, the first 18 singular values retain all the information, but in the case of experiment and synthetic with noise, it is spread out across all the singular values

Fig. 19

IoU (first row) and Loss (second row) performance for a Model 1, b Model 2 and c Model 3

To begin with, consider Model 1 (Fig. 19a), which was trained and validated solely on the small dataset of the measurement EOFs. For the first 50 epochs, the model fails to generalize its learning from the training data onto the unseen validation data. The validation IoU gradually improves from around the 50th epoch and eventually lingers around 0.75. As the dataset was labelled manually and the ground truth was verified with the actual sample defect positions, it is safe to say that the highest achievable performance for this task (human-level performance) is around 0.95 IoU (taking a conservative estimate). The deficit between the training IoU and the highest achievable performance indicates that the model is unable fully to tap into the potential of the data and can improve its performance if more data is available for its training. Furthermore, consider the difference between the training and validation IoUs, which shows that the model is not generalizing well to the unseen data of the validation set, indicating overfitting, i.e., good performance on the train set but not on the validation set, which is a common problem when dealing with small datasets. The above-discussed points emphasize the need for a larger representative dataset, which, as discussed before, is the biggest challenge.

Synthetic data can help overcome this inherent lack of data, and to evaluate their effectiveness, Model 2 and Model 3 were trained purely on a large portion of synthetic EOFs (w/o and with noise, respectively) and validated on the remaining synthetic EOFs and measurement EOFs. Validating the model performance on the measurement dataset helps understand how well the learning on the synthetic data generalizes to real-world scenarios, i.e. how representative the synthetic data is to the real data. To evaluate the effectiveness of synthetic EOF w/o noise, consider Model 2. In contrast to Model 1, the improvements in the validation IoU (Fig. 19b, “val syn w/o noise” and “val exp”) can be seen within the first ten epochs, indicating that increasing the training data with more diverse examples to learn from leads to an earlier performance improvement and faster performance convergence. Also, the training IoU has improved and is above 0.95. When comparing training and validation IoU for the model, the model generalizes well to the unseen data from the same distribution, i.e. synthetic EOFs w/o noise (“val syn w/o noise”). However, it struggles to generalize well on the measurement EOFs, this can be observed in the chaotic validation curves for the measurement EOFs (“val exp”). This phenomenon can be attributed to the absence of noise in the synthetic dataset on which the model was trained. In the case of Model 2, the synthetic dataset does not encapsulate all the characteristics of the real-world data, i.e. it does not consist of artefacts such as measurement noise present in the measurement data. Figure 21b shows a few predictions of Model 2 on the measurement EOFs; it can be seen that the false positives by the model are due to noise present in the measurement EOFs.

Table 5 Best average IoU on measurement validation dataset

Fig. 20

Visualization of the segmentation results for Model 1. The pink masks represent the segmentations, and the black contours represent the ground truth boundary. a Few measurement EOFs from the validation dataset; b obtained segmentation results

Model 3 showcases the model’s performance when trained on synthetic EOFs with noise (Fig. 19c). It has characteristics similar to Model 2, such as early performance improvement, convergence, and higher train IoU. However, the highlight of Model 3 is its improvement in the measurement validation set, where its performance convincingly converges at around 0.79 IoU. This improvement in performance on an unseen real-world dataset indicates that the synthetic data on which Model 3 was trained is sufficiently diverse and a better representative of the actual measurement dataset. Figure 21c shows a few predictions of Model 3 on the measurement EOFs; it can be seen that the model is robust to the noise present in the measurement EOFs.

Further dissecting the performance of Model 3 on the measurement EOFs, it was observed that the loss in the IoU of the model on the measurement dataset is mainly on the defect boundaries (Fig. 21c); this is because of difficulties in the precise annotation of the defect boundaries for the measurement dataset. In the case of annotation of the synthetic data, the precise location and boundary of the defects are well known. As a result, the masks generated are accurate and precise. However, this is not true for masks generated for the measurement dataset, where lateral heat diffusion makes it difficult to mark the defect boundaries consistently. This issue of precise annotation of the defect boundaries for the measurement dataset also explains why the IoU performance of Model 3 on the measurement validation set plateaus at around 0.79 (Fig. 19c) despite all defects being detected and improved performance in the presence of noise. Thus, IoU, as the evaluation metric, does not fully capture the model performance where the annotation of the defect boundary is challenging.

Fig. 21

Visualization of the segmentation results for Model 2 and Model 3. The pink masks represent the segmentations, and the black contours represent the ground truth boundary. a Few of the measurement EOFs for samples with varying numbers of defects. b Segmentation results for Model 2 (Top) and the absolute difference between ground truth and segmentation where false positives can be seen due to present noise (Bottom). c Segmentation results for Model 3 (Top) and the absolute difference between ground truth and segmentation (Bottom) show improvements over Model 2

Robustness assessment: inference on new images

The feasibility of the trained models on the new PT dataset was evaluated using two new datasets. Here, the previously trained models (Table 4) are used to make predictions on two new datasets covering two scenarios: (1) when the previously used experimental samples are measured on an entirely different experimental setup and (2) when both the samples and the experimental setup are different.

To begin with, consider the first scenario where the previously used experimental samples are measured on a different experimental setup. Figure 22 shows the schematic of the new experimental setup where the infrared camera (Optris Xi 400) is placed coaxially with the single flash ring directly above the sample. The detector resolution of the new infrared camera is $382 \times 288$ IR pixels, and the thermal resolution of 80 mK. The sampling rate of the camera was 80 Hz with an acquisition time of 12.5 s. Table 6 lists changes between the previously used experimental setup in Sect. “Samples and experimental setup” and the new experimental setup. As the experiment aimed to examine if the models could still detect defects when the experimental setup changes considerably, no new ground truth masks were created for the dataset. PCT was performed on the new measurements as described in Sect. “Synthetic data: generation and pre-processing”. The first four EOFs were used for inference. Figure 23 shows a few of the predictions on the new EOFs from all three models. All three models showed good immunity to the change in the experimental setup, i.e., the defects in the samples were detected successfully, and the performance was consistent with the measurement from the previous experimental setup. Model 2 did struggle with the noise in the EOF image, as experienced in the previous sections.

The second dataset is the Fraunhofer IZFP dataset from Wei et al. (2023), which consists of 19 PT measurements and masks for samples made up of PVC with artificially induced defects in the form of cylindrical holes. In the paper, the authors have the following dataset split: 13 samples for the training set, 3 for the validation and 3 for the test set. The measurement sampling rate is 10 Hz with a total acquisition time of 181 s.

Fig. 22

Schematic of the new experimental setup with single flash source and the IR camera placed directly above the sample

Table 6 Comparison between the previously used experimental setup (Setup 1) as described in Sect. “Samples and experimental setup” and the new experimental setup (Setup 2). The robustness of the trained models against the change in the experimental setup is assessed based on their prediction performance on the measurement data from the changed experimental setup (Setup 2)

Figures 24 and 25 show the segmentation results of the models on the test set of the Fraunhofer IZFP dataset. Inference was made on the first 10 EOFs of the test samples, and the EOF with the highest IoU is presented here. In the paper, the authors reported an average IoU of 0.638 on the validation dataset for the U-Net model trained on PCT; no information on the average IoU score for the test set was provided for the U-Net model trained on PCT. Table 7 shows the average IoU score of each model on the provided test set. From Table 7, and Figs. 24 and 25, show that all three models can generalize well on the unseen dataset indicating that they have learned the useful features for defect detection. Model 1 and Model 3 have marginal differences in their IoU scores, and both performed better than Model 2. It can also be seen that even though most of the defects were detected, the loss in the IoU score is mainly around the defect boundaries, further showcasing the difficulty in marking the defect boundaries precisely due to lateral heat dispersion around the defect.

Thus, the performance of the models on these unseen datasets, especially Model 2 and Model 3, demonstrate that models trained on representative synthetic data generalize well on new datasets. Thus, further strengthing the stand of physics-based synthetic datasets as a valuable resource in data deprived real world.

Lastly, to demonstrate the effectiveness of the proposed methodology, consider the predictions on the EOF of an independently simulated sample with added noise as shown in Fig. 26a. The sample helps examine the defect pattern not present in the training set distribution. At the edges of the sample, where the effect of uneven heating is dominant, there are two defects: D1, a relatively smaller diameter (1.5 mm) at a deeper depth (0.3 mm) and a quarter defect, D4 (depth = 0.1 mm). Furthermore, two contrasting defects in size and depth are positioned close to each other: D2 (diameter = 7 mm, depth = 0.1 mm) and D3 (diameter = 2 mm, depth = 0.3 mm).

Fig. 23

Visualization of the segmentation results when the samples are measured on an entirely different experimental setup. a Few of the EOFs from the measurement dataset followed by inference results (pink masks) from b Model 1, c Model 2 and d Model 3. All the models showed good immunity against the change in experimental setup

Fig. 24

Visualization of the segmentation results on EOFs with the highest IoU from the Fraunhofer IZFP test dataset (Wei et al. 2023). Column description from left to right: EOF, inference on the EOF from Models 1, 2, and 3. The pink masks represent the segmentations, and the black contours represent the ground truth boundary. a Second EOF of sample Z004 and b fourth EOF of sample Z009

Fig. 25

Visualization of the segmentation results on the EOF with the highest IoU of the sample Z013 from the Fraunhofer IZFP test dataset Wei et al. (2023); a Second EOF of Z013 (Top), Model 1 inference (Bottom); b fourth EOF of Z013, Model 2 inference (Bottom); c second EOF of Z013 (Top), Model 3 inference (Bottom)

From the predictions, it can be seen that Model 1 fails to detect defects D1 and D3; this can be attributed to the limited training dataset of Model 1. As a result, Model 1 cannot generalize well on the new unseen data. Although Model 2 detects all the defects, its underperformance in detecting D4 due to noise can be seen. Finally, Model 3, trained on a large and representative dataset, convincingly detects all the defects. This performance aligns with the conclusions drawn from Fig. 19.

Conclusions and outlook

The presented work begins with its sight set on sustainable and reliable zero-defect manufacturing using automated defect detection based on PT setup. However, the lack of meaningful data in manufacturing is the biggest challenge in realizing an intelligent defect detection system. The research taps into the potential of physics-based synthetic data generation using FEM to bridge the data gap. The proposed end-to-end framework was thoroughly investigated at each step, from generating synthetic data to evaluating the model performance. With 20 experimental samples and 517 representative synthetic samples, the PT dataset in this research is more extensive than any of the previously used PT datasets.

Inherently synthetic datasets generated using FEM are noise-free, and their representativeness can be improved by adding noise intrinsically present in the experimental setup. Noise from the experimental setup was extracted using the temperature response of a defect-free sample to the experimental setup. To answer the important question of how representative is the synthetic dataset of the real-world data, three different datasets were generated: experiment, synthetic w/o noise and synthetic with noise. A comparative analysis of the dataset was carried out by comparing: surface temperature distribution from the time series PT measurement set, the obtained PC, EOFs and singular values and lastly, the performance of the U-Net model when trained on these datasets separately. The comparative analysis revealed that the synthetic dataset with noise was a better representative of the experiment dataset.

The U-Net model was trained individually on each of the three datasets. Analysis of the performance curves of Model 1, which was trained and validated on the limited experimental EOFs, revealed the need for more data for better performance. Investigation of performance curves for Model 2, which was trained on a large portion of synthetic EOFs w/o noise and validated on the remaining synthetic EOFs w/o noise and experimental EOFs, motivated the improvement in the representativeness synthetic datasets by the addition of noise to encapsulate more characteristics of the real-world data. Exploration of the performance curves for Model 3, which was trained on a large portion of synthetic EOFs with noise and validated on the remaining synthetic EOFs with noise and experimental EOFs, shows that the synthetic dataset with noise is sufficiently diverse and a better representative of the actual measurement dataset.

The robustness assessment of the models on two new datasets highlights the effectiveness of the synthetic datasets and the potential benefits they provide when real data is not readily available or is expensive to procure.

Table 7 Results on the test set of Fraunhofer IZFP dataset

Fig. 26

a EOF of noise added simulated sample with four defects and the corresponding predictions from b Model 1, c Model 2 and d Model 3. The example demonstrates the effectiveness of training on a diverse and representative dataset

Having reached the current milestone, one of the focuses for the upcoming iteration of this work will be on improving the annotation approach for the defect. The aim will be to acknowledge the difficulties in precisely annotating defect boundaries in the measurement data due to lateral heat dispersion. One of the potential solutions is to reduce the emphasis on pixel-perfect annotation and allow some tolerance in exact defect boundaries. Thus, a more nuanced representation of defects, accounting for the lack of well-defined defect boundaries due to lateral heat dispersion, would help improve the evaluation metrics. Furthermore, the aim is to adapt the proposed framework for samples with more complicated structure and defects, such as delamination, voids and cracks between the interface of two materials, and to evaluate the performance of other segmentation algorithms.