Introduction

The shift from mass production to mass customization and personalization (Hu, 2013) requires high standards on production processes. In spite of the high variance between different products and small batch sizes of the products to be manufactured, the product quality in mass customization has to be comparable to the quality of products from established mass production processes. It is therefore essential to keep process ramp-up times low and to achieve the required product quality as directly as possible. This requires a profound and solid understanding of the dependencies between process parameters and quality criteria of the final product, even before the start of production (SOP). Various ways exist to gain this kind of process knowledge: for example, by carrying out experiments, setting up simulations, or exploiting available expert knowledge. In production, expert knowledge in particular plays a central role. This is because complex cause–effect relationships operate between the input–output parameters during machining, and these parameters generally have to be set in a result-oriented manner in a short amount of time without recourse to real-time data sets. Indeed, process ramp-up is still commonly done by process experts purely based on their knowledge. Furthermore, many processes are controlled by experts during production to ensure that consistently high quality is produced.

In the course of digitalization, the acquisition of and the access to data in manufacturing have increased significantly in recent years. Sensors, extended data acquisition by the controllers themselves, and the continuous development of low-cost sensors allow for the acquisition of large amounts of data (Wuest et al., 2016). Accordingly, more and more data-driven approaches, most notably machine learning (ML) methods, are used in manufacturing to describe the dependencies between process parameters and quality parameters (Weichert et al., 2019). In principle, such data-driven methods are suitable for the rapid generation of quality prediction models in production, but the quality of ML models crucially depends on the amount and the information content of the available data. The data can be generated from experiments or from simulations. In general, experiments for process development or improvement are expensive and accordingly the number of experiments to be performed should be kept to a minimum. In this context, design of experiment can be used to obtain maximum information about the process behavior with as few experiments as possible (Montgomery, 2017; Fedorov & Leonov, 2014). Similarly, the generation of data using realistic simulation models can be expensive as well, because the models must be created, calibrated, and—depending on the process—high computing capacities are required to generate the data. Concluding, the data available in manufacturing before the SOP is typically rather small.

This paper introduces a novel and general methodology to leverage expert knowledge in order to compensate such data sparsities and to arrive at prediction models with good predictive power in spite of small datasets. Specifically, the proposed methodology is dedicated to shape expert knowledge, that is, expert knowledge about the qualitative shape of the input–output relationship to be learned. Simple examples of such shape knowledge are prior monotonicity or prior convexity knowledge, for instance. Additionally, the proposed methodology directly involves process experts in capturing and in incorporating their shape knowledge into the resulting prediction model.

In more detail, the proposed methodology starts out from an initial, purely data-based prediction model and then proceeds in the following steps. In a first step, a process expert inspects selected, particularly informative graphs of this model. In a second step, the expert then specifies in what way these graphs confirm or contradict his shape expectations. And in a third and last step, the thus specified shape expert knowledge is incorporated into a new prediction model which strictly complies with all the imposed shape constraints. In order to compute this new model, the semi-infinite optimization approach to shape-constrained regression (SIASCOR) is taken, based on the algorithms from (Schmid & Poursanidis, 2021). In the following, this approach is referred to as the SIASCOR method for brevity. While a semi-infinite optimization approach has also been pursued in von Kurnatowski et al. (2021), the algorithm used here is superior to the reference-grid algorithm from von Kurnatowski et al. (2021), both from a theoretical and from a practical point of view. Additionally, von Kurnatowski et al. (2021) treat only a single kind of shape constraints, namely monotonicity constraints. Apart from this reference, there is, to the best of our knowledge, only one other reference that treats shape constraints by means of semi-infinite optimization, namely Cozad et al. (2015). Compared to the algorithm used here, however, the algorithm from Cozad et al. (2015) is less satisfactory. In particular, it does not guarantee the strict fulfilment of the imposed shape constraints.

The general methodology is applied to the exemplary process of grinding with brushes. In spite of the small set of available measurement data, the methodology proposed here leads to a high-quality prediction model for the surface roughness of the brushed workpiece. Aside from the brushing process, the SIASCOR method can also be successfully applied to the glass-bending and press-hardening processes described in von Kurnatowski et al. (2021).

The paper is organized as follows. The section “Related works” gives an overview of the related work. In the section “A methodology to capture and incorporate shape expert knowledge”, the general methodology to capture and incorporate shape expert knowledge is introduced, and its individual steps are explained in detail. The section “Application example” describes the application example, that is, the brushing process. The section “Results and discussion” discusses the resulting prediction models applied to the brushing process and compares them to more traditional ML models. The section “Conclusion and future work” concludes the paper with a summary and an outlook on future research.

Related works

Quality prediction is essential to optimize processes in manufacturing. It can help to quickly ramp up processes and to document product quality. Quality prediction models can be analytical or data-driven. Benardos and Vosniakos (2003) review both approaches in the context of machining processes to describe the surface roughness as a function of different process variables. Data-driven quality prediction models for process optimization have recently been applied to a machining process in Proteau et al. (2021), to textile drapping processes in Pfrommer et al. (2018), and to a laser cutting process in Chaki et al. (2015), just to name a few.

Weichert et al. (2019) show that ML models used for optimization of production processes are often trained with relatively small datasets. In this context, attempts are often made to represent complex relationships with complex models and small datasets. Also in other domains, such as process engineering (Napoli & Xibilia, 2011) or medical applications (Shaikhina & Khovanova, 2017), small amounts of data play an important role in the use of ML methods—and will continue to do so (Kang et al., 2021). Accordingly, there already exist quite many methods to train complex models with small datasets in the literature. These known approaches to sparse-data learning can be categorized as purely data-based methods on the one hand and as expert-knowledge-based methods on the other hand.

In the following literature review, expert-knowledge-based approaches that typically require large—or, at least, non-sparse—datasets are not included. In particular, the projection- and rearrangement-based approaches to monotonic regression from Lin and Dunson (2014), Schmid (2021) and Dette and Scheder (2006), Chernozhukov et al. (2009) are not reviewed in detail here. Similarly, the kernel-based approach to shape-constrained regression from Aubin-Frankowski and Szabo (2020) is only mentioned here but not discussed in detail, because the way the shape-knowledge is integrated differs completely from our semi-infinite optimization approach.

Purely data-based methods for sparse-data learning in manufacturing

An important method for training ML models with small datasets is to generate additional, artificial data. Among these virtual-data methods the mega-trend-diffusion (MTD) technique is particularly common. It was developed by Li et al. (2007) using flexible manufacturing system scheduling as an example. In Li et al. (2013) virtual data is generated using a combination of MTD and a plausibility assessment mechanism. In the second step, the generated data is used to train an artificial neural network (ANN) and a support vector regression model with sample data from the manufacturing of liquid-crystal-display (LCD) panels. Using multi-layer ceramic capacitor manufacturing as an example, bootstrapping is used in Tsai and Li (2008) to generate additional virtual data and then train an ANN. Napoli and Xibilia (2011) also use bootstrapping and noise injection to generate virtual data and consequently improve the prediction of an ANN. The methodology is applied to estimate the freezing point of kerosene in a topping unit in chemical engineering. In Chen et al. (2017) virtual data is generated using particle swarm optimization to improve the prediction quality of an extreme learning machine model.

In addition to the methods for generating virtual data and the use of simple ML methods such as linear regression, lasso or ridge regression (Bishop, 2006), other ML methods from the literature can also be used in the context of small datasets. For example, the multi-model approaches in Li et al. (2012) and in Chang et al. (2015) can be mentioned here. The multi-model approaches are used in the field of LCD panel manufacturing to improve the prediction quality. Another concrete example are the models described by Torre et al. (2019), which are based on polynomial chaos expansion. These models are also suitable for learning complex relationships in spite of few data points.

Expert-knowledge-based methods for sparse-data learning in manufacturing

An extensive general survey about integrating prior knowledge in learning systems is given in Rueden et al. (2021). The integration of knowledge depends on the source and the representation of the knowledge: for example, algebraic equations or simulation results represent scientific knowledge and can be integrated into the learning algorithm or the training data, respectively.

Apart from this general reference, the recent years brought about various papers on leveraging expert knowledge in specific manufacturing applications. Among other things, these papers are motivated by the fact that production planning becomes more and more difficult for companies due to mass customization. In order to improve the quality of production planning, Schuh et al. (2019) show that enriching production data with domain knowledge leads to an improvement in the calculation of the transition time with regression trees.

Another broad field of research is knowledge integration via Bayesian networks. In Zhang et al. (2020) domain knowledge is incorporated using a Bayesian network to predict the energy consumption during injection molding. Lokrantz et al. (2018) present an ML framework for root cause analysis of faults and quality deviations, in which knowledge is integrated via Bayesian networks. Based on synthetically generated manufacturing data, an improvement of the inferences could be shown compared to models without expert knowledge. He et al. (2019) show a way to use a Bayesian network to inject expert knowledge about the manufacturing process of a cylinder head to evaluate the functional state of manufacturing on the one hand, and to identify causes of functional defects of the final product on the other hand.

Another possibility of root cause analysis using domain-specific knowledge is described by Rahm et al. (2018). Here, knowledge is acquired within an assistance system and combined with ML methods to support the operator in the diagnosis and elimination of faults occurring at packaging machines. Xu et al. (2018) suggested an intelligent knowledge-driven system to solve quality problems in the automotive industry. In that approach, an intelligent module structures and analyzes the knowledge database. The intelligent module provides additional information to experts responsible for solving quality problems.

Lu et al. (2017) incorporate knowledge of the electrochemical micro-machining process into the structure of a neural network. It is demonstrated that integrating knowledge achieves better prediction accuracy compared to classical neural networks. Another way to integrate knowledge about the additive manufacturing process into neural networks is based on causal graphs and proposed by Nagarajan et al. (2019). This approach leads to a more robust model with better generalization capabilities. In Ning et al. (2019), a control system for a grinding process is presented in which, among other things, a fuzzy neural network is used to control the surface roughness of the workpiece. Incorporating knowledge into models using fuzzy logic is a well-known and proven method, especially in the field of grinding (Brinksmeier et al., 2006).

In contrast to the methodology proposed in the present paper, the references mentioned above are not devoted to shape expert knowledge but to other kinds of expert knowledge, which relate to the input–output function to be learned only indirectly. Indeed, He et al. (2019), Lokrantz et al. (2018), Nagarajan et al. (2019), and Zhang et al. (2020) are concerned with expert knowledge in the form of cause–effect relationships and they integrate this kind of knowledge into the model’s architecture. Also, Ning et al. (2019), Lu et al. (2017), and Schuh et al. (2019) are concerned with expert knowledge in the form of explicit physical equation relationships and they integrate these equations into the models, for instance, in the form of new features.

A paper that does consider shape constraints in a manufacturing context is Hao et al. (2020). In contrast to the present paper, the mentioned paper is confined to (piecewise) monotonicity constraints and incorporates these constraints in a completely different way. Indeed, it incorporates the monotonicity constraints into Gaussian process surrogate models (Riihimäki & Vehtari, 2010). In order to get better surrogate models, these models are trained on an iteratively increasing number of sample points determined by Bayesian optimization. In particular, as in Riihimäki and Vehtari (2010), the monotonicity constraints are understood only in a probabilistic sense and their fulfilment is enforced only at a finite number of sampling points, namely at the sampling points that are proposed by the acquisition function for the Bayesian optimization in Hao et al. (2020). Another important difference to the methodology proposed here is that Hao et al. (2020) do not discuss methods of capturing the shape constraints or, in other words, of supporting the expert in working out and specifying their piecewise monotonicity constraints.

A methodology to capture and incorporate shape expert knowledge

As has been pointed out in the previous section, there are expert-knowledge-free and expert-knowledge-based methods to cope with small datasets in the training of ML models in manufacturing. An obvious advantage of expert-knowledge-based approaches is that they typically yield models with superior predictive power, because they take into account more information than the pure data. Another clear advantage of expert-knowledge-based approaches is that their models tend to enjoy higher acceptance among process experts, because the experts are directly involved in the training of these models.

Therefore, this paper proposes a general methodology to capture and incorporate expert knowledge into the training of a powerful prediction model for certain process output quantities of interest. Specifically, the proposed methodology is dedicated to shape expert knowledge, that is, prior knowledge about the qualitative shape of the considered output quantity y as a function

$$\begin{aligned} y = y(\varvec{x}) = y(x_{1}, \ldots , x_{d}) \end{aligned}$$
(1)

of relevant process input parameters \(x_1, \ldots , x_d\). Such shape expert knowledge can come in many forms. An expert might know, for instance, that the considered output quantity y is monotonically increasing with respect to (w.r.t.) \(x_1\), concave w.r.t. \(x_2\), and monotonically decreasing and convex w.r.t. \(x_3\).

In a nutshell, the proposed methodology to capture and incorporate shape expert knowledge starts out from an initial purely data-based prediction model and then proceeds in the following three steps.

  1. (1)

    Inspection of the initial model by a process expert,

  2. (2)

    Specification of shape expert knowledge by the expert,

  3. (3)

    Integration of the specified shape expert knowledge into the training of a new prediction model which strictly complies with the imposed shape knowledge.

This new and shape-knowledge-compliant prediction model is computed with the help of the SIASCOR method (Schmid & Poursanidis, 2021) and it is therefore referred to as the SIASCOR model in the following. After a first run through the steps above, the shape of the SIASCOR model can still be insufficient in some respects, because the shape knowledge specified at the first run might not have been complete, yet. In this case, the steps one to three can be passed through again (with the initial model replaced by the current SIASCOR model), until the expert notices no more shape knowledge violations in the final SIASCOR model. Schematically, this cyclic procedure of obtaining more and more refined shape-knowledge-compliant models from an initial purely data-based model is sketched in Fig. 1.

Fig. 1
figure 1

Schematic of the proposed three-step methodology with an initial purely data-based model as its input and a shape-knowledge-compliant model as its output

Full size image

In the remainder of this section, the individual steps of the proposed methodology are explained in detail. The input parameter range on which the models are supposed to make reasonable predictions is always denoted by the symbol X. It is further assumed that X is a rectangular set, that is,

$$\begin{aligned} X = \{\varvec{x} \in {\mathbb {R}}^{d}: a_{i} \le x_{i} \le b_{i} \text { for all } i \in \{1,\ldots ,d\}\} \end{aligned}$$
(2)

with lower and upper bounds \(a_i\) and \(b_i\) for the ith input parameter \(x_i\). Additionally, the—typically small—set of measurement data available for the relationship (1) is always denoted by the symbol

$$\begin{aligned} {\mathcal {D}} = \{(\varvec{x}^{j}, y^{j}): j \in \{1, \ldots , N\}\}. \end{aligned}$$
(3)

Initial prediction model

As a starting and reference point of the proposed methodology, an initial purely data-based model \({\hat{y}}^0\) is trained for (1), using standard polynomial regression with ridge or lasso regularization (Bishop, 2006). Its sole purpose is to visually assist the process expert in specifying shape knowledge for the SIASCOR model. So, the initial model \({\hat{y}}^0\) is assumed to be a multivariate polynomial

$$\begin{aligned} {\hat{y}}^{0}(\varvec{x}) = {\hat{y}}_{\varvec{w}}^{0}(\varvec{x}) = \varvec{w}^{\top } \varvec{\phi }^{0}(\varvec{x}) \quad (\varvec{x} \in X) \end{aligned}$$
(4)

of some degree \(m^0 \in {\mathbb {N}}\), where \(\varvec{\phi }^0(\varvec{x})\) is the vector consisting of all monomials \(x_1^{p_1} \cdots x_d^{p_d}\) of degree less than or equal to \(m^0\) and where \(\varvec{w}\) is the vector of the corresponding monomial coefficients. In training, these monomial coefficients \(\varvec{w}\) are tuned such that \({\hat{y}}_{\varvec{w}}^0\) optimally fits the data \({\mathcal {D}}\) and such that, at the same time, the ridge or lasso regularization term is not too large. In other words, one has to solve the simple unconstrained regression problem

$$\begin{aligned} \min _{\varvec{w}} \sum _{j=1}^{N}\left( {\hat{y}}_{\varvec{w}}(\varvec{x}^{j}) - y^{j}\right) ^{2} + \lambda \Vert \varvec{w}\Vert _{q}^{q}, \end{aligned}$$
(5)

where \(\lambda \in (0,\infty )\) and \(q \in \{1, 2\}\) are suitable regularization hyperparameters (\(q=1\) corresponding to lasso and \(q=2\) corresponding to ridge regression). As usual, these hyperparameters are chosen such that some cross-validation error becomes minimal.

Inspection of the initial prediction model

In the first step of the proposed methodology, a process expert inspects the initial model in order to get an overview of its shape. To do so, the expert has to look at 1- or 2-dimensional graphs of the initial model. Such 1- and 2-dimensional graphs are obtained by keeping all input parameters except one (two) constant to some fixed value(s) of choice and by then considering the model as a function of the one (two) remaining parameter(s). As soon as the number d of inputs is larger than two, there are infinitely many of these graphs and it is notoriously difficult for humans to piece them together to a clear and coherent picture of the model’s shape (Oesterling, 2016). It is therefore crucial to provide the expert with a small selection of particularly informative graphs, namely graphs with particularly high model confidence and graphs with particularly low model confidence.

A simple method of arriving at such high- and low-fidelity graphs is as follows. Choose those two points \(\hat{\varvec{x}}^{\mathrm {min}}\), \(\hat{\varvec{x}}^{\mathrm {max}}\) from a given grid

$$\begin{aligned} {\mathcal {G}} = \{\hat{\varvec{x}}^{k}: k \in \{1,\ldots ,K\}\} \end{aligned}$$
(6)

in X with minimal or maximal accumulated distances from the data points, respectively. In other words,

$$\begin{aligned} \hat{\varvec{x}}^{\mathrm {min}} := \hat{\varvec{x}}^{k_{\mathrm {min}}} \quad \text {and} \quad \hat{\varvec{x}}^{\mathrm {max}} := \hat{\varvec{x}}^{k_{\mathrm {max}}}, \end{aligned}$$
(7)

where the gridpoint indices \(k_{\mathrm {min}}\) and \(k_{\mathrm {max}}\) are defined by

$$\begin{aligned} k_{\mathrm {min}}:= & {} {\mathop {\mathrm{argmin}}\limits _{k\in \{1,\ldots ,K\}}} \sum _{j=1}^{N} \Vert (\varvec{x}^{j}, y^{j}) - (\hat{\varvec{x}}^{k}, {\hat{y}}^k)\Vert _{2}, \end{aligned}$$
(8)
$$\begin{aligned} k_{\mathrm {max}}:= & {} {\mathop {\mathrm{argmax}}\limits _{k\in \{1,\ldots ,K\}}} \sum _{j=1}^N \Vert (\varvec{x}^{j}, y^{j}) - (\hat{\varvec{x}}^{k}, {\hat{y}}^k)\Vert _{2}, \end{aligned}$$
(9)

with \({\hat{y}}^k := {\hat{y}}^0(\hat{\varvec{x}}^k)\) being the initial model’s prediction at the gridpoint \(\hat{\varvec{x}}^k\). Starting from the two points \(\hat{\varvec{x}}^{\mathrm {min}}\) and \(\hat{\varvec{x}}^{\mathrm {max}}\), one then traverses each input dimension range. In this manner, one obtains, for each input dimension i, a 1-dimensional graph of the initial model of particularly high fidelity (namely the function \(x_i \mapsto {\hat{y}}^0({\hat{x}}_1^{\mathrm {min}}, \ldots , x_i, \dots , {\hat{x}}_d^{\mathrm {min}})\)) and a 1-dimensional graph of particularly low fidelity (namely the function \(x_i \mapsto {\hat{y}}^0({\hat{x}}_1^{\mathrm {max}}, \ldots , x_i, \dots , {\hat{x}}_d^{\mathrm {max}})\)). See Fig. 2 for exemplary high- and low-fidelity graphs as defined above.

An alternative method of obtaining low- and high-fidelity input parameters and graphs is to use design-of-experiments techniques (Fedorov & Leonov, 2014), but this alternative approach is not pursued here.

After inspecting particularly informative graphs as defined above, the expert can further explore the initial model’s shape by navigating through and investigating arbitrary graphs of the initial model with the help of commercial software or standard slider tools (from Python Dash or PyQt, for instance).

Fig. 2
figure 2

Sample high- (a) and low-fidelity (b) graphs of the initial model

Full size image

Specification of shape expert knowledge

In the second step of the proposed methodology, the process expert specifies his shape expert knowledge about the input–output relationship (1) of interest. In this process, the expert can greatly benefit from the initial model and especially from the high- and low-fidelity graphs generated in the first step. Indeed, with the help of these graphs, the expert can, on the one hand, easily detect shape behavior that contradicts his expectations and, on the other hand, identify shape behavior that already matches his expectations for the shape of (1). When inspecting the graphs from Fig. 2, for instance, the expert might notice that the initial model exceeds or deceeds physically meaningful bounds. Similarly, the expert might notice that the initial model

  • is convex w.r.t. \(x_1\) (as he expects),

  • is not monotonically decreasing w.r.t. \(x_1\) (contrary to what he expects).

All the shape knowledge that is noticed and worked out in this manner can then be specified and expressed pictorially in the form of simple schematic graphs like the ones from Fig. 3.

Integration of shape expert knowledge into the training of a new prediction model

In the third step of the proposed methodology, the shape expert knowledge specified in the second step is integrated into the training of a new and shape-knowledge-compliant prediction model, using the SIASCOR method. Similarly to the initial model, the SIASCOR model \({\hat{y}}\) is assumed to be a multivariate polynomial

$$\begin{aligned} {\hat{y}}(\varvec{x}) = {\hat{y}}_{\varvec{w}}(\varvec{x}) = \varvec{w}^{\top } \varvec{\phi }(\varvec{x}) \quad (\varvec{x} \in X) \end{aligned}$$
(10)

of some degree \(m \in {\mathbb {N}}\) (not necessarily equal to the degree of the initial model) and \(\varvec{\phi }(\varvec{x})\), \(\varvec{w}\) represent the monomials and the corresponding monomial coefficients as in (4). In contrast to the initial model training, however, the monomial coefficients \(\varvec{w}\) are now tuned such that \({\hat{y}}_{\varvec{w}}\) not only optimally fits the data \({\mathcal {D}}\) but also strictly satisfies all the shape constraints specified in the second step. In other words, one has to solve the constrained regression problem

$$\begin{aligned}&\min _{\varvec{w}} \sum _{j=1}^N \left( {\hat{y}}_{\varvec{w}}(\varvec{x}^j) - y^j\right) ^2 \quad \text {subject to the}\nonumber \\&\text {shape constraints specified in the second step.} \end{aligned}$$
(11)

In order to do so, the core semi-infinite optimization algorithm from Schmid and Poursanidis (2021) is used, which covers a large variety of allowable shape constraints.

Some simple examples of shape constraints covered by the algorithm are boundedness constraints

$$\begin{aligned} {\underline{b}} \le {\hat{y}}_{\varvec{w}}(\varvec{x}) \le {\overline{b}} \quad (\varvec{x} \in X) \end{aligned}$$
(12)

with given lower and upper bounds \({\underline{b}}, {\overline{b}}\), monotonic increasingness or decreasingness constraints

$$\begin{aligned}&\partial _{x_{i}} {\hat{y}}_{\varvec{w}}(\varvec{x}) \ge 0 \quad (\varvec{x} \in X), \end{aligned}$$
(13)
$$\begin{aligned}&\partial _{x_{i}} {\hat{y}}_{\varvec{w}}(\varvec{x}) \le 0 \quad (\varvec{x} \in X) \end{aligned}$$
(14)

in a given input dimension i, as well as convexity or concavity constraints

$$\begin{aligned}&\partial _{x_i}^{2} {\hat{y}}_{\varvec{w}}(\varvec{x}) \ge 0 \quad (\varvec{x} \in X), \end{aligned}$$
(15)
$$\begin{aligned}&\partial _{x_i}^{2} {\hat{y}}_{\varvec{w}}(\varvec{x}) \le 0 \quad (\varvec{x} \in X) \end{aligned}$$
(16)

in a specified input dimension i. A more complex kind of shape constraint that is also covered by the employed algorithm is the so-called rebound constraint. It constrains the amount the model can rise after a descent to be no larger than a given rebound factor r. In mathematically precise terms, a rebound constraint in the ith input dimension takes the following form:

$$\begin{aligned}&{\hat{y}}_{\varvec{w}}(x_{1}, \ldots , b_{i}, \ldots , x_d) - {\hat{y}}_{\varvec{w}}^*\nonumber \\&\quad \le r \cdot ({\hat{y}}_{\varvec{w}}(x_{1}, \ldots , a_{i}, \ldots , x_d) - {\hat{y}}_{\varvec{w}}^*) \end{aligned}$$
(17)

for all values \(x_j \in [a_j,b_j]\) of the input parameters in the remaining dimensions \(j \ne i\), where

$$\begin{aligned} {\hat{y}}_{\varvec{w}}^{*} := \min _{x_{i} \in [a_{i},b_{i}]} {\hat{y}}_{\varvec{w}}(x_{1}, \ldots , x_{i}, \ldots , x_{d}) \end{aligned}$$
(18)

and where \(r \in (0,1]\) is the prescribed rebound factor. Sample graphs of a model that satisfies this rebound constraint with \(r = 1/2\) can be seen in Fig. 3.

Fig. 3
figure 3

Sample graphs satisfying the rebound constraint with \(r=1/2\). In these graphs, \({\Delta }_{\downarrow i}\) is the total descent and \({\Delta }_{\uparrow i}\) is the imposed upper bound on the rebound of the model in the ith input dimension. In other words, \({\Delta }_{\uparrow i} = r \cdot {\Delta }_{\downarrow i}\) is the right-hand side of (17)

Full size image

An important asset of the approach to shape-constrained regression taken here is that the core algorithm can handle arbitrary combinations of the kinds of shape constraints mentioned above, in an efficient manner. Also, the core algorithm is entirely implemented in Python which makes it particularly easy to use and interface. Another asset of the proposed approach is that the considered shape-constrained regression problem (11) features no hyperparameter except for the polynomial degree m. Consequently, no tuning of hard-to-interpret hyperparameters is necessary. Concerning other, more theoretical, merits of the employed semi-infinite optimization algorithm, the reader is referred to Schmid and Poursanidis (2021).

Application example

The brushing process

The brushing process is a metal-cutting process used for the grinding of metallic surfaces with the help of brushes. Its main applications are the deburring of precision components (Gillespie, 1979), the structuring of decorative surfaces of glass (Novotný et al., 2017), and the functional surface preparation of metals for subsequent process steps of joining (Teicher et al., 2018). Common to all these applications is that the brushing process functions as a finishing process for components with a high inherent added value. Additionally, brushing processes have established themselves in certain highly automated mass production processes (Kim et al., 2012).

While the focus of Deutsches Institut für Normung (2003–2009) is still on steel wires as brushing filaments, in recent years filaments made of plastic with interstratified abrasive grits have become much more important. Such filaments act only as carrier elements of the machining substrate and, accordingly, the corresponding brushing process can be classified as a process with a geometrically undefined cutting edge. In view of their increased relevance, only brushing filaments with interstratified abrasive grits are considered here. See Fig. 4 for a schematic representation of the considered brushing processes.

Apart from the material parameters of the workpiece, the machining process is influenced, on the one hand, by technological parameters of the process and, on the other hand, by a multitude of material parameters of the brush. Important technological parameters are the numbers of revolutions \(n_b\) and \(n_w\) of the brush and of the workpiece, the cutting depth \(a_e\), and the cutting time \(t_c\). The brush parameters relate to the individual filaments (length \(l_f\), diameter \(d_f\), modulus of elasticity, and other technical properties), their arrangement (axial, radial), and their coupling to the base body (cast, plugged). The cutting substrate as an abrasive grain is characterized, among other things, by the grain material, the grain concentration and the grain diameter dia. In addition, the shape of the brush is determined by its width and its diameter \(d_b\).

Fig. 4
figure 4

Schematic of the brushing process

Full size image

In view of this large variety of technological and material parameters, it is a challenging task to choose the tool and the tool settings such that a prescribed target value for the roughness of the brushed workpiece is reached quickly but also robustly. It is therefore important to have good prediction models for the surface roughness of the brushed workpiece. In principle, such prediction models can be obtained from a comprehensive simulation of the brushing process (Wahab et al., 2007; Novotný et al., 2017). Such simulation-based models are expensive and complex because—in addition to the many process parameters mentioned above—the dynamic behavior of the tool has to be broken down to the filaments and microscopically to the individual grain in engagement. In particular, the dynamically changing tool diameter (Matuszak & Zaleski, 2015) has to be taken into account. Another paper that highlights the complexity of the underlying physics of the brushing process is Pandiyan et al. (2020). In addition to the challenging modeling procedure, the resulting models are typically expensive to evaluate. Currently, these factors still limit the applicability of simulation-based models in real-world process design and process control. And therefore it is important to build good alternative prediction models in brushing, for example, by using ML. A basic overview of ML approaches used for the modeling of grinding and abrasive finishing processes, which are comparable to brushing, is given in Brinksmeier et al. (1998) and in Pandiyan et al. (2020), for instance.

Input parameters, output parameter, and dataset

In this paper, such an alternative, ML model is built. Specifically, the modeled output quantity is the arithmetic-mean surface roughness of the brushed workpiece,

$$\begin{aligned} y {:}{=} R_{a}. \end{aligned}$$
(19)

It is modeled as a function of five particularly important process parameters \(\varvec{x} = (x_1, \ldots , x_5)\) of the brushing process, namely

$$\begin{aligned} \varvec{x} = (x_{1}, \ldots , x_5) := (dia, \, t_{c}, \, n_{b}, \, n_{w}, \, a_{e}). \end{aligned}$$
(20)

The dataset used for the training of the prediction model consists of \(N = 125\) measurement points. Table 1 shows the ranges of the process and quality parameters covered by the measurement data.

Table 1 The ranges of the process input and output parameters
Full size table

Results and discussion

In this section, SIASCOR is applied to the brushing process example. In particular, shape expert knowledge is integrated according to the methodology described in the section “A methodology to capture and incorporate shape expert knowledge”. Aside from SIASCOR, a purely data-driven Gaussian process regression (GPR) was conducted for the brushing example. GPR was chosen because it is particularly suitable for small amounts of data. Therefore, it is expected to produce a model with a high predictive power for the comparison with the SIASCOR model. In the end, the two regression models are compared and their advantages and shortcomings are discussed.

Initial model

As a first step, an initial purely data-based model was trained as a reference model to visually assist the process expert in specifying shape knowledge for the SIASCOR model. A polynomial model (4) with the relatively small degree \(m^0=3\) was used to prevent an overfit to the small dataset. The parameters of the model were computed via lasso regression with a learning rate \(\lambda \) selected by means of cross-validation using scikit-learn (Pedregosa et al., 2011). Additionally, prior to training the input variables were transformed with the standard transformation (Kuhn & Johnson, 2013) \(x_i' := \sqrt{x_i}\) for all \(i=1, \ldots , 5\) and then scaled to the unit hypercube. The standard transformation with the square root function led to a better generalization performance.

Capturing shape expert knowledge

As a second step, for the inspection of the initial model, two points \(\hat{\varvec{x}}^{\mathrm {min}}\), \(\hat{\varvec{x}} ^{\mathrm {max}}\) of particularly high fidelity and of particularly low fidelity were computed according to (6)–(89) (Table 2). The corresponding 1-dimensional graphs of the initial model (anchored in these two points) are visualized in Fig. 5. When inspecting and analyzing the shape of these graphs, the process expert detected several physical inconsistencies. For example, some of the initial model’s predictions for \(R_a\) are significantly lower than the surface roughness that is technologically achievable with the brushing process. Another example is the violation of convexity along the \(n_w\) direction.

With these observations in mind, the expert specified shape constraints for the SIASCOR model in the form of the schematic graphs from Fig. 6. Specifically, the expert imposed the boundedness constraint \(0.1 \le R_a \le 0.5\) upon the surface roughness. Along the \(t_c\) direction, the expert required monotonic decreasingness and convexity. In the direction of \(n_b\) and \(n_w\), the model was required to be convex and to satisfy the rebound constraint (17) with \(r = 1/2\). And finally, the model was constrained to be convex w.r.t. \(a_e\) and monotonically increasing w.r.t. dia.

The way the expert arrived at the convexity constraints w.r.t. \(n_b\) and \(n_w\) is through the following physical consideration. As the tool speed \(n_b\) and workpiece speed \(n_w\) increase, the roughness decreases because the equivalent chip thickness is reduced (Hänel et al., 2017). A further increase of \(n_b\) or \(n_w\), however, leads to increased process discontinuities due to centrifugal forces, for example, and can thus cause the roughness to increase again. The other shape constraints were obtained through similar physical considerations.

Table 2 Anchor points \(\hat{\varvec{x}}^{\mathrm {min}}\) and \(\hat{\varvec{x}}^{\mathrm {max}}\) for the high- and low-fidelity graphs
Full size table
Fig. 5
figure 5

Comparison of the high- (solid green) and low-fidelity (dashed red) graphs of the initial model. The high- and low-fidelity graphs are anchored in different points, namely the point \(\hat{\varvec{x}}^{\mathrm {min}}\) or \(\hat{\varvec{x}}^{\mathrm {max}}\), respectively, from Table 2 (Color figure online)

Full size image
Fig. 6
figure 6

Shape constraints specified by the process expert

Full size image

SIASCOR model

With the aforementioned shape constraints and the data described in the section “Input parameters, output parameter, and dataset”, the SIASCOR model was trained as explained in the section “Integration of shape expert knowledge into the training of a new prediction model”. For the degree of the polynomial model, \(m=4\) was found to produce the best fits compared to \(m \in \{3,4,5,6\}\). Moreover, the variables were transformed with the root function \(x_i' = \sqrt{x_i}\) for all \(i=1, \ldots , 5\) and then scaled to the unit hypercube. Table 3 lists various performance indices and Fig. 9 shows two plots of the final SIASCOR model.

GPR model

In addition to the SIASCOR model, a GPR model was trained for the sake of comparison since GPR with an appropriately chosen kernel is well-suited for small datasets. As a kernel, the sum of an anisotropic Matérn kernel with \(\nu = 3/2\) and a white-noise kernel was chosen:

$$\begin{aligned}&k(\varvec{x},\varvec{x}') = k_{\varvec{l}}(\varvec{x},\varvec{x}') + k_{n}(\varvec{x},\varvec{x}') \nonumber \\&\quad = ( 1 \!+\! \sqrt{3} \Vert \varvec{x}-\varvec{x}'\Vert _{2,\varvec{l}} ) \exp ( \!-\!\sqrt{3} \Vert \varvec{x} \!-\! \varvec{x}'\Vert _{2,\varvec{l}} ) \!+\! n \cdot \delta _{\varvec{x},\varvec{x}'}, \end{aligned}$$
(21)

where \(\Vert \varvec{z} \Vert _{2,\varvec{l}} := \Vert (z_1/l_1, \ldots , z_d/l_d)\Vert _2\) denotes the aniso-tropic norm of the d-component vector \(\varvec{z}\) and where \(\delta _{\varvec{x},\varvec{x}'}\) is 1 if \(\varvec{x}=\varvec{x}'\) and 0 otherwise. As usual, to optimize the hyperparameters \( \varvec{l} \) and n, the marginal likelihood was maximized according to Williams and Rasmussen (2006), using the Python package scikit-learn (Pedregosa et al., 2011). Due to the anisotropy of the Matérn kernel, for each input dimension i, a separate hyperparameter \(l_i \) is calculated. As for the SIASCOR model, the input variables were transformed with the root function \(x_i' = \sqrt{x_i}\) for all \(i=1, \ldots , 5\) and then scaled to the unit hypercube. Table 3 reports the pertinent performance indices and Fig. 10 shows two plots of the final GPR model.

Comparison of SIASCOR and GPR

Table 3 compares the predictive power of the initial lasso, the SIASCOR and the GPR model obtained by 10-fold cross-validation (10% of the data was taken for the test set in each fold). The predictive power is measured in terms of three averaged performance measures, namely the averaged root-mean-square error (RMSE), the averaged mean-absolute error (MAE), and the averaged coefficient of determination (\(\text {R}^2\)). In formulas, these averaged performance indices are defined as follows:

$$\begin{aligned}&\text {RMSE} := \frac{1}{10} \sum _{t=1}^{10} \text {RMSE}_{{\mathcal {T}}_t}, \end{aligned}$$
(22)
$$\begin{aligned}&\text {MAE} := \frac{1}{10} \sum _{t=1}^{10} \text {MAE}_{{\mathcal {T}}_t}, \end{aligned}$$
(23)
$$\begin{aligned}&\text {R}^{2} := \frac{1}{10} \sum _{t=1}^{10} \text {R}^{2}_{{\mathcal {T}}_t}, \end{aligned}$$
(24)

where \(({\mathcal {T}}_1, {\mathcal {D}}\setminus {\mathcal {T}}_1), \ldots , ({\mathcal {T}}_{10}, {\mathcal {D}}\setminus {\mathcal {T}}_{10})\) are the ten different test-training splits of the overall dataset \({\mathcal {D}}\) obtained by 10-fold cross-validation, and

$$\begin{aligned}&\text {RMSE}_{{\mathcal {T}}} = \Big (\frac{1}{|{\mathcal {T}}|}\sum _{\varvec{x}^{j} \in {\mathcal {T}}}(y^{j} - {\hat{y}}_{{\mathcal {D}}\setminus {\mathcal {T}}}(\varvec{x}^{j}) )^{2}\Big )^{1/2}, \\&\text {MAE}_{{\mathcal {T}}} = \frac{1}{|{\mathcal {T}}|} \sum _{\varvec{x}^{j} \in {\mathcal {T}}} \left|y^{j} - {\hat{y}}_{{\mathcal {D}}\setminus {\mathcal {T}}}(\varvec{x}^j) \right|, \\&\text {R}^{2}_{{\mathcal {T}}} = 1 - \Big ( \sum _{\varvec{x}^{j} \in {\mathcal {T}}} (y^{j} - {\hat{y}}_{{\mathcal {D}}\setminus {\mathcal {T}}}(\varvec{x}^j))^{2} \Big ) / \Big ( \sum _{\varvec{x}^{j} \in {\mathcal {T}}} (y^{j} - {\bar{y}}_{{\mathcal {T}}})^{2} \Big ). \end{aligned}$$

In the last three equations, \(({\mathcal {T}}, {\mathcal {D}}\setminus {\mathcal {T}})\) is any of the test-training dataset pairs, \({\hat{y}}_{{\mathcal {D}}\setminus {\mathcal {T}}}\) denotes the lasso, SIASCOR, or GPR model trained on \({\mathcal {D}} \setminus {\mathcal {T}}\), and

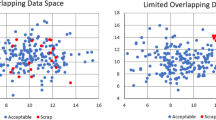
$$\begin{aligned} {\bar{y}}_{{\mathcal {T}}} = \frac{1}{|{\mathcal {T}}|} \sum _{\varvec{x}^{j} \in {\mathcal {T}}} y^{j}. \end{aligned}$$
(25)

It can be seen from Table 3 that the lasso and the SIASCOR models have similar averaged prediction errors and a similar averaged coefficient of determination on the test data, while the purely data-based GPR model features slightly better averaged prediction errors (but a slightly worse averaged coefficient of determination). This can also be seen from Figs. 7 and 8.

Table 3 Various averaged performance measures for the SIASCOR and the GPR models based on 10-fold cross-validation: root-mean-square error (RMSE), mean-absolute error (MAE), coefficient of determination (\(\text {R}^2\)). See (22)–(24)
Full size table
Fig. 7
figure 7

Comparison of measured vs. predicted values for the SIASCOR model

Full size image
Fig. 8
figure 8

Comparison of measured vs. predicted values for the GPR model

Full size image

Figures 9 and 10 juxtapose two plots of the SIASCOR and the GPR model, respectively. As can be seen, in contrast to the SIASCOR model, the GPR model is starkly non-convex w.r.t. \(n_w\). Consequently, the GPR model is at odds with physical shape expert knowledge, while the SIASCOR model is not. As has been explained in the section “A methodology to capture and incorporate shape expert knowledge”, the reason is that SIASCOR explicitly incorporates all the shape knowledge provided by the process expert, while the GPR model relies on the scarce and inherently noisy data alone. In other words, the discrepancies between the GPR model’s shape and the expected shape behavior can be traced back to the sparsity and the noisiness of the available measurement data.

Another downside of the GPR approach is that the resulting models are typically quite sensitive w.r.t. the selected kernel class and that the selection of this kernel class is typically not very systematic but rather based on heuristic rules of thumb. Accordingly, the model selection in GPR is typically quite time-consuming and cumbersome. In the SIASCOR method, by contrast, model selection is simple because the SIASCOR models have only one hyperparameter, namely the polynomial degree m. Also, the interpretation of the shape constraints needed for the SIASCOR method is straightforward and, in any case, much clearer than the interpretation and selection of different GPR kernel classes.

As a matter of fact, the solution of the SIASCOR training problem (10) with the algorithm from Schmid and Poursanidis (2021) takes a bit more computational time than the hyperparameter optimization in GPR because semi-infinite optimization problems have a more complex (bi-level) structure than the (unconstrained) marginal likelihood maximization problems used in GPR. Indeed, in the 5-dimensional brushing example considered here, the training of the SIASCOR model typically took around 30 min calculated with a standard office computer. Yet, this is negligible in view of the aforementioned clear advantages of SIASCOR over GPR in terms of shape-knowledge compliance, model selection, and interpretability.

Fig. 9
figure 9

Sample 2-dimensional graphs of the SIASCOR model (data points in blue). In a, \((dia, n_b, n_w)\) are fixed to (400, 2000, 500) and in b, \((dia, t_c, a_e)\) are fixed to (400, 60, 1) (Color figure online)

Full size image
Fig. 10
figure 10

Sample 2-dimensional graphs of the GPR model (data points in blue). In a, \((dia, n_b, n_w)\) are fixed to (400, 2000, 500) and in b, \((dia, t_c, a_e)\) are fixed to (400, 60, 1) (Color figure online)

Full size image

Conclusion and future work

In order to achieve target product qualities quickly and consistently in manufacturing, reliable prediction models for the quality of process outcomes as a function of selected process parameters are essential. Since the datasets available in manufacturing—and especially before SOP—are typically small, the construction of data-driven prediction models is a challenging task. The present paper addresses this challenge by systematically leveraging expert knowledge. Specifically, this paper introduces a general methodology to capture and incorporate shape expert knowledge into ML models for quality prediction in manufacturing. It is based on the SIASCOR method.

The resulting SIASCOR model is mathematically guaranteed to satisfy all the shape constraints imposed by the expert. Conventional purely data-based models, by contrast, do not come with such a guarantee but, on the contrary, often exhibit an unphysical shape behavior in the sparse-data case considered here. Additionally, the direct involvement of process experts in the training of the SIASCOR model increases the acceptance of and the confidence in this model. Another asset of the SIASCOR method is that, in contrast to many conventional ML methods, it does not involve a time-consuming and unsystematic hyperparameter tuning or model selection step.

The proposed general methodology was applied to an exemplary brushing process in order to obtain a prediction model for the arithmetic-mean surface roughness of the brushed workpiece as a function of five process parameters. The dataset available in this application consisted of only 125 measurement points. After inspecting the initial lasso model based solely on these data, the expert defined shape constraints in all five input parameter dimensions. The SIASCOR model trained with these shape constraints was compared to a purely data-based GPR model. As opposed to the SIASCOR model, the GPR model contradicts the physical shape knowledge about the surface roughness in various ways. Also, the selection of an appropriate GPR kernel class is rather heuristic and time-consuming. In any case, the interpretation of the GPR kernel class is certainly less clear than the interpretation of the shape constraints used in the SIASCOR method.

A possible topic of future research is to develop a more sophisticated definition of high- and low-fidelity graphs, using techniques from the optimal design of experiments. Additionally, to further support the user in collecting and leveraging shape expert knowledge, additional information, e.g. from assistance systems similar to the ones from Rahm et al. (2018) or Xu et al. (2018), can be presented to the expert in a preliminary step. Another topic of future research is the further improvement of the SIASCOR algorithm’s runtimes. In addition, a methodology will be developed for assessing the model and for uncovering possible conflicts between the imposed shape constraints and the data. Such conflicts might arise especially as soon as more data is available towards or after the SOP, and the model can then be retrained, using the new and larger dataset and a more refined and consolidated set of shape constraints. And finally, a graphical user interface will be implemented allowing the domain experts to apply the proposed methodology completely independently of external support from data scientists or mathematicians. In particular, this user interface will no longer require a manual translation of the shape knowledge specified pictorially by the expert into mathematical constraints in the form expected by the SIASCOR algorithm.