Abstract
Wooden pallets are commonly used as load carriers in many industrial and logistic applications. This article investigates and formalizes the production planning for a highly automated but customized pallet production and provides a solution approach. For completing a specific pallet, the required boards must be cut and stacked in advance to meet the demand at the assembly line. The arising planning problem for producing the required boards consists of both a cutting stock and a constraining open stack problem. Further, both the changeover of raw material at the cutting process and the number of fully automated internal storages, for stacked boards, are restricted. The proposed solution heuristic aims at minimizing the cutting waste. Additionally, feasibility with regard to the buffers is tested using discrete event simulation. Different approaches to generate, select and sequence the cutting patterns are investigated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In many industries, wooden pallets are needed to transport cargo. In contrast to the high volume production of standardized pallets, the production facility investigated here is producing disposable pallets in small batches. A highly automated production plant was newly built for this purpose. Supplying customers within a lead time smaller than one working day for small batches with a minimum order quantity of one piece requires a fast and flexible production planning and production process.
Pallets are constructed of up to four layers of boards and one layer of standardized blocks which are nailed together. For each layer, boards of different length and dimension can be used, whereby the dimension refers to the width and thickness of the board. The main processes can be summarized in two production steps. In the first production step, the boards for each layer are cut to length out of longer boards. In the second step, the pallets are assembled by nailing them together. In the following, it is examined in detail how the production processes are implemented in the highly automated environment of the investigated production site.
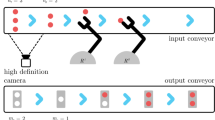
In Fig. 1 the shop floor layout of the pallet producer investigated is illustrated. Furthermore the two main material flows of the production process are pictured. In the first step of the process analysed, the raw material is cut to length, stored and transported to the appropriate material feeding, shown in red. The blue part is the pallet assembly line, the next step of the process. Here the boards are assembled fully automated by nailing them together. More specifically, two operators at the saw (1) load wood from a package into the saw’s feeder and build stacks that are cut simultaneously using the same cutting pattern.
At the end of the saw the items are autonomously stacked by two industrial robots (2 and 3) onto six available stacks (4). However, it must be considered that only one type of item is allowed on each stack. When the last element is placed on a stack, it is released.
Each stack of items is assigned to a production lot and a particular material feeding (6–9). Hence, as next step the stack is picked up by an automated handling system. This system can bring it directly to the material feed or to the small buffer in front of it if it is next one to be produced. Otherwise, it is stored in the temporary storage (5) until it is the next in sequence. Based on these processes, the arising combinatorial problems for the production planning, which are addressed in this article, are discussed next. The first issue is the creation and selection of cutting patterns, defining the way a larger object is cut into smaller items. In this case, the items refer to the boards, which are assembled to pallets. The raw material represents the large objects that are processed with the use of cutting patterns. The overall objective is to minimize the trim loss and exactly meet a given demand of items at the assembly line. Furthermore, several large objects are available and can be used if they have the same width and thickness as the items included in the pattern.
The next problem arises at the stacking of boards after cutting. Due to the limited number of stacks and as a stack can only be released when all items of a production batch are placed, the cutting patterns have to be selected and sequenced in a feasible order as part of production planning. The production schedule for the pallet assembling is generated by sorting from short to long in order to cope with arising setup times. These depend on the length delta of the top boards of two successive pallets. A simplified description of this planning problem and pre-tests are shown in Kaltenbrunner et al. (2020).
Literature review and preparatory work
The first arising problem where small items have to be cut out of larger objects is refered to as cutting stock problem (CSP) in research. This problem can be used with various objectives like minimal production costs, minimal waste, minimal raw material costs or maximum revenue. Each of the small items is defined by a given length and a needed demand that has to be satisfied. Furthermore, the number of available large objects can be limited by an existing stock. The cutting patterns indicate how often an item is included in a cutting pattern. The number of existing cutting patterns for a given set of items and large objects is easy to using combinatorics but hard to compute in optimization models. The problem, then, is to find the optimal amount of patterns to satisfy demand while minimizing waste. Cui et al. (2015), for example, use a two-step approach to solve the problem. In the first step, they generate patterns with a column-generation based approach which are then used to solve the integer linear program. Thus, near optimum solutions are found when minimizing the number of patterns without increasing trimloss. CSP and packing problems have been studied thoroughly in the last decades, for the most recent review see (Melega et al. 2018).
Another directly related challenge in the investigated production environment is defining an order of applied cutting patterns which is not violating the constraint of available stacks. This is a special case of the well defined minimization of open stacks problem (MOSP) which has the goal of minimizing the maximal number of open stacks by defining a sequence of patterns. A stack is called open when the first pattern that contains the item is cut and it stays open until the last pattern including this item is processed, as defined by Linhares and Yanasse (2002). They show that the problem is NP-hard and related to problems in the field of very large-scale integration (VLSI) design, minimization of order spread, the minimisation of tool switches and the minimization of discontinuities.
A well-illustrated definition of the MOSP problem and model formulation is given by Frinhani et al. (2018). Additionally, they formalize a graph modelling approach to state the problem. They perform numerous tests with data found in literature for the introduced PageRank based heuristic and the authors conclude the suitability of the heuristic based on its ability to obtain quality solutions in short runtimes. The problem was first formalized by Yanasse (1997) and is based on the work of Tang and Denardo (1988), which investigates the minimization of tool switches. For the latest review see Yanasse and Senne (2010) and for the most recent solution approaches see Gonçalves et al. (2016) and Lima and Carvalho (2017).
A third problem in the manufacturing process under consideration is the change of raw boards at the start of the process, which is the saw. When solving the CSP with an integrated MOSP, no consideration is given to the raw material sequence needed for the optimal pattern selection. This aspect needs consideration to ensure that changing the raw material does not become too time-consuming. A few articles deal with the combination of simultaneously solving trim-loss and scheduling problems. The common approach is to integrate penalty costs for changing the raw material into the objective function. Ferreira et al. (1990) introduce a heuristic based on automatic sequential search application to solve the contradictory objective of trim-loss and pattern usage in the iron and steel industry. Chen et al. (1996) use simulated annealing to solve the one-dimensional CSP to address the general problem of trim-loss and scheduling. For applications in the paper industry see Haessler and Talbot (1983), Harjunkoski et al. (1998), Westerlund and Isaksson (1998), Östermark (1999), Giannelos and Georgiadis (2001), Beraldi et al. (2009)) and Deep et al. (2009). These articles use mixed integer programming, genetic hybrid algorithm, hybrid particle swarm optimization or stochastic models to solve the particular problems investigated. In addition, Golfeto et al. (2009) compare different solution approaches for the general trim-loss and scheduling problem.
Although there are many publications on the CSP and the MOSP, very few deal with a combination of both problems which are very common in industry. For a thorough analysis of the integrated model see Yanasse and Lamosa (2007). They use Lagrangian relaxation to solve the decomposed model. In a feedback loop, the models are repeatedly solved, column generation is used for the CSP and the sequencing problem is addressed by an exact approach.
A different modelling approach for the integrated model is developed by Arbib et al. (2016). This formulation has exponentially many variables, like the one used by Yanasse and Lamosa (2007). However, the number of lots has only a quadratic effect on the number of constraints
An application in the steel industry is investigated by Armbruster (2002). They optimize the cutting of steel reinforcing bars with the special constraint that the buffers after cutting consist of so-called ways which have different departments. These departments can be combined to hold orders that exceed the compartment length. In their solution approach, they focus on the pattern sequencing problem.
Belov and Scheithauer (2007) introduce a sequential heuristic to solve a one-dimensional CSP. They also show how this heuristic can be further developed to include minimization of open stacks and setups or a maximum number of open stacks in the CSP. The applied sequential heuristic is an algorithm that iteratively calculates new patterns by solving a knapsack problem with the usage of so-called pseudo-prices. These prices represent the waste in the patterns and are updated within each iteration depending on the included items in the previously used patterns.
Matsumoto et al. (2011) solve the one-dimensional CSP with Tabu Search for an application in the paper tube industry. In this industrial application article, tubes have to be cut to length using various cutting patterns. Thereby the demand has to be fulfilled exactly with the goal of minimizing the total length of used stock rolls. Similar to the problem of pallet production, the authors combine the CSP and the open stack problem and also constrain the number of setups of each raw material type to a maximum of once per planning period per type. Contrary to the articles mentioned above, where penalty costs are introduced to the objective function, Matsumoto et al. (2011) use constraints for the paper tube cutting stock problem (PTCSP). They introduce cutting groups to reduce the PTCSP to a number of bin packing problems. These groups represent pieces which have to be cut from available stock rolls of the same type. A Tabu Search algorithm, based on a shift neighbourhood, is used to solve the problem by the first-fit decreasing heuristic algorithm.
The integrated problem arising when working centres with nesting capabilities are used in combination with automated feeders and stackers is investigated by Arbib et al. (2012). The introduced Tabu Search algorithm addresses both the pattern and batch sequencing problem simultaneously. Thereby no more stacks than buffers are opened, the order spread is kept under control and the batch compatibility/precedence constraint is satisfied. The heuristic is tested on 920 problems found in the literature, 25% are solved to optimality and nearly all have a gap below 1 percent with only a maximal computation time of several minutes.
Kim et al. (2016) propose a MIP model and a knapsack based heuristic algorithm for the one-dimensional CSP of window frame manufacturing. For each frame four different types of bars have to be produced from aluminum profiles. Thereby the weighted objective function of trim loss, sequence of the same bar type and degree of order spreading is minimized. The proposed solution methods are tested with different weights.
Although there is literature on similar problems, production planning of a pallet production factory has not been studied yet. This industrial problem represents another challenging research opportunity especially due to the high variability of small items. This is caused by the small lot sizes and the interlacing of the problems, which complicates the production process. Short-term planning makes the problem even more complicated. To address this industrial problem and integrate it at the interface between ERP and MES, we propose a greedy construction heuristic. This heuristic always generates a feasible solution within acceptable computation time for daily use. Furthermore, we use discrete event simulation to verify if the computed production sequence can be processed by the intralogistics system. Hence, in the following section the solution approach and the parameters used are presented. In the next part, numerical experiments are carried out and the results are shown and analysed for their industrial application. Followed by the managerial implications that focus on the need and the advantages of planning algorithms in a modern production environment. The final section of the article summarizes the problem and highlights the results.
This work considerably extends the contribution of Kaltenbrunner et al. (2020) by introducing some new parameters for the heuristic and combine the heuristic with a newly developed simulation model for the internal logistics. Additionally, extensive experiments and analyzes are carried out.
Solution approach
Since both the cutting stock problem and the open stack problem as well as the resulting combination problem are NP-hard, see Yanasse and Lamosa (2007), a heuristic is developed to find solutions for the industrial application of pallet production. The cutting stock problem is greatly restricted by the integrated MOSP, although this problem is reduced from a minimization to a satisfaction problem. The cutting stock problem combined with the minimization of open stacks is presented as mixed integer program in Yanasse and Lamosa (2007). A modified model is given in Kaltenbrunner et al. (2020) where the minimization of open stacks is changed to a constraint with a maximum number of open stacks. This model is given in Eqs. (1)–(16) using the indices, parameters and variables in Table 1. Where the Eqs. (1)–(4) state the cutting stock problem with the objective to minimize the total costs, which corresponds to the waste in this application case. In Eqs. (5)–(13) the MOSP is defined with the modification that the number of open stacks is no longer an optimization goal, but instead it is included as a constraint. The following equations ensure a feasible cutting sequence and link the two problems.
Finding a feasible solution for the industrial problem even more complicated because the number of open stacks is very small in relation to the items to be cut. The ratio is six to several hundred, depending on the planned order situation. Thus, a pattern based construction heuristic is introduced and summarized as pseudocode below. Afterwards the main steps are described in more detail.
Heuristic solution approach
The definitions of the sets used to parameterise the solution approach are shown in Table 2. To provide an overview and to summarize the developed solution approach, the main steps and functions are given as pseudocode in Algorithm 1. At the beginning, the available raw material and the pallet orders, which are sequenced according to minimize the set up times at the assembly line, are initialized. Next, based on these pallet orders, the items required are calculated and re-sorted applying the re-order range r. In the following steps the cutting patterns are generated, including the trivial patterns as well as randomly generated patterns, using the available raw material and allowed order spread within one pattern p. The number of generated patterns is defined by the number of unique boards times the pattern generation multiplier f. These patterns are sorted according to their included items and the produced waste. Afterwards, eligible patterns are selected to create a feasible cutting pattern sequence. This selection is constraint by the number of available stacks and the material switch threshold w. When the production plans for all parameter combinations and their repetitions have been computed, the list of cutting patterns is sorted according to their waste. Finally, a discrete event simulation checks if the internal logistics can process the production plan and if it is feasible the production plan is returned and approved for production.

Since the proposed solution approach generates all trivial patterns, a feasible solution for the combined cutting stock and open stack problem is always found, provided that sufficient raw boards are in stock. If all open stacks are occupied at one time and there is no randomly generated pattern that contains a combination of the partially produced items, there is always a trivial pattern that produces the item with the lowest production order, regardless of its waste. Therefore, one stack becomes available again and can be used for another pattern with at least one new item, while satisfying the demand of the remaining items. The essential steps and the implementation of the heuristics are now presented in detail.
Data preparation
When a new planning run is started (say for the next shift), the assembly orders for pallets are loaded from a database. Based on the predefined assembling sequence, the bill of material of the production orders is used to determine the boards needed in the assembly process. Each bill of material consists of three or four different types of items that are used multiple times for the different layers of the pallet. At the saw, these items are ordered according to the assembly sequence of pallets. Since the bill of material for a pallet contains items of different dimensions, the items have to be re-sorted to avoid a high and unnecessary number of raw material changes. Hence, the aim of the re-sorting is to group items with the same dimensions and thus need the same set of raw materials. The applied sorting algorithm starts at the beginning of the current order and advances the production of items of the same dimensions if they are within a certain range of the production order. Therefore, the sorting algorithm puts the first item to the new list. Afterwards, it checks if items within a range of r have the same dimensions, if so, it removes them from the old list, adds them one after another to the new list and increases r by one for each added item. If there are no more items within r, the first item in the old list is used and the grouping is repeated with the new dimension and r is reset to the starting value. This procedure is repeated until the old list is empty and the new list includes all newly ordered items.
Pattern generation
First, the trivial patterns are created. For this purpose, all items are assigned to each suitable raw material with the same width and height. In a second step, the same item is iteratively added one more time to the pattern. In each of these steps, the patterns are saved for further use. In a next step, additional random patterns are generated. To this end, the items that require the same raw material are combined, whereby the spread of production order p for the contained items is limited within each pattern. The number of random patterns generated is determined by the number of different items to be produced. These are multiplied by a factor f to generate an adequate number of patterns. This results in a generic algorithm that can be applied to problems of different sizes.
Pattern selection
Once all necessary patterns have been generated, the heuristic sorts them by the items they contain and their production order. Items required for production jobs that are assembled earlier will be given a lower production order. Accordingly, patterns containing these items are ranked first.
The heuristic then sorts all generated patterns within a group that contains the same lowest ranked item according to their trim loss, from lowest to highest waste.
To develop the production plan, appropriate patterns are selected as follows: First, the pattern with the lowest waste is selected from the group of patterns containing at least one item with the lowest rank. The next step is to ensure that the pattern is producible. In order to reduce the number of raw material switches at the beginning of the process, the pattern is eligible if it uses the same raw material as the predecessor or if the difference in waste compared to the next successor with the currently used raw material in the sorted pattern list is higher than a threshold of w. Secondly, the heuristic checks whether there are enough open stacks available for de-stacking the cut items. If producible, it is calculated how often the pattern can be cut until either the demand for one of the included items is met or no raw material is left. Afterwards, the demand and the raw material availability are updated. If the item with the lowest production order has not been fulfilled in line with demand yet, the next pattern of the group with a higher waste is selected. Again, it is calculated how often the sample can be used. As soon as the demand for the item with the lowest position is fulfilled, the next item is selected. This approach is repeated until the demand for all items is met and thus a complete production schedule is developed.
Discrete event simulation
The simulation model covers the cutting and stacking process, the fully automated transport system at the assembly line and the limited number of intermediate buffers before the material feedings. With this material flow simulation the utilization of buffers can easily be observed. The preceding steps of the algorithm already create a feasible solution for the CSP and the MOSP which is used as input for the simulation model. However, in most cases the assembly plan is limited due to the parameters used, which allow some re-sorting of the cutting and stacking plan. In order to verify that the number of buffers is sufficient to re-sort the stacks and to bring them to the different material feedings in the sequence required for assembly, the control logic of the fully automated transport system is modelled exactly. If the material can not be provided to the material feedings in the correct order, the production plan is infeasible and rejected.
In the next section, numerical experiments are carried out on an industrial test data sample with a extensive range of values the parameters introduced. Afterwards, the impact of the parameters is analysed and the ranges of the sets for a daily industrial use are reduced.
Numerical experiments
Next, the heuristic is parameterized and tested on real life industrial data with a typical planning horizon of one shift (eight hours). To generate the test data production orders from the past are used. Each order consists of a specified pallet (type and dimensions) and the needed number of this pallet. The material used can differ in length, width and height. In total 1527 production orders are taken into account. In the top graph in Fig. 2, the distribution of the order sizes is pictured and small lot sizes are indicated. From this pool, orders are randomly selected until the assembling time for one shift is reached. The order size distribution of this sample, including 52 production orders, is displayed in the lower graph in Fig. 2 and it shows that overall distribution is well represented in the sample.
Detailed information of the test data set for the cutting stock and the open stack problem is given in Table 3, where the number of different lengths, number of items and the total length per raw material type are shown. In total 16,993 items have to be cut using seven different raw material dimensions. Each of these raw material dimensions (A–G), defined by its width and thickness, that indicate for which items it can be used, is available in three different lengths. Hence, according to the introduced MIP model M = 162 and O = 21. Additionally, it reveals that the raw material dimension A is the most common material as it has more than 50% of the total demanded lengths, about 50% of all required items and approximately 40% of the required material. The distribution of the length of the items per each raw material type is shown in Fig. 3. It displays that raw material dimensions A, B, D, E and G have a wide range of different lengths. On the contrary, raw materials of type C and F have a smaller range of lengths and are only used for long items. This is explained by the dimensions of C and F. These boards are thicker than the others and hence, there is a mechanical reason to use them for statically loaded parts in larger pallets.
For the numerical studies a set of values for each parameter of the previously described heuristic is defined. The material change threshold f is set to 0.0, 0.1 and 0.2. To get a baseline on the overall waste, 0.0 is used, where the material is changed each time the best cutting pattern needs a different raw material. The maximum delay parameter r and the parameter p, the production order spread, are tested with a step size of two in a range from two to 18. Thereby 18 corresponds to three times the available number of stacks. The random pattern factor f is tested in tenfolds \(\lbrace \)10, 100\(\rbrace \) to analyze a wide range. These sets are summarized in Table 4. The heuristic is tested with every possible value combination of the parameter set (= 486) and the thoroughly described industrial test data set is used. Furthermore, for each combination 50 repetitions are performed due to the random creation of patterns. In total this sums up to 24,300 test runs.
Results and discussion
In this section, the results of the numerical experiments are shown and discussed. It is analysed if the parameters have the expected impact and additionally, the set of values for each parameter is reduced to decrease the number of combinations. This is necessary to gain a reliable heuristic which is fast enough for a daily industrial application.
The best feasible solution with a waste of 3.3% is found using the parameters of \(w=0.0\), \(r=4\), \(p=10\) and \(f=100\). The results of the numerical studies are summarized in Fig. 4, showing the calculated waste of all 24,300 instances as boxplots. The first two plots show the waste of the 14,317 feasible solutions and the second plot the 9983 infeasible solutions. For all 24,300 test runs a feasible cutting plan is developed and hence, the infeasible runs are not producible due to the limits of the internal logistics, which is tested by the discrete event simulation model. For simplification these infeasible results are not included in upcoming figures.
In the next group of plots, the impact of the raw material switching threshold w is shown and it reveals that the threshold has a big influence on the waste. This is reasonable because the threshold is directly applied when the next pattern is selected according to its waste. Hence, the higher the raw material switching threshold w the higher the chance to neglect a good pattern and to continue with the same raw material but using a pattern with a higher waste. In Fig. 5, the correlation between raw material switches and waste is plotted for each feasible test run and the different thresholds are indicated by the colours. It becomes apparent that the results are well grouped for each threshold and there is little overlap between these groups. Furthermore, it is remarkable that all parameters generate acceptable results for an industrial application with less than 6% waste. This can be explained by the fact that in some cases a higher waste due to a prohibited material change allows the use of many patterns with a low waste. The best results in term of waste is of course obtained by a threshold of 0. On the other hand all of these results require close to one hundred or even more material switches during one shift. In the industrial application, this is not workable, hence, a threshold of 0 must not be considered in real life production planning.
The next analysed parameter is the maximal delay of an item order when the orders are resorted according to their raw material dimension used at the beginning of the heuristic, see r in Fig. 4. It can be seen that the best found solution by each value is quite similar and if the parameter is chosen too high (\(r \ge 14\)) only very little or no feasible solutions are found. As the increase of this parameter increases the mixing of the cutting sequence compared to the assembling sequence, the rise of infeasible solutions is caused by the limited number of intermediate buffers. This parameter is integrated in the heuristic to reduce the number of raw material switches. Thus, the impact of the parameter r on the number of switches is shown in Fig. 6. It can be seen that the median number of switches is reduced by increasing the maximal delay r until no more feasible solutions are found. Nevertheless, the impact on the raw material switches is rather small compared to other parameters. This is caused by the fact that most material changes are made within a raw material by using different lengths and the parameter only affects the number of changes between different raw materials by re-sorting. For the final heuristic the value set of r is reduced to \(\lbrace \)4,6,8,10\(\rbrace \) because it contains good solutions of waste and raw material switches.
The next investigated parameter in Fig. 4 is p, the maximal spread of the order sequence within one pattern. It can be seen that if the spread within the order sequence in patterns is increased, the waste is significantly reduced at the beginning, before going up again. This is due to the limited number of stacks and the prioritising of the patterns including the item of the lowest production order, which has not been finished yet. Hence, with a large maximal spread, an item might block a stack for a longer time until it is finished and therefore, prohibit the usage of good patterns that need an additional stack. Another indication that the stacks are blocked longer with a larger p is that the number of infeasible solutions does not increase significantly in contrast to an increase of the parameter r. For the industrial application p is reduced to 8, 10, 12 and 14.
As the last parameter, the results of the random pattern factor f, which determines the number of generated random pattern by multiplying it with the number of items, is shown in Fig. 4. It is evident that an increase in the number of randomly generated patterns decreases the waste. Unfortunately, the increase of this factor by an additional tenfold would lead to unacceptable long computation times and furthermore, in some cases, when the maximal allowed spread is small, not enough unique patterns are existing. Regarding this factor, it is obvious that \(f=100\) is used for the industrial application.
Finally, the set of each value for the industrial application is shown in Table 5. These reduced sets of values ensure an acceptable computation time for the industrial application, because the number of combinations is reduced from 486 to 32. In terms of generated production plans, this implies that the number is reduced from 24,300 to 1600 when 50 repetitions per combinations are calculated. Furthermore, for the industrial application it is not necessary to test each cutting plan for its producibility with the discrete event simulation model. Instead, the solutions found are sorted according to their waste and only the best one is simulated. If it is feasible, no further simulations are necessary. Otherwise, the next one is tested and this is repeated until a feasible one is found.
The applicability of the reduced parameter set is not limited by the problem size, in terms of the total number of items and pallets, due to the greedy properties of the algorithm. If, however, a change in customer orders is observed which leads to shifts in the length distribution within raw material, between raw materials or a new raw material is . Then new analyses using the large parameter set have to be done and if necessary the small parameter set has to be adapted. In the case of structural changes to the production system, such as an additional stacking robot or a different number of buffers, the large parameter set has to be adopted and new tests have to be performed to reduce the set. In the case of a sufficient number of buffers, which is not practically in an industrial application due to the limited space and the costs of the automated buffers, the resorting parameter r needs not to be restricted.
The proposed solution approach combines a heuristic with a discrete event simulation. This combination of methods is necessary, as not all requirements can be included in the heuristic. Compared to other research the heuristic does not include a local search or another type of metaheuristic, because when the next pattern is selected for the production sequence the whole system is in a very dedicated state. This means, that normally all stacks are occupied by an item and hence, the set of usable patterns is rather small and if this set is further reduced, for example by some kind of Tabu Search, the result becomes worse. This might be acceptable, if the worse result leads to a solution area where better results are obtained. Nevertheless, pre-tests during the heuristic design showed that the sequence of patterns is soon the same after a pattern was prohibited. It has also turned out that it is not efficient to generate many shorter feasible sub-sequences and combine them to a feasible sequence, because the merging of them is too expensive in terms of solution quality and computation time. Instead, the heuristic is designed as a construction heuristic with a random part and a set of parameters to control it.
Other methods summarized in Sect. 2 do not appear suitable for the investigated problem because many of them are focusing on one of the integrated problems, like the PageRank based heuristic introduced by Frinhani et al. (2018) for the MOSP. The previous researches on industrial problems, which combine CSP and MOSP, include application specific solution approaches for the constraints inherited from the application case. Armbruster (2002) for example have to consider to combine departments to store the cut steel bars. The unique requirements of the industrial application in a highly automated customer oriented pallet production is on the one hand the different types of raw material that have to be considered. On the other hand, the integration of the production order at the assembly line and the fully automated internal transportation system, including the limited number of buffers, requires the stacks to be within an order range. The simulation model checks whether the number of buffers is sufficient. Thus, it is not reasonable to judge the proposed solution approach in terms of runtime or solution quality and compare it with other approaches found in literature.
Hence, the repetitive random search in the solution space, guided by parameters, based on domain knowledge about the processes and the influence of decisions, appears more promising.
Managerial implication
The new era of automated production is enabled by algorithms that support short-term production. This article shows how these algorithms are supporting the operation of a newly built pallet factory. Beside the obvious power of the method, the integration in a corresponding ERP and MES system are the actual steps in order to complete the efforts. For this, the described problems have to be customized and extended to exactly meet the process requirements which are mostly defined by the used machine tools. Hence, a configurable planning environment based on the algorithm developed is implemented. In the introductory phase for daily use, an additional benefit can be derived from the animated simulation model. In addition to insights that are provided to users who are not simulation experts, it allows to verify the results obtained and helps to build confidence in the established system. The parameters used for the algorithm are based on domain knowledge of the processes and how different aims and constraints interact with the solutions. A large range for these parameters is tested in the numerical experiments on a representative industrial dataset. Afterwards, the range is reduced without neglecting too many good solutions and to meet computation time requirements for a daily usage as part of the MES. If additional data is available in the future or a change in the structure of the customer orders occurs, additional analyses must be carried out to readjust the parameter settings. Another important aspect is the possibility to readjust the planning when sudden changes occur on the production line, like the break down of a robot or an automated storage. In this case, the planning must be restarted with fewer available machines and the new production data, which is always up to date due to the integration of the algorithm with the EMS. The new solution is of course worse because of new restrictions, but, after a short interruption, it allows continuous production until the failed machines are repaired and a replanning is done.
Conclusion
This article investigates the production planning for a highly automated pallet production that produces pallets in small lots down to lot size one. This combination is rather new to this industry as normally large lots of standardized pallets are produced on specialised and automated production lines and small lots of customized pallets are produced with a high degree of manual labour involvement. The examined production process consists of cutting boards into smaller items, which are dedicated to a specific assembling order, can be made of several different raw materials and need to be combined to cutting patterns. This can be modelled by the well-studied cutting stock problem. Further, the cut items are stacked automatically by industrial robots on a limited number of homogeneous stacks, which can be formalized as a minimal open stack problem. These two models are combined to one model where the number of stacks is no longer minimized, but instead becomes a constraint limiting the available number of open stacks. The complete stacks are transported automatically to the dedicated material feeding at the assembly line, where on each feeding the material has to arrive in the correct order. To ensure this sequence a limited number of intermediate storages is available. To handle these challenges a greedy construction heuristic is developed with the overall aim of minimizing the cutting loss, which arises from the cutting patterns at the saw, and ensure a continuous production flow at the assembly line. This heuristic consists of the creation of a cutting and stacking plan. Subsequently, these feasible plans are further checked for their producibility. Furthermore, the heuristic is adjustable by parameters, which are selected on domain knowledge. The results of the numerical experiments on a representative industrial test data set reveal that the set of parameters can be reduced. These parameters can be neglected because they do not generate feasible or practicable solutions above a certain threshold. Further, trends and overlaps can be observed which lead to obsolete values. This reduction is also necessary to meet computation time requirements for the daily industrial usage of the developed method as part of the MES.
Future research will focus on a new solution approach to include the requirements of the internal logistics both in a heuristic and the MIP. With this advanced heuristic the whole planning problem will be solved at once. Numerical experiments can clarify whether the current approach including a simulation model or the new approach is superior. Another possible extension with an even more integrated approach is to develop the solution approach to an inline algorithm which runs totally autonomously. Every new placed order of a pallet or newly delivered raw material is immediately considered in the planning, resulting in no or a very short frozen time period. Hence, this solution approach must also optimize the production sequence of the pallets, their due dates, setup costs and combine delivery runs.
References
Arbib, C., Marinelli, F., & Pezzella, F. (2012). An LP-based tabu search for batch scheduling in a cutting process with finite buffers. International Journal of Production Economics, 136(2), 287–296.
Arbib, C., Marinelli, F., & Ventura, P. (2016). One-dimensional cutting stock with a limited number of open stacks: Bounds and solutions from a new integer linear programming model. International Transactions in Operational Research, 23(1–2), 47–63.
Armbruster, M. (2002). A solution procedure for a pattern sequencing problem as part of a one-dimensional cutting stock problem in the steel industry. European Journal of Operational Research, 141(2), 328–340.
Belov, G., & Scheithauer, G. (2007). Setup and open-stacks minimization in one-dimensional stock cutting. INFORMS Journal on Computing, 19(1), 27–35.
Beraldi, P., Bruni, M. E., & Conforti, D. (2009). The stochastic trim-loss problem. European Journal of Operational Research, 197(1), 42–49.
Chen, C. L. S., Hart, S. M., & Tham, W. M. (1996). A simulated annealing heuristic for the one-dimensional cutting stock problem. European journal of operational research, 93(3), 522–535.
Cui, Y., Cui, Y. P., & Zhao, Z. (2015). Pattern-set generation algorithm for the one-dimensional multiple stock sizes cutting stock problem. Engineering Optimization, 47(9), 1289–1301. https://doi.org/10.1080/0305215X.2014.969726
Deep, K., Chauhan, P., & Bansal, J. C. (2009). Solving nonconvex trim loss problem using an efficient hybrid particle swarm optimization. In 2009 world congress on nature & biologically inspired computing (NaBIC) (pp. 1608–1611). IEEE.
Ferreira, J. S., Neves, M. A., & e Castro PF,. (1990). A two-phase roll cutting problem. European Journal of Operational Research, 44(2), 185–196.
Frinhani, R. D. M. D., de Carvalho, M. A. M., & Soma, N. Y. (2018). A pagerank-based heuristic for the minimization of open stacks problem. PLoS One, 13(8), e0203076.
Giannelos, N., & Georgiadis, M. (2001). Scheduling of cutting-stock processes on multiple parallel machines. Chemical Engineering Research and Design, 79(7), 747–753.
Golfeto, R. R., Moretti, A. C., & Salles Neto, LLd. (2009). A genetic symbiotic algorithm applied to the one-dimensional cutting stock problem. Pesquisa Operacional, 29(2), 365–382.
Gonçalves, J. F., Resende, M. G., & Costa, M. D. (2016). A biased random-key genetic algorithm for the minimization of open stacks problem. International Transactions in Operational Research, 23(1–2), 25–46.
Haessler, R. W., & Talbot, F. B. (1983). A 0–1 model for solving the corrugator trim problem. Management science, 29(2), 200–209.
Harjunkoski, I., Westerlund, T., Pörn, R., & Skrifvars, H. (1998). Different transformations for solving non-convex trim-loss problems by minlp. European Journal of Operational Research, 105(3), 594–603.
Kaltenbrunner, M., Huka, M. A., & Gronalt, M. (2020). Automating production planning and control in pallet manufacturing—A case study. Procedia Manufacturing, 42, 119–124.
Kim, B. I., Ki, Y., Son, D., Bae, B., & Park, J. S. (2016). An algorithm for a cutting problem in window frame production. International Journal of Production Research, 54(14), 4327–4339.
Lima, J. R., & Carvalho, M. A. M. (2017). Descent search approaches applied to the minimization of open stacks. Computers& Industrial Engineering, 112, 175–186.
Linhares, A., & Yanasse, H. H. (2002). Connections between cutting-pattern sequencing, VLSI design, and flexible machines. Computers& Operations Research, 29(12), 1759–1772.
Matsumoto, K., Umetani, S., & Nagamochi, H. (2011). On the one-dimensional stock cutting problem in the paper tube industry. Journal of Scheduling, 14(3), 281–290.
Melega, G. M., de Araujo, S. A., & Jans, R. (2018). Classification and literature review of integrated lot-sizing and cutting stock problems. European Journal of Operational Research, 271(1), 1–19.
Östermark, R. (1999). Solving a nonlinear non-convex trim loss problem with a genetic hybrid algorithm. Computers& Operations Research, 26(6), 623–635.
Tang, C. S., & Denardo, E. V. (1988). Models arising from a flexible manufacturing machine, Part I: Minimization of the number of tool switches. Operations Research, 36(5), 767–777.
Westerlund, T., & Isaksson, J. (1998). Some efficient formulations for the simultaneous solution of trim-loss and scheduling problems in the paper-converting industry. Chemical Engineering Research and Design, 76(6), 677–684.
Yanasse, H. H. (1997). On a pattern sequencing problem to minimize the maximum number of open stacks. European Journal of Operational Research, 100(3), 454–463.
Yanasse, H. H., & Lamosa, M. J. P. (2007). An integrated cutting stock and sequencing problem. European Journal of Operational Research, 183(3), 1353–1370.
Yanasse, H. H., & Senne, E. L. F. (2010). The minimization of open stacks problem: A review of some properties and their use in pre-processing operations. European Journal of Operational Research, 203(3), 559–567.
Funding
Open access funding provided by University of Natural Resources and Life Sciences Vienna (BOKU).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kaltenbrunner, M., Huka, M.A. & Gronalt, M. Heuristic based approach for short term production planning in highly automated customer oriented pallet production. J Intell Manuf 33, 1087–1098 (2022). https://doi.org/10.1007/s10845-021-01901-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-021-01901-0