Abstract
Highly complex data streams from in-situ additive manufacturing (AM) monitoring systems are becoming increasingly prevalent, yet finding physically actionable patterns remains a key challenge. Recent AM literature utilising machine learning methods tend to make predictions about flaws or porosity without considering the dynamical nature of the process. This leads to increases in false detections as useful information about the signal is lost. This study takes a different approach and investigates learning a physical model of the laser powder bed fusion process dynamics. In addition, deep representation learning enables this to be achieved directly from high speed videos. This representation is combined with a predictive state space model which is learned in a semi-supervised manner, requiring only the optimal laser parameter to be characterised. The model, referred to as FlawNet, was exploited to measure offsets between predicted and observed states resulting in a highly robust metric, known as the dynamic signature. This feature also correlated strongly with a global material quality metric, namely porosity. The model achieved state-of-the-art results with a receiver operating characteristic (ROC) area under curve (AUC) of 0.999 when differentiating between optimal and unstable laser parameters. Furthermore, there was a demonstrated potential to detect changes in ultra-dense, 0.1% porosity, materials with an ROC AUC of 0.944, suggesting an ability to detect anomalous events prior to the onset of significant material degradation. The method has merit for the purposes of detecting out of process distributions, while maintaining data efficiency. Subsequently, the generality of the methodology would suggest the solution is applicable to different laser processing systems and can potentially be adapted to a number of different sensing modalities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As sensor data fidelity improves in additive manufacturing (AM) monitoring systems, so does the challenge of extracting useful and meaningful patterns efficiently. The AM processes are physically driven, yet underlying phenomena are poorly understood and highly challenging to simulate during the build process (Francois et al. 2017). However, causal patterns are present in the data suggesting a place for data-driven models which have the potential to be much faster than their simulated counterparts. There is, therefore, a need for developing such causal dynamics models capable of exploiting underlying physical patterns, enabling detection of anomalous events, leading to on-line quality monitoring of the AM process.
This need is particularly evident in Laser Powder Bed Fusion (L-PBF), the most widely used metal 3D printing process. A thin layer of powder is spread across a build plate, which is then fused with a rapidly scanning laser; the cycle is repeated until a 3D metal component is formed. This enables an efficient manufacturing process, while minimising material and energy usage (Ford and Despeisse 2016). Furthermore, the design freedom reduces the number of standard components and allows engineers to greatly optimise the design process (Gao et al. 2015). Finally, the mass production of end-use components would disrupt manufacturing as it is understood today (Attaran 2017).
However, a complex set of interactions occur at the micro scale between the laser, powder and the chamber environment resulting in variability (Khairallah et al. 2020). The variability from part-to-part is caused by the accumulation of defects, including porosity and micro-cracks, that are inherently generated from the stochastic nature of the process (Grasso and Colosimo 2017). Parts are, therefore, not repeatable enough to meet stringent qualification and certification standards. This means that costly post-build inspection, such as Computed Tomography (CT) scanning or functional testing, is required to qualify components for end-use applications. (Debroy et al. 2019).
This has motivated the development of advanced in-situ monitoring systems, with the aim of online quality monitoring. This includes advanced imaging such as co-axial high speed cameras (Hooper 2018), off-axis imaging (Grasso and Colosimo 2017) and in-situ X-ray imaging (Cunningham et al. 2019). These systems have shown the ability to detect process signatures which lead to porosity and other flaws (Grasso and Colosimo 2017). However, a vast amount of complex data is generated and proves challenging to analyse, beyond simple experiments, using traditional methods.
This study seeks to fill a gap in the AM literature of learning a data-driven dynamics model of the L-PBF process directly from images to enable efficient anomaly detection. This is in contrast to recent studies, where important time correlations are not considered and independent and identically distributed (i.i.d.) data is assumed when machine learning is applied. Though vast quantities of high dimensional data can be captured with high frequency, the application may also be susceptible to potential sampling bias, where only a small portion of the state space can be captured in each experiment. Since the AM process has a large number of process parameters (Grasso and Colosimo 2017), collecting enough data to model each signature is potentially intractable. To improve data efficiency, the input and output information as well as time-correlations can be modelled to explicitly learn the process dynamics which is a more complex task. It is hypothesised that this encourages sampling efficiency, which would agree with recent literature (Buesing et al. 2018). In this study, the laser dynamics are learned while the residual error between the predictions and measurement is monitored. This is referred to as the dynamic signature. Furthermore, an extension to the variational recurrent neural network (VRNN) is proposed, where a semi-supervised model is capable of drastically improving detection of anomalies. The model was originally inspired by the Kalman filter, while dynamics are modelled in latent space (Chung et al. 2015). The method is therefore referred to as Filtering Latent Anomalies with Neural Networks (FlawNet).
Literature review
A natural step in AM is to build intelligent systems capable of automating the detection of flaws during the process. This has driven research in AM towards machine learning including anomaly detection with photodiodes (Okaro et al. 2019), as well as high speed imaging (Mitchell et al. 2020). Deep learning has also proven to be effective at detecting defective melt pools (Scime and Beuth 2019) and predicting material surface height from images (Yuan et al. 2019). Meanwhile, image features have also been classified using convolutional neural networks (CNNs) with labelled data (Zhang et al. 2018). Furthermore, autoencoders have been used to detect anomalies (Tan et al. 2019). Though these studies use signals from a highly dynamic process, an i.i.d. assumption is made, where the useful time-series information becomes lost. This loss of granularity limits further development of monitoring systems in AM.
However, sequential patterns in the data have been shown to improve results. Zhang et al. (2019) used a hybrid CNN to classify images over multiple frames to account for the temporal and spatial aspects of the data. Nonetheless, the correlations between each frame were not directly modelled.
There is, presently, a gap in the AM literature related to modelling dynamics directly from data for anomaly detection. Since sequential data can often be highly autocorrelated, failing to account for it can increase the number of false alarms (Alwan 1992). Efforts to model dynamics in AM for the purposes of control have previously been demonstrated using linear models from photodiodes (Kruth et al. 2007; Craeghs et al. 2010). Thermal fields have also been predicted from simulated data (Ren et al. 2020). However, a lack of AM literature is present where sequential data points are modelled directly from in-situ cameras for anomaly detection. The data has simply been too complex and high dimensional for this to be technically feasible.
Deep learning has shown great potential in anomaly detection of high dimensionality sensors, where the ability to reduce dimensionality with autoencoders makes this problem tractable (Hinton and Salakhutdinov 2006). Recent development of the variational autoencoder (VAE) have allowed anomalies to be detected directly from images using a method grounded in probability theory (Kingma and Welling 2013). This has subsequently been used in industrial applications for anomaly detection in images (Han et al. 2020) and complex sensor data (Lee et al. 2019). However, the VAE also assumes i.i.d. and these studies have not needed to account for temporal structure in the data.
Neural networks have a long history in modelling dynamics and system identification (Chen et al. 1990). Furthermore, using a structured probabilistic models improve the efficiency of representing probability distributions, where only the interactions of interest are modelled (Goodfellow et al. 2016). This has led to deep learning being combined with idea of state space modelling (SSM), extending the application of the VAE to a VRNN (Krishnan et al. 2015; Chung et al. 2015; Karl et al. 2016; Buesing et al. 2018). Since predictions are made in low dimensional latent state space, these models are more computationally efficient for fast prediction. Furthermore, accuracy is improved by explicit modelling of uncertainty in the dynamics (Buesing et al. 2018).
There are also a wide range of studies exploring the use of time-series neural networks for detecting anomalies and learning dynamics. Recurrent neural networks (RNNs) have been widely used for anomaly detection in time-series data (Hundman et al. 2018), while anomaly detection in video data has also been studied (Morais et al. 2019). Tan et al. (2020) used a long short-term memory (LSTM) neural network to detect anomalies in simulated non-linear fluid dynamics. Sölch et al. (2016) used a latent dynamics model to detect anomalies in a robotics time-series data. Slavic et al. (2020) used a time-series anomaly detection approach in a self-driving application. Through modelling of time-series correlations, these studies show improved performance compared to assuming independent data in each sample interval.
AM monitoring systems could potentially greatly benefit from exploiting time-series modelling methods. Sequential representation learning models are especially suited to high dimensional data such as video feeds. However, less literature exists in detecting anomalies using this method in an AM context. Combining the newer representation learning methods and well studied dynamics modelling approaches would enable approaches for modelling dynamics directly from images without hand engineering features. The great variety of AM monitoring systems available suggest a need for such flexible methods. Meanwhile, modelling causal patterns, such as input/output correlations, through structured models enables the physical nature of the problem to be captured inductively.
Method
Problem description
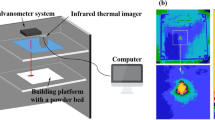
Figure 1 shows a simplified schematic of the L-PBF machine considered. Two 100 kHz high speed cameras (Photron Fastcam SA5) capture data at near-infrared wavelengths (700 nm and 950 nm) to detect high temperature information (Hooper 2018). The cameras are mounted co-axial with the laser and therefore the laser is measured in a Lagrangian perspective, where the camera is aligned with the laser as it moves. This co-axial setup captures the process signatures as the material is being fused. This enables the capture of flaw formation, which could be caused by damage in previous layers, laser obstructions from spatter, under-melting or unstable laser keyholing (Grasso and Colosimo 2017; Khairallah et al. 2020). The overall aim is to detect any such anomalous events leading to a degradation of material quality.
The dynamic anomaly detection problem involves identifying an anomalous event where a list of sequential observations are present, \((\mathbf {x}_1, \mathbf {x}_2, \ldots , \mathbf {x}_t)\) with controlled input \((\mathbf {u}_1, \mathbf {u}_2,\ldots , \mathbf {u}_t)\). Images are the observations and the laser power is the input in the present case. An anomalous sequence is one which does not conform to standard operating conditions based on pre-defined set points or decision boundaries. The dynamic model is required to make predictions and the residual error is measured to identify an anomaly. Specifically, this involves predicting the state at the present time step (\({\hat{\mathbf{z}}}_{t}\)) given previous observations (\(\mathbf {x}_{< t}\)), states (\(\mathbf {z}_{< t}\)) and inputs (\(\mathbf {u}_{< t}\)). A new observation (\(\mathbf {x}_{t}\)) is used to update the state, meaning the residual error can be measured, (\(||\mathbf {z}_{t} - {\hat{\mathbf{z}}}_{t} ||\)). This is referred to as the dynamic signature.
The model, therefore, detects anomalous events by exploiting the sequential patterns in the data. With an ideal predictor, the dynamic signature becomes a random variable independent of time. This enables the use of traditional process monitoring methods (Montgomery 2007). A reduction in false positive rate (FPR) is the main effect seen (Alwan 1992). This is important in AM because of two requirements: (1) true positive rate (TPR) needs to be maximised as false negatives pose a larger potential downside risk, (2) detection from a minimum number of samples is required to increase resolution, without requiring the increased cost of a large number of additional sensors.
Models
Autoregressive model
Markov Models exploit the sequential nature of temporal data (Bishop 2006). A first-order Markov chain is shown in Fig. 2a where the conditional distribution is given by \(p(\mathbf {x}_n|\mathbf {x}_{n-1}, \mathbf {u}_{n-1})\), and each observation is considered independent of previous observations given only the most recent. If each observation is assumed to be a continuous normal distribution, in which the mean is a linear function of the parent nodes, then this is referred to as the autoregressive (AR) model (Bishop 2006). The addition of inputs result in the AR with extra inputs (ARX) model and can be expressed as a stochastic difference equation as follows (Ljung 1999):
where \(\mathbf {x}_t\) and \(\mathbf {u}_t\) are observations and inputs. The parameters, \(\text {A}\) and \(\text {B}\) are calculated from data using the ordinary least squares (OLS) method, and comes under the class of models known as linear time invariant (LTI) in system identification (Ljung 1999). A similar first order model has been used for control applications in AM (Kruth et al. 2007; Craeghs et al. 2010).
In this work the ARX model, referred to as the linear model, is considered a comparative baseline. The mean peak image intensity and laser power are used as observations and inputs respectively. The model parameters, A, and B, are fitted to a sequence length of 20 samples. The mean values are then calculated for 1300 sequences.
Variational autoencoder
When considering high dimensional data such as images, it is often useful to consider latent variable models, giving a higher level of abstraction to represent the data. One method of calculating latent variables is by compressing data to a lower dimension referred to as a bottleneck, the objective being to reconstruct the input data. A well known probabilistic method of achieving this is the VAE (Kingma and Welling 2013; Rezende et al. 2014). The graphical model of the VAE can be seen in Fig. 2b.
The VAE utilises the concept of variational inference to estimate the latent variable distribution. Given an observation, \(\mathbf {x}_i\), the likelihood is given by \(p(\mathbf {x}_i|\mathbf {z})\). Using Bayes rule, the posterior is given by \(p(\mathbf {z}|\mathbf {x}_i)\). However, the evidence, \(p(\mathbf {x}_i)=\int p(\mathbf {x}_i|\mathbf {z})p(\mathbf {z})dz\), is intractable for high dimensional problems, therefore, approximate inference is required. The VAE relies on a variational distribution to approximate the posterior \(q_\phi (\mathbf {z}|\mathbf {x}_i)\), where \(\phi \) are parameters of a neural network. The prior, \(p(\mathbf {z})\), can be set to be an isotropic Gaussian distribution, encouraging the posterior to take a Gaussian form acting as a regulizer. Similarly, the likelihood is given by a generative network \(p_\theta (\mathbf {x}_i|\mathbf {z})\), where \(\theta \) are the parameters of a neural network.
Therefore, since the Kullback–Leibler (KL) divergence is always greater than or equal to zero between the true and approximate posteriors, by Jensen’s inequality, maximizing the Evidence Lower Bound (ELBO) is equivalent to minimizing the KL divergence. The objective function is then given by (Kingma and Welling 2013):
Anomaly detection can be applied in a number of ways. Firstly, the reconstruction term can be used to compare the input and output of the model. However, novel images can be reconstructed in unexpected ways and therefore may not always be detected (Denouden et al. 2018). Additionally, the KL divergence can be used as another measure. More recently, the Mahalanobis distance has also been used for out of distribution detection (Denouden et al. 2018). This is a method of calculating the distance from a pre-defined distribution. The Mahalanobis distance is described as:
where \(\bar{\mathbf {z}}\) and \(\varSigma \) are the optimal mean vector and covariance matrix, while \(\mathbf {z}_t\) is the sampled variable. The Mahalanobis distance is the foundation of the Hotelling \(T^2\) statistic, which has been applied to in-situ monitoring in AM (Grasso and Colosimo 2017).
The Mahalanobis distance can be calculated directly from the latent variables of the VAE. However, Principal Component Analysis (PCA) can also be applied to calculate a reduced dimensionality, which is widely applied in process monitoring on higher dimensional data (Kourti and MacGregor 1995). The PCA reconstruction error, also referred to as the Square Prediction Error (SPE), can then be used to detect any out of distribution data (Kourti and MacGregor 1995).
In the present study, the latter approach was applied to the VAE benchmark model, where the \(\beta \)-VAE implementation is followed (Higgins et al. 2016). PCA was applied to the mean of the latent variables of the training data, where 99.9% of the variance was preserved. The Mahalanobis distance was then calculated using the preserved n components. The resulting error metrics calculated at each time step are the \(D^2\) score, SPE, KL divergence and VAE reconstruction error.
Variational recurrent neural network
The graphical illustration of a first order SSM can be seen in Fig. 2c. The introduction of latent variables overcomes the severe limitations of the AR model, similar to the VAE, where a higher level abstraction can be achieved. If the latent variables are considered Gaussian then the SSM becomes the linear dynamical system leading to the Kalman Filter, while the discrete case results in the Hidden Markov Model (HMM) (Bishop 2006).
RNNs have more expressive power than the linear SSM structure and are capable of modelling complex sequences with longer time dependencies (Chung et al. 2015). The RNN can be considered as a non-linear mapping, which recursively processes a sequence while maintaining a hidden state, \(\mathbf {h}\):
However, the internal state of the RNN is fully deterministic and the output is limited to modelling simpler unimodal and bimodal distributions. This can be inappropriate when the model is highly structured and complex relationships exist between outputs in time (Chung et al. 2015). Consequently, additional stochastic terms can be used to model the uncertainty in the dynamics, which motivates the VRNN (Chung et al. 2015). Since the VAE is capable of modelling complex multi-modal distributions, the same idea can be applied to the SSM. Subsequently, complex relationships between the latent random variables can be modelled across time with the RNN. This has shown to improve modelling accuracy while preserving efficiency (Buesing et al. 2018).
The graphical model of the VRNN can be seen in Fig. 2d. The deterministic nodes are modelled with a RNN. Since the images are high dimensional, an embedding is formed with an encoder, \(\varphi _\tau ^\mathbf {x}(\mathbf {x}_t)\), for example a CNN. Additional neural networks map inputs (\(\varphi _\tau ^\mathbf {u}(\mathbf {u}_t)\)) and states (\(\varphi _\tau ^\mathbf {z}(\mathbf {z}_t)\)), resulting in the following RNN:
The new hidden state, \(\mathbf {h}_t\), can then be used to predict the probability distribution of next state, \(p(\mathbf {z}_t | \mathbf {x}_{< t}, \mathbf {u}_{< t}, \mathbf {z}_{< t})\), or combined with the latest observation to estimate the new state distribution, \(q(\mathbf {z}_t|\mathbf {x}_{\le t}, \mathbf {u}_{< t}, \mathbf {z}_{< t})\), resulting in the variational lower bound:
Additionally, the term \(\alpha \) is applied to allow the model to become semi-supervised:
where S is the set of optimal dynamics, determined through ex-situ characterisation. With all values of \(\alpha \) set to 1, the VRNN model is recovered, all observations are considered optimal and the model becomes self-supervised. Therefore, the prediction error is only calculated for the labelled inputs, while the model can still improve state representation by having access to more varied data. Finally, the regularization term from (2) is also added.
A schematic diagram of the FlawNet model. The sequence of observations is embedded into latent space, where a dynamics model utilising an RNN is trained to predict the next state distribution based on previous observations. A binary classification method is then applied to the dynamic signature to detect out of process distributions
Furthermore, the reconstruction error in this work is affected by the pulsing of the laser. This requires the signal to noise ratio (SNR) to be taken into account. The reconstruction error in (6) can be calculated by maximum likelihood estimation (MLE). This is normalised by the mean pixel intensity to give the normalised mean square error (NMSE):
where \(\bar{x}_t\) is the mean pixel intensity. This increases the penalty at low SNR images encouraging learning of the fast dynamics.
The model follows the implementation from Chung et al. (2015) and Buesing et al. (2018) but differs in that the deterministic hidden state is not used in the reconstruction of the image. Instead, only an indirect path exists through the latent random variable. This adds additional regularization to the model. The reconstruction term can be useful in facilitating state representation. However, there are redundant states that are not essential for dynamics predictions in this application. This, therefore, facilitates a simpler, more general and transferable solution.
The model architecture can be seen in Fig. 3. A CNN encoder is used to reduce the dimensions of the images at each time step into latent space. The melt pool states are then calculated, both with observations (\(\mathbf {z}\)) and without (\({\hat{\mathbf{z}}}\)). The difference between each state distribution is minimised with the KL divergence term to facilitate accurate predictions. A gated recurrent unit (GRU) is used as the RNN (Cho et al. 2014). Meanwhile, the reparameterization trick allows the calculation of gradients through backpropagation which is similar to the VAE (Kingma and Welling 2013). A generative network, composed of transposed convolutions, is then sampled and the reconstruction error is calculated using (8). Finally, the model is optimised using the lower bound from (6). The inference and generative networks are the same for both the VAE and the FlawNet model in this study. The encoder and generator architectures are shown in Table 1, an adaptation similar to many VAE network architectures, see e.g. (Ha and Schmidhuber 2018). The neural network models were implemented in PyTorch (Paszke et al. 2019).
VRNN for anomaly detection
In this paper, several scores are used to detect anomalies at test time. The prediction and reconstruction terms are used from (6) as well as the regulizer term. Furthermore, a multi-step prediction error is computed at every time step. This involves predicting ahead N steps, where the KL divergence is computed between the observed and predicted state at each step:
where N is the number of steps predicted.
Once scores are computed by the model a simple decision boundary is calculated to demonstrate the effect of the dynamic signature. Specifically, Logistic Regression is used to automate the decision boundary calculation. A statistical test such as the Hotelling \(T^2\) could be used in the absence of sub-optimal data, however, an empirical boundary gives more flexibility in adjusting the trade-off between true and false positive rates.
Experiments
Experimental setup
The aim of the experiment was to test whether quality degradation could be detected with the model and to ascertain the level of granularity. To simulate this, the focus height of the laser was adjusted from the optimal value, 0 mm, in both directions. This was then expected to cause an increase in the porosity of the samples. Adjusting focus also mimics the potential adverse effects of thermal lensing, where laser focal shift may change due to heating of focal elements of the machine (Goossens et al. 2018). The degradation was not expected to be symmetrical since the laser-material interaction varies depending on the defocus direction (Metelkova et al. 2018). The AM machine in this work is a Renishaw AM250 which utilises a modulated continuous wave laser system. The parameters followed the manufacturers pre-set optimal parameters (laser power, 200 W, point distance, 60 \(\upmu \)m, exposure time, 80 \(\upmu \)s) for the material (316L stainless steel).
The experimental setup involved the printing of 5 mm diameter cylinders at nine focus heights. The experiment was repeated three times and is referred to as Build 1, 2 and 3. Therefore, there were 27 cylinders in total, where each focus height had three samples. The focus height was adjusted from − 20 to 12 mm in increments of 4 mm. This meant that the process would traverse the optimal region, from instability through marginal and optimal stability, then return to instability. The stable region is known as the process window in AM literature (Fig. 4) (Grasso and Colosimo 2017).
The laser focus was adjusted between \({-}\) 20 and 12 mm, where each experiment was repeated three times. No significant difference was found between porosity for \({-}\) 4, 0, 4 and 8 mm, therefore this was considered within the process window. Meanwhile, the other parameters were considered unstable. In addition, \({-}\) 4 and 8 mm were considered marginally stable
Build 1 was used for training the model as well as setting decision boundaries for the binary classifiers. Meanwhile, Build 2 and 3 were utilised as validation and test sets. The position of each cylinder was randomized between each experiment to prevent this becoming a confounding variable. The separation of data was important in analysing the transferability of the model to new data. It was expected that processing conditions may vary for different types of geometries, due to the different processing variables. For example, it has been shown that inter-layer cooling time may have an effect (Williams et al. 2019). However, the present study controlled for geometric variation, which may be considered a limitation compared to true build conditions.
The parameter groupings were based on an empirical analysis of the material quality. The material quality metric that is widely used in AM is porosity (Ronneberg et al. 2020). Each sample’s porosity was assessed from optical micrographs (Hirox RH-2000 with MXB-5000REZ lens at 600\(\times \) optical zoom stitched, Fig. 5). This resulted in a total of nine focus height groupings containing three samples each. A Shapiro–Wilk test for normality and an independent samples t-test or non-parametric equivalent was used to compare the optimal parameter cylinder, 0 mm, individually to the other cylinders: − 20, − 16, − 12, − 8, − 4, 4, 8, and 12 mm. There was no statistically significant difference found between 0 mm and − 4, 4 and 8 mm, \(p \ge 0.05\). There was a statistically significant difference found between 0 mm and − 20, − 16, − 12, − 8, 12 mm, \(p<\) 0.05.
The above analysis formed the basis for four parameter groupings and three comparative tasks (Table 2). The first group compared stable versus unstable, which can be thought of as within and outside the process window. In addition, two other groups were added. 0 and 4 mm were considered optimal while − 4 and 8 mm were considered marginally stable. Therefore, task 2 considered optimal versus stable while task 3 considered optimal versus marginal. This boundary was considered marginal since these parameters were closest to unstable and therefore, potentially detectable.
The performance of the binary classifiers are evaluated with the receiver operating characteristic (ROC). The true positive rate (TPR) and false positive rate (FPR) are calculated for a set of decision thresholds giving FPR and TPR as a function of the threshold. The area under curve (AUC) is typically used to summarise this in a single number, where a score of 0.5 indicates a random guess. This metric is widely used when evaluating binary classifiers (see Murphy 2012 for an overview).
Data pre-processing
The data were captured from a single layer of the cylinder. The images from each camera were initially \(128\times 128\) pixels in size. These were cropped to \(28\times 28\) pixels around the peak intensity. The image intensities were also normalised by the bit depth (\(2^{12}\)). The images were then divided into sequences. Each 5 mm diameter layer resulted in approximately 38,000 frames. These were divided into sequences of 20 frames giving 1900 sequences.
At test time, each of the 38,000 frames then had its associated anomaly features, depending on the model. A moving average of each feature was calculated depending on the resolution requirement. The results show a nine time step moving average unless stated otherwise. This was equivalent to a single laser pulse or 90 \(\upmu s\).
ROC curves from a one-versus-one validation, where the optimal model from task 2 and 3 is scored individually against each material sample. a Unstable samples have a clear decision boundary. Due to the high value of the macro AUC (0.9994), four samples are highlighted on a semi-log axis to fully investigate the limits of FPR. b Marginal samples are more difficult to distinguish compared with unstable. This is due to the high material quality of these samples which becomes apparent at lower levels of FPR
The input data, \(\mathbf {u}\), in these experiments was the laser power. The power was sampled with a picoscope (PicoScope 5444) at 1 MHz. A filtering operation was carried out with low pass Finite Impulse Response (FIR) filter with a cutoff frequency of 100 kHz. The signal was then downsampled to match the video data at 100 kHz. The power data was then normalised by the maximum power of 200 W.
Results
The model performance across three tasks can be seen in (Table 3). The most clear distinction arose between the optimal and unstable parameters, with a mean AUC ROC of 0.9994. This reduced slightly on differentiating parameters that were stable and unstable, where an AUC of 0.9851 was achieved. Finally, the more challenging task of distinguishing between optimal and marginal groups resulted in a mean AUC of 0.9440.
A comparison between the three models across the three tasks is shown in Fig. 6. In task 1, FlawNet, VAE and linear models achieved an AUC 0.985, 0.916, 0.871 respectively. In task 2 this increased by 1.4% to 0.999 for FlawNet and 11.9% to 0.975 for the VAE. It reduced by 4.6% to 0.874 for the linear model. In task 3 FlawNet achieved 0.944 decreasing by 4.2% compared with task 1. Meanwhile, the VAE reduced by 5.7% to 0.821 while the linear model reduced by 36.3% to 0.555 compared with task 1.
Figure 7 shows a number of ROC curves for the optimal parameter model versus individual focus height samples. Firstly, in Fig. 7a, the unstable group shows four ROC curves highlighted of the 10 samples indicating limits of TPRs for a range of FPRs. At 0.01, the TPR is \(0.987\pm 0.010\). As the FPR reduces to 0.001 the TPR is reduced by 2.5% to \(0.962\pm 0.027\). Finally, as the FPR is reduced to 0.0001, the lower end of the TPR drops below 0.5, dropping by 28.4% to \(0.689\pm 0.287\). In the marginal group, Fig. 7b, the four samples from Build 2 and 3 are shown. At an FPR value of 0.5, the TPR was \(0.978\pm 0.014\). This decreased by 15.5% to \(0.826\pm 0.037\) at 0.1. At 0.01, the value decreased by another 27.5% to \(0.599\pm 0.101\). Finally, at an FPR of 0.001, the TPR drops to levels which would result in more false detections in the positive class, at \(0.368\pm 0.146\).
The dynamic signature was investigated further as a lone metric since it had highest feature importance. This revealed a positive correlation between porosity and the mean dynamic signature of the layer. Figure 8 shows the mean dynamic signature for each build, where samples are taken from the onset of porosity, i.e. the unstable group. This revealed a strong linear relationship between the dynamic signature and porosity, with an \(\text {R}^2\) value of 0.904. The onset was only achieved at 12 mm, therefore, more data is required to see if it is also linear in the positive direction.
To better understand the potential granularity of the model, Fig. 9 shows a comparison of resolution, when detecting different porosity amounts at 0.999 TPR. For very low porosity, around three laser pulses were required to achieve an FPR below 0.1. Meanwhile, for higher porosities, a single laser pulse was required.
To investigate the critical components of the model, an ablation study was conducted, where several critical components of the network were systematically removed. The input, multi-step prediction (MSP) and semi-supervision (SS) components were removed individually (Fig. 10a). Compared with FlawNet in task 1, a reduction of 2.9%, 0.7% and 6.7% can be seen when removing the input, MSP and SS respectively. Similarly for task 2, very little change was observed when removing the input and MSP (0.3%, 0.1%), whereas removing SS resulted in a larger reduction (5.5%). Finally, task 3 saw a slight difference of 5.0% and 3.9% when removing the input and MSP, whereas a large change of 24.8% was observed when removing SS.
Removal of semi-supervision resulted in a large reduction in performance. This is explored in Fig. 10b. The peak image intensities were compared between the true image (\(\mathbf {x}\)), the input (\(\mathbf {u}\)), and reconstructed images of the predicted posterior (\(\hat{\mathbf{z}}\)) and observed posterior (\(\mathbf {z}\)) based on 50 MC samples of the generative model and an error of one standard deviation. Firstly, the states are better represented in the low amplitude regimes which was important for capturing fast dynamics. Secondly, the observation model was better capable of reconstructing the intensity of low signal images.
a Ablation study of FlawNet, where the input, multi-step prediction (MSP) as well as semi-supervision (SS) were systematically removed. b Comparison of models trained with and without semi-supervision. Two improvements can be seen: (1) The ability to represent low amplitude regimes important for fast dynamics. (2) Improved reconstruction of sub-optimal process data, essential for detecting an anomalous dynamic signature
Discussion
There were two key factors that contributed to the model’s performance: predictive accuracy and state representation. The better state representation results in a better ability to model variability, which became apparent with the inclusion of the additional anomalous data. This allowed the model to improve since a larger variety of data was available (Halevy et al. 2009). Furthermore, there is better representation of the low signal states, where the cooling rate is captured. Since cooling rate is a good indicator of the process being in control, it is important to capture it in this application (Hooper 2018). The predictive accuracy is also important since this is needed to compute the dynamic signature. However, for a high performing model, the predictions should better match the optimal dynamics, rather than the observed state. The model prefers to base predictions on the input parameter over the previous observations. This is apparent from the performance degradation when removing the input in the ablation study. Therefore, the model should be capable of strong predictive posteriors weighted towards optimal conditions, while the observed posterior should follow the observation closely.
To further elucidate this result, the resolution was compared at differing numbers of samples (Fig. 9). A rapid convergence resulted from the sequential errors becoming more independent compared to assuming i.i.d. data. Since predictive errors will take on a randomness with respect to time, fewer samples are required to improve accuracy. However, when the correlation is not accounted for this assumption does not hold and a larger FPR will result (Alwan 1992). Since the laser modulates at regular frequency, the resulting variability is part of the process and not anomalous. Hence, needs to be modelled to account for the resulting seasonality. The autocorrelation is, therefore, an important consideration in many industrial problems such as AM and the improved results agree with process monitoring literature, where a predictive model is used (Montgomery 2007). This has not been feasible in many industrial applications with high dimensional non-linear dynamics and would suggest an effective predictive model for this application domain.
The model was also robust to non-linearity in the captured data. The laser modulates at a very high frequency of around 11 kHz. However, the off-time is much shorter, lasting only 10 \(\upmu \)s. This is the same as the camera frame rate and therefore greater than the Nyquist criterion, i.e. the off-pulse lasts for 10 \(\upmu \)s while the camera sample spacing is 10 \(\upmu \)s. Therefore, a mild aliasing effect occurs between pulses and creates additional non-linearity. This does not seem to have degraded results for this experiment. It is thought that this was aided by accounting for the uncertainty in the model, where explicit modelling of uncertainty improves accuracy (Buesing et al. 2018).
A key advantage of the system is that no hand labelled data is required, automating the learning of dynamics. Beyond the ex-situ characterisation of the optimal parameter, new data can be added as it becomes available. Similarly, semi-supervised prediction of single tracks has been reported in AM (Yuan et al. 2019). However, the method required more complex characterisation than porosity to achieve labels, whereas this method only requires the input power as the label. Therefore, the present method is easily adapted to current industrial monitoring systems. Furthermore, since system performance improves with the use of additional unstable process parameters, it indicates the model’s potential to improve over time as more data is collected. This is important when scaling the model, where data may be needed for additional process parameters and inputs.
The model also performed well when distinguishing between highly dense, yet unstable, materials. The model was capable of differentiating between parameters that produce \(0.09 \pm 0.04\%\) and \(0.21 \pm 0.02\%\) density, achieving an AUC of 0.999. The results indicate the potential to detect changes at a level of 0.1% porosity. This is approaching the level required for monitoring of the microstructure. This would open up a large potential for AM combined with monitoring systems, where microstructure could be locally tailored within the material. Control of microstructure can therefore reduce the need for post-processing and speed up the qualification of the final component (Gockel and Beuth 2013). This is a strong indicator of the granularity of the system, however, adjustment of additional parameters is required to confirm this finding.
Meanwhile, false detections were significantly reduced for the unstable parameters (Fig. 7). The system performed well to an FPR of 0.001, maintaining a TPR of \(0.962\pm 0.027\), with predictions made from nine frames or one laser pulse, equating to around 12,600 data points in total when comparing the two optimal samples against the defective sample for that build. This would indicate a system which has potential to maintain usefulness at locating defects at high resolution, even with respect to rarely observed defects, at approximately 4 false positives per layer with no defects present. The dataset in this study was not large enough to fully evaluate lower levels of FPR but performance appears to greatly decrease at 0.0001. Porosity is a rare event, hence most detections will be in the negative class. Therefore, even at this level the FPR may be unacceptably high, suggesting larger datasets are needed to better understand these ramifications. The data points in an entire build would easily reach 10\(^6\). Hence, evaluation datasets need to be at least this size or larger to fully characterise the system.
Similarly, the model is also capable of high resolution while maintaining 99.9% TPR (Fig. 9). This is an important requirement in critical applications, where a single false negative could be dangerous. Therefore, it becomes important to have high confidence in the system, even at the cost of increased false positives. However, it was also shown that this may come at a cost of resolution. Higher porosity values typically needed one to three laser pulses to achieve sub 10% FPR while maintaining 99.9% TPR. Meanwhile, lower porosity material (i.e. − 8 mm and 12 mm) needed three pulses or more. Given that a relatively small 5 mm cylinder of these experiments had around 38,000 captured images, if it is crudely assumed that nine samples is equivalent to one melt pool and the material has 0.1% porosity, an estimate would be to consider that four melt pools were anomalous. With a 10% FPR, the system correctly detects approximately 1 in 100 samples and is overwhelmed by false positives. Hence, a trade-off between resolution and FPR needs to be made. The results from this work would suggest that additional systems would be required to accurately and repeatably locate flaws below 150 \(\upmu \text {m}\) in size. However, additional spatial correlations in the x, y and z directions may also improve this result if data was captured over multiple layers.
Though the model performed well in the first two tasks tested, performance reduced slightly in the optimal vs. marginal task. This was due to the challenge of differentiating signatures at near optimal conditions in ultra-dense materials. Since, at least some of the time, the marginal parameters are in the optimal high density regime, there is unavoidable reduced performance. However, this high performance is a good sign for early detection of the onset of increased variability. This is highly useful in a monitoring system since an early warning could allow corrective action. Parameters could then be adjusted if there is the onset of variability due to specific geometrical features. This is a key requirement of future research in AM (Debroy et al. 2019).
There was a clear trend observed between porosity and the mean dynamic signature for the layer. This would suggest that global properties can be inferred very accurately, in the context of parameter selection. Since each cylinder layer has around 38,000 time steps, the mean of the dynamic signature will approach its population mean for that experiment. Therefore, this study indicates the dynamic signature to work well as a global quality metric. This is useful in the context of optimising parameters for a new material or a challenging geometry. Instead of taking the time to measure porosity or conduct destructive test, the monitoring data could be directly used to estimate the quality. This could enable automated material development, rapidly increasing the pace at which new material parameters could be found.
There are no public benchmarks for AM. However, in comparison to other recent work in AM anomaly detection the model achieved state-of-the-art results. Mitchell et al. (2020) utilised features from high speed images and applied outlier detection using a k–d tree. This is an effective method but at lower porosity the model FPR was between 23% and 58%. In comparison, this work indicates the potential to locate material degradation at lower FPR even while maintaining 0.999 TPR, though more data is required to quantify this to localisation. Jayasinghe et al. (2020) were capable of differentiating porosity below 99% with an AUC of 0.946 using three photodiodes. This is equivalent to − 8 mm unstable parameter in the present work, where a mean AUC of 0.999 was achieved with a single laser pulse. This would indicate the advantage of camera monitoring, allowing additional information to be utilised. However, the present method is also highly suitable for this type of sensor.
A limitation of the study was that the part geometry was fixed. Though many experiments in AM use only single track experiments, this study has gone one step further where solid material was considered. However, complex geometries may cause new types of dynamic signatures, which arise due to changes in the melt pool state. The present study achieved high performance without requiring the modelling of geometry related inputs, e.g. the laser turning at the edge of a geometric feature causes a change in velocity. However, it is likely that highly complex geometries will require further inputs that relate the melt pool to the geometry. Similarly, global surface temperatures are also likely to effect the melt pool state. These areas were out of the scope of the present study and are topics of an ongoing study.
Conclusion
In this study, a data-driven modelling paradigm, FlawNet, was introduced to model the laser dynamics of the L-PBF process directly from high speed images. The method exploits the correlations between observed images and the laser input, as well as the time-series correlations between images to reduce the rate of false detections. A novel monitoring metric known as the dynamic signature was introduced to facilitate this aim. The model was tested on various porosity levels and demonstrated state-of-the-art results with an ability to differentiate between optimal processing and defective materials down to 0.2% porosity with an AUC of 0.999. Furthermore, the model was capable of distinguishing between process signatures at porosity levels of 0.1% with an AUC of 0.944. The model is a useful tool for predicting both local and part-wide porosity which has application in parameter selection and in-situ quality control. The model also demonstrated a potential to detect the early onset of material degradation allowing potential corrective action to be taken. The dynamic signature presented adds an important metric to the AM flaw detection toolbox and the FlawNet model brings about a significant leap towards in-situ quality control.
References
Alwan, L. C. (1992). Effects of autocorrelation on control chart performance. Communications in Statistics-Theory and Methods, 21(4), 1025–1049. https://doi.org/10.1080/03610929208830829
Attaran, M. (2017). The rise of 3-d printing: The advantages of additive manufacturing over traditional manufacturing. Business Horizons, 60(5), 677–688. https://doi.org/10.1016/j.bushor.2017.05.011
Bishop, C. M. (2006). Pattern recognition and machine learning (pp. 605–652). Berlin: Springer.
Buesing, L., Weber, T., Racaniere, S., Eslami, S., Rezende, D., Reichert, D. P., et al. (2018). Learning and querying fast generative models for reinforcement learning. arXiv preprint arXiv:1802.03006.
Chen, S., Billings, S., & Grant, P. (1990). Non-linear system identification using neural networks. International Journal of Control, 51(6), 1191–1214. https://doi.org/10.1080/00207179008934126
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder–decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
Chung, J., Kastner, K., Dinh, L., Goel, K., Courville, A. C., & Bengio, Y. (2015). A recurrent latent variable model for sequential data. In Advances in neural information processing systems (pp. 2980–2988). arXiv:1506.02216.
Craeghs, T., Bechmann, F., Berumen, S., & Kruth, J. P. (2010). Feedback control of layerwise laser melting using optical sensors. Physics Procedia, 5, 505–514. https://doi.org/10.1016/j.phpro.2010.08.078
Cunningham, R., Zhao, C., Parab, N., Kantzos, C., Pauza, J., et al. (2019). Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed X-ray imaging. Science, 363(6429), 849–852. https://doi.org/10.1126/science.aav4687
Debroy, T., Mukherjee, T., Milewski, J., Elmer, J., Ribic, B., Blecher, J., et al. (2019). Scientific, technological and economic issues in metal printing and their solutions. Nature Materials. https://doi.org/10.1038/s41563-019-0408-2
Denouden, T., Salay, R., Czarnecki, K., Abdelzad, V., Phan, B., & Vernekar, S. (2018). Improving reconstruction autoencoder out-of-distribution detection with mahalanobis distance. arXiv preprint arXiv:1812.02765.
Ford, S., & Despeisse, M. (2016). Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. Journal of cleaner Production, 137, 1573–1587. https://doi.org/10.1016/j.jclepro.2016.04.150
Francois, M. M., Sun, A., King, W. E., Henson, N. J., Tourret, D., Bronkhorst, C. A., Carlson, N. N., Newman, C. K., Haut, T. S., Bakosi, J., et al. (2017). Modeling of additive manufacturing processes for metals: Challenges and opportunities. Current Opinion in Solid State and Materials Science. https://doi.org/10.1016/j.cossms.2016.12.001
Gao, W., Zhang, Y., Ramanujan, D., Ramani, K., Chen, Y., Williams, C. B., Wang, C. C., Shin, Y. C., Zhang, S., & Zavattieri, P. D. (2015). The status, challenges, and future of additive manufacturing in engineering. Computer-Aided Design, 69, 65–89. https://doi.org/10.1016/j.cad.2015.04.001
Gockel, J., & Beuth, J. (2013). Understanding Ti–6Al–4V microstructure control in additive manufacturing via process maps. In Solid freeform fabrication proceedings (pp. 666–674). Univ. Tex. Austin. http://utw10945.utweb.utexas.edu/Manuscripts/2013/2013-53-Gockel.pdf.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. Cambridge: MIT Press.
Goossens, L. R., Kinds, Y., Kruth, J. P., & Van Hooreweder, B. (2018). On the influence of thermal lensing during selective laser melting. In Solid freeform fabrication symposium proceedings (SFF Symp 2018) (pp. 2267–2274). Austin: University of Texas. https://lirias.kuleuven.be/2114088?limo=0.
Grasso, M., & Colosimo, B. M. (2017). Process defects and in situ monitoring methods in metal powder bed fusion: A review. Measurement Science and Technology, 28(4), 044005. https://doi.org/10.1088/1361-6501/aa5c4f
Ha, D., & Schmidhuber, J. (2018). World models. arXiv preprint arXiv:1803.10122.
Halevy, A., Norvig, P., & Pereira, F. (2009). The unreasonable effectiveness of data. IEEE Intelligent Systems, 24(2), 8–12. https://doi.org/10.1109/MIS.2009.36
Han, Z., Hossain, M. M., Wang, Y., Li, J., & Xu, C. (2020). Combustion stability monitoring through flame imaging and stacked sparse autoencoder based deep neural network. Applied Energy, 259, 114159. https://doi.org/10.1016/j.apenergy.2019.114159
Higgins, I., Matthey, L., Pal, A., Burgess, C., Glorot, X., Botvinick, M., Mohamed, S., & Lerchner, A. (2016). beta-vae: Learning basic visual concepts with a constrained variational framework. https://openreview.net/pdf?id=Sy2fzU9gl.
Hinton, G. E., & Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313(5786), 504–507. https://doi.org/10.1126/science.1127647
Hooper, P. A. (2018). Melt pool temperature and cooling rates in laser powder bed fusion. Additive Manufacturing, 22, 548–559. https://doi.org/10.1016/j.addma.2018.05.032
Hundman, K., Constantinou, V., Laporte, C., Colwell, I., & Soderstrom, T. (2018). Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery and data mining (pp. 387–395). https://doi.org/10.1145/3219819.3219845.
Jayasinghe, S., Paoletti, P., Sutcliffe, C., Dardis, J., Jones, N., & Green, P. (2020). Automatic quality assessments of laser powder bed fusion builds from photodiode sensor measurements. https://www.preprints.org/manuscript/202004.0055/v1.
Karl, M., Soelch, M., Bayer, J., & Van der Smagt, P. (2016). Deep variational bayes filters: Unsupervised learning of state space models from raw data. arXiv preprint arXiv:1605.06432.
Khairallah, S. A., Martin, A. A., Lee, J. R., Guss, G., Calta, N. P., Hammons, J. A., et al. (2020). Controlling interdependent meso-nanosecond dynamics and defect generation in metal 3d printing. Science, 368(6491), 660–665. https://doi.org/10.1126/science.aay7830
Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
Kourti, T., & MacGregor, J. F. (1995). Process analysis, monitoring and diagnosis, using multivariate projection methods. Chemometrics and Intelligent Laboratory Systems, 28(1), 3–21. https://doi.org/10.1016/0169-7439(95)80036-9
Krishnan, R. G., Shalit, U., & Sontag, D. (2015). Deep kalman filters. arXiv preprint arXiv:1511.05121.
Kruth, J. P., Mercelis, P., Van Vaerenbergh, J., & Craeghs, T. (2007). Feedback control of selective laser melting. In Proceedings of the 3rd international conference on advanced research in virtual and rapid prototyping (pp. 521–527). Taylor & Francis Ltd. https://lirias.kuleuven.be/66104?limo=0.
Lee, S., Kwak, M., Tsui, K. L., & Kim, S. B. (2019). Process monitoring using variational autoencoder for high-dimensional nonlinear processes. Engineering Applications of Artificial Intelligence, 83, 13–27. https://doi.org/10.1016/j.engappai.2019.04.013
Ljung, L. (1999). System identification Wiley encyclopedia of electrical and electronics engineering (pp. 1–19). Hoboken: Wiley.
Metelkova, J., Kinds, Y., Kempen, K., de Formanoir, C., Witvrouw, A., & Van Hooreweder, B. (2018). On the influence of laser defocusing in selective laser melting of 316l. Additive Manufacturing, 23, 161–169. https://doi.org/10.1016/j.addma.2018.08.006
Mitchell, J. A., Ivanoff, T. A., Dagel, D., Madison, J. D., & Jared, B. (2020). Linking pyrometry to porosity in additively manufactured metals. Additive Manufacturing, 31, 100946. https://doi.org/10.1016/j.addma.2019.100946
Montgomery, D. C. (2007). Introduction to statistical quality control (pp. 419–423). Hoboken: Wiley.
Morais, R., Le, V., Tran, T., Saha, B., Mansour, M., & Venkatesh, S. (2019). Learning regularity in skeleton trajectories for anomaly detection in videos. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 11996–12004). https://doi.org/10.1109/cvpr.2019.01227.
Murphy, K. P. (2012). Machine learning: A probabilistic perspective (pp. 183–184). Cambridge: MIT Press.
Okaro, I. A., Jayasinghe, S., Sutcliffe, C., Black, K., Paoletti, P., & Green, P. L. (2019). Automatic fault detection for laser powder-bed fusion using semi-supervised machine learning. Additive Manufacturing, 27, 42–53. https://doi.org/10.1016/j.addma.2019.01.006
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J., & Chintala, S. (2019). Pytorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems 32 (pp. 8024–8035). Red Hook: Curran Associates, Inc.
Ren, K., Chew, Y., Zhang, Y., Fuh, J., & Bi, G. (2020). Thermal field prediction for laser scanning paths in laser aided additive manufacturing by physics-based machine learning. Computer Methods in Applied Mechanics and Engineering, 362, 112734. https://doi.org/10.1016/j.cma.2019.112734
Rezende, D. J., Mohamed, S., & Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. arXiv preprint arXiv:14014082. http://proceedings.mlr.press/v32/rezende14.pdf.
Ronneberg, T., Davies, C. M., & Hooper, P. A. (2020). Revealing relationships between porosity, microstructure and mechanical properties of laser powder bed fusion 316l stainless steel through heat treatment. Materials and Design, 189, 108481. https://doi.org/10.1016/j.matdes.2020.108481
Scime, L., & Beuth, J. (2019). Using machine learning to identify in-situ melt pool signatures indicative of flaw formation in a laser powder bed fusion additive manufacturing process. Additive Manufacturing, 25, 151–165. https://doi.org/10.1016/j.addma.2018.11.010
Slavic, G., Campo, D., Baydoun, M., Marin, P., Martin, D., Marcenaro, L., & Regazzoni, C. (2020). Anomaly detection in video data based on probabilistic latent space models. In 2020 IEEE conference on evolving and adaptive intelligent systems (EAIS) (pp. 1–8). IEEE. https://doi.org/10.1109/EAIS48028.2020.9122766.
Sölch, M., Bayer, J., Ludersdorfer, M., & van der Smagt, P. (2016). Variational inference for on-line anomaly detection in high-dimensional time series. arXiv preprint arXiv:1602.07109.
Tan, Y., Hu, C., Zhang, K., Zheng, K., Davis, E. A., & Park, J. S. (2020). LSTM-based anomaly detection for non-linear dynamical system. IEEE Access, 8, 103301–103308. https://doi.org/10.1109/access.2020.2999065
Tan, Y., Jin, B., Nettekoven, A., Chen, Y., Yue, Y., Topcu, U., & Sangiovanni-Vincentelli, A. (2019). An encoder–decoder based approach for anomaly detection with application in additive manufacturing. In 2019 18th IEEE international conference on machine learning and applications (ICMLA) (pp. 1008–1015). IEEE. https://doi.org/10.1109/icmla.2019.00171.
Williams, R. J., Piglione, A., Rønneberg, T., Jones, C., Pham, M. S., Davies, C. M., & Hooper, P. A. (2019). In situ thermography for laser powder bed fusion: Effects of layer temperature on porosity, microstructure and mechanical properties. Additive Manufacturing, 30, 100880. https://doi.org/10.1016/j.addma.2019.100880
Yuan, B., Giera, B., Guss, G., Matthews, I., & McMains, S. (2019). Semi-supervised convolutional neural networks for in-situ video monitoring of selective laser melting. In 2019 IEEE winter conference on applications of computer vision (WACV) (pp. 744–753). IEEE. https://doi.org/10.1109/wacv.2019.00084.
Zhang, Y., Hong, G. S., Ye, D., Zhu, K., & Fuh, J. Y. (2018). Extraction and evaluation of melt pool, plume and spatter information for powder-bed fusion am process monitoring. Materials and Design, 156, 458–469. https://doi.org/10.1016/j.matdes.2018.07.002
Zhang, Y., Soon, H. G., Ye, D., Fuh, J. Y. H., & Zhu, K. (2019). Powder-bed fusion process monitoring by machine vision with hybrid convolutional neural networks. IEEE Transactions on Industrial Informatics, 16(9), 5769–5779. https://doi.org/10.1109/tii.2019.2956078
Acknowledgements
The authors thank A. Terenin for suggesting generative networks as a research direction. The authors also thank H. De Winton for processing samples and analysing optical micrographs. The authors thank AWE plc (contract 30338995) and EPSRC (EP/K503733/1) for their financial support for this research.
Funding
Partial financial support was received from AWE plc (contract 30338995) and EPSRC (EP/K503733/1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Larsen, S., Hooper, P.A. Deep semi-supervised learning of dynamics for anomaly detection in laser powder bed fusion. J Intell Manuf 33, 457–471 (2022). https://doi.org/10.1007/s10845-021-01842-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-021-01842-8