Modular production control using deep reinforcement learning: proximal policy optimization

Abstract

EU regulations on $\textit{CO}_2$ limits and the trend of individualization are pushing the automotive industry towards greater flexibility and robustness in production. One approach to address these challenges is modular production, where workstations are decoupled by automated guided vehicles, requiring new control concepts. Modular production control aims at throughput-optimal coordination of products, workstations, and vehicles. For this np-hard problem, conventional control approaches lack in computing efficiency, do not find optimal solutions, or are not generalizable. In contrast, Deep Reinforcement Learning offers powerful and generalizable algorithms, able to deal with varying environments and high complexity. One of these algorithms is Proximal Policy Optimization, which is used in this article to address modular production control. Experiments in several modular production control settings demonstrate stable, reliable, optimal, and generalizable learning behavior. The agent successfully adapts its strategies with respect to the given problem configuration. We explain how to get to this learning behavior, especially focusing on the agent’s action, state, and reward design.

Introduction to modular production systems

Manufacturing systems in the automotive industry are undergoing a systematic change. The trade-off between following the customer’s needs and handling the economic pressure requires novel approaches to manufacturing (Kern et al. 2015). On one side, EU regulations defining a $\textit{CO}_2$ threshold of $95 \frac{g \textit{CO}_2}{km}$ averaged over the fleet require car manufacturers to expand their engine portfolio to electric drives and other alternative more sustainable engine concepts. The threshold regulation is phased for $95\%$ of cars at the beginning of 2020, with full compliance by 2021 (Mock 2014). On the other side, customers expect more individual products that closely match their needs and taste. Individualization and customization need to be balanced with resource management to keep the costs as low as possible. In a highly competitive market, as the automotive market is, this is essential for a company to persist over time (McKinsey 2013, 2016).

Fig. 1

Modular production system consisting of a source, where products are released into the system, stations, where products are processed, automated guided vehicles (AGV) for material transport moving on a transport network, and a sink, where products are finished

Modular production systems are an up-and-coming solution to this challenge. In contrast to classical production lines, such as mixed-model assembly lines (Boysen 2007), modular production drops the concept of sequential processing and allows for more flexibility of routing diversified products through workstations¹. This flexibility is inherently characterized by the application of automated guided vehicles (AGV). They enable flexible transportation of products and essentially decouple workstations, making AGVs a core feature of modular production systems (Kern et al. 2015; Bochmann 2018; Greschke 2016; Foith-Förster and Bauernhansl 2015).

Figure 1 depicts a modular production system, as considered in this work. Different products are released into the production system on workpiece carriers (WPC) at a production source. AGVs handle the material transport between the decoupled workstations utilizing a transport network. Each decoupled workstation comprises a buffer at its input and its output (IB and OB), allowing to buffer products on WPCs in front of and behind a station’s processing location (PROC). Finally, finished products are brought to the system’s sink. The next section describes how complex the control of these systems is.

Modular production control problem formulation

In order to utilize the flexibility advantage of such modular production systems, an optimal coordination of products, stations, and AGVs is required. At the same time, real dynamic production environments require robustness against unexpected events like machine down-times (Ouelhadj and Petrovic 2009). Being a scheduling-like problem, modular production control (MPC) belongs to the complexity class of np-hard problems. Because modular production is a new field in the automotive industry, descriptions of the complex control problems are rarely found in literature. Instead, our earlier work has introduced five sub-problems (Mayer and Endisch 2019; Mayer et al. 2019a, b, c). Each sub-problem represents specific scheduling decisions to be made:

• Job release management (JReM): Release jobs of different product types into the production system at certain points in time out of a given job pool.

• Job routing management (JRoM): Define the operations’ order and choose a workstation for each operation.

• Workstation management (WM): Time jobs’ operations at a workstation and sequence competing jobs.

• Vehicle management (VM): Assign transports to AGVs and coordinate them deadlock-free.

• Deviation management (DM): React on dynamics like machine down-times and operation time fluctuations.

A more formal description of the control context orients itself on a scheduling formulation by Watermeyer (2016) and is as follows: A set of $n_J$ jobs J is processed by a set of $n_M$ modular workstations M and transported by $n_V$ AGVs V with speed $v_V$. Each workstation $M_k$ comprises an Inbound- and an Outbound-Buffer (IB and OB) with equal capacity $n_{buf}$ utilizing First In - First Out (FIFO). A vehicle’s $V_j$ transport time is denoted by $t_T$. Jobs $J_i$ represent certain product types PT and can be flexible according to their operations’ order and the choice of an operation’s station. Firstly, order flexibility is represented by $n_{P}$ process plans $P_i$. A process plan $P_{ip}$ consists of $n_O$ operations $O_{ip}$ defining their order. Operations’ $O_{ipl}$ processing times are denoted by $t_{ipl}$, their start times at stations by $S_{ipl}$. Secondly, operation flexibility is defined as the ability of at least one job operation $O_{ipl}$ to be processed by at least two stations (Kacem et al. 2002). $S_{J_i}$ denotes the point in time, a job $J_i$ is released at the source. Jobs are released on WPCs, whose number is limited to $n_{WPC}$. A job and a respective WPC remain linked until a job has finished all of its operations. After finishing all operations, an AGV transports a job to the production system’s sink and the WPC becomes available again. All descriptive sets are listed below:

$$\begin{aligned} J&:=\{J_1,J_2,\ldots ,J_i,\ldots ,J_{n_J}\} \end{aligned}$$

(1)

$$\begin{aligned} M&:=\{M_1,M_2,\ldots ,M_k,\ldots ,M_{n_M}\} \end{aligned}$$

(2)

$$\begin{aligned} V&:=\{V_1,V_2,\ldots ,V_j,\ldots ,V_{n_V}\} \end{aligned}$$

(3)

$$\begin{aligned} PT&:=\{PT_1,PT_2,\ldots ,PT_x,\ldots ,PT_{n_{PT}}\} \end{aligned}$$

(4)

$$\begin{aligned} P_i&:=\{P_{i1},P_{i2},\ldots ,P_{ip},\ldots ,P_{in_{p}}\} \end{aligned}$$

(5)

$$\begin{aligned} O_{ip}&:=\{O_{ip1},O_{ip2},\ldots ,O_{ipl},\ldots ,O_{ipn_O}\} \end{aligned}$$

(6)

In order to complement the above model, further boundary conditions are: The release order and the job release time points $S_{J_i}$ are arbitrary, but limited by the number of WPCs $n_{WPC}$. Jobs J are initially available and independent. A job’s operations cannot be processed in parallel. A workstation cannot process more than one job at a time. Operation times $t_{ipl}$ are known and independent from the station. Preemption of operations is not allowed. An AGV can only transport one job at a time.

The production control’s goal is to be generalizable in dealing with diverse modular production environments. Furthermore, MPC aims at robustness against dynamics and a minimized makespan for all jobs J² by maximizing the production throughput.

Earlier work leads to reinforcement learning closing the research gap

From a high-level perspective, control approaches are divided into centralized and decentralized approaches, where centralized describes one entity solving the problem and decentralized describes several collaborative entities finding solutions (Leitão 2009).

As no plug-and-play algorithms for the new problem of MPC exist in literature, our earlier work addressed MPC with rather conventional scheduling approaches. Firstly, we implemented a centralized approach using a Genetic Algorithm for scheduling (Mayer and Endisch 2019) and secondly, a decentralized multi-agent-system, where resource and product agents negotiated for their allocation (Mayer et al. 2019b, c). Both control approaches lacked in topics like computing efficiency for large scale problems, finding the optimal solution reliably, and their generalizability.

In order to close this research gap in MPC, this work addresses the previously mentioned problem by applying an intelligent computing method called Reinforcement Learning (RL) (Teti and Kumara 1997). Firstly, RL is applicable to sequential decision problems, for instance, using Markov Decision Processes (MDP). Secondly, RL’s applicability to related adaptive control problems in manufacturing systems has already been shown (Chen et al. 2015; Stricker et al. 2018; Usuga Cadavid et al. 2020). Especially Deep Reinforcement Learning’s (DRL) success in the gaming industry (Mnih et al. 2013; Silver et al. 2016) proved the method’s generalizability and its solution quality, being applied to complex, dynamic optimization problems.

Overview on reinforcement learning

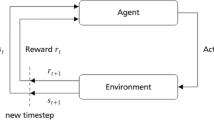
In RL, an agent tries to solve the underlying problem optimally by interacting with its environment and adapting its strategy through trial-and-error. At timesteps t, the agent takes actions $A_t$ that lead to rewards $R_{t+1}$ and new states $S_{t+1}$ in the environment. It collects this experience to adapt its policy $\pi$ iteratively, in order to maximize the collected rewards and find an optimal policy $\pi _*$ (Sutton and Barto 2018).

RL methods can be divided into tabular methods like Q-Learning, and DRL methods, where value-based, policy gradient, and actor-critic methods are distinguished. DRL methods utilize a Neural Network (NN) to acquire and store experience over time. In comparison, tabular methodologies utilize a lookup table to store the respective knowledge. The main difference between value-based and policy gradient methods is that value-based methods approximate the mentioned lookup table with the NN and thereof deduce the optimal policy, whereas policy gradient methods directly approximate a policy (Sutton and Barto 2018; Morales 2020). Morales (2020) also describes that generally, tasks of an RL agent are divided into two aspects: episodic tasks, having a natural ending, and continuous tasks that do not end naturally.

Applied to MPC, an episodic task is defined to finish a fixed number of jobs and to minimize their makespan, where the episode’s terminal state is reached when the last job enters the production system’s sink. Whereas, a continuous task describes a production system running 24 hours, seven days a week, and the throughput, describing the production’s output of products per hour, is aimed to be maximized. Here, we focus on a continuous setting.

Contribution and structure

This article closes the research gap in the field of MPC for the automotive industry in mainly three ways: Firstly, we derive the first application of RL in the field of automotive MPC. Secondly, to reliably find throughput-maximized control solutions, we give implementation guidance by documenting our learnings. Thirdly, the article demonstrates the generalization capabilities of RL in the context of MPC to meet one of the main goals of RL appliance in MPC.

Accordingly, the article is structured as follows: In order to choose an RL method for MPC, “Related work on reinforcement learning in production” section reviews literature on the appliance of RL algorithms for MPC-related production control problems. “Deep reinforcement learning with policy gradient methods: proximal policy optimization” section introduces the chosen DRL method Proximal Policy Optimization (PPO) and concludes with the respective pseudocode. These basics are then used in “Implementation: PPO agent and environment” section for the agent’s implementation, the interaction with its environment, and the environment itself, especially focusing on the action, state, and reward design. Finally, “Experimental results” section documents the experiments and discusses its results on PPO’s learning and generalization capabilities in MPC. The article closes with a conclusion in “Conclusion and future work” section.

Related work on reinforcement learning in production control

RL is getting more attention in MPC-related production control research in the last years, especially in the semiconductor industry, where production systems are highly complex. This section analyses a cross-section of RL in production control or related areas focusing on tabular RL methods as well as value-based DRL, and policy gradient DRL methods. Actor-critic methods are not involved, being a newer field in DRL research and no applications to production control have been found. The section categorizes the different approaches along the introduced dimensions of MPC and concludes their applicability to MPC. Finally, a suitable RL method for MPC is chosen.

Tabular methods

Aydin and Öztemel (2000) developed an improved version of the Q-Learning algorithm termed Q-III featuring faster learning and a higher probability to converge to a global optimum. Applied to a dynamic job-shop scheduling problem consisting of nine workstations and five jobs, the centralized agent intelligently chose priority rules for the current production situation in real-time and showed better performance than benchmark priority rules. The publication focused on workstation management and deviation management.

In contrast to optimizing performance and convergence issues of Q-Learning, Creighton and Nahavandi (2002) focused on minimizing the required memory space of the centralized RL agent. They managed to reduce the state space significantly with a mapping technique, which enabled the evaluation of larger size problems with tabular methods and available computing power. Although little is stated about the problem setting and exact tabular methodology applied, the approach is considered valuable for the expansion to large state spaces. The authors addressed workstation and vehicle management.

Wang (2020) showed the applicability of a Q-Learning algorithm in combination with a multi-agent bidding system for job-shop scheduling. The centralized Q-Learning instance selected the best fit between tasks and resources based on the bids at hand. A clustering method was used to reduce the state space. The overall approach demonstrated superior performance compared to respective benchmarks. Wang (2020) addressed the sub-problems of deviation and workstation management.

Shiue et al. (2018) developed a Q-Learning agent to control the workstation within the factory and perform scheduling tasks. As a discrete-event environment, the Tecnomatix Plant Simulation software was utilized, just as within this article. Shiue et al. (2018) described better performance results of the Q-Learning RL approach compared to previous implementations of their work as well as to benchmark heuristic dispatching rules. The RL agent took a centralized perspective and addressed the sub-problem of workstation management. Little was stated about the exact problem setting.

Value-based DRL methods

Mahadevan and Theocharous (1998) investigated transfer lines to integrate methods of lean manufacturing and thereby minimize inventory levels using RL. Their SMART model outperformed the Kanban benchmark on inventory levels as well as workstation failure prevention. The SMART algorithm was developed as a centralized approach addressing the sub-problems of job release, workstation, and deviation management, as maintenance policies were learned.

The center figure for the following three examples of value-based methods in production control is Mr. Riedmiller who contributed to a large extent to the development of the Deep Q-Network (DQN) architecture (Riedmiller and Riedmiller 1999; Gabel and Riedmiller 2007; Mnih et al. 2015, 2013). Riedmiller’s first RL application in production control featured a multilayer-perceptron network that approximated the value function Q. The problem set was rather small with an experiment consisting of three workstations and the smaller experiment including a single workstation. The architecture is characterized as decentralized with individual agents representing a single workstation. Riedmiller and Riedmiller (1999) addressed the sub-problem of workstation management. Upon successful completion of a process, the workstation could select the next job to be produced to minimize the overall tardiness of all jobs. The authors described successful learning for both cases with one and three workstations. Additionally, the approach demonstrated basic generalization capabilities to previously unseen scenarios.

In 2008, the next evolution of value function approximation, now featuring multiple agents learning simultaneously, was presented. The new architecture was termed Fitted Q Iteration with NNs and Optimistic Assumption featuring various tweaks to increase data efficiency and inter-agent coordination to enhance learning. Additionally, the problem size had increased significantly, now featuring up to 15 workstations and 20 jobs. Gabel and Riedmiller (2007) showed successful learning, promising results compared to benchmark problems and stated adequate generalization to unseen scenarios. The approach is again characterized as decentralized due to the multi-agent characteristic and addressed the sub-problem of workstation management.

Waschneck et al. (2018a, 2018b) applied a multi-agent DQN architecture to the problem setting of the semiconductor industry. The theoretical foundation for their work was based on the publications of the DQN architecture by the Google DeepMind team, where Riedmiller is listed as a co-author in the initial publications (Mnih et al. 2015; Silver et al. 2016). Waschneck et al. (2018a, 2018b) adapted the DQN method to the semiconductor manufacturing industry. They followed the concept of the multi-agent approach and assigned individual agents to a respective workstation to handle dispatching actions. They concluded successful learning of the agents and satisfying results compared to benchmark dispatching heuristics. However, direct comparison and adaption to our work are not straightforward because of the specific problem setting in the semiconductor industry. Though, the overall results and complexity of the problem hint towards feasible implementation in MPC as well. Altogether, the presented approach is characterized as decentralized and addressed the sub-problems of workstation and deviation management.

In contrast to Waschneck et al. (2018a, 2018b), Altenmüller et al. (2020) implemented the DQN architecture as a centralized instance within the semiconductor industry. The problem size consisted of 10 workstations being of five distinct workstation groups and two product types. The agent addressed the sub-problems of workstation and deviation management. A discrete-event simulation handled the job release by feeding a new job into the system every 70 seconds, whereas the particular job type was selected randomly. The performance of the algorithm beat heuristic rules like FIFO. Within the article, Altenmüller et al. (2020) gave detailed insights into the state and action space as well as reward function modeling. They specified the reward to be a critical part of successful learning behavior and included further optimization of it as well as the state space in the outlook. Additionally, Altenmüller et al. (2020) pointed out that policy-based methods depict a viable alternative to value-based methods as they proved to be robust to changing problem settings.

Qu et al. (2016) utilized Q-Learning with function approximation to solve the scheduling task in a multi-skill production scenario. The problem size consisted of six workstations being grouped into three distinct types. The factory simulation displayed a sequential setup of the respective workstation groups, where the output of one group served as input for the next one. This sequential process order was fixed. Each job required processing at one workstation of each group. The RL agents acted in a decentralized manner and addressed the sub-problems of workstation and job routing management. Jobs were stochastically introduced into the factory simulation. A conclusion about the performance is not feasible, as Qu et al. (2016) only compared the performance of the algorithm to parameter variations but not to general benchmarks.

Policy gradient DRL methods

Table 1 Overview of RL methods within literature review and their categorization

Wang and Dietterich (2003) presented an improvement of the REINFORCE algorithm termed model-based policy gradient RL. By minimizing the variance of Monte Carlo exploration of the environment, they reduced the number of required training samples. This lead to faster learning and higher data efficiency. Applied to the NASA space shuttle payload processing problem, they demonstrated successful learning paired with better performance in comparison to their previous developments. The NASA space shuttle payload processing problem is highly complex, featuring various constraints of resources and a sequence of between 40 and more than 100 actions until termination (Zhang and Dietterich 1995). Generally, the presented approach is categorized as centralized and addressed the sub-problems of workstation and job routing management.

Kuhnle et al. (2019a, 2019b) utilized a Trust Region Policy Optimization (TRPO) architecture for their production scenario in the semiconductor industry. The problem focus lay on minimizing the lead time of a predefined number of product batches in the production system. The problem size featured eight workstations, three sources for order entries, and one AGV. The RL agent was centralized and focused on the sub-problems of job release, workstation, vehicle, and deviation management. Kuhnle et al. detailed that the implementation outperformed existing benchmark heuristics. In a succeeding work from Kuhnle et al. (2021), they focused on state, action, and reward designs in RL production control and concluded their importance for successful learning. Even if the semiconductor example is not directly transferable to our work, inspiration about the state and action representation, as well as the reward function, and other setup parameters can be generated, especially from their 2021 publication.

Another approach combined robust optimization models with RL presented by Echsler Minguillon and Lanza (2019). The robust optimization model was the centralized unit computing a robust global production schedule that aimed to be very close to the optimum. The RL implementation served as a rescheduling unit to the production plan once disturbances such as workstation breakdowns occured. This setup aimed at incorporating the advantages of both approaches to increase optimality, robustness, and online reaction to disturbances. As an RL architecture, a distributed policy search RL approach based on the work of Gabel and Riedmiller (2012) was utilized. The implementation is categorized as decentralized with individual station rescheduling agents. The approach addressed the sub-problems of workstation, job routing, and deviation management.

Finally, May et al. (2021) proposed an adaptable and scalable decentralized DRL architecture for a matrix-structured job-shop problem introducing three agent types: Part Agents, Station Agents, and Transport Agents. The Part Agents bid in auctions of the Station and Transport Agents to be routed through the system, where each agent wanted to generate maximum profit for itself. The decisions for bids could either be made with priority rules or with decisions by RL agents utilizing the PPO algorithm. Also, stations’ decisions could be supported by RL agents. The authors mentioned the approach’s generalizability and concluded that decentralized DRL algorithms were able to outperform traditional approaches in certain production settings. Therefore, May et al. (2021) proposed a hybrid structure consisting of priority rules and some learning components. The paper addressed job routing, workstation, and vehicle management and is categorized as decentralized comprising several agents.

Summary and deductions for this article

Table 1 summarizes the related work for both tabular and DRL methods. DRL is split up into value-based and policy gradient methods. Most publications have shown promising results in comparison to benchmarks, mostly for small-sized problems. None of the presented research focused on all the five sub-problems of MPC, though. The publications primarily used discrete-event simulators like Tecnomatix Plant Simulation to model the agent’s environment.

As tabular RL methods are not as scalable as DRL methods, because they are limited by the size of the used tables growing exponentially with problem size, this article focuses on DRL. Many of the reviewed DRL methods focused on semiconductor industry problems, for instance, the works of Waschneck et al. (2018a, 2018b), Kuhnle et al. (2019a, 2019b, 2021), or Altenmüller et al. (2020) which are all closely related and promising. As the semiconductor problem strongly focuses on dispatching problems, the presented solutions cannot be directly used for MPC. But especially Kuhnle et al. solved a wide variety of MPC’s sub-problems and offered a detailed documentation of state, action, and reward designs in RL production control being helpful for designing DRL-controlled MPC.

In DRL-controlled production systems, value-based and policy gradient methods both demonstrated their applicability. Especially, DQN and PPO were highlighted as powerful and generalizable methods, which aligns well with MPC’s goals. Furthermore, PPO is known as an easy-to-implement method that solves a variety of complex problem settings in a reliably stable way (Schulman et al. 2017). Considering the successes of May et al. (2021) with PPO and Altenmüller et al. (2020)’s outlook to PPO as a viable alternative to DQN, we decided to start our work on MPC with a centralized policy-gradient PPO implementation.

Applying PPO and utilizing the findings for state, action, and reward designs, the article’s implementation of MPC is focused on the sub-problems of workstation, job release, and vehicle management, especially because they are the core functions of MPC. This leads to the following additional assumptions, complementing the problem description:

• No job routing management: Order and operation flexibility of Jobs J is not considered.

• No deviation management: Resource availabilities are set to $100\%$ for this article’s implementation.

The next section explains the basics of PPO as a policy gradient method and concludes with the respective pseudocode.

Deep reinforcement learning with policy gradient methods: proximal policy optimization

Policy gradient methods directly learn a parameterized policy $\pi$ without the necessity for an intermediate step learning an action-value function to deduce the optimal policy. Instead of lookup tables, they use function approximation with NNs to learn and execute respective policies. The theoretical basis regarding concepts and equations builds upon Sutton and Barto (2018), Morales (2020), Schulman et al. (2017), and Williams (1992).

Policy gradient methods aim at maximizing the performance of the parameterized policy $\pi$. The iterative update step on the performance measure $J(\theta )$ is performed through gradient ascent, as shown in Eq. (7):

$$\begin{aligned}&\theta ' = \theta + \alpha \widehat{\nabla J(\theta )}, \end{aligned}$$

(7)

where $\theta$ is the policy’s parameter vector, $\alpha$ the learning rate, and $\widehat{\nabla J(\theta )}$ an estimate that approximates the gradient of the performance measure $J(\theta )$. The notation of the policy parameter vector $\theta$ is equivalent to the notation of the weights of a NN, but is more commonly used with policy gradient methods.

The agent’s learning mechanism is to adjust the probabilities of taking a specific action, in order to increase the overall reward received in one episode. The event sequence per episode is described as a trajectory $\tau$. The challenge remains on how to adapt the weights $\theta$, in order to increase the likelihood of a trajectory $\tau$ that leads to an optimal return $G_{\tau }$.

Before we get to the PPO policy update step, the REINFORCE algorithm sets the baseline. It was first introduced by Williams (1992). REINFORCE estimates the gradient of $J(\theta )$ by utilizing one trajectory $\tau$ described in the REINFORCE update in Eq. (8).

$$\begin{aligned}&\theta ' = \theta + \alpha \sum _t G_{\tau } \frac{\nabla \pi (A_t \mid S_t, \theta )}{\pi (A_t \mid S_t, \theta )} \end{aligned}$$

(8)

The gradient of $J(\theta )$ is estimated by a sum over all visited state-action pairs in the trajectory $\tau$. For each state-action pair, the gradient of its probability over the actual probability is multiplied by the overall return $G_{\tau }$ of $\tau$. The gradient describes the direction within the parameter space that in- or decreases the probability of performing an action $A_t$ for future visits of state $S_t$. Actions that have a low probability of being taken will be adapted faster than actions with a high probability.

Building on top of that, PPO was developed by Schulman et al. (2017). Mainly, the PPO version that we implement addresses three weak spots of REINFORCE and solves them:

• 1. REINFORCE utilizes one full trajectory together with the collected return to update the NN weights $\theta$. There is no clear credit assignment. It is not able to distinguish which specific actions within a trajectory have a high or low impact on the return.

• 2. REINFORCE is subjected to noisy input as it performs the update only on a single trajectory. One trajectory alone might not be representative of the current policy though, and thus be misguiding for the gradient ascent update step.

• 3. REINFORCE lacks in data efficiency as each trajectory is utilized only once for updating the network’s parameters and is then discarded.

Firstly, addressing the credit assignment problem, PPO introduces the concept of future rewards. Instead of using the trajectory’s complete return $G_{\tau }$ for the update step, only the rewards received after the respective action at timestep t are considered with a discount factor $0 \le \gamma \le 1$. Equation (9) illustrates this concept for a trajectory of length T.

$$\begin{aligned}&R_{t}^{future} = R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + \ldots = \sum _{k=0}^{T-t} \gamma ^k R_{t+k+1} \end{aligned}$$

(9)

Secondly, the noisy input problem is addressed equivalently to momentum-based learning for NNs, where instead of entirely relying on the current direction of the gradient, the average of the past n gradient directions is included in the update step. Similarly, instead of completely trusting a single trajectory, PPO collects several trajectories and updates the policy parameters in the direction of the gradient averaged over all trajectories. Additionally, noise is reduced by normalizing the collected rewards.

Thirdly, PPO aims at increasing data efficiency by performing multiple gradient update steps based on a set of trajectories. This is essentially the core feature of the PPO algorithm and distinguishes it from other algorithms such as TRPO (Schulman et al. 2015) and Advantage Actor-Critic (A2C) (Morales 2020). Schulman et al. (2017) utilize the mathematical concept of importance sampling to solve this issue by introducing a re-weighting factor $\frac{P(\tau ;\theta ')}{P(\tau ;\theta )}$ to the gradient of the performance measure $\nabla J(\theta )$ in Eq. (8) leading to Eq. (10):

$$\begin{aligned}&\nabla J(\theta ) = \frac{P(\tau ;\theta ')}{P(\tau ;\theta )}*\sum _t R_{t}^{future}\frac{\nabla \pi (A_t \mid S_t, \theta ')}{\pi (A_t \mid S_t, \theta ')}, \end{aligned}$$

(10)

where $P(\tau ;\theta )$ describes the probability of a trajectory $\tau$ occurring under the old policy parameters $\theta$ and $P(\tau ;\theta ')$ the probability of the same trajectory occurring under the new policy parameters $\theta '$. The re-weighting factor describes how over- or under-represented the respective trajectory is according to the new policy.

The following equation shows the resulting gradient estimation after some reworking of Eq. (10) and under the assumption that the new policy with $\theta '$ is close to the old policy with $\theta$:

$$\begin{aligned}&\nabla L_{sur}(\theta ', \theta ) = \sum _t R_{t}^{future}\frac{\nabla \pi (A_t \mid S_t, \theta ')}{\pi (A_t \mid S_t, \theta )}, \end{aligned}$$

(11)

where $L_{sur}$ denotes the surrogate objective. The surrogate replaces the performance measure J in the case of performing multiple update steps, but essentially features the same objective of being maximized. The gradients in Eqs. (11) and (8) look quite similar, with the critical difference that Eq. (11) calculates the gradient with respect to the new policy.

Updating the policy multiple times based on an initial trajectory might lead to a significant divergence of the estimated and actual performance. This problem is characterized as the reward cliff. At a reward cliff, the surrogate function suggests the performance will increase in the proposed direction. In contrast, the actual performance drops drastically, which is pictured as a cliff. PPO introduces the clipped surrogate function to inhibit the reward cliff scenario from occurring and ensuring the old and new policy to be sufficiently similar. The clipped surrogate function $L_{sur}^{clip}(\theta ', \theta )$ is mathematically defined as follows:

$$\begin{aligned} \begin{aligned}&L_{sur}^{clip}(\theta ', \theta ) = \sum _t min\{r_t(\theta )R_{t}^{future}, \\&clip(r_t(\theta ), 1- \epsilon , 1+\epsilon )R_{t}^{future}\}, \end{aligned} \end{aligned}$$

(12)

where $r_t(\theta )= \frac{\pi (A_t \mid S_t, \theta ')}{\pi (A_t \mid S_t, \theta )}$. The clipping parameter $\epsilon$ is utilized as the clip boundary. Essentially, $r_t(\theta )$ describes the probability ratio of the old and new policy, and $\epsilon$ defines the amount in which both are allowed to differ. This clipping minimizes the risk of encountering a reward cliff by ensuring similarity. Additionally, clipping the probability ratio inhibits potentially large step sizes caused by different policies. Furthermore, by focusing on the minimum of unclipped and clipped estimation, the surrogate function ignores highly optimistic policy improvements but considers pessimistic adjustments (Morales 2020; Schulman et al. 2017).

Finally, the clipped surrogate function is utilized to perform gradient ascent in combination with Eq. (7) to adjust the policy parameters in order to increase the performance, summarized in Eq. (13):

$$\begin{aligned}&\theta ' = \theta + \alpha \nabla _{\theta '} L_{sur}^{clip}(\theta ', \theta ) \end{aligned}$$

(13)

This section concludes by summarizing PPO with its pseudocode in Algorithm 1. The PPO algorithm starts by initializing the essential hyperparameters. The number of epochs $n_{epochs}$ defines, how many update loops the algorithm performs, based on a collected set of $n_{env}$ trajectories. R is the roll-out length, which defines the length of each collected trajectory. The parameter $\epsilon$ defines the clipping parameter necessary for the calculation of the clipped surrogate function, and $\alpha$ is the step size. Additionally, the policy within the NN as well as the parallel environments have to be initialized. The learning process starts by collecting $n_{env}$ trajectories either utilizing parallel environments or by re-running a single environment $n_{env}$ times where each trajectory is of length R. In contrast to the REINFORCE algorithm, the policy update step based on a set of trajectories is now performed $n_{epochs}$ times as described above. According to Schulman et al. (2017), PPO was applied successfully to episodic, but especially to continuous control tasks fitting our problem setting.

Implementation: PPO agent and environment

This section sets the context for the agent to learn, describing its environment interaction, the environment itself, the action, state, and reward design, and its learning setup.

Interaction cycle

Figure 2 displays the interaction cycle between the agent and the environment. The environment represents the modular production system that the agent learns to control. The DRL agent is implemented in Python, whereas the environment is programmed in Tecnomatix Plant Simulation, a state-of-the-art discrete-event process simulation software, e.g. used by Shiue et al. (2018) and especially used in the automotive industry. In order to handle the large number of messages between agent and environment during learning, a TCP/IP interface was selected.

Fig. 2

Agent-environment interaction cycle, where the environment and the agent communicate via TCP/IP exchanging action, state, and reward information

The cyclic learning process always begins by starting the simulation on the environment side. Once the simulation is started or restarted, it performs the respective simulation events until an action request point is encountered. The simulation raises an action request, if an AGV becomes available again and has no subsequent action to perform. The simulation is lacking information on how to proceed and thus consults the RL agent. Firstly, the simulation and the respective internal timer is paused. Secondly, the required data for the representation of the current state $S_{t+1}$ is collected and packaged into a message. Lastly, the environment sends the state information together with the reward $R_{t+1}$ for the last action to the RL agent through the TCP/IP socket. Once the agent receives the message containing the state information and reward, it unbundles the message into the state information and reward $R_t$ in order to update its internal knowledge represented by the NN. Finally, the RL agent selects a next action $A_t$ based on the current state $S_t$ and sends the information to the environment through the same TCP/IP Socket and waits until another action request is received. With the received action, the environment continues its simulation until another action request is raised.

Fig. 3

Environment for the agent, implemented as discrete-event simulation with 6 red-dotted action-request triggers, machines comprising an Inbound-Buffer (IB), a processing position, an Outbound-Buffer (OB), as well as a parking area, a transport network for the movement of automated guided vehicles (AGV), a source for products’ releases, and a sink for finishing products

Environment description

In order to prove DRL’s applicability to MPC solving the derived sub-problems of job release, workstation, and vehicle management, we implemented the environment given in Fig. 3. Each workstation $M_k$ comprises an IB and an OB with equal capacity $n_{buf}$ utilizing FIFO as detailed in the figure. Products are released into the production system by an AGV’s action to go to the production system’s source, choosing a specific product type, and loading the product together with a WPC. For this article, the number of AGVs $n_{V}$ is set to one: $V := \{V_1\}$ and the number of machines $n_{M}$ is set to two: $M := \{M_1, M_2\}$.

The red dots in Fig. 3 mark the discrete events, where the environment sends an action request to the DRL agent following the interaction scheme in Fig. 2. There are two different types of action request events: Firstly, each time an AGV becomes available because of a product delivery to a machine’s IB or the sink, the environment initiates an action request. And secondly, each time an AGV picks up a product with its WPC at the source or one of the machines’ OBs, an action is requested to decide on the next machine to go to for the specific product. If the chosen action is going from one machine’s IB position to the same machine’s OB position, the AGV can utilize a space for parking to be able to wait for a product to be finished at the station.

For any action, the AGV is traveling between two action request points. Table 2 depicts the respective static transport times in the given environment for all possible actions. The table is symmetric except for two actions: the action within a machine going from the IB to the OB utilizing the parking (1s), compared to the reverse action going from OB to IB, where the transport network has to be used (15s).

Action design

In case of an action request from the environment, the agent can select an action out of the set of all actions (14). These actions also represent the six red-dotted action request positions in Fig. 3. The subscripts of the actions denote the AGV’s destinations, e.g. to the OB-Buffer of machine $M_1$ for action $A_{M_{1OB}}$. For the general understanding, $A_{all}$ can be split into two different types of actions: pickup-actions $A_{pick}$ (see Eq. (15)) from the source or the OB of a machine, where a product is loaded to the AGV, or dropdown-actions $A_{drop}$ (see Eq. (16)), where a loaded product is dropped off at the IB of a machine or at the production system’s sink.

$$\begin{aligned}&A_{all} := \{A_{source}, A_{M_{1IB}}, A_{M_{1OB}}, A_{M_{2IB}}, A_{M_{2OB}}, A_{sink}\}\end{aligned}$$

(14)

$$\begin{aligned}&A_{pick}:= \{A_{source}, A_{M_{1OB}}, A_{M_{2OB}}\}, \;\;A_{pick} \subseteq A \end{aligned}$$

(15)

$$\begin{aligned}&A_{drop} := \{A_{M_{1IB}}, A_{M_{2IB}}, A_{sink}\}, \;\;A_{drop} \subseteq A \end{aligned}$$

(16)

At each point in time t of the interaction cycle in Fig. 2, there exists a set of valid actions $A_{t, val} \subseteq A$ with $A_{t, val} \ne \emptyset$, known only by the environment. For instance, if a product is loaded on an AGV, another pickup-action is not valid, just a dropdown-action is meaningful. This definition orients itself on May et al. (2021) and Kuhnle et al. (2021). A dropdown action is also not valid if a machine and its respective buffers are already full or have reached a fixed capacity limit of $n_{dl}$ being set as a parameter. Therefore, pickup actions leading to one of those invalid dropdown actions are invalid, too. This should avoid deadlocks in the production system.

How these actions solve the problem formulation: In order to solve the control task for the introduced factory setting, the RL agent’s actions are designed to directly manage the AGV fleet. Thereby, it directly addresses the sub-problem of vehicle management. Additionally, this setup indirectly deals with the problems of job release and workstation management. Job release management is enabled through the source design in the environment described in Fig. 3. If a product is available at the source, the agent can decide if it wants to go there and pick the product up, by choosing action $A_{Source}$. Therefore, job release management is entirely handled by the agent. Workstation management is handled quite similarly by the agent. As the agent has access to the information of workstation occupancy, it can reasonably assign transportation tasks to indirectly control the workstations’ efficiency, occupancy, and product sequence by bringing the products to the workstations.

In future iterations, we aim to implement job routing and deviation management in a similar way.

Table 2 Transport times in given modular production system

State design

Taking into account the learnings from May et al. (2021) and especially Kuhnle et al. (2021), we developed a state representation for the given environment in Fig. 3. The state comprises all information needed for learning in this scenario. It is defined by the state of the source, the occupation of the machines, the occupation and position of the AGV, and the valid actions at the time of an action request. Where applicable, one-hot-encoding is applied to the state variables. This has shown reliable success to improve learning, e.g. in Waschneck et al. (2018a)’s work.

The source state ss determines whether a product and how many products could be picked up according to the currently available number of WPCs $N_{source,occ}$ at the production source. This defines the validity and importance of action $A_{source}$:

$$\begin{aligned} ss := {\left\{ \begin{array}{ll}N_{source,occ} &{}\text {if }\; N_{source,occ} \ge 1 \\ 0 &{}\text {else} \end{array}\right. } \end{aligned}$$

(17)

For each machine $M_k$ in the environment, there exist three bits in the state representation giving the agent the needed information: one for the occupation of its IB $ib_k$ (Eq. (18)), one for the machine workload itself, where the product is processed $p_k$ (Eq. (19)), and one for the machine’s OB’s occupation $ob_k$ (Eq. (20)). The value of the IB’s and OB’s state represents the current number of products in the respective buffers $N_{k,IB,occ} \le n_{buf}$ and $N_{k,OB,occ} \le n_{buf}$. And, $N_{k,proc,occ} \in [0,1]$ represents the occupation of the machine itself, being either occupied (1) or not (0).

$$\begin{aligned} ib_k&:= {\left\{ \begin{array}{ll}N_{k,IB,occ} &{}\text {if }\;N_{k,IB,occ} > 0, \; N_{k,IB,occ} \le n_{buf} \\ 0 &{}\text {else}\end{array}\right. }\end{aligned}$$

(18)

$$\begin{aligned} p_k&:= {\left\{ \begin{array}{ll}1 &{}\;\;\;\;\;\;\;\;\;\;\;\;\;\text {if }\;N_{k,proc,occ} == 1\\ 0 &{}\;\;\;\;\;\;\;\;\;\;\;\;\;\text {else}\end{array}\right. }\end{aligned}$$

(19)

$$\begin{aligned} ob_k&:= {\left\{ \begin{array}{ll}N_{k,OB,occ} &{}\text {if }\;N_{k,OB,occ} > 0, \; N_{k,OB,occ} \le n_{buf} \\ 0 &{}\text {else}\end{array}\right. } \end{aligned}$$

(20)

Equation (21) defines the vehicle occupation vo, meaning if the AGV is occupied ($N_{AGV,occ} = 1$) or not ($N_{AGV,occ} = 0$).

$$\begin{aligned} vo := {\left\{ \begin{array}{ll}1 &{}\text {if }\;N_{AGV,occ} == 1\\ 0 &{}\text {else}\end{array}\right. } \end{aligned}$$

(21)

Additionally, the agent has to know, where the AGV is located for an action request. These locations are defined by the six red-dotted action request positions in Fig. 3, denoted by vehicle positions $vp_{y}, y \in [1,2,3,4,5,6]$. If the AGV is requesting an action from position y, the respective bit in the state representation is set to 1, all others are set to 0.

$$\begin{aligned} vp_{y} := {\left\{ \begin{array}{ll}1 &{}\text {if AGV at location y}\\ 0 &{}\text {else}\end{array}\right. } \end{aligned}$$

(22)

Lastly, the agent learns faster having information about the valid and meaningful actions at time t. As there are six available actions in $A_{all}$, the state comprises six bits for their validity $va_{z}, z \in [1,2,3,4,5,6]$, being set to 1, if valid and 0, if invalid. This enables distinguishing between valid and invalid actions. An action is not valid in the following cases: if a product is transported to the wrong destination, if the destination is a machine that is fully occupied, if a dropdown is planned but no product is loaded, if a pickup is planned but no product is to be picked up, and if a pickup action is selected even though the AGV is already occupied.

$$\begin{aligned} va_{z} := {\left\{ \begin{array}{ll}1 &{}\text {if }\;A_{z} \in A_{val}\\ 0 &{}\text {else}\end{array}\right. } \end{aligned}$$

(23)

Summarizing the state design, Fig. 4 describes one sample state $S_t$, where the production setting consists of two machines $M_1$ and $M_2$ and one AGV $V_1$ leading to a state size of 20 digits, where each one is fed into the respective neuron in the input layer of the NN. The source state ss is set to 4 meaning that there are four WPCs with products at the source that are ready to be picked up by the AGV. Then, three bits each describe the occupancy of the machines $M_1$ and $M_2$, separated in $ib_k$, $p_k$, and $ob_k$. For instance, at $M_1$ no product is in the IB-Buffer, one product is being processed, and the OB-Buffer is occupied by two products. The AGV $V_1$ currently carries a product ($vo=1$) that has been seemingly picked up at the source, as the first AGV location bit $vp_1$ is set to 1 representing the source location. The valid action bits highlight that currently, just one action $va_2=1$ would be valid, the dropdown action to machine $M_1$ being the first operation of the product to be carried out.

Fig. 4

Exemplary state in an environment with two machines $M_1$ and $M_2$ and one AGV $V_1$

Reward design

The section on PPO presents the learning objective of the RL agent to maximize the overall reward. It is defined by optimizing the policy to maximize the equivalent state value function of the starting state. This optimization objective is framed as a maximization task, by performing gradient ascent.

For the agent’s goal to maximize the throughput of modular production systems, the environment calculates dense rewards according to Eq. (24), where, as stated by Kuhnle et al. (2021), the term “dense reward” applies to a reward given for each concluded action. Maximizing throughput, the collected reward in one trajectory has to encourage finishing as many products as possible in the shortest possible amount of time. Therefore, for each action, the environment returns the passed time $-t_{T, S_{t-1} \rightarrow S_t}$ as a negative reward, additionally gives a positive bonus reward $R_{bonus}$ in case a product is finished with the respective action, or punishes the agent with a negative reward $R_{punish}$ for invalid actions.

$$\begin{aligned} R_{t}&:= {\left\{ \begin{array}{ll} -t_{T, S_{t-1} \rightarrow S_t} + R_{bonus} &{}\text {if } \;A_{t-1} == A_{sink} \in A_{t-1,val} \\ R_{punish} &{}\text {if } A_{t-1} \notin A_{t-1,val}\\ -t_{T, S_{t-1} \rightarrow S_t} &{}\text {else}\end{array}\right. } \end{aligned}$$

(24)

Concerning the throughput maximization, this setting has shown success, as it is demonstrated in the “Experimental results” section.

PPO learning setup for continuous control task

Utilizing the previous defined action, state, and reward design, the PPO agent follows the depictions in the PPO section, essentially described by algorithm 1. The implementation is built upon a codebase from a DRL Udacity course³ and utilizes the PyTorch library⁴. The agent’s task is modeled as a continuous task, where an episode or a trajectory consists of a certain number of R actions. After R actions, the $n_{env}$ collected trajectories are used to update the NN weights. After that, each environment continues from the last state of the previous trajectory. The applied reward function is a measure for throughput that the agent aims to optimize.

The learning objective is set to be relative. The increased system complexity makes it infeasible to sufficiently estimate or empirically deduce a reasonable absolute target value before the start of the learning process. Thus, a relative learning objective is more flexible and preferable for this case. The relative performance criterion is met if 10 consecutive trajectories yield a reward that is within $0.1\%$ deviation concerning the previous 100 trajectories. Essentially, this performance criterion measures the stability of the NN weights. In that case, the applied relative learning objective has performed satisfactorily and has reliably signalled convergence. Alternatively, the learning process stops reaching a maximum number of episodes $n_{episodes}$.

The underlying NN architecture for approximating the optimal policy has a fully connected architecture consisting of 20 input neurons representing the state bits, $h1_{size}=80$ and $h2_{size}=40$ neurons in the first and second hidden layers, and six output neurons in the final layer representing the six possible actions in $A_{all}$. The fully connected hidden layers utilize a ReLU activation function, whereas a Softmax activation layer feeds the output of the NN into the six output neurons so that a probability distribution describes the likelihood of each action being the optimal choice regarding the overall return. In turn, the agent samples an action out of the probability distribution of actions upon an action request. Regarding the update mechanism, the Adam optimizer is selected. It is characterized by its momentum-based learning approach as well as other performance-enhancing characteristics and is thus, commonly selected within Deep Learning tasks. This setup has performed satisfactorily on the targeted problem size.

Lastly, the set of valid actions $A_{val, t}$ is known by the environment for each time step t. If the agent selects a non-valid action, though, the environment does not conduct this action and gives the punish reward $R_{punish, t}$. Therefore, the environment stays in the same state and sends the same action request to the agent again until an action out of the set of valid actions is selected. Essentially, the punish reward ensures that the respective action probability of invalid actions is decreased. Repeating this process many times artificially favors the subset of valid actions. The agent is thus incentivized to explore only the valid actions and eventually to be able to select an action out of this valid subset according to the expected return.

Experimental results

Fig. 5

Learning curves for the default environment, default product, and default PPO agent depending on the number of parallel environments with $n_{env}=2$ a $n_{env}=4$ b and $n_{env}=6$ c where the black curve indicates the mean rewards over all environments and the environment-specific rewards are color-coded, each parameter set was simulated 10 times, reliably converging to the optimum

The PPO algorithm is applied to a rather small problem, based on a case study from the automotive industry, in order to identify first learnings and to guarantee functionality of the developed agent-environment framework. The computations are carried out on an Intel(R) Core i7-7700HQ CPU with 2.8GHz and 16GB RAM.

The default environment is according to the setup in Fig. 3 and consists of $n_M=2$ machines $M_1$ and $M_2$ as well as one AGV $V_1$ doing the transports and conducting the agent’s actions with a vehicle speed of $v_V=2\frac{m}{s}$ that leads to the transport times documented in Table 2. Machines are configured with a buffer size of $n_{buf}=3$ for both IB and OB. Lastly, the available number of WPCs $n_{WPC}$ is set to 10.

The default product consists of $n_O=2$ operations being processed sequentially, first at $M_1$, then at $M_2$, with a processing time of 50s each. There are no alternative process plans ($n_p=1$) and there is only this one product type ($n_{PT}=1$).

The PPO agent used for the experiments is configured as documented in Table 3. This configuration is the result of empirical tests and shows stable and reliable results on a large number of learning runs.

Table 3 PPO default settings

PPO’s learning capabilities for MPC

Figure 5 displays the learning curves for the given environment and PPO default settings, varying the number of used parallel environments from two on the left to six on the right. Because of the random seed settings, all three learning setups are simulated 10 times and lead reliably to an optimal throughput of $72 \frac{1}{hour}$⁵. This learning behavior indicates successful control of the AGV’s behavior to coordinate the modular production system. The more parallel environments are used, the steeper the learning curves get. Further, if some of the environments start more explorative trajectories during the learning process, the other environments keep aiming for convergence and stabilize the learning process. The learning curves hint towards stability by parallelization, whereas the difference in learning stability between two (a) and four (b) environments is more apparent than between four (b) and six (c) environments. These findings confirm PPO’s improvements on noisy input and data efficiency compared to the REINFORCE algorithm mentioned in the section about PPO.

Fig. 6

Learned optimal strategy for the default settings consisting of six actions to keep the production system in an equilibrium for optimal throughput: $A_{source} \rightarrow A_{M_{1IB}} \rightarrow A_{M_{1OB}} \rightarrow A_{M_{2IB}} \rightarrow A_{M_{2OB}} \rightarrow A_{sink}$

Learned strategy: The learned optimal strategy⁶ achieving the respective throughput optimum is shown in Fig. 6. This strategy shows how the agent learns to reach a production equilibrium consisting of two products at machine $M_1$ and two products at machine $M_2$ and the AGV being positioned at the sink currently finishing a product. From this equilibrium state on, the agent always chooses a sequence of six actions marked red and enumerated in the figure. With this sequence, the agent iteratively gets back to the showed equilibrium state and manages to utilize the two machines continuously without breaks and therefore achieves the maximum throughput. The sequence of optimal actions is defined by the following equation and comprises all available actions $A_{all}$ getting them into the optimal order:

$$\begin{aligned} A_{source} \rightarrow A_{M_{1IB}} \rightarrow A_{M_{1OB}} \rightarrow A_{M_{2IB}} \rightarrow A_{M_{2OB}} \rightarrow A_{sink} \end{aligned}$$

(25)

Thus, the agent picks up a new product from the source, brings it to $M_1$, picks up a finished product at $M_1$, and brings it to $M_2$, does another pickup there, and finally brings the finished product to the sink, being back in the root state of the sequence.

On rare occasions, if the learning process is too long, the agent learns this optimal sequence, but seems to focus too much on repeating the sequence of these six actions in order to stay in the equilibrium. This focus in the agent’s policy leads to forgetting the production’s ramp-up process from an initial configuration, where no products are in the system yet. Essentially, the agent forgets knowledge about how to get into the equilibrium. Thus, when resetting the environment and applying the learned policy for evaluation, the agent converges to a suboptimal throughput. In the future, a combination of two agents could improve the system, one managing the ramp-up actions and the other one managing the equilibrium actions. Alternatively, one could think about resetting the environment every once in a while during the learning process to deepen the agent’s knowledge about the optimal ramp-up process. That leads to a hybrid learning setting comprising both episodic and continuous aspects.

In order to get the agent to learn the optimal control, the state as well as the reward design play a key role, which confirms the findings of Kuhnle et al. (2021).

Table 4 Five parameter settings for generalization experiments

State learnings: As it turned out, the state design had more impact on the learning behaviour than did the hyperparameter values throughout the experiments. On the one side, this confirms PPO’s robustness. On the other side, it emphasizes the importance of a well-designed state. Two main learnings can be emphasized here: Firstly, the information depicted within the state should be reduced to the minimum required for successful learning behavior. This is favorable in terms of general data efficiency, because the state is negligibly small. Furthermore, it is rather difficult to debug a DRL method as the NN mostly presents a blackbox, and clear deduction of learning inhibiting factors is not always possible. Thus, minimizing the information within the state helps to indicate these inhibiting factors as well as identifying the central and essential state variables that are relevant for learning and describing the system. Secondly, in order to achieve a state with the minimum required information for successful learning behaviour, an iterative state development is recommendable. It enables adding the necessary information step by step and prevents the designer from overinforming the agent. Additionally, after some iterations, the developer gets the necessary intuition about which information the agent requires, how it perceives the environment, and how it learns. Next to having knowledge about the source’s, the stations’, and the AGV’s occupation as well as the AGV’s location, the binary encoded information about valid actions (Eq. (23)) is to be highlighted here. It extensively accelerates the learning process by offering the agent available domain knowledge about currently valid actions for the requesting AGV.

Reward learnings: In order to enable this accelerated learning process with the state bits about valid actions, the punish reward $R_{punish}$ plays a crucial role. The punish reward’s task is to negatively accentuate invalid actions with the aim to guide the agent towards the valid actions flagged by a one in the state. Therefore, it must be high enough to clearly make the agent distinguish between valid and invalid actions. But being too high, $-1000$ for instance instead of $-100$, it also tends to distort the learning process, making it a performance-relevant parameter to be tuned by the designer. Besides, the main reward design question was how to optimize throughput. This was successfully achieved by combining the idea of passed time for an action and additionally rewarding actions that complete products. Accordingly, the agent maximizes throughput by being encouraged to finish as many products as possible in the shortest possible amount of time. Thus, the agent optimizes throughput indirectly. A direct throughput optimization will be investigated in the future. Conclusively, the dense reward design from Eq. (24) trains the agent how to act validly first, and in a second phase how to act optimally.

Overall learnings: Concluding this section, the PPO agent manages to coordinate the production system optimally and solves the problem of MPC reliably. Using parallel environments and utilizing collected trajectories several times for updating the policy offers a stable and powerful learning environment for the given example. The goal is to show this for higher complexity problems in the future, too. But first, this article’s next subsection investigates PPO’s generalization capabilities for the given MPC problem.

PPO’s generalization capabilities for MPC

In order to show generalization for the given default environment, product, and agent, we vary parameters following the five parameter sets in Table 4, where parameter set 1 represents all the default settings. The table also documents the achieved production throughputs.

Parameter set 1: This experiment comprises the default settings for product, agent, and environment from above and leads to the displayed optimal strategy in Fig. 6, and the respective optimal throughput of 72 products per hour (PPH). It sets the baseline for the following experiments.

Parameter set 2: For the optimal strategy in Fig. 6, only five of ten available WPCs are utilized. Therefore, parameter set 2 should also be able to learn this strategy having just these five WPCs available ($n_{WPC}=5$). Apparently, the agent finds a strategy leading to 70 PPH, slightly below the optimum. This performance decline of $2.8\%$ is probably due to the fact that the agent’s playground of only five instead of ten available WPCs decreases. Possibly, the agent’s motivation to go to the source and pick the last available WPC before finishing a product is not high enough. Playing with the bonus reward as well as with the number of episodes does not compensate the throughput decrease.

Parameter set 3: Increasing the number of $n_O$ operations to be done for the product to four with a machine sequence of $M_1 \rightarrow M_2 \rightarrow M_1 \rightarrow M_2$ and a processing time of 50s each, leads to a throughput decrease of $50\%$, because each product doubles the processing time at each of the machines. This leads to an optimal PPH of 36 in this setting, which is also reached by the agent. Thus, the agent successfully learns to optimally conduct the four operations and to finally bring the finished products to the production system’s sink.

Parameter set 4: Varying the processing time of the product’s second operation to 100s instead of 50s leads to a learned throughput of 36 PPH, being also the theoretical optimum, because of the production’s new bottleneck with the operation at machine $M_2$ leading to $\frac{3600\frac{s}{h}}{100 s}=36\frac{1}{hour}$. In its strategy, the agent utilizes the IB of machine $M_2$ and the OB of machine $M_1$ extensively, continuously providing products for being processed at the $M_2$-bottleneck. Figure 7 documents this behavior with the learned optimal sequence of again all six available actions $A_{all}$, but differently organized than in Fig. 6 and comprising a different equilibrium state being maintained by the action sequence:

$$\begin{aligned} A_{M_{1OB}} \rightarrow A_{M_{2IB}} \rightarrow A_{source} \rightarrow A_{M_{1IB}} \rightarrow A_{M_{2OB}} \rightarrow A_{sink} \end{aligned}$$

(26)

Fig. 7

Learned optimal strategy for parameter set 4 consisting of six actions to keep the production system in an equilibrium for optimal throughput: $A_{M_{1OB}} \rightarrow A_{M_{2IB}} \rightarrow A_{source} \rightarrow A_{M_{1IB}} \rightarrow A_{M_{2OB}} \rightarrow A_{sink}$

Parameter set 5: Lastly, a decrease in the buffer capacity from three to $n_{buf}=1$ is tested in comparison to the default parameter set. Based on the findings in the optimal strategy of Fig. 6, we expect that $n_{buf}=1$ should be high enough to reach the optimal throughput. A successful learning performance of the agent confirms this expectation. But, it is to keep in mind that there will be machine breakdowns in future implementations, where buffer capacity can help dealing with these uncertainties.

Generalization yes or no? The five experiment settings indicate good generalization capabilities of the implemented PPO algorithm, learning optimal strategies with a slight performance loss in parameter set 2. The agent is capable of dealing with different numbers of WPCs, higher numbers of operations, varying processing times, and also a smaller buffer capacity. Essentially, the agent learns reliably for all settings how to reach an equilibrium configuration of the production system and how to stay there, utilizing the six available actions in an optimal order. The learned strategies in Figs. 6 and 7 highlight this behaviour and emphasize the agent’s strategy adaptation to varying production settings.

Conclusion and future work

Modular production systems are a new field in the automotive industry. These systems are complex to control and often diverse in their configuration. The powerful and generalizable nature of RL algorithms addresses these challenges.

Based on a literature review on RL in the production control field, this article applies the DRL method PPO to the problem of MPC. The conducted experiments demonstrate the agent’s stable, reliable, and generalizable learning towards the optimal solution utilizing parallel environments. The article’s contributions to the field of MPC closing the introduced research gap unfold in mainly three ways:

• MPC application: To the best of our knowledge, this article constitutes the first DRL application to the concrete problem of MPC in the automotive industry.

• Agent design: Documenting implementation learnings.

  • Two-phase learning: In order to reach throughput-optimal control, the agent needs to successfully coordinate the production’s ramp-up process as well as the settled production equilibrium. The agent’s designer has to ensure that the agent sees both ramp-up and equilibrium states often enough.

  • State design: The state design has shown more impact on successful learning behaviour than tuning the hyperparameters. An iterative state development is recommendable to produce a state design with the minimum required information for successful learning. A minimalistic state improves data efficiency and supports identifying inhibiting factors as well as essential state variables. Adding available domain knowledge like valid action information accelerates the learning process.

  • Reward design: The reward design’s aim is to train the agent first how to act validly and second how to act optimally. Acting validly is achieved by using punish rewards combined with state information about currently valid actions. Acting throughput-optimally is indirectly achieved by negatively rewarding passed time for actions and especially positively rewarding actions leading to product completion.

• RL’s generalizability: Generalization experiments demonstrate that the agent is capable of reliably learning how to reach an equilibrium configuration and keep the production setting in this settled state. As Figs. 6 and 7 highlight, the agent generalizes by adapting its strategy to varying production settings. That meets one of MPC’s main needs.

Conclusively, the article demonstrates DRL’s applicability and its generalization capabilities for MPC, while thoroughly documenting implementation issues. Next steps are to integrate job routing and deviation management. After that, scaling the problem to real-world production cases of about 20 stations and AGVs becomes relevant. We assume that the steep learning curves in Fig. 5 let room for these more complex settings. Finally, lifting policy-gradient to actor-critic PPO is desirable to unleash PPO’s full potential.