Abstract
Modern production systems face enormous challenges due to rising customer requirements resulting in complex production systems. The operational efficiency in the competitive industry is ensured by an adequate production control system that manages all operations in order to optimize key performance indicators. Currently, control systems are mostly based on static and model-based heuristics, requiring significant human domain knowledge and, hence, do not match the dynamic environment of manufacturing companies. Data-driven reinforcement learning (RL) showed compelling results in applications such as board and computer games as well as first production applications. This paper addresses the design of RL to create an adaptive production control system by the real-world example of order dispatching in a complex job shop. As RL algorithms are “black box” approaches, they inherently prohibit a comprehensive understanding. Furthermore, the experience with advanced RL algorithms is still limited to single successful applications, which limits the transferability of results. In this paper, we examine the performance of the state, action, and reward function RL design. When analyzing the results, we identify robust RL designs. This makes RL an advantageous control system for highly dynamic and complex production systems, mainly when domain knowledge is limited.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Manufacturing companies face ever-increasing complexity in their internal operational processes driven by versatile and fast changing market environments (Abele and Reinhart 2011). These external conditions require manufacturing companies to create flexible production and logistics processes in order to remain competitive (Mönch et al. 2013). The usage of data collected along the entire value chain is one promising technological enabler to address these challenges (Henke et al. 2016). Autonomous systems and learning-based algorithms provide tools to exploit and leverage these potentials and, eventually, optimize the operational performance (Monostori et al. 2016). Thereby, the focus of manufacturing is shifting from knowledge-based to data-driven and knowledge-based manufacturing (Tao et al. 2019).
The application of machine learning (ML) gains relevance in research and practice due to the increased computing capacity and availability of information in the production processes (Schuh et al. 2017). Reinforcement learning, in particular, offers the potential to solve complex and dynamic decision-making problems as an alternative to prevailing methods such as heuristics and mathematical optimization by training agents that learn a generalizing strategy (Waschneck et al. 2016; Silver et al. 2017).
However, the degree of freedom when modeling a real-world decision-making problem as RL-problem and applying an RL solution algorithm raises numerous issues (Kuhnle et al. 2019). Questions that need to be clarified in advance concern the type of learning algorithm, the configuration of the actual decision-making agent as well as the way in which information is integrated from the environment so that the agent learns a desired behavior. Furthermore, the trade-off between exploration, i.e., exploring new knowledge, and exploitation, i.e., strengthening existing assumptions, and the design of the reward function are essential features. In general, RL has been applied in recent years to a variety of control tasks, such as playing video and board games (Mnih et al. 2013). However, a methodical approach for modeling RL-agents and their environment is not or only partially known.
The relevant fundamentals and literature are summarized in Sect. 2, and the RL-modeling and design are explained in Sect. 3. The evaluation of the methodical approach and various RL-modeling alternatives is based on a simulation framework, representing a generic job shop manufacturing system. Finally, the real-world example of a semiconductor manufacturer is applied in Sect. 4. Conclusively, this paper contributes to the research of combining digital twins and cyber-physical systems towards the vision of smart manufacturing (Tao et al. 2019; Singh et al. 2019).
Fundamentals and literature review
This section starts with an overview of production planning and control fundamentals. By the example of a semiconductor manufacturing system, the properties of complex manufacturing systems are explained. The following outlines the theoretical background of advanced RL-algorithms. Finally, related research work is summarized in an overview of the state of the art.
Production planning and control
Production planning and control involves the planning, control and administration of all processes necessary for the production of goods (Günther 2005). It plays a central role for any manufacturing company in order to manage the utilization of their production factors in the best way possible, optimizing the operational performance (Schuh 2006). According to Wiendahl (1997), four performance indicators are suitable for evaluating the operational performance: capacity utilization, delivery time, adherence to due dates, and stock levels. These are also called logistical performance measures (Lödding 2016).
Nowadays, manufacturing systems are broadly seen as complex systems due to various unprecedented challenges such as globally spread manufacturing operations (e.g., the number of partners, communication), volatile future development (e.g., dynamic changes), and uncertain influencing factors (e.g., limited information) (ElMaraghy et al. 2012). The semiconductor industry investigated in this paper is, in particular, characterized by a high degree of complexity due to complex manufacturing operations related to the wafer fabrication that strives for ever-miniature structures (Mönch et al. 2013).
A reference model by Bischoff (1999) and Wiendahl (1997) structures the production planning and control activities according to their time horizon. The result of the first planning phase is a production schedule that covers a period from weeks to months. It contains the type, amount, and due date of orders and is based on the available resource capacity, inventory levels, and available demand (forecast) information. The second phase starts when the production orders are released and the production is started. Hence, it mainly focuses on the control of the operations with respect to the schedule determined in the previous phase. The control operations are of particular interest due to their direct effect on the operational performance (Lödding 2016). Moreover, a wide range of activities and real-time decision-making are required in order to react to disturbances such as machine breakdowns or material shortages (Nyhuis 2008).
Simple heuristic approaches such as priority rules are the standard prevailing in practice, particularly in the semiconductor industry (Sarin et al. 2011; Mönch et al. 2013; Waschneck et al. 2016). Their advantage in terms of computational efficiency, simplicity, and real-time ability leads to a broad application. They are, for instance, carried out by the so-called “Real-Time Dispatcher”, which allows easy programming of multi-level priority rules (Mönch et al. 2013; Waschneck et al. 2016). It determines which job is processed or transported next. Widespread examples of priority rules are: First In First Out (FIFO), Earliest Due Date (EDD), Shortest Setup Time (SST), etc. They are listed and described by the following authors Panwalkar and Iskander (1977), Blackstone et al. (1982), Haupt (1989), Mönch et al. (2013) and Klemmt (2012). Significant disadvantages of priority rules are their static nature and the required domain knowledge to implement them in the best way (Stricker et al. 2018).
Order dispatching problem
The production control problem that is considered in this paper is described by Brucker and Knust (2012) as an optimization problem to optimize a set of l performance measures \(K_1, \ldots , K_l\). Thereby, n orders \(O_1, \ldots , O_n\) have to be dispatched to m machines \(M_1, \ldots , M_m\). Each order \(O_j\) consists of \(k_j\) operations \(S_{i,j}\) (\(i=1, \ldots , k_j\)) that have to be executed in a defined sequence \(S_{1,j} \rightarrow S_{2,j} \rightarrow \ldots \rightarrow S_{k_j,j}\). Each operation must be performed on an assigned machine \(\mu _{i,j} \in \{ M_1, \ldots , M_m \}\) with a processing time of \(p_{i,j} > 0\). Two consecutive operations must always be carried out on different machines.
Reinforcement learning
Reinforcement learning is applicable to optimization problems that can be modeled as sequential decision-making processes, i.e., Markov Decision Processes (MDP). Therefore, they are applicable as an adaptive control system in manufacturing setups (Stricker et al. 2018). The following fundamental descriptions of RL are based on the formulations of Sutton and Barto (2018) and we refer to it for further definitions and detailed explanation.
In general, RL does not necessarily require a model of the environment system’s dynamics and, hence, they are called model-free. By interacting with the environment in a closed-loop, an RL-agent learns to optimally solve the underlying MDP (see Fig. 1). Based on the state \(s_t \in S\) (S is the set of all possible states) of the environment observed in time period t, the agent selects an action \(a_t \in A\) (A is the set of all possible actions) according to its strategy \(\pi \). Carrying out this action transforms the environment into a subsequent state \(s_{t+1}\), according to the dynamics of the underlying MDP. The agent then receives a reward \(r_{t+1}\), which is dependent on the observed state \(s_t\), the taken action \(a_t\), and the subsequent state \(s_{t+1}\) of the environment. Through repeated interaction with the environment, the agent’s learning algorithm tries to maximize the discounted sum of rewards, which is called the long-term return \(G_t\), and adapts the strategy \(\pi \) accordingly. A strategy \(\pi *\) that maximizes \(G_t\) is called the optimal strategy. This strategy optimally solves the MDP according to the given reward function \(R(S_t, A_t, S_{t+1})\) which determines the reward \(r_{t+1}\).
Model-free RL algorithms can be divided into value-based and policy-based approaches. In general, both exhibit different characteristics that match specific problem domains. While policy-based approaches like REINFORCE (Williams 1992) can naturally handle continuous state and action spaces and learn stochastic policies (Wang et al. 2016b; Sutton et al. 1999; Kober et al. 2013), they are sample inefficient and show poor robustness (Nachum et al. 2017; Schulman et al. 2017). Basic off-policy value-based approaches like Q-Learning (Mnih et al. 2013; Watkins and Dayan 1992) show better sample efficiency but are often unstable when integrated with function approximators (Kober et al. 2013; Nachum et al. 2017).
In recent years, algorithmic advances have been made to address the above-mentioned deficits. The development of the so-called TRPO (Schulman et al. 2015) and PPO (Schulman et al. 2017) algorithms led to further improvement of sample efficiency and robustness when using policy-based approaches. Several attempts to boost the performance of DQN (Mnih et al. 2013), the most common value-based algorithm, have also seen successful results. To combine the advantages of policy-based and value-based methods while minimizing their shortcomings, current research efforts include actor-critic methods (Haarnoja et al. 2018; Wang et al. 2016b).
According to Sutton and Barto (2018), RL-problems have the following two main characteristics: First, the agent gains knowledge about the environment and its dynamics solely by performing actions that change the state of the environment, which again gets observed by the agent. Second, an action impacts the reward received in the future, e.g., winning at the end of a game. Both characteristics need to be addressed in practice.
The first is also known as exploitation-exploration trade-off (Sutton and Barto 2018). At each time step, the agent has two kinds of actions to perform. The agent can either execute the so far best-known action based on the learned strategy, which presumably gains the highest reward. However, there might be an even better action, which has not been discovered (learned) yet. Therefore, the alternative kind of action is to explore and deliberately execute suboptimal actions. Second, due to the various and unknown lengths of an action’s impact on the rewards observed in future interactions, the agent faces the so-called Credit-Assignment-Problem (Sutton and Barto 2018). Only some of the actions may be the actual reason for the resulting reward. Hence, the agent has to learn to distinguish between actions performed in specific states that are beneficial to achieving high rewards and those that have no significant impact.
Application of RL in production control
Table 1 gives an overview of RL approaches that are relevant to the present work. The approaches are compared based on the following requirements: job shop manufacturing system as considered use case with its degrees of freedom, highly volatile environment conditions in terms of high volume and many product variants, complex internal material flow due to the job shop setup, stochastics such as machine breakdowns are considered, order dispatching with respect to transport or processing, adaptive production control system, near real-time decision-making, multi-objective target system for optimization, dynamic evaluation of performance, order- or resource-related performance indicators, RL as solution algorithm, discrete-event simulation for validation, and recommendations of the RL-design.
From this literature review, it can be seen that there is previous work dealing with the control of complex job shop manufacturing systems as well as approaches in which RL has been successfully implemented in exemplary investigations. The research deficit can thus be summarized as follows: A complex real-world application has hardly been considered for RL-methods. Existing adaptive control approaches use a state-dependent rule selection or rule parameterization and, thus, the adaptivity is only partially implemented, i.e., to changing parameters of static rules. Heuristics and mathematical optimization are static, model-based production control approaches and require much adaptation in case of changes. Approaches that analyze the comprehensibility of the RL-agent behavior as well as the direct comparison with a benchmark procedure have not been carried out yet. A methodological procedure that supports the RL design for applications in production planning and control is not yet available, and authors often provide only a few details on their RL design.
Methodical approach for designing an adaptive production control system
When applying RL, a learning data generation process is required. Performing this in real production environments is uneconomical and takes far too much time, as it is limited by the actual speed of production processes. Moreover, the operational performance is directly affected by the initial worse performance of the RL-agent. Hence, a simulation environment representing the behavior of the real production system with sufficient accuracy is used in this paper to train RL-agents and, thereby, speed up their learning process. Discrete-event simulations are commonly used in production planning and control to evaluate production systems and identify the potential of improvement measures (Law 2014; Rabe et al. 2008). Therefore, this section first deals with the overall architecture of the discrete-event simulation and, second, continues with the modeling and implementation of the RL-based adaptive production control system.
Simulation of the production environment
One central element of the simulated job shop production system is production orders. They enter the system via entry resources called sources. Each order is processed on a single processing resource called machine, and leaves the production system afterward again via a sink. Hence, an order can be in one of the three states: waiting, in-transport, or in-process. Each state corresponds to a specific type of production resource. Processing is done by machines, and transportation is handled by a dispatching resource called dispatcher. While orders are waiting, they are placed in buffers, which can be intermediate buffers such as entry or exit buffers of machines. Every machine has an entry and an exit buffer.
During the simulation, actions are carried out on orders. These decision-making points are related to the release, transport, or processing of orders. As a result, buffer levels change, e.g., when machines are done with processing or the dispatcher finishes transportation. For such a change, all production resources currently not in use are triggered to decide on their next action to perform, given the new production state (see Fig. 2). In particular, these decisions are the object of interest of this paper. While machines select the next order to be processed according to a FIFO-rule, i.e., the order waiting longest in the entry buffer, an RL-agent is used to decide which order to dispatch next. After each resource has decided on its next action, these are carried out by the simulation to continue the ongoing production processes.
To exhibit real-world production characteristics, the discrete-event simulation model is parameterized with historical data and assumptions on stochastic probability distributions. The following characteristics and assumptions are considered:
-
Machines are organized in groups, where each machine in a group has similar order processing capabilities. Therefore, an order assigned to one specific machine can, in fact, be processed by each machine of the respective group.
-
Order release and machine assignement are performed based on a predefined probability distribution, and orders are released in the sources.
-
The processing time of an order incorporates setup times and is also stochastically determined based on the machine’s specific probability distribution. Every order is of the same type, i.e., no further order-specific distinction is considered and no prioritization scheduling of orders is required.
-
No batching processes are considered and, hence, a machine can only process one order at a time.
-
The production system is subjected to random machine failures, which lead to limited availability of machines. Again the machine failures are stochastically determined according to two parameters: mean time between failures (MTBF) and mean time off-line (MTOL).
-
The number of dispatching agents is fixed and a single agent can carry just one order at the time.
-
The buffer capacities at the machines as well as the queue of incoming orders are limited.
Modeling the RL dispatching agent
To obtain an adaptive production control system, a single RL-agent is determining the next action of the dispatcher. Hence, the agent is the decision-maker of the dispatcher and, hereinafter, also called RL dispatching agent. Note that the modeling is independent of the number of dispatchers (instances) because the decision-making process is, in principle, identical for any dispatcher, also if there are more than one. In any case, the decision-relevant state information and evaluation in terms of the reward signal are identical. This assumption was already introduced by Crites and Barto (1998).
Whereas in most use cases of RL that are not related to production control, the definition of the action space is rather apparent, e.g., the allowed moves in a game. For the examined dispatching agent, this is a design choice. The following definition is used in this paper, based on the available resources in the production environment: An action consists of the source and destination resource of the transport to perform by the dispatcher. Such action is denoted with \(a_{I \rightarrow J}\), where I is the source and J the destination of that action. If the dispatching agent is not yet located at resource I, the agent first has to move to I from the current location to pick up the order. This activity is included implicitly in \(a_{I \rightarrow J}\). As this definition does not distinctively determine the unique production order, this is subsequently determined by the resource, i.e., it determines which order to release for transport. Here again, a FIFO-rule is assumed as decision-making heuristic, and always the longest waiting order is released from the resource. It is important to have a static rule in place to not increase the stochastic dynamics within the production processes and possibly cause artificial effects that are not related to the RL dispatching agent’s actions.
The set A of all possible actions of the dispatching agent is separated into pairwise disjoint subsets (see Table 2). The subsets are divided by the type of source and destination resource. There are machines M and sources and sinks, which are both denoted with S as they are located in the real-world production system in the same place. It is important to note that a source resource can only be an action’s source as well as a sink can only be an action’s destination. However, some actions, such as waiting or moving without transporting an order, do not have an actual source or destination and, thus, \(\varnothing \) is also an option. The subset \(A_{S \rightarrow M}\) denotes actions transporting an order from a source to a machine. The opposite direction to a sink is given by \(A_{M \rightarrow S}\), and transports between two machines are represented by \(A_{M \rightarrow M}\). Actions from a source to a sink are not allowed, because at no time such a transport would be possible due to the processing required by every order. As the source of an action specifies where to pick up an order, an action with the source \(\varnothing \) instructs the dispatcher to move to the given destination without transporting any order. The subset \(A_{empty}\) is the collection of those actions. In case the destination equals to \(\varnothing \), the dispatcher would pick up an order but not put it anywhere. Thus, this kind of action is not available in A. Finally, \(A_{waiting}\) contains a single action with both source and destination being empty. This action results in no movement of the dispatcher but the waiting at its current position for a defined amount of time \(t_w\). The waiting time is a parameter that needs to be specified. All in all, the available actions are not all value-adding, as the waiting action. Hence, the RL-agent needs to learn to distinguish the action subsets or make use of waiting actions tactically, i.e., waiting for an order that finishes processing soon.
The overall learning process of the RL-agent is equivalent to Sect. 2.3. To determine the next action, the RL dispatching agent is given information on the current production state. This state \(s_t\) can contain various data such as the number of available orders, their location, and where they can be transported. Based on the given state, the RL dispatching agent determines an output scalar \(o_t\) according to its strategy, which is then mapped to an executable action \(a_t\). According to the chosen action and the production state, the agent receives a reward \(r_{t+1}\) in the next iteration, which is determined by the reward function.
The RL-agent is implemented in a modular manner. Thus, it can be configured at the beginning of each run. The modules and their relationships are shown in Fig. 3. The following subsections describe them in detail.
Action module
Of the previously mentioned subsets of actions (see Table 2), not all are directly affecting the operations of the production. Thus, the set \(A_{exec}\) is defined as the union of the relevant subsets. \(A_{S \rightarrow M}\) and \(A_{M \rightarrow S}\) are always part of \(A_{exec}\) to ensure that orders are actually processed. Additionally, \(A_{empty}\) and \(A_{waiting}\) are relevant in this paper. Due to just a single process step needed for each order in the considered production scenario, \(A_{M \rightarrow M}\) is ignored hereinafter.
The output of the RL algorithm is a discrete value. To interpret this, the output value needs to be uniquely mapped to one of the executable actions. The action module implements this mapping. Two alternative action mappings are considered:
-
The first mapping type, which we call direct mapping, enumerates every single action of \(A_{exec}\). The RL-agent is accordingly configured to output a discrete action value in the range of 0 to \(n=|A_{exec}|\) discrete action values. This value can easily be mapped to one distinctive action.
-
In the second mapping type, the so-called resource mapping, the RL-agent is configured to output a pair of two discrete values. These pairs are directly interpreted as the source and destination resource, which define the action to execute.
Each time the agent has to choose an action, not necessarily every single action of \(A_{exec}\) can be performed. This depends on the current state of the production system at the time of decision-making t. For example, the action \(a_{I \rightarrow J}\) from source I to machine J can be performed only if there is an order at source I that can be processed next at machine J and if there is free space in the entry buffer of machine J. Thus, each action is either valid or invalid at time t and accordingly \(A^t_{valid} \subset A_{exec}\) and \(A^t_{invalid} \subset A_{exec}\) are defined.
Both types of action mapping do not prohibit the RL-algorithm to output an invalid action. To handle this, a maximum recursion parameter is introduced. Immediately after selecting an invalid action, the RL-agent is given a zero-valued reward and called again for a new decision. This is repeated up to a maximum recursion count. If the decision is still an invalid action, the waiting action \(A_{waiting}\) is performed instead.
State module
Providing information on the current production state enables the RL-agent to make decisions and choose actions that maximize the reward. The state module combines different parts of the theoretically available information in an idealistic scenario, which contains all information. In general, a simulation environment allows any type of information to process. Therefore, note that only data that is available in the real-world can be integrated into the state representation to ensure the transferability of the simulated production system to the real system. The decision-relevant information is combined to a single numeric state vector, which the RL-algorithm can interpret. Hence, the reasoning for determining an adequate state vector is an important question and investigated in the following. If the state vector contains too much information, the RL-agent might not be able to capture the relevant parts and not converge.
The elements of the state vector are calculated based on the simulation state at simulation time t. However, for improved readability, the following formulas neglect the time reference t if not explicitly needed. The rest of the sections list possible state elements that are investigated in Sect. 4.
First of all, the state always contains information indicating for every available action \(a_i \in A_{exec}\) whether it is valid or not. The information is represented by the binary variables \(as_i\) and the state is named \(S_{AS}\):
Next, the state can provide information on the dispatcher’s current position within the production system. This is encoded by a one-hot vector for the each resource and the state is named \(S_L\). Thus, there is a binary variable \(l_i\) for every resource in the production system.
As machines break down, the state may contain \(S_{MF}\) with information on the current failure state of each machine \(M_i\). The according variables \(mf_i\) are defined as follows:
Apart from the machine’s state, it is also of interest whether the machine is currently processing an order or not and if it is processing, what the remaining processing time is. \(S_{RPT}\) summarizes \(rpt_i\) for every machine \(M_i\). The value represents the remaining processing time \(RPT_i\) divided, i.e., scaled, by the average processing time \(APT_i\) at machine \(M_i\). As \(RPT_i\) is 0 if no order is at the machine, the state value automatically equals 0:
Next, \(S_{BEN}\) indicates for every machine \(M_i\) the remaining free buffer spaces in its entry buffer. The information is derived from its capacity \(CAP_i^{EN}\) and the number of occupied buffer spaces \(OCC_i^{EN}\). Analogously, the same information is available for the exit buffers in \(S_{BEX}\) and calculated based on \(CAP_i^{EX}\) and \(OCC_i^{EX}\).
In addition to the number of loaded buffer spaces, the total processing time of the orders waiting in front of the machine is provided as state information \(S_{BPT}\) with the values \(bpt_i\). They are scaled by \(APT_i\) multiplied with the entry buffer’s capacity and shifted by \(-1\) to be negative if the sum of processing times is below the average. \(PT^k_i\) denotes the actual processing time of every order k in the entry buffer of machine \(M_i\).
The state information \(S_{WT}\) deals with the waiting times of orders that are waiting for transport. For every source and machine, it represents the longest waiting time \(WT_i^{max}\) of an order in the respective exit buffer. Two normalizers take the average and standard deviation of the waiting time of orders being transported from a source or machine into account. \(WT_i^{mean}\) and \(WT_i^{std}\) refer to those values.
To allow the agent to get a grasp of the temporal effects of an action selection, the state information on the action time \(S_{AT}\) is introduced. It contains one value for each action of \(A_{exec}\), indicating the time that passes by when the specific action is chosen. For any invalid action, the value is 0. The other values are calculated based on the time it takes to walk from the agent’s current location to the resource where the order to be transported is currently located \(t_{\rightarrow O}\) as well as the time it takes subsequently to transport the order to its destination \(t_{O \rightarrow D}\). Additionally, loading \(t_{load}\) and unloading times \(t_{unload}\) are considered. Finally, all values are divided by \(at_{max}\), which is the maximum of those values, to achieve a scaled value range from 0 to 1.
Reward module
In order to learn the desired behavior that fulfills the operational performance indicators and to continuously evaluate the performed actions, an RL-agent is given feedback in the form of a numeric reward signal. Looking at the reward frequency, there are two categories of reward signals to differentiate: a reward can either be given after every step (dense reward) or after an episode of steps (sparse reward). Note that hereinafter the term step refers to a full iteration of state, action, and reward. Sparse and dense rewards have different effects on the RL-agent’s learning, their own specific advantages and disadvantages and, hence, are evaluated in Sect. 4.
The designer, who wants to apply an RL-agent, can influence the agent’s behavior with the reward function, as it directs the behavior of the agent in any decision situation towards the objectives. Some objectives are long-term, which means that their evaluation in every step is not useful. A sparse reward setting focuses on such scenarios. The agent is provided with feedback when enough time has passed to reevaluate the objective. In doing so, the agent has to find a way to achieve the objective over multiple steps entirely on its own. While this may enable the agent to learn an unknown behavior strategy performing better than, e.g., any human player (Silver et al. 2017), it is, at the same time, a tough challenge due to its complexity.
By rewarding the agent after every step, additional domain knowledge can be incorporated, the complex task can be simplified and the agent can be directed step-by-step towards the objective. However, by using domain knowledge, the risk arises that the agent can no longer find the optimal strategy, as that is usually not known by any domain expert. In this paper, both alternatives are evaluated.
Dense reward functions: To examine the influence of rewarding the main action subsets \(A_{S \rightarrow M}\) and \(A_{M \rightarrow S}\) differently, \(R_{const}\) is introduced. The agent receives the constant reward values \(\omega _1\) and \(\omega _2\) dependent on the subset of the chosen action.
While \(R_{const}\) depends the reward on the selected action, the functions \(R_{uti}\) and \(R_{wt}\) directly target operational performance indicators. \(R_{uti}\) rewards the agent with respect to the current average utilization U when carrying out a valid action. The exponential function is applied to incorporate an increasing gradient towards the optimal point with the maximum utilization. This modeling choice facilitates the learning process of RL-algorithms (Sutton and Barto 2018). Moreover, two discrete values are added to align the \(R_{uti}\) to the expected performance level.
To reduce the throughput time of orders in the production system, one has to minimize the average waiting time of the orders. Note that the processing times are stochastically determined and fixed, as the agent is not able to influence it e.g., by alternative machines with varying processing times. We, therefore, design reward function \(R_{wt}\) to reward the agent based on the waiting time of the order transported. Actions transporting no order are rewarded with the value 0. To account for the fact that orders entering the system have by default a lower waiting time than orders leaving the system, the waiting times \(WT_i\) are already normalized by the resource group (source or machine).
The reward functions \(R_{w-util}\) and \(R_{w-wt}\) combine the ideas behind the reward functions \(R_{const}\) with \(R_{uti}\) and \(R_{wt}\), respectively. The resulting reward functions might utilize the advantages of both single reward functions.
Sparse reward functions: A sparse reward function is defined by two independent characteristics. First of all, it is assumed in this paper that the sparse reward is always given at the end of an episode. The explanation of an episode is given in the following Secti. 3.2.4. The second characteristic is the actual value of the reward. As a matter of fact, we designed the sparse to be very similar to the dense reward functions already introduced above.
Analogously to \(R_{const}\) the function \(R_{const-ep}\) rewards with a constant value:
Next, there are \(R_{uti-ep}\) and \(R_{wt-ep}\) as the sparse counterparts of \(R_{uti}\) and \(R_{wt}\). While the function definitions are very similar, there are different calculations of the values of utilization and waiting time. In the sparse version, U is calculated for the completed episode, instead of the last step. Likewise, WT is defined as the average waiting time of orders that have been transported to a sink in the past episode.
However, due to the computational results of \(R_{const-ep}\) described in the evaluation section, \(R_{uti-ep}\) and \(R_{wt-ep}\) are not used explicitly. Nonetheless, we show that there are numerous aspects when designing a reward function that needs to be considered.
Last but not least, it is possible to combine different reward functions in a weighted sum with weighting factors \(\alpha _n\) to allow for multi-criteria optimization. This also enables the combination of dense and sparse reward functions.
Agent module
The agent module implements substitutions of different RL-algorithms and their respective parameter configurations. Available RL-algorithms are policy-gradient-based methods like TRPO by Schulman et al. (2015) and taken from the implementations of the Python framework tensorforce (Kuhnle et al. 2017).
Some RL-algorithms require the definition of episodes to optimize the strategy. Due to the nature of production operation processes as continuous processes, a fixed definition of episodes is not possible and, therefore, it represents another modeling design choice. Note that this is a fundamental difference comparing to well-known applications of RL in board or computer games. In order to examine the influence of the episode design choice, time-based and action-based definitions are proposed in this work.
The time-based nature of the production process, such as shifts or a working day, represents the most intuitive variant of episode definition. An episode is given by a time period of a fixed length. The action-based episode definition refers to a fixed number of actions carried out. As actions can belong to different subsets, this definition can also be detailed on action subsets. Investigated in this paper are episodes denominated by a fixed number of actions belonging to the following subsets:
-
\(A_{S \rightarrow M}\): source to machine actions, also called entry actions
-
\(A_{M \rightarrow S}\): machine to source actions, also called exit actions
-
\(A^t_{valid}\): valid actions
Rule-based benchmark heuristics
In the already mentioned production system simulation, several heuristic dispatching approaches are implemented for benchmarking purposes. Their concept is described in the following section.
The RANDOM heuristic is the most simple dispatching approach, choosing any action randomly from \(A_{exec}\). The actions chosen are not necessarily valid. Because of this, the VALID heuristic is considered as an enhancement, selecting randomly from \(A^t_{valid}\) and, by this, ensuring the selection of only valid actions.
A more sophisticated heuristic is based on the orders’ waiting times. The FIFO heuristic determines the order to be transported as the one with the highest total waiting time within the production system. Depending on its location, the action’s source is determined. From that source, the order is transported to the machine with the lowest entry buffer level of all machines being able to process that order. For transporting a processed order from a machine, the nearest sink is selected as the destination.
Additionally, the nearest job fist (NJF) heuristic is implemented. It selects the nearest order being ready for transport and determines the destination based on the order’s destination. If the order has not yet been processed, it is being transported to the machine the next process step is intended. Again, the nearest sink is selected as the destination for all complete orders.
Use case description and computational results
Especially in the semiconductor industry and wafer fabs, the material handling system fulfills a critical function (Sturm 2006; Mönch et al. 2013). Nowadays, automated material handling systems are broadly established and responsible for the material flow between work centers and inside a work center between the machines (Lin et al. 2001). An efficient material handling directly influences the cycle time and machine utilization.
Currently, a rule-based real-time dispatching system is used, and the rules are developed by engineers and reflect specific work center requirements under certain production scenarios. However, these rules such as FIFO and NJF are too rigid (Waschneck et al. 2016). Therefore, an adaptive order dispatching optimizing material handling routes under consideration of machine utilization and order throughput time is required that, at the same time, does not require a considerable amount of domain expertise. The previously described approach to design RL-agents is applied and investigated in the following section. It extends the research presented in Kuhnle et al. (2019).
Use case description
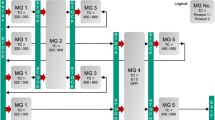
The production system considered in this paper represents one work center of a wafer frontend fab and consists of eight machines \(M_1, \ldots , M_8\) as well as three sources \(S_1, S_2, S_3\) which simultaneously serve as sinks. Each source \(S_i\) is assigned to one of three work areas \(W_i\), representing separated areas in the manufacturing building. These work areas group the machines as follows: \(W_1 = \{M_1, M_2\}\), \(W_2 = \{M_3, M_4, M_5\}\), and \(W_3 = \{M_6, M_7, M_8\}\). Additionally, those machines being able to perform the same operations are grouped in machine groups \(G_1 = \{M_1\}\), \(G_2=\{M_2, M_3, M_4, M_5\}\) and \(G_3 = \{M_6, M_7, M_8\}\).
Orders released in the system are generated with a specific machine intended for processing and get assigned randomly to any source that has the intended machine’s group in its responsible work area. Therefore, \(S_1\) provides orders for both \(G_1\) and \(G_2\), while \(S_2\) and \(S_3\) serve only \(G_2\) and \(G_3\). Thus, transports between work areas are possible.
The actual layout of the production system is depicted in Fig. 4. The bold lines indicate the transportation routes on which the dispatching agent can move. Thin lines cover the work areas. Based on the layout, the four relevant subsets of actions mentioned in Sect. 3.2 are specifically made up of the following actions:
-
1.
\(A_{S \rightarrow M}\) = {\(a_{S_1 \rightarrow M_1}\), ..., \(a_{S_1 \rightarrow M_5}\), \(a_{S_2 \rightarrow M_2}\), ..., \(a_{S_2 \rightarrow M_5}\), \(a_{S_3 \rightarrow M_6}\), ..., \(a_{S_3 \rightarrow M_8}\)} (12 actions)
-
2.
\(A_{M \rightarrow S}\) = {\(a_{M_1 \rightarrow S_1}\), \(a_{M_2 \rightarrow S_1}\), \(a_{M_3 \rightarrow S_2}\), \(a_{M_4 \rightarrow S_2}\), \(a_{M_5 \rightarrow S_2}\), \(a_{M_6 \rightarrow S_3}\), \(a_{M_7 \rightarrow S_3}\), \(a_{M_8 \rightarrow S_3}\)} (8 actions)
-
3.
\(A_{empty}\) = {\(a_{\varnothing \rightarrow S_1}\), \(a_{\varnothing \rightarrow S_2}\), \(a_{\varnothing \rightarrow S_3}\), \(a_{\varnothing \rightarrow M_1}\), ..., \(a_{\varnothing \rightarrow M_8}\)} (11 actions)
-
4.
\(A_{waiting}\) = {\(a_{\varnothing \rightarrow \varnothing }\)} (1 action)
Thus, the use case-specific version of the generic Table 2 is shown in Table 3.
Evaluation and computational results
For the majority of the computational evaluations, only a limited number of parameters are varied, keeping most of them fixed. By doing this, we are able to examine the influence of those varied parameters on the agent’s behavior and performance. When not stated differently, the used configuration is summarized by Table 4.
Default RL-agent configuration
Due to the broad scope of evaluations and the high operational performance, we chose the TRPO agent because of its robustness (Schulman et al. 2015). The remaining parameters of the default configuration are selected with the intention to enable a fast and reliable convergence. The maximum recursion number and waiting time are set to be 5 and 2, respectively. Both parameters support the agent in distinguishing between valid and invalid actions and have almost no effect on the production environment in the state when the agent converged because then the number of invalid actions is negligible. The last two parameters prevent the agent from getting trapped in a loop of choosing invalid actions over and over again.
Performance indicators
A simulation experiment run contains many stochastic processes. To ensure the reproducibility of the results, every random number is controlled by a seed value. However, some randomness still remains due to the “black box” behavior of the RL-agent that cannot be controlled. Therefore, multiple simulation runs with the same configuration are performed. Preliminary studies showed that three runs per configuration result in a sufficiently small confidence interval, allowing quantitative comparisons. During each simulation run, characteristic performance indicators are recorded. Once the simulation experiment is finished, these recordings are analyzed for comparison and evaluation. The key figures include the following:
-
Reward given to the agent
-
Average utilization of the machines ignoring downtimes (U)
-
Average waiting time of orders (WT)
-
Utilization of the dispatching agent
-
Throughput of the entire production system
-
Average inventory level (I)
-
Alpha value (\(\alpha \))
The \(\alpha \) value has its origins in the operating curve management theory (Boebel and Ruelle 1996), which in return references Kingman’s Equation and Little’s Law. For the theoretical background and mathematical calculation of the alpha value, we refer to the related literature (Schoemig 1999). For the understanding of this paper, it suffices to understand the basic concept as follows: The main denominators are the flow factor and machine utilization. The flow factor is a value describing by which factor an order’s cycle time is higher than its raw process time. Alpha is proportional to the flow factor and to the inverse of the machine utilization. By combining multiple performance indicators, alpha can be used to evaluate the performance of the production system, where a small alpha value means better performance.
However, to understand the actual reasoning for the achieved performance, one has to examine the key figures in detail. In order to do this, the raw values of the recording are processed and summarized. This includes the calculation of a moving average and standard deviations for every performance indicator of every single simulation run as well as the combination of all three runs, as before via mean and standard deviation values. Additionally, the time of the agent’s convergence is calculated. In this paper, convergence is defined as the point in time, in which the moving average of the reward signal varies in a range specified by a threshold relative to the value of the moving average of the reward. The finale performance evaluation values are derived from convergence onward and, hence, the training period is not considered. These are the values mainly used for comparing different configurations.
Furthermore, the course of the performance indicators are plotted and visualized, which can be seen in Fig. 5. The raw utilization data as well as a moving average, the simulation step in which the convergence of the agent is assumed, the moving average and standard deviation, and a Box-plot of the utilization data after the state of convergence are shown as example. However, for means of readability and comprehensiveness, we try to limit the plots to a minimum and focus the evaluations of the converged performance values.
Evaluation setup
To optimize the operational performance, the agent has to solve two types of problems summarized under the term order dispatching: These are order sequencing and route planning. This is important to state, as the dispatching agent is not only deciding where to move next but also to which machine to take the order (out of the possible machines in the same machine group). Depending on the actual production scenario, the importance of those two problems shifts from one to the other. If the transport resource is the limiting factor (bottleneck) of the entire system, it is crucial to utilize this resource by an optimized route planning effectively. On the other hand, if the transport resource’s capacity is not limited and the machines are the bottleneck, the importance shifts to an effective order sequencing.
To examine both scenarios, each RL-agent configuration is tested in two different production scenarios focusing on one problem each. In the first scenario, the dispatching agent, i.e., the system’s transport resource, has a relatively slow speed (factor 0.3) and the machine entry and exit buffers are small (factor 0.5). This puts the focus on route planning, as the transport agent is the limiting factor. Inversely, the second scenario features a relatively fast agent (factor 1.0) and large buffers (factor 1.0). The aim in the second scenario is to sequence the orders in a way that the machines are optimally utilized.
Table 5 shows the performance indicators of the rule-based benchmark heuristics mentioned in Sect. 3.3 for both scenarios. The performance is evaluated based on the average machine utilization U, average order waiting time WT in an arbitrary time unit TU, average inventory level I, and the \(\alpha \)-factor. In general, the average inventory is lower in Scenario 1 due to the slower agent and the limited buffer capacity. Accordingly, there are fewer orders in the system and in front of the machines, which results in lower average machine utilization. However, on the other hand, the average waiting time is lower, because the orders do not have to wait that long to be processed and transported.
Moreover, the performance gives further insights into the behavior of the benchmark heuristics. It is not surprising that the RANDOM heuristic performs worst in both scenarios. A better heuristic is the VALID heuristic, but FIFO and NJF achieve an even better performance in both scenarios. As the FIFO heuristic performs the transport of the longest waiting order, it achieves the lowest average waiting time in both scenarios. In Scenario 2, where the waiting times tend to be higher due to the large inventory, FIFO also performs best, as indicated by the \(\alpha \) value. In Scenario 1, however, the NJF heuristic achieves the best results, because it minimizes empty walks and, thereby, the bottleneck transport resource is used efficiently. This results in higher machine utilization.
However, it can be seen that the heuristics suffer from the trade-off between the performance indicators. The higher machine utilization of the NJF comes with an increase in the average waiting time, while, on the other hand, lowering the average waiting time by applying a FIFO heuristic consequently lowers the machine utilization. This represents the intention of using an RL-agent, as described in the introduction of this paper. The aim of the RL-agent is to use the available information to enable multi-criteria optimization and simultaneously minimize conflicts arising due to the inherent trade-off.
When learning an optimal order dispatching strategy, the RL-agent has to solve the two problems mentioned above, i.e., order sequencing and route planning, and in addition to that, perform a two-phased learning process: First, it must learn to distinguish valid and invalid actions to choose only the former ones. Next, the agent has to learn the interplay between state information, the selected action, and the reward received from those three elements to optimize the performance indicators.
Evaluation results
Distinction between valid and invalid actions
Dense reward: To determine first whether an RL-agent is able to distinct between valid and invalid actions, the examined agents receive only the action state \(S_{AS}\) as information. The dense reward function \(R_{const}\) with different values for \(\omega _1\) and \(\omega _2\) is used. The results are presented in Table 6 for both scenarios.
The results show that even for changing weight factors, the agents are able to identify and select valid actions. Especially noteworthy are the extreme cases of agents 1 and 5, in which only one particular subset of actions is rewarded. Nonetheless, these agents are not neglecting the actions from the subset that is not rewarded and, thus, keep the production running. At the beginning of a simulation run, each agent selects on average 1.5 to 3 invalid actions per actually performed action. Note that, because of the implemented recursion, only after the selection of six consecutive invalid actions, the waiting action is performed. The rate of invalid actions decreases fast and continuously. Within the last one million steps, the average count of selected invalid actions per 100 valid actions is shown in the column \(A_{invalid}^t\). It varies in the range of 0.09 to 0.25, whereas the agents of the extreme cases have higher rates due to the more complex credit-assignment problem. Due to the recursion, only a small effect on the performance indicators can be observed.
When looking at the performance indicators U, WT, and I, we can show that shifting the reward between action subsets directly affects them. By emphasizing entry actions with a higher weighting factor \(\omega _1\), these actions are carried out by the agent preferably. As a consequence, the average inventory level increases and together with the lower preference of exit actions, the waiting times increase as well. Additionally, higher inventory levels have two effects on the machines. First, it is less likely that an entry buffer is empty and the machine has no order to process. Second, it is more likely that an exit buffer is full and the machine has to wait until it can unload a processed order. Despite those opposing effects, higher inventory levels always come along with higher machine utilization. Analogous considerations can be made in the opposite case, where exit actions are rewarded by a higher \(\omega _2\) value. In this case, the average levels of inventory and waiting times decrease and, accordingly, does the machine utilization.
This shifting of the reward from \(\omega _1\) to \(\omega _2\) is similar to the transition from a push to a pull production principle.
Sparse reward: We also train an agent rewarded with the sparse reward function \(R_{const-ep}\) to distinguish between valid and invalid actions. This, however, did not succeed. While the count of selected invalid actions for agents 1 to 5 diminishes down to 0.1 per 100 valid actions, the sparsely rewarded agents still have way higher counts. Agents similar to 1, 3, and 5 rewarded every 100th valid action, do not achieve a counter below 100, which means that the agent selects exclusively invalid actions for over 1 million steps. By rewarding the agents more frequently, the counts show a positive, declining trend. However, they are still significantly higher than the ones of their dense counterparts and the agents still show an inferior performance.
All in all, we observe that a sparse reward function, although theoretically well-suited, comes with significant disadvantages when investigating the learning performance. Due to these facts and especially because of an increased training effort requiring significantly more computation time, we decide not to investigate the sparse reward functions any further.
Relationship between state information and reward function
In contrast to the basic RL-agents in the previous section, we now introduce more complex agents with additional state information and reward functions \(R_{uti}\) and \(R_{wt}\). These agents are designed to incentivize the agent in the desired way according to the performance indicator.
In the first part of Table 7, the results are shown for agents 9 and 10, which are extensions of agent 3 with additional state information. Agent 9 receives \(S_{AT}\), containing information on the execution times of actions, whereas the new state information \(S_{WT}\) for agent 10 represents the waiting times of orders in the production system.
First, one can see that additional state information leads to a decrease in machine utilization for both scenarios when comparing agents 9 and 10 to agent 3. On the other hand, agent 10 manages to decrease the average order waiting times as well as the average inventory levels in both scenarios. State information \(S_{AT}\) (agent 9) leads to worse overall performance in Scenario 1 and comparable performance in Scenario 2 relative to agent 3 regarding WT, I, and \(\alpha \). We, therefore, conclude that an agent does not necessarily benefit from additional state information when it does not directly assist the agent to exploit the given reward function and collect higher long-term returns.
To evaluate this hypothesis, we train further agents with additional state information and the reward function \(R_{uti}\) aiming to increase machine utilization and \(R_{wt}\) to minimize the average order waiting time. The results are shown in the lower part of Table 7. To bring the conclusion first, we can show that optimizing a specific performance indicator by designing an accordingly reward function is possible in both scenarios. This can easily be seen by comparing the performance of agents 3 and 11, where the latter is again an extension of the former by the reward signal \(R_{uti}\). Additional data in the state that does not provide any information towards the performance indicator on that the reward is based, again, reduces the performance of the RL-agent. This is shown by agent 12, whose performance in both scenarios is worse than the one of agent 11. In addition, it can be noted that, in contrast to the other agents, it requires significantly more simulation interactions for this agent to converge. We attribute this to the fact that the agent gets somehow “confused” by the state information. This restrains the learning and results in reduced performance. On the other hand, state information with a more obvious relation to the reward function enables the agent to optimize the respective performance indicator (cf. agents 13 and 14). Analogous observations can be made in both scenarios for agents trained with \(R_{wt}\).
When comparing agents trained with \(R_{uti}\) and \(R_{wt}\), we can see that both agents suffer from conflicting objectives. While agents rewarded with \(R_{uti}\), in both scenarios, operate on a higher inventory level and subsequently higher order waiting times, the agents rewarded with \(R_{wt}\) were not able to reduce the latter without a significant drop in machine utilization.
Evaluating the overall performance based on the \(\alpha \) value, we conclude that a matching choice of reward and state representation for an RL-agent leads to a significant performance increase (cf. agents 3, 11, and 14). However, there is the risk that agents designed to aim at one optimizing performance indicator specifically may do so on a disproportionate cost of other indicators (cf. agents 15 and 16). This problem is, in particular, addressed by the domain of multi-criteria optimization, which is investigated in Sect. 4.4.5.
Influence of episode design and action mapping on the RL-agent’s performance
In this section, we test the influence of basic configuration parameters different from the default setup given in Table 4. In particular, agents with an adjusted episode definition and action mapping are examined. The results are displayed in Table 8 and Table 9.
First of all, we observe that regardless of the episode definition, all agents converge (see Table 8). Thus, the dynamics of a dispatching control system can be learned with different episode designs. As discovered in the previous section, agents rewarded with \(R_{uti}\) come with higher waiting times and the ones rewarded with \(R_{wt}\) reach a lower machine utilization. Nonetheless, there are minor differences regarding the performance indicators when looking deeper into it. Recall that, because of the episode-wise characteristic, the agent’s goal is to collect as much reward as possible within one episode. The agent has no incentive to collect a lower reward in this episode, just to increase its reward in the next one. Accordingly, when the episode ends, e.g., after 100 entry actions, the agent collects additional reward by performing exit actions without getting closer to the episode end. These actions, however, decrease the inventory level and average order waiting time. Vice versa holds true if the episode ends after 100 exit actions, an increase in machine utilization can be observed. As there is no direct link between the passed simulation time and the reward, no apparent influence of a time-based episode definition can be discovered.
In contrast to the episode definition, the agents show a significant behavior change when the action mapping is altered. Again, all agents converge regardless of the action mapping used (see Table 9). The resource mapping is, by nature, harder to learn, which contributes to the worse overall performance of agents 26 and 27, as indicated by the \(\alpha \) value. Furthermore, this mapping allows the agent to select actions, which are not even in \(A_{exec}\). Agents 26 and 27 can select 12 x 12 distinctive actions (11 resources and 1 empty option for both source and destination), while agent 25 has 32 options and agent 17 only 20. Due to that fact, the agents with resource mapping need significantly longer to distinguish valid and invalid actions. Therefore, fewer order transports are performed, which results in lower inventory levels and subsequent effects on the other performance indicators.
By enabling the execution of empty walks and waiting actions, we obtain agents 25 and 27 from their respective counterparts. These perform better with regard to \(\alpha \) in both production scenarios, with the only exception of agent 25 in Scenario 2. Hence, the agents learn to perform empty walks and waiting actions in favor of the operational performance indicators’ fulfillment. However, this slightly better performance resulted in a slower converging speed of the agent. We can state that giving the RL-agent more freedom in the action selection by using the resource mapping comes with a significantly more extended learning period, and adding irrelevant actions to \(A_{exec}\) increases the performance slightly and, at the same time, slows down the convergence.
Directing the reward on a specific action type
Next, we combine the weighting of the reward for the different action types like in \(R_{const}\) (see Sect. 4.4.1) with the reward signals \(R_{uti}\) and \(R_{wt}\) to get the reward \(R_{w-util}\) and \(R_{w-wt}\). By doing so, either entry or exit actions are rewarded with a higher value. The aim is to actively influence the inventory level, being of central importance for any production system (Wiendahl et al. 2014), and subsequently the other performance indicators, as observed in Sect. 4.4.1. Additionally, an extended state representation with sufficient information is applied in the following investigations. The RL-agents rewarded with \(R_{w-wt}\) receive all state information described in Sect. 3.2.2. The ones rewarded with \(R_{w-util}\) do get the same state information except for \(S_{WT}\). This is because agent 12, which is rewarded with \(R_{uti}\) and has this state information, requires significantly longer to converge. The computational results are summarized in Table 10.
Due to the identical weighting factors for both action types for agents 32 and 35, the resulting reward signal is identical to \(R_{uti}\) and \(R_{wt}\) scaled by the factor 0.5. In comparison to their counterpart agents 17 and 21, which are provided with less state information, we observe for both a superior performance in both scenarios. Thus we conclude that the additional state information in total is used in a positive way.
The expected behavior regarding the achieved inventory level can also be observed. By increasing the reward weight \(\omega _2\) for exit actions, the agent performs these actions preferably, which results in a lower inventory level and subsequently lower waiting times. When entry actions are relatively more rewarded than exit actions, inverse behavior can be observed.
The effect on the machine utilization performance indicator is not that straightforward. For the agents trained with \(R_{w-util}\), the highest machine utilization is achieved in both scenarios when both action types are rewarded equally. This is because the prioritization of one action type above the other results in a higher chance of empty entry buffers or full exit buffers, respectively. Both situations reduce machine utilization.
Due to the typically low inventory level when using \(R_{w-wt}\), agents rewarded with this signal achieve only a relatively low machine utilization. By putting the focus on entry actions, the agent increases the inventory level significantly and, thus, the machine utilization rises, too. It is noticeable that agent 33 in both scenarios and agent 31 in Scenario 1 achieve a lower average order waiting time than their counterparts, agents 34 and 36.
Overall, the agents rewarded with \(R_{w-util}\) achieve superior performance in terms of \(\alpha \). We are not able to identify the exact reason for that, but there are many possibilities. For instance, the fact that the reward signal or the state information or even both are not well designed to achieve an optimization of waiting time per se. Also, there might be reasons intrinsic to the production system, which have not been accounted for. Nonetheless, we further investigate these hindrances by applying multi-criteria optimization in the next section.
Multi-criteria optimization
In Sect. 4.4.2, we find that training an agent to optimize a single performance indicator might result in poor performance regarding the other indicators. For this reason, we examine multi-criteria optimization in this section.
The previously used reward functions \(R_{uti}\) and \(R_{wt}\) are combined into a single one. By using weighting factors, as shown in Eq. 18, we are able to shift the focus between the two basic reward functions and, thus, emphasize one above the other. The simulation results are presented in Table 11. Again, we provide the agents with all state information described in Sect. 3.2.2.
Although the usage of \(R_{wt}\) by itself comes with relatively low inventory levels in the experiments before, the addition of \(R_{wt}\) to \(R_{uti}\) results for all three agents 37, 38, and 39 in increased inventory levels and order waiting times in Scenario 1 (cf. agent 32). With an increasing weight of \(R_{wt}\), the inventory level and average order waiting time decrease only in Scenario 2 and for Scenario 1 the inverse can be observed. However, by increasing the weight of \(R_{wt}\), the utilization always rises. This might be due to the fact that the agent is not able to find the correct correlation between state information and reward signal in this scenario. Hence, its optimization is based on false assumptions.
In comparison to the agents of Table 8, it can be stated that the multi-criteria reward signal does not help to achieve a better performance, although the agents received additional state information. The multi-criteria agents achieve \(\alpha \) values between the ones of agents 32 and 35, but not below. By increasing the weight of \(R_{uti}\), the \(\alpha \) value is closer to the one of agent 32 and vice versa. While this may indeed result from multi-criteria optimization, it cannot be generalized. As mentioned before, it is hard for the RL-agent to grasp the elements of the reward function. In the case of combining three or more reward signals, it is, therefore, concluded that the training of an agent would be not possible.
Behavior of agent and heuristics when changing scenarios
Figure 6 summarizes the performance indicators utilization and waiting time of all RL-agents and benchmark heuristics in a two-dimensional scatter plot. Herein, the aforementioned results are visualized, and one can clearly see the potential of RL-agents in comparison to rule-based heuristics. Firstly, RL enables far more and more detailed adjustments of the desired performance, i.e., more different operation states of the production system can be achieved. Secondly, the performance of the heuristics varies largely when the scenario is changed. Note that not only the location in the scatter plot changes but also the ranking of the heuristics, as for instance, VALID and FIFO are spread in the first scenario, whereas in the second scenario, they are close to each other. This is also due to the fact that the rule-based heuristics do not take into account the bottleneck of the systems. That is enforced by the poor performance of NJF in Scenario 2 comparing to Scenario 1. Finally, the highlighted RL-agents 31 and 32 are almost robust when changing the scenario. Additionally, they show an overall superior performance when looking at both performance indicators and comparing it to all heuristics as well as other RL-agents.
So far, the two scenarios are only considered separately. Figure 7 shows the course of the moving average of the machine utilization U and the average waiting time WT of the orders over the simulated environment steps for the heuristics FIFO and NJF as well as for agent 17. Agent 17 was chosen due to its simplicity and excellent performance in both scenarios. The rule-based heuristics and the RL-agent first operate in a production system that is parametrized as in Scenario 1, before the scenario changes to the second after 10 million steps.
After the scenario changed, both, the heuristics and the agent reach performance values of U and WT that are characteristic for Scenario 2 (see Table 8). This is what one would expect from the static heuristics, since they always select deterministically, which action is executed next. However, agent 17 reaches almost identical performance values compared to a separated training in Scenario 1 and 2. Only the waiting times are slightly better in the case of changing scenarios.
We, therefore, conclude that RL-agents can adapt to changing production conditions. No significant training phase is required, because the performance indicators of the RL-agent in Fig. 7 are adjusted over the same amount of steps as the heuristics need to adjust their performance. Additionally, it has to be noted that training the agent in Scenario 1 and then changing to Scenario 2 has a negligible effect on the final performance.
Comparison of time consumption when training RL-agents
Our experiments were conducted on a Linux system with an Intel Xeon E5-2698 v4 CPU with 20 cores running at 2.2 GHz, 256 GB RDIMM DDR4 system memory, and an SSD for storage. The simulation environment as well as the RL-agents are implemented in Python 3.6 using the packages simpy and tensorforce.
For agents rewarded with a dense reward function, the computation of one million simulation steps requires approximately 1 h. The longer a simulation runs, a slight decrease in the computation speed can be observed due to an increased effort of data handling and recording. Sparse agents, on the other hand, require approximately three times the computation time, as the updates of the neural network are far more complex.
In general, the RL-agents converge in Scenario 2 faster than in Scenario 1. Simple agents like the ones in the Tables 6 and 7 require in Scenario 1 three to five million simulation steps, while in Scenario 2 it is achieved after one to three million steps. Adding additional state information and using more complex reward functions entails increased time consumption. Complex agents shown in the Tables 11 and 10 require 20 to 25 million simulation steps in Scenario 1 and 10 to 13 million steps in Scenario 2 to converge.
The only exception to these general statements is agent 12, which needed 45 million simulation steps to converge. The reason for this is in the combination of state and reward. While the agent received state information on the current waiting time of orders, this is not related to the reward signal \(R_{uti}\). Nonetheless, the agent eventually found a correlation.
Conclusion and outlook
Achieving operational excellence in the competitive environment of manufacturing companies, conventional production control methods are no longer sufficient. With increasing digitization, reinforcement learning offers an alternative approach to control production systems. In this paper, we comprehensively present and apply a methodology for the design of an adaptive production control system that is based on reinforcement learning. Thereby, existing challenges in the application of reinforcement learning methods are identified and addressed: First, designing the state information passed to the agent and based on which the agent makes the decision has an influence on the learned performance. Second, the modeling of the reward signal is of central importance as it represents the optimization objective.
All presented modeling choices are analyzed based on two real-world production scenarios taken from the semiconductor industry. The results reveal that RL-agents are able to perform adaptive control strategies successfully and can be flexibly adapted to different objectives, and thus to different application scenarios. “Simple” RL-agents, e.g., with a constant reward function, achieve a performance superior to random heuristics. Specific RL-agents are able to outperform existing rule-based benchmark heuristics. Moreover, an extended state representation clearly improves the performance if there is a relation between it and the objectives. The reward signal can be designed in such a way to enable the optimization of multiple objectives more easily. Finally, specific RL-agent configurations reach a high performance independent of the production scenario.
Further research is required in order to analyze and understand the performance, and in particular, the strategy the RL-agents learn in more detail. This will offer a huge advantage in building trust and enlarging the acceptance of “black box” learning algorithms such as reinforcement learning. Furthermore, the transferability of the results in further production systems needs to be evaluated.
References
Abele, E., & Reinhart, G. (2011). Zukunft der Produktion. München: Carl Hanser Verlag.
Arviv, K., Stern, H., & Edan, Y. (2016). Collaborative reinforcement learning for a two-robot job transfer flow-shop scheduling problem. International Journal of Production Research, 54(4), 1196–1209.
Aydin, M., & Öztemel, E. (2000). Dynamic job-shop scheduling using reinforcement learning agents. Robotics and Autonomous Systems, 33(2–3), 169–178.
Bischoff, J. (1999). Ein Verfahren zur zielorientierten Auftragseinplanung für teilautonome Leistungseinheiten. Berlin, Heidelberg: Springer.
Blackstone, J. H., Phillips, D. T., & Hogg, G. L. (1982). A state-of-the-art survey of dispatching rules for manufacturing job shop operations. International Journal of Production Research, 20(1), 27–45.
Boebel, F. G., & Ruelle, O. (1996). Cycle time reduction program at acl. In IEEE/SEMI 1996 advanced semiconductor manufacturing conference and workshop. Theme-innovative approaches to growth in the semiconductor industry. ASMC 96 Proceedings (pp 165–168). IEEE
Brucker, P., & Knust, S. (2012). Complex scheduling (2nd ed.). Heidelberg and New York: GOR publications, Springer.
Chen, C., Xia, B., Zhou, Bh, & Xi, L. (2015). A reinforcement learning based approach for a multiple-load carrier scheduling problem. Journal of Intelligent Manufacturing, 26(6), 1233–1245.
Crites, R. H., & Barto, A. G. (1998). Elevator group control using multiple reinforcement learning agents. Machine Learning, 33(2/3), 235–262.
ElMaraghy, W., ElMaraghy, H., Tomiyama, T., & Monostori, L. (2012). Complexity in engineering design and manufacturing. CIRP Annals, 61(2), 793–814.
Freitag, M., & Hildebrandt, T. (2016). Automatic design of scheduling rules for complex manufacturing systems by multi-objective simulation-based optimization. CIRP Annals, 65(1), 433–436.
Gabel, T. (2009). Multi-agent reinforcement learning approaches for distributed job-shop scheduling problems. Ph.D. thesis, University of Osnabruck, Osnabruck
Gabel, T., & Riedmiller, M. (2008). Adaptive reactive job-shop scheduling with reinforcement learning agents. International Journal of Information Technology and Intelligent Computing, 24(4), 14–18.
Günther, H. O. (2005). Produktion und Logistik (6th ed.). Berlin: Springer-Lehrbuch.
Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In J. Dy, & A. Krause (Eds.), Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholmsmässan, Stockholm Sweden, proceedings of machine learning research (Vol. 80, pp. 1861–1870)
Haupt, R. (1989). A survey of priority rule-based scheduling. OR Spektrum, 11(1), 3–16.
Heger, J. (2014). Dynamische Regelselektion in der Reihenfolgeplanung. Wiesbaden: Springer Fachmedien Wiesbaden.
Heger, J., Branke, J., Hildebrandt, T., & Scholz-Reiter, B. (2016). Dynamic adjustment of dispatching rule parameters in flow shops with sequence-dependent set-up times. International Journal of Production Research, 54(22), 6812–6824.
Henke, N., Bughin, J., Chui, M., Manyika, J., Saleh, T., Wiseman, B., & Sethupathy, G. (2016). The age of analytics: Competing in a data-driven world. New York: McKinsey Global Institute.
Kim, G. H., & Lee, C. (1998). Genetic reinforcement learning approach to the heterogeneous machine scheduling problem. IEEE Transactions on Robotics and Automation, 14(6), 879–893.
Klemmt, A. (2012). Ablaufplanung in der Halbleiter- und Elektronikproduktion. Wiesbaden: Vieweg+Teubner Verlag.
Kober, J., Bagnell, J. A., & Peters, J. (2013). Reinforcement learning in robotics: A survey. The International Journal of Robotics Research, 32(11), 1238–1274.
Kuhnle, A. (2020). SimRLFab: Simulation and reinforcement learning framework for production planning and control of complex job shop manufacturing systems. GitHub. https://github.com/AndreasKuhnle/SimRLFab
Kuhnle, A., Schaarschmidt, M., & Fricke, K. (2017). Tensorforce: a tensorflow library for applied reinforcement learning. GitHub. https://github.com/tensorforce/tensorforce
Kuhnle, A., Schäfer, L., Stricker, N., & Lanza, G. (2019). Design, implementation and evaluation of reinforcement learning for an adaptive order dispatching in job shop manufacturing systems. Procedia CIRP, 81, 234–239.
Law, A. M. (2014). Simulation modeling and analysis. McGraw-Hill series in industrial engineering and management science (5th ed.). New York: McGraw-Hill Education.
Lin, J. T., Wang, F. K., & Yen, P. Y. (2001). Simulation analysis of dispatching rules for an automated interbay material handling system in wafer fab. International Journal of Production Research, 39(6), 1221–1238.
Lödding, H. (2016). Verfahren der Fertigungssteuerung. Berlin, Heidelberg: Springer.
Mahadevan, S., & Theocharous, G. (1998). Optimizing production manufacturing using reinforcement learning. In Proceedings of the eleventh international florida artificial intelligence research society conference (pp 372–377). AAAI Press
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., et al. (2013). Playing atari with deep reinforcement learning. NIPS Deep Learning Workshop, 2013, 1–9.
Mönch, L., Fowler, J. W., & Mason, S. J. (2013). Production planning and control for semiconductor wafer fabrication facilities, operations research/computer science interfaces series (Vol. 52). New York, NY: Springer.
Monostori, L., Csáji, B., & Kádár, B. (2004). Adaptation and learning in distributed production control. CIRP Annals, 53(1), 349–352.
Monostori, L., Kádár, B., Bauernhansl, T., Kondoh, S., Kumara, S., Reinhart, G., et al. (2016). Cyber-physical systems in manufacturing. CIRP Annals, 65(2), 621–641.
Monostori, L., Váncza, J., & Kumara, S. (2006). Agent-based systems for manufacturing. CIRP Annals, 55(2), 697–720.
Nachum, O., Norouzi, M., Xu, K., & Schuurmans, D. (2017). Bridging the gap between value and policy based reinforcement learning. In Proceedings of the 31st international conference on neural information processing systems (NIPS’17) (pp. 2772–2782). Curran Associates Inc, USA.
Niehues, M. R. (2017). Adaptive Produktionssteuerung für Werkstattfertigungssysteme durch fertigungsbegleitende Reihenfolgebildung, Forschungsberichte IWB (Vol. 329). Herbert, München: Utz.
Nyhuis, P. (2008). Beiträge zu einer Theorie der Logistik. Berlin: Springer.
Panwalkar, S. S., & Iskander, W. (1977). A survey of scheduling rules. Operations Research, 25(1), 45–61.
Paternina-Arboleda, C. D., & Das, T. K. (2001). Intelligent dynamic control policies for serial production lines. IIE Transactions (Institute of Industrial Engineers), 33(1), 65–77.
Qu, S., Wang, J., Govil, S., & Leckie, J. O. (2016). Optimized adaptive scheduling of a manufacturing process system with multi-skill workforce and multiple machine types: An ontology-based, multi-agent reinforcement learning approach. Procedia CIRP, 57, 55–60.
Rabe, M., Spieckermann, S., & Wenzel, S. (2008). Verifikation und Validierung für die Simulation in Produktion und Logistik: Vorgehensmodelle und Techniken. Dordrecht: Springer.
Riedmiller, S., & Riedmiller, M. (1999). A neural reinforcement learning approach to learn local dispatching policies in production scheduling. In Proceedings of the 16th international joint conference on artificial intelligence (IJCAI’99) (Vol. 2, pp 764–769). San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Sarin, S. C., Varadarajan, A., & Wang, L. (2011). A survey of dispatching rules for operational control in wafer fabrication. Production Planning & Control, 22(1), 4–24.
Schoemig, A. K. (1999). On the corrupting influence of variability in semiconductor manufacturing. In P. A. E. Farrington (Ed.), 1999 Winter simulation conference proceedings (vol 1, pp. 837–842). IEEE
Scholz-Reiter, B., & Hamann, T. (2008). The behaviour of learning production control. CIRP Annals, 57(1), 459–462.
Schuh, G. (2006). Produktionsplanung und -steuerung: Grundlagen, Gestaltung und Konzepte (3rd ed.). Berlin: VDI-Buch, Springer.
Schuh, G., Reuter, C., Prote, J. P., Brambring, F., & Ays, J. (2017). Increasing data integrity for improving decision making in production planning and control. CIRP Annals, 66(1), 425–428.
Schulman, J., Levine, S., Moritz, P., Jordan, MI., & Abbeel, P. (2015). Trust region policy optimization. arXiv:1502.05477
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv:1707.06347
Shah, P., Gosavi, A., & Nagi, R. (2010). A machine learning approach to optimise the usage of recycled material in a remanufacturing environment. International Journal of Production Research, 48(4), 933–955.
Shahrabi, J., Adibi, M. A., & Mahootchi, M. (2017). A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Computers & Industrial Engineering, 110, 75–82.
Shiue, Y. R., Lee, K. C., & Su, C. T. (2018). Real-time scheduling for a smart factory using a reinforcement learning approach. Computers & Industrial Engineering, 125, 604–614.
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., et al. (2017). Mastering the game of go without human knowledge. Nature, 550(7676), 354–359.
Singh, S., Barde, A., Mahanty, B., & Tiwari, M. K. (2019). Digital twin driven inclusive manufacturing using emerging technologies. IFAC-PapersOnLine, 52(13), 2225–2230.
Stegherr, F. (2000). Reinforcement-Learning zur dispositiven Auftragssteuerung in der Variantenreihenproduktion. Materialfluss, Logistik, Utz, Wiss, München: Fördertechnik.
Stricker, N., Kuhnle, A., Sturm, R., & Friess, S. (2018). Reinforcement learning for adaptive order dispatching in the semiconductor industry. CIRP Annals, 67(1), 511–514.
Sturm, R. (2006). Modellbasiertes Verfahren zur Online-Leistungsbewertung von automatisierten Transportsystemen in der Halbleiterfertigung, IPA-IAO Forschung und Praxis (Vol. 450). Stuttgart and Heimsheim: Univ and Jost-Jetter-Verl.
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction, second (edition ed.). Adaptive computation and machine learning: The MIT Press, Cambridge, Massachusetts.
Sutton, R. S., McAllester, D., Singh, S., & Mansour, Y. (1999). Policy gradient methods for reinforcement learning with function approximation. In Proceedings of the 12th international conference on neural information processing systems (NIPS’99) (pp 1057–1063). Cambridge, MA, USA: MIT Press.
Tao, F., Qi, Q., Wang, L., & Nee, A. Y. (2019). Digital twins and cyber–physical systems toward smart manufacturing and industry 4.0: Correlation and comparison. Engineering, 5(4), 653–661.
Wang, J., Li, X., & Zhu, X. (2012). Intelligent dynamic control of stochastic economic lot scheduling by agent-based reinforcement learning. International Journal of Production Research, 50(16), 4381–4395.
Wang, X., Wang, H., & Qi, C. (2016a). Multi-agent reinforcement learning based maintenance policy for a resource constrained flow line system. Journal of Intelligent Manufacturing, 27(2), 325–333.
Wang, Y. C., & Usher, J. M. (2004). Learning policies for single machine job dispatching. Robotics and Computer-Integrated Manufacturing, 20(6), 553–562.
Wang, Y. C., & Usher, J. M. (2005). Application of reinforcement learning for agent-based production scheduling. Engineering Applications of Artificial Intelligence, 18(1), 73–82.
Wang, Z., Bapst, V., Heess, N., Mnih, V., Munos, R., Kavukcuoglu, K., & de Freitas, N. (2016b) Sample efficient actor-critic with experience replay. arXiv:1611.01224
Waschneck, B., Altenmüller, T., Bauernhansl, T., & Kyek, A. (2016). Production scheduling in complex job shops from an industrie 4.0 perspective: A review and challenges in the semiconductor industry. In R. Kern, G. Reiner, O. Bluder (Eds.), Proceedings of the 1st international workshop on science, application and methods in industry 4.0, CEUR workshop proceedings (pp. 1–12)
Waschneck, B., Reichstaller, A., Belzner, L., Altenmuller, T., Bauernhansl, T., Knapp, A., & Kyek, A. (2018). Deep reinforcement learning for semiconductor production scheduling. In 29th annual SEMI advanced semiconductor manufacturing conference (ASMC) (pp 301–306)
Watkins, C., & Dayan, P. (1992). Q-learning. Machine Learning, 8(3–4), 279–292.
Wauters, T., Verbeeck, K., Berghe, G. V., & de Causmaecker, P. (2011). Learning agents for the multi-mode project scheduling problem. Journal of the Operational Research Society, 62(2), 281–290.
Wiendahl, H. P. (1997). Fertigungsregelung: Logistische Beherrschung von Fertigungsabläufen auf Basis des Trichtermodells. München: Carl Hanser Verlag.
Wiendahl, H. P., Reichardt, J., & Nyhuis, P. (2014). Handbuch Fabrikplanung. München: Carl Hanser Verlag.
Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8(3–4), 229–256.
Zeng, Q., Yang, Z., & Lai, L. (2009). Models and algorithms for multi-crane oriented scheduling method in container terminals. Transport Policy, 16(5), 271–278.
Zhang, W., & Dietterich, T. G. (1996). High-performance job-shop scheduling with a time-delay TD(\(\lambda \)) network. In D. S. Touretzky, M. C. Mozer, & M. E. Hasselmo (Eds.), Advances in Neural Information Processing Systems 8 (pp. 1024–1030). Cambridge: MIT Press.
Zhang, Z., Zheng, L., Hou, F., & Li, N. (2011). Semiconductor final test scheduling with Sarsa(\(\lambda \), k) algorithm. European Journal of Operational Research, 215(2), 446–458.
Acknowledgements
Open Access funding provided by Projekt DEAL. We extend our sincere thanks to the German Federal Ministry of Education and Research (BMBF) for supporting this research project 02P14B161 “Empowerment and Implementation Strategies for Industry 4.0”.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
All readers that are eager to extend this research are referred to the open source repository SimRLFab (Kuhnle 2020). This repository contains the simulation as well as RL-agent framework for order dispatching in a complex job shop manufacturing system as described in the present work. The scenario parameters are set to arbitrary default numbers.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuhnle, A., Kaiser, JP., Theiß, F. et al. Designing an adaptive production control system using reinforcement learning. J Intell Manuf 32, 855–876 (2021). https://doi.org/10.1007/s10845-020-01612-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-020-01612-y