PARASOL: a hybrid approximation approach for scalable frequent itemset mining in streaming data

Abstract

Here, we present a novel algorithm for frequent itemset mining in streaming data (FIM-SD). For the past decade, various FIM-SD methods in one-pass approximation settings that allow to approximate the support of each itemset have been proposed. They can be categorized into two approximation types: parameter-constrained (PC) mining and resource-constrained (RC) mining. PC methods control the maximum error that can be included in the approximate support based on a pre-defined parameter. In contrast, RC methods limit the maximum memory consumption based on resource constraints. However, the existing PC methods can exponentially increase the memory consumption, while the existing RC methods can rapidly increase the maximum error. In this study, we address this problem by introducing a hybrid approach of PC-RC approximations, called PARASOL. For any streaming data, PARASOL ensures to provide a condensed representation, called a Δ-covered set, which is regarded as an extension of the closedness compression; when Δ = 0, the solution corresponds to the ordinary closed itemsets. PARASOL searches for such approximate closed itemsets that can restore the frequent itemsets and their supports while the maximum error is bounded by an integer, Δ. Then, we empirically demonstrate that the proposed algorithm significantly outperforms the state-of-the-art PC and RC methods for FIM-SD.

Introduction

Streaming data analysis is a central issue in many domains such as computer system monitoring (Du and Li 2016), online text analysis (Iwata et al. 2010; Hoffman et al. 2010), financial and economic analyses (Zhao et al. 2013; Zhu and Shasha 2002), and medical and health record data analysis (Ginsberg et al. 2009; Keogh et al. 2001). Streaming data is an infinite and continuous sequence of data, and, nowadays, is generated and collected rapidly. The sudden emergence of an intensive bursty event, called concept drift, in streaming data can make it difficult to extract meaningful information from such data. Therefore, there is a strong and growing need for powerful methods that are robust against concept drift in large-scale streaming data analysis.

Frequent itemset mining in streaming data (FIM-SD) (Han et al. 2007; Mala and Dhanaseelan 2011; Lee et al. 2014) is the most fundamental and well-used task in streaming data analysis. It is used to find frequently occurring itemsets (in this study, sets of non-negative integers) in streaming data (in this study, a sequence of itemsets). FIM-SD must exhibit two important properties; (i) the real time property, which is the ability to process a huge volume of itemsets continuously arriving at high speed and simultaneously (on-the-fly) output the detected frequent itemsets (FIs); and (ii) memory efficiency, which is the ability to enumerate FIs while managing an exponential number of candidate FIs with limited memory. Concept drift suddenly introduces huge itemsets that must be processed, which demands a huge amount of memory. This makes it difficult to design scalable and efficient FIM-SD. Thus, the development of a space-efficient FIM-SD that is especially robust against concept drift is an important open challenge that must be solved to enable large-scale streaming data analysis.

One reasonable approach for memory efficiency is to compress the FIs. There are two major classes of solutions: closed FIs, which have no frequent supersets with the same support (i.e., occurrence frequency), and maximal FIs, which are not contained in any other FI. The maximal FIs can restore the original FIs, though their supports are lost. In contrast, the closed FIs can exactly restore every FI and its support, though memory efficiency is bounded by limitation of lossless compression. For an intermediate solution between the closedness and maximality, various lossy condensed representations have been proposed in Xin et al. (2005), Cheng et al. (2006, 2008), Shin et al. (2014) and Quadrana et al. (2015).

A common approach among them is using an error parameter 𝜖 (0 ≤ 𝜖 < 1) to control the maximum error that can be included in the approximate supports. In the following, we call this approach parameter-constrained (PC) approximation. The value of 𝜖 is fixed in advance, however it is difficult to keep the initial value when concept drift emerges beyond user’s expectation. Let us explain this situation using MOA-IncMine (Quadrana et al. 2015), which is the state-of-the-art PC method for FIM-SD. This method incrementally manages approximate closed FIs, called semi-frequent closed itemsets (SFCIs), for each segment of streaming transactions. Figure 1 shows the number of SFCIs stored at each segment of 1,000 transactions generated from a part of the Yahoo! Hadoop grid logs dataset.¹ Then, we observe that the SFCIs rapidly increase on the way to process an intermediate segment. When 𝜖 is less than or equal to 0.1, the process terminates due to out-of-memory exception (with 2GB JavaVM Heap size). Such sudden and intensive increase of memory consumption is a common drawback of PC mining in streaming data.

There is an alternative approximation approach, called resource-constrained (RC) approximation, working under resource (ex. memory and response time) constraint. The Skip LC-SS (Yamamoto et al. 2014) is a representative RC method which works in a constant O(k) space and returns approximate FIs, where k is a size constant associated with the available memory resource. By setting a relevant k, the Skip LC-SS can avoid the out-of-memory; this represents a significant advantage. However, it involves another drawback: due to the combinatorial explosion of candidate FIs, the maximum error becomes extremely high in accordance with k, rendering some solutions in the output useless (Yamamoto et al. 2014).

In this study, we tackle the limitation of those PC and RC mining. First, to address the maximum error issue in RC mining, we introduce a lossy condensed representation of the FIs, called Δ-covered set. The notion of Δ-cover is regarded as an extension of closedness compression and allows the original FIs to be compressed while bounding the maximum error by an integer, Δ. Secondly, to address the memory consumption issue in PC mining, we introduce a hybrid approach of PC and RC approximation. As shown in Fig. 1, sudden and intensive memory consumption can be considered a temporary phenomenon. Indeed, normal PC approximation is sufficient except for within a brief period. From the viewpoint of memory efficiency, it is reasonable to dynamically switch between PC and RC approximations. We call this hybrid approach PARASOL (an acronym for Parameter- and Resource-constrained Approximation for Soft and Lazy mining).

Fig. 1

Time-series on the number of SFCIs

In this paper, we propose the first PARASOL method to find a Δ-covered set of the FIs. The proposed method is based on two key techniques: incremental intersection, which is an incremental way to compute the closed itemsets (Borgelt et al. 2011; Yen et al. 2011), and minimum entry deletion, which is a space-saving technique for PC and RC approximation (Manku and Motwani 2002; Metwally et al. 2005; Yamamoto et al. 2014). We firstly show that the output obtained from these existing techniques composes a Δ-covered set of the FIs. Based on this finding, the proposed method controls the memory consumption and maximum error using an error parameter and takes an RC approximation using a size constant k only in certain scenarios. Consequently, the following characteristics are exhibited:

On-the-fly manner::

it can process any transaction that has L items in O(k) space in almost O(kL) time.

Anytime feature::

it can monitor the maximum error, Δ, and return the output, T, at anytime.

Quality of output::

for every FI α, T contains some superset β of α such that the difference between the frequencies of α and β is at most Δ.

We also propose a post-processing technique, called Δ-compression, which enables to reduce the size of the raw output for more concise solution. Then, we develop a novel data structure, called weeping tree, to efficiently carry out the three key operations (i.e., incremental intersection, minimal entry deletion, and Δ-compression). Finally, we empirically show that the proposed method outperforms the existing PC and RC methods when applied to various real datasets.

The remainder of the paper is organized as follows. Section 2 presents a brief review of the related works. Section 3 is a preliminary. Section 4 describes the baseline algorithm used to compute a Δ-covered set, and Section 5 describes PARASOL and Δ-compression. The data structure is discussed in Section 6. The experimental results are summarized in Section 7. Then, we conclude in Section 8.

Related works

Here, we clarify our contribution through the comparison with the related works. There are many previous works (Xin et al. 2005; Cheng et al. 2006, 2008; Song et al.2007; Boley et al. 2009, 2010; Liu et al. 2012; Quadrana et al. 2015; Hu and Imielinski 2017) on PC mining that deal with lossy condensed representations of the FIs. However, most of those previous works, expect for Song et al. (2007), Cheng et al. (2008), and Quadrana et al. (2015), are oriented to a transactional database that tolerates multiple scanning and allows us to assume a stable distribution of occurrences. It is infeasible to apply them for SD where concept drift can emerge.

Song et al. (2007) proposed an online PC approximation algorithm called CLAIM to compute relaxed closed itemsets. Like the notion of a Δ-covered set, their solution (i.e., relaxed closed itemsets) can bound the maximum error in the approximate support of any FI. In this sense, CLAIM has the anytime feature. However, its update process involves exhaustive computation including set enumeration and generate-and-test based search. In contrast, the proposed method always performs the update processing in O(kL) time for any transaction of length L.

Cheng et al. (2008) also proposed an online PC approximation algorithm called IncMine to compute semi-frequent closed itemsets (SFCIs). IncMine incrementally maintains SCFIs for each segment (i.e., each set of transactions) in two steps: computing the SFCIs in the current segment followed by updating whole set of SFCIs based on the newly computed ones. IncMine utilizes various pruning techniques and efficient data structure to avoid redundant computation in the update process. To our knowledge, IncMine is one of the state-of-the-art PC methods for condensed representation mining. Indeed, IncMine has been implemented in a massive online analysis (MOA) platform which enables it to be widely distributed (Quadrana et al. 2015). However, as shown in Fig. 1, a large number of SFCIs emerges temporarily, causing sudden and intensive memory consumption. In contrast, the proposed method based on PARASOL never issues the out-of-memory. Besides, it is unknown if the obtained SFCIs can restore the support of each FI within a bounded error.

StreamMining (Jin and Agrawal 2005) is a PC approximation method that seeks the FIs. Based on an error parameter, 𝜖, it deletes itemsets that are not promising as they have supports less than or equal to 𝜖 × i for each timestamp i. The accuracy of the solution (i.e., the maximum error in the approximate supports) can be directly controlled by 𝜖. However, this involves a combinatorial explosion of candidates itemsets to be managed, causing huge memory consumption. In contrast, the proposed method focuses the solution on a Δ-covered set of the FIs. Then, the memory consumption becomes much smaller than the one of StreamMining.

CloStream (Yen et al. 2011) is a non-constrained (NC) online method that computes the closed FIs exactly. The update process is based on the incremental intersection that never requires set enumeration computation. However, the memory consumption increases as the whole stream becomes large. This is due to the limitation of closedness compression. In contrast, the proposed method can control the memory consumption using the space-saving technique based on minimal-entry deletion (Manku and Motwani 2002; Metwally et al. 2005; Yamamoto et al. 2014). On the other hand, the proposed method is incomplete for finding the closed itemsets. This is a drawback of the proposed method. Note that there exists the notion of strong closedness, called Δ-closed set (Boley et al. 2009). The Δ-closed set is defined as a characteristic subset of the closed FIs, capturing the interesting patterns. Then, the proposed method is complete for finding this Δ-closed set (i.e., any Δ-covered set contains the Δ-closed set), as detailed in the Appendices A and B.

Skip LC-SS (Yamamoto et al. 2014) is an RC method that seeks FIs based on minimal-entry deletion. Given a size constant k, it can process any transaction of length L in O(k) space and O(kL) time, keeping the top-k itemsets with respect to their approximate supports. However, Skip LC-SS must increment the maximum error Δ by one, whenever a transaction t_i that satisfies $2^{|t_{i}|} > k$ is processed; hence, it suffers from a rapid increase in Δ in accordance with k. By introducing the condensed representation (i.e., Δ-covered set), the proposed method enables to reduce the maximum error, as demonstrated in the experiment later.

Hence, our important contribution lies in proposing the first online PARASOL method that seeks a Δ-covered set of the FIs. It can process any transaction of length L in O(k) space and almost in O(kL) time, unlike to the existing online PC and NC methods (Manku and Motwani 2002; Karp and Shenker 2003; Jin and Agrawal 2005; Chi et al. 2004; Jiang and Gruenwald 2006; Song et al. 2007; Li et al. 2008; Cheng et al. 2008; Yen et al. 2011; Shin et al. 2014; Quadrana et al. 2015). Compared with the existing RC method (Yamamoto et al. 2014), our solution is more accurate in the sense that Δ is much smaller, while the support of every FI can be restored within an error bounded by Δ.

We also highlight the issue on data structure to efficiently perform the key operations of the proposed method. Especially, we focus on a binomial spanning tree, called weeping tree. Unlike the previously proposed data structures, such as prefix trees (Borgelt et al. 2011; Shin et al. 2014) and vertical format index (Yen et al. 2011), the weeping tree captures not only each itemset but its occurrence sequence in the transactions. As a result, the weeping tree exhibits several interesting features that are essential to prune redundant update process. To our knowledge, this is the first attempt to demonstrate the applicability of binomial spanning trees in the context of FIM-SD.

Notation and terminology

Let I = {1,2,…, N} be the universal set of items. Itemset t is a non-empty subset of I, i.e., t ⊂ I. Data stream ${\mathcal S}_{n}$ is the sequence of itemsets 〈t₁, t₂,…, t_n〉 for which t_i ⊂ I for i = 1,2,..., n where n denotes the timestamp for which an output is requested by the user. Each t_i is called transaction at timestamp i. The number of items in t_i (i.e., the cardinality) is denoted as |t_i| and is referred to as the length of t_i. L denotes the maximum length of the transactions in ${\mathcal S}_{n}$. For itemset α ⊂ I and timestamp i, tran(α, i) denotes the family of itemsets each of which includes α as a subset at timestamp i (i.e., $tran(\alpha , i) = \{t_{j}~|~\alpha \subseteq t_{j},\ 1\leq j \leq i\})$. Supportsup(α, i) of itemset α at timestamp i is defined as |tran(α, i)|. Given a minimum support threshold σ (0 ≤ σ ≤ 1), if sup(α, n) > σn, then α is frequent with respect to σ in ${\mathcal S}_{n}$. $\mathcal {F}_{n}$ denotes the family of FIs with respect to σ at timestamp n in ${\mathcal S}_{n}$, i.e., $\mathcal {F}_{n} = \{\alpha \subset I~|~ \sup (\alpha , n) > \sigma n\}$. FI α is closed if there is no α’s proper superset whose support is equal to α’s support in $\mathcal {F}_{n}$. On the other hand, FI α is maximal if there is no α’s proper superset in $\mathcal {F}_{n}$.

Next, we define two key notions to describe a condensed representation of the FIs as follows:

Definition 1 (Δ-cover)

Let α and β be two itemsets. If $\alpha \subseteq \beta$ and sup(α, i) ≤ sup(β, i) + Δ for a non-negative integer Δ, then α is Δ-covered by β at timestamp i; this state is denoted by $\alpha \preceq _{\Delta }^{i} \beta$.

Definition 2 (Δ-covered set)

Let P and Q be two families of itemsets. If ∀α ∈ P ∃β ∈ Q such that $\alpha \preceq _{\Delta }^{i} \beta$ for a non-negative integer Δ, then Q is a Δ-covered set of P at timestamp i.

Example 1

Consider the family, P of four itemsets α₁, α₂, α₃, and α₄, shown in Fig. 2. For Q₀ = {α₁, α₃, α₄}, Q₁ = {α₃, α₄} and Q₂ = {α₄}. Hence, Q₀, Q₁ and Q₂ are 0-covered, 1-covered and 2-covered sets of P, respectively. Note also that there exists another 1-covered set $Q_{1}^{\prime } = \{\alpha _{1}, \alpha _{4}\}$ of P.

Fig. 2

Example of a Δ-covered set

A Δ-covered set is a generalization of the closed itemsets. The closed itemsets of the family $\mathcal {F}_{n}$ of FIs compose a 0-covered set of $\mathcal {F}_{n}$. Note also that each FI and its support can be recovered from a Δ-covered set within an error bounded by Δ; in the following, this property is called Δ-deficiency. Let us consider again the 2-covered set Q₂, in Example 1. By anti-monotonicity with respect to support, sup(α₄, n) ≤ sup(α_j, n) (1 ≤ j ≤ 3) holds for a timestamp n. Since Q₂ is a 2-covered set of P, $\alpha _{4}{\preceq _{2}^{n}} \alpha _{j}$, so sup(α_j, n) ≤ sup(α₄, n) + 2. Since both 3 ≤ sup(α_j, n) and sup(α_j, n) ≤ 5 hold, the maximum error is bounded by 2.

The objective is to find a Δ-covered set of $\mathcal {F}_{n}$ for a non-negative integer, Δ, while processing each transaction t_i (1 ≤ i ≤ n) only once. As explained before, PC mining and RC mining approaches for FIM-SD have been established. PC mining controls Δ according to an error parameter, 𝜖, such that Δ ≤ 𝜖 × i for each timestamp i; however, in the worst case, an exponential number of candidate itemsets must be stored with this approach. Indeed, it is not feasible for any PC method to solve this problem in O(k) space for a constant k.

Hence, we aim to design a novel method by integrating PC and RC mining approaches so that Δ is kept as small as possible based on a given value of k, which bounds the memory consumption. Herein, we present a baseline method to find a Δ-covered set of $\mathcal {F}_{n}$ for a given k in O(kLn) time and O(k) space, where L is the maximum length of transactions and n is the end timestamp.

Baseline algorithm for online Δ-covered set mining

The baseline algorithm is built on two key techniques: incremental intersection and minimum entry deletion, which are described in detail in this section.

Incremental intersection (Borgelt et al. 2011; Yen et al. 2011) is used for computing the closed itemsets. It is based on the following cumulative and incremental features of the closed itemsets. Let $\mathcal {C}_{i}$ be the family of closed itemsets in $\mathcal {S}_{i}$.

Theorem 1

(Borgelt et al. 2011; Yen et al. 2011) Given$\mathcal {C}_{i-1}$at timestamp i − 1 and transactiont_iat timestamp i, $\mathcal {C}_{i}$is given as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{C}_{i} &=& \emptyset ~~ \text{for}~~ i = 0 \\ \mathcal{C}_{i} &=& \mathcal{C}_{i-1} \cup \{t_{i}\} \cup \{\ \beta ~|~ \beta = \alpha\ \cap\ t_{i},\ \beta\neq\emptyset,\ \alpha\in \mathcal{C}_{i-1}\ \} ~~ \text{for} ~~ i \geq 1 \end{array} $$

Proof

This recursive relationship has been revealed in the literature (Borgelt et al. 2011; Yen et al. 2011). We also give a brief sketch of the proof in Appendices A and B. □

Theorem 1 ensures that $\mathcal {C}_{i}$ can be computed from the intersection of each itemset in $\mathcal {C}_{i-1}$ with t_i.

Example 2

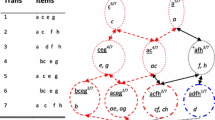
Let I = {1,2,3,4,5} and the stream $\mathcal {S}_{4}^{1} = \langle t_{1}, t_{2}, t_{3}, t_{4} \rangle$ where t_i = I −{i} for each i (1 ≤ i ≤ 4). Figure 3 illustrates how $\mathcal {C}_{i}$ is incrementally generated until i = 3. $\mathcal {C}_{1}$ consists of the first transaction. $\mathcal {C}_{2}$ newly contains α₂ and α₃, which correspond to the second transaction and its intersection with α₁, respectively. Finally, $\mathcal {C}_{3}$ and $\mathcal {C}_{4}$ consist of the seven and fifteen closed itemsets, respectively.

Fig. 3

Example of incremental intersection

An incremental intersection never unfolds a transaction to intermediate subsets. We just intersect each stored itemset by the transaction. Then, the update operation never involves the subset enumeration of itemsets. Besides, we do not need to check if the generated one is a closed itemset by Theorem 1. In this sense, incremental intersection can simply but efficiently compute only the closed itemsets. On the other hand, lossless compression based on closedness cannot necessarily control an exponential increase of the closed itemsets; in the worst case, Ω(2^L) closed itemsets can be generated. In Example 2, there is a total of fifteen closed itemsets from $\mathcal {S}_{4}^{1}$, which is almost the same as the 2^L closed itemsets that are attained for L = 4.

Hence, it is required to embed a space-saving technique into incremental intersection. In this paper, we introduce the notion of minimum entry deletion which has been proposed in RC mining (Metwally et al. 2005; Yamamoto et al. 2014). Given a size constant, k, minimal entry deletion is performed when the number of stored itemsets exceeds k to keep only the top-k itemsets; in other words, the itemset with the lowest approximate support must be deleted iteratively as long as the number of stored itemsets is greater than k. The maximum value in the approximate supports of the deleted itemsets is then maintained as the maximum error, Δ. It is reasonable for space-saving to embed the same scheme into the update process by incremental intersection.

The baseline algorithm manages two types of information for each stored itemset: its approximate support count and maximum error count. They are represented as a tuple entry of the form 〈α, c,Δ〉, which represents the stored itemset, the approximate support count, and maximum error count, respectively. In the following, we call c and Δ the frequency count and error count of α, respectively. Besides, the itemset, frequency count, and error count of an entry, e, are often denoted by α_e, c_e, and Δ_e, respectively.

Example 3

Consider $\mathcal {S}_{4}^{1}$ again. Let k = 3. The number of $\mathcal {C}_{3}$ is beyond k = 3 at timestamp i = 3. As shown in Fig. 4, we remove four closed itemsets in order of increasing frequency count; the highest count of those that are removed is two. The next transaction, t₄, is stored in the entry 〈t₄,3,2〉, meaning that the support of t₄ is between one and three (i.e., 1 ≤ sup(t₄,4) ≤ 3).

Fig. 4

Example of minimal entry deletion

In the following, T_i denotes the collection of entries used at timestamp i, k(i) denotes the number of entries in T_i, and Δ(i) denotes the maximum error at timestamp i. A minimum entry in T_i is an entry whose frequency count is the lowest of those in T_i. Then, the baseline algorithm is described in Algorithm 1. The updating process is composed of entry addition and entry deletion for each timestamp. The addition operation is carried out by the function intersect(T_i− 1, t_i), which performs the incremental intersection. The deletion operation is realized by the function delete(T_i), which performs the minimum entry deletion.

Example 4

Consider T₄ again as shown in Fig. 4. T₄ corresponds to the output of Line 5 in Algorithm 1 at i = 4 for the input stream $\mathcal {S}_{4}^{1}$ and k = 3. By the deletion process of Line 6, Δ(4) becomes three. Now, we assume that the top three entries in T₄ remain as shown in Fig. 5. Next, let the transaction arriving at i = 5 be t₅ = {1,3,5}. Then, by the addition process, we first add the entry 〈t₅,3,3〉 to T₄, since there is no entry for t₅ in T₄. After that, the intersection of each stored itemset in T₄ with t₅ is computed and stored in C. In total, C consists of three entries. Then, T₅ is obtained by updating T₄ with C by way of Lines 26-33 in the intersect function. Finally, the minimum entry, 〈{2,5},3,0〉, is deleted from T₅ to ensure that k(5) ≤ k.

Fig. 5

Example of the baseline algorithm

Next, we clarify the quality of the output by the baseline algorithm.

Theorem 2

Algorithm 1 outputs a Δ(n)-covered set of the FIs wrt σ, provided that Δ(n) ≤ σn.

This implies that for every FI, α, T_n must contain an entry, e, in which α is Δ(n)-covered by α_e. To demonstrate this feature, we introduce the notion of a representative entry.

Definition 3

Let α be an itemset. Given T_i, $T_{i}^{\alpha }$ is used to denote the set of entries in T_i that contains such an itemset β that $\alpha \subseteq \beta$. If $T_{i}^{\alpha }$ is not empty, a representative entry, r, for α is defined as an entry that has the maximum frequency count of those in $T_{i}^{\alpha }$ (i.e., $r = argmax_{e \in T_{i}^{\alpha }} (c_{e})$).

Then, for every FI, α, and a representative entry, r, of α, we claim that α is Δ(n)-covered by α_r. This claim can be explained as shown in Fig. 5: Since Δ(5) = 3, we set σ = 0.6 to ensure that Δ(5) ≤ σ × 5. There exist five FIs {1},{3},{5},{1,5},{3,5} wrt σ in $\mathcal {S}_{5}^{1}$ (that is, $\mathcal {S}_{5}^{1} = \mathcal {S}_{4}^{1} \circ \langle t_{5}=\{1,3,5\}\rangle$). Let α be the FI {3,5}. $T_{5}^{\alpha }$ uniquely contains the entry r = 〈{1,3,5},4,3〉. Hence, r is the representative entry of α. Note that α = {3,5} is 1-covered by α_r = {1,3,5}, since sup({1,3,5},5) = 3 and sup({3,5},5) = 4.

First, we prove the following proposition and two lemmas.

Proposition 1

Let ebe an entry in T_i. Then, eis a representative entry for α_e.

Proof. Suppose that e is not a representative entry. Then, there exists another entry, $e^{\prime }\in T_{i}$, such that $\alpha _{e}\subseteq \alpha _{e^{\prime }}$ and $c_{e} < c_{e^{\prime }}$. This contradicts the anti-monotonicity in T_i, which is proved by using the mathematical induction, following the below argument. First, since T₁ contains only one entry, T₁ satisfies the anti-monotonicity property. Assume that T_i satisfies this property (i.e., for every two entries, e and $e^{\prime }$, if $\alpha _{e}\subseteq \alpha _{e^{\prime }}$ then $c_{e} \geq c_{e^{\prime }}$ holds). Then, by the cumulative feature of the incremental intersection, the output of the function intersect(T_i, t_i+ 1) also exhibits anti-monotonicity. Moreover, this property is preserved by the deletion process. Therefore, T_i+ 1 also exhibits the anti-monotonicity. $\Box$

Lemma 1

Let αbe an itemset. Given T_i, if there exists a representative entry rfor αin T_i, then it holds that

$$c_{r} - {\Delta}_{r} \leq sup(\alpha, i) \leq c_{r}.$$

Proof

We use the mathematical induction. T₁ consists of only one entry, 〈t₁,1,0〉. Since k > 0, this entry is not deleted. Accordingly, this lemma is true in the case of T₁. Assume that T_i satisfies the claim of the lemma. Let α be an itemset whose representative entry, r_i+ 1, exists in T_i+ 1. Now, we consider two cases for the existence of a representative entry r_i for α in T_i.

• Case 1:r_i exists. Based on the assumption, we have $c_{r_{i}} - {\Delta }_{r_{i}} \leq sup(\alpha , i) \leq c_{r_{i}}$. If $\alpha \not \subseteq t_{i+1}$, then $c_{r_{i+1}} = c_{r_{i}}$ because $T_{i}^{\alpha } \supseteq T_{i+1}^{\alpha }$ and $T_{i+1}^{\alpha } \neq \emptyset$ (i.e., the maximum frequency count in $T_{i}^{\alpha }$ is preserved in $T_{i+1}^{\alpha }$ by the minimum entry deletion); thus, since sup(α, i + 1) = sup(α, i), $c_{r_{i+1}} - {\Delta }_{r_{i}} \leq sup(\alpha , i+1) \leq c_{r_{i+1}}$. Otherwise, since $\alpha \subseteq t_{i+1}$, $c_{r_{i+1}} = c_{r_{i}} + 1$ holds because T_i+ 1 contains the entry for $\alpha _{r_{i}}\cap t_{i+1}$ which has a frequency count of $c_{r_{i}} + 1$. Since sup(α, i + 1) = sup(α, i) + 1, $c_{r_{i+1}} - {\Delta }_{r_{i}} \leq sup(\alpha , i+1) \leq c_{r_{i+1}}$. Finally, since ${\Delta }_{r_{i}} \leq {\Delta }_{r_{i+1}}$, we have $c_{r_{i+1}} - {\Delta }_{r_{i+1}} \leq sup(\alpha , i+1) \leq c_{r_{i+1}}$.

• Case 2:r_i does not exist. This means that α or its supersets never appear or have been deleted before the time i. Hence, sup(α, i) is at most Δ(i), because Δ(i) is the upper bound of the frequencies of the deleted itemsets. Since r_i+ 1 exists but r_i does not, r_i+ 1 corresponds to 〈t_i+ 1,1 + Δ(i),Δ(i)〉. Hence, $\alpha \subseteq t_{i+1}$ holds. Accordingly, 1 ≤ sup(α, i + 1) ≤ 1 + Δ(i) holds. Since $c_{r_{i+1}} = 1 + {\Delta }(i)$ and ${\Delta }_{r_{i+1}} = {\Delta }(i)$, it holds that $c_{r_{i+1}} - {\Delta }_{r_{i+1}} \leq sup(\alpha , i+1) \leq c_{r_{i+1}}$.

In both cases, T_i+ 1 also satisfies the claim of the lemma.

□

Lemma 2

For every itemset, α, such that sup(α, i) > Δ(i), there exists a representative entry r ∈ T_ifor α.

Proof

We also use the mathematical induction. The lemma is obviously true in the case of T₁ since Δ(1) = 0 holds. Assume that T_i satisfies the claim of this lemma; we show the induction step by contradiction. Assume that ∃α such that sup(α, i + 1) > Δ(i + 1) but there is no representative entry for α in T_i+ 1. We can consider two cases: whether or not a representative entry, r, has existed in T_i+ 1 before the deletion operation (i.e., in the intermediate T_i+ 1 at the moment when the incremental intersection has been completed, as depicted in the middle T_i+ 1 in Fig. 6).

• Case 1: such an r exists in T_i+ 1 but was deleted. By Lemma 1, we have c_r −Δ_r ≤ sup(α, i + 1) ≤ c_r. Since r was deleted, c_r ≤Δ(i + 1) should hold. Thus, sup(α, i + 1) ≤Δ(i + 1) also holds. However, this is a contradiction.

• Case 2: such an r does not exist in T_i+ 1. Here, T_i+ 1 captures the entry table before the deletion operation. Thus, $T_{i}^{\alpha } \subseteq T_{i+1}^{\alpha }$ holds. Since there is no representative entry for α in T_i+ 1, it holds that $T_{i+1}^{\alpha } = \emptyset$ and $T_{i}^{\alpha } = \emptyset$. Note that T_i+ 1 should contain the entry for t_i+ 1. Hence, $\alpha \not \subseteq t_{i+1}$ because $T_{i+1}^{\alpha } = \emptyset$. Therefore, sup(α, i) = sup(α, i + 1). Since sup(α, i + 1) > Δ(i + 1) and Δ(i + 1) ≥Δ(i), it should hold that sup(α, i) > Δ(i). Then, by the assumption for T_i, there should exist a representative entry for α in T_i. However, this contradicts the conclusion that $T_{i}^{\alpha } = \emptyset$.

Fig. 6

Sketch of updating T_i to T_i+ 1 with t_i+ 1

In both cases, there is a contradiction. Therefore, for every α such that sup(α, i + 1) > Δ(i + 1), there exists a representative entry for α in T_i+ 1. □

Now, we prove Theorem 2 as follows:

Proof of Theorem 2

Suppose that the condition of σ (i.e., Δ(n) ≤ σn) is satisfied. Then, by Lemma 2, for every FI α wrt σ, there exists a representative entry, r, in T_n for α. By Lemma 1, c_r −Δ_r ≤ sup(α, n) ≤ c_r holds. By Proposition 1, r is also a representative entry for α_r. Thus, we have c_r −Δ_r ≤ sup(α_r, n) ≤ c_r. Hence, sup(α, n) ≤ sup(α_r, n) + Δ_r holds. Since $\alpha _{r}\supseteq \alpha$, α is Δ_r-covered by α_r. Since Δ_r ≤Δ(n), we can claim that for every FI α, there exists an entry, r , such that α is Δ(n)-covered by α_r. Note that c_r > σn holds because sup(α, n) > σn. Hence, r is contained in the output because of Lines 9-11 in Algorithm 1. □

Next, we clarify the complexity of the baseline algorithm. Incremental intersection generates at most k(i) + 1 new entries for the intersections of the entries in T_i with t_i+ 1 as well as t_i+ 1 itself; these new entries are added to C in Lines 16 and 21 of the intersect function. Thus, the total number of stored entries is at most 2 × k(i) + 1, and k(i) is always bounded by the size constant k. Hence, the complexity of the baseline algorithm can be described as follows:

Theorem 3

For a size constant kand the maximum transaction length L, Algorithm 1 processes every transaction in$O(kL+k\log k)$time and O(k) space.

Proof

First, the number of stored entries is at most 2k + 1 for every time point. Thus, the space required to store them is O(k). In addition, it takes at most O(2L) time to compute the intersection of a stored itemset with a transaction. Thus, the incremental intersection is performed in O(kL) time. It takes at most $O(\log k)$ time to delete a minimum entry and add a new entry by using a heap structure. Hence, the total time required to update the table is at most $O(kL + k\log k)$. □

Based on Theorems 2 and 3, Algorithm 1 can extract a Δ-covered set of the FIs wrt $\sigma \geq \frac {\Delta }{n}$ for an integer Δ and can process each transaction in O(kL) time and O(k) space for a size constant k (k < 2^L). Therefore, Algorithm 1 satisfies the three characteristics (i.e., on-the-fly manner, anytime feature, and quality of output) presented in Section 1.

Parasol: a hybrid of PC and RC approximation

We observe in Fig. 1 that a sudden and intensive memory consumption may occur as a temporary phenomenon. In other words, the PC approximation is feasible unless all of the memory is consumed during this short period. Hence, it is reasonable to take a hybrid of PC and RC approximation; the memory consumption is generally controlled by using an error parameter 𝜖 and an RC approximation using a size constant k is taken only when the number of used entries exceeds k. We call this hybrid approximation approach PARASOL (an acronym for Parameter- and Resource-constrained Approximation for Soft and Lazy mining).

Our proposed PARASOL method can be realized just by replacing the delete function in Algorithm 1 with the following function:

The main difference appears in the condition of Line 3. Unless sudden and intensive memory consumption occurs (i.e., k < k(i) holds), the proposed PARASOL method performs the minimal-entry deletion in the PC approximation manner. For this ordinary scenario, it always ensures Δ(i) ≤ 𝜖 × i. Otherwise, it performs the minimal-entry deletion in the RC approximation manner due to the constant space constraint. For this exceptional scenario, it allows Δ(i) to exceed 𝜖 × i. Since sudden and intensive memory consumption is a temporal phenomenon, the RC approximation is only required for a short period. Therefore, the error ratio, $\frac {\Delta (i)}{i}$ gradually converges to 𝜖 after this short period. This self-sustained recovery of the error ratio is a unique and advantageous characteristic of the proposed PARASOL method, and will be empirically demonstrated in experiment later.

Furthermore improvement

Note that the solution to our problem setting is not unique: there can exist many Δ-covered sets of $\mathcal {F}$. Then, it is reasonable to extract a concise Δ-covered set. Here, we propose a fast post-processing technique to reduce the original output to a more concise one based on the maximum error, Δ(n).

First, we explain the intuition using T₅ (the right-most table in Fig. 5) in Example 4. Since Δ(5) = 3, the three itemsets stored in T₅ compose a 3-covered set of the FIs. Interestingly, even if {1,5} was deleted from T₅, the two remaining itemsets could compose a 3-covered set. Let us consider the entry r = 〈{1,5},4,0〉, and let α be an itemset whose representative entry is r. By Lemma 1, the support of α is at most c_r. Since c_r is the same as the frequency count for {1,3,5}, α is also 3-covered by {1,3,5}. Therefore, there is no need to keep r in T₅ for restoring the support of α when Δ = 3.

There is another choice point to delete the entry for {5} from T₅. In exchange for deletion, we need to update the entry for {1,5} by 〈{1,5},5,1〉 (i.e., incrementing the frequency and error counts by one). In this way, the support of {5} can be restored from the entry for {1,5}.

In general, it is infeasible to identify such itemsets to be deleted from an original Δ(n)-covered set so that the remaining set keeps the Δ(n)-deficiency. However, some of them can be simply detected based on the following corollary:

Corollary 1

For every entry e ∈ T_n, if there exists r ∈ T_nsuch that$\alpha _{e}\subsetneq \alpha _{r}$and c_e ≤ c_r −Δ_r + Δ(n), then the itemsets of T_n −{e} compose a Δ(n)-covered set of the FIs wrt σ, provided that Δ(n) ≤ σn.

Proof

Let e be an entry in T_n and α an arbitrary itemset whose representative entry is e. Suppose that there exists an entry r such that $\alpha _{e}\subsetneq \alpha _{r}$ and c_e ≤ c_r −Δ_r + Δ(n). We claim that α is Δ(n)-covered by α_r. By Lemma 1, it holds that sup(α, n) ≤ c_e, followed by sup(α, n) ≤ c_r −Δ_r + Δ(n). Since c_r −Δ_r ≤ sup(α_r, n), we have sup(α, n) ≤ sup(α_r, n) + Δ(n). Since $\alpha \subseteq \alpha _{e}$ and $\alpha _{e}\subsetneq \alpha _{r}$, we also have $\alpha \subsetneq \alpha _{r}$. Hence, α is Δ(n)-covered by α_r. The claim implies that even if e was removed, the support of α can be recovered using r, while Δ(n) remains as it is. □

Now, we propose a post-processing technique, called Δ-compression, which incrementally deletes the entry from T_n according to Corollary 1, as described in Algorithm 2. In exchange for deleting e, Δ_r is updated by increasing it by the difference between c_e and c_r, and c_r is updated to c_e in Lines 3 and 4.

Note that the output produced by Algorithm 2 does not necessarily compose a minimal Δ(n)-covered set of the FIs. The counter example is derived by using T₅ of Example 4. After applying Algorithm 2, T₅ contains two itemsets {1,3,5} and {5} (alternatively, {1,3,5} and {1,5}). However, only {1,3,5} is enough to compose a 3-covered set of the FIs (σn is now assumed to be greater than or equal to 3). Thus, the output is not a minimal 3-covered set. A simple implementation of Algorithm 2 is that for each entry e, we search T_n for a corresponding r. This can be achieved in O(k²) time, since |k(n)|≤ k.

Data structure

Here, we address the issue of the data structure that is needed to efficiently realize the three key operations of the proposed algorithm: incremental intersection, deletion, and Δ-compression. Of these, incremental intersection incurs the majority of the computational cost. This operation imposes the traverse of every entry, e, to compute its intersection with a transaction, t_i, for each timestamp i. This computation is often redundant: for example, if α_e has no common items with t_i, it is redundant to compute the intersection of α_e with t_i.

Based on this observation, Yen et al. (2011) proposed an indexing data structure, called cid_list, corresponding to the vertical format of the stored itemsets: for each item, x, cid_list(x) maintains the indexes of the entries corresponding to the itemsets that contain x. Using cid_list, we can focus only on the entries whose indexes are contained in $\bigcup _{x\in t_{i}} cid\_list(x)$ and compute their intersections with t_i. However, the computational cost of updating cid_list is relatively high: the entire cid_list is dynamically changed by addition and deletion operations. This overhead becomes especially high for dense datasets since most itemsets stored in T_i have some of the same items as t_i.

Borgelt et al. (2011) proposed a fast two-pass FIM method, called ISTA, based on incremental intersection. In this implementation, the prefix tree (as well as patricia) was introduced to efficiently maintain T_i and perform the incremental intersection. Although it is reasonable to represent T_i with such a concise data structure, it is not directly applicable in the one-pass approximation setting that is used here. For example, we cannot use the item support as static information, while it is available in the transactional database that allows multi-pass scanning. This information is crucial to constructing a compact trie by sorting items in a pre-processing step. Note that the trie size can be directly affected by the order of (sorted) transactions. Indeed, ISTA constructs the trie with 306 nodes by treating it as a retail problem (No. 3 in Table 1), compared to 244,938 nodes when the pre-processing technique is not applied. Besides, in the context of the SD that emerges concept drift, it is not appropriate to assume a static distribution.

Table 1 Characteristics of the used datasets

Thus, it is necessary to design a more suitable data structure for our proposed algorithm, which enables to prune redundant computations in incremental intersections, as well as quickly access both the minimum entries and Δ-covered entries required for PARASOL deletion and Δ-compression, respectively.

Weeping tree

Now, we propose a variation of the binomial spanning tree (Johnsson and Ho 1989; Chang 2005), called weeping tree, in which a collection of entries, T_n, can be represented in a binary n-cube as follows: Let e be an entry in T_n. By Theorem 1, α_e corresponds to the intersection of a certain set S of transactions. This set can be represented as a binary address (x₁, x₂,…, x_n) where each x_j is one if S contains t_j and zero otherwise. Every α_e has its own binary address. Thus, T_n can be represented as a set of binary addresses, denoted by V (n), each of which identifies α_e for an entry e ∈ T_n. Each binary address can be described by an integer, $x = {\Sigma }_{j=1}^{n} (x_{j}\times 2^{n-j})$. Then, V (n) corresponds to a subset of {1,…,2ⁿ − 1}.

Let x and y be two integers (1 ≤ x, y ≤ 2ⁿ − 1) with the addresses $(x_{1},x_{2},\ldots , x_{n})$ and $(y_{1},y_{2},\ldots , y_{n})$, respectively. p(x) is the position in x that satisfies two conditions: x_p(x) = 1 and x_j = 0 for each j(p(x) + 1 ≤ j ≤ n). In other words, p(x) is the least significant set bit of x. We say that x covers y if y_j = x_j for each j where 1 ≤ j ≤ p(x). For example, if x = 12 and y = 15 in 4-cube with addresses (1100) and (1111) then, p(x) = 2, y₁ = x₁, and y₂ = x₂ so x covers y. We assume that zero covers every integer.

Now, we define the binomial spanning tree of V (n), following the notion in the literature (Chang 2005).

Definition 4 (Binomial spanning tree)

Let V (n) be a subset of {1,…,2ⁿ − 1}, x be an integer such that 0 ≤ x ≤ 2ⁿ − 1, and C(x) be the set of integers in V (n) each of which is covered by x. The binomial spanning tree of V (n) is the tree in which the root node, r, is zero and the other nodes are V (n). The children of each node, x, correspond to the following set:

$$\{ y~|~y\in C(x)\ and \not\exists y^{\prime}\in C(x)\ s.t.\ y \neq y^{\prime}\ and\ y \in C(y^{\prime})\}.$$

The siblings y⁽¹⁾, y⁽²⁾,…, y^(m) are sorted in the descending order (i.e., y^(j) is the left sibling of y^(j+ 1)). We say that a non-root node, y, is a descendant of node x if y ∈ C(x), a precursor of x if y∉C(x) and y > x, and a successor of x if y < x. The precursors and successors of x are denoted at P(x) and S(x), respectively.

The weeping tree at time n, denoted by W(n), is the binomial spanning tree of V (n) obtained by associating each node, x, with its corresponding entry e (i.e., α_e is the intersection of the transactions indicated by the address x).

Example 5

Consider again the stream $\mathcal {S}_{4}^{1}$ in Example 2. Let 𝜖 and k be 0.2 and 15, respectively. PARASOL uses the 15 entries in T(4) for all closed itemsets (i.e., V (4) = {1,2,…,15}). The corresponding weeping tree, W(4), is described in Fig. 7. Each node, x, is associated with its own entry, e. For example, the node x = 6 (0110) corresponds to the entry for α = t₂ ∩ t₃, i.e., α = {1,4,5}. Note also that C(6) = {7}, P(6) = {8,9,…,15} and S(6) = {1,2,…,5}.

Fig. 7

The weeping tree W(4) wrt ${\mathcal S}_{4}^{2}$

One crucial feature of the weeping tree is that it captures inclusion relationships among the stored itemsets in T_n.

Proposition 2

Let two nodes xand ybe associated with two entries e_xand e_y. If xcovers y, then$\alpha _{e_{y}}\subseteq \alpha _{e_{x}}$

Proof

The address of y can be written as (x₁,…, x_p(x), y_p(x)+ 1,…, y_n), since x covers y. Accordingly, $\alpha _{e_{y}}$ is written as $(\bigcap _{x_{j} = 1, 1\leq j \leq p(x)} t_{j})\ \cap \ I$ where $I = \bigcap _{y_{j} = 1, p(x)+1\leq j \leq n} t_{j}$. Since p(x) is the position of the least significant set bit, $\alpha _{e_{x}}=\bigcap _{x_{j} = 1, 1\leq j \leq p(x)} t_{j}$ holds, followed by $\alpha _{e_{y}} = \alpha _{e_{x}}\cap I$. □

Proposition 2 has three useful implications. First, it is applicable for pruning the intersection computations. Suppose that during the updating process at time i, an entry, e, is found such that $\alpha _{e} \subseteq t_{i}$. Since every descendant of e must be included in t_i, it is not necessary to compute the intersections for these descendants. Proposition 2 also implies that every minimum entry must be located in the shallowest layer in the tree due to the anti-monotonicity of T_i. This feature is useful for the minimum entry deletion (in practice, it is reasonable to use min-heap for the shallowest layer).

Finally, Proposition 2 is applicable to the pairwise checking involved in Δ-compression. Suppose that we found a parent entry, e_p, and its child entry, e_c such that $C_{e_{c}} \leq C_{e_{p}}-{\Delta }_{e_{p}} + {\Delta }(n)$. Then, $\alpha _{e_{c}}$ must be Δ(n)-covered by $\alpha _{e_{p}}$ according to Corollary 1. Hence, a quick check can be done to determine if each child is Δ(n)-covered by its parent. Note that a brute-force approach requires O(k²) time for Δ-compression while the quick pairwise checking can be completed in O(k) time. Thus, it is useful as a pre-processing step preceding Δ-compression.

Weeping tree updating

Here, we explain how to incrementally update W(i) at each time i. Suppose that an itemset, α, is newly stored in W(i + 1). An address (x₁,…, x_i,1) is then assigned to α, where (x₁,…, x_i) is the address of the node, r, in W(i) that corresponds to a representative entry of α if such an r exists; if there is no such node, r is the root node. Thus, the entry for α is newly located as a child of node r.

Example 6

Consider Example 5 again. Let α be the itemset {2,5} that is newly added in W(4). There exists a representative entry r = 〈{2,4,5},2,0〉, for α (see Fig. 4) in T(3). Since r is given the address (101) at time i = 3, the address of α becomes (1011), and the entry for α is located as a child of r.

We can interpret the meaning of the address assigned to each entry. Let e be an entry of node x with the address (x₁,…, x_n). We denote the least and greatest significant bit sets of x as p(x) and q(x), respectively. Then, e is written as 〈α,Δ(q(x) − 1) + B,Δ(q(x) − 1)〉, where $\alpha = \bigcap _{x_{j}=1, q(x)\leq j\leq p(x)} t_{j}$, Δ(q(x) − 1) is the maximum error at time q(x) − 1 and B is the bit count of x (See Fig. 8). This observation leads to the following proposition:

Fig. 8

Relation between address and entry

Proposition 3

Consider two nodes, xand y, of entries e_x and e_y, respectively, in a weeping tree. If$\alpha _{e_{y}}\subseteq \alpha _{e_{x}}$, then yis either a descendant or a precursor of x.

Proof

We derive a contradiction in the case that $\alpha _{e_{y}}\subseteq \alpha _{e_{x}}$ and y < x. Let v be the address obtained by the bitwise OR operation between x and y. Since y < x and x ≤ v, y < v. We write v as (v₁,…, v_n) and denote by α_v the intersection $\bigcap _{v_{j} = 1, 1\leq j\leq n} t_{j}$. Since $\alpha _{e_{y}}\subseteq \alpha _{e_{x}}$, we have $\alpha _{v}=\alpha _{e_{y}}$. Thus, node v should not appear in the tree, since its duplicate never occurs in T_n. Without losing generality, this implies that v has been deleted at some time, which is referred to as time m. Accordingly, the tree never contains such a node, u, with an address (u₁,…, u_n) such that q(u) = q(v); moreover, the bit count of the m-prefix (u₁,…, u_m) is lower than the bit count of the m-prefix (v₁,…, v_m). This is because every node with such an address has been deleted at time m, along with v (i.e., u has a lower frequency count than v). Hence, no node can have an address in which the m-prefix matches (u₁,…, u_m) or (v₁,…, v_m). Next, we consider the address of node x. Since y < x and v is obtained by a bitwise OR operation between x and y, we have q(x) = q(v). In addition, (x₁,…, x_m) is either equal to (v₁,…, v_m) or has a lower bit count than (v₁,…, v_m). Hence, x should not appear in the tree. This is a contradiction. □

For example, consider node 6 for the itemset {1,4,5} as shown in Fig. 7. There are three nodes 7,14,15 that have subsets of this itemset and each of these nodes is either a descendant or a precursor of the node 6.

Proposition 3 is useful for pruning the computation for incremental intersection. Suppose that for some entry C, t_i ⊂ α_C holds. Thus, the intersection computations for every successor of C with t_i can be skipped as they do not store any subset of t_i (See Fig. 9).

Fig. 9

Reasoning for Proposition 3

The weeping tree can be used to perform the incremental intersection by traversing the weeping tree in a depth-first, left-to-right manner. Algorithm 3 sketches the process for updating a node x in W(i) with an itemset E. Note that E is initially a transaction.

In the algorithm, a node, x, is identified with its associated entry, e_x. Here, α_x, c_x and Δ_x are the itemset, frequency, and error count of e_x, respectively. Given the transaction t_i+ 1 and W(i), the next tree, W(i + 1), is obtained by calling the function update(root, t_i+ 1, W(i)). Note that W(0) is defined as the initial tree consisting of the root node.

A few characteristics of the update(x, E, W(i)) algorithm should be noted:

• Line 4 means that $\alpha _{y}\subseteq E$. By Proposition 2, the descendants of y are included by E. Thus, the frequency count of each node, z ∈ C(y), can be simply incremented without computing the intersection except for α_y itself. This is called descendant-intersect-skipping (DIS).

• In Line 9, we continue the updating process. In the recursive call, the intersection, I, is used instead of the original itemset, E. It follows that $\alpha _{y^{\prime }}\cap E = \alpha _{y^{\prime }}\cap I$ for each child $y^{\prime }$ of y since I = α_y ∩ E. By reducing E to I (i.e., I is a subset of E), the computational cost of the recursive call after Line 9 is reduced. This pruning technique is called masking.

• If I = ∅, every descendant of y has no items in common E so the descendants need not be updated. This is called descendant-update-skipping (DUS).

• Line 11 checks if $E \subseteq \alpha _{y}$ or not. If so, every right sibling of y need not be updated. This follows from the observation in Proposition 3 that the entry for any subset of E to be updated never appears in the successors of y. This is called successor-update-skipping (SUS).

• Finally, if there is no entry for E in W(i), the new entry for E is added as the right-most child of x. Note that if x is the root node, we set c_x = 0 and Δ_x = Δ(i).

Example 7

We explain how Algorithm 3 works using

$${\mathcal S}^{2}_{4} = \langle \{1,2,3,5\},\{1,2,4\},\{2,3,4\},\{1,2,5\}\rangle.$$

W(3) corresponds to the left tree in Fig. 10. The function update(root, t₄, W(3)) is called to derive W(4) from W(3). For the left-most child e₁, the intersection, I₁ = {1,2,5} of e₁ with t₄ is computed. Since I₁≠∅, we call update(e₁, I₁, W(3)) as shown in Line 9. For the left-most child, e₂, of e₁, the intersection I₂ = {1,2} of e₂ with I₁ is computed using I₁ by masking. Since $I_{2} = \alpha _{e_{2}}$, DIS is applied in Lines 5-7. Then, $c_{e_{5}}$ is simply incremented by one. Moving to the right sibling, e₄, the intersection I₄ = {2} of e₄ with I₂ is computed. Since I₄≠∅, update(e₄, I₄, W(3)) is called. Since e₄ does not have any children, the algorithm checks if there exists the entry for I₄ then backtrack to the second call (i.e., update(e₁, I₁, W(3))). Since there is no sibling of e₄, the algorithm returns to Line 15 and a new entry, e₇, for I₁ is added as the right most child of e₁. After backtracking to the first call, SUS is applied in Line 11 since I₁ = t₄. Thus, the updating of the two right-most sibling nodes, e₃ and e₆, is skipped and the algorithm proceeds to Line 15. Since an entry for t₄ exists, the updated tree, W(4), is returned as the output.

Fig. 10

The weeping trees W(3) and W(4) wrt ${\mathcal S}^{2}_{4}$

In this way, the update function realizes the incremental intersection. Note that every node in W(i) is visited at most once, which implies that Algorithm 3 efficiently runs update(root, t_i+ 1, W(i)) to return W(i + 1) in O(kL) time.

Next, we show how PARASOL realizes the minimum entry deletion in the weeping tree. As explained before, the minimum entries to be deleted are allocated in the shallowest layer relative to the root. Recall Example 5, in which 𝜖 was set to 0.25 and PARASOL was used to delete the entries with frequency counts of one at time i = 4. These minimum entries can be quickly accessed by applying min-heap to the shallowest layer. The reduced weeping tree is obtained by reconnecting the children of the deleted nodes with the root as shown in Fig. 11.

Fig. 11

The reduced weeping tree of W(4)

The weeping tree can be used as a pre-processing step for the Δ-compression in such a way that we find such a child node e that c_e ≤ c_r −Δ_r + Δ(n) where r is the parent node of e. By Corollary 1, e can be deleted from the tree.

Figure 11 shows the reduced tree obtained by searching the weeping tree W(4) in a bottom up manner from the left-most leaf to the root; this process results in the removal of four nodes (7, 11, 13, and 15). Note that Δ-compression requires O(k²) time to completely check every pair of nodes. Thus, it is reasonable to carry out the Δ-compression in a two-step procedure; first checking each pair of parent-child nodes in a one-time scan and subsequently performing the brute-force search of the remaining nodes.

Experiment

Now, we empirically evaluate the performances of the baseline algorithm, PARASOL, and Δ-compression, respectively. They have been implemented with the weeping tree (in C language²). Ten real datasets were collected from Yamamoto et al. (2014) (Nos. 1-2), the FIMI repository³ (Nos. 3-9), and a new benchmark (No. 10) created from the Yahoo! Hadoop grid logs dataset⁴ as shown in Table 1. Note that n, |I|, L, and L_ave are the end time, the number of different types of items, the maximum transaction length, and the average transaction length, respectively.

First, the baseline algorithm was compared with the state-of-the-art RC method, Skip LC-SS (Yamamoto et al. 2014), on the existing real datasets (Nos. 1-9). Then, the scalability of the baseline algorithm was demonstrated on the synthesized datasets generated by the IBM market basket generator. Next, the performance of PARASOL was compared with those of the baseline algorithm and the state-of-the-art PC method, MOA-IncMine (Quadrana et al. 2015), when applied to the large-scale dataset (No. 10). Finally, we evaluated the effectiveness of Δ-compression in reducing the output. Table 2 describes the overall improvement that has been realized by the baseline algorithm, compared with Skip LC-SS, for each dataset in terms of the maximum error, Δ(n), the error ratio, $\frac {\Delta (n)}{n}$, and the average updating time (msec). In this experiment, the size constant, k, was fixed as 12,000. The results show that the baseline algorithm drastically reduced the error. Notably, in datasets 4, 5, 6, 8, and 9, the error ratio with Skip LC-SS reached one, meaning that the FIs could not be found for any σ (0 < σ < 1), while the baseline provided a Δ(n)-covered set of the FIs for which Δ(n) ≤ σn. Moreover, the updating time of the baseline algorithm was lower than the one of Skip LC-SS.

Table 2 Skip LC-SS versus the baseline algorithm

Skip LC-SS was compared with the baseline algorithm with a range of size constants for the dataset 7, on which Skip LC-SS performed the best in terms of the error ratio. The results are summarized in Fig. 12a.

Fig. 12

Performance of the baseline algorithm

The data shows that the baseline algorithm (bold lines) performed better than Skip LC-SS in terms of maximum error and execution time for all values of k. Moreover, the execution time decreased linearly and Δ(n) increased as k was decreased.

Next, the scalability of the baseline algorithm was evaluated by varying the maximum transaction length, L, as it is applied to the synthesis data. This dataset was generated by the IBM market basket generator; its stream size, n, was 10,000 and the number of types of items, |I|, was about 24,000. Figure 12b describes the average updating time and the error ratio, $\frac {\Delta (n)}{n}$, as functions of L. As the time complexity for the updating process is O(kL), the execution time linearly increased as L was increased. In an ordinary problem setting, we need to focus the solution space on 2^L itemsets for L, resulting in a rapid increase in the error count. In contrast, the proposed solution can tolerate such large transactions that always contain 5,000 items. In addition, the change in the error ratio as a function of k in the range of 1,000,000 to 7,000,000 was evaluated with the dataset 6, for which the error ratio achieved by the baseline algorithm was the largest. The results are shown in Fig. 12c. Then, the error ratio linearly decreased while the execution time increased as k was increased. Note that a simple open MP parallelization was used for this computation. Such a parallelization scheme can be used in RC approximation with a fixed memory resource (Yamamoto et al. 2016) but the issue of efficient implementation of such a scheme is beyond the scope of this paper.

Figures 13 and 14 show the time series changes of the number of used entries, k(i), and the error ratio, $\frac {\Delta (i)}{i}$, respectively, which are obtained by applying PARASOL to the hadoop dataset (No. 10) with respect to k = 10,000 and 𝜖 = 0.015. The results show that PARASOL violates the original 𝜖 value due to the RC approximation that was applied earlier in the time series period. However, after this period, the error ratio recovers to 𝜖. This autonomous recover of 𝜖 is an interesting characteristic of PARASOL. Note that PARASOL finally derives T_n of 1,626 entries while the baseline algorithm always uses the 10,000 entries. Another characteristic of PARASOL lies in this observation that T_n becomes smaller than k due to the PC approximation. In contrast, MOA-IncMine generates 770,995 SFCIs for some intermediate segment when 𝜖 = 0.1 and a segment size of w = 1,000; thus, it could not finish updating the SFCIs (this was true for other values of w, as well). The drastic decrease in performance due to streaming transactions (or segments) is a common drawback among the existing PC methods. PARASOL can avoid it and remains sustainable by switching between PC and RC approximations.

Fig. 13

Time series of the stored entries, k

Fig. 14

Time series of the error ratio, Δ

Table 3 compares the performance of MOA-IncMine with that of PARASOL with Δ-compression when applied to the other datasets in terms of execution time and number of entries in the output. Given 𝜖 = 0.1, MOA-IncMine was run with 1 GB Java heap size for six hours (the segment size was fixed as the default (1,000)). PARASOL was run with k = 100,000 and 𝜖 = 0.1.

Table 3 MOA-IncMine versus PARASOL

The results show that MOA-IncMine results in out-of-memory (OM) and time-out (TO) exceptions when applied to datasets 4, 5, 6, and 8. On the other hand, PARASOL successfully processed all of these datasets, however the error ratio ($\frac {\Delta (n)}{n}$), exceeded the initial value of 𝜖. In datasets, 1, 3, 7, MOA-IncMine was faster than PARASOL. These datasets were relatively sparse, implying that MOA-IncMine may tend to be more powerful for sparse datasets, although the speed also depends on the segment size (as well as the size constant k for PARASOL). The output of PARASOL was generally smaller than that of MOA-IncMine due to Δ-compression as shown by number of used entries, k(n).

Table 4 shows the pruning effect of using the weeping tree structure (parameters were set as k = 12,000 and 𝜖 = 0). The average ratio between traversing nodes and total nodes for each timestamp (i.e., Visiting ratio) and the average ratio between nodes that have non-empty intersections and total nodes for each timestamp (i.e., Non-empty ratio) are shown. The standard indexing technique (i.e., cid_list) forces us to compute all the non-empty intersections. Interestingly, the weeping tree succeeds in reducing this search space by the indexing technique in datasets 2, 4, 5, 6, and 8. Those datasets are relatively dense. Note that the execution time with the weeping tree was faster than cid_list for every dataset. This is due to the additional cost for maintaining the indexing data structure for each timestamp. The #Num⁻ and #Num⁺ columns show the number of entries after pre-processing and number of entries that were output by the Δ-compression, respectively. For example in dataset 6, the ordinal 12,000 entries were reduced to 3,418 by pre-processing and 535 of these entries remained in the output after the second filtering step. The Time⁻ and Time⁺ columns show the execution time of the Δ-compression with and without the pre-processing step, respectively. It is reasonable for Δ-compression to apply the pre-processing with the weeping tree.

Table 4 Pruning effects of using the weeping tree

Conclusion and future work

In this study, we have proposed a novel solution for FIM-SD that involves seeking a Δ-deficient condensed representation, from which every FI and its support can be restored, while bounding the maximum error by an integer, Δ. While the existing FIM-SD methods are limited to strictly PC and RC methods, we have mitigated the drawbacks of each approach by introducing a unified PC and RC-approximation scheme called PARASOL. We furthermore introduce a post-filtering technique called Δ-compression and a novel data structure called the weeping tree. Experimental trials on ten datasets show that the proposed technique outperforms the existing FIM-SD methods. Moreover, the proposed algorithm is scalable in terms of the transactional length; in other words, it can tolerate any bursty transaction without running into an OM exception. This feature is favorable for analyzing large volumes of streaming transactions that consistently contain many items. Such large streaming transactions are often encountered in surveillance domains of sensor networks and cloud servers. In addition, along with the recent success achieved with deep learning, it is now necessary to analyze the cognitive correlations among mid-level objects for explanatory domains. We believe that integrating modern online learning with the solution presented here will give rise to a new methodology for streaming data analysis. From a technical standpoint, it will be important to introduce novel parallel-processing techniques to further improve the scalability of this technique. In addition, it will be fruitful to study how such techniques can be efficiently embedded into the proposed weeping tree structure.

Appendices

Appendix : A: Relation between Δ-closed set and Δ-covered set

The Δ-covered set has an interesting relationship with the so-called Δ-closed set (Boley et al. 2009), which is known as a condensed representation for FIs. An itemset α is Δ-closed if there exists no itemset β such that $\beta \succeq _{\Delta }^{n}\alpha$. Let $\mathcal {F}_{\Delta }$ denote the family of Δ-closed FIs. $\mathcal {F}_{\Delta }$ is uniquely determined but does not have the Δ-deficiency property. Consider again Example 1 and assume that every α_i ∈ P is frequent at some timestamp. Then, we have $\mathcal {F}_{1} = \{\alpha _{4}\}$ (i.e., Δ = 1), since α_i (1 ≤ i ≤ 3) is not 1-closed. $\mathcal {F}_{1}$ is unique but no longer 1-covered set of P. Indeed, the support of α₁ cannot be restored only by α₄ within the error range below one.

In contrast, there exist two 1-covered sets Q₁ = {α₃, α₄} and $Q_{1}^{\prime } = \{\alpha _{2}, \alpha _{4}\}$. Note that $\mathcal {F}_{1}$ corresponds to the intersection of Q₁ and $Q_{1}^{\prime }$. This characteristic is described as follows:

Proposition 4

Let$\mathcal F$be the family of FIs and Δ an integer. Then, $\mathcal {F}_{\Delta }$is included by any Δ-covered set of$\mathcal {F}$.

Proof

Assume that there exist a Δ-closed FI α such that α∉T for some Δ-covered set T of $\mathcal {F}$. Since α is a FI but is not included in T, there should exist a β ∈ T such that $\beta \succeq _{\Delta }^{n} \alpha$. However, this contradicts that α is Δ-closed. □

Appendix B: Proof of Theorem 1

Let α be an itemset and $\mathcal {S}_{i}$ a stream at timestamp i. We define the function $f(\alpha , i) = \bigcap _{t\in tran(\alpha , i)} t$. Then, it is well-known that α is a closed itemset at timestamp i, that is, $\alpha \in \mathcal {C}_{i}$ if and only if α = f(α, i) holds. Now, we prove that $\mathcal {C}_{i}\subseteq \mathcal {C}_{i-1}\cup \{t_{i}\}\cup \{\beta ~|~\beta =\alpha \cap t_{i}, \beta \neq \emptyset , \alpha \in C_{i-1}\}$ (*). Assume that $\alpha \in \mathcal {C}_{i}$. If tran(α, i − 1) = ∅, α should be equal to t_i, since $\alpha = \bigcap _{t\in tran(\alpha , i)} t$ holds. Else if tran(α, i − 1)≠∅ and $\alpha \subseteq t_{i}$, we have α = t_i ∩ β where β = f(α, i − 1). Otherwise, α should be equal to β. Since $\beta \in \mathcal {C}_{i-1}$, $\alpha \in \mathcal {C}_{i-1}\cup \{t_{i}\}\cup \{\beta ~|~\beta =\alpha \cap t_{i}, \beta \neq \emptyset , \alpha \in C_{i-1}\}$ holds. In turn, the reverse inclusion relation of (*) is proven in the same argument. Note that Theorem 1 is regarded as an instance of Theorem 2 when the minimal-entry deletion does not happen.