1 Introduction

The aim of this paper is to investigate how firms’ incentives to invest in process research and development (R&D) are affected by the network effects arising in the product market. In the presence of network effects, the value of a good or a service depends not only on its intrinsic characteristics, but also on its network of users (cf., Katz and Shapiro 1994). Network effects are pervasive in many industries, i.e., telecommunications, e-commerce, media, entertainment, financial services, and fashion, among others.

Since the seminal studies by Katz and Shapiro (1985, 1994), researchers have been interested in understanding how technology adoption may be affected by the existence of network effects (see the Section 2 below). While this literature addressed many important issues, there are still open questions regarding (i) firms’ incentives to invest in R&D in markets with network effects, and (ii) private and social outcomes of R&D cooperation under such market characteristics.

In this article, we set out to investigate the above questions. Our study is limited to process innovations in markets with network effects. Already such a scope of interest is sufficient to be relevant to a significant piece of a modern economy (Calvano and Polo 2020). Innovations mentioned above refer to telecom networks, computers, game consoles, video recorders, hardware components, digital music systems, among many others. The real-world examples of businesses with process innovations and network effects also include credit cards with their technological protections, production of ATMs, ticket machines with digital cameras, production of smartphones. As Laguna de Paz (2015) observes, cooperative process R&D works became a norm in the mobile sector. Telecom firms undertake cooperative R&D projects in order to enhance compatibility and interoperability between their networks via extending or restructuring both passive (e.g., BTS shelters) and active (e.g., switches, microwave devices) infrastructure (cf., Laguna de Paz 2015).

From the public policy point of view, it is important to determine the effects of R&D cooperation between enterprises operating in such industries. Is cooperative R&D in markets with process innovations and network effects socially beneficial? Should cooperative R&D be promoted in such industries? Are the benefits from R&D cooperation in markets with process innovations and network effects large enough compared with possible social costs related to cooperative R&D? The above questions constitute a very practical rationale for the present study.

Based on the game-theoretic model, we show that the presence of network effects increases the firms’ R&D investments, both under R&D competition and R&D cooperation. Three scenarios were considered, in which companies decide on R&D investments and production volumes. These scenarios include: N—companies compete with each other in both stages, C—companies cooperate in the R&D stage and compete in the product market, M—cooperate in the R&D stage and collude in the product market.

The result stating that cooperation in R&D increases firms’ R&D investments when the size of technological spillovers is large enough, has been here confirmed. However, in presence of network effects, the level of spillovers necessary to attain this increase rises to a very high level. Further, collusion in both R&D and production stage leads to large investments which dominate those under R&D competition or R&D cooperation, if spillovers are sufficiently large and network effects are small enough.

Moreover, for comparison purposes, we consider two other scenarios: W1—the social planner determines the amount of R&D expenditures, but also the production volumes (this is a benchmark scenario), and W2—the social planner decides on the size of the investments, but companies compete in the product market.

Comparing these scenarios we state that coordination is socially beneficial if spillovers are large enough. In the presence of network effects, the level of spillovers required for cooperation to be socially preferred has to be higher than in a case without network externalities. Moreover, if network effect is sufficiently large and knowledge spillover is small enough, the competition makes firms invest a lot in cost reductions, and the amount of investments can reach the level required from the welfare maximizing perspective.

From the firms’ point of view the most preferred scenario is monopoly, since it consists of maximizing joint payoff by coordinating strategies in both stages. But this kind of behavior is illegal, even when firms are allowed to form a cooperation in the R&D stage. So, in fact firms can legally choose between two scenarios: independent R&D investments or cooperation in R&D. However, the risk of cartelization in case of legal R&D cooperation is pronounced, since there is a strong incentive to collude also in the product market.

The model we develop in this paper has some limitations, i.e., to keep analytical tractability we consider only two symmetric firms competing in Cournot fashion.

The remainder of this paper is as follows. The next section contains the review of relevant literature. Next, we present the game-theoretic model of firms’ process innovation in markets with network effects. Then, we study the case of R&D competition between firms. In Section 5, we consider the case of R&D cooperation, whereas Section 6 is devoted to the analysis of enterprise collusion both in R&D and production stage. Section 7 deals with public policy and welfare issues. Discussion and concluding remarks follow.

2 Literature Review

The following research is meant to contribute to the three strands of innovation literature: (1) works on firms’ R&D investments (Atallah 2007; Marini et al. 2014; Geldes et al. 2017), (2) works on markets with network effects (Choi et al. 2010; Dan 2018; Bond-Smith 2019), and (3) innovation policy literature (Eklinder-Frick and Age 2017; Cabon-Dhersin and Gibert 2019).

The first strand focuses on models of firms’ investments in process R&D (see, e.g., d’Aspremont and Jacquemin 1988; Kamien et al. 1992; Kamien and Zang 2000; Marini et al. 2014). These are usually sequential models, in which firms decide upon their R&D investments and engage in the product market competition. Innovations resulting from the investments in R&D affect the competitive position of all firms operating in the product market.

One of the key questions in this area of research is the impact of R&D cooperation of firms competing in the product market on the enterprise investment levels, firms’ profits, and total welfare (Becker and Dietz 2004; Belderbos et al. 2006; Van Beers and Zand 2014; Marini et al. 2014). In particular, it is thoroughly studied which types of agreements between firms are particularly beneficial from the welfare point of view, and whether such cooperation is likely to increase firms’ incentives for anti-competitive behavior in the product market (see, e.g., Ziss 1994; Martin 2006; Miyagiwa 2009).

The second strand deals with so called network externalities. As regards process innovations in markets with network effects, Boivin and Vencatachellum (2002) state that the presence of network effects increases the level of firms’ investments in process R&D. Saaskilahti (2006) follows this research alley, and studies the issues of compatibility in the presence of price competition. More recently, Naskar and Pal (2020) compare the investments in process innovation under different models of competition. However, none of those studies confront the effects of R&D competition, R&D cooperation and industry collusion with socially optimal outcomes.

The key innovation policy issues concerning R&D in markets with network effects are identified by Gandal (2002). These issues refer to the social and private incentives to achieve compatibility, and the interaction between compatibility and technological progress. Two general results can be derived from this literature, i.e., compatibility results in the optimal timing of new product introduction, and, second, incompatibility speeds up new product introduction (Katz and Shapiro 1992; Regibeau and Rockett 1996; Kristiansen 1998; Gandal 2002). As regards welfare issues, Kristiansen (1996) shows that network effects may lead to divergence between R&D projects that are socially or privately optimal. In the context of incompatible technologies between the incumbent firm (with an installed base) and the entrant, a welfare loss occurs due to the fact that the technology introduced by the entrant succeeds too often. As Bond-Smith (2019) shows, the incumbent firm can however discourage R&D investments made by the entrant by exploiting the dominant position and the likely threat of incompatibility which is clear to the entrants.

In correspondence with the above literature, we construct a model of process R&D in markets with network effects. The model utilizes the approach proposed by Crémer et al. (2000). Within this framework, we consider different R&D regimes and market setups, as discussed in seminal papers by d’Aspremont and Jacquemin (1988) or Kamien et al. (1992). Based on the game-theoretic analysis, we show that, if there is no full compatibility, both first best and second best welfare levels of R&D investments can be reached under R&D competition. R&D competition makes firms invest a lot, especially if the level of spillovers is not very large. Without network effects, first best level of investment cannot be reached. Higher compatibility of networks decreases the spillover value required for the competitive R&D investment to reach the socially optimal one. R&D cooperation, in turn, always leads to the R&D investment levels lower than the welfare optimal ones.

3 The Model of Process Innovation in Markets with Network Effects

To model market competition we use the model of backbone market as in Crémer et al. (2000). This is an extension of the canonical (Katz and Shapiro 1985).

There is a continuum of potential consumers who differ in tastes, which is denoted by a value of 𝜃 ∈ [0,1]. The distribution of 𝜃 is uniform. The parameter 𝜃 expresses a consumer’s valuation for the stand alone benefits of a network good. All consumers are the same in terms of valuation of the network benefit, v, i.e., their utility function can be described in the following way:

$$ U(\theta)=\theta a+vn^{e} $$

where a = 1 for simplicity, ne is the expected size of the network, and v < 1/2, to guarantee that there is no full market coverage and consumers’ tipping is avoided.

There are two producers of a network good. The firms compete for the new consumers. Each firm has an installed base of consumers, denoted βi ≥ 0,i = 1,2. We assume that the installed bases are locked in, by previously signed contracts, and cannot be changed.

Parameter γ ∈ [0,1] measures the level of compatibility between the products of the firms. γ = 0 means incompatibility, hence each good makes up its own network, γ = 1 means that there is full compatibility, hence there is one unified network. Moreover, we consider values of γ being in-between, and 0 < γ < 1 means partial compatibility.Footnote 1 Each firm chooses quantity qi in order to maximize its profit on new consumers, since the profits associated with the installed base of consumers are constant. We consider simultaneous quantity competition between firms.

Let \({q_{i}^{e}}\) be the number of new consumers of firm i (as it expects), then expected size of the network is given by \({n_{i}^{e}}={q_{i}^{e}}+\beta _{i}\).

When a new consumer of type 𝜃 adopts a good of firm i at price pi, her utility is Ui(𝜃) = 𝜃 + gi − pi, where \(g_{i}=v\left [\left (\beta _{i}+{q_{i}^{e}}\right )+\gamma \left (\beta _{j}+{q_{j}^{e}}\right )\right ]\), and it measures expected network benefit from good i.

The goods are perfect substitutes for the consumers who are unattached. This means that their quality-adjusted prices are the same: \(p_{1}-g_{1}=p_{2}-g_{2}=\hat {p}\). This implies that for the consumer who is indifferent to adopt a good or not, \(\theta _{0}=\hat {p}\), so the joint demand for both technologies is 1 − 𝜃0. For fulfilled-expectations, we obtain that \(q_{1}+q_{2}=1-\hat {p}\).

Hence, \(p_{i}=1-\left (q_{i}+q_{j}\right )+g_{i}=1+v\left (\beta _{i}+\gamma \beta _{j}\right )-(1-v)q_{i}-(1-\gamma v)q_{j}\) for i≠j.

Finally, firm i strives to attract consumers to maximize its profit \(\pi _{i}=\left (p_{i}-c_{i}\right )q_{i}=\left [1+v\left (\beta _{i}+\gamma \beta _{j}\right )-(1-v)q_{i}-(1-\gamma v)q_{j}-c_{i}\right ]q_{i}\), where ci denotes unit production cost of producer i.

In equilibrium, we have the following quantities:

$$ q_{i}=\frac{2(1-v)\left( 1-c_{i}+v\left( \beta_{i}+\gamma \beta_{j}\right)\right)-\left( 1-\gamma v\right) \left( 1-c_{j}+v\left( \beta_{j}+\gamma \beta_{i}\right)\right) }{D_{1}D_{2}} $$
(1)

where \(D_{1}=2\left (1-v\right ) -\left (1-v\gamma \right ) ,D_{2}=2\left (1-v\right ) +\left (1-v\gamma \right ) \), and the following profits:

$$ \pi_{i}=\left( 1-v\right) {q_{i}^{2}}. $$
(2)

Now, we introduce the possibility of investing in process R&D which allows to decrease the unit costs of production. As in d’Aspremont and Jacquemin (1988), we assume the possibility of knowledge spillovers. \(z\in \left [ 0,1\right ] \) is the spillover parameter. Let \(x_{1}\in \left [ 0,c_{1}\right ] \) and \(x_{2}\in \left [ 0,c_{2}\right ] \) denote the autonomous cost reductions (or individual R&D investments) made by firm 1 and firm 2, respectively. To attain this level of cost reduction, each firm has to pay a cost given by \( C(x_{i})=\frac {k}{2}{x_{i}^{2}},i=1,2\). Due to the existence of knowledge spillovers, the effective cost reductions are xi + zxj and xj + zxi.

We consider a two-stage game: in the first stage, firms choose x1 and x2 to maximize payoffs from the second stage of the game, i.e., product market quantity competition. Assume that the initial unit costs are equal, then, a pure strategy for firm i is a pair \(\left (x_{i},q_{i}\right )\), where \(x_{i}\in \left [ 0,c\right ] \) and \(q_{i}:\left [ 0,c\right ]^{2}\rightarrow R_{+}\). We restrict our attention to subgame perfect Nash equilibria of this game. After investments are made, unit costs are of the form ci = c − xi − zxj, and the payoff to be maximized is given by

$$ F_{i}=\left( 1-v\right) \left( \frac{B_{1}x_{i}-B_{2}x_{j}+B_{3}}{D_{1}D_{2}} \right)^{2}-k\frac{{x_{i}^{2}}}{2}, $$

where B1 = \(2\left (1-v\right ) -z\left (1-v\gamma \right ) ,\) \( B_{2}=\left (1-v\gamma \right ) -2z\left (1-v\right ) \) and \(B_{3}=2\left (1-v\right ) \left (1-c+v\left (\beta _{i}+\gamma \beta _{j}\right ) \right ) -\left (1-v\gamma \right ) \left (1-c+v\left (\beta _{j}+\gamma \beta _{i}\right ) \right ) \), and D1 and D2 have been defined in Eq. (1).

We assume that demand, taking into account the network benefit, is high enough in relation to the initial unit cost, i.e.,

A1 :

1 + v(βi + γβj) > c,i,j = 1,2

Due to the above assumption we can be sure that the quantity competition admits a unique pure strategy Nash equilibrium where both firms are active for all possible R&D levels chosen.

d’Aspremont and Jacquemin (1988) found that the level of spillover z plays an important role in properties of the equilibiria of their model. When the level of spillover is low, below 1/2, the autonomous cost reductions made by firms are strategic substitutes, i.e., the more one firm reduces its cost, the more it lowers marginal profitability of the other firm from cost reduction. When the opposite inequality holds, we have strategic complements, i.e., the more one firm invests, the larger is the profitability of cost reducing investment achieved by the other firm. To find the threshold level of z, one has to compute the cross partial derivative of the payoff function with respect to xi and xj and see when this derivative is negative and when is positive. If the cross partial derivative is negative, firms’ autonomous cost reductions are strategic substitutes. They are strategic complements in the opposite case. For the model presented in this section, note that the sign of the cross partial derivative depends on the sign of B2, i.e., if B2 > 0, we have \(z<\frac {1}{2}\frac {1-v\gamma }{1-v}\), and firms’ autonomous cost reductions are strategic substitutes. They are strategic complements in the opposite case.

We are going to study the impact of network effects, measured by v, on firms’ process R&D investments. We compare the following scenarios: first, when firms decide upon their cost reductions independently and remain competitors in the product market (R&D competition), second, when they cooperate in R&D, but compete in the product market (R&D cooperation), third, when they coordinate both R&D and product market decisions in order to maximize joint profit (full industry collusion or monopoly), fourth, when the social planner selects both R&D investments and quantities to maximize welfare (first best welfare solution), and fifth, when the social planner selects R&D investments only (second best welfare solution).

4 R&D Competition

For the rest of the paper, we assume that both firms have the same initial network size, βi = βj = β. The payoff of a firm is then as follows:

$$ F_{i}=\left( 1-v\right) \left( \frac{\left( 1-c+v\beta \left( 1+\gamma \right) \right) D_{1}+x_{i}B_{1}- B_{2}x_{j}}{D_{1}D_{2}}\right)^{2}-k\frac{{x_{i}^{2}}}{2}. $$

Firms aim to maximize payoffs choosing the levels of cost reductions, xi and xj, respectively. To assure that there is an meaningful interior solution, we have to make standard assumptions on the parameter values.

  1. N1

    \(k>\frac {2\left (1-v\right ){B_{1}^{2}}}{{D_{1}^{2}}{D_{2}^{2}}}\)

This condition is required for Fi(i = 1,2) to be strictly concave in own R&D level, which means that the second-order conditions of payoff maximization are satisfied.

  1. N2

    \(k>\frac {2\left (1-v\right ){B_{1}^{2}}}{{D_{1}^{2}}{D_{2}^{2}}} \frac {D_{1}}{B_{1}}\left (\frac {1+ v\beta \left (1+\gamma \right ) }{c}+z\right )\)

This assumption assures that the effective cost reduction is positive and not larger than the initial cost.

Observe that for the relatively large v, close to \(\frac {1}{2}\), these conditions cannot be satisfied since the denominator tends to zero. One can observe that N2 is not more (or less) stringent than N1, since \(\frac {D_{1}}{B_{1}}\) can be both larger or smaller than 1.

4.1 R&D Competition Equilibrium

If firms independently choose the autonomous cost reductions, they are equal:

$$ {x_{i}^{N}}={x_{j}^{N}}=x^{N}=\frac{2\left( 1-v\right) B_{1}\left( 1-c+v\beta \left( 1+\gamma \right) \right) }{{D_{2}^{2}}D_{1} k-2\left( z+1\right) \left( 1-v\right) B_{1}}, $$
(3)

and the effective cost reduction is equal xN(1 + z).

We start with analyzing the impact of the network effect on the cost reduction.

Proposition 1

Assume N1 and N2 hold. Then the individual investment in process R&D is increasing with v.

Proof

See the A. □

This means that network effect enhances the firm’s investment in process R&D. This is due to the fact that consumer utility is an increasing function of the number of the network users, hence the cost reduction exerts the impact also on consumers’ expectations and network formation. If price falls, due to a decrease in costs, more consumers buy the product, so the demand rises. From the firms’ point of view, this is an additional positive effect of the R&D investment, therefore, network effects provide firms with greater incentives to invest in R&D, cf., Boivin and Vencatachellum (2002) and Naskar and Pal (2020). We can see the above demand effect by studying the equilibrium output.

$$ Q^{N}= \frac{2kD_{2}D_{1}\left( 1-c+v\beta \left( 1+\gamma \right) \right) }{{D_{2}^{2}}D_{1} k-2\left( z+1\right) \left( 1-v\right) B_{1}}. $$

Proposition 2

Assume N1 and N2 hold. QN is increasing with v.

Proof

Observe that the partial derivative of QN can be decomposed as follows:

$$ \frac{d}{dv}Q^{N}=\frac{\partial Q\left( x_{i},x_{j}\right)}{\partial v}|_{x_{i}=x_{j}=x^{N}}+\frac{\partial Q\left( x_{i},x_{j}\right)}{\partial x_{i}}\frac{\partial x^{N}}{\partial v}, $$

where

$$ \begin{array}{@{}rcl@{}} \frac{\partial Q\left( x_{i},x_{j}\right)}{\partial v} &=&\frac{2\left( 6\left( \gamma +1\right) \beta +\left( \gamma +2\right) \left( 2\left( 1-c\right) +\left( z+1\right) \left( x_{i}+x_{j}\right) \right) \right)}{{D_{2}^{2}}} >0 \\ \frac{\partial Q\left( x_{i},x_{j}\right)}{\partial x_{i}} &=& \frac{\left( z+1\right)}{D_{2} } >0 \end{array} $$

and \(\frac {\partial x^{N}}{\partial v}>0\) as derived in the proof of Proposition 1.

Hence, we can conclude that the equilibrium quantity increases with the network effect. □

Consider now the possible change in compatibility of the products. Increase in the compatibility means that the competing firms have access not only to the own consumers, but also to (at least a part of) the consumers of the rival. This suggests that for higher compatibility, firms invest less. The larger the compatibility, the less prone to invest in R&D firms should be, since they should avoid investing in something which might be of use for the customers of the competing network. This intuition confirms the result of Viecens (2009) stating that compatibility may harm innovations. Observe however that result obtained by Viecens (2009) applies to a market with a dominant firm. We show in turn that compatibility may harm innovation even without the presence of a dominant firm.

We also show that this intuition is not always valid, i.e., it holds for the network effect strong enough. For low values of v, the opposite reaction of firms to the increase in compatibility is possible. The following example illustrates the role of the network effect in the reaction of the R&D investment to the changes in compatibility.

Example 1

Take the following parameters’ values: z = 0.2,β = 0.3,c = 0.95,v = 0.1,k = 2. Then for γ = 0, we have xN = 2.5352 × 10− 2, and for γ = 0.1, we have xN = 2.157 × 10− 2, so the investment increased. However if v = 0.4, xN|γ= 0 = 0.41129 > xN|γ= 0.1 = 0.27939, so the investment decreased.

When we use the decomposition of the derivative of QN as in the proof of Proposition 2, we can conclude that the equilibrium output can increase or decrease with the increase of the compatibility between products.

$$ \frac{d}{d\gamma}Q^{N}=\frac{\partial Q\left( x_{i},x_{j}\right)}{\partial \gamma}|_{x_{i}=x_{j}=x^{N}}+\frac{\partial Q\left( x_{i},x_{j}\right)}{\partial x_{i}}\frac{\partial x^{N}}{\partial \gamma}, $$

where

$$ \begin{array}{@{}rcl@{}} \frac{\partial Q\left( x_{i},x_{j}\right)}{\partial \gamma}&=& \frac{v\left( 4\beta +2\left( 1-c+\beta (1-v)\right) +\left( z+1\right) \left( x_{i}+x_{j}\right) \right) }{{D_{2}^{2}}}>0 \\ \frac{\partial Q\left( x_{i},x_{j}\right)}{\partial x_{i}} &=& \frac{\left( z+1\right)}{D_{2} } >0 \end{array} $$

The derivative of xN with respect to γ can be both positive and negative, hence we cannot be sure about the sign of the reaction of the equilibrium output due to an increase in compatibility (see, the following example).

Example 2

Consider the following parameters’ values: z = 0.2,β = 0.3,v = 0.4,k = 3,c = 0.95. If γ = 0, QN = 0.30656. When γ = 0.1, the equilibrium output is smaller and equal 0.29674. For γ = 0.2, the equilibrium output is larger compared with γ = 0.1 and equal QN = 0.29882, so the output can rise with γ.

Next, we examine the impact of network effects on the equilibrium payoff. This is given by

$$ \begin{array}{@{}rcl@{}} F^{N}= \frac{\left( {D_{2}^{2}}{D_{1}^{2}}k-2\left( 1-v\right) {B_{1}^{2}} \right) k\left( 1-v\right) \left( 1-c+v\beta \left( 1+\gamma \right) \right)^{2}}{\left( k{D_{2}^{2}}D_{1} -2\left( 1-v\right) \left( z+1\right) B_{1}\right)^{2}}. \end{array} $$

Observe that although the impact of the network effect on output is positive, the payoff is not always increasing with v.

Example 3

Take the following parameters’ values β = 0.3,z = 0.2,c = 0.5,k = 2,γ = 0. If v = 0.1 then \(\frac {d}{dv}F_{i}=\) 8.2898 × 10− 3. If v = 0.2 then \(\frac {d}{dv}F_{i}=-0.114 85\).

We can express \(\frac {\partial }{\partial v}F^{N}\) as follows:

$$ \frac{d}{dv}F^{N}=\frac{\partial F_{i}}{\partial v}|_{x_{i}=x_{j}=x^{N}}+\left( \frac{\partial F_{i}}{ \partial x_{i}}\frac{\partial x_{i} }{\partial v}\right)|_{x_{i}=x_{j}=x^{N}}+\left( \frac{\partial F_{i} }{ \partial x_{j}}\frac{\partial x_{j}}{\partial v}\right)|_{x_{i}=x_{j}=x^{N}}, $$

and analyze each term separately.

$$ \begin{array}{@{}rcl@{}} \frac{\partial F_{i}}{\partial v}|_{x_{i}=x_{j}=x^{N}}&=&\left( \left( 2v^{2}-9v+6\right) \beta +\left( 1-2v\right) \left( 1-c+x^{N}\left( 1+z\right) \right) \right) \\&& \times\frac{1-c+x^{N}\left( 1+z\right) +v\beta }{\left( 2(1-v)+1\right)^{3}} \end{array} $$

The latter is positive, since \(\left (2v^{2}-9v+6\right )>0\) for v ∈ [0,1/2]. Moreover, \(\frac {\partial }{ \partial x_{i}}F_{i}=0\) in equilibrium. Finally,

$$ \frac{\partial F_{i}}{\partial x_{j}}=2\left( 1-v\right) \left( \frac{\left( 1-c+v\beta \left( 1+\gamma \right) \right) D_{1}+x_{i}D_{1}- D_{2}x_{j}}{D_{1}D_{2}}\right) \frac{- D_{2}}{D_{1}D_{2}} $$

and the latter is positive when R&D investments are strategic complements, and negative when R&D investments are strategic substitutes. The last term, \( \frac {\partial x_{j}}{\partial v}\), is given by Eq. (A.1) in the A; hence, it is positive.

We can now formulate the following proposition.

Proposition 3

Firm’s equilibrium payoff is increasing with v, when R&D investments are strategic complements.

Proof

Follows from the above reasoning. □

If R&D investments are strategic substitutes, the impact of v on the equilibrium payoff is ambiguous. It results from the two opposite effects, the direct effect, which is positive, and the strategic effect, which is negative. Depending on the parameters’ values, each of them can dominate.

The compatibility between products has also an ambiguous impact on the equilibrium payoffs.

Example 4

Consider the following parameters’ values: z = 0.2,β = 0.3,v = 0.4,k = 2,c = 0.5 Then \(F\left (x^{N},x^{N}\right )|_{\gamma =0}= 0.636\) \(>F\left (x^{N},x^{N}\right )|_{\gamma =1}=0.229 52\). However, if k = 3, we have \(F\left (x^{N},x^{N}\right )|_{\gamma =0}= 0.133 93<\) \(F\left (x^{N},x^{N}\right )|_{\gamma =1}=0.152 37\).

5 R&D Cooperation

Assume now that the firms can cooperate in R&D, whereas they remain competitors in the production stage. We consider a scenario in which firms choose the joint profit-maximizing levels of cost reductions, taking into account the exogenous spillover rate. This is the case considered by d’Aspremont and Jacquemin (1988), but for markets without network effects. The authors mentioned above provide conditions when the R&D cooperation leads to the higher cost reductions compared with R&D competition. We test the latter result for a market with network effects.

Again, we need the standard assumptions to secure the second-order condition to be satisfied and the level of the effective cost reduction to be not larger than the initial cost.

The following assumptions are required.

  1. C1

    \(k>\frac {2\left (z+1\right )^{2}\left (1-v\right ) }{{D_{2}^{2}}}\).

  2. C2

    \(k>\frac {2\left (z+1\right )^{2}\left (1-v\right )}{{D_{2}^{2}}}\left (\frac {1+ v\beta \left (1+\gamma \right ) }{c}+z\right )\).

The first assumption is responsible for the behavior of the second-order condition and the second assumption guarantees that the effective cost reductions do not exceed the initial cost level.

Observe also that C2 implies C1, since from A1 we know that \(\frac {1+ v\beta \left (1+\gamma \right ) }{c}>1\). Henceforth we use C2 alone to guarantee the existence of equilibrium in the scenario of R&D cooperation.

Firms form an R&D cooperation and they choose their investment levels in order to maximize the sum of their profits, taking into account the fact that in the production stage they remain competitors. The optimal autonomous cost reduction is as follows:

$$ x^{C}=\frac{2\left( z+1\right) \left( 1-v\right) \left( 1-c+v\beta \left( 1+\gamma \right) \right) }{{D_{2}^{2}}k-2\left( z+1\right)^{2}\left( 1-v\right) }. $$

First, observe that, as in R&D competition, we have the enhancing impact of the network effect on the firms’ R&D investments. Moreover, in this case we can clearly conclude about the effect of product compatibility. The above is formulated by the following proposition.

Proposition 4

Assume C2 holds. Then xC is increasing with v and with γ.

Proof

See the A. □

The positive impact of compatibility on the R&D investment under R&D cooperation is intuitive: the more both firms invest, the more they benefit, since every growth of the rival’s network makes the other firm gain due to the compatibility between the networks.

Now, we can test if the result of d’Aspremont and Jacquemin (1988) holds in the presence of the network effects.

Proposition 5

Assume N1, N2 and C2 hold. Then xN > xC if cost reductions are strategic substitutes and xN < xC if cost reductions are strategic complements.

Proof

See the A. □

The cost reductions are strategic substitutes when

$$ z<\frac{1}{2}\frac{1-v\gamma}{1-v} $$
(4)

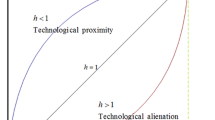
and they are strategic complements if the opposite condition holds. In the Figure (cf., Fig. 1) we can see the scope of parameter values (when γ = 0) where autonomous cost reductions are strategic substitutes or strategic complements.

Fig. 1
figure 1

The scope of parameter values (for γ = 0) where autonomous cost reductions are strategic substitutes or strategic complements. For parameter values below the red line xN > xC

Full size image

Below the red line they are strategic substitutes—in this area the autonomous cost reductions under R&D competition dominate these resulting from the R&D cooperation. The stronger the network effect, the higher must be the spillover rate for the advantage of R&D cooperation over the competitive case. For v = 0, we arrive exactly at the result obtained by d’Aspremont and Jacquemin (1988).

The illustration in Fig. 1 is for γ = 0. The area where cooperative R&D investments dominate the competitive ones is increasing with γ, i.e., the more compatible the networks, the smaller spillover rate is needed for cooperative investments dominate the competitive levels.

The equilibrium quantity is given by

$$ Q^{C} =\frac{ 2kD_{2}\left( 1-c+v\beta \left( 1+\gamma \right) \right) }{{D_{2}^{2}}k-2\left( z+1\right)^{2}\left( 1-v\right) } . $$

It has the following properties.

Proposition 6

Assume N1, N2 and C2 hold. Then

  1. 1.

    QC is increasing with v.

  2. 2.

    QC is increasing with γ.

  3. 3.

    QC < QN, when the R&D investments are strategic substitutes, the opposite holds when they are strategic complements.

Proof

See the A. □

The equilibrium payoff is given by

$$ F^{C}= k\left( 1-v\right) \frac{\left( 1-c+v\beta \left( 1+\gamma \right) \right)^{2}}{{D_{2}^{2}}k-2\left( z+1\right)^{2}\left( 1-v\right) }. $$

There is no strategic effect in this case, hence the payoff is an increasing function of v, z, γ and β and decreasing of k. The payoff under R&D cooperation is always larger than the payoff under R&D competition.

6 Monopoly

We now consider a situation of a monopoly, i.e., firms cooperate in R&D and also they collude in the final product market. They choose quantities so as to maximize the sum of profits πi + πj, where

$$ \pi_{i}=\left( p_{i}-c_{i}\right)q_{i}=\left( 1+v\beta (1+\gamma )-(1-v)q_{i}-(1-v\gamma )q_{j}-c_{i}\right) q_{i}. $$

This leads to the following optimal quantities:

$$ q_{i}^{\ast }= \frac{1}{2}\frac{ c_{i}\left( 1-v\right) -\left( 1-v\gamma \right) c_{j}+v\left( 1-\gamma \right) \left( v\beta \left( 1+\gamma \right) +1\right) }{v\left( 1-\gamma \right) D_{3} }, $$

where \(D_{3}=\left (2-v\left (1+\gamma \right ) \right )\).

Solving the problem of joint profit maximization by setting autonomous cost reductions requires usual assumptions, which guarantee that the second-order condition is satisfied and that the effective cost reductions are smaller than the initial cost:

M1 :

\(k>\frac {\left (z+1\right )^{2}}{2D_{3} }\).

M2 :

\(k>\frac {\left (z+1\right ) }{2D_{3} }\left (\frac {1+v\beta \left (1+\gamma \right ) }{c}+z\right )\).

Similarly to the R&D cooperation scenario, also here M2 implies M1, since from A1 it follows that \(\frac {1+v\beta \left (1+\gamma \right ) }{c}+z>1+z\).

Autonomous cost reductions maximizing the sum of profits are given by

$$ x^{M}=\frac{\left( z+1\right) \left( 1-c+v\beta \left( 1+\gamma \right) \right) }{ 2D_{3} k-\left( z+1\right)^{2}} $$

Proposition 7

Assume C2 and M2 hold. Then

  1. 1.

    xM is increasing with v.

  2. 2.

    xM is increasing with γ.

  3. 3.

    xM > xC.

Proof

See the A. □

The above proposition states that R&D investment under R&D cooperation is smaller than the R&D investment under monopoly. It is because less competition in the product market allows the firms to capture more of the surplus created by their research and induce more R&D expenditures. The stronger the network effect, the larger the difference between xM and xC. However, as we can see in the next proposition, competition can make firms invest in R&D more than under monopoly.

Proposition 8

Assume N1, N2 and M2 hold. Then xM < xN if and only if

$$ z <\frac{8(1-v)^{2}D_{3}-D_{1}{D_{2}^{2}} }{D_{1}{D_{2}^{2}}+4(1-v\gamma)(1-v)D_{3} }. $$
(5)

Proof

See the A. □

Based on the above proposition, we can observe that under monopoly the R&D investment is larger than under R&D competition if knowledge spillovers are sufficiently high and the network effect is small enough. The investment under monopoly is smaller than under R&D competition for a relatively wide range of spillover parameter values, if the network effect is sufficiently strong.

The equilibrium quantity is given by

$$ Q^{M}= 2k\frac{1-c+v\beta \left( 1+\gamma \right) }{2D_{3} k-\left( z+1\right)^{2}}. $$

Let us now compare the value of equilibrium quantity under monopoly with the corresponding values from the previous cases (R&D competition and R&D cooperation).

Proposition 9

Assume N1, N2, C2 and M2 hold. Then the following is true:

  1. 1.

    QMis increasing with v and γ.

  2. 2.

    If

    $$ k<\frac{\left( z+1\right)^{2}}{D_{2}} $$
    (6)

    then QM > QC.

  3. 3.

    If

    $$ k< \frac{\left( z+1\right) \left( \left( z+1\right) D_{1}D_{2}-2\left( 1-v\right) B_{1}\right) }{D_{1}D_{2}\left( 1-v\gamma \right) } $$
    (7)

    then QM > QN.

Proof

See the A. □

Observe that condition (7) is meaningful only for \(z>\frac {\left (1-v\gamma \right )^{2}}{\left (D_{1}D_{2}+2\left (1-v\gamma \right ) \left (1-v\right ) \right ) }\), since for smaller values of z the right-hand side is negative.

Based on the above proposition, we can conclude that for a relatively small cost of innovation and sufficiently large spillover value, the quantities chosen by a monopoly can be larger than these resulting from the R&D competition or R&D cooperation, provided the network effect is not too strong. Higher spillover makes the monopoly invest more, while the competing firms hold their investment effort. An example is given below.

Example 5

Observe that it is possible that the monopoly produces the largest equilibrium output, e.g., c = 0.99,β = 0.3,z = 0.48,v = .05,γ = 0,k = 0.6. One may check that all the assumptions listed in the A, required for the existence of interior solutions to exist, are satisfied. Then QM = 0.20053,QN = 0.14279 and QC = 0.09839.

7 Policy and Welfare

7.1 First Best

We now compare the results obtained in the previous sections with the results for the first best welfare optimum. In this case, the social planner decides on the R&D investments and on the production output. This scenario (and the next one, called second best welfare optimum, where no intervention in the product market is assumed) is considered as a benchmark only. In practice, any planner does not intervene in companies’ decisions on their outputs or their R&D levels. But in this way a socially optimal level of these variables is found and public policy can be set to approach this socially optimal objective.

To find first best welfare optimum we build welfare function, summing up firms’ profits and consumer surplus. Optimal production level of one firm, given a cost reduction x, is given by

$$ q_{i}^{\ast }= \frac{1-c+x(1+z)+v\beta \left( 1+\gamma \right) }{ 2-v\left( 1+\gamma \right) }. $$

which leads to the following welfare function:

$$ \begin{array}{@{}rcl@{}} W_{1}&=&\frac{ \left( z+1\right)^{2}x^{2}+2\left( z+1\right) \left( 1-c+v\beta \left( 1+\gamma \right) \right) x}{D_{3}} +\\&&+ \frac{ c^{2}-2\left( v\beta \left( 1+\gamma \right) +1\right)c+ \left( v\beta \left( 1+\gamma \right) +1\right)^{2} -kx^{2}D_{3} }{D_{3}} \end{array} $$

To find welfare optimum level of x, we need to take the usual assumptions associated with the second-order condition and with the fact that the effective cost reduction cannot exceed the initial cost level.

W1 :

\(k>\frac {\left (z+1\right )^{2}}{D_{3} }\).

W2 :

\(k>\frac {\left (z+1\right ) }{ D_{3} }\left (\frac {1+v\beta \left (\gamma +1\right )}{c}+z\right )\)

Observe that again W2 implies W1, moreover it implies M2 and C2.

Then, the optimal level of the autonomous cost reduction is given by

$$ x^{W1}=\frac{\left( z+1\right) \left( 1-c+v\beta (1+\gamma )\right) }{D_{3} k-\left( z+1\right)^{2}} $$

The optimal joint output and the corresponding welfare are as follows:

$$ \begin{array}{@{}rcl@{}} Q^{W1} &=&2k\frac{1-c+v\beta\left( 1+\gamma\right) }{D_{3} k-\left( z+1\right)^{2}} \\ W_{1} &=& k\frac{\left( 1-c+v\beta \left( 1+\gamma\right)\right)^{2}}{ D_{3} k-\left( z+1\right)^{2}}. \end{array} $$

We can now show that the following properties hold.

Proposition 10

Assume W2 holds. Then

  1. 1.

    xW1 is increasing with v and γ.

  2. 2.

    QW1 is increasing with v and γ.

Proof

See the A. □

Now, we can compare the R&D investment in all three scenarios already considered with that optimal from the welfare viewpoint. To this end we formulate the following proposition.

Proposition 11

Assume N1, N2 and W2 hold. Then

  1. 1.

    xM < xW1.

  2. 2.

    xC < xW1.

  3. 3.

    xN < xW1 if and only if

    $$ z>\frac{4(1-v)^{2}D_{3}-{D_{2}^{2}}D_{1}}{{D_{2}^{2}}D_{1}+2(1-v\gamma)(1-v)D_{3}}. $$
    (8)

Proof

See the A. □

If the network effect is relatively weak, the welfare optimal investment is always the largest one, which confirms the result obtained by d’Aspremont and Jacquemin (1988). But, if there is a sufficiently strong network effect, the investment under R&D competition increases so strongly that it exceeds the welfare optimum level.

7.2 Second Best

Consider now the second best welfare solution, i.e., the social planner decides on the R&D investments, but not on the firms’ output which is established by the market competition. In this case, optimal cost reductions result from the maximizing the following welfare function:

$$ W_{2}(x)=\left( 4-v\left( 3+\gamma \right) \right) \frac{\left( 1-c+x\left( 1+z\right) +v\beta \left( 1+\gamma \right) \right)^{2}}{{D_{2}^{2}}} -kx^{2}. $$

In order to find the interior equilibrium, we need the usual assumptions:

  1. S1

    \(k>\frac { \left (z+1\right )^{2}\left (4-v\left (3+\gamma \right ) \right )}{{D_{2}^{2}}}\)

  2. S2

    \(k>\frac {\left (z+1\right )\left (4-v\left (3+\gamma \right ) \right )}{{D_{2}^{2}}}\left (\frac {1+v\beta \left (1+\gamma \right )}{c}+z\right )\)

Again, S2 implies S1, which follows from A1. Moreover, it implies M2 and C2. Observe also that S2 is implied by W2.

If S2 is satisfied, the optimal autonomous cost reduction is given by the following expression:

$$ x^{W2}=\frac{\left( z+1\right) \left( 4-v\left( 3+\gamma \right) \right) \left( 1-c+v\beta \left( 1+\gamma \right) \right) }{ {D_{2}^{2}}k-\left( z+1\right)^{2}\left( 4-v\left( 3+\gamma \right) \right) }. $$

The second best welfare optimum level of R&D investment is increasing with the network effect, and with the product compatibility.

Proposition 12

Assume S2 holds, then

  1. 1.

    xW2 is increasing with v.

  2. 2.

    xW2 is increasing with γ.

Proof

See the A. □

We can now compare the second best level of investments with the investment levels obtained previously and we arrive at the following results:

Proposition 13

Assume N1, N2 and W2 hold, then

  1. 1.

    xW1 > xW2.

  2. 2.

    xN ≤ xW2 when

    $$ \frac{v\left( 1-\gamma\right)}{ 2(1-v)-v(1+\gamma) }\leq z. $$
    (9)
  3. 3.

    xM < xW2.

Proof

See the A. □

The second best investment level is always smaller than the first best, and the second best investment level dominates the investment under monopoly, which in turn dominates the investment under R&D cooperation (cf., Proposition 7). Only the competitive scenario can lead the firms to invest as much (or more) as in the welfare optimum, e.g., for γ = 0, v = 0.2 and z ≈ 0.45 \(x^{N}\simeq x^{W2}\simeq 0.188\). If the level of spillover is smaller, with the same size of a network effect, the competition in both R&D and on the product market leads to the higher investment compared with the optimal from the welfare point of view.

Based on the previous propositions, we can now complete a ranking of the R&D investments under different market regimes. There are five possible orders listed below and illustrated in Fig. 2.

Fig. 2
figure 2

Areas of different order of R&D investments for γ = 0

Full size image
I:

xW1 > xN > xW2 > xM > xC,

I\(^{\prime }\):

xW1 > xW2 > xN > xM > xC,

I\(^{\prime \prime }\):

xN > xW1 > xW2 > xM > xC,

II:

xW1 > xW2 > xM > xN > xC,

III:

xW1 > xW2 > xM > xC > xN.

Next proposition states that the network effects and higher compatibility are welfare enhancing.

Proposition 14

Assume S2 holds, then \( W_{2}\left (x^{W2}\right )\) is increasing with v and with γ.

Proof

See the A. □

To sum up the section on welfare, we can stress the fact that both the first best and the second best level of R&D investments can be attained by firms competing both in R&D and in the product market with network effects, if there is no full compatibility. Competition forces firms to invest a lot, especially if the level of spillovers is not very large. For sufficiently strong network effect and spillover value low enough, the competing firms invest more than in the welfare optimum, but this is in favor of consumers, since the equilibrium output rises, so does consumer surplus.

Note that, for markets with network effects, R&D cooperation always leads to R&D investments lower than the welfare optimal level. Further, the network effect increases welfare and without this effect the first best level of investment cannot be attained by competing firms.

Figure 3 (below) illustrates the levels of spillover and network effect which are required for the competitive level of cost reduction to achieve the welfare optimal one. Generally speaking, both the first best and the second best levels can be attained, but not without the network externality. The compatibility of the networks decreases the required spillover, and for full product compatibility, the area where the competitive investments equal or exceed the welfare optimal level is empty.

Fig. 3
figure 3

The illustration of conditions (8) and (9) for different levels of compatibility. Curves indicate where the competitive level of R&D investments is equal to the welfare optimal one. Black lines denote the first best and the red lines the second best welfare solution. Compatibility levels from the top: γ = 0,γ = 0.5,γ = 1

Full size image

8 Discussion and Conclusions

Our analysis brings some interesting theoretical implications. First, we extend the results obtained by Boivin and Vencatachellum (2002) and Naskar and Pal (2020) who show that the presence of network effects increases firms’ incentives to invest in process R&D under competition. We develop the latter result and show that network effects increase firms’ incentives to undertake process R&D not only under R&D competition, but also under R&D cooperation and collusion of firms in both R&D and production stage (monopoly case). It means that in general network effects can stimulate process R&D.

Second, as regards the relationship between product compatibility and process innovation, observe that for R&D competition, the effect (on investment) of an increase in product compatibility is ambiguous. When the network effect is relatively weak, the rising product compatibility serves process innovation, the opposite holds when the network effect is strong enough. Interestingly, for R&D cooperation, investments increase with the product compatibility independently of the strength of the network effects.

From the industrial innovation viewpoint, it turns out that for markets with strong network effects, R&D investments are higher under R&D competition compared with both R&D cooperation and monopoly. Further, both first best and second best levels of R&D investments can be attained under R&D competition. R&D cooperation, in turn, always leads to the R&D investment levels lower than the welfare optimal ones. It means that under incomplete product compatibility, the positive role of R&D cooperation is limited. The well-known conclusion drawn by d’Aspremont and Jacquemin (1988) stating that cooperation increases the R&D investments, when the spillover level is large enough, is still valid, but in presence of network effects, the level of spillovers needed to attain the result obtained by d’Aspremont and Jacquemin (1988) increases to a very high level. If the network effect is sufficiently large, for most of the spillover values, the non-cooperative investments prevail. The above results allow us to at least partially explain the failure of Nintendo and Sony collaborative R&D project on the new game console. Only about 200 prototypes of Nintendo PlayStation game console were produced and the console never entered the commercial volume production. The R&D cooperation between Nintendo and Sony in the market with strong network effects turned out to be unsuccessful despite the large knowledge spillovers between cooperating partners.

IO scholars can be also interested in the theoretical trade-off present in this paper (here, we are indebted to the anonymous Reviewer). On one hand, the motivation to dominate a closed network may increase the enterprise incentive to undertake R&D investment. On the other hand, R&D investment may be further reduced if the network effect creates a sufficient market power for a dominant provider.

Importantly, our analysis brings some interesting policy implications. The possible benefits of R&D cooperation higher investments of firms in R&D, higher outputs) postulated by policy-makers (see, e.g., Cassiman 2000; Barajas et al. 2012) do not need to be a case in markets with network externalities. On the contrary, for markets with network effects strong enough, we should rather expect higher investments of firms under R&D competition than under R&D cooperation, in particular under low network compatibility. As a result, promoting R&D cooperation between enterprises does not need to be a desirable innovation policy as regards markets exhibiting strong network effects. The latter constitutes the particularly important contribution which is relevant to mobile sector, online entertainment industry or financial services.

From the policy point of view, it is also interesting to note that the sufficiently strong network effects can lead to the situation when competing firms invest so much in R&D that they reach the welfare optimal investment levels (both first and second best). This kind of situation does not occur in markets without network effects. However, the sufficiently strong network effects can also result in the wasteful overinvestments in R&D when the investments made by competing firms exceed the welfare optimal levels. The latter constitutes a risk of innovation policy oriented at promoting R&D competition in markets with relatively strong network externalities. Competition authorities should monitor for that.