Abstract
The Hotelling model is extended where not only can consumers choose to buy from both sellers (multi-brand purchase), buying multiple units from one seller is also considered (within-brand multi-unit purchase). When an increase of the demand for within-brand multi-purchase exceeds a threshold: (i) firms’ strategies are switched from single-brand equilibrium with higher prices to multi-brand equilibrium with lower prices, if the incremental value from consuming an additional unit of the same product is independent of the preference for diversity; (ii) the direction of such equilibrium-switch is reversed if the two types of multi-purchase are substitutes.




Similar content being viewed by others
Notes
If one firm is subscripted by i, the other firm is subscripted by − i. Besides, marginal costs of production are normalized to be zero.
From the standpoint of a particular consumer, μi is known. In addition, our primary interest is to solve interior solutions, i.e., both types of multi-purchase are potentially active evaluated at equilibrium; hence, we restrict μ ∈ [t, 3t] and \( \beta \in [0,\sqrt {2}t] \) for a binary distributed μi in this section. In Section 3, β is allowed to be greater than \( \sqrt {2}t \) for a comparison between two types of preferences.
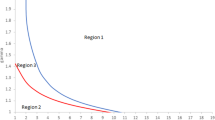
The inequalities shall be compared through the β-rA plane (fixing μ and rB), which adds complexity—this can be done by using the “inequal” command in Maple to check the intersections between two sets (see Fig. 2).
For the sign of \( \frac {\partial p_{i}^{*}}{\partial r_{i}} \) when ri≠r−i: (i) for the boundary solution, i.e., \( {{{p}_{A}^{M}}}^{*}<\mu \Leftrightarrow \beta <\mu +t \), which implies that \( \frac {\partial {{{p}_{A}^{M}}}^{*}}{\partial r_{A}}=\frac {\mu +t-\beta }{(1+r_{A})^{2}} > 0 \) when β + rAμ ≥ 2t; (ii) when \( \frac {\sqrt {2}}{3}(r_{A}-r_{B})\mu +\sqrt {2}t < \beta +r_{A}\mu <2t \), \( \frac {\partial {{{p}_{A}^{M}}}^{*}}{\partial r_{A}} = \frac {1}{2}\frac {\mu -\beta }{(1+r_{A})^{2}} \gtrless 0 \) provided that \( \beta \lessgtr \mu \), i.e., an increase of rA pushes \( {{{p}_{A}^{M}}}^{*} \) upward when μ is large relative to β; (iii) when \( \beta +r_{A}\mu < \frac {\sqrt {2}}{3}(r_{A}-r_{B})\mu +\sqrt {2}t \), \( \frac {\partial {{{p}_{A}^{S}}}^{*}}{\partial r_{A}} =\frac {(1+r_{B})\mu -3t}{3(1+r_{A})^{2}} \gtrless 0 \) provided that \( (1+r_{B})\mu \gtrless 3t \), i.e., an increase of rA pushes \( {{{p}_{A}^{S}}}^{*} \) downward evaluated at a lower rBμ because of strategic complements.
The threshold is numerically approximated by using “evalf(.)” command in Maple, where the equation (e.g., \( {\pi _{A}^{S}}|_{{{p}_{B}^{M}}\left (a=0,b=\frac {1}{2}\right )} = {\pi _{A}^{M}}|_{a=0,b=\frac {1}{2}} \)) in bracket (.) gives the solution of β + rμ that is replaced by an arbitrary variable.
References
Anderson SP, Foros Ø, Kind HJ (2017) Product functionality, competition, and multipurchasing. Int Econ Rev 58:183–210
Conitzer V, Taylor CR, Wagman L (2012) Hide and seek: costly consumer privacy in a market with repeat purchases. Market Sci 31:277–292
d’Aspremont C, Gabszewicz JJ, Thisse J-F (1979) On hotelling’s stability in competition. Econometrica 47(5):1145–1150
Hotelling H (1929) Stability in competition. Econ J 39:41–57
Jeitschko TD, Jung Y, Kim J (2017) Bundling and joint marketing by rival firms. J Econ Management Strategy 26:571–589
Kim H, Serfes K (2006) A location model with preference for variety. J Indust Econ 54:569–595
Acknowledgments
We thank Chong-En Bai, Alexander White, Jie Zheng, Ching-To Albert Ma, Ming Gao, Matthew Shi, and Yong Chao for very valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
Supplemental Proof for Proposition 1
In this section, we provide more details regarding the inequalities that shall be compared through case (a-1) to case (c-3), assuming that rA ≥ rB.
First, we rule out the possibility that one firm charges \( {p_{i}^{M}} \) whereas the other firm charges \( p_{-i}^{S} \). Suppose firm A charges \( {{p}_{A}^{M}} \) evaluated at \( {{p}_{B}^{S}}({{p}_{A}^{M}}) < \hat {p}_{B}\Leftrightarrow \)
When Eq. A.1 holds, the condition \( {{p}_{A}^{M}} > \hat {p}_{A} \Leftrightarrow \)
cannot hold evaluated at μ < 3t. Therefore, firm B will not charge \( {{p}_{B}^{S}} \). Similarly, suppose firm A charges \( {{p}_{A}^{S}}({{p}_{B}^{M}}) \) evaluated at \( {{p}_{B}^{M}} > \hat {p}_{B}\Leftrightarrow \beta +r_{A} \mu < \frac {1}{2\sqrt {2}-1}(r_{A}-r_{B}) \mu + \frac {2}{2\sqrt {2}-1}t \), the condition \( {{p}_{A}^{S}}({{p}_{B}^{M}}) < \hat {p}_{A}\Leftrightarrow \beta +r_{A} \mu >\frac {23(29-8\sqrt {2})}{713}(r_{A}-r_{B})\mu +\frac {(29-8\sqrt {2})(18 + 24\sqrt {2})}{713}t \) cannot hold, i.e., firm B will not charge \( {{p}_{B}^{M}} \).
-
(a)
When \( \hat {p}_{A} < {{p}_{A}^{M}} \), the following condition holds:
$$ \beta+r_{A}\mu < \frac{2(\sqrt{2}-1)}{2\sqrt{2}-1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t. $$(A.2)Suppose \( \hat {p}_{B} > {{p}_{B}^{M}} \), then
$$ \beta+r_{A}\mu>\frac{1}{2\sqrt{2}-1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t, $$which contradicts Eq. A.2. Therefore, for case (a), Eq. A.2 holds such that \( \hat {p}_{B} < {{p}_{B}^{M}} \), i.e., \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \) is a unique equilibrium.
-
(b)
When \( {{p}_{A}^{M}} < \hat {p}_{A} < \sqrt {2}{{p}_{A}^{M}} \), it follows that
$$ \frac{2(\sqrt{2}-1)}{2\sqrt{2}-1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t < \beta+r_{A}\mu < (2-\sqrt{2})(r_{A}-r_{B})\mu+\sqrt{2}t. $$(A.3)-
(1)
The intersection of Eq. A.3 and \( \hat {p}_{B} < {{p}_{B}^{M}} \) is
$$ \frac{2(\sqrt{2} - 1)}{2\sqrt{2} - 1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t \!<\! \beta+r_{A}\mu \!<\!\frac{1}{2\sqrt{2}-1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t. $$(A.4)Therefore, when Eq. A.4 holds, the unique equilibrium is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).
-
(2)
The intersection of Eq. A.3 and \( {{p}_{B}^{M}} < \hat {p}_{B} < \sqrt {2} {{p}_{B}^{M}} \) is
$$ \frac{1}{2\sqrt{2}-1}(r_{A}-r_{B})\mu+\frac{2}{2\sqrt{2}-1}t < \beta+r_{A}\mu < (\sqrt{2}-1)(r_{A}-r_{B})\mu + \sqrt{2}t. $$(A.5)However, evaluated at Eq. A.5, there are two equilibria. For firm A,
$$ {\pi_{A}^{M}}\left( {{p}_{A}^{M}},{{p}_{B}^{M}}\right)<{\pi_{A}^{S}} \left( {{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right)\Leftrightarrow \beta+r_{A}\mu < \frac{\sqrt{2}}{3}(r_{A}-r_{B})\mu+\sqrt{2}t, $$(A.6)which is a sufficient condition for
$$ {\pi_{B}^{M}}\left( {{p}_{A}^{M}},{{p}_{B}^{M}}\right)<{\pi_{B}^{S}} \left( {{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right)\Leftrightarrow\beta+r_{A}\mu < \left( 1-\frac{\sqrt{2}}{3}\right)(r_{A}-r_{B})\mu+\sqrt{2}t. $$(A.7)Evaluated at Eq. A.5, both Eq. A.6 and Eq. A.7 hold. That is, \( \left ({{p}_{A}^{M}},{{p}_{B}^{M}}\right ) \) is not a stable equilibrium because both firms have incentives to deviate to \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).
-
(3)
The intersection of Eq. A.3 and \( \sqrt {2}{{p}_{B}^{M}} < \hat {p}_{B} \) is
$$ (\sqrt{2}-1)(r_{A}-r_{B})\mu+\sqrt{2}t<\beta+r_{A}\mu < (2-\sqrt{2})(r_{A}-r_{B})\mu+\sqrt{2}t. $$(A.8)Evaluated at Eq. A.8, the intersection of \( {{p}_{A}^{M}} \) and \( {{p}_{B}^{M}} \) exists. But the existence of the intersection of \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) depends crucially on the relative size of β + rAμ, in particular:
-
(i)
If \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) intersects, we have \( {{p}_{B}^{S}}|_{p_{A}= \sqrt {2}{{p}_{A}^{M}}} > \hat {p}_{B} \Leftrightarrow \)
$$ (\sqrt{2}-1)(r_{A}-r_{B})\mu+\sqrt{2}t<\beta+r_{A}\mu < \frac{\sqrt{2}}{3}(r_{A}-r_{B})\mu+\sqrt{2}t. $$(A.9)If Eq. A.9 holds, there are two equilibria. However, the second inequality of Eq. A.9 is equivalent to Eq. A.6, which is also a sufficient condition for Eq. A.7. Therefore, evaluated at Eq. A.9, the stable equilibrium is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).
-
(ii)
Evaluated at Eq. A.8, if \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) do not intersect, the parametric values correspond to
$$ \frac{\sqrt{2}}{3}(r_{A}-r_{B})\mu+\sqrt{2}t<\beta+r_{A}\mu < (2-\sqrt{2})(r_{A}-r_{B})\mu +\sqrt{2}t. $$(A.10)Then, the unique equilibrium is \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \).
-
(i)
-
(1)
-
(c)
When \( \sqrt {2}{{p}_{A}^{M}} <\hat {p}_{A} \),
$$ \beta+r_{A}\mu > (2-\sqrt{2})(r_{A}-r_{B})\mu +\sqrt{2}t. $$(A.11)Suppose \( \hat {p}_{B} < \sqrt {2}{{p}_{B}^{M}} \), then
$$ \beta+r_{A}\mu < (\sqrt{2}-1)(r_{A}-r_{B})\mu +\sqrt{2}t, $$which contradicts Eq. A.11. Therefore, when Eq. A.11 holds, the unique equilibrium is \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \). The cutoff conditions derived above are summarized in Fig. 2.
□
Supplemental Proof for Proposition 3
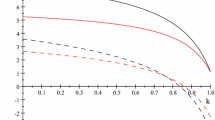
The intersection points of the best responses given by Eq. 9 are determined by the relative positions of \( {p_{i}^{M}}(p_{-i}) \), \( {p_{i}^{S}}(p_{-i}) \) and \( \tilde {p}_{-i} \) (see Fig. 3). Evaluated at \( \tilde {p}_{-i} \), \( {p_{i}^{M}}(\tilde {p}_{-i})=\frac {\left ((1+r)(\beta -r\mu )-rt \right )\left (2r\sqrt {2(1+r^{2})} + (1+r)(1+r^{2}) \right ) }{2(1-r)(1+r^{2})(1+4r+r^{2})} \), \( {p_{i}^{S}}(\tilde {p}_{-i})= \frac {\left ((1+r)(\beta -r\mu )-rt\right ) \left ((1+r)\sqrt {2(1+r^{2})}+4r\right ) }{2(1-r)(1+r)(1+4r+r^{2})} \), and when 1 ≥ r ≥ 0,
In the proof of Proposition 1, we have shown the relative slopes of \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \). Here, \( {{p}_{A}^{M}} \) and \( {{p}_{B}^{M}} \) are also upward sloping, where \( \frac {\partial {{p}_{A}^{M}}}{\partial p_{B}} = \frac {r}{1+r^{2}} < \frac {1}{2} = \frac {\partial {{p}_{A}^{S}}}{\partial p_{B}} \) and \( \left (\frac {\partial {{p}_{B}^{S}}}{\partial p_{A}}\right )^{-1} = 2 > \left (\frac {\partial {{p}_{B}^{M}}}{\partial p_{A}}\right )^{-1} = \frac {1+r^{2}}{r}>\frac {1}{2} \).
-
(i)
When \( \tilde {p}_{-i}<{p_{i}^{M}}(\tilde {p}_{-i}) < {p_{i}^{S}}(\tilde {p}_{-i}) \Leftrightarrow \)
$$ \beta-r\mu < K^{S}:= \frac{4(1-r+r^{2})\sqrt{2(1+r^{2})} +2-7r+2r^{2}-5r^{3} }{(1-r)(7-2r+7r^{2})}t, $$(A.12)the unique intersection point is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).
-
(ii)
When \( {p_{i}^{M}}(\tilde {p}_{-i}) < {p_{i}^{S}}(\tilde {p}_{-i})< \tilde {p}_{-i} \Leftrightarrow \)
$$ \beta-r\mu>K^{M}:= \frac{(1+r)\sqrt{2(1+r^{2})}-3r-r^{2}}{(1-r)(1+r)}t, $$(A.13)the unique intersection point is \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \).
-
(iii)
When \( {p_{i}^{M}}(\tilde {p}_{-i})<\tilde {p}_{-i}<{p_{i}^{S}}(\tilde {p}_{-i})\Leftrightarrow K^{S}<\beta -r\mu <K^{M} \), there are two points of intersection: \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \) and \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \). However, evaluated at KS < β − rμ < KM, the condition
$$ \beta-r\mu < \frac{\sqrt{2}(1-r+r^{2})+r\sqrt{1+r^{2}}}{(1-r)\sqrt{1+r^{2}}}t $$(A.14)holds such that ∀i and 0 < r < 1, \( {\pi _{i}^{S}}\left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) > {\pi _{i}^{M}}\left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \). That is, KS < β − rμ < KM is a sufficient condition of (i.e., a subset of) Eq. A.14.
Finally, we validate the above arguments by checking whether the equilibrium prices are offered consistently with consumers’ decisions. Evaluated at \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \), the demand for multi-brand purchase is positive, i.e., \( \tilde {x}_{B}\left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) < \tilde {x}_{A}\left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right )\Leftrightarrow \)
where Eq. A.15 is a necessary condition of Eq. A.13. Evaluated at \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \), the demand for multi-brand purchase is eliminated, i.e., \( \tilde {x}_{B}\left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right )>\tilde {x}_{A}\left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right )\Leftrightarrow \)
where Eq. A.16 is implied by β − rμ < KM. □
To summarize (Fig. 4), when β − rμ is greater than the threshold given by Eq. A.13, the equilibrium prices are \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \); when β − rμ is lower than the threshold given by Eq. A.13, the equilibrium prices are \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).
Equilibria with Quadratic Costs and Fixed Locations
When prices are higher relative to β and μ, the demand for multi-brand purchase is zero. A consumer who is indifferent between choosing brand A and B locates at \( \hat {x}^{S} \). When prices are lower relative to β and μ, the demand for multi-brand purchase is positive. A consumer who is indifferent between buying brand A only and both brands, and the one who is indifferent between buying brand B only and both brands, locate at
respectively.
The remaining procedure follows the similar manner as shown by Proposition 1. When \( \hat {x}_{B}>\hat {x}_{A} \), given pB, firm A solves \( {{p}_{A}^{S}}=\arg \max_{p_{A}}(1+r)p_{A}\hat {x}^{S} \); Given pA, firm B solves \( {{p}_{B}^{S}}=\arg \max_{p_{B}}(1+r)p_{B}(1-\hat {x}^{S}) \). When \( \hat {x}_{B}<\hat {x}_{A} \), firm A solves \( {{p}_{A}^{M}}=\arg \max_{p_{A}}(1+r)p_{A}\hat {x}_{A} \) and firm B solves \( {{p}_{B}^{M}}=\arg \max_{p_{B}}(1+r)p_{B}(1-\hat {x}_{B}) \). Evaluated at \( \hat {p}_{-i} \), charging \( {p_{i}^{S}} \) according to \( \hat {x}_{B}>\hat {x}_{A} \) and charging \( {p_{i}^{M}} \) according to \( \hat {x}_{B}<\hat {x}_{A} \) are equally profitable, i.e., \( {\pi _{i}^{M}}({p_{i}^{M}})={\pi _{i}^{S}}(\hat {p}_{-i}) \). Hence, the conditional reactions are given by
Next, by checking the relative positions of \( {p_{i}^{M}} \), \( {p_{i}^{S}}(\hat {p}_{-i}) \) and \( \hat {p}_{i} \) and the resulting points of intersection of \( {p}_{A}^{BR} \) and \( {p}_{B}^{BR} \), the symmetric equilibrium is given by
□
Supplemental Proof for Proposition 4
In Proposition 4, the threshold for regime switch, denoted \( \widehat {\beta +r\mu }:=-\frac {t}{12} + \frac {t}{12}\left [(28+3\sqrt {87})^{\frac {1}{3}} +\frac {1}{(28+3\sqrt {87})^{\frac {1}{3}}}-1\right ]^{2} \), is found by \( {\pi _{i}^{S}}|_{a=0,b=1} = {\pi _{i}^{M}}|_{a=b=\frac {1}{2}}\left (\widehat {\beta +r\mu }\right ) \). For the remaining, we complete the proof by ruling out possible deviations.
Suppose that the initial equilibrium corresponds to the multi-brand equilibrium, i.e., when \( \beta +r\mu >\widehat {\beta +r\mu } \) holds with minimum differentiation. By Eq. 12, price deviation in stage 2 is unprofitable. Consider the deviations in stage 1 by relocating at a = 0, given \( b=\frac {1}{2} \), and then search for the optimal prices in stage 2.
Given a = 0 and \( b=\frac {1}{2} \) chosen in stage 1, and the demand for multi-brand satisfies the condition \( \hat {x}_{b}>\hat {x}_{a} \) (single-brand equilibrium), then the equilibrium prices in stage 2 are \( {{p}_{A}^{S}}|_{a=0,b=\frac {1}{2}} = \frac {5}{12}\frac {t}{1+r} \) and \( {{p}_{B}^{S}}|_{a=0,b=\frac {1}{2}} = \frac {7}{12}\frac {t}{1+r} \) (by plugging a = 0 and \( b=\frac {1}{2} \) into Eq. 11). The equilibrium profits are \( {\pi _{A}^{S}}|_{a=0,b=\frac {1}{2}}=\frac {25}{144}t \) and \( {\pi _{B}^{S}}|_{a=0,b=\frac {1}{2}} = \frac {49}{144}t \). If firm A deviates its price by setting \( {{p}_{A}^{M}} \) such that \( \hat {x}_{b}<\hat {x}_{a} \) (multi-brand equilibrium), then the equilibrium price and profit are \( {{p}_{A}^{M}}|_{a=0,b=\frac {1}{2}} = \frac {2}{3}\frac {\beta +r\mu }{1+r} \) and \( {\pi _{A}^{M}}|_{a=0,b=\frac {1}{2}} = \frac {2\sqrt {3}(\beta +r\mu )^{\frac {3}{2}}}{9\sqrt {t}} \). Charging \( {{p}_{A}^{M}}|_{a=0,b=\frac {1}{2}} \) is less profitable than charging \( {{p}_{A}^{S}}|_{a=0,b=\frac {1}{2}} \) provided that \( \beta +r\mu < \frac {450^{\frac {2}{3}}3^{\frac {1}{3}}}{144}t \). Similarly, if firm B deviates by setting \( {{p}_{B}^{M}} \) such that \( \hat {x}_{b} < \hat {x}_{a} \), such deviation is not profitable provided that \( {\pi _{B}^{M}}|_{a=0,b=\frac {1}{2}} < {\pi _{B}^{S}}|_{a=0,b=\frac {1}{2}} \Leftrightarrow \beta +r\mu < -\frac {t}{12}+\frac {t}{12}\left (\frac {1}{2}(155+7\sqrt {489})^{\frac {1}{3}}+\frac {2}{(155+7\sqrt {489})^{\frac {1}{3}}}-1\right )^{2} \), under which, the condition \( \beta +r\mu < \frac {450^{\frac {2}{3}}3^{\frac {1}{3}}}{144}t \) holds such that neither firm will deviate.
Next, if the demand for multi-brand satisfies the condition \( \hat {x}_{b}<\hat {x}_{a} \) and given \( a=0 < b=\frac {1}{2} \) chosen in stage 1, consider the possible price deviations in stage 2. Before deviation, prices and profits are given by Eq. 12 where location parameters are replaced by a = 0 and \( b = \frac {1}{2} \). Given \( {{p}_{B}^{M}}|_{a=0,b=\frac {1}{2}} \), if firm A deviates by setting \( {{p}_{A}^{S}} = \frac {24(\beta +r\mu )+7t+2\sqrt {\left (12(\beta +r\mu )+t\right )t} }{72(1+r)} \) such that \( \hat {x}_{b}>\hat {x}_{a} \), the profit is \( {\pi _{A}^{S}}|_{{{p}_{B}^{M}}\left (a=0,b=\frac {1}{2}\right )} = \frac {\left (24(\beta +r\mu )+7t+2\sqrt {\left (12(\beta +r\mu )+t\right )t } \right )^{2}}{5184t} \). Deviating is unprofitable provided that \( {\pi _{A}^{S}}|_{{{p}_{B}^{M}}\left (a=0,b=\frac {1}{2}\right )} < {\pi _{A}^{M}}|_{a=0,b=\frac {1}{2}}\Leftrightarrow \beta +r\mu >0.32t \).Footnote 5 Similarly, given \( {{p}_{A}^{M}}|_{a=0,b=\frac {1}{2}} \), if firm B deviates by setting \( {{p}_{B}^{S}} = \frac {8(\beta +r\mu )+9t}{24(1+r)} \), it gives \( {\pi _{B}^{S}}|_{{{p}_{A}^{M}}\left (a=0,b=\frac {1}{2}\right )} = \frac {\left [8(\beta +r\mu )+9t\right ]^{2}}{576t} \). Such deviation is unprofitable provided that \( {\pi _{B}^{S}}|_{{{p}_{A}^{M}}\left (a=0,b=\frac {1}{2}\right )}<{\pi _{B}^{M}}|_{a=0,b=\frac {1}{2}}\Leftrightarrow \beta +r\mu > 0.41t \).
Therefore, when \( \beta +r\mu > -\frac {t}{12}+\frac {t}{12}\left (\frac {1}{2}(155+7\sqrt {489})^{\frac {1}{3}}+\frac {2}{(155+7\sqrt {489})^{\frac {1}{3}}}-1\right )^{2} \), given a = 0 and \( b=\frac {1}{2} \), both firms will deviate to offer prices such that the demand for multi-brand is positive. However, when the demand for multi-brand is positive, firm A has no incentive to relocate at a = 0 in stage 1, as shown by Eq. 12, where \( \frac {\partial {\pi _{A}^{M}}}{\partial a} > 0 \). When β + rμ < 0.41t, both firms will charge \( {p_{i}^{S}} \) to eliminate multi-brand purchase. In such a case, the location \( (a,b)=\left (0,\frac {1}{2}\right ) \) is not optimal, because moving b to 1 makes firm B strictly better off. Similarly when \( 0.41t < \beta +r\mu < -\frac {t}{12}+\frac {t}{12}\left (\frac {1}{2}(155+7\sqrt {489})^{\frac {1}{3}}+\frac {2}{(155+7\sqrt {489})^{\frac {1}{3}}}-1\right )^{2} \), deviating to \( (a,b)=\left (0,\frac {1}{2}\right ) \) in stage 1 is not profitable, because \( -\frac {t}{12}+\frac {t}{12}\left (\frac {1}{2}(155+7\sqrt {489})^{\frac {1}{3}}+\frac {2}{(155+7\sqrt {489})^{\frac {1}{3}}}-1\right )^{2} < \widehat {\beta +r\mu } \) and \( {\pi _{i}^{M}}|_{\beta +r\mu <\widehat {\beta +r\mu }} < {\pi _{i}^{S}}|_{\beta +r\mu <\widehat {\beta +r\mu }} \).
Now suppose the initial condition satisfies \( \beta +r\mu < \widehat {\beta +r\mu } \) with maximum differentiation given by Eq. 13. Clearly, when fixing (a,b) = (0, 1), price deviation in stage 2 is unprofitable. Consider firm B deviates by relocate at \( b=\frac {1}{2} \), given a = 0. Evaluated at \( (a,b)=\left (0,\frac {1}{2}\right ) \), charging \( {{p}_{B}^{S}} \) in stage 2 must generate an incentive to move b to 1 in stage 1. Alternatively, charging \( {{p}_{B}^{M}} = \frac {12(\beta +r\mu )-t+\sqrt {\left (12(\beta +r\mu )+t\right )t}}{18(1+r)} \) according to \( \hat {x}_{b} < \hat {x}_{a} \) gives \( {\pi _{B}^{M}}|_{a=0,b=\frac {1}{2}} \), which is less profitable than that before deviating in stage 1, i.e., \( {\pi _{B}^{M}}|_{a=0,b=\frac {1}{2}} < {\pi _{B}^{S}}|_{a=0,b=1}=\frac {t}{2} \) provided that \( \beta +r\mu < \widehat {\beta +r\mu } \). □
Rights and permissions
About this article
Cite this article
Shao, X. Diversity and Quantity Choice in a Horizontally Differentiated Duopoly. J Ind Compet Trade 20, 689–708 (2020). https://doi.org/10.1007/s10842-020-00337-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10842-020-00337-1