Strategic CSR in Asymmetric Cournot Duopoly

Abstract

We examine the strategic use of corporate social responsibility (CSR) in Cournot competition between two firms that differ in their marginal costs of production. The level of CSR determines the weight a firm puts on consumer surplus in its objective function before it decides upon supply. We show that the more efficient firm chooses a higher CSR level, reinforcing its dominant position. If there are sufficiently large fixed costs of CSR, only the more efficient firm will engage in CSR.

Introduction

Corporate social responsibility (CSR) refers to all social and environmentally friendly activities of a firm beyond its legal requirements (Kitzmueller and Shimshack 2012). In the past decades, CSR has increasingly become a concern for many firms, particularly large- and mid-cap companies (Benn and Bolton 2011; KPMG 2017). Among the various motives for CSR, its strategic use in markets with imperfect competition plays an important role (Garriga and Melé 2004; Bénabou and Tirole 2010). The basic idea is that even pure profit-maximizing firms engage in CSR because it may serve as a commitment device for their strategy choices.

Although overall empirical evidence on the relation between firms’ CSR activities and their financial performance is mixed, meta-analyses such as Aguinis and Glavas (2012) confirm a small positive relation. Indeed, many recent studies find a positive correlation (Jo and Harjoto 2011; Eccles et al. 2014; Flammer 2015). This raises the question about causality: does CSR boost profits or can more profitable firms afford more CSR?

We address this question within a simple model of Cournot competition between two firms that differ in their marginal costs of production. The level of CSR determines the weight a firm puts on consumer surplus in its objective function before it decides upon supply. We find a mutual causality: the more efficient firm chooses a higher CSR level, reinforcing its dominant position. If there are sufficiently large fixed costs of CSR, an equilibrium will arise in which only the more efficient firm chooses a positive level of CSR.

The Model

We consider Cournot competition between two profit-maximizing firms on the market for some homogeneous good with (normalized) linear inverse demand¹p = 1 − (q₁ + q₂), where p denotes the price of the good and q_i denotes the output of firm i ∈{1,2}. Marginal costs of production are assumed to be constant with c₁ = 0 (normalization) and c₂ = c, where 0 ≤ c ≤ 1, i.e., firm 1 is (possibly) more efficient than firm 2.

Competition between firms is modeled as a two-stage game. In the first stage of the game, the firms simultaneously choose their level of CSR. The CSR level of firm i ∈{1,2} is understood as the weight 𝜃_i ≥ 0 on consumer surplus CS in addition to profits π_i in its objective function:²

$$ V_{i} = \pi_{i} + \theta_{i} \cdot CS = (1-q_{i}-q_{j}-c_{i})q_{i} - K_{i} + \frac{1}{2}\theta_{i}(q_{i}+q_{j})^{2}, $$

where K_i represents a quasi-fixed cost of CSR, i.e., K_i = 0 if 𝜃_i = 0 and K_i = Z ≥ 0 if 𝜃_i > 0.³ Such a commitment to an objective function can be thought of as signing an appropriate corporate charter or hiring a manager known to have appropriate preferences. Our framework may thus also be interpreted as a model of strategic delegation (Vickers 1985; Fershtman and Judd 1987; Sklivas 1987).

In the second stage of the game, firms decide simultaneously on their output levels q_i ≥ 0 in order to maximize their objective functions V_i.

Analysis

In this section, we abstract from costs of CSR (Z = 0) and solve the game by backward induction for its subgame perfect equilibria (SPE). We focus on potential SPE in which 𝜃_i ∈ [0,1] for i ∈{1,2}, i.e., no firm puts more weight on consumer surplus than on profits.

At the second stage of the game, the first-order conditions ∂V_i/∂q_i = 0 imply the reaction functions

$$ \begin{array}{@{}rcl@{}} q_{1}(q_{2})&=& \frac{1-(1-\theta_{1})q_{2}}{2-\theta_{1}},\\ q_{2}(q_{1})&=& \frac{1-c-(1-\theta_{2})q_{1}}{2-\theta_{2}}, \end{array} $$

and thus, the second stage quantity choices as functions of the CSR levels:

$$ \begin{array}{@{}rcl@{}} q_{1}&=& \frac{1-\theta_{2}+\theta_{1}+c(1-\theta_{1})}{3-\theta_{1}-\theta_{2}}, \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} q_{2}&=& \frac{1-\theta_{1}+\theta_{2}-c(2-\theta_{1})}{3-\theta_{1}-\theta_{2}}. \end{array} $$

(2)

At the first stage, the firms anticipate these choices and maximize their respective profits

$$ \begin{array}{@{}rcl@{}} \pi_{1}&=& \frac{(1-\theta_{2}+c-\theta_{1})(1-\theta_{2}+c+(1-c)\theta_{1})}{(3-\theta_{1}-\theta_{2})^{2}}, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} \pi_{2}&=& \frac{(1-2c-(1-c)\theta_{1}-(1-c)\theta_{2})(1-2c-(1-c)\theta_{1}+\theta_{2})}{(3-\theta_{1}-\theta_{2})^{2}}, \end{array} $$

(4)

by the choice of their CSR levels. The first-order conditions ∂π_i/∂𝜃_i = 0 imply

$$ \begin{array}{@{}rcl@{}} \theta_{1}(\theta_{2})&=& \frac{(1-\theta_{2})^{2}+(1-\theta_{2})c}{3-\theta_{2}-c}, \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \theta_{2}(\theta_{1})&=& \frac{(1-\theta_{1})^{2}-(1-\theta_{1})(2-\theta_{1})c}{3-\theta_{1}-(2-\theta_{1})c}. \end{array} $$

(6)

It is straightforward to show that 0 ≤ 𝜃₁(𝜃₂) < 1 for all 0 < c < 1 and all 𝜃₂ ∈ [0,1] as well as 𝜃₂(𝜃₁) < 1 for all 0 < c < 1 and all 𝜃₁ ∈ [0,1]. Moreover, 0 < 𝜃₂(𝜃₁) for 0 < c < 1 and 𝜃₁ ∈ [0,1] if and only if

$$ \theta_{1} < \frac{1-2c}{1-c}. $$

(7)

Consequently, for all 0 < c < 1 and 𝜃₁,𝜃₂ ∈ [0,1], the first stage best responses of the firms are given by the reaction functions r₁(𝜃₂) := 𝜃₁(𝜃₂) and $r_{2}(\theta _{1}):=\max \limits \{\theta _{2}(\theta _{1}),0\}$, where 𝜃₁(𝜃₂) and 𝜃₂(𝜃₁) are defined by Eqs. 5 and 6, respectively.

Figure 1 illustrates the equilibrium CSR levels depicting the reaction functions r₁ and r₂ for the cost differentials c = 0, c = 1/4, and c = 1/3, respectively. Lemma 1 in the Appendix provides the comparative statics properties of the reaction functions. In particular, it shows that an increase in c increases r₁ and decreases r₂ wherever positive. For c = 1/3, we have r₁(0) = 𝜃₁(0) = 1/2 and r₂(1/2) = 𝜃₂(1/2) = 0 according to Eqs. 5 and 6, and thus, r₁ and r₂ intersect at (𝜃₁,𝜃₂) = (1/2,0). Lemma 1 then implies that, for any c ≥ 1/3, we always have 𝜃₂ = 0 where r₁ and r₂ intersect. If 𝜃₂ = 0, however, Eq. 5 implies the best response 𝜃₁ = (1 + c)/(3 − c), and thus, q₂ < 0 for all c > 1/3 by Eq. 2, i.e., the non-negativity constraint on the quantity of firm 2 will be violated. This proves

Fig. 1

CSR levels in the SPE with asymmetric marginal costs

Proposition 1

If c ≥ 1/3, the less efficient firm will leave the market.

Notice that, without the strategic use of CSR (𝜃₁ = 𝜃₂ = 0), the threshold marginal cost above which the less efficient firm leaves the market is larger (c = 1/2). Strategic CSR may thus increase the market power of more efficient firms and foster market consolidation as well as the adaption of new technologies.

For smaller marginal costs, the intersection of the reaction functions r₁ and r₂ constitutes a SPE. We asterisk the corresponding equilibrium values.

Proposition 2

For all c ∈ (0,1/3), the two-stage game with strategic CSR and Cournot competition between two asymmetric firms has a SPE in which

• (a) The firm with the lower marginal costs chooses a higher CSR level, produces more output, and earns higher profits, i.e., $\theta ^{*}_{1} > \theta ^{*}_{2} > 0$, $q^{*}_{1}>q^{*}_{2} > 0$, and $\pi ^{*}_{1}>\pi ^{*}_{2} > 0$ for all 0 < c < 1/3.

• (b) An increase in the cost differential increases the CSR level of the advantaged firm and decreases the CSR level of the disadvantaged firm, i.e., $d\theta ^{*}_{1}/dc > 0$ and $d\theta ^{*}_{2}/dc < 0$ for all c ∈ (0,1/3).

The proof can be found in the Appendix. For the intuition behind these results, note that in this model a higher CSR level (i.e., more weight on consumer surplus) represents a strategic commitment to a higher output. Since the more efficient firm faces lower costs of production, increasing its output is less costly for this firm. Therefore, it has stronger incentives to use this commitment device.⁴ The model thus applies particularly well to environments in which CSR measures aim at a high market coverage, e.g., in the provision of pharmaceuticals in developing countries.

Proposition 2 is in line with several findings in the recent literature on strategic delegation. Straume (2006) and Fanti and Meccheri (2017) also find that the more efficient firm chooses a higher weight on the additional objective if managers maximize a weighted combination of profits and sales. For revenues as additional objective, Delbono et al. (2016) show that the more efficient firm earns higher equilibrium profits.⁵ Moreover, Colombo (2019) finds that for sufficiently high cost differences the more efficient firm may even earn higher profits in the delegation equilibrium than if both firms abstained from delegation.

Inclusion of Fixed Costs for CSR

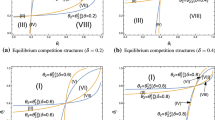
Fixed costs for CSR may induce firms to shy away from its strategic use. Based on numerical computations, we demonstrate that, depending on the level of fixed costs Z, different types of equilibria may exist: as Fig. 2 illustrates (for c = 0.02), we may find not only interior solutions, I, in which both firms choose positive CSR levels, but also right (left) corner solutions, R (L), in which only the more (less) efficient firm chooses a positive CSR level, or an equilibrium, O, in which neither firm engages in CSR.

Fig. 2

Best responses and equilibria at different levels of Z (c = 0.02)

Figure 3 depicts which equilibria may occur for different combinations of asymmetric marginal costs of production, c, and symmetric quasi-fixed costs of CSR, Z. Using Eqs. 3 through 6, we compute the threshold values for Z for each given c in the following way:

$$ \begin{array}{@{}rcl@{}} Z_{0}&=&\pi_{2}(\theta_{1}(0),\theta_{2}(\theta_{1}(0)))-\pi_{2}(\theta_{1}(0),0), \\ Z_{1}&=&\pi_{2}(\theta_{1}^{*},\theta_{2}^{*})-\pi_{2}(\theta_{1}^{*},0), \\ Z_{2}&=&\pi_{1}(\theta_{1}(\theta_{2}(0)),\theta_{2}(0))-\pi_{1}(0,\theta_{2}(0)), \\ Z_{3}&=&\pi_{2}(0,\theta_{2}(0))-\pi_{2}(0,0), \\ Z_{4}&=&\pi_{1}(\theta_{1}(0),0)-\pi_{1}(0,0). \end{array} $$

Intuitively, if the costs of CSR are sufficiently small (below Z₁), it may pay off for both firms to choose positive CSR levels resulting in an interior solution (I). By contrast, if the costs of CSR are prohibitively large (above Z₄), both firms will abandon CSR in equilibrium (O). In the range of intermediate costs of CSR (above Z₀ and below Z₄), corner solutions may arise: investing these costs and choosing a sufficiently high level of CSR, one firm can “take the lead” and commit to a quantity that makes such a costly commitment unprofitable for the other firm. Since a commitment to a larger quantity is less attractive for the less efficient firm (and the less so the higher its production costs c), the range of parameters for a left corner solution (L), where only the less efficient firm engages in CSR, is restricted to the area above Z₂ and below Z₃. By contrast, in the whole area between Z₀ and Z₄, there always exists a right corner solution (R), where only the more efficient firm engages in CSR.

Fig. 3

Occurrence of equilibria depending on c and Z

Including fixed costs for CSR, our model thus provides an explanation why firms with and without CSR engagement may coexist.

Conclusion

We have examined the strategic use of corporate social responsibility (CSR) in Cournot competition between two firms that differ in their marginal costs of production. The level of CSR determines the weight a firm puts on consumer surplus in its objective function before it decides upon supply. The results demonstrate that the strategic use of CSR complements cost advantages and reinforces differences in market power. Moreover, (symmetric) fixed costs of CSR provide an explanation for the coexistence of (highly profitable) firms that engage in CSR and (less profitable) firms that abstain from CSR. In the long-run, strategic CSR may thus foster market consolidation and accelerate the adoption of superior technologies.

The lessons for policymakers are twofold: First, the observation of differing CSR levels may convey information on differing costs of production. On markets with imperfect competition, a firm’s CSR level may also be an indicator of market power. Thus, such information may be useful for regulatory purposes. Second, if politics can control the fixed costs of CSR, e.g., by establishing an official CSR label, it may be able to influence the (type of) market equilibrium and outcome. We find both cases in which the government can increase consumer surplus by reducing the fixed costs of CSR and cases in which it can do so by raising them.⁶

A comprehensive welfare analysis is, however, beyond the scope of this short paper.

Appendix: Proof of Proposition 2

In order to prove part (a) of Proposition 2, first notice that for c = 0, a (unique) SPE exists (Planer-Friedrich and Sahm 2020) and is symmetric with $\theta ^{*}_{1}=\theta _{2}^{*}=(5-\sqrt {17})/4$ according to Eqs. 5 and 6. Now, suppose that an SPE with $\theta ^{*}_{i} \in [0,1]$ for i ∈{1, 2} exists for all 0 < c < 1 and has the properties stated in part (b) of Proposition 2. Then these properties imply $\theta ^{*}_{1} > \theta ^{*}_{2}$ for all 0 < c < 1, which, in turn, implies $q^{*}_{1}>q^{*}_{2}$ according to Eqs. 1 and 2, and, consequently, $\pi ^{*}_{1}>\pi ^{*}_{2}$.

It remains to show that an SPE with $\theta ^{*}_{i} \in [0,1]$ for i ∈{1, 2} exists for all 0 < c < 1 and has the properties stated in part (b). Notice that r₁(1) = r₂(1) = 0 and r₁(0) > 0 for all 0 < c < 1. For c = 1/3, we have r₁(0) = 𝜃₁(0) = 1/2 and r₂(1/2) = 𝜃₂(1/2) = 0 according to Eqs. 5 and 6, and thus, $\theta ^{*}_{1}=1/2$ and $\theta _{2}^{*}=0$ constitute an SPE. The existence of an SPE for all 0 < c < 1 in which $\theta ^{*}_{i} \in [0,1]$ for i ∈{1, 2} and the respective comparative statics $d\theta ^{*}_{1}/dc > 0$ for all c ∈ (0, 1) and $d\theta ^{*}_{2}/dc < 0$ for all c ∈ (0, 1/3) as well as $\theta ^{*}_{2}=0$ for all c ∈ [1/3, 1) now result from the following:

Lemma 1

For all 0 < c < 1 and 𝜃₁,𝜃₂ ∈ [0, 1], the reaction function

• (a) r₁ strictly decreases in 𝜃₂, i.e., ∂r₁/∂𝜃₂ < 0,

• (b) r₂ strictly decreases in 𝜃₁, i.e., ∂r₂/∂𝜃₁ < 0, wherever positive.

• (c) r₁ shifts strictly upward in c, i.e., ∂r₁/∂c > 0, for all 𝜃₂ ∈ [0, 1)

• (d) r₂ shifts strictly downward in c, i.e., ∂r₂/∂c < 0, for all 𝜃₁ ∈ [0, 1) wherever positive.

Proof

• (a) Using Eq. 5, it is straightforward to show that ∂r₁/∂𝜃₂ = ∂𝜃₁(𝜃₂)/∂𝜃₂ < 0 is equivalent to

  $$ -5+c^{2}-2c\theta_{2}+6\theta_{2}-{\theta_{2}^{2}} < 0. $$

  For 𝜃₂ = 1, the expression on the left-hand side (LHS) of this inequality is obviously negative for all 0 ≤ c ≤ 1. As a function of c, the LHS is convex and takes its minimum at c = 𝜃₂ ∈ [0, 1]. Consequently, depending on 𝜃₂, the LHS takes its maximum either at c = 0 or at c = 1. For 0 ≤ 𝜃₂ ≤ 1/2 the LHS has a maximum of $-4+4\theta _{2}-{\theta _{2}^{2}}<0$ at c = 1, and for 1/2 < 𝜃₂ < 1 the LHS has a maximum of $-5+6\theta _{2}-{\theta _{2}^{2}}<0$ at c = 0. The maximum of the LHS is thus always negative and, a fortiori, the inequality is correct for all 0 < c < 1 and 𝜃₂ ∈ [0, 1].

• (b) Wherever r₂ is positive, r₂(𝜃₁) = 𝜃₂(𝜃₁). Using Eq. 6, it is straightforward to show that ∂𝜃₂(𝜃₁)/∂𝜃₁ < 0 is equivalent to

  $$ (6-10c+4c^{2})\theta_{1}-(1-c)^{2}{\theta_{1}^{2}} < 5-10c+4c^{2}. $$

  (8)

  The expression on the left-hand side (LHS) of inequality (8) strictly increases in 𝜃₁, because straightforward calculations show that

  $$ \frac{6-10c+4c^{2}}{2(1-c)} > 1 \geq \theta_{1} $$

  for all 0 < c < 1 and 𝜃₁ ∈ [0, 1]. According to inequality (7), 𝜃₁ < (1 − 2c)/(1 − c) wherever r₂ positive. Consequently, wherever r₂ positive, the LHS of inequality Eq. 8 is smaller than

  $$ (6-10c^{2}+4c^{2}) \cdot \frac{1-2c}{1-c}-(1-c)^{2} \cdot \left( \frac{1-2c}{1-c}\right)^{2} = 5-12c+4c^{2} $$

  and thus obviously smaller than the right-hand side of inequality (8) for all 0 < c < 1.

• (c) Using Eq. 5, it is straightforward to show that ∂r₁/∂c = ∂𝜃₁(𝜃₂)/∂c > 0 is equivalent to

  $$ 2-3\theta_{2}+{\theta_{2}^{2}} > 0, $$

  which is obviously true for all 𝜃₂ ∈ [0, 1) as the expression on the left-hand side of this inequality strictly decreases for all 𝜃₂ ∈ [0, 1] and thus takes its minimum 0 at the corner 𝜃₂ = 1.

• (d) Wherever r₂ is positive, r₂(𝜃₁) = 𝜃₂(𝜃₁). Using Eq. 6, straightforward calculations show that ∂𝜃₂(𝜃₁)/∂c < 0 for all 𝜃₁ ∈ [0, 1).

□