Abstract
Optical memristive switches are particularly interesting for the use as latching optical switches, as a novel optical memory or as a digital optical switch. The optical memristive effect has recently enabled a miniaturization of optical devices far beyond of what seemed feasible. The smallest optical – or plasmonic – switch has now atomic scale and in fact is switched by moving single atoms. In this review, we summarize the development of optical memristive switches on their path from the micro- to the atomic scale. Three memristive effects that are important to the optical field are discussed in more detail. Among them are the phase transition effect, the valency change effect and the electrochemical metallization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Optical memristive switches are versatile integrated optical circuit elements [1–7]. They are digital optical switches with distinct transmission states based on a resistive switching with memory and thus feature characteristics of optical modulators and optical memories in one structure. Typically, they are controlled by electrical signals – but sometimes by optical signals. Normally, the operation speed is moderate and in the MHz range. The application range includes usage as a new kind of memory which can be electrically written and optically read, or usage as a latching switch that only needs to be triggered once and that can keep the state with little or no energy consumption. In addition, they represent a new logical element that complements the toolbox of optical computing.
The optical memristive effect has been discovered only recently [1]. It is of particular interest because of strong electro-optical interaction with distinct transmission states and because of low power consumption and scalability [8]. Such devices rely in part on exploiting the electrical memristive effect to optically probe the material changes. In another aspect, they rely on plasmonics to enhance light-matter interaction and the switching effect.
In electrical resistive switching, a wide range of resistance switching processes are known [8–11]. Although all of them can be induced electrically, switching happens through mechanical, chemical, thermal or other effects or as a combination of them. Only four mechanisms have also been shown to work for optical devices [1, 3–7, 12]. These are the phase transition effect, the valency change effect, the electrochemical metallization and the phase change effect.
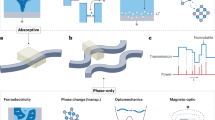
Fig. 1 show a classification overview of optical memristive switches. The phase transition effect is based on Joule heating and thermally induces a transition from insulating to metallic properties. The valency change effect is caused by the motion of oxygen vacancies in transition metal oxides, which causes local changes in the composition of the material. Through biasing, conductive paths are formed and destroyed whose resistance shows the typical memristive behavior. Electrochemical metallization occurs by the motion of metal ions, which forms a conductive path, or filament, that once connecting the electrodes causes a drastic reduction in the resistance. Lastly, the phase change effect switches materials between a crystalline and an amorphous phase by heating pulses just above the crystallization or melting temperature.
Classification of optical memristive switches. They are based on either the phase transition effect, the valency change effect, the electrochemical metallization or the phase change effect. All four effects were shown in electro-optic devices while the phase transition and the phase change effect were also applied in all-optical (O) configuration. Switches based on phase transitions between insulating and metallic states were volatile as the change was induced by Joule heating. The valency change effect and the electrochemical metallization are both based on forming a conductive path. This path is generally stable which classifies these switches for use as nonvolatile optical memory. The phase change effect influences the crystalline structure through short heating pulses. The new structure is kept after the pulse and hence the state is nonvolatile
If the memristive section is in or close to an optical waveguide, then a change in resistance can be detected by an optical signal – which makes the effect an optical memristive effect. Optical transmission measurements showed a clear hysteresis with well distinguishable transmission levels depending on the device’s resistance state [1, 3–7]. All effects were demonstrated in electro-optic configurations and with the exception of the phase change effect also shown to work as optical memristive switches such that both the electrical resistance and the optical transmission switching could be observed in the same device. Still, the inherent connection of the two switching mechanisms in phase change materials is well known [13–15]. Phase transition effect based optical memories are volatile due to the thermal activation that is needed to keep the state [5, 16–19]. Valency change effect or electrochemical metallization based optical memories are generally nonvolatile (or latching) since the conductive path remains open or closed, respectively, even without bias [1, 3, 4]. Likewise, phase change effect based optical memories are nonvolatile also since the disorder in the crystallinity is kept after the heat pulse [13, 20].
Memristive switches at the nanoscale are already widely implemented in electronics [8–10, 21–26] while optical memristive device are only explored now. The reason for this is in fact that memristive effects typically are performed in a few nanometers thin layers with areas below 1 μm2. The memristive effect thus remains mostly unnoticed by an optical signal. While a photonic wave has a rather low power density and is too large to detect a sub-micrometer material change, a plasmonic wave can confine the optical intensity to the active region and therefore is a good fit to detect a memristive material change [27]. And indeed, latest research used strong material changes and plasmonics as means to increase light-matter interaction by orders of magnitude [27, 28]. The ultimate scaling limit was reached in 2015 when an atomic scale plasmonic switch was reported [7]. The next challenge now is to increase the integration density of optical switches. This way, optical circuits can be scaled down from the micro- to the nanoscale. The space requirements of optical devices will be reaching electronic scales ultimately enabling the long awaited co-integration of optics and electronics on the same chip.
This review is organized in three parts. In the first part, the optical and electrical concepts of optical memristive switches are discussed with a focus on plasmonics as a mean to enhance light-matter interaction. The second part shows the latest progress in the field and an example of optical switching for each of the electrically induced resistive switching mechanism presented above. The third part covers the progress from the micro- to the atomic scale and presents the atomic origin of resistance switching by electrochemical metallization and its first implementation as an optical switch.
2 Optical & electrical concepts
The successful implementation of optical memristive switches requires an understanding of the underlying concepts of both the optical and electrical dynamics and their interaction. Therefore, this chapter introduces the concept of plasmonics, which exploits strong light confinement on metal surfaces to enhance light-matter interaction and a brief explanation of resistive switching.
2.1 Plasmonics
Plasmonics describes a field of optics where electromagnetic waves are coupled to electron oscillations within a conductor. In integrated optical circuits, surface plasmon polaritons (SPPs) are used to guide light along a metal surface. The simplest case is an electromagnetic wave on a flat metal-dielectric interface with field components as schematically shown in Fig. 2 [29]. The figure also shows how charge and light are coupled and propagate along the interface. The intensity plot of the perpendicular electric field component describes how the field is strongly confined to the interface and how it exponentially decays with typical penetration depths of a few tens of nanometers.
An SPP propagating along a metal-dielectric interface. (a) Schematic showing the electric (red) and magnetic field (blue) orientations and the interaction of the electromagnetic wave with the charge of the metal. (b) Exponential field decay leading to strong field confinement to the interface. Typical penetration depths are in the order of tens of nanometers
The strong field confinement and the high field intensities on the metal surface make plasmonics particularly suitable for modulators and switches since any light-matter interaction in an active material close to the metal is strongly enhanced [27–29]. For maximum light confinement, also the lateral dimension can be reduced. This is done in plasmonic waveguides by structuring the metal or the dielectric similar to standard photonic waveguides. Since SPPs can only be excited when light has an electric field component perpendicular to the metal surface, different waveguide designs have to be used for the two polarizations of light. Common choices are a hybrid plasmonic waveguide (HPW) for a transverse magnetic (TM) polarization and metal-insulator-metal (MIM) waveguide for a transverse electric (TE) polarization.
The hybrid plasmonic waveguide is composed of a standard photonic waveguide, which is covered by a metal, see Fig. 3(a). For nonlinear applications like switching, an active material is sandwiched in between. The intensity of the electric field is maximum beneath the metal and its polarization must be TM due to the horizontal orientation of the metal-dielectric interface. Fig. 3(b) shows the electric field norm of the fundamental mode in a typical HPW. As desired, the field is strongly confined to the active material to boost light-matter interaction. An advantage of the HPW is the simplicity to couple from and to standard photonics because of its direct implementation on top [30].
(a) 3D structure of a typical HPW consisting of a Si photonic waveguide (dark blue, Si) covered by an active material (purple, A) and a metal (gold, M). (b) Electric field norm (color) of the fundamental TM mode and its transverse orientation (arrows). The field is strongly confined to the active material below the metal to maximize light-matter interaction
A standard plasmonic waveguide for TE polarized light is a MIM waveguide. It consists of two metal patches, which are separated by a small gap (~100 nm) as shown in Fig. 4(a). The gap is often filled with an active material to use the MIM waveguide as a modulator or switch. Light is strongly confined to the slot of the MIM waveguide, which can be seen from the electric field norm depicted in Fig. 4(b). The field is TE polarized because of the vertical orientation of the metal walls. Coupling to a MIM waveguide is more challenging than for the HPW. However, efficient solutions have already been shown by tapering a Si waveguide into an MIM slot [31, 32] or by evanescent coupling from a waveguide beneath [7].
(a) 3D structure of a typical MIM waveguide consisting of a slot between two metal patches (gold, M). An active material (purple, A) can be deposited in the slot for device applications. (b) Electric field norm (color) of the fundamental TE mode and its transverse orientation (arrows). The field is strongly confined within the slot for enhanced light-matter interaction
Plasmonics offers the possibility to convert light into an electromagnetic wave coupled to free charge oscillations on a conducting surface. The plasmonic wave can be confined to nanoscale dimensions and therefore can overcome the diffraction limit of photonics. The strong field enhancement multiplies light-matter interaction at the price of higher propagation losses along the metals. Fortunately, there is a trade-off since the required propagation distances are reduced from mm’s to μm’s. Hence, the total losses remain reasonable. Typical plasmonic devices have an area of about 10 μm2 or below. The compact size has advantages. First, capacitive device limitations are necessarily low and plasmonic devices can thus in principle be fast. Second, the high confinement on such a compact space allows for lowest power operation [27].
Currently more and more plasmonic devices are added to the toolbox of plasmonics. This encompasses devices for light generation, modulation, amplification and detection. While first plasmonic circuit elements are emerging [33], fully conceived all-plasmonic circuits are still to come [34–36].
2.2 Resistive switching
The underlying electrical concept of the optical memristive switches to be presented below is “resistive switching” within a material or a material arrangement. The origin can be manifold but their electrical behavior is of the same kind [8]. Fig. 5(a) and (b) show typical I-V curves for nonvolatile and volatile resistive switching, respectively. If a device is initially in the high resistance (off) state, it stays in the off state until the bias reaches the set voltage. Above the set voltage, a low resistance (on) state is activated which remains even when reducing the bias below the set voltage. Only if a bias below the reset voltage is applied the device switches back to the off state. The main difference between the nonvolatile and volatile memristive switches is the position of the reset voltage with respect to zero bias. Nonvolatile switches remain in the on state in a unbiased configuration while volatile ones have already switched back to the off state. Because of the hysteresis in the I-V curve, such devices are often called memristors [10, 37], i.e., a resistor with memory.
Typical I-V curves of (a) nonvolatile and (b) volatile memristive switches. Initially, the device is in the off state. When it is biased with a voltage above the set voltage, a low resistance state is activated. The device is in the on state, which is maintained even below the set voltage. When the bias is reduced below the reset voltage, the resistance increases and the device switches off again. In nonvolatile resistive switching, the reset voltage is negative and the low resistance state is maintained even without bias. In the volatile case, however, the reset occurs at positives voltages and the switch is always in the off state at zero bias
2.3 Electro-optical interaction
The electro-optical interaction between the light in the waveguide and the electrical resistive switching may rely on different possibilities to interact and the exact mechanisms can be difficult to determine. A first possibility is a refractive index change of the active material by resistive switching which in turn changes the propagation constant of the optical mode. A second possibility is via irregularities or defects in the waveguide caused by the switching operation. They will perturb the optical mode and therefore change the propagation losses. Alternatively, the increased conductivity through switching to the on state could lead to a stronger coupling to charge oscillations of SPPs on the metal walls and influence the plasmonic character of the mode. Lastly, also a resonance effect is probable where the resistive switching alters the resonance condition. These electro-optical interactions are not necessarily independent and combinations are expected to be observed.
3 Optical memristive switches
The investigation of memristors as optical switches evolved only in the last few years. As mentioned in the introduction, four types of memristive effects were shown for electro-optical switching; the phase transition effect, the valency change effect, electrochemical metallization and the phase change effect, c.f. Fig. 1. The phase transition effect changes electrical and optical properties from insulating to metallic through Joule heating. Since the device at room temperature is always in the insulating state, its state is volatile and must be kept actively. Both the valency change effect and the electrochemical metallization are based on building and destroying a conductive path. This path and hence the device state generally endure during ambient conditions which renders the device nonvolatile. Nonvolatility is beneficial since no power is required to keep the current state. This could be especially interesting for optical memory applications. The nonvolatility is also given in devices based on the phase change effect where short heating pulses swap the material phase from crystalline to amorphous and back.
In this chapter, we first introduce the best performing optical memristive device. Then, we show the first three memristive effects on the basis of an exemplary paper each. We omit the phase change effect since its implementation in an optical memristive switch is still ongoing research. Recent work demonstrates electrically controlled displays based on a phase change material [12] and hereby indicates great potential for the application as electro-optical switches. However, they did not show active optical switching.
3.1 State-of-the-art
An optical memristive switch featuring an exemplary performance with respect to extinction ratio and modulation speed is the latching optical switch shown in Fig. 6, adapted from Ref. [4]. The device was 10 μm in length and had an extinction ratio (ER) of 12 dB. The latching optical switch in [4] was based on a hybrid plasmonic waveguide, consisting of silicon photonic waveguide with a plasmonic stack on top, see Fig. 6. The plasmonic stack was made of a transparent ITO electrode covered by an insulating SiO2 layer and a top gold electrode for plasmonic guiding and confinement of the optical field to the active region.
Cross-section of the plasmonic latching switch [4]. The hybrid plasmonic structure confines light to the active area in SiO2 and ITO. A voltage is applied between the ITO and the gold (Au) electrode to form a conductive path
It should be noted, that the same device structure might be used for operation of an ultrafast modulator based on the free carrier dispersion effect in indium-tin-oxide (ITO) [38, 39]. A material study in the visible showed a tunability of the refractive index in the order of unity [40]. Later, a waveguide integrated device showed absorption modulation within a ITO-SiO2-Au stack [30]. However, the origin of the modulation remains uncertain as long as no fast response times are demonstrated.
The switching operation of the device is depicted in Fig. 7. To change the state of transmission, a voltage was applied between the electrodes. This caused the formation or elimination of conductive paths in ITO and the insulating SiO2 layer for positive or negative voltages, respectively. The memristive behavior of this process can be seen from Fig. 7(a) where the voltage is cycled between –3 V and +3 V. The existence of a conductive path perturbs the plasmonic mode, which leads to the absorbing state of the switch while its absence represents the transmitting state. By changing the voltage between ±2 V, an optical ER of 12 dB was found, see Fig. 7(b). The device required an operating power of 200 nW to switch and showed a flat frequency response up to 30 MHz which is claimed to be improvable towards the GHz range by optimizing the device design.
(a) I-V curve of the latching optical switch. The hysteresis proves the memristive origin of the switching. (b) Normalized transmission of a latching switch of 5 μm or 10 μm length. A clear hysteresis and ERs up to 12 dB were achieved. The state of transmission is well preserved when turning the voltage off which enables the possibility for use as a nonvolatile optical memory. Adapted from [4]
The formation of a conductive path was the key to this switch. However, the underlying physics could not be fully resolved. Literature suggests that the switching happens through the formation of either a conductive path of oxygen vacancies [41, 42] or a metal filament [43], c.f. section 3.3 or 3.4, respectively, or even a combination of them.
3.2 Phase transition effect
Optical memristive switches exploiting a reversible phase transition from insulating to metallic phase were reported using vanadium dioxide (VO2) as active material [5, 16–19]. The phase transition can be activated by substrate heating [16], optical absorption [44–47] or electrical currents [5, 48–50]. Here, we present the most recent publication of a VO2 switch where electrically induced Joule heating is exploited to achieve the phase transition [5]. The switch reached an ER of 12 dB on a length of 1 μm and showed operation across at least 100 nm.
The design of the phase transition switch consisted of a Si ridge waveguide, which was covered by VO2. On the sides, the VO2 was contacted by two gold pads to apply a current through VO2, controlling the material phase by Joule heating. Fig. 8 shows the cross-section of the switch and the optical electric field distribution in the insulating off state and the metallic on state. In the off state, the optical mode shows a typical photonic shape. In the on state however, the mode has a plasmonic character similar to a gap plasmon in a MIM waveguide. The plasmonic character and the highly lossy properties of VO2 in its metallic phase lead to strong optical absorption.
Cross-section of the VO2 phase transition switch with insets showing optical mode in the off and on state. The electric field has a photonic mode profile when VO2 is in the insulating off state (n = 2.9 + 0.4i). In the on state, VO2 is in a lossy metallic state (n = 2.0 + 3i) giving the mode a plasmonic shape. Adapted from [5]
To access optical and electrical performance of the phase transition switch, the optical transmission and the current through the device were measured for voltage cycles between 0 V and 8 V and devices of either 5 μm or 10 μm length. The measured data is depicted in Fig. 9(a) and (b) for transmission and current, respectively. The electrical measurement clearly shows the memristive behavior of the phase transition effect. When the bias crosses the set voltage, the resistance of VO2 drops by orders of magnitude and the device is in the on state. Only below a much smaller reset voltage, the VO2 goes back to the insulating state and hence the off state. Optically, the transmission follows the hysteresis of the current. The device is transmitting in the high resistance state and absorbing in the low resistance state leading to a memristive optical switch. ERs of 12 dB for 1 μm long device and of 4 dB for a 0.5 μm long device were measured. These are probably the highest ERs per length ever demonstrated experimentally. Due to the hysteresis in the optical transmission, this phase transition switch could also be used as an optical memory. However, a constant bias above the reset voltage has to applied to maintain the transmission state which limits to the use as volatile memory.
(a) Electrical current measured through the device for voltage cycles from 0 V to 8 V and back and devices of 0.5 μm and 1 μm length. The jumps in the current show the resistance change in VO2 by orders of magnitude when the phase changes. Due to the observed hysteresis, the switch clearly is a memristive device. (b) Optical transmission through the VO2 switch for the same configuration as in (a). An ER of 12 dB or 4 dB was shown for a 1 μm or 0.5 μm long device, respectively. In both cases, a clear hysteresis was observed. Because of the missing hysteresis at 0 V, such a switch would act as volatile memory. Adapted from [5]
The authors investigated the switching dynamics by means of time-resolved transmission measurements [5]. They show in pulsed measurements (period of 1 s) that the transmitting state can be preserved for one or a few microseconds. From the measured phase transition times, sub-GHz switching speeds are estimated but not shown since speed measurements are very challenging due to thermal accumulation. The authors claim that high switching speeds of tens of GHz are potentially possible by activating the phase transition through electron injection, which happens on picosecond timescales. However, this comes most probably at the price of losing the memory effect.
3.3 Valency change effect
Optical switching exploiting an oxygen vacancy filament growth to form a conductive path was recently shown in [3]. They fabricated a grating of aluminum (Al) on top of an 80 nm thick ZnO layer on silicon (Si) and measured the response in reflection at mid-IR frequencies, see Fig. 10.
(a) Device structure consisting of structured Al on 80 nm thick ZnO on highly doped p-Si. A voltage is applied between the Si substrate and the metal pad to control the resistive switching. (b) Reflection versus applied voltage when the grating section of the device is illuminated by light with 8 μm wavelength. A clear hysteresis was observed and the reflection state was preserved at zero bias, which indicates potential use as nonvolatile memory. Adapted from [3]
Two distinct reflection states were observed with a difference of about 5% in reflection corresponding to an ER of about 0.35 dB. The hysteresis in reflection gives an indication of the memristive nature of the switch, which was also shown electrically. Since the reflection states are preserved without bias, such devices allow use as a nonvolatile optical memory.
The filamentary origin of resistance switching was proven by inspecting transmission electron microscope (TEM) images, see Fig. 11(a), where the darker areas in the ZnO layer indicate a filament. To justify the claim that oxygen vacancies are forming the conductive paths, an energy dispersive X-ray spectroscopy (EDX) was carried out along the dashed line drawn in Fig. 11(a) to determine the oxygen concentration. Measurements of the difference between Zn and O concentration gave a value of 5% in the low resistance state and of 1.85% in the high resistance state, respectively. Fig. 11(b) concludes the electronic investigation by schematically showing the resistance switching mechanism through oxygen migration or removal. The low and high resistance states directly correspond to the high and low reflection states in Fig. 10(b), respectively.
(a) TEM image showing oxygen filaments in the ZnO layer. The dashed line indicates the location for EDX measurements to determine the oxygen concentration in the filaments. A difference in concentration between Zn and O of 5% or 1.85% was measured in the low or high resistance state, respectively. (b) Schematic showing the process of oxygen accumulation or depletion to switch between the two resistance states, i.e., the optical reflection states. Adapted from [3]
The growth and rupture of a conductive path of charge vacancies is governed by the motion of oxygen ions under a voltage bias [8, 51]. The carrier dynamics are key to understand the resistive switching mechanism and the interaction with light. Recently developed measurement techniques are capable to separate different current contribution and hence to access material diffusion parameters [51]. This insight paves the way towards more compact switches – potentially even reaching the atomic scale.
3.4 Electrochemical metallization
Optical switching based on the formation of a metal filament was first reported in [1]. The switching works via a controlled diffusion of silver ions in an amorphous silicon (a-Si) layer, which modifies the optical absorption within a hybrid plasmonic waveguide, see Fig. 12(a). Light is strongly confined to the a-Si layer across which a voltage bias is applied to control the silver ion diffusion. Fig. 12(b)/(c) show the on- and off state with respect to the voltage bias of the device. The on state corresponds to the optical absorbing state while the off state is optically transmitting.
(a) Schematic depicting the hybrid plasmonic waveguide structure of the optical memristive switch. A voltage is applied between the silver (Ag) electrode and the Si waveguide to grow or shrink the metal filament in the a-Si layer. (b) Fully evolved metal filament in the electrical on state or optical absorbing state. (c) Annihilated metal filament in the off state, which is optically transmitting. Adapted from [1]
To measure the optical transmission, light at a wavelength of 1.5 μm from a diode laser was sent through the device and measured using a photodetector connected to a digital oscilloscope. By slowly sweeping the voltage between −3 V and + 9 V, a hysteresis in both the electrical and the optical signal was observed, see Fig. 13. The hysteresis in the electrical signal clearly shows the memristive nature of the switching mechanism. The hysteresis in the optical signal has a modulation depth of about 1% and validates the applicability for optical memory. Although a reduced ER and no electrical hysteresis are found at zero bias, the two optical transmission states can still be distinguished which renders the memory nonvolatile.
Current (black) flowing through the a-Si layer and optical signal (green) transmitted through the waveguide for a voltage sweep between −3 V and + 9 V. A clear hysteresis in the optical signal allows use as a nonvolatile optical memory. Adapted from [1]
The full potential of the memristive effect based on metal filament formation could not be exploited in the current device configuration due to limitations from the design. A deeper understanding of carrier dynamics in electrochemical metallization switches, i.e., the metal ion transport and their redox reactions [8, 52], was opening new possibilities. Recently, the atomic origin of resistive switching [53] and quantized conductance levels [54] were demonstrated in electrochemical metallization switches showing that the underlying physics are an atomic process. This fact enabled scaling the device from the micro- down to the nano-scale as shown below.
4 From the micro- to the atomic scale
The need for higher integration density and lower energy consumption drives the development of optical switches to the nanoscale. Electronic components are already at nanoscale dimensions and atomic scale transistors or switches were demonstrated in the last two decades [8, 9, 21, 22, 55–58]. Optically, this is a very new but quickly growing research field. State-of-the-art research in plasmonics is expected to show efficient and highly compact solutions for light generation and detection on-chip in the near future calling for optical modulators and switches on the nanoscale. With the development of atomic scale CMOS processes, the co-integration of electronic and optical devices on a new energy efficient platform will eventually emerge.
Standard optical switches are still based on photonic waveguides of mm lengths whose size reduction is limited by diffraction and rather weak light-matter interaction. In the last years, plasmonics evolved quickly and reported switches, c.f. chapter 3, could reduce the interaction lengths to several μm. Only recently, quantum plasmonic devices [59–64] and the first atomic scale plasmonic switch [7] were reported. The authors showed digital optical switching of 9.2 dB based on electrochemical metallization. The grown filament showed discrete quantum conductance levels proving the atomic scale origin of the switching mechanism.
4.1 Atomic scale resistance switching
The exact process of atomic scale filament formation is difficult to access by experiment. Still, atomic scale resistance switching was already demonstrated [21, 22, 55–57]. Atomistic simulations [53, 65–71] are an accurate and promising tool to describe the exact processes happening during the growth and the destruction of a filament in electrochemical metallization cells. Such a model must incorporate and couple electronic transport, nucleation, electrochemical reactions and the diffusion of ions [72, 73]. In 2015, Onofrio, et al., presented a technique based on reactive molecular dynamics augmented with a charge equilibrium method which was able to describe the full dynamics during electrochemical metallization [53]. They demonstrated the atomic origin of resistance switching at the example of a copper filament growing within amorphous silicon dioxide.
The simulated devices consisted of two copper electrodes with an area 7.4 × 7.4 nm2, which were separated by at least 1 nm. One electrode was either triangular or conical to fix the position of filamentation. Between the electrodes, a-SiO2 was used as dielectric. Altogether, this gave a simulation cell consisting of about 20,000 atoms. The simulations consisted of three phases; a forming phase, a reset phase and a set phase. In the forming phase, a positive voltage of +8 V was applied to initiate the growth of the filament and to reach a stable condition, see Fig. 14. Once a stable condition is reached, the device is in the low resistance on state. In the reset phase, the bias is reversed to –8 V. The filament gets destroyed and after a few nanoseconds a stable high resistance off state is reached. Finally, the bias is set back to +8 V in the set phase which causes an ultrafast switching to a stable on state. In true device operation, the forming phase is only performed once to initialize the cell. Afterwards, the set and reset phases are used to operate the switch.
Atomic configurations during the three phases of an atomistic electrochemical metallization switch. The top graph shows the switching between the high resistance (HR) and the low resistance (LR) state and the instants of time when the four snapshots were taken. Initially, the switch consists of two electrodes – one of them conically formed to a sharp tip – as shown in the 1st snapshot. A positive voltage is applied between the left and the right electrode to initiate the filament growth in the a-SiO2 matrix. Once a stable filament is formed (2nd snapshot), the device is prepared for switching operation. Reversing the bias starts the reset phase, destroys the filament and switches the device off (3rd snapshot). Lastly, a forward bias is applied in the set phase to switch the device back on by forming a new conductive bridge (4th snapshot). In all snapshots, the blue and red color indicate negative and positive charge distributions, respectively. Adapted from [53]
The shape of the filament changes during switching operation, which has an impact on the stability of the conductive bridge. Fig. 15 shows two examples of copper filaments. While the first filament is formed by single atom chain and therefore is only meta-stable, the second has a higher metallic coordination and hence is more stable. By comparing various simulation, the authors find that percolation of clusters and high metallic coordination numbers are required to achieve stable switching.
Two examples for the atomic configuration of the copper filament. In the first case, a meta-stable single atom chain is formed. In the second example, the copper ions are more clustered and a stronger and therefore more stable filament is grown. The blue and red color indicate negative and positive charge distributions, respectively. Adapted from [53]
4.2 Atomic scale plasmonic switching
The atomic scale plasmonic switch presented in [7] explores the ultimate limits of atomic scale resistance switching since the quantum conductance of a single silver filament is used to switch light on or off. A similar resistance switching has also been found in memristive plasmonic antennas where resonances are shifted by single atoms [74–77].
The work in [7] is the first optical switch implementation on a single atom scale. This work actually scaled the active area of optical on-chip devices to sizes never reported before. Furthermore, the device introduced in Ref. [7] had an ER of 12 dB, was operated with MHz speed and consumed as little as 12.5 fJ/bit.
The structure of the atomic scale plasmonic switch is depicted in Fig. 16 together with two zoom-ins illustrating off- and on states of the device. The device was composed of a Si waveguide which is narrowed down to couple light into a plasmonic MIM waveguide which itself is adiabatically tapered to a slot width of 20 nm where the single filament growth will happen. The MIM slot is filled with a-Si as a matrix for filament forming. As shown in the two zoom-ins of Fig. 16, a filament is created at the tip of the silver electrode by diffusion of silver atoms. In the disconnected (resistive) off state, a localized surface plasmon (LSP) is created between the electrodes which reflects the incoming light. The device shows low optical transmission. In the connected (conductive) on state, light can pass the filament and the device is transmitting. This switching behavior is opposite to what was previously reported in a similar structure [1], see section 3.4, which is due to the resonant origin of the atomic scale switching. However, further investigation of electro-optic interactions on quantum scales are still required to fully explain the optical switching mechanism.
3D structure of the atomic scale plasmonic switch. It consists of a Si waveguide to couple light into the plasmonic MIM waveguide on top. One electrode is tapered to a sharp tip to fix the number of filaments to one. The zoom-ins on the right show off and on state of the switch. Light is reflected in the resistive off state while it is transmitted in the conductive on state. Adapted from [7]
The switching performance of the device was characterized by applying a sinusoidal driving voltage signal at 1 kHz. The measured optical output signal showed clear switching between two transmittance states, see Fig. 17. When the electrical signal exceeds a voltage of 1.25 V, the device switches to the on state and transmits light. This state is maintained until the voltage falls below 0.25 V. Then, the device switches off and is in a stable reflecting state. The switching cycle was reproduced repeatedly proving the stability of the switching mechanism.
Digital optical output power measured when applying a sinusoidal electrical signal of 1 kHz. The high and low transmittance state can be assigned to a conductive and resistive filament, respectively, as highlighted by the two insets. Adapted from [7]
To prove the atomic origin of the switching process, the authors derived the conductance levels of the switch by measuring the current while increasing the applied bias voltage. From this measurement, they derived the conductance of the switch as shown in Fig. 18. The conductance shows three distinct levels, which can be associated to three quantum states of the filament connection. Ab initio simulations using a nonequilibrium Green’s function formalism [68, 71] give the same conductance levels as three distinct atomic configurations of the silver filament. Hence, the authors showed a strong indication that optical switching is achieved by only moving one or at most a few atoms in a single filament.
Conductance measurement to confirm the atomic origin of the switching. While the voltage was steadily increased, clear discrete jumps in the conductance were observed. The three quantized conductance levels can be associated to three distinct atomic configurations of the filament giving strong indication for the atomic origin of the switching process. Adapted from [7]
5 Summary
This review presented the research on optical memristive switches. These optical switches are based on the phase transition effect, the valency change effect or the electrochemical metallization. State-of-the-art devices and examples for each effect were presented. Finally, it was shown how the concept of resistive switching can be exploited in an atomic scale plasmonic switch.
Table 1 gives an overview over the optical memristive switches, which were presented in this review. It shows that ERs up to 12 dB were shown on sub-μm2 areas. Switching with a speed of 30 MHz was achieved. By going to atomic scales, very low power consumption of 12.5 nW corresponding to 12.5 fJ/bit were reported.
In the future, it can be expected that the performance of optical memristive switches will be further improved towards higher speed and lower energy consumption. The exploration of other resistive switching mechanisms integrated into optical devices could lead to further improvements. Finally, the use as optical memory might attract more attention on the path towards all-optical computing.
References
A. Emboras, I. Goykhman, B. Desiatov, N. Mazurski, L. Stern, J. Shappir, U. Levy, Nanoscale plasmonic memristor with optical readout functionality. Nano Lett. 13(12), 6151–6155 (2013)
C. Hoessbacher, Y. Fedoryshyn, A. Emboras, D. Hillerkuss, A. Melikyan, M. Kohl, M. Sommer, C. Hafner, and J. Leuthold, Latching Plasmonic Switch with High Extinction Ratio. in CLEO: 2014, (San Jose, California, 2014), p. FTu3K.6
E. Battal, A. Ozcan, A.K. Okyay, Resistive switching-based electro-optical modulation. Adv. Opt. Mater. 2(12), 1149–1154 (2014)
C. Hoessbacher, Y. Fedoryshyn, A. Emboras, A. Melikyan, M. Kohl, D. Hillerkuss, C. Hafner, J. Leuthold, The plasmonic memristor: A latching optical switch. Optica 1(4), 198–202 (2014)
A. Joushaghani, J. Jeong, S. Paradis, D. Alain, J. Stewart Aitchison, J.K.S. Poon, Wavelength-size hybrid Si-VO2 waveguide electroabsorption optical switches and photodetectors. Opt. Express 23(3), 3657–3668 (2015)
C. Ríos, M. Stegmaier, P. Hosseini, D. Wang, T. Scherer, C.D. Wright, H. Bhaskaran, W.H.P. Pernice, Integrated all-photonic non-volatile multi-level memory. Nat. Photonics 9(11), 725–732 (2015)
A. Emboras, J. Niegemann, P. Ma, C. Haffner, A. Pedersen, M. Luisier, C. Hafner, T. Schimmel, J. Leuthold, Atomic Scale Plasmonic Switch. Nano Lett. 16(1), 709–714 (2016)
R. Waser, R. Dittmann, G. Staikov, K. Szot, Redox-based resistive switching memories – Nanoionic mechanisms, prospects, and challenges. Adv. Mater. 21(25–26), 2632–2663 (2009)
R. Waser, M. Aono, Nanoionics-based resistive switching memories. Nat. Mater. 6(11), 833–840 (2007)
D.B. Strukov, G.S. Snider, D.R. Stewart, R.S. Williams, The missing memristor found. Nature 453(7191), 80–83 (2008)
J. Doo Seok, T. Reji, R.S. Katiyar, J.F. Scott, H. Kohlstedt, A. Petraru, H. Cheol Seong, Emerging memories: Resistive switching mechanisms and current status. Rep. Prog. Phys. 75(7), 076502 (2012)
P. Hosseini, C.D. Wright, H. Bhaskaran, An optoelectronic framework enabled by low-dimensional phase-change films. Nature 511(7508), 206–211 (2014)
S.R. Ovshinsky, Reversible electrical switching phenomena in disordered structures. Phys. Rev. Lett. 21(20), 1450–1453 (1968)
J. Feinleib, J. deNeufville, S.C. Moss, S.R. Ovshinsky, Rapid Reversible Light-Induced Crystallization of Amorphous Semiconductors. Appl. Phys. Lett. 18(6), 254–257 (1971)
M. Wuttig, N. Yamada, Phase-change materials for rewriteable data storage. Nat. Mater. 6(11), 824–832 (2007)
R.M. Briggs, I.M. Pryce, H.A. Atwater, Compact silicon photonic waveguide modulator based on the vanadium dioxide metal-insulator phase transition. Opt. Express 18(11), 11192–11201 (2010)
A. Joushaghani, B.A. Kruger, S. Paradis, D. Alain, J. Stewart Aitchison, J.K.S. Poon, Sub-volt broadband hybrid plasmonic-vanadium dioxide switches. Appl. Phys. Lett. 102(6), 061101 (2013)
A. Joushaghani, J. Jeong, S. Paradis, D. Alain, J. Stewart Aitchison, J.K.S. Poon, Voltage-controlled switching and thermal effects in VO2 nano-gap junctions. Appl. Phys. Lett. 104(22), 221904 (2014)
A. Joushaghani, J. Jeong, S. Paradis, D. Alain, J. Aitchison, J. Poon, Characteristics of the Current-Controlled Phase Transition of VO2 Microwires for Hybrid Optoelectronic Devices. Photonics 2(3), 916 (2015)
A.V. Kolobov, P. Fons, A.I. Frenkel, A.L. Ankudinov, J. Tominaga, T. Uruga, Understanding the phase-change mechanism of rewritable optical media. Nat. Mater. 3(10), 703–708 (2004)
K. Terabe, T. Hasegawa, T. Nakayama, M. Aono, Quantized conductance atomic switch. Nature 433(7021), 47–50 (2005)
T. Hasegawa, K. Terabe, T. Sakamoto, M. Aono, Nanoionics switching devices: “Atomic switches”. MRS Bull. 34(12), 929–934 (2009)
J. Borghetti, G.S. Snider, P.J. Kuekes, J.J. Yang, D.R. Stewart, R.S. Williams, 'Memristive' switches enable 'stateful' logic operations via material implication. Nature 464(7290), 873–876 (2010)
W. Lu, D.S. Jeong, M. Kozicki, R. Waser, Electrochemical metallization cells—Blending nanoionics into nanoelectronics? MRS Bull. 37(2), 124–130 (2012)
J.J. Yang, D.B. Strukov, D.R. Stewart, Memristive devices for computing. Nat. Nanotechnol. 8(1), 13–24 (2013)
W. Lu, Memristors: Going active. Nat. Mater. 12(2), 93–94 (2013)
A. Emboras, C. Hoessbacher, C. Haffner, W. Heni, U. Koch, P. Ma, Y. Fedoryshyn, J. Niegemann, C. Hafner, J. Leuthold, Electrically controlled plasmonic switches and modulators. IEEE J. Sel. Top. Quantum Electron. 21(4), 276–283 (2015)
M. Kauranen, A.V. Zayats, Nonlinear plasmonics. Nat. Photonics 6(11), 737–748 (2012)
O. Benson, Assembly of hybrid photonic architectures from nanophotonic constituents. Nature 480(7376), 193–199 (2011)
V.J. Sorger, N.D. Lanzillotti-Kimura, R.-M. Ma, X. Zhang, Ultra-compact silicon nanophotonic modulator with broadband response. Nanophotonics 1(1), 17 (2012)
D.F.P. Pile, D.K. Gramotnev, Adiabatic and nonadiabatic nanofocusing of plasmons by tapered gap plasmon waveguides. Appl. Phys. Lett. 89(4), 041111 (2006)
A. Melikyan, L. Alloatti, A. Muslija, D. Hillerkuss, P.C. Schindler, J. Li, R. Palmer, D. Korn, S. Muehlbrandt, D. Van Thourhout, B. Chen, R. Dinu, M. Sommer, C. Koos, M. Kohl, W. Freude, J. Leuthold, High-speed plasmonic phase modulators. Nat. Photonics 8(3), 229–233 (2014)
C. Haffner, W. Heni, Y. Fedoryshyn, J. Niegemann, A. Melikyan, D.L. Elder, B. Baeuerle, Y. Salamin, A. Josten, U. Koch, C. Hoessbacher, F. Ducry, L. Juchli, A. Emboras, D. Hillerkuss, M. Kohl, L.R. Dalton, C. Hafner, J. Leuthold, All-plasmonic Mach–Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 9(8), 525–528 (2015)
T.W. Ebbesen, C. Genet, S.I. Bozhevolnyi, Surface-plasmon circuitry. Phys. Today 61(5), 44–50 (2008)
V.J. Sorger, R.F. Oulton, R.-M. Ma, X. Zhang, Toward integrated plasmonic circuits. MRS Bull. 37(8), 728–738 (2012)
Y. Fang, M. Sun, Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 4, e294 (2015)
L. Chua, Memristor-the missing circuit element. IEEE Trans. Circuit Theory 18(5), 507–519 (1971)
A. Melikyan, T. Vallaitis, N. Lindenmann, T. Schimmel, W. Freude, and J. Leuthold, A Surface Plasmon Polariton Absorption Modulator. in Conference on Lasers and Electro-Optics 2010, (San Jose, California, 2010), p. JThE77
A. Melikyan, N. Lindenmann, S. Walheim, P.M. Leufke, S. Ulrich, J. Ye, P. Vincze, H. Hahn, T. Schimmel, C. Koos, W. Freude, J. Leuthold, Surface plasmon polariton absorption modulator. Opt. Express 19(9), 8855–8869 (2011)
E. Feigenbaum, K. Diest, H.A. Atwater, Unity-order index change in transparent conducting oxides at visible frequencies. Nano Lett. 10(6), 2111–2116 (2010)
A. Mehonic, S. Cueff, M. Wojdak, S. Hudziak, C. Labbé, R. Rizk, A.J. Kenyon, Electrically tailored resistance switching in silicon oxide. Nanotechnology 23(45), 455201 (2012)
A. Mehonic, A. Vrajitoarea, S. Cueff, S. Hudziak, H. Howe, C. Labbé, R. Rizk, M. Pepper, A.J. Kenyon, Quantum conductance in silicon oxide resistive memory devices. Sci. Rep. 3, 2708 (2013)
Y. Yang, P. Gao, S. Gaba, T. Chang, X. Pan, W. Lu, Observation of conducting filament growth in nanoscale resistive memories. Nat. Commun. 3, 732 (2012)
A. Cavalleri, C. Tóth, C.W. Siders, J.A. Squier, F. Ráksi, P. Forget, J.C. Kieffer, Femtosecond Structural Dynamics in VO2 during an Ultrafast Solid-Solid Phase Transition. Phys. Rev. Lett. 87(23), 237401 (2001)
S. Lysenko, V. Vikhnin, A. Rúa, F. Fernández, H. Liu, Critical behavior and size effects in light-induced transition of nanostructured VO2 films. Phys. Rev. B 82(20), 205425 (2010)
J.D. Ryckman, V. Diez-Blanco, J. Nag, R.E. Marvel, B.K. Choi, R.F. Haglund, S.M. Weiss, Photothermal optical modulation of ultra-compact hybrid Si-VO2 ring resonators. Opt. Express 20(12), 13215–13225 (2012)
J.D. Ryckman, K.A. Hallman, R.E. Marvel, R.F. Haglund, S.M. Weiss, Ultra-compact silicon photonic devices reconfigured by an optically induced semiconductor-to-metal transition. Opt. Express 21(9), 10753–10763 (2013)
G. Stefanovich, A. Pergament, D. Stefanovich, Electrical switching and Mott transition in VO2. J. Phys. Condens. Matter 12(41), 8837 (2000)
J. Jeong, N. Aetukuri, T. Graf, T.D. Schladt, M.G. Samant, S.S.P. Parkin, Suppression of metal-insulator transition in VO2 by electric field–induced oxygen vacancy formation. Science 339(6126), 1402–1405 (2013)
P. Markov, J. D. Ryckman, R. E. Marvel, K. A. Hallman, R. F. Haglund, and S. M. Weiss, Silicon-VO2 Hybrid Electro-optic Modulator. in CLEO: 2013, (San Jose, California, 2013), p. CTu2F.7
F. Messerschmitt, M. Kubicek, S. Schweiger, J.L.M. Rupp, Memristor kinetics and diffusion characteristics for mixed anionic-electronic SrTiO3-δ bits: The memristor-based Cottrell analysis connecting material to device performance. Adv. Funct. Mater. 24(47), 7448–7460 (2014)
S. Tappertzhofen, H. Mundelein, I. Valov, R. Waser, Nanoionic transport and electrochemical reactions in resistively switching silicon dioxide. Nanoscale 4(10), 3040–3043 (2012)
N. Onofrio, D. Guzman, A. Strachan, Atomic origin of ultrafast resistance switching in nanoscale electrometallization cells. Nat. Mater. 14(4), 440–446 (2015)
S. Tappertzhofen, E. Linn, S. Menzel, A.J. Kenyon, R. Waser, I. Valov, Modeling of quantized conductance effects in electrochemical metallization cells. IEEE Trans. Nanotechnol. 14(3), 505–512 (2015)
N. Agraїt, A.L. Yeyati, J.M. van Ruitenbeek, Quantum properties of atomic-sized conductors. Phys. Rep. 377(2–3), 81–279 (2003)
F.Q. Xie, L. Nittler, C. Obermair, T. Schimmel, Gate-Controlled Atomic Quantum Switch. Phys. Rev. Lett. 93(12), 128303 (2004)
C. Obermair, F.-Q. Xie, T. Schimmel, The single-atom transistor: Perspectives for quantum electronics on the atomic-scale. Europhys. News 41(4), 25–28 (2010)
M. Fuechsle, J.A. Miwa, S. Mahapatra, H. Ryu, S. Lee, O. Warschkow, L.C.L. Hollenberg, G. Klimeck, M.Y. Simmons, A single-atom transistor. Nat. Nanotechnol. 7(4), 242–246 (2012)
J. Zuloaga, E. Prodan, P. Nordlander, Quantum description of the Plasmon resonances of a nanoparticle dimer. Nano Lett. 9(2), 887–891 (2009)
O. Pérez-González, N. Zabala, A.G. Borisov, N.J. Halas, P. Nordlander, J. Aizpurua, Optical spectroscopy of conductive junctions in plasmonic cavities. Nano Lett. 10(8), 3090–3095 (2010)
K.J. Savage, M.M. Hawkeye, R. Esteban, A.G. Borisov, J. Aizpurua, J.J. Baumberg, Revealing the quantum regime in tunnelling plasmonics. Nature 491(7425), 574–577 (2012)
F. Benz, C. Tserkezis, L.O. Herrmann, B. de Nijs, A. Sanders, D.O. Sigle, L. Pukenas, S.D. Evans, J. Aizpurua, J.J. Baumberg, Nanooptics of molecular-shunted plasmonic Nanojunctions. Nano Lett. 15(1), 669–674 (2015)
M. Barbry, P. Koval, F. Marchesin, R. Esteban, A.G. Borisov, J. Aizpurua, D. Sánchez-Portal, Atomistic near-field Nanoplasmonics: Reaching atomic-scale resolution in Nanooptics. Nano Lett. 15(5), 3410–3419 (2015)
T. Wang, C.A. Nijhuis, Molecular electronic plasmonics. Appl. Mater. Today 3, 73–86 (2016)
J. Aichelin, “quantum” molecular dynamics—A dynamical microscopic n-body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys. Rep. 202(5), 233–360 (1991)
J. Zhang, H. Zeng, Theory and application of quantum molecular dynamics (World Scientific, Singapore, 1999)
S. Datta, Nanoscale device modeling: The Green’s function method. Superlattice. Microst. 28(4), 253–278 (2000)
M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor, K. Stokbro, Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65(16), 165401 (2002)
M. Ben-Nun, T.J. Martínez, in Advances in Chemical Physics, ed. Ab Initio Quantum Molecular Dynamics (John Wiley & Sons, Inc., New York, 2002), pp. 439–512
S. Datta, Electronic transport in mesoscopic systems, (sixth printing) ed (Cambridge University Press, Cambridge, 2005)
M. Luisier, Atomistic simulation of transport phenomena in nanoelectronic devices. Chem. Soc. Rev. 43(13), 4357–4367 (2014)
Y.C. Yang, F. Pan, Q. Liu, M. Liu, F. Zeng, Fully room-temperature-fabricated nonvolatile resistive memory for ultrafast and high-density memory application. Nano Lett. 9(4), 1636–1643 (2009)
V.V. Zhirnov, R. Meade, R.K. Cavin, G. Sandhu, Scaling limits of resistive memories. Nanotechnology 22(25), 254027 (2011)
T.P. Rossi, A. Zugarramurdi, M.J. Puska, R.M. Nieminen, Quantized Evolution of the Plasmonic Response in a Stretched Nanorod. Phys. Rev. Lett. 115(23), 236804 (2015)
R. Chikkaraddy, B. de Nijs, F. Benz, S.J. Barrow, O.A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess, J.J. Baumberg, Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 535(7610), 127–130 (2016)
S. Dong, K. Zhang, Z. Yu, J.A. Fan, Electrochemically programmable plasmonic antennas. ACS Nano. 10(7), 6716–6724 (2016)
D.T. Schoen, A.L. Holsteen, M.L. Brongersma, Probing the electrical switching of a memristive optical antenna by STEM EELS. Nat. Commun. 7, 12162 (2016)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Koch, U., Hoessbacher, C., Emboras, A. et al. Optical memristive switches. J Electroceram 39, 239–250 (2017). https://doi.org/10.1007/s10832-017-0072-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10832-017-0072-3