Functional identification of biological neural networks using reservoir adaptation for point processes

Abstract

The complexity of biological neural networks does not allow to directly relate their biophysical properties to the dynamics of their electrical activity. We present a reservoir computing approach for functionally identifying a biological neural network, i.e. for building an artificial system that is functionally equivalent to the reference biological network. Employing feed-forward and recurrent networks with fading memory, i.e. reservoirs, we propose a point process based learning algorithm to train the internal parameters of the reservoir and the connectivity between the reservoir and the memoryless readout neurons. Specifically, the model is an Echo State Network (ESN) with leaky integrator neurons, whose individual leakage time constants are also adapted. The proposed ESN algorithm learns a predictive model of stimulus-response relations in in vitro and simulated networks, i.e. it models their response dynamics. Receiver Operating Characteristic (ROC) curve analysis indicates that these ESNs can imitate the response signal of a reference biological network. Reservoir adaptation improved the performance of an ESN over readout-only training methods in many cases. This also held for adaptive feed-forward reservoirs, which had no recurrent dynamics. We demonstrate the predictive power of these ESNs on various tasks with cultured and simulated biological neural networks.

1 Introduction

One central goal in neuroscience is to understand how the brain represents, processes, and conveys information. Starting from Hebb’s cell assemblies (Brown and Milner 2003; Hebb 1949), many neurobiologically founded theories and hypotheses have been developed towards this goal. It stands clear now that spikes are the elemental quanta of information processing in the mammalian cortex (Hodgkin and Huxley 1952; Kandel et al. 2000). As a result of extensive experiments of cortical recordings, it has been widely postulated and accepted that function and information of the cortex are encoded in the spatio-temporal network dynamics (Abeles et al. 1993; Lindsey et al. 1997; Mainen and Sejnowski 1995; Prut et al. 1998; Riehle et al. 1997; Villa et al. 1999). The right level of describing the dynamics, however, is a matter of intensive discussions (Prut et al. 1998; Rieke et al. 1999). Are spike rates or spike timings more relevant? What is the right temporal precision if the latter proves significant? What should be the spatial resolution of this description? How far can the population activity of neurons be related to function or behavior? Does the correlated activity of multiple neurons indicate a functionally relevant state?

Depending on the answers to the above questions one would preferably apply different models to relate the network activity to function. Another approach is to employ a generic network model, which can be assumed to be universal for problems of neural encoding. The parameters of the model would be learned by adaptive algorithms. Obviously, such a model should be able to deal with single spikes with high temporal precision as well as population rates. It should also be able to catch, with the appropriate parameters, network synchrony and polychrony (Izhikevich 2006).

1.1 Reservoir computing

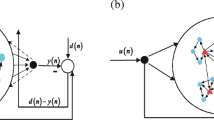
Liquid State Machines (LSM) and Echo State Networks (ESN) have been introduced as efficiently learning recurrent neural networks (Jaeger 2001; Maass et al. 2002). The common key contribution of these approaches is the proposal of a recurrent neural network with a fixed connectivity, i.e. a reservoir, which does not have stable states and has a fading memory of the previous inputs and network states. In response to an input stream, the reservoir generates a higher-dimensional spatio-temporal dynamics reflecting the structure in the input stream. The higher dimensional reservoir state can be mapped to a target output stream online, with a second module, namely a readout. LSMs are networks of spiking integrate-and-fire (IAF) neurons whereas ESNs use continuous valued sigmoid neurons and a single layer of readout neurons (see Section 2).

With the appropriate parameters, reservoir dynamics can be sensitive to different features of the input such as correlations, polychronous and synchronous spikes, different frequency bands or even temporally precise single spikes. For instance, LSMs can approximate any time invariant filter with fading memory if their traces of internal states differ at least for one time point in response to any two different input streams (Separation Property, SP) and if the readout modules can approximate any continuous function from ℝ^m → ℝ, where m ∈ ℕ (Approximation Property, AP) (Maass et al. 2002). Satisfying the separation property depends on whether the reservoir is composed of sufficient basis filters. A random reservoir needs to have a rich repertoire of basis filters in order to approximate the target time-invariant filter. This could be achieved for several tasks with sufficiently large random reservoirs (Maass et al. 2002). Furthermore, reservoirs have been shown to simulate a large class of higher order differential equations with appropriate feedback and readout functions (Maass et al. 2007). These findings suggest that reservoir computing can be used as a generic tool for the problems of neural encoding.

Biological neural networks, in vivo, process a continuous stream of inputs in real time. Moreover, they prove successful to react and compute fast, independent of their instantaneous state and ongoing activity, when prompted by sudden changes in stimuli. In other words, they perform any time computing. Reservoir computing has also been suggested as a model of cortical information processing for their capability of online and anytime computing, for their fading memory and for their separation properties. It has been argued that specific cortical circuitry is possible to build into generic LSM framework (Maass et al. 2004). Bringing reservoir computing into the problem will not only deliver expressive models that can distinguish a rich set of input patterns, but also may provide more biological relevance to the theoretical tool.

1.2 Neuronal cell cultures as biological neural networks

While brain tissue has highly specialized architecture and developmental history, generic biological networks can be created as cell cultures of mammalian cortical neurons that have been dissociated and regrown outside an organism. They are closed system in vitro living networks, which are frequently used to study physiological properties of neural systems (Marom and Shahaf 2002). Although the anatomical structure of the brain is not preserved in cultures, their inherent properties as networks of real neurons, their accessibility and small size make them very attractive for investigating information processing in biological networks. Using cultured networks also eliminates the problem of interference with ongoing activity from different parts of the brain. Compared to in vitro brain slices, cultured networks are more accessible in terms of ratio of the recorded neurons to the whole network. In other words, they pose a less serious under-sampling problem. Studying such networks can provide insight into the generic properties biological neural networks, independent of a specific anatomy (Marom and Shahaf 2002). Another motivation to study cultures is understanding and employing them as biological computers. For instance, neuronal cell cultures have been shown to be able to learn. Shahaf and Marom (2001) demonstrated how the response of the network to a stimulus can be ‘improved’ by systematically training the culture. Jimbo et al. (1999) showed how neuronal cultures can increase or decrease their overall response to pulse inputs stimulus by tetanic stimuli training.

Micro-Electrode Arrays (MEA) have commonly been employed to both stimulate and record from neuronal cultures and slices (Egert et al. 2002; Marom and Shahaf 2002) (Fig. 1). Standard MEAs allow for simultaneous recordings and stimulations from up to 60 electrodes from a surface area of around 2 mm$^\text{2}$. Each electrode picks up the extracellular electrical field of one or several (1 to 3) neurons. Neurons transmit information by action potentials, or spikes, which can be extracted by adaptive high-pass filtering of the extracellular signals (Egert et al. 2002; Wagenaar et al. 2005).

Fig. 1

A photo image of a neuronal culture with MEA electrodes. We aim at generating an equivalent network in terms of input–output relations. Photo was taken by Steffen Kandler from BCCN Freiburg

The activity in neuronal cultures is composed of irregular network-wide bursts of spikes, even in absence of an external stimulation (Marom and Shahaf 2002). These networks display little or no spiking activity most of the time (that is, between bursts) and very high spiking activity during the bursts (Fig. 2). Although the inter-burst intervals are not necessarily regular, there seem to be spatio-temporal patterns that occur within bursts (Feber le et al. 2007; Rolston et al. 2007). For example, a burst might always start with the activity of the same channel and continue with the activity of another particular channel.

Fig. 2

Spike activity in neuronal cultures. Burst activity (left). Zoom into a burst. Each dot shows a spike detected on the corresponding electrode at the corresponding time (right)

1.3 Problem statement

Although we cannot relate the activity dynamics to a physiological function in random in vitro BNNs, by studying their activity dynamics, we gain experience and information about generic network properties forming the basis of in vivo networks. Moreover, one can assign pseudo-functions to random BNNs by artificially mapping network states to a predefined set of actions (Chao et al. 2008). One can also regard the response spike train of a BNN to a stream of various stimuli as a very detailed characterization of its pseudo-function and aim at modeling stimulus-response relations. In the present work, we take this approach. We record the output responses of simulated and cultured BNNs to random multivariate streams of stimuli. We tackle the question whether it is possible to train an artificial neural network that predicts the response of a reference biological neural network under the applied stimulus range. In other words, we aim at generating an equivalent network of a BNN in terms of stimulus-response relations. Given the same stimulus, the equivalent network should predict the output of the biological neural network.

A model or a predictor for biological neural networks can be useful for relating the physiological and physical determinants of its activity and thereby, can be a tool for analyzing information coding in these networks. It can also be helpful for interacting with BNNs by means of electrical stimulation. Here, we employ Echo State Networks (ESN) as a reservoir computing tool and propose an algorithm to find appropriate models for the relations between continuous input streams and multi-unit recordings in biological neural networks. The algorithm uses point process log-likelihood as an optimization criterion and adapts the readout and reservoir parameters of ESNs accordingly. Moreover, we investigate the performance of our approach on different feed-forward and recurrent reservoir structures and demonstrate its applicability to stimulus-response modeling problem in BNNs.

We shortly review ESNs in Section 2 and point process modeling of spike data in Section 3. An elaboration of ESN adaptation for point processes is presented in Section 4. In Section 5 we present our evaluation methods. A detailed experimental section and their implications can be found in Sections 6 and 7, respectively.

2 Echo State Networks

Echo State Networks (ESN) (Jaeger 2001) consist of a recurrent neural network (RNN) reservoir and a readout module (Fig. 3). Recurrent neural networks (RNN) are in general difficult to train with gradient descent methods (Bengio et al. 1994). The echo state approach to RNNs is motivated by the observation that a fixed (untrained) RNN can be very useful for discriminating multivariate time series if the RNN is gradually forgetting internal states and thereby also the inputs at previous time steps. This property is described as generating the echo states of the input. Existence of echo states is independent of the specific structure of the reservoir, but strongly determined by the extension of the eigenvalues of its connectivity matrix. The input stream is used to stimulate a higher dimensional dynamical system, which can be mapped to a target output stream by adaptive linear or sigmoidal readout units. Even with random fixed reservoirs, ESNs make up a successful reservoir computing framework with applications in several engineering and nonlinear modeling tasks (Jaeger 2003; Jaeger and Eck 2006; Jaeger and Haas 2004).

Fig. 3

Architecture of Echo State Networks

2.1 Dynamics

The ESN dynamics is described as

$$ x^{n+1} = f\left(W^{in}\,u^{n+1} + W\,x^{n}\right) $$

$$ y^{n} = f^{out}\left(W^{out}\,\left[u^{n};x^{n}\right]\right), $$

where,

W:

N × N internal reservoir weight matrix,

Wⁱⁿ:

N × K input weight matrix,

W^out:

L × (N + K) output weight matrix,

xⁿ:

N × 1 state vector for time step n,

uⁿ:

K × 1 input vector for time step n,

yⁿ:

L × 1 output vector for time step n,

’;’:

vertical vector concatenation.

Note that ESNs can have feedback projections from the readout module to the reservoir (Jaeger 2001). Throughout this note, however, we employ ESN architectures without such feedback projections. We choose $f(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}$, which allows for existence of echo states.

2.2 ESN with leaky integrators

Fading memory in the reservoir is due to recurrent connectivity if the individual neurons are memoryless. Using leaky integrator neurons results in a reservoir made from a network of low pass filters, which can be referred to as Leaky Integrator Echo State Networks (LI-ESN). LI-ESNs have been shown to work well on noisy systems with slowly changing dynamics (Jaeger et al. 2007). The leakage time constant is another aspect of fading memory. For instance, even a purely feed-forward reservoir will have a fading memory due the memory of the individual neurons. We describe the LI-ESN dynamics with

$$ x^{n+1} = \left(1 - \frac{1}{\tau}\right) \, x^{n} + \frac{1}{\tau} \, f\left(W^{in}\,u^{n+1} + W\,x^{n}\right), \ \ \tau \ge 1. $$

$$ y^{n} = f^{out}\left(W^{out} \, \left[u^{n};x^{n}\right]\right), $$

where τ is a global parameter for all reservoir neurons.

2.3 Feed-Forward Echo State Networks

Acyclic random neural networks with leaky integrator neurons can be used as reservoirs, as they also have fading memory. We refer an ESN with such a reservoir as a Feed-Forward Echo State Network (FF-ESN). Naturally, it can be asked whether FF-ESNs can have the same expressive power as the recurrent ESNs. Intuitively, it can be expected that a recurrent ESN with the same number of neurons discriminates between more input patterns than a FF-ESN, i.e. the recurrent ESN has a much more powerful separation property. In case of adaptive reservoirs, however, it is worthwhile to test whether the reservoir adaptation algorithm works especially better on feed-forward reservoirs than on recurrent ones. Here, we also propose the use of FF-ESNs for functional identification of biological neural networks. A recurrent reservoir can easily be made acyclic by inverting the connections that cause recurrence (Fig. 4).

Fig. 4

A recurrent sparse random reservoir (left) and a feed-forward sparse random reservoir (right). Numbers denote the neuron indices. A reservoir is guaranteed to be acyclic if connections are allowed only from neurons with lower indices to neurons with higher indices. A recurrent reservoir (left) can be converted into a feed-forward one by inverting the connections that are from higher indexed neurons to lower indexed ones (dashed lines, right)

2.4 ESN learning

Learning in Echo State Networks will typically include learning readout parameters by linear regression, e.g. using the pseudo inverse matrix

$$ \tilde{W}^{out} = Y \, [X;U]^+, $$

where L × T matrix Y is the collection of target vectors y for T time steps, X , U are the same collection for reservoir states and input vectors. ⁺ is pseudo inverse operation. Much more efficient is the use of the Wiener-Hopf equation for ESN readout learning (Jaeger 2001). Steil (2004) proposed the backpropagation- decorrelation algorithm, which seeks a trade-off between error minimization and decorrelation of the reservoir activity.

Although ESN learning is restricted to readout learning in many cases, there have recently been several approaches to adapt reservoirs, among which a significant improvement over untrained reservoirs was reported by Steil (2007). Adopting the intrinsic plasticity rule from real biological systems improved the performance of the backpropagation-decorrelation algorithm.

In the current approach, we adapt the reservoir connectivity and individual neuronal time constants with a one-step propagation of the log-likelihood into the reservoir. This is basically a gradient descent approach, where the log-likelihood of a point process is used as an optimization criterion. We elaborate our approach in Section 4.

3 Point process modeling of spike data

Signals that are comprised of point-like events in time, e.g. trains of action potentials generated by neurons, can be characterized in terms of stochastic point processes (Brown et al. 2001; Chornoboy et al. 1988; Okatan et al. 2005; Rajaram et al. 2005). A spiking process, modeled as a point process, is in turn fully characterized by its conditional intensity function (Cox and Isham 1980; Daley and Vere-Jones 2003).

The instantaneous firing rate is defined as a conditional intensity function

$$ \lambda_i(t|I_t,H_t) = \lim\limits_{\Delta \rightarrow 0}\frac{P\big( N_i(t+\Delta) - N_i(t) = 1 |I_t,H_t \big)}{\Delta} , $$

where N _i(t) is the cumulative spike count of unit i. λ_i(t|I _t,H _t) represents the conditional probability density that a spiking event occurs at unit i. I _t and H _t stand for input history and spike history, respectively. For small Δ, the probability of a spike can be computed by Bernoulli approximation to the point process (Daley and Vere-Jones 2003; Brown et al. 2003)

$$ P\big(\delta_{N_i(t)} = 1 | I_t, H_t \big) \approx \lambda_i\big(t|I_t,H_t\big) \, \Delta, $$

where $\delta_{N_i(t)} = N_i(t+\Delta) - N_i(t)$. If λ is a function of I _t, H _t and parameter set θ, the log-likelihood $\mathcal{L}$ of a sample count path for a node (electrode) i is expressed as in Chornoboy et al. (1988):

$$ \begin{array}{rcl} \mathcal{L}_i (\theta|N_i) &=& \log p(N_i|\theta)\\[3pt] &=& \int_0^T \log\lambda_i\left(t|I_t,H_t,\theta\right) \: dN_i(t)\\[3pt] &&- \int_0^T \lambda_i(t|I_t,H_t,\theta) \: dt , \end{array} $$

where p(N _i|θ) is the conditional probability density for the count path. The instantaneous log-likelihood (Brown et al. 2001) of a point process trajectory (spike train) is defined as

$$ \ell_i(t,\theta) = \log\lambda_i(t|I_t,H_t,\theta) \,\frac{dN_i(t)}{dt} - \lambda_i(t|I_t,H_t,\theta) $$

(1)

Note that

$$ \mathcal{L}_i (\theta|N_i) = \int_0^T \ell_i(t,\theta) \: dt . $$

With a conversion to discrete time, i.e. t → n, Δ → 1, instantaneous log-likelihood becomes,

$$ \ell_i^n = \log\lambda_i^n \: \delta_{N_i}^n - \lambda_i^n, $$

(2)

where n is the discrete time step index. Any parameter θ _j of the model is then learned then by the standard gradient descent learning.

$$ \theta^{n+1}_j \leftarrow \theta^n_j + \eta \, \left. \frac{\partial{\ell^n_i}}{\partial{\theta_j } } \right |_{\theta_j = \theta^n_j }, $$

where η is the learning rate. For the sake of readability, we will leave the calculation points of partial derivatives out and simply use the notation $\theta^{n+1}_j \leftarrow \theta^n_j + \eta \, \frac{\partial{\ell^n_i}}{\partial{\theta_j}}$.

The quality of point process modeling strongly depends on the expressive power of function λ(t|I _t,H _t,θ). Linear or log-linear models might be preferable for successful adaptation by gradient descent, whereas nonlinear functions allow for more expressive models. In the current work, we model this function by an Echo State Network, which inherently incorporates input and network history into the instantaneous network states.

4 Point process modeling with ESN and log likelihood propagation

We relate input and reservoir state to the conditional intensity function in discrete time as

$$ \lambda(t|I_t,H_t,\theta) \approx \lambda^n = f^{out}\left(W^{out} \, \left[u^n;x^n\right]\right), $$

(3)

where λⁿ is an L-dimensional vector of conditional intensity estimations for time step n. We use an exponential f ^out

$$ f^{out}(\xi) = \exp(A \: \xi), $$

(4)

where 0 ≤ A ≤ 1 is a constant. Exponential functions were already applied in point process modeling and shown to have desirable properties such as avoiding local minima in Generalized Linear Models (GLM) (Paninski 2004).

ESN readout learning can be trivially adapted to point process data, where the output of the ESN estimates the conditional intensity function in batch mode

$$ {W}_{ij}^{out} \leftarrow {W}_{ij}^{out} + \eta \, \frac{\partial{\mathcal{L}_i}}{\partial{{W}_{ij}^{out}}}, $$

(5)

and also in online mode

$$ {W}_{ij}^{out} \leftarrow {W}_{ij}^{out} + \eta_{out} \, \frac{\partial{\ell_i^n}}{\partial{{W}_{ij}^{out}}}. $$

(6)

We are going to provide the expansion of the above learning rule and its extension to reservoir adaptation assuming an online mode. Combining Eqs. (2), (3), and (4) yields

$$ \begin{array}{lll} \frac{\partial{\ell^n_i}}{\partial{{W}_{ij}^{out}}} &=& A\; x_j^n\;\delta_{N_i^n} - A\;x^n_j\;f^{out}\left(\xi^n\right)\nonumber\\ &=& A\; x_j^n\;\delta_{N_i^n} - A\;x_j^n\;\lambda_i^n, \end{array} $$

(7)

where $\xi^n = W^{out}\,\left[u^n;x^n\right]$.

4.1 Reservoir adaptation

One interesting question is whether it is sufficient to learn the output weights or whether one needs to adapt the reservoir using the point process log-likelihood as the fitness criterion. In the current work, we adapt recurrent and feed-forward reservoirs with one step propagation of the point process log-likelihood into the reservoir and compare the results to non-adaptive reservoirs.

Any connectivity weight W _kl within the reservoir can also be adapted with the gradient descent rule,

$$ {W}^n_{kl} \leftarrow {W}^{n-1}_{kl} + \eta_{res} \, \frac{\partial{\ell^n}}{\partial{{W}_{kl}}}. $$

(8)

As we assume the output channels are mutually independent given the parameters,

$$ \frac{\partial{\ell^n}}{\partial{{W}_{kl}}} = \sum\limits^L_{i=1} \frac{\partial{\ell_i^n}}{\partial{{W}_{kl}}}. $$

(9)

Obviously, $\ell^n_i$ has a long term dependency on W _kl due to reservoir memory, i.e. $\ell^n_i$ not only depends on $W^{n-1}_{kl}$ but also on $W^{n-h}_{kl}$, where h > 1. However, for the sake of computational efficiency, and in view of the fact that long term partial derivatives tend to vanish exponentially with respect to time (Bengio et al. 1994), we utilize a one-step propagation of the instantaneous log-likelihood into the reservoir.

$$ \frac{\partial{\ell_i^n}}{\partial W_{kl}} \approx \frac{\partial{\ell_i^n}}{\partial W^{n-1}_{kl}}. $$

(10)

Note that if neuron ψ projects to the readouts, any connection to ψ is updated with one-step propagation. As every reservoir neuron is projecting to the readout units, every reservoir connection is updated with the learning rule.

$$ x^n = \left(1 - \frac{1}{\tau}\right)\,x^{n-1} + \frac{1}{\tau} \, f\left(W^{in}\,u^n + W^{n-1}\,x^{n-1}\right), $$

(11)

$W^{n-1}_{kl}$ contributes to ${\ell_i^n}$ for all i, k and l through $x^n_k$. We can now utilize the chain rule,

$$ \frac{\partial{\ell_i^n}}{\partial W^{n-1}_{kl}} = \frac{\partial{\ell_i^n}}{\partial{x^n_k}} \, \frac {\partial x^n_k} {\partial{W^{n-1}_{kl}}}. $$

(12)

Partial derivatives with respect to state variables can be computed by combining Eqs. (2), (3), and (4).

$$ \frac{\partial{\ell^n_i}}{\partial x^n_k} = A \; W^{out}_{ik} \; \delta_{N_i}^n - A \; W^{out}_{ik} \; \lambda_i^n. $$

(13)

Again following Eq. (11),

$$ \frac{\partial{x_k^n}}{\partial{ W^{n-1}_{kl} }} = \alpha_k \, \frac {\partial {f_k\left(a_k^n\right)} } {\partial a_k^n} \, x^{n-1}_l, $$

(14)

where $a_k^n$ is the k − th element of the vector W ^inp u ⁿ + W ^n − 1 x ^n − 1 and $f_k (a_k^n)$ is the k-th element of the resulting state vector. We define α _k as the inverse of the time constant for reservoir unit k, 0 < α _k = 1/τ_k < 1. With Eqs. (9), (10), (12), (13) and (14), the update rule in Eq. (8) is completed.

4.1.1 Adapting neuronal time constants

Gradient descent is also used for adapting the time constants of the reservoir neurons. Note that in this case time constant is not a global parameter anymore. Let $\alpha^n_j =1/\tau^n_j = g(\alpha^{\prime n}_j) = 1/ (1 + \exp(\alpha^{\prime n}_j))$, to have a continuity over all $\alpha^n_j$ and to keep them in the desired range.

$$ \frac{\partial{\ell^{n}_i}}{\partial \alpha^{\prime n-1}_j} = \frac{\partial{\ell^{n}_i}}{\partial{x^n_j}} \, \frac{\partial{x^n_j}}{\partial{\alpha^{\prime n-1}_j}} $$

(15)

$$ \frac{\partial{x_j^n}}{\partial \alpha^{\prime n-1}_j} = \left\{-x^{n-1}_j + f_j\left(W^{inp} \, u^{n} + W \, x^{n-1}\right)\right\} \frac{dg\left(\alpha_j^{\prime n-1}\right)}{d\alpha_j^{\prime n-1}} $$

(16)

$$ \alpha_j^{\prime n} \leftarrow \alpha_j^{\prime n-1} + \eta_{\alpha} \, \frac{\partial{\ell^{n}}}{\partial \alpha_j^{\prime n-1} }, $$

(17)

The complexity of the readout-only learning is O(L N) for each time step, where L is the number of readout units. Running the trained ESN on the test input stream has also a complexity of O(L N) for sparse reservoirs, where the number of connections linearly scales with the number of reservoir units. All the reservoirs we use belong to this sparse type. In this case, the complexity of the one-step log-likelihood propagation is also O(L N).

4.2 Existence of local maxima and confidence intervals

Due to deep architecture and reservoir transfer function, we cannot guarantee that gradient descent in the reservoir parameters yields uniquely true, i.e. globally optimal, parameters. Point process log-likelihood is not concave with respect to the whole set of parameters. Reservoir adaptation, as a result, is not a tool for finding a globally optimal equivalent of a given BNN. The quality of reservoir adaptation is evaluated based on its improvement on the predictive performance over fixed reservoirs. For a fixed reservoir, on the other hand, learning reduces to redout-only learning, and hence, to adapting the parameters of a Generalized Linear Model (Mccullagh and Nelder 1989; Paninski 2004), which maps reservoir states and input to the conditional intensity. In this case, point-process log-likelihood is a concave function of readout parameters (see Appendix 2) and does not have non-global local maxima with respect to them (Paninski 2004). This shows that gradient descent in the readout parameters will asymptotically result in a global maximum. The absence of local minima holds for readout parameters under a fixed reservoir or if an adaptive reservoir is fixed after some epochs of training. Note that we take an online (stochastic) gradient descent approach in this work. Although online gradient descent takes a stochastic path in the parameter space for maximization of the log-likelihood, empirical evidence suggests that the average behavior of gradient descent is not affected by online updates (Bottou 2004).

Upon training, the observed Fisher Information Matrix can be used to approximate the covariance matrix and confidence intervals on the readout parameters,

$$ \Sigma^{-1}_{out} = -\nabla^2_{W^{out}} \mathcal{L} \left(W^{out}|N\right), $$

where Σ _out is the estimation of the covariance matrix and $\nabla^2_{W^{out}} \mathcal{L} (W^{out}|N)$ is the Hessian of the log-likelihood. The Hessian matrix is computed at the final point estimates of the readout parameters. Confidence intervals are computed using the standard deviations obtained from the diagonal of the covariance matrix. It should be noted that we do not perform a full probabilistic learning of the parameters. We approximate the distribution on the readout parameters by the asymptotic normal distribution of the maximum likelihood estimator (Davison 2003; Pawitan 2001).

5 Evaluation of the learned models

We compared our results with feed-forward and recurrent architectures to the baseline method where only the readout weights were adapted. For different ESN types and architectures, we comparatively evaluated their capabilities on modeling BNN stimulus-response relations by testing the predictive power of the ESN on the observed spike trains. The continuous ESN output signal was tested for compatibility with the actual observed spikes.

Receiver Operating Characteristic (ROC) curve analysis was employed to test the quality of prediction. ROC curves are extensively used in signal detection theory and machine learning to evaluate prediction performance on binary variables. In a binary classification problem (here spike or no spike), a ROC curve is a plot of true positive rate vs. false positive rate. True positive rate is defined as

$$ TPR = \frac{\#\,True\;Positives}{\#\,All\;Positives}. $$

Similarly, false positive rate is defined as

$$ FPR = \frac{\#\,False\;Positives}{\#\,All\;Negatives}. $$

As the ESN output is continuous, true positive rate and false positive rate will vary with respect to a moving threshold. An example ROC curve is shown in Fig. 6 (bottom). In contrast to classification accuracy, the area under a ROC curve (AUC) is more robust with respect to prior class probabilities (Bradley 1997). An AUC around 0.5 indicates a random prediction whereas an AUC for a perfect prediction will equal 1.0.

6 Experimental results

We employed Echo State Networks with different types and sizes of reservoirs on spike prediction tasks, where the spikes were recorded from simulations of random cortical networks and from cultured networks of cortical neurons. We investigated whether ESNs successfully predict output spikes of BNNs when they are presented with the same input streams.

6.1 Simulations of random cortical networks

We simulated 10 surrogate cortical neural networks of 1000 neurons each with 0.1 random connectivity. We used the Izhikevich neuron model and included spike-timing dependent plasticity (STDP) in our simulations (Izhikevich 2006). At each 5 ms, one of the 100 input channels was randomly selected from a uniform distribution and a pulse of 5 ms width was sent to the network. Each input channel had excitatory projections to 10 % of the neurons in the network. The networks were simulated for 2 h in real time with STDP and 0.5 h in real time with frozen synapses thereafter. In each network, the spikes from a randomly selected excitatory neuron were recorded with 5 ms discretization. We then trained ESNs to estimate the conditional intensity of the selected neuron’s spiking process from the history of the input pulses.

LI-ESNs with three different reservoir types of various sizes were used for this task, namely recurrent fixed recurrent reservoirs (R-fxd), recurrent adaptive reservoirs (R-adp) and feed-forward adaptive (FF-adp) reservoirs. Reservoir connectivity and each individual time constant were adapted using the method described in Section 4. For each of the 10 surrogate biological neural networks, we used reservoirs of sizes 100, 500 and 1000. A separate random sparse reservoir for each size and for each surrogate biological network was generated, where each reservoir unit was connected to 10 other units. For each random reservoir, a feed-forward reservoir was generated by inverting the edges that cause recurrence as described in Fig. 4. Note that the same sized feed-forward and the recurrent reservoirs for the same biological neural network had the same topology apart from edge directions. This yielded 60 different reservoirs for the whole experiment.

From each of the 10 BNN simulations we recorded data for 30 min in real time. Using a discretization time bin of 5 ms, the simulation yielded time series data for 360,000 time steps, of which 328,000 time steps for were used for training and 30,000 time steps were used for testing in each sub-experiment. For the adaptive reservoirs, the training phase included 20 full adaptation iterations of the reservoirs and 60 readout adaptation iterations. One iteration covered one forward traversal of the training data in time. No learning was performed on the test data.

Results of the ROC curve analysis show that the ESN approach performs well in conditional intensity estimation (Table 1). For all the experiments on 10 different BNNs, the estimated conditional intensity predicts output firing far better than random prediction. For BNN2, point estimates and uncertainty measures of readout parameters after readout-only-training were also presented. (Fig. 5, see Section 4.2 for computation of uncertainty measures).

Table 1 Areas under ROC curves (in %) for the prediction of activity in 10 simulated biological neural networks with fixed recurrent (R-fxd), feed-forward adaptive (FF-adp) and recurrent adaptive (R-adp) reservoirs

Fig. 5

Confidence intervals on the readout parameters of 3 reservoir types of size 100 for a selected biological neural network. The learned readout weights and 99% confidence intervals (±2.576σ) are shown. Confidence intervals are computed by assuming a multivariate normal distribution and an infinite prior covariance matrix. Hence, inverse of the observed Fisher information matrix is used to compute confidence intervals. The weights indexed from 1 to 100 are reservoir-to-output parameters, whereas the weights indexed from 101 to 200 are direct input-to-output parameters. Greater uncertainty for input-to-output parameters are noticeable, which results from low density of the input pulses per channel

We further investigated whether the predictive power of ESNs with feed-forward adaptive reservoirs of leaky integrator neurons is comparable to that of recurrent reservoirs. Adaptive reservoirs are in general better than non-adaptive reservoirs. This difference, however, vanishes with increasing reservoir size (Table 1). In these experiments, feed-forward adaptive reservoirs significantly outperformed the non-adaptive recurrent reservoirs of all sizes. Furthermore, they significantly outperformed recurrent adaptive reservoirs for sizes of 100 and 500. Although adaptation brought significant improvement also to recurrent reservoirs for sizes 100 and 1000, feed-forward adaptation performed in general better than recurrent adaptation in estimating the conditional intensity. Small reservoirs (i.e. for N = 100) of the feed-forward architecture were drastically superior to the recurrent reservoirs.

One can gain some insight on the comparative performances of different reservoirs by looking at the development of the log-likelihood during training (Fig. 6). Note that we adapted the reservoir connectivity and the time constants only in the first 20 iterations. The remaining 60 iterations included only learning of readout parameters. This allowed for observing the effects of two learning phases separately. The log-likelihood clearly increases with fewer iterations in adaptive reservoirs. A sudden drop of training log-likelihood is remarkable at the transition from the full training phase to the readout training phase. Although this transition significantly reduces the fitness and might make the adaptive reservoirs worse than non-adaptive ones, previous full reservoir training pays out in the upcoming iterations.

Fig. 6

Changes of the training log-likelihood with the number of iterations for reservoirs with different number of neurons (N) and reservoir types (color coded). The performance of the reservoirs is shown for fixed recurrent (blue, dashed), adaptive recurrent (black, continuous) and adaptive feed-forward types (red, ∗)

Note that Table 1 refers only to the prediction of output spikes from input pulse trains. If the spike history of the output neuron is also taken into account, the prediction performance increases considerably. In this case, the output spike history is also fed into the ESN through an additional input channel. For BNN2, we visualize the conditional intensity estimation that takes also the output spike history into account (Fig. 7). Note the increased area under the ROC curve when compared to the second row in Table 1. Cross-correlation coefficients around 0 time lag between the conditional intensity estimation and the target spike train also improve when the output spike history is used (Fig. 8), indicating an increased similarity of estimations and observations. Cross-correlation coefficients are computed as

$$ c_{s\lambda}(m) = \frac{1}{T-1}\frac{ \sum_n \left[s(n+m)-\tilde{s}\right] \left[\lambda(n) -\tilde{\lambda}\right]}{\sigma_s \sigma_{\lambda}}, $$

where m is the time lag, s is the binary valued discrete-time signal for the target spike train and λ(n) is the conditional intensity estimation at time step n. $\tilde{s}$ and $\tilde{\lambda}$ stand for mean values, whereas σ _s and σ _λ denote standard deviations. T is the data length in time steps. As for ROC curve areas, the peak around zero lag indicates the similarity between the conditional intensity estimation and the reference spike train.

Fig. 7

Estimated conditional intensity for a selected biological neural network (BNN2) using input history and the output spike history together. Conditional intensity estimations λ for all time steps in the testing period are shown in decreasing order (top). A bar is shown if there was indeed a spike observed in the corresponding time step (top). Distributions of conditional intensity, λ, for time steps with observed spikes and without spikes (middle). By a varying threshold on λ, true positive rates vs. false positive rates can be calculated (bottom)

Fig. 8

Cross-correlation coefficients between the conditional intensity estimation and the observed spike patterns for the output neuron of a selected biological neural network (BNN2) with feed-forward ESN adaptation for a reservoir of 1000 neurons. Using only the input stream, AUC = 85.5% (top). Using the input stream and the spike history of the output neurons, AUC = 91.6% (bottom). Each bar shows the correlation coefficient for 1 time step of the ESN (5 ms). Around 0 time lag, the conditional intensity that uses the spike history has a higher correlation with the observed spikes. Note that there is negative correlation for some negative time lags (− 90 < time lag < 0). This results from the fact that conditional intensity estimation is very low after an observed spike since the algorithm learns the negative auto-correlation of the output spikes for this time lag interval. In other words, the learned model is reflecting the inter-spike interval in its output

6.1.1 Approximating gradient vectors with one-step propagation

In order to investigate the consequences of one-step approximation to gradient descent, we compared the gradient vectors obtained by full gradient computation and those obtained by one-step approximation. Full gradient computation would replace Eqs. (14) and (16) as

$$ \begin{array}{rcl} \frac{\partial{x_j^n}}{\partial{ W_{kl} }} &=& \left(1-\alpha_j\right) \frac{\partial{x_j^{n-1}}}{\partial{ W_{kl} }}\\[3pt] &&+\, \alpha_j \, \frac {\partial {f_j\left(a_j^n\right)} } {\partial a_j^n} \left[\delta_{jk}\; x^{n-1}_l + \sum_m W_{\!jm} \frac{\partial{x_m^{n-1}}}{\partial{ W_{kl} }} \right] \end{array} $$

and

$$ \begin{array}{rcl} \frac{\partial{x_j^n}}{\partial \alpha_k} &=& \left(1-\alpha_j\right) \frac{\partial{x_j^{n-1}}}{\partial \alpha_k} \\[3pt] &&+\,\left[\alpha_j \frac {\partial {f_j\left(a_j^n\right)} } {\partial a_j^n} \sum_m W_{\!jm} \frac{\partial{x_m^{n-1}}}{\partial{ \alpha_{k} }} \right]\\[3pt] &&+\, \delta_{jk} \left[-x^{n-1}_j + f_j\left(a_j^n\right)\right], \end{array} $$

respectively. The resulting learning rule would be an adaptation of the Real Time Recurrent Learning (Williams and Zipser 1989) for point processes, which is computationally very expensive for our data and reservoir sizes. It is, however, still viable to compare the gradients obtained by one-step propagation to those obtained by full gradient computation for a limited number of time steps. Here, we compared gradient vectors of the log likelihood with respect to all reservoir parameters for 19,000 time steps. We computed the correlation and the cosine between full and one-step gradients for each time step separately,

$$ \begin{array}{rcl} c^n &=& \frac{1}{R-1}\frac{\sum_r \left(\displaystyle\frac{\partial \ell^n}{\partial W^{n-1}_r} - \mu^n_{one}\right) \left(\displaystyle\frac{\partial \ell^n}{\partial W_r} -\mu^n_{full}\right)} { \sigma^n_{one} \sigma^n_{full} }\\[6pt] \cos\left(\Omega^n\right)&=& \frac{<\nabla^{n-1} \ell^n, \nabla \ell^n >}{|\nabla^{n-1} \ell^n| \; |\nabla \ell^n|}, \end{array} $$

where $\nabla^{n-1} \ell^n$ and $\nabla \ell^n$ are the gradient vectors at time step n obtained by one-step propagation and by full gradient computation, respectively; $\frac{\partial \ell^n}{\partial W^{n-1}_r}$ and $\frac{\partial \ell^n}{\partial W_r}$ are their r-th components; $\mu^n_{one/full}$ and $\sigma^n_{one/full}$ are the mean values and the standard deviations for the components of the gradient vector; c ⁿ and Ω ⁿ are the correlation and the angle between the full and one-step gradient vectors at time step n, respectively.

The distribution of the correlations and cosines provides insight to the consequences of one-step approximation in feed-forward and recurrent reservoirs. Over 19,000 time steps, the correlations between the one-step and full gradient vectors in a selected random reservoir are distributed around a mean value of 0.61 with a standard deviation of 0.034. The mean and standard values are 0.77 and 0.022 for the corresponding feed-forward reservoir (Fig. 9). Cosines constitute a very similar distribution, as the gradient vector components for each time step have approximately a mean value of 0. Strong correlations between the full and one-step gradients deliver additional explanation for the better performance adaptive reservoirs. The fact that the log-likelihood propagates to every reservoir parameter in one-step (due to full reservoir-to-output connectivity) and that one-step gradient is the dominant component of the full gradient information are possible reasons for the detected similarity. Stronger correlations for feed-forward reservoirs are in agreement with the relative better performance of the feed-forward reservoir adaptation.

Fig. 9

Distributions of the correlations (left) and cosines (right) between fully recursive and one-step computations of gradients vectors, $\nabla \ell^n$ and $\nabla^{n-1} \ell^n$, respectively. Results are shown for a selected sparse recurrent reservoir of size 100 and its feed-forward version

6.1.2 Information encoded in reservoir activity

A canonical correlation analysis of the reservoir activity and the output spiking activity also revealed that output spikes are encoded in the reservoir activity. Prior to readout-only learning, we recorded the reservoir states for one traversal of the training data and performed a canonical correlation analysis (CCA) (Chatfield and Collins 2000) with the observed training spikes. We then used parameters obtained by CCA for relating reservoir states to output spikes in the test data and detected maximum correlations for all of the 10 experiments in Table 1. Although not as good as in readout learning, CCA also reveals the correlation of the reservoir activity with output spikes (Fig. 10), indicating the spike encoding in the reservoir activity.

Fig. 10

Correlation of reservoir activity with the observed spike activity for a selected recurrent reservoir with 100 neurons and its feed-forward version. Canonical correlation analysis (CCA) results also indicate that output spikes are encoded in reservoir activity. Point process readout learning proves more efficient in relating the reservoir activity to output spikes than CCA

In addition to CCA of reservoir states and output spikes, we further visualized the memory traces of the input pulses in reservoir states. We compared how past inputs are reflected in the reservoir activity for different reservoir types by considering input triggered averages (ITA). We define the input triggered average for an input-neuron pair as

$$ \mathrm{ITA}_{hj}(m) = \frac{\sum_{n=1}^T u_h^n \; x^{n+m}_j}{\sum_{n=1}^T u_h^n}, $$

where m is the time lag, $u_h^n$ is the input pulse from channel h at time step n (1 or 0), $x^{n+m}_j$ is the state of the j-th neuron at time step n + m. The normalized ITA is then

$$ \widehat{\mathrm{ITA}}_{hj}(m) = \frac{\mathrm{ITA}_{hj}(m) - \bar{x}_j}{\sigma_{x_j}}, $$

(18)

where $\bar{x}_j$ and $\sigma_{x_j}$ are the mean value and the standard deviation for x _j, respectively. Figure 11 depicts the $\widehat{\mathrm{ITA}}_{hj}$ curves for 800 input neuron pairs in 3 different reservoir types for a selected biological neural network. Memory traces for adaptive reservoirs, especially for recurrent adaptive reservoirs, are more scattered over time. This increased heterogeneity in the responses is very likely a reflection of time constants in adaptive reservoirs.

Fig. 11

Normalized input triggered averages (see Eq. (18)) for 20 different input pulses on 40 different reservoir neurons (background, gray). Randomly selected 30 combinations, are highlighted (darker, red) for three different reservoir types. Adaptive reservoirs display more diffused memory traces, i.e. their time lags for the peaks vary more

6.2 Prediction of spontaneous events in neuronal cultures

To test our approach on living neural networks, we aimed at predicting spontaneous events in neuronal cultures. We defined an event as a group of spikes recorded by the same MEA electrode, whose maximum inter spike interval is less than 60 ms. The time of the first spike in the group is regarded as the event time. It should be noted again that the activity in neuronal cultures is typically a sequence of network bursts. If there were at least 100 ms between two successive events, we regarded them as parts of different bursts. These criteria mostly excluded isolated spikes from network bursts and clustered fast repetitive firings at an electrode, e.g. a cellular burst, into a single event. We recorded spikes from a neuronal cell culture for 30 min, detecting bursts and events according to the above definition. We used the data for training except for the last 200 s, which were reserved for testing. We selected approximately 3/4th of the 60 MEA electrodes and treated their events as the input stream; and the remaining electrodes as output. This selection was based on spatial order of the electrodes, i.e. input and output electrodes occupied two distinct areas in the culture. If an electrode had never recorded spikes in the training event train, it was regarded as inactive and was excluded from the learning and testing processes. The evaluation task was to estimate the conditional intensity of the output events for each output electrode at time step n using the total input event stream until time step n (1 ms bin size). Note that only very few events occur outside the bursts. Therefore, the algorithm performs learning and prediction only during bursts.

Based on estimates for all time steps during network bursts in the last 200 s, we evaluated the predictive performance of the learned ESN models using ROC curve analysis on the target events and estimated conditional intensity. We selected the electrodes that recorded at least 15 events within the evaluation window of 200 s.

Figure 12 (left) shows the AUC for each electrode using reservoirs of different types all with 500 neurons. Note that the prediction results in Fig. 12 is based only on input event streams, i.e. the event history of the output electrodes is excluded. Except for output electrode 3, all AUC measures are far above the random level. This supports the notion that most output neurons in the culture do not fire randomly but they rather follow patterns (Shahaf et al. 2008). Even electrode 3 is above the chance level but it has low predictability compared to other electrodes. Aggregated test data AUC over active electrodes (except electrode 3) for different ratios of training data is shown in Fig. 12 (right). As expected, AUC improved with more training data. The improvement, however, was not dramatic. For a selected output electrode the details of the ROC analysis is illustrated in Fig. 13.

Fig. 12

Areas under ROC curves (AUC) for the event prediction task at the active output electrodes (left) and aggregated AUC for different ratios of training data (right) using fixed recurrent (R-fxd), feed-forward adaptive (FF-adp) and recurrent adaptive (R-adp) reservoirs, all with 500 neurons

Fig. 13

ROC curve analysis of the event timing prediction for active output electrode 1 using a recurrent adaptive reservoir with 500 neurons without using the spike history. Conditional intensity estimations λ for all time steps in the testing period are shown in decreasing order (top). A bar for each observed spike in the corresponding time step (top). Distributions of of conditional intensity, λ, for time steps with and without observed spikes (middle). By a varying threshold on λ, true positive rates vs. false positive rates can be calculated (bottom)

Table 2 shows aggregated areas under ROC curves over all active electrodes except electrode 3 for a selected culture (Culture 1), without (top) and with (middle) using the output event history. Each entry in the table was obtained with a single reservoir of the corresponding size. As expected, the prediction performance usually increased with the reservoir size. Using the event history of the output electrodes did not improve the prediction performance, thus, no additional information could be found in the output event history. Note that utilizing the event history results in an approximately 25% increase in the input dimensionality. Possible redundancy of the event history with the already existing input might have caused a suboptimal performance of the learning algorithm, decreasing the prediction accuracy in several reservoirs. Feed-forward adaptive and recurrent adaptive reservoirs performed better than the fixed reservoirs for most reservoir sizes. As a baseline for comparison purposes, we used the input event rate (regardless of the spatial information, i.e. without using the electrode number) for the conditional intensity estimation (Table 2, below). Although this method proved to have some predictive power especially for a rate kernel of 20 ms, it is obviously not as good as ESN predictors. Cross-correlation analysis reveals further information about comparative performances of different methods (Fig. 14). The higher peak and the smaller width of the cross-correlogram is an indicator for the better performance of recurrent adaptive reservoirs. To further compare different reservoir types, we experimented with 3 different cultures and employed 10 randomly generated reservoirs of size 500. We used the acyclic forms of the same reservoirs for feed-forward adaptation. In 2 of these 3 cultures (1 and 3), the recurrent adaptive reservoirs had the best average predictive power (Table 3). In the same 2 cultures, the prediction of the recurrent adaptive reservoirs significantly outperformed the others for several output electrodes (Table 4).

Table 2 Areas under ROC curves for the event timing prediction task aggregated over active output electrodes

Fig. 14

Cross-correlation coefficients between the conditional intensity estimation and the observed output events for a selected (1) active output electrode without using the output spike history (res. size of 500). Coefficients are shown for fixed recurrent (a), feed-forward adaptive (b), and recurrent adaptive reservoirs (c). Each bar shows the correlation coefficient for 5 time steps of the ESN (5 ms). As a baseline a prediction based on event rate (without an ESN, conditional intensity proportional to event rate) is also shown (d). The recurrent adaptive reservoir performs better here, considering the height of the peak and the width of the cross-correlogram

Table 3 Mean AUC (%) in the event timing prediction task in 3 different cultures

Table 4 Pairwise comparison of the reservoir types and methods in the event timing prediction task in 3 different cultures using 10 random reservoirs all with size 500

6.3 Next-event prediction in neuronal cultures

Recent findings indicate that the temporal order of the events in neuronal cultures carries significant information about the type of stimuli (Shahaf et al. 2008). In this experimental setting, we investigated whether the ESNs can model the structure in the temporal order of the events. We deleted timing information of the events from the previous setting and, as a result, we obtained data of temporally ordered events. More precisely, we used operational time steps for ESN analysis, i.e. each event appeared only in 1 time step and each time step contained only 1 event.

In this setting, we treated every electrode as output and used the whole event history for prediction. The task was again to estimate the conditional intensity of the output events for each electrode at time step n using the total event stream until time step n. Note that point process modeling is not necessarily the optimal tool for this data, where each abstract time step can contain only 1 event. The general framework taken in the current work, however, can still be employed for predictive modeling of temporal event orders. Again, ROC curve analysis indicates a good average prediction quality with larger reservoirs, feed-forward adaptive reservoirs outperforming the recurrent reservoirs up to sizes of 500 (Table 5, Fig. 15).

Table 5 AUC (%) for the next-event prediction task aggregated over all active output electrodes in a selected neuronal culture (1)

Fig. 15

Estimated conditional intensity for a selected output electrode (5) of the neuronal culture in the next-event-prediction task using a feed-forward adaptive reservoir with 500 neurons. Conditional intensity estimations λ for all time steps in the testing period are shown in decreasing order (top). A bar is shown if there was indeed a spike observed in the corresponding time step (top). Distributions of of conditional intensity, λ, for time steps where there was an observed spike and where there was no spike (middle). By a varying threshold on λ, true positive rates vs. false positive rates can be calculated (bottom)

To further compare different reservoir types, 10 random reservoirs of 300 neurons together with their acyclic forms were tested on 3 different cultures (Table 6). The predictability varied with respect to the electrode that recorded the event, with AUC ranging from 50.5% to 93.4%. In pairwise comparison of the 3 reservoir types, FF-adp reservoirs significantly (signed-rank test, p < 0.05) outperformed other methods for many electrodes (Table 7). Conversely, the number of electrodes, for which the other methods performed better, was much smaller.

Table 6 Mean AUC (%) in the next-event prediction task in 3 different cultures

Table 7 Pairwise comparison of the reservoir types and methods in the next-event prediction task in 3 different cultures using 10 random reservoirs all with size 300

7 Conclusion

The implications of our results are manifold. Firstly, our results indicate that reservoir computing is a potential candidate for modeling neural activity including neural encoding and decoding. With their expressive power for different activity measures (e.g. spike rates, correlations etc.), reservoir computing tools might help for analysis of neural data. In our experiments, ESNs of leaky integrator neurons proved successful for modeling response-dynamics (e.g. stimulus-response relations and spatio-temporal dynamics) of simulated and cultured biological neural neural networks.

On the methodological side, we showed that ESN learning algorithms can be adapted for event data, such as spikes or spike groups, using a point process framework. We proposed a reservoir adaptation method for event data, which can be used to adapt connectivity and time constants of the reservoir neurons. The experimental results indicate that reservoir adaptation can significantly improve the ESN performance over readout-only training.

We utilized feed-forward networks with leaky-integrator neurons as reservoirs with a comparable predictive power to recurrent reservoirs when trained with log-likelihood propagation. In modeling stimulus-response relations of simulated BNNs, feed-forward reservoir adaptation outperformed other methods up to 500 neurons. This outperformance was statistically significant. For the event timing prediction task in neuronal cultures, adaptive recurrent reservoir adaptation outperformed the other methods (in 2 of 3 cultures), whereas feed-forward adaptation were better in the next-event type prediction task in all 3 cultures. This might indicate that the type of encoding in neural systems (order or timing) favors different architectures for decoding. An analysis of the structure-coding relations, however, is beyond the scope of this note. Why feed-forward reservoir adaptation can work better than recurrent reservoir adaptation necessitates also more theoretical analysis. We manually optimized global parameters (spectral radius, learning rates and A) for recurrent fixed reservoirs. Recurrent adaptive reservoirs started from these values. Although we can think of no obvious disadvantage for recurrent reservoirs, feed-forward adaptation outperformed recurrent adaptation in some tasks. We experimentally showed that one-step propagation approximates the gradients better in feed-forward reservoirs than in recurrent ones. In our opinion, better structuring of the reservoir parameters, i.e. separation of the memory parameters from the reservoir connectivity, might further underlie the relative better performance of feed-forward adaptation. For instance, a small connectivity change in the recurrent adaptation might have a more dramatic effect on the reservoir memory than in case of feed-forward adaptation. Our findings on feed-forward networks are also in accordance with the recent work by Ganguli et al. (2008), Goldman (2009), Murphy and Miller (2009), who show that stable fading memory can be realized by feed-forward or functionally feed-forward networks and that feed-forward networks have desirable properties in terms of trade-off between noise amplification and memory capacity.

Appendices

Appendix 1: Implementation details

For all the experimental settings, we generated recurrent sparse random reservoirs. Regardless of the reservoir size, each reservoir unit was connected to 10 other units. The initial connection strengths were drawn from a uniform distribution over the interval [−0.5 0.5]. The entries of the input weight matrix W ⁱⁿ were drawn from a uniform distribution over [−1 1]. We normalized the connectivity so that the maximum absolute eigenvalue, i.e. the spectral radius, was 1, with which the ESNs were experimentally detected to work well on all experiments. We additionally generated the feed-forward form of the each recurrent reservoir as described in Fig. 4. After changing from recurrent to feed-forward architecture, we did not manually modify the connectivity parameters. The leakage time constants, τ _j = 1/α _j, were initialized according to

$$ \alpha_j = 1/\left(1+ \exp\big(\alpha^{\prime}_j\big)\right), $$

where $\alpha^{\prime}_j$ were uniformly drawn from [−1.5 1.5].

Note that the initial value of the spectral radius and the initial range for time constants were manually arranged to work well with recurrent fixed reservoirs. Adaptive reservoirs used this fixed settings as starting parameters.

For fixed reservoirs, we used 80 epochs of readout-only training. Initially, we set η _out = 0.7 and gradually decreased the output learning rate with

$$ \eta_{out} \leftarrow \frac{\eta_{out}}{E+1}, $$

where E was the epoch number. This was done for fast learning and convergence of the algorithm.

For adaptive reservoirs, we used 20 epochs for reservoir and readout training and 60 epochs for readout-only training. The readout-only learning employed the same time dependent η _out as the fixed reservoirs. For reservoir training, we set the initial values η _out = η _res = η _α = η = 0.2 and decreased it with

$$ \eta \leftarrow 0.5\;\eta, $$

when the increase in the training log-likelihood dropped below 0.0003 per output channel and time step.

The parameter A in $f^{out}(\xi) = \exp(A \: \xi)$ was set to 0.2, which was manually found to work well for the selected learning rates.

The ESN learning algorithm described in this note was implemented in MATLAB and C++ languages. The results reported here were produced by the C++ implementation. The source code is available under http://www.informatik.uni-freiburg.de/~guerel/PP_ESN.zip"/> (currently only MATLAB).

Appendix 2: Concavity of the log-likelihood with respect to readout parameters

The second order partial derivative of the instantaneous log-likelihood with respect to output parameters is computed as

$$ \frac{\partial^2{\ell^n_i}}{\partial{{W}_{ij}^{out}}\partial{{W}_{ik}^{out}}} = -A^2 \; x_j^n \; x_k^n\; \lambda_i^n, $$

resulting in a Hessian,

$$ H_{\ell_i^n} = -A^2 \; \lambda_i^n \; \left[x^n;u^n\right]\;\left[x^n;u^n\right]^\mathrm{T}, $$

where [x ⁿ;u ⁿ]^T is the transpose of the column vector [x ⁿ;u ⁿ]. $H_{\ell_i^n}$ is obviously a non-positive definite matrix, since for any non-zero row vector b

$$ \begin{array}{lll} b\;H_{\ell_i^n} \; b^\mathrm{T}& = &-\left(A^2 \; \lambda_i^n\right)\;b \left[x^n;u^n\right]\;\left[x^n;u^n\right]^\mathrm{T}\; b^\mathrm{T}\\ & = &-(A^2 \; \lambda_i^n)\;\left(b \left[x^n;u^n\right]\right)^2\\ &\leq&0. \end{array} $$

Consequently, the Hessian of the total log-likelihood is also non-positive definite as $H_{\mathcal{L}} \!=\! \sum_i \sum_n H_{\ell_i^n}$. Therefore, we conclude that under fixed reservoir parameters, the log-likelihood is a concave function with respect to output parameters. This indicates that output parameters will not get stuck in the local maxima for a fixed reservoir. For adaptive reservoirs, the concavity holds for the readout-only learning phase of the training. An overview of the concavity of the point process log-likelihood for generalized linear models and its extension to different conditional intensity functions is given in Paninski (2004).