1 Introduction

Parkinson’s disease (PD) is a chronic, progressive disorder of the central nervous system, characterised mainly by a difficulty in performing movements smoothly and fluently. Bradykinesia, or slowness of movement, is one of the most debilitating symptoms of PD. Experimental evidence indicates that bradykinesia is more pronounced in the execution of complex movements, i.e. sequential or simultaneous motor tasks, than in the execution of simple movements. PD patients exhibit abnormal pauses between movement segments and a more pronounced movement time when a task is performed within a sequence of moves (Suri et al. 1998; Berardelli et al. 2001). Several mechanisms have been proposed to explain the extra deficits observed in complex movements, such as insufficient dopamine resources for multiple simultaneous movements, difficulty in switching between movement segments due to impaired force control, interference from competing motor programs, and impaired preparation of movement sequences (Agostino et al. 2003; Levy et al. 2002). Cutsuridis and Perantonis (2006) have developed a basal ganglia–cortico–spinal network model for control of voluntary arm movements by incorporating dopaminergic innervation of cells in the cortical and spinal components of the circuit. The basal ganglia, however, were not included in this model. The output of this system, i.e., the activity of the internal part of the globus pallidus (GPi), was represented by a scaled step function that, according to the authors, initiates movement. One of the conclusions of this study is that the disrupted basal ganglia output has the strongest effect on movement when dopamine levels are reduced.

In the current study we have developed a computational model that simulates basal ganglia activity related to movement control under normal and parkinsonian conditions that may explain the increased difficulty to perform complex movements and even the requirement of a repetitive output from basal ganglia to complete the movement.

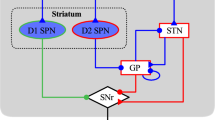
The basal ganglia (BG) play a vital role in the regulation of voluntary movement. This group of subcortical nuclei receive input from the cerebral cortex and project back to the cortex via the thalamus in a closed loop called the BG–thalamocortical circuit. The classic view of the pathways through the BG, first proposed by Albin et al. (1989) and De Long (1990), considers two major connections between the input and output nuclei of the BG, namely the ‘direct’ and ‘indirect’ pathways. The direct pathway, arising from inhibitory striatal efferents containing GABA, substance P and dynorphin, projects directly to the internal part of the globus pallidus (GPi), whereas the indirect pathway, arising from striatal efferents containing both GABA and enkephalin, projects to the GPi via the external part of the globus pallidus (GPe) and subthalamic nucleus (STN). The centre-surround model, described by Nambu et al. (2002), includes an additional pathway called the ‘hyperdirect’ pathway from the cerebral cortex to the GPi via the STN, bypassing the striatum. The hyperdirect pathway, which provides a widespread excitation of the GPi (Mink 1996), is thought to suppress large areas of the thalamus and cerebral cortex related to both the selected motor program and competing programs before movement begins. According to the ‘scaling’ hypothesis, the direct pathway then facilitates movement in a small focal area via disinhibition of the thalamus, while the indirect pathway acts to scale or brake the facilitation (Alexander and Crutcher 1990). The general scheme of the basal ganglia–thalamocortical circuit, shown in Fig. 1, illustrates these pathways through the basal ganglia.

Fig. 1
figure 1

General scheme of the BG–thalamocortical circuit showing the ‘direct’, ‘indirect’ and ‘hyperdirect’ pathways. Excitatory glutamatergic projections are illustrated with a ‘+’, inhibitory GABAergic projections with a ‘−’. The projection from SNc to the striatum uses dopamine (DA) as a neurotransmitter, and is inhibitory or excitatory depending on the striatal receptor to which it binds. SNc Substantia nigra pars compacta; STN subthalamic nucleus; GPe and GPi external and internal part of the globus pallidus, respectively

Full size image

Dopaminergic neurons in the substantia nigra pars compacta (SNc) of the BG project mainly to the striatum. The effect of dopamine (DA) is determined by the type of striatal receptor to which it binds. DA increases the activity of the direct pathway via D1 receptors and decreases the activity of the indirect pathway via D2 receptors. The net effect of DA is thus to reinforce the activation of the particular BG–thalamocortical circuit that has been initiated by the cortex (Mink 1996). The primary pathological feature of PD is the degeneration of dopaminergic neurons in the SNc, which upsets the critical balance between the direct and indirect pathways, resulting in a reduction in transmission through the direct pathway and an increase in transmission through the indirect pathway. This ultimately leads to an excessive inhibition of the thalamus by the GPi, resulting in the symptoms of bradykinesia.

The preservation of body maps throughout the various nuclei of the BG suggests that the BG–thalamocortical circuit is characterised by individual parallel modules, related to specific body parts, spatially segregated in a somatotopic fashion (Romanelli et al. 2005; Strafella et al. 2005). Furthermore, single cell studies have shown that neurons in the BG are direction-specific (Nambu et al. 2002) and fire in relation to movement about a particular joint in a particular limb (Teulings et al. 1997). In neurodegenerative diseases, a certain degree of distortion of the body maps occurs, which is thought to lead to a loss of functional segregation between neurons in neighbouring modules. It has been proposed that a loss of segregation may result in increased difficulty in inhibiting unwanted movements and facilitating desired movements (Romanelli et al. 2005; Strafella et al. 2005).

Several computational models of the BG have been developed based on their predicted role in the control of movement. Of the firing rate models that are directly related to the production of movement, the main roles assigned to the BG are serial processing (Albin et al. 1989; De Long 1990), movement gating and velocity regulation (Contreras-Vidal and Stelmach 1995), and action selection (Gurney et al. 2001a, b). Focused selection of the desired motor program and inhibition of competing motor programs have also been proposed as an important role of the BG, as the simultaneous activation of competing motor programs could cause inappropriate muscular co-contraction, resulting in ineffective action (Mink 1996). It is thought that during movement, in addition to reinforcing the intended motor pattern, a multitude of potentially competing motor mechanisms should be suppressed to prevent them from interfering with the intended movement.

Despite a huge amount of anatomical and physiological data regarding the BG and their connections, the computational processes performed by these nuclei in health and disease are still under debate. Moreover, there is currently no known cure for PD. Medication and surgery provide only symptomatic relief, and do not stop the neurodegenerative process. To develop better treatments for this devastating disease, further research is needed to clarify the role of the BG in normal movement and the changes that occur in the BG and related motor circuits due to PD. In addition, the reason for the extra delay observed in the performance of complex movements by PD patients requires further investigation. Although deep brain stimulation (DBS), which involves high-frequency (>100 Hz) electrical stimulation of BG structures, has proven to be an effective treatment for the symptoms of bradykinesia, the mechanisms of operation remain a mystery. It is hypothesised that DBS works by altering the GPi efferent signals projecting to the thalamus, though there is considerable debate as to whether DBS excites or inhibits its target structures, and as to which neuronal elements are influenced by DBS. In order to define optimal stimulation settings and optimal sites for electrode placement, further investigation into possible mechanisms of DBS is required.

The present research focuses on the role of the BG in the control of voluntary limb movement and the factors influencing the pathogenesis of bradykinesia in the performance of simple and complex movements. Voluntary movement was simulated using feedforward control from the cortex. The assumption that no proprioceptive feedback from the limb is required for movement is valid for fast ballistic arm movements (Caselli et al. 2006). The functional scheme of the ‘motor’ BG–thalamocortical circuit was described by a mathematical model, based on the mean firing rates of BG nuclei. A single-joint elbow flexion/extension movement was used in all simulations. A separate BG–thalamocortical circuit was modelled for the control of each muscle group involved in the movement and the interaction between two competing motor modules, controlling flexion and extension at the elbow joint, was examined. The purpose of the model was to investigate possible causes for the increased movement times observed in parkinsonian patients in the execution of both simple and complex motor tasks. PD was simulated as a reduction in the level of striatal DA, as well as a loss of functional segregation between the two motor modules.

While there is little argument that Deep Brain Stimulation (DBS) of the STN, GPi and thalamus has been an effective tool in the treatment of the various symptoms of Parkinson’s disease, there remains considerable debate concerning the methods underlying the beneficial effect of DBS and its mechanisms of action are still unknown (Montgomery and Baker 2000; Benabid et al. 2002; McIntyre et al. 2004, Rubin and Terman 2004). Therefore, possible mechanisms of DBS based on the firing rate of BG nuclei were investigated.

2 Methods

The computational model of the BG–thalamocortical circuit is based on a model developed by Contreras-Vidal and Stelmach (1995), which describes normal and parkinsonian movement based on changes in the mean firing rate of BG nuclei. In this paper of Contreras-Vidal and Stelmach, the BG gate the initiation of voluntary movement and modulate movement velocity via the thalamus. The thalamic output signal is input to a model of the motor cortex, which generates a desired movement trajectory that is sent to the spinal cord. The loss of striatal DA that occurs in PD leads to an imbalance in the neurotransmitter dynamics in the direct and indirect pathways, producing smaller-than-normal BG output signals. The dynamics used in the present research were based on the model of Contreras-Vidal and Stelmach. However, enhancements were made to make the model more realistic and to allow the simulation of complex movements and DBS. In Section 2.1 the physiological background is given on which the equations, described in Section 2.2 (the ‘intact model’), are based. Section 2.3 describes the physiological changes in Parkinson’s disease that, when implemented in the model, transform the intact model into a ‘parkinsonian model’. Several possible mechanisms of DBS are implemented in the model as described in Section 2.4. Finally, Sections 2.5 and 2.6 give details of the movements that are simulated and experimental verification, respectively.

2.1 Intact model

Realistic tonic firing rates for each nucleus were implemented, based on human data specified by Squire et al. (2003), as shown in Table 1. In addition, all lower bounds on neural firing were set to zero to ensure that the negative firing rates seen in the Contreras-Vidal and Stelmach model would not occur. Delays were introduced into all pathways within the BG–thalamocortical circuit based on conduction time values found in literature (Squire et al. 2003; Suri et al. 1997; Romo and Schultz 1992). The time required for a cortical signal to propagate through the BG and thalamus and back to the cortex depends on the path taken and the various synaptic delays encountered along the way. Of the three main routes through the BG, the shortest is the hyperdirect pathway at about 5 ms, then the direct pathway at 20 ms, and finally the indirect pathway at 30 ms (Suri et al. 1997). Table 2 contains the delays that were introduced in the model. The conduction times of the individual connections along the indirect pathway (striatum–GPe–STN–GPi) could not be found in literature. Therefore, these pathway delays have been estimated based on the documented 30 ms conduction time along the entire indirect pathway. During limb movement, changes in STN activity have been recorded on average 30 ms before changes in striatal activity. It is assumed therefore, that cortical input to the STN occurs earlier than cortical input to the striatum. Hence a delay of 30 ms in cortical input to the striatum has been implemented to ensure that STN activity changes occur first.

Table 1 Tonic firing rates cited by Squire et al. (2003)
Full size table
Table 2 Delays in pathways of BG–thalamocortical circuit
Full size table

To ensure that thalamic excitation of the cortex would initiate movement only if a sufficient number of thalamic neurons were active, a threshold on thalamic activity was set just above the tonic activity of the thalamus under normal conditions. The ‘hyperdirect’ pathway from the cortex to the GPi via the STN was added, providing a direct route to the output nucleus of the BG, as illustrated in Fig. 2. The widespread excitation of the GPi by the hyperdirect pathway is achieved via a cortical input to both the area of the STN involved in the desired movement (active module) and the immediately adjacent areas (inactive modules).

Fig. 2
figure 2

Two-module BG–thalamocortical circuit for the simulation of simple and complex movements. SMA Supplementary motor area; PPV present position vector; TPV target position vector

Full size image

To enable the simulation of complex movements, the model was extended to include multiple functionally segregated BG–thalamocortical circuits. The majority of movements require the sequential and temporally precise activation of many muscles. Georgopoulos et al. (1982) propose that the direction of movement of a limb is determined not by the action of single neurons, but by the net activity of large populations of cortical neurons. The contribution of each neuron to movement in a particular direction may be represented as a vector whose length is an indication of the level of activity during movement in that direction. The contributions of individual neurons can then be added vectorially to produce a population vector, whose direction matches the direction of movement. Thus, motor cortex activity signals ‘higher-level’ parameters related to the trajectory of the limb, as well as ‘lower-level’ parameters such as muscle force. In the model, each individual muscle group, controlling a separate degree-of-freedom i.e. elbow flexion or elbow extension, is controlled by a separate circuit or ‘module’. The ‘active’ module refers to the circuit corresponding to the currently executing motor program, while the ‘inactive’ modules refer to surrounding circuits that are not involved in the current movement. To simulate the simultaneous movement of several joints, two or more modules are activated at the same time. To simulate sequential movements, a second module is activated immediately after the first has finished. The model was initially extended to include two modules, as shown in Fig. 2, but more modules can be added as necessary to model each degree-of-freedom.

Lateral inhibition between modules was implemented at the level of the striatum as there is evidence for inhibitory recurrent connections among striatal projection neurons (Tunstall et al. 2002). An additional inhibitory input from the axon collaterals of striatal projection neurons in neighbouring motor modules was included to model this effect, as shown in Fig. 2. During movement, increased striatal activity in the active module should serve to inhibit striatal neurons in neighbouring modules, thus reducing the activity of unwanted modules, and suppressing undesired movements.

2.2 Model equations

The model consists of a set of delay differential equations (ODEs), which represent the mean firing rate of each of the nuclei of the BG and the neurotransmitter dynamics in the direct and indirect pathways. Calculation of the mean firing rate of each nucleus, measured in spikes per second, is based on the sum of the inhibitory and excitatory projections to the nucleus, as well as a passive decay component.

Each inhibitory and excitatory input is multiplied by a constant, representing the connection strength. However, while the inhibitory vs. excitatory nature of each of the BG pathways is known for the most part, the relative strength of the connections between nuclei has not been reliably quantified. In the present model, the connection strengths were estimated based on data found in literature regarding the degree of connectivity between various nuclei, and therefore express relative differences for the different connections.

According to Hamani et al. (2004), approximately 69% of STN neurons and 32% of GPe neurons project to the GPi. From this, it has been concluded that the STN exerts a greater influence than the GPe on the GPi. Therefore, the weight of the STN→GPi connection should be greater than the GPe→GPi connection. These pathways have been given strengths of 10 and 3, respectively.

The reciprocal connection from GPi→GPe has been given the same strength as the GPe→GPi connection (3). Approximately 83% of STN neurons project to the GPe, and 84% of GPe neurons project back to the STN (Hamani et al. 2004). Therefore these connections have been given equal strengths (10). Approximately half of striatal neurons project to the GPi and half to the GPe, so the striatal→GPe and striatal→GPi projections have been given equal strength. The number of striatal neurons greatly outweighs the number of GPe and GPi neurons by two to three orders of magnitude, so the strength of these connections has been set to 500.

According to Contreras-Vidal and Stelmach (1995), the parameter values used by the authors were obtained by fitting the model to experimental data. For example, decay rates (A i ) were chosen so as to shape the pattern of average firing rate for each BG cell population to experimental data. In the absence of any other data, the decay rate values of Contreras-Vidal et al. were used in the present research.

In the following equations, A i is the passive decay rate of neural activity, B i is the upper bound of neural activity and D i is the lower bound of neural activity, where ‘i’ represents the nucleus under discussion (i.e. Sr, Gi, Ge, Stn or Th).

The mean firing rate of the striatal projection neurons (Sr) is modelled as:

$$\frac{d}{{dt}}{\text{Sr}}\left( t \right) = - A_{{\text{Sr}}} {\text{Sr}}\left( t \right) + \left( {B_{{\text{Sr}}} - {\text{Sr}}\left( t \right)} \right)\left( {I_{{\text{CorSr}}} \left( {t - \tau _{{\text{CorSr}}} } \right) + I_{{\text{tonicSr}}} } \right) - \left( {{\text{Sr}}\left( t \right) - D_{{\text{Sr}}} } \right)\sum\limits_{\begin{array}{*{20}c} {x \ne {\text{current}}} \\ {{\text{module}}} \\ \end{array} } {{\text{Sr}}_x \left( t \right)} $$
(1)

where I CorSr is an excitatory input from the cortex, I tonicSr represents the level of tonic activity within the striatum, and ΣSr x (t) represents the inhibition by axon collaterals from striatal neurons in neighbouring motor modules, i.e., lateral inhibition.

The mean firing rate of the output nucleus of the BG, the GPi (Gi), which corresponds to the ‘GO’ signal sent to the thalamus, is modelled as:

$$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Gi}}\left( t \right) = - A_{{\text{Gi}}} {\text{Gi}}\left( t \right) + \left( {B_{{\text{Gi}}} - {\text{Gi}}\left( t \right)} \right)10{\text{Stn}}\left( {t - \tau _{{\text{StnGi}}} } \right)} \\ { - \left( {{\text{Gi}}\left( t \right) - D_{{\text{Gi}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGi}}} } \right) * {\text{Nd}}\left( t \right) + 3{\text{Ge}}\left( {t - \tau _{{\text{GeGi}}} } \right)} \right)} \\ \end{array} $$
(2)

where Stn is an excitatory input from the STN, and Sr and Ge are inhibitory inputs from the striatum and GPe respectively, with delays τ StnGi, τ SrGi, and τ GeGi. The striatal inputs are weighted by the amount of neuromodulator (substance P and dynorphin) available for transmission on the direct pathway (Nd). Sr*Nd denotes the coexistence of GABA/substance P/dynorphin neurotransmitters. Synaptic failure of STN efferent projections to the GPi due to DBS was modelled as a decrease in the weight of the STN input to the GPi.

The mean firing rate of the GPe (Ge) is modelled as:

$$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Ge}}\left( t \right) = - A_{{\text{Ge}}} {\text{Ge}}\left( t \right) + \left( {B_{{\text{Ge}}} - {\text{Ge}}\left( t \right)} \right)10{\text{Stn}}\left( {t - \tau _{{\text{StnGe}}} } \right)} \\ { - \left( {{\text{Ge}}\left( t \right) - D_{{\text{Ge}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGe}}} } \right) * {\text{Ni}}\left( t \right) + 3{\text{Gi}}\left( {t - \tau _{{\text{GiGe}}} } \right)} \right)} \\ \end{array} $$
(3)

where Stn is an excitatory input from the STN, and Sr and Gi are inhibitory inputs from the striatum and GPi respectively, with delays τ StnGe, τ SrGe, and τ GiGe. The striatal inputs are weighted by the amount of neuromodulator (enkephalin) available for transmission on the indirect pathway (Ni). Sr*Ni denotes the coexistence of GABA/enkephalin neurotransmitters. Synaptic failure of STN efferent projections to the GPe due to DBS was modelled as a decrease in the weight of the STN input to the GPe.

The mean firing rate of the STN (Stn) is modelled as:

$$\frac{d}{{dt}}{\text{Stn}}\left( t \right) = - A_{{\text{Stn}}} {\text{Stn}}\left( t \right) + \left( {B_{{\text{Stn}}} - {\text{Stn}}\left( t \right)} \right)\left( {I_{{\text{CorStn}}} + I_{{\text{tonicStn}}} } \right) - \left( {{\text{Stn}}\left( t \right) - D_{{\text{Stn}}} } \right)10{\text{Ge}}\left( {t - \tau _{{\text{GeStn}}} } \right)$$
(4)

where I CorStn is the hyperdirect pathway excitatory input from the cortex, I tonicStn represents the tonic activity of the STN, and Ge is an inhibitory input from the GPe with delay τ GeStn.

The mean firing rate of the thalamus (Th), the target of BG output, is modelled as:

$$\frac{d}{{dt}}{\text{Th}}\left( t \right) = - A_{{\text{Th}}} {\text{Th}}\left( t \right) + \left( {B_{{\text{Th}}} - {\text{Th}}\left( t \right)} \right)I_{{\text{tonicTh}}} - \left( {{\text{Th}}\left( t \right) - D_{{\text{Th}}} } \right)0.5{\text{Gi}}\left( {t - \tau _{{\text{GiTh}}} } \right)$$
(5)

where I tonicTh represents the level of tonic activity within the thalamus and Gi is an inhibitory input from GPi neurons with delay τ GiTh.

Striatal neurotransmitters have a modulatory effect on the activity of the direct and indirect pathways. This modulation has a medium-term effect (i.e. the effect unfolds over hundreds of milliseconds and may last a minute or more) on neural activity in the BG, which is consistent with the metabotropic action of DA (McGeer and McGeer 1989). The dynamics of neurotransmitter levels in the striatum were modelled using differential equations to account for the accumulation and depletion processes that occur during movement. The neurotransmitter dynamics on the direct and indirect pathways respectively are:

$$\frac{d}{{dt}}{\text{Nd}}\left( t \right) = b\left( {B_{{\text{SP/DYN}}} \left( {{\text{DA}}} \right) - {\text{Nd}}\left( t \right)} \right) - c * {\text{Sr}}\left( t \right) * {\text{Nd}}\left( t \right)$$
(6)
$$\frac{d}{{dt}}{\text{Ni}}\left( t \right) = b\left( {B_{{\text{ENK}}} \left( {{\text{DA}}} \right) - {\text{Ni}}\left( t \right)} \right) - c * {\text{Sr}}\left( t \right) * {\text{Ni}}\left( t \right)$$
(7)

where Nd and Ni are the amount of neurotransmitter available for signalling in the direct (substance P and dynorphin), and indirect pathway (enkephalin), respectively; b is the re-accumulation rate of neurotransmitter, and c is the neurotransmitter depletion constant. B SP/DYN(DA) and B ENK(DA) are the maximum amount of neurotransmitter in the direct and indirect pathway, respectively, and Sr is the striatal activity.

The maximum amount of neurotransmitter available on each of the striato-pallidal pathways varies non-linearly with the concentration of striatal DA (DA), according to:

$$B_{{\text{SP/DYN}}} \left( {{\text{DA}}} \right) = {\text{DA}}^2 $$
(8)
$$B_{{\text{ENK}}} \left( {{\text{DA}}} \right) = 1 + e^{ - 4.6{\text{DA}}} $$
(9)

Figure 3 shows the DA-dependencies of B SP/DYN and B ENK.

Fig. 3
figure 3

The maximum amount of neurotransmitters available in direct (B SP/DYN) and indirect (B ENK) pathway as a function of the concentration of striatal dopamine (DA). DA = 1 (100%) means no loss of dopamine; DA < 1 (<100%) means dopamine depletion. Dopamine depletion produces increases in dopamine D2 receptors and decreases in dopamine D1 receptors in the two subpopulations of striatal neurons, which match an increase in enkephalin expression (increased by 100% at DA = 0), and the decrease in substance P expression (decreased to 0 at DA = 0) in the striatum, respectively

Full size image

The majority of BG neurons are activated before the onset of movement, but after agonist muscle activity. Thus, they are unlikely to be involved in the initiation of movement. Instead, it is hypothesised that BG neurons are responsible for the facilitation, gating or scaling of cortically initiated movement. As explained in Section 2.1, motor cortical neurons are responsible for signalling higher-level movement parameters related to limb trajectory to the spinal cord, as well as lower-level parameters such as muscle force. The Vector-Integration-To-Endpoint or VITE model as described in detail by Bullock and Grossberg (1988) was used to generate a movement trajectory that could be used to verify the output of the model by movement experiments. The VITE circuit models motor cortical operations performed during arm pointing movements, and generates an outflow signal, representing the desired arm trajectory, which is sent to the lower spinal centres.

The inclusion of the VITE circuit in the model has the advantage of allowing the actual movement trajectory to be observed, rather than just the firing rates of the nuclei. The trajectory can be used to determine whether or not the BG output was sufficient to complete the movement, or whether additional bursts of activity are required, allowing the simulation of sub-movements.

Input to the VITE circuit, indicating the target position of the current movement to be performed, originates in the SMA. The movement may involve only a single segment or may be part of a complex sequence of moves. For sequential movements, the movement plan consists of a sequence of motor subprograms, specified in terms of a sequence of Target Position Vectors (TPVs). The VITE circuit automatically translates the target-position command into a complete movement trajectory via a mechanism of continuous vector updating and integration. In the model, each motor program is loaded into the TPV, which specifies the desired target location for the limb movement. The TPV is continuously compared with the Present Position Vector (PPV) to compute a Difference Vector (V), which codes information about the direction and magnitude of the desired movement.

$$\frac{d}{{dt}}V\left( t \right) = 25\left( { - V\left( t \right) + {\text{TPV}} - {\text{PPV}}\left( t \right)} \right)$$
(10)

V is modulated by the BG-controlled pallido-thalamic signal, which gates the initiation of movement and modulates velocity. PPV is gradually updated in the direction of the vector difference by integrating the outflow command from the pallidal-gated thalamus through time until PPV is equal to TPV, in which case the V will be zero. Updating of PPV is modelled as:

$$\frac{d}{{dt}}{\text{PPV}}\left( t \right) = 5.75{\text{Th}}\left( {t - \tau _{{\text{ThCor}}} } \right)\left[ {V\left( t \right)} \right]^ + $$
(11)

where Th is the pallidal-gated thalamic signal, with a threshold level of 0.713 coinciding with thalamic resting activity in the intact model, and [V]+ = V if V > 0, or zero otherwise. PPV generates an outflow movement command to update the movement trajectory (e.g. onset timing and velocity).

The integration constants for the Difference Vector (V) and Present Position Vector (PPV) equations was set to 25 and 5.75 respectively to fit the modelled velocity data to the experimental movement times obtained in the present research. The output of the VITE circuit is the movement velocity (degrees per second).

All simulations were performed using Matlab version 7.0.1, release 14 (MathWorks™). Equations were numerically integrated using the Matlab ODE solver dde23, which is based on the explicit Runge–Kutta (2,3) pair integration method with a maximum step size of 0.001. The dde23 solver integrates a system of delay differential equations \(y'\left( t \right) = f\left( {t,y\left( t \right),y\left( {t - \tau _1 } \right), \ldots ,y\left( {t - \tau _k } \right)} \right)\), with the constant, positive delays τ 1,…, τ k . Parameter values used in the simulations are described in the “Appendix”. The total time span of simulation was 5 s for elbow flexion, and 6 s for elbow flexion–extension (time = −3 to 2 s and 3 s, respectively); the first 3 s are used to stabilize the system and the results are shown starting from t = 0.(The model code is available on request; contact the corresponding author.)

2.3 Parkinsonian model

The tonic concentration of DA available to the striatum was defined as a constant between 0 and 1, with normal DA levels given a value of 1 (100%), and total DA depletion given a value of 0. PD was modelled as a depletion of striatal DA to 80% (DA = 0.8) or 70% (DA = 0.7) of normal levels. As compensatory mechanisms have not been included in the model, there is not a one-to-one relationship between the actual DA level in parkinsonian patients and the modelled DA level. In patients, symptoms do not become evident until DA levels fall below about 20%. However, in the model, any depletion in DA below the normal level of 1 immediately displays bradykinetic symptoms. Thus, the modelled symptoms at 80% DA levels should correspond to parkinsonian symptoms at about 16% of normal DA levels in reality.

Due to the neuronal plasticity of the brain, several mechanisms are capable, to a certain extent, of functionally compensating for the progressive loss of DA. The extent of this compensation can be seen in the fact that PD symptoms do not become clinically manifest until neuronal death exceeds a critical threshold: about 70–80% of striatal nerve terminals and 50–60% of SNc DA neurons (Bezard et al. 2003). The increased efficiency of residual dopaminergic neurons is sufficient to mask PD symptoms in the early stages (Blandini et al. 2000).

Initially, dopaminergic efficiency is such that the death of a few DA nerve endings does not necessitate any compensatory response. As cell degeneration progresses, adaptive changes occur in the nigrostriatal DA system which attempt to maximise the physiologic effectiveness of the remaining DA neurons so as to maintain extracellular DA concentrations near normal levels despite severe DA neuron loss. The major compensatory nigrostriatal changes that occur, as described by Bezard and Gross (1998), are (1) increased synthesis and release of DA in the surviving DA neurons; (2) reduced uptake of synaptically released DA from the extracellular fluid; (3) increased responsiveness of striatal neurons to DA input from the SNc, and (4) diffusion of released DA over large distances before being eliminated by reuptake. This ‘volume transmission’, which occurs when DA leaves the synaptic cleft, usually only occurs in pathological conditions and is activated by nigral degeneration. The normal mode of DA communication is synaptic transmission.

Romanelli et al. (2005) have proposed that a loss of functional segregation between BG motor modules may occur in PD patients. In the present study loss of segregation was modelled as originating in the striatum, due to the fact that DA loss mainly affects the striatum and it is known that communication exists between different functional striatal areas via lateral inhibition. In order to implement loss of striatal segregation, cortical input is allowed to excite both the desired striatal area and areas in neighbouring modules, corresponding to undesired movements. The loss of striatal segregation propagates through the circuit, affecting the activity of all BG nuclei, and ultimately the thalamus and cortex.

2.4 Deep brain stimulation (DBS) model

The model was extended to allow DBS of the STN to be simulated by inhibition/excitation of various neuronal elements. Due to the comparable effects of high frequency stimulation to a lesion of the nucleus, it appears that DBS of the STN induces a functional inhibition of the stimulated region, and thus to decreased neuronal activity. However, on the basis of physiological principles, one would expect that the effects of DBS are due to excitation of the neural elements (axons, soma) surrounding the tip of the electrode, and thus to increased firing of the axons projecting away from the stimulated region (Montgomery and Baker 2000; Benabid et al. 2002; McIntyre et al. 2004). DBS was investigated according to the following possible mechanisms:

  1. Mechanism 1

    Direct inhibition of the STN cell body is accomplished by I DBS,inh = 1200:

    $$\frac{d}{{dt}}{\text{Stn}}\left( t \right) = - A_{{\text{Stn}}} {\text{Stn}}\left( t \right) + \left( {B_{{\text{Stn}}} - {\text{Stn}}\left( t \right)} \right)\left( {I_{{\text{CorStn}}} + I_{{\text{tonicStn}}} } \right) - \left( {{\text{Stn}}\left( t \right) - D_{{\text{Stn}}} } \right)\left[ {10{\text{Ge}}\left( {t - \tau _{{\text{GeStn}}} } \right) + I_{{\text{DBS,inh}}} } \right]$$
    (12)
  2. Mechanism 2

    Excitation of inhibitory afferent axons projecting to STN by setting a weight factor w DBS,aff = 7:

    $$\frac{d}{{dt}}{\text{Stn}}\left( t \right) = - A_{{\text{Stn}}} {\text{Stn}}\left( t \right) + \left( {B_{{\text{Stn}}} - {\text{Stn}}\left( t \right)} \right)\left( {I_{{\text{CorStn}}} + I_{{\text{tonicStn}}} } \right) - \left( {{\text{Stn}}\left( t \right) - D_{{\text{Stn}}} } \right)\left[ {w_{{\text{DBS,aff}}} 10{\text{Ge}}\left( {t - \tau _{{\text{GeStn}}} } \right)} \right]$$
    (13)
  3. Mechanism 3

    Partial synaptic failure of STN efferent projections to target nuclei by setting a weight factor w DBS,eff = 0.4:

    $$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Gi}}\left( t \right) = - A_{{\text{Gi}}} {\text{Gi}}\left( t \right) + \left( {B_{{\text{Gi}}} - {\text{Gi}}\left( t \right)} \right)w_{{\text{DBS,eff}}} 10{\text{Stn}}\left( {t - \tau _{{\text{StnGi}}} } \right)} \\ { - \left( {{\text{Gi}}\left( t \right) - D_{{\text{Gi}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGi}}} } \right) * {\text{Nd}}\left( t \right) + 3{\text{Ge}}\left( {t - \tau _{{\text{GeGi}}} } \right)} \right)} \\ \end{array} $$
    (14)
    $$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Ge}}\left( t \right) = - A_{{\text{Ge}}} {\text{Ge}}\left( t \right) + \left( {B_{{\text{Ge}}} - {\text{Ge}}\left( t \right)} \right)w_{{\text{DBS,eff}}} 10{\text{Stn}}\left( {t - \tau _{{\text{StnGe}}} } \right)} \\ { - \left( {{\text{Ge}}\left( t \right) - D_{{\text{Ge}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGe}}} } \right) * {\text{Ni}}\left( t \right) + 3{\text{Gi}}\left( {t - \tau _{{\text{GiGe}}} } \right)} \right)} \\ \end{array} $$
    (15)
  4. Mechanism 4

    Excitation of excitatory efferent axons projecting to GPi and GPe by setting the weight factor w DBS,eff = 7 in previous two equations.

  5. Mechanism 5

    Direct excitation of STN cell body by adding an excitatory input I DBS,exc = 20:

    $$\frac{d}{{dt}}{\text{Stn}}\left( t \right) = - A_{{\text{Stn}}} {\text{Stn}}\left( t \right) + \left( {B_{{\text{Stn,DBS}}} - {\text{Stn}}\left( t \right)} \right)\left( {I_{{\text{corStn}}} + I_{{\text{tonicStn}}} + I_{{\text{DBS,exc}}} } \right) - \left( {{\text{Stn}}\left( t \right) - D_{{\text{Stn}}} } \right)10{\text{Ge}}\left( {t - \tau _{{\text{GeStn}}} } \right)$$
    (16)

    In this situation the upper limit of the STN firing rate (B Stn,DBS) is set at 200 spikes per second, since it is known that STN neurons are capable of firing at frequencies beyond their normal frequency range when stimulated at high frequencies (Nakanishi et al. 1987; Bevan and Wilson 1999; Rubin and Terman 2004).

  6. Mechanism 6

    Orthodromic excitation of efferent nuclei (GPi and GPe) by adding input I DBS,exc,eff = 20:

    $$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Gi}}\left( t \right) = - A_{{\text{Gi}}} {\text{Gi}}\left( t \right) + \left( {B_{{\text{Gi}}} - {\text{Gi}}\left( t \right)} \right)\left[ {10{\text{Stn}}\left( {t - \tau _{{\text{StnGe}}} } \right) + I_{{\text{DBS,exc,eff}}} } \right]} \\ { - \left( {{\text{Gi}}\left( t \right) - D_{{\text{Gi}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGi}}} } \right) * {\text{Nd}}\left( t \right) + 3{\text{Ge}}\left( {t - \tau _{{\text{GeGi}}} } \right)} \right)} \\ \end{array} $$
    (17)
    $$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Ge}}\left( t \right) = - A_{{\text{Ge}}} {\text{Ge}}\left( t \right) + \left( {B_{{\text{Ge}}} - {\text{Ge}}\left( t \right)} \right)\left[ {10{\text{Stn}}\left( {t - \tau _{{\text{StnGe}}} } \right) + I_{{\text{DBS,exc,eff}}} } \right]} \\ { - \left( {{\text{Ge}}\left( t \right) - D_{{\text{Ge}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGe}}} } \right)*{\text{Ni}}\left( t \right) + 3{\text{Gi}}\left( {t - \tau _{{\text{GiGe}}} } \right)} \right)} \\ \end{array} $$
    (18)
  7. Mechanism 7

    Antidromic excitation of afferent nucleus (GPe) by adding input I DBS,exc,aff = 20:

    $$\begin{array}{*{20}c} {\frac{d}{{dt}}{\text{Ge}}\left( t \right) = - A_{{\text{Ge}}} {\text{Ge}}\left( t \right) + \left( {B_{{\text{Ge}}} - {\text{Ge}}\left( t \right)} \right)\left[ {10{\text{Stn}}\left( {t - \tau _{{\text{StnGe}}} } \right) + I_{{\text{DBS,exc,aff}}} } \right]} \\ { - \left( {{\text{Ge}}\left( t \right) - D_{{\text{Ge}}} } \right)\left( {500{\text{Sr}}\left( {t - \tau _{{\text{SrGe}}} } \right) * {\text{Ni}}\left( t \right) + 3{\text{Gi}}\left( {t - \tau _{{\text{GiGe}}} } \right)} \right)} \\ \end{array} $$
    (19)

    In all seven simulations, DA was set to 0.7 to simulate severe Parkinsonism. For those mechanisms that improved the PD symptoms the parameters related to DBS were chosen such that the movement trajectory resembled the trajectory of the intact model best.

2.5 Testing the model

The model was tested with both a simple 90° elbow flexion movement (TPV = 90) and a complex sequential movement, consisting of a 90° elbow flexion followed immediately by a 90° elbow extension (TPV = 90, and TPV = −90, respectively). The ultimate goal of each simulated movement was to reach the assigned target. Movement was initiated by a burst of cortical input to the striatum of module 1, consisting of a signal of magnitude 25 spikes per second, input at a time of 0.1 s, for a duration of 1 s. Movement was not required in module 2 during the simple movement, so no cortical input was assigned to the striatum of this module. For the complex movement a burst of cortical input was applied to the striatum of module 1, and sequentially to the striatum of module 2, in both cases consisting of a signal of magnitude 25 spikes per second. The end of the burst to module 1 and the start of the burst to module 2 was determined by the moment the velocity induced by module 1 was reduced to 15°/s. For both movements the STN received a cortical signal to both modules, corresponding to the more widespread effect of the STN projections. The STN signal was the same magnitude and duration as the corticostriatal input. Cortical inputs to the BG and Target Position Vectors (TPVs) are illustrated in Figs. 4 and 6 for the simple and complex movement, respectively.

Fig. 4
figure 4

Cortical input into module 1 (a), and module 2 (b) for the intact (broken line) and parkinsonian (solid line) model. Striatum as well as STN receive the cortical input, however, striatum receives the input with a delay of 30 ms. Due to loss of functional segregation in the parkinsonian situation module 2 also receives part of the input. The resulting GPi activity in module 1 (c) and module 2 (d) show a reduced facilitation of desired movement and reduced suppression of unwanted movement in the parkinsonian model following dopamine loss and loss of functional segregation, resulting from a reduced inhibition in module 1 and a slight inhibition of module 2, respectively. N.B. Cortical input continues for 1 s in both models, however, any input after movement has completed has no effect on velocity output. In reality, cortical input would stop (see Fig. 6)

Full size image

PD was modelled as a depletion of striatal DA to 80% of normal levels (DA = 0.8), combined with a loss of functional segregation between the active and inactive modules. The normal and parkinsonian models were first compared for a simple movement, and the extra deficits observed in the parkinsonian model during execution of the complex movement were then examined. In addition, several mechanisms of deep brain stimulation (DBS) were explored during the performance of a simple movement in the parkinsonian model to determine their ability to improve the symptoms of bradykinesia. These simulations were performed with a lower DA level of 70% (DA = 0.7), as DBS is normally performed in the more advanced stages of PD. The input to the model in all cases was a single burst of cortical activity to the striatum and STN.

A sensitivity analysis was performed for the intact model in order to determine whether any of the parameters has a disproportionately large effect on the system, or whether any had no effect at all. The sensitivity of the thalamic output was investigated for changes in each of the parameter values within a range of 10% above and below the values that were used. It was concluded that the thalamus was not particularly sensitive to changes in any one parameter.

2.6 Experimental verification

A series of movement experiments were carried out to provide an initial high-level verification of the computational model and to substantiate some of the model assumptions. The experiments were performed in the Medisch Spectrum Twente (MST), Enschede, and were approved by the ethical committee (METC) of the MST. Kinematic, electromyographic (EMG) and movement time data were collected in a series of four experiments, ranging in complexity from a simple single-joint movement to a sequential double-joint movement. The first experiment was a simple single-joint 90° elbow extension, while the second was a sequential single-joint movement, consisting of a 90° elbow flexion followed immediately by a 90° elbow extension. Two additional experiments were performed: the third experiment was a single-segment, double-joint movement involving a simultaneous elbow extension and horizontal shoulder flexion, and the fourth experiment consisted of two double-joint movements in sequence, an elbow flexion and shoulder extension followed by an elbow extension and shoulder flexion. Three PD patients (1: male age 50, 2: male age 59, 3: female age 59), and three age-matched control subjects (1: male age 50, 2: male 59, 3: female 60) participated in the experiments. One of the patients was classified as I (patient 1), and two were classified as II on the Hoehn and Yahr scale (Goetz et al. 2004). A visual stimulus (LED flashing on) was provided at random intervals ranging from 3 to 4 s. On presentation of the stimulus, the subject was requested to perform the required movement, completing the action by pressing a button on the measurement box. All subjects performed 20 trials of each of the four experiments.

Kinematic data was obtained using an MT-9 3D acceleration sensor (Xsens™), which was fixed to the back of the subject’s hand. Data was continuously acquired at a rate of 100 Hz throughout the duration of the 20 trials. EMG activity was recorded bipolarly using Ag/AgCl surface monitoring electrodes (3M™ 2259) from the biceps brachii (elbow flexion), the long head of the triceps brachii (elbow extension) and anterior deltoid muscles (horizontal shoulder flexion). During experiments 1 and 2, EMG data was collected from the biceps and triceps; during experiments 3 and 4, data was collected from the biceps and deltoid. Optimal electrode placement, orientation and inter-electrode distance were determined according to the SENIAM guidelines (Hermens et al. 1999). Reference electrodes were placed on the inside of the wrist. EMG data was sampled for 3 s after presentation of the stimulus in experiments 1 and 3, and for 4 s in experiments 2 and 4, at a rate of 2000 Hz. The data was pre-amplified at a gain of 5000. Kinematic and EMG data were synchronised using an external trigger signal.

Kinematic data of each trial was band-pass filtered with a dual pass Butterworth filter, having a low cut-off frequency of 0.5 Hz to remove the gravitational acceleration component and a high cut-off of 30 Hz to remove the upper unwanted frequencies. The data was then numerically integrated to obtain velocity (m/s). All EMG data was extracted and rectified. The power density function of surface EMG signals has negligible contributions outside the range 5–10 Hz to 400–450 Hz (Merletti 1999). Therefore, the rectified data was band-pass filtered with a dual pass Butterworth filter, having a pass band of 5 to 450 Hz. Smoothing was performed with a second-order low-pass Butterworth filter, with a cut-off frequency of 25 Hz. As the experimental verification was a pilot study, the results were analysed only to a level of detail sufficient for the current purpose.

3 Results

In this section, the computational results of the simulated elbow movements are presented, along with the results of the experimental verification.

3.1 Mathematical model

3.1.1 Simple movement

The simulated 90° elbow flexion was performed by module 1 (active module), while module 2 represented antagonist muscles (inactive module), which should be suppressed to prevent interference with the desired movement. PD was modelled as a reduction of DA to 80% (DA = 0.8) of normal levels as well as a loss of functional segregation between the two modules.

In the intact model, GPi activity in the active module decreased during movement, disinhibiting the thalamus and allowing the elbow flexion to proceed, as seen in Fig. 4. In the inactive module, GPi activity increased slightly, further inhibiting the thalamus and thus suppressing unwanted movements. In the parkinsonian case, the amount of disinhibition by the GPi was reduced in the active module, resulting in less facilitation and thus slower movements. In the inactive module, GPi activity decreased slightly, resulting in a slight facilitation rather than a suppression of unwanted movements, i.e. co-contractions.

The resulting velocity profiles, as seen in Fig. 5(a), indicate that the movement time increased from 480 ms in the intact model to 624 ms in the parkinsonian model and the peak angular velocity decreased compared to the intact model. Figure 5(b) the elbow joint angle is shown. In all simulations, the start and end of movement is defined as the time when the velocity first exceeds/goes below 15°/s.

Fig. 5
figure 5

(a) Increased movement time and lower peak angular velocity in the parkinsonian model (DA = 0.8) in contrast to the intact model, i.e. control. A reduction in DA to 70% of normal levels (DA = 0.7) was enough to prevent the action from being fully executed in one smooth movement. (b) Elbow joint angle in parkinsonian and intact model. In order to complete the movement at DA = 0.7 additional cortical inputs need to be applied (not shown)

Full size image

Simulations revealed that the more reduced level of DA had a profound effect on the ability to execute the required movement. A reduction in Dopamine to 70% (DA = 0.7) resulted in an abrupt interruption of the movement. The velocity profile as well as the elbow joint angle for this situation is included in Fig. 5(a) and (b), respectively. Multiple pulses would be required to complete the movement.

3.1.2 Complex movement

The simulated complex movement was a sequential task involving a 90° elbow flexion followed immediately by a 90° elbow extension (TPV = 90, and −90, respectively). Module 1 was activated during the elbow flexion, while module 2 was activated during the elbow extension. Each segment of the movement was initiated by a burst of cortical activity, input to the striatum of the relevant module. Cortical input was removed when the movement segment was complete. Inputs to the striatum of both modules in the PD and control scenarios are illustrated in Fig. 6. PD was modelled as a reduction of DA to 80% of normal levels as well as a loss of functional segregation between the two modules.

Fig. 6
figure 6

Inhibition of GPi is reduced in the second segment of a sequential movement in PD patients compared to the first segment

Full size image

In the intact model, an inhibition of GPi activity in module 1 followed by an inhibition in module 2 allowed the flexion/extension movement segments to proceed in turn, with the degree of inhibition being similar for both segments of the movement, as illustrated in Fig. 6. During the inactive phases of each module, GPi activity increased slightly, thereby suppressing unwanted movements. As was the case for the simple movement, the parkinsonian model displayed less facilitation of the desired movement and a slight facilitation rather than suppression of the unwanted movement in each phase of the complex task. In addition, it was observed that GPi activity was inhibited to a lesser degree in the second segment of the movement (module 2 active) than in the first segment, even though the cortical input for both segments was the same.

During execution of the first segment of the movement, an undesired decrease in neurotransmitter levels was observed in module 2 of the parkinsonian model, as illustrated in Fig. 7. This was due to activity in module 2 during its inactive phase resulting from a loss of segregation between the two modules. As the second segment of the movement was initiated immediately after completion of the first segment, the neurotransmitters did not have sufficient time to re-accumulate to normal levels.

Fig. 7
figure 7

In the parkinsonian model, neurotransmitter levels in module 2 decrease slightly during execution of the first movement segment, and have not re-accumulated before segment 2 is started

Full size image

In the control situation, both segments of the movement were performed in approximately the same length of time, 480 ms for both the flexion and extension component, as illustrated in Fig. 8. In contrast, the parkinsonian model displayed a significantly increased movement time for the second segment (656 ms), in comparison to the first segment (624 ms). The slower movement during the second segment was caused by the reduced level of neurotransmitter available on activation of module 2.

Fig. 8
figure 8

Angular velocity profiles demonstrating flexion and extension movements of patient vs. control

Full size image

3.1.3 Deep brain stimulation

The model demonstrated that changes in the ‘firing rate’ of BG nuclei induced by several possible DBS mechanisms were capable of transforming the output of the parkinsonian model into a near normal output. Table 3 indicates the effectiveness of the mechanisms that were investigated. Figure 9 shows the simulation results of two DBS mechanisms that result in movement performance comparable to the normal model: A, C, and E showing GPi activity, STN activity, and angular velocity profile, respectively, resulting from excitation of afferent axons; B, D, and F showing GPi activity, STN activity, and angular velocity profile, respectively, resulting from partial synaptic failure. Figure 10 shows the ineffectiveness of orthodromic excitation of GPi and GPe. In this situation bradykinesia is worsened such that repetitive output from basal ganglia would be required to complete the movement. In Figs. 9 and 10 the curves for the intact model and the parkinsonian model (DA = 0.8) are included in each graph.

Fig. 9
figure 9

GPi activity (a, b), STN activity (c, d), and angular velocity (e, f), resulting from simulation of the parkinsonian model (DA = 0.7) including DBS mechanism 2 (excitation of afferent axons), and 3 (partial synaptic failure), respectively. In addition, the curves for the intact model (control) and the parkinsonian model (DA = 0.8) are included in each graph

Full size image
Fig. 10
figure 10

The angular velocity profile resulting from the simulation of parkinsonian model (DA = 0.7) including DBS mechanism 5 (excitation of efferent nuclei, GPe and GPi). In addition, the curves for the intact model and the parkinsonian model (DA = 0.8) are included in each graph

Full size image
Table 3 Possible DBS mechanisms and their effects
Full size table

3.1.4 Lateral inhibition and hyperdirect pathway

The effects of lateral inhibition and the inclusion of the hyperdirect pathway in the model were investigated. The main observed benefit of striatal lateral inhibition was its focusing effect on the desired movement via suppression of movement in undesired modules. The hyperdirect pathway also demonstrated its beneficial effects in the inhibition of undesired movements in the inactive module, preventing interference with the desired movement, in agreement with the role of the hyperdirect pathway in the widespread inhibition of movement in competing modules, as proposed by Nambu et al. (2002).

3.2 Experimental verification

In all four experiments, PD patients took longer to complete each movement and reached lower peak velocities than the age-matched control subjects, an example of which is illustrated in Fig. 11. The difference in movement time between patients and controls in the simple single-joint movement was quite small, with patients requiring an average of 8% longer than controls. However, the more complex experiments involving a double-joint movement of the elbow and shoulder showed a much larger difference, with patients requiring on average 81% longer than controls to complete the movement. The reduced peak velocity of patients was also more obvious in double-joint than in single-joint movements.

Fig. 11
figure 11

Sample mean velocity profiles averaged over 20 trials for an elbow flexion/extension movement, comparing patient 3 to control 3. The patient (solid line) took longer to complete the movement and exhibited lower peak velocities than the age-matched control (dotted line)

Full size image

One of the patients in the more advanced stages of PD demonstrated particular difficulties in the performance of double-joint movements, requiring several sub-movements to complete each task. In both the single-segment movement and in each segment of the two-segment movement, two main peaks were present in the velocity curve, instead of the expected single peak.

It was observed that PD patients tended to build up to a peak of EMG activity more slowly than control subjects and had a more irregular EMG pattern, with many separate bursts of activity during movement. In several trials, patients demonstrated muscular co-contraction during execution of the elbow flexion/extension movement. A sample trial is illustrated in Fig. 12, in which the EMG activity of one of the patients is compared to the EMG activity of one of the control subjects. The control subject demonstrated an increased biceps activity at the start and end of elbow flexion and an increased triceps activity during elbow extension whereas the parkinsonian subject demonstrated a delayed increase in both biceps (agonist) and triceps (antagonist) activity during the elbow flexion segment of the movement, which also indicates co-contraction of antagonist muscles.

Fig. 12
figure 12

Sample trial in which control subject 1 (a) shows increased biceps activity during elbow flexion (segment 1) and increased triceps activity during elbow extension (segment 2), whereas patient 3 (b) shows a simultaneous increase in both biceps and triceps activity

Full size image

4 Discussion

The present research concentrates purely on the motor execution aspects of the BG. The model was fitted to represent elbow flexion and extension, however, it could easily be adapted to represent different movements around different joints, and extended by additional modules to simulate more complex movements, i.e., more than two degrees of freedom.

In addition to the facilitation of desired movements, the model demonstrates that suppression of unwanted movements, as proposed by Mink (1996), may be an important function of the BG. The proposal by Tunstall et al. (2002) that lateral inhibition among medium spiny neurons of the striatum serves to focus neural activity to the desired movement is further strengthened by the model. The model also provides support for the functional role of the hyperdirect pathway in the suppression of unwanted movements that could potentially interfere with the planned action, as proposed by Nambu et al. (2002). Results have shown that the primary deficits in movement arise directly from a degeneration of dopaminergic neurons in the nigrostriatal pathway. Depletion of DA produces smaller-than-normal pallidothalamic gating signals, which fail to sufficiently reinforce cortical input, producing smaller-than-normal movement amplitudes and velocities.

The research also demonstrates the importance of maintaining functional segregation between competing motor modules in the smooth execution of movement. There is ample evidence to suggest that loss of segregation between modules occurs in PD. Physiologically, loss of segregation may originate from the compensatory mechanisms that occur in an attempt to counteract the DA deficiency, such as a larger area of DA diffusion from the surviving neurons, enlarged receptive fields in the striatum, GPi, GPe, STN and thalamus, and increased corticostriatal transmission (Strafella et al. 2005; Romanelli et al. 2005; Pessiglione et al. 2005; Calabresi et al. 2000). Loss of segregation resulting from an enlargement of the receptive fields of striatal neurons is illustrated in Fig. 13. Due to loss of segregation, cortical input which is destined for a particular set of striatal neurons activates not only the desired neurons, but also several neurons in the surrounding motor pathways. Loss of segregation at the striatal level propagates through the entire BG–thalamocortical circuit. The model reveals that a loss of segregation may contribute to bradykinesia due to an inability to fully suppress competing motor programs. Activity in competing modules causes a slight activation of undesired muscles. The simultaneous activation of competing programs may be interpreted as the co-activation of antagonist muscles, which would result in co-contraction of muscles around a particular joint. Co-contraction of opposing muscles creates additional movement difficulties due to the greater effort required by the agonist muscles to overcome the opposing effect of the antagonists. Furthermore, the model shows that increased striatal activity in the undesired module inhibits neural activity slightly in the desired module via striatal lateral inhibition, thereby reducing the ability to facilitate the desired movement.

Fig. 13
figure 13

Normal situation (left) in which functional segregation between modules is maintained, and parkinsonian situation (right) in which loss of segregation originates in the striatum and propagates throughout the BG

Full size image

The model predicts that abnormal neurotransmitter depletion may contribute to the additional delays experienced by PD patients in the execution of complex movements. Abnormal activity in the inactive module, due to a loss of functional segregation, may lead to an excessive depletion of the available neurotransmitters, which can have severe consequences for subsequent movements if the neurotransmitter has not re-accumulated sufficiently before the following movement begins. The continual depletion of neurotransmitters during a long sequence of movements may explain the progressive slowing of each step of the sequence (‘sequencing effect’) observed by Berardelli et al. (2001) and Levy et al. (2002). In order to test the model further, a more advanced stage of PD, simulated by a reduction in DA to 70% of normal levels, was investigated. Results demonstrated that in the more advanced stages of PD, neurotransmitters in a particular module may be depleted to such an extent that further movement by that module is completely prevented until the neurotransmitters have been allowed to re-accumulate to a certain level. This may explain the increased inter-segment delay observed in PD patients between movement segments of a sequential movement (Berardelli et al. 2001; Agostino et al. 2003; Kelly and Bastian 2005).

Based on changes in the firing rate of BG nuclei, the model has demonstrated that stimulation induced inhibition of STN, partial synaptic failure of efferent projections, or excitation of inhibitory afferent axons could explain the beneficial effects of DBS in improving the symptoms of bradykinesia. The underlying methods of action may be quite different for the different mechanisms. For example, although both mechanisms as shown in Fig. 9 produced a decrease in GPi activity, the methods of action were quite different. Stimulation of the afferents [Fig. 9(a), (c), and (e)], which is assumed to cause a release of the inhibitory GABAergic neurotransmitter, resulted in a decrease in STN activity. Increased axonal firing rate combined with a decrease in STN cell body firing rate is a realistic scenario due to the possibility of functional decoupling between the cell body and axon of a nucleus (McIntyre et al. 2004). On the other hand, stimulation of the efferents [Fig. 9(b), (d), and (f)], which is assumed to cause synaptic failure due to an inability of the stimulated neurons to follow the rapid train of electrical stimuli produced by DBS, resulted in an increase in STN activity. However, according to Rubin and Terman (2004), the STN is capable of following the rapid train of stimuli produced by DBS. According to the model simulations, a direct inhibition of STN cell body firing could also be a possible mechanism of action of DBS, whereas an improvement in PD symptoms by a direct excitation of the STN cell body could not be explained by the firing rate model. Further investigations are required to determine whether the STN cell body is directly stimulated by DBS, and if so, whether stimulation causes an increase or decrease in the firing rate.

In general, DBS shifts the firing rates up or down, depending on the mechanism. In the model firing rates were prevented to exceed non-physiological values: the upper levels of firing rate were set by Dx; the lower bound was zero in all cases. A higher amplitude of the stimulation pulses in general means that the volume that is affected by stimulation is increased, and thus the number of neurons and/or axons that are responding to stimulation is increased. A decrease (inhibitory effect) or increase (excitatory effect) in average firing rate may be the result of an increase in the number of cells/axons responding to stimulation and a high firing rate of these cells/axons induced by high frequency stimulation (~130 Hz). These two effects were included in the parameters that were used to investigate the different mechanisms. While the firing rate of the neuronal cell types were kept within their physiological range, the number of cells or axons that were required to respond to stimulation may be larger than the number of cells or fibers that are physically present within the particular module in order to obtain a movement trajectory and velocity profile similar to the intact model for mechanism 1 to 3.

The mechanism of DBS may also be due to a change in the firing pattern of nuclei rather than a change in the firing rate. Rubin and Terman (2004) presented a network model, consisting of single compartment conductance based models of STN, GPe, GPi and thalamus. In this model the thalamus is simplified into a relaying station whose role it is to respond faithfully to incoming sensorimotor signals, while this function is disturbed by rhythmic GPi firing under parkinsonian conditions. According to their simulation the mechanism of DBS may be a replacement of the pathological firing pattern with high frequency firing. Although the results presented are insightful, the model is based on numerous assumptions (Rubin and Terman 2004; Pascual et al. 2006). The therapeutic mechanisms that underlie DBS, however, most likely represent a combination of several phenomena (McIntyre et al. 2004; Benabid et al. 2002).

The proposed somatotopic organisation of the STN (e.g. as proposed by Nambu et al. 2002) indicates the relevance of viewing the basal ganglia as a system consisting of multiple modules. These modules may be affected differently by DBS and may therefore be relevant for optimal positioning of the electrode in the STN.

As expected, when a simple movement was simulated with PD modelled only as a depletion of DA, with no loss of functional segregation, the results produced were similar to those obtained by Contreras-Vidal and Stelmach (1995). The results of the present model can also be compared to the action selection model of Gurney et al. (2001a, b), in which one of several competing actions (comparable to modules in the present study) is selected based on varying cortical inputs. However, the model of Gurney et al. (2001a, b) does not incorporate much of the known physiological data regarding the BG, in particular the changes in neurotransmitter dynamics on the direct and indirect pathways that occur during movement and following loss of DA. Furthermore, the performance of complex movements in comparison to simple movements is not investigated.

Results of the movement experiments provided an initial verification of the model output. Similar trends in movement time and peak velocity were observed in the simulated and experimental data. While PD patients were slower than controls in both simple and complex movement experiments, the slowness became much more noticeable as the complexity of the tasks increased. The greater increase in movement time and decrease in peak velocity, observed in the execution of double-joint movements by parkinsonian patients compared to controls, verifies the premise of the model that complex movements are more affected than simple movements in PD. The presence of sub-movements in the double-joint movements but not in the single-joint movements of one of the parkinsonian patients further indicates the greater difficulty of patients in executing more complex movements. The sub-movements may result from a deliberate decision to reduce the velocity mid-way through the movement in order to accurately arrive at the target, or the initial muscle activation may not have been sufficient to reach the target in one movement, requiring a second movement to complete the task. Co-contraction of the agonist and antagonist muscles, as predicted by the model, was also observed in parkinsonian patients during execution of the elbow flexion/extension movement.

4.1 Experimental and model limitations

The experimental study was limited by the small size of the population, making it difficult to obtain statistically significant results. In addition, all of the patients who took part in the study were taking medication at the time of the experiments, which presumably masked the symptoms. While the modelled velocity output is qualitatively comparable to the experimental results, the shape of the velocity curve in the deceleration phase is much more gradual in the model than was observed in reality. This is due to the VITE model simplification, which assumes that movements are very accurately aimed, and therefore have a much longer deceleration than acceleration phase. However, in the experimental study, movements were performed as fast as possible, and therefore do not demonstrate a gradual slowing to the target.

The present model implements only the primary motor cortex (M1) related aspects of BG processing. Beiser and Houk (1998) propose that the BG use input from the supplementary motor area (SMA) to determine the next movement in the sequence, and use this information to prepare the cortex for subsequent movements. A dysfunction in SMA-related areas of the BG could result in a deficit in the preparation of the next movement in the sequence. The current implementation of BG processing may need to be expanded to include SMA-related processing in order to fully explain the additional deficits observed in the performance of complex movements by PD patients.

Compensatory mechanisms that occur in the BG following dopaminergic denervation have largely been ignored in the model. Therefore, PD symptoms become evident in the model with only a small loss of DA, whereas in reality symptoms are not clinically manifest until about 70–80% DA depletion. In addition, dopaminergic projections from the SNc to the STN and GPi have not been included in the model. The direct effect of dopamine loss on the STN and GPi may be important in the pathogenesis of PD.