Abstract
Objectives
Evolutionary theory predicts grandmothers to invest more in their daughter’s children than in their son’s children, because of the higher likelihood of being genetically related to their daughter’s children. At the same time, most African cultures are characterized by male dominance, which might make it more profitable to invest in sons than in daughters. Here, the relative importance of paternal versus maternal grandmothers for children’s schooling is studied as well as how this grandmother gender effect varies across circumstances.
Methods
The importance of paternal versus maternal grandmothers for children’s schooling is studied using multilevel logistic regression analysis on data for 896,073 children aged 7–15, living in 33 sub-Saharan African countries. We control for demographic and socio-economic factors at household and context level and study the role of circumstances using interaction analysis.
Results
Children living with a paternal grandmother have a higher chance of being in school than children living with a maternal grandmother. This effect is larger for boys, when the father is higher educated and when a grandfather is present. It is reduced when mother’s education level is higher.
Conclusions
Children living with a paternal grandmother have better schooling outcomes relative to those living with a maternal grandmother. This advantage of living with a paternal grandmother is stronger for boys and when the father is higher educated. Male dominance as a cultural factor seems to be more important for grandmother’s investments than certainty about genetic relatedness. Only a higher education level of the mother seems to counterbalance this tendency to a certain extent.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
In recent years, several studies have paid attention to the importance of grandmothers for their grandchildren’s well-being in sub-Saharan African (SSA) countries (e.g., Duflo 2003; Lachaud et al. 2017; Lu and Treiman 2011; Parker and Short 2009; Schrijner and Smits 2018a, 2018b). This is highly relevant, as in these countries extended household structures with three generations living under one roof are still common practice. In about 16% of the households in the SSA region a grandmother is co-residing (Schrijner and Smits 2018a).
Grandmothers are generally thought to be good caretakers and expected to contribute in a positive sense to the success in life of their young grandchildren. According to the classical grandmother theory the prolonged survival of women after their fertile ages has developed as a positive trait during human evolution. It offers them the possibility to increase their own reproductive success by helping their children raising their children (e.g., Hawkes et al. 1997; Hawkes 2004; Hrdy 1999, 2009; Sear and Mace 2008). For example in Ethiopia non-reproductive grandmothers were positively associated with child height (Gibson and Mace 2005) and in rural Gambia the presence of grandmothers doubled the survival chances of a Mandinka child (Sear et al. 2000). In particular, grandmothers are supposed to help their daughters during their fertile ages, when they face the workload of raising multiple children (Coall and Hertwig 2010; Hawkes 2003, 2004; Sear and Mace 2008).
Evolutionary theory has often been used to explain grandparental investment in general, and—more specifically—differences in investment between the maternal and paternal grandmother (e.g., Gaulin and Schlegel 1980; Strassmann and Garrard 2011; Bishop et al. 2009; Euler and Michalski 2007; Laham et al. 2005). A major expectation in this respect is that grandparental investment depends on the likelihood of being genetically related to a certain grandchild. This expectation is called the confidence of paternity hypothesis (Gaulin and Schlegel 1980; Strassmann and Garrard 2011). The idea behind this hypothesis is that grandparental investment depends on the likelihood of being genetically related to a certain grandchild. As is explained in Fig. 1, the likelihood of being genetically related to a grandchild is higher for the maternal grandmother than for the paternal grandmother. Mother’s mother knows for certain that her daughter is her daughter and that her grandchild is her descendant. For her there are no uncertain generational links (arrows 1a and 1b). Father’s mother is also certain that her son is her son (arrow 2a). However she is less certain that her grandchildren are genetically related to her, because her son might be cuckolded by her daughter in law. There is thus an uncertain generational link (arrow 2b). Because of this uncertainty regarding whether her son’s children bear her genes, the paternal grandmother might be less willing to invest in her grandchildren than the maternal grandmother. The willingness to invest in her son’s children is expected to further diminish when the paternal grandmother has grandchildren through her daughter as well. She might then invest more in the offspring of her daughter than in the children of her son, because there are no uncertain generational links.
It remains to be seen, however, whether this genetic mechanism—if it exists—is strong enough to overcome the effect of other factors. Research does not unequivocally support a certain direction in the relation between grandchild investment and grandmother’s lineage. Some studies show indeed stronger effects of the presence of maternal grandmothers (Sear et al. 2000; Voland and Beise 2002), but others find no differences (Beise 2005; Gibson and Mace 2005), or even a more positive effect of the presence of paternal grandmothers (Borgerhoff Mulder 2007; Sear 2008). Paternity uncertainty is reduced by the fact that human mating generally takes place in a family context, whereby both males and females give up external mating opportunities in exchange for fitness gains through investments into long-run parental care (Gavrilets 2012; Korn 2000; Vyrastekova et al. 2014).
There are also indications that maternal grandmothers are more important in industrialized societies and paternal grandmothers in traditional societies (Coall et al. 2018; Kaptijn et al. 2013; Snopkowski and Sear 2015). Many traditional societies are patriarchally oriented, with sons being considered more important than daughters. This preference for sons over daughters appears for instance in restriction of land ownership to men, poor inheritance rights of women, restrictions on the possibilities of women to move freely in the public domain and difficulties experienced by them in filing claims through the judicial system (Cooper 2012; International African Institute 1950; Jütting et al. 2008; Richardson 2004; UNICEF 2006; Smits and Gündüz-Hosgör 2006). This could led grandmothers to invest more in their son’s children than in their daughter’s children, even though they are less sure that his children are genetically related to them. This social dominance of males over females—and the social prestige associated with having sons—might make it more socially rewarding for grandmothers to invest in offspring of her son(s) than of her daughter(s), even though the genetic relatedness is less certain. Hence, according to the male dominance hypothesis, a positive effect of a co-residing grandmother on the schooling of her grandchildren will be stronger for her sons’ children than for her daughters’ children.
Besides paternity uncertainty and male dominance, differences between paternal and maternal grandmothers might also be influenced by circumstances in which a household is living. An important perspective in this respect is the Trivers–Willard hypothesis (Trivers 1972; Trivers and Willard 1973; Hopcroft 2005), which supposes investments in the male lineage to be larger under resource-rich circumstances and investments in the female lineage under resource-poor circumstances The explanation given for this is that women prefer high status men over low status men when it comes to reproduction, whereas men are more indifferent regarding the status of their partner. Under poor circumstances, low status men will therefore have fewer opportunities to marry, and if they find a partner it might be one with lower reproductive prospects. For low status women, the chances to marry are better, as high status men are less concerned about the status of their wife than high-status women. Under poor circumstances, women might still have the option to become the second or third wife of a wealthy husband instead of becoming the first wife of a poor husband. Investing in daughters and their families might therefore be the best evolutionary strategy for (grand)parents in poor households, whereas investing in sons would be the best strategy for them in wealthy households.
Circumstances of scarcity and resource competition might also affect altruistic behaviour of family members more directly (e.g., Borgerhoff Mulder 2007; Sear and Mace 2008). Borgerhoff Mulder (2007) observed, using within-population variation in land ownership in Kenya, that wealth affects the extent of kin altruism. Paternal relatives (specifically father’s brothers) appear to buffer young children from mortality much more effectively in rich than in poor households. Strassmann (2011) found that under poor circumstances (Dogon in Mali) co-residence of a paternal grandmother was associated with a higher hazard of death of a grandchild by the age of five. One of the explanations given is that in resource-poor societies elderly grandmothers are net-consumers and therefore become competitors with their grandchildren. Strassmann (2011) also noticed that girls sometimes grow slower when they are living with their maternal grandmother. A possible reason is the hard work these girls perform for their maternal grandmothers, like fetching water and weeding the garden.
This study aims to contribute to the literature by testing three hypotheses regarding the effect of co-residence of paternal versus maternal grandmothers on the schooling of their grandchildren. First, the paternity uncertainty hypothesis which predicts maternal grandmothers in SSA to invest more in the schooling of their grandchildren than paternal grandmothers, because maternal grandmothers are more certain about the genetic connection with their grandchildren. Second, the male dominance hypothesis, predicting the positive effect of a co-residing grandmother on the schooling of her grandchildren to be strongest for her son’s children, because under circumstances of male dominance—as is the case in many SSA regions—it is more socially rewarding to invest in children of sons than in children of daughters. Third, regarding the context in which the household is living, the Trivers–Willard hypothesis predicts investments in the male lineage to be higher under resource-rich circumstances and investments in the female lineage to be higher under resource-poor circumstances, because of the asymmetry in marriage chances of women and men in resource-poor versus resource-rich situations.
Method
Participants
To test the hypotheses we use data derived from the Demographic and Health Surveys (DHS; www.dhsprogram.com) made available for this study by the Global Data Lab (www.globaldatalab.org). DHS are large, nationally representative household surveys, sponsored by USAID. We combined datasets of 69 DHS surveys, held between 1998 and 2013 in 33 sub-Saharan African countries. The dataset created in this way contained information on 917,788 children aged 7–15. The individual/household data was supplemented with context information at the DHS sample cluster level (29,925 observations) and the level of urban and rural areas within subnational regions, called ‘districts’ henceforth (1,164 observations). Given the large size of our database, cluster and district variables could be created by aggregating data from the household level. Because of missing cases on the variables parental education, (grand)parental age, polygamy, number of brothers and sisters, wealth, educational participation and some unrealistic cases for (grand)parental age (mothers under 12 and grandmothers under 24 at the children’s birth), in total 21,715 (2.4%) children had to be removed from the initial dataset. Our analysis therefore included 896,073 children, of which 456,265 were boys and 439,808 girls. Additional information about the sample, such as which countries were included and the year in which the surveys were conducted can be found in the Supplementary Materials section. The response rates of DHS surveys are generally very high, over 95% in most countries. The team responsible for conducting the DHS ensures protection of human subjects in agreement with local and international laws.
Procedure
The sampling procedure used for collecting the DHS data consists of two steps. In the first step, in cooperation with local statistical offices, a representative set of sample clusters is selected, consisting of local communities, villages, or city neighborhoods. In the second step, each cluster is visited by an interview team that first prepares a list of all households living in the cluster. From this list subsequently a random sample of 25–30 households is selected. These households first get an oral interview in which basic information is collected on the household and all household members. On the basis of this information, women aged 15–49 are selected for a separate oral interview in which detailed information on socioeconomic, demographic, and health related issues is collected. In the database created for our analyses, information from the household surveys and the women’s surveys is combined.
Measures
The major independent variable is a dummy variable that indicates the difference between the co-residence of a paternal grandmother and the co-residence of a maternal grandmother (chosen as reference category). In the rest of the paper, this variable will be called the grandmother gender effect. When studying the size of this effect, the focus is on the more or less ‘normal’ situation where a grandmother co-resides in the household of (one of her) children. This situation is separated in the analysis from the situation of fostering, where a child is co-residing in the household of the grandmother without its parents being present. This separation is implemented by including an extra ‘fostering’ dummy for this situation. There were 317 children in our sample who were living together with both their paternal and maternal grandmother. Given the very small size of this group (0.03%), these children were left out of the analysis.
Next to the main independent variable, several other variables were included in the analysis to control for demographic and socio-economic factors at the household and context level. As demographic factors at the household level we included the presence of parents, age and sex of the child, age of the parents, age of the grandmother, birth order, number of brothers and sisters, presence of a grandfather. Absence of parents is measured with two dummies for each parent, one indicating whether (1) or not (0) the parent is absent from the household and one indicating whether (1) or not (0) the parent is deceased. Birth order, age of the child, age of its parents and grandmother, and the number of brothers and sisters were measured by interval variables. The presence of a grandfather is measured by a dummy variable.
Socio-economic control factors at the level of the household are wealth, employment and education. Because income is lacking in the data, household wealth was measured by the International Wealth Index (IWI; Smits and Steendijk 2015), a comparative asset-based wealth index. IWI indicates to what extent households own a basic set of assets, valued highly by people across the globe. Education of the mother, father and grandmother is measured in years of education completed. Occupation of the father is measured by three dummy variables: (1) Farm, (2) Lower non-farm (sales, services, manual), (3) Upper non-farm (professional, technical, managerial, clerical). Work status of the mother is a dummy variable indicating whether (1) or not (0) the mother was employed.
To control for the relative position of women at both the household and context level, the age difference between husbands and wives was used, calculated by subtracting the age of the father of that of the mother. The smaller or more positive the age difference, the stronger the relative position of women is supposed to be. For the relative position of women at the context level, the average of the age difference between parents in the district was used. The larger the age difference to the disadvantage of the women in the area, the weaker their position is considered to be.
Other context factors are urbanization, wealth, education and polygamy. Urbanization was measured by a dummy variable indicating whether (1) or not (0) the child lived in a rural area. The context level of development was measured as the mean International Wealth Index score of households in the district. The context variable polygamy is calculated as the percentage of polygamous households in the district. Context education was measured by aggregating the variable years of education to the level of the DHS sample cluster. Kravdal (2006) shows that average cluster-level education can effectively be used to indicate context educational achievement.
Data Analyses
The relative importance of paternal versus maternal grandmothers and the effect on schooling is studied using multilevel logistic regression analysis. Multilevel analysis is used to address the nesting of the households within sample clusters and districts. It is the appropriate method to analyse such clustered data (Khan and Shaw 2011). To control for the nesting within countries fixed effects dummies at the national level are included in the analysis. This strategy allows us to control for clustering and confounding at the national level while retaining the possibility to study the role of context factors at the district and cluster level. In the model the dependent variable comprises educational participation, which is a dummy variable indicating whether (1) or not (0) children aged 7–15 were attending school at the time of the interview. The upper age limit of 15 years was chosen because above that age already a substantial number of children is not living with their parents anymore (e.g. because of early marriage, for educational reasons, or parental death). The lower age limit was set at 7 years to avoid excluding children in countries where many children start schooling later than the compulsory age (Huisman and Smits 2009). Because the dependent variable is dichotomous, it violates the assumption of a normal distribution of errors and of homoscedasticity for OLS regression (Allison 1999; Pampel 2000). Therefore, logistic regression models were applied. The models are estimated with MLwiN, using second-order penalized quasi-likelihood (PQL2), the recommended estimating technique for multilevel logistic regression analysis (Goldstein and Rasbash 1996).
To find out whether the grandmother gender effect differs according to the situation in which the household lives, interactions between the grandmother gender effect and the other independent variables in the model are studied. In this interaction analysis centred versions of these independent variables were used. The coefficients of the grandmother gender effect in the interaction model are thus for an average situation concerning the other variables. Given the explorative nature of the interaction analysis and the potentially large number of interactions, only significant interactions are included in the model. Children with a missing parent or grandparent were given the mean score of the other children on the (grand)parents characteristics. Because dummy variables were included, indicating whether (1) or not (0) the (grand)parent was missing, this procedure leads to unbiased estimates of these variables (Allison 1999; Little and Rubin 2002).
Results
In Table 1 descriptive statistics of our sample are presented. In 16.2% of the cases children aged 7–15 years are living with their grandmother of which 3.3% with their maternal grandmother and 4.6% with their paternal grandmother. In nearly 7% of the cases children are living with their grandfather. At the time of the interview 73% of the children were attending school. The average age of grandmothers in the sample was almost 63 years. For more than 23% of the children the mother was absent or deceased, whereas regarding fathers this accounts for 35% of the children. More than two third of the children were living in a rural area.
The results of the three-level logistic regression models are presented in Table 2. Model 1 contains only main effects. Model 2 contains main effects plus all significant interaction effects. The central variable in the models is the indicator for the grandmother gender effect, which measures the difference in educational participation between children in households with (only) a paternal grandmother and children in households with (only) a maternal grandmother (the reference category). The positive grandmother gender coefficients that can be observed in Table 2 indicate that children in households with (only) a paternal grandmother have significantly higher odds of being in school. The effect is opposite to the prediction of the paternity uncertainty hypothesis: grandmothers seem to support the children of their sons more than those of their daughters. Compared to grandchildren living with a maternal grandmother, the odds of being in school are on average 19% higher for grandchildren living with their paternal grandmother (Model 1).
The dummy for fostering shows a strong significant positive effect, thus indicating that in the generally more extreme situation that no parents are present—e.g. with aids orphans—it is particularly important that a child co-resides in the household of one of its grandmothers. Children without a grandmother in the household are worst off and have a significant lower chance of being in school than children in any of the situations with a grandmother.
The second aim of this study is to shed light on how the strength of the grandmother gender effect is moderated by varying circumstances. To test for this, interactions between the grandmother gender effect and all other household and context variables were estimated. Significant interactions were found with the gender of the child, parental education and the presence of a grandfather in the household. Model 2 includes all significant interactions.
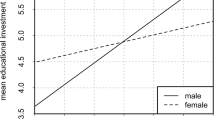
The grandmother gender effect is significantly stronger for boys than for girls. This difference is about 13% to the advantage of boys (odds ratio of interaction with sex is 0.87). Hence boys profit more of living with a paternal instead of a maternal grandmother than girls. Parental education is known to be an important factor in relation to children’s schooling (Huisman and Smits 2009). The interaction analysis makes clear that parental education is also significantly associated with the grandmother gender effect. Interestingly, the grandmother gender effect is negatively related to maternal education and positively to paternal education. This implies that the advantage children have when living with a paternal grandmother becomes larger if their father is higher educated. At the same time, this advantage is smaller when their mother’s education level is higher. The strength of these effects is almost similar. In both cases, an increase of parental education by one year is associated with a change of the grandmother gender effect of about 3%. In Fig. 2, these interaction effects are depicted graphically.
This figure shows that when the father has no education, the grandmother gender effect is close to zero. Indicating that there is no difference in effect on children’s schooling between paternal and maternal grandmothers. As the education level of the father rises, this has a positive impact on the grandmother gender effect: The higher father’s education, the more important the paternal grandmother is for children’s schooling. A higher education level of the mother on the other hand, pushes the grandmother gender effect into the opposite direction. It decreases towards zero and for higher educated mothers it may become even negative, indicating a more positive role for maternal grandmothers compared to paternal grandmothers with respect to children’s schooling.
The last significant interaction effect is with the presence of a grandfather in the household. Given that there are very few cases in the data (less than 0.01% of households with a grandmother) where both a paternal grandmother and a maternal grandfather or a maternal grandmother and a paternal grandfather are living in the same household, the co-resident grandfather is in almost all cases the husband of the grandmother. The presence of a grandfather significantly strengthens the grandmother gender effect, thus indicating that the combination of a paternal grandmother with the paternal grandfather is particularly favourable for children’s schooling.
Discussion
According to the classical grandmother hypothesis the prolonged survival of women after their fertile ages has developed during human evolution, because it offers them the possibility to increase their own reproductive success by helping their daughters raising their children (Hawkes 2004; Hawkes et al. 1997). The expectation that they would invest more in their daughters’ children is based on the so called paternity uncertainty hypothesis. Grandparental investment is supposed to depend on the likelihood of being genetically related to a certain grandchild, which is more certain for maternal than for paternal grandmothers. This hypothesis was tested against the male dominance hypothesis which predicts the effect of a co-residing grandmother on the schooling of her grandchildren to be more positive for her son’s children than for her daughter’s children. As discussed in the introduction, many regions of Africa are characterized by a patriarchal culture in which men, sons and grandsons are considered to be more important than women, daughters and granddaughters (Giovarelli et al. 2013; Jütting et al. 2008; Kandiyoti 1988). In such a culture, the effect of genetic relatedness—if it exists—might easily be overruled by the greater societal importance attached to male offspring.
In addition to paternity uncertainty and male dominance, a third important hypothesis, the Trivers–Willard hypothesis was tested. According to this hypothesis differences in investment between paternal and maternal grandmothers might also be influenced by the circumstances in which the household is living. Because of asymmetry in the marriage chances of males versus females under poor and rich circumstances, investments in the male lineage are expected to be higher under resource-rich circumstances and investments in the female lineage to be higher under resource-poor circumstances.
To test these hypotheses, the importance of co-residing maternal and paternal grandmothers for the educational attendance of young (aged 7–15 years) children was studied by applying multilevel logistic regression analysis on data for 896,073 children in 33 sub-Saharan African (SSA) countries. Our analysis did not provide any support for the paternity uncertainty hypothesis. In fact the opposite effect was observed. Children living with their paternal grandmother are associated with better schooling outcomes relative to those who are living with their maternal grandmother. This result is in line with the prediction of the male dominance hypothesis. It suggests that the preference for sons over daughters in the SSA context is so strong that grandmothers tend to favour their son’s children over their daughter’s children even though the genetic relatedness to their son’s children is less certain.
The importance of male dominance is further supported by two additional outcomes of the interaction analysis. First, it was found that the grandmother gender effect is particularly strong for boys. This implies that grandmothers do not only invest more in their son’s children than in their daughter’s children, but also that they invest more in their son’s sons than in their son’s daughters. Second, the observation that the presence of a grandfather more or less doubles the grandmother gender effect. Given that in almost all cases that the grandfather is the husband of the grandmother, this indicates that grandfathers have a similar tendency as grandmothers to invest more in the children of their sons than in the children of their daughters.
The interaction analysis further revealed that the grandmother gender effect depends on the education level of both parents. The interaction effects with father’s and mother’s education have about the same strength, but work in opposite directions. Father’s education strengthens the grandmother gender effect and mother’s education weakens this effect. This means that the tendency of grandmothers to invest in the children of their sons or their daughters is also influenced by the resources in the form of human capital those sons and daughters have at their disposal. If their sons have more human capital their investments go more into the direction of their son’s children and if their daughters have more human capital they invest relatively more the children of their daughters.
No significant interaction was found between the grandmother gender effect and wealth. Both household and regional wealth did not influence the association between the lineage of grandmothers and the educational participation of their grandchildren. Hence, the Trivers Willard hypothesis is not supported by the findings.
Limitations
Our study has some limitations and therefore caution is required regarding our conclusions. First, our analysis is based on cross-sectional data. Although important new information is obtained on the association between the lineage of grandmothers and children’s schooling, no strict conclusions in terms of causal relationships can be drawn. Second, educational attendance seems to be a rather weak indicator for the educational achievement of grandchildren, as it is not an accumulative investment indicator—like e.g. years of education completed—nor does it say anything about educational quality. This would be a problem in more developed regions, but in the sub-Saharan African region differences in attendance are still highly relevant, as many children do not go to school at all and others drop out early, even before completing primary education (Huisman and Smits 2009, 2015). Third, the results of this study are restricted to children from 7–15 years old living in the SSA region. It remains to be seen to what extent grandmother’s lineage still makes a difference at higher levels of education and in low-income countries in other parts of the world. Patriarchy in SSA is known to differ from patriarchy in other regions. In SSA women are much more economically active than women in for example the Middle East or South and East Asia (Dodoo and Frost 2008; Kandiyoti 1988). Hence, the patterns observed in this study should not be uncritically generalized to other regions. Fourth, a study covering 33 SSA countries provides a birds-eye view of the prevailing patterns of grandmother care on the continent. This has the advantage that broader patterns are discerned much better than with data for one or only a few countries. It has the disadvantage that the unique forms in which the patterns are expressed in specific areas and groups is overlooked. It is therefore important that the current study is supplemented with small scale studies focussing on how the broader pattern found here works out under specific circumstances.
References
Allison, P. (1999). Comparing Logit and Probit Coefficients Across Groups. Sociological Methods & Research, 28(2), 186–208. https://doi.org/10.1177/0049124199028002003.
Beise, J. (2005). The helping grandmother and the helpful grandmother: the role of maternal and paternal grandmothers in child mortality in the 17th and 18th century population of French settlers in Quebec, Canada. In E. Voland, A. Chasiotis & W. Schiefenhövel (Eds.), Grandmotherhood: the evolutionary significance of the second half of female life (pp. 215–238). New Brunswick: Rutgers University Press.
Bishop, D. I., Meyer, B. C., Schmidt, T. M., & Gray, B. R. (2009). Differential investment behavior between grandparents and grandchildren: the role of paternity uncertainty. Evolutionary Psychology, 7(1), 66–77.
Borgerhoff Mulder, M. (2007). Hamilton’s rule and kin competition: the Kipsigis case. Evolution and Human Behavior, 28(5), 299–312. https://doi.org/10.1016/j.evolhumbehav.2007.05.009.
Coall, D. A., Hilbrand, S., Sear, R., & Hertwig, R. (2018). Interdisciplinary perspectives on grandparental investment: a journey towards causality. Journal of the Academy of Social Sciences, 13(2), 159–174. https://doi.org/10.1080/21582041.2018.1433317.
Coall, Da, & Hertwig, R. (2010). Grandparental investment: past, present, and future. Behavioral and Brain Sciences, 33(1), 1–59. https://doi.org/10.1017/S0140525X09991105.
Cooper, E. (2012). Women and Inheritance in Sub-Saharan Africa: what can change? Development Policy Review, 30(5), 641–657.
Dodoo, F. N.-A., & Frost, A. E. (2008). Gender in African Population Research: the fertility/reproductive health example. Annual Review of Sociology, 34(1), 431–452. https://doi.org/10.1146/annurev.soc.34.040507.134552.
Duflo, E. (2003). Grandmothers and granddaughters: old-age pensions and intrahousehold allocation in South Africa. The World Bank Economic Review, 17(1), 1–25. https://doi.org/10.1093/wber/lhg013.
Euler, H. A., & Michalski, R. L. (2007). Grand parental and extended kin relationships. In C. A. Salmon & T. K. Shackelford (Eds.), Family relationships: an evolutionary perspective (pp. 230–255). New York, NY: Oxford University Press.
Gaulin, S. J. C., & Schlegel, A. (1980). Paternal confidence and paternal investment: a cross cultural test of a sociobiological hypothesis. Ethology and Sociobiology, 1(4), 301–309. https://doi.org/10.1016/0162-3095(80)90015-1.
Gavrilets, S. (2012). Human origins and the transition from promiscuity to pair-bonding. Proceedings of the National Academy of Sciences, 109(25), 9923–9928. https://doi.org/10.1073/pnas.1200717109.
Gibson, M., & Mace, R. (2005). Helpful grandmothers in rural Ethiopia: a study of the effect of kin on child survival and growth. Evolution and Human Behavior, 26(6), 469–482. https://doi.org/10.1016/j.evolhumbehav.2005.03.004.
Giovarelli, R., Wamalwa, B., & Hannay, L. (2013). Land Tenure, Property Rights, and Gender Challenges and Approaches For Strenghtening Women’s Land Tenure and Property Rights. USAID Issue Brief, 1–15.
Goldstein, H., & Rasbash, J. (1996). Improved approximations for multilevel models with binary responses. Journal of the Royal Statistical Society, 159(3), 505–513.
Hawkes, K. (2003). Grandmothers and the evolution of human longevity. American Journal of Human Biology, 15(3), 380–400. https://doi.org/10.1002/ajhb.10156.
Hawkes, K. (2004). The grandmother effect. Nature, 428(March), 128–129.
Hawkes, K., O’Connell, J. F., & Blurton Jones, N. G. (1997). Hadza women’ s time allocation, offspring provisioning, and the evolution of long postmenopausal life spans. Current Anthropology, 38(4), 551–577.
Hopcroft, R. L. (2005). Parental status and differential investment in sons and daughters: Trivers–Willard revisited. Social Forces, 83(3), 1111–1136.
Hrdy, S. B. (1999). Mother Nature: a history of mothers, infants, and natural selection. New York: Pantheon.
Hrdy, S. B. (2009). Mothers and others: the evolutionary origins of mutual understanding. Cambridge: Harvard University Press.
Huisman, J., & Smits, J. (2009). Effects of household- and district-level factors on primary school enrollment in 30 developing countries. World Development, 37(1), 179–193. https://doi.org/10.1016/j.worlddev.2008.01.007.
Huisman, J., & Smits, J. (2015). Keeping children in school: household and district-level determinants of school dropout in 363 districts of 30 developing countries. Sage Open, 2015(Oct), 1–38. https://doi.org/10.1177/2158244015609666.
International African Institute (1950). African systems of kinship and marriage. In: A. R. Radcliffe-Brown (Ed.), London: Oxford University Press.
Jütting, J. P., Morrisson, C., Dayton-Johnson, J., & Drechsler, D. (2008). Measuring gender (In)equality: the OECD gender, institutions and development data base. Journal of Human Development, 9(1), 65–86. https://doi.org/10.1080/14649880701811401.
Kandiyoti, D. (1988). Bargaining with patriarchy. Gender and Society, 2(3), 274–290. https://doi.org/10.2307/190357.
Kaptijn, R., Thomese, F., Liefbroer, A. C., & Silverstein, M. (2013). Testing evolutionary theories of discriminative grandparental investment. Journal of Biosocial Science, 45(3), 289–310. https://doi.org/10.1017/S0021932012000612.
Khan, M. H. R., & Shaw, J. E. H. (2011). Multilevel logistic regression analysis applied to binary contraceptive prevalence data. Journal of Data Science, 9(1), 93–110.
Korn, E. (2000). On the formation of family structures. Public Choice, 3–4(1996), 357–372. https://doi.org/10.1023/A:1005198714654.
Kravdal, Ø. (2006). A simulation-based assessment of the bias produced when using averages from small DHS clusters as contextual variables in multilevel models. Demographic Research, 15(1), 1–20. https://doi.org/10.4054/DemRes.2006.15.1.
Lachaud, J., LeGrand, T. K., & Kobiané, J.-F. (2017). Intergenerational transmission of educational disadvantage in the context of the decline of family size in urban Africa. Population Review, 56(1). https://doi.org/10.1353/prv.2017.0004.
Laham, S. M., Gonsalkorale, K., & von Hippel, W. (2005). Darwinian grandparenting: preferential investment in more certain kin. Personality & Social Psychology Bulletin, 31(1), 63–72. https://doi.org/10.1177/0146167204271318.
Little, R. J. H., & Rubin, D. B. (2002). Statistical Analysis with Missing Data. New Jersey: John Wiley & Sons, Inc.
Lu, Y., & Treiman, D. J. (2011). Migration, remittances and educational stratification among Blacks in Apartheid and Post-Apartheid South Africa migration. Social Forces, 89(4), 1119–1143. https://doi.org/10.1353/sof.2011.0063.
Pampel, F. C. (2000). Logistic regression: A primer. London: Sage Publications.
Parker, E. M., & Short, S. E. (2009). Grandmother coresidence, maternal orphans, and school enrollment in Sub-Saharan Africa. Journal of Family Issues, 30(6), 813–836.
Richardson, A. M. (2004). Women’s inheritance rights in Africa: the need to intergrate cultural understanding and legal reform. Human Rights Brief, 11(2), 19–22.
Schrijner, S., & Smits, J. (2018a). Grandmothers and children’s schooling in Sub-Saharan Africa. Human Nature, 29(1), 65–89. https://doi.org/10.1007/s12110-017-9306-y.
Schrijner, S., & Smits, J. (2018b). Grandparents and children’s stunting in sub-Saharan Africa. Social Science and Medicine, 205(Mar), 90–98. https://doi.org/10.1016/j.socscimed.2018.03.037.
Sear, R. (2008). Kin and child survival in rural Malawi. Human Nature, 19(3), 277–293. https://doi.org/10.1007/s12110-008-9042-4.
Sear, R., & Mace, R. (2008). Who keeps children alive? a review of the effects of kin on child survival. Evolution and Human Behavior, 29(1), 1–18. https://doi.org/10.1016/j.evolhumbehav.2007.10.001.
Sear, R., Mace, R., & McGregor, I. A. (2000). Maternal grandmothers improve nutritional status and survival of children in rural Gambia. Proceedings of the Royal Society B Biological Sciences, 267(1453), 1641–1647. https://doi.org/10.1098/rspb.2000.1190.
Smits, A., & Gündüz Hoşgör, J. (2006). Effects of family background characteristics on educational participation in Turkey. International Journal of Educational Development 26(5):545–560. https://doi.org/10.1016/j.ijedudev.2006.02.002.
Smits, J., & Steendijk, R. (2015). The International Wealth Index (IWI). Social Indicators Research, 122(1), 65–85. https://doi.org/10.1007/s11205-014-0683-x.
Snopkowski, K., & Sear, R. (2015). Grandparental help in Indonesia is directed preferentially towards needier descendants: a potential confounder when exploring grandparental influences on child health. Social Science and Medicine, 128, 105–114. https://doi.org/10.1016/j.socscimed.2015.01.012.
Strassmann, B. I. (2011). Cooperation and competition in a cliff-dwelling people. Proceedings of the National Academy of Sciences of the United States of America, 108(Supplement 2), 10894–10901. https://doi.org/10.1073/pnas.1100306108.
Strassmann, B. I., & Garrard, W. M. (2011). Alternatives to the grandmother hypothesis: a meta-analysis of the association between grandparental and grandchild survival in patrilineal populations. Human Nature Hawthorne NY, 22(1–2), 201–222. https://doi.org/10.1007/s12110-011-9114-8.
Trivers, R. (1972). Parental investment and sexual selection. In B. Campbell (Ed.), Sexual selection and the descent of man (pp. 136–179). New York: Aldine de Gruyter.
Trivers, R. L., & Willard, D. E. (1973). Natural selection of parental ability to vary the sex ratio of offspring. Science, 179, 90–92.
UNICEF (2006). Women and Children: The Double Dividend of gender Equality. The State of the World’s Children 2007. New York.
Voland, E., & Beise, J. (2002). Opposite effects of maternal and paternal grandmothers on infant survival in historical Krummhörn. Behavioral Ecology and Sociobiology, 52(6), 435–443. https://doi.org/10.1007/s00265-002-0539-2.
Vyrastekova, J., Huisman, J., Mosha, I., & Smits, J. (2014). Mothers more altruistic than fathers, but only when bearing responsibility alone: evidence from parental choice experiments in Tanzania. PLoS ONE, 9(6). https://doi.org/10.1371/journal.pone.0099952.
Acknowledgements
The authors thank the Demographic and Health Surveys program (www.dhsprogram.org) for generously providing the data for this study.
Author Contributions
S.S. constructed the database, performed the literature review, conducted the analyses and wrote the paper. J.S. assisted in the design, analysis and writing of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Ethical Approval
This research is entirely based on existing data obtained from the Demographic and Health Survey (DHS) program. The team executing the DHS program ensures protection of human subjects in agreement with local and international laws.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schrijner, S., Smits, J. Paternity Uncertainty or Male Dominance? Paternal versus Maternal Grandmothers’ Contribution to Children’s Schooling in Sub-Saharan Africa. J Child Fam Stud 29, 2930–2939 (2020). https://doi.org/10.1007/s10826-019-01632-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10826-019-01632-0