Application of the tight-binding method onto the Von Neumann equation

Abstract

This paper presents a numerical framework for the analysis of quantum devices based on the Von Neumann (VN) equation, which involves the concept of the Tight-Binding Method (TBM). The model is based on the application of the Tight-Binding Hamiltonian within Quantum Liouville Type Equations and has the advantage that the atomic structure of the materials used is taken into account. Furthermore, the influence of a Complex Absorbing Potential (CAP) as a complementary boundary condition and its essential contribution to the system stability with respect to the eigenvalue spectrum is discussed.

1 Introduction

The Tight-Binding Method (TBM) is a widely used method for modeling electronic states in a solid-state system, describing the behavior of electrons in a crystal lattice in terms of their interactions with neighboring atoms [1]. In the field of quantum transport, approved models were developed that can accurately describe the quantum transport in realistic device geometries and materials, including the Wigner formalism [2] and the non-equilibrium Green’s function (NEGF) [3] method. More recently, by solving the Von Neumann Equation (VNE) numerically in center of mass coordinates and representing it in the phase space using basis transformations, the so-called Quantum Liouville type Equations (QLTE) were introduced [4]. The QLTE combines the benefits of a real space method with those of a phase space representation. This way, a model is established, which alleviates the computational high demanding time-resolved simulations of the NEGF formalism for scattering problems while maintaining the advantage of the Wigner formalism to determine time-resolved quantum transport in both, the coherent as well as the incoherent regime.

Previous studies indicate that the incorporation of TBM schemes can lead to better runtimes, exemplified by the use within a NEGF formalism for the evaluation of self-energy matrices [5]. Furthermore, the TBM is well-suited for the study of large-scale systems, as done for the quantum transport in ballistic graphene [6]. By combining the TBM with Quantum Liouville type Equations it is not only possible to study the electron transport in semiconductors and nanoscale devices in a computationally efficient manner but to handle realistic device geometries and materials in an atomistic Tight Binding basis.

The TBM can be seamlessly integrated into the QLTE for dynamic or transient algorithm implementation. Scattering can be conceptually integrated within the methodology. Unlike conventional schemes used for the numerical solution of Wigner Equations in quantum transport, the TBM directly maps the atomic structure onto the computational grid, which prevents inherent errors or inconsistencies due to inaccurate discretizations [7,8,9].

Following this approach, the QLTE is combined with the Tight-Binding Hamiltonian to investigate the steady-state and transient behavior of a double barrier resonant tunneling diode (RTD). The approach is initially implemented in a one-dimensional system to illustrate the core idea. However, it can also be extended to more complex systems by applying the general Hamiltonian defined here to various materials, considering their physical properties such as spin-oriented formulations [1, 10].

The derivation of the transport equations in form of the VNE takes place in Sect. 2; whereas, the transformation into the phase space via the Wigner–Weyl Transform is described in Sect. 3. The work proceeds with the numerical evaluation in Sect. 4. Another aspect of this work, which will therefore be discussed in more detail in Sect. 5, revolves around the influence of the CAP on the numerical stability and accuracy of the results. When simulating open quantum systems, it is common to encounter problems with boundary conditions due to the finiteness of the system. The use of a CAP can help stabilize the numerical calculations and prevent the occurrence of unphysical solutions [9]. Finally, a conclusion is drawn in Sect. 6.

2 Fundamentals

The Tight-Binding Hamiltonian is a general formulation that describes the hopping of electrons between atomic orbitals in a crystalline solid. Throughout this paper a set of orthonormal atomic orbitals between different lattice sites is considered, what leads to a simple orthogonal Tight-Binding formalism. The Tight-Binding model is demonstrated here with an s-band model in means of one single s-orbital as the orbital function for each atom.

2.1 Tight-binding method

For the sake of clarity and for further derivations the Tight-Binding Method is briefly demonstrated here. The main idea is that the wave functions $\Psi _n$ can be expanded dependent on a set of orbital functions $\phi _n$ which span an orthonormal basis

$$\begin{aligned} |\Psi _n\rangle =\sum _n {\hat{c}}_n|\phi _n\rangle \, \end{aligned}$$

(1)

with ${\hat{c}}_n$ being the expansion coefficients. The Tight-Binding Hamiltonian $H$ can be written in Dirac notation as in [10]

$$\begin{aligned} {\hat{H}} = \sum _{n}\epsilon _n|n\rangle \langle n|+\sum _{ n,m }\gamma _{nm}|n\rangle \langle m| \end{aligned}$$

(2)

with the general states

$$\begin{aligned} |\phi _n\rangle =|n\rangle \,, \, |\phi _m\rangle = |m\rangle \,, \end{aligned}$$

(3)

where $\epsilon _n$ is the on-site energy of the atomic orbital at site n, $\gamma _{nm}$ is the hopping parameter between the atomic orbitals at sites n and m, and the sum is taken over all pairs of sites n and m. This formulation allows to capture the effects of long-range interactions between the electrons in the material [10]. This type of Hamiltonian directly arises from a physical system’s approximative atomic description, in which case the lattice sites are equivalent to atoms or molecules.

Before proceeding to the reformulation and derivation of the transport equations with the Tight-Binding Hamiltonian, the important relations regarding the Hamiltonian are pointed out. For that, the expression

$$\begin{aligned} \langle l |{\hat{H}}| k\rangle = \sum _{n'm'}\gamma _{n'm'}\langle l|n'\rangle \langle m'|k\rangle =\gamma _{lk} \end{aligned}$$

(4)

is evaluated by inserting the second term of the right hand side of (2) into the Hamiltonian ${\hat{H}}$ and multiplying the left side by the eigenstate $\langle l|$ and the right side by $|k \rangle$. This expression holds the relation for the hopping terms. In the case of being at the same lattice site with the states ($l=k$), which are correspondingly the same, the on-site energy holds

$$\begin{aligned} \langle l |{\hat{H}}| k\rangle = \sum _{n}\epsilon _{n}\langle l|n\rangle \langle n|k\rangle =\epsilon _{k} \delta _{lk}\,. \end{aligned}$$

(5)

Both relations will be used for the derivation of the transport equations in the next section.

2.2 Von Neumann equation

The Von Neumann equation is used to describe the time evolution of the density matrix $\hat{\rho }$ as follows:

$$\begin{aligned} i\hbar \frac{d\hat{\rho }}{dt} = [{\hat{H}}, \hat{\rho }]. \end{aligned}$$

(6)

The density matrix $\hat{\rho }$ then can be expressed in terms of the wave functions, respectively, with the ansatz defined in (1)

$$\begin{aligned} \begin{aligned} \hat{\rho }&= |\Psi \rangle \langle \Psi | \\&=\sum _{n,m} {\hat{c}}_n {\hat{c}}_m^\dagger |n\rangle \langle m|. \end{aligned} \end{aligned}$$

(7)

The location under consideration can be identified by the parameters $n$ and $m$. They indicate the location of the lattice sites in terms of the density matrix elements in the computational domain as illustrated in Fig. 1.

Fig. 1

Elements of the density matrix in real space arranged in a staggered grid due to the TBM formalism. The sub-grids are identified by crosses or circles

The density matrix formed from the orbital functions (7) can now be substituted into the Von Neumann Eq. (6), which leads to the expression

$$\begin{aligned} \begin{aligned} i\hbar \frac{\partial }{\partial t}\sum _{n,m} {\hat{c}}_n {\hat{c}}_m^\dagger |n\rangle \langle m|&= \sum _{n,m} {\hat{c}}_n {\hat{c}}_m^\dagger {\hat{H}}|n\rangle \langle m| \\&-\sum _{n,m} {\hat{c}}_n {\hat{c}}_m ^\dagger |n\rangle \langle m|{\hat{H}}. \end{aligned} \end{aligned}$$

(8)

The orthogonalities of the orbital functions can be exploited to express the density operator $\hat{\rho }$ in a position based basis as for instance $\langle x|\hat{\rho }|x'\rangle$ with $\hat{\rho } = |\Psi (x)\rangle \langle \Psi (x')|$ or in an orbital functions based basis given by $\langle l|\hat{\rho }|k\rangle$. The latter option is chosen. For this purpose, the Von Neumann Eq. (8) is multiplied by $\langle l|$ from the left and by $|k\rangle$ from the right. The resulting equation holds

$$\begin{aligned} \begin{aligned} \sum _{n,m}\langle l|n\rangle \langle m|k\rangle i\hbar \frac{\partial }{\partial t}{\hat{c}}_n {\hat{c}}_m ^\dagger&= \sum _{n,m} {\hat{c}}_{n}{\hat{c}}_m^\dagger \langle l|{\hat{H}}|n\rangle \langle m|k\rangle \\&-\sum _{n,m} {\hat{c}}_{n}{\hat{c}}_{m}^\dagger \langle l|n\rangle \langle m|{\hat{H}}|k\rangle . \end{aligned} \end{aligned}$$

(9)

In general, the relations $\langle l| n\rangle =\delta _{ln}$ and $\langle m| k\rangle =\delta _{mk}$ are utilized. Together with the relations for the Hamiltonian matrix elements defined in (4) and (5), the Eq. (9) can be rewritten as

$$\begin{aligned} \begin{aligned} i\hbar \frac{\partial }{\partial t}{\hat{C}}_{lk}&= \sum _n\gamma _{ln}{\hat{C}}_{lk} - \sum _m \gamma _{mk}{\hat{C}}_{lk} \\&+(\epsilon _n-\epsilon _m){\hat{C}}_{lk} \end{aligned} \end{aligned}$$

(10)

introducing

$$\begin{aligned} {\hat{C}}_{lk}={\hat{c}}_n{\hat{c}}^\dagger _m. \end{aligned}$$

(11)

The $\gamma$-coefficients contain the hopping terms between each lattice site and the self-consistent Hartree potential, the static conduction band energy and the externally applied bias are included in the Potentials $\epsilon _n$ and $\epsilon _m$ and can be summarized according to

$$\begin{aligned} {\mathcal {E}}_{nm}=\epsilon _n-\epsilon _m. \end{aligned}$$

(12)

3 Phase-space representation

The obtained formulation for the density matrix is now transformed into center of mass coordinates $\xi$ and $\chi$ before a transformation with basis functions representing plane waves is carried out in $\xi$-direction. Hence, the Von Neumann equation in center of mass coordinates $\chi ,\xi$ is transformed into a Quantum Liouville type equation defined in the phase space $k$. The reason for this transformation is that inflow and outflow boundary conditions with regard to the $\chi$-direction must be integrated into the model by representing it in phase space. These boundary conditions originate from the Wigner formalism [11]. Moreover, a complex absorbing potential (CAP) is applied in $\xi$-direction to suppress artificial reflections due to the finiteness of the computational domain [9].

To begin with, (10) is transformed into center of mass coordinates in compliance with the transformation rules to define the locations of the density matrix elements in position space

$$\begin{aligned} \chi =\frac{(n+m)}{2} \quad \textrm{and}\quad \xi =n-m. \end{aligned}$$

(13)

Then, the Von Neumann equation becomes a two-staggered grid formulation which differ by the positions of the density matrix elements for each grid. Both sub-grids are offset from each other by half of the discretization width $\Delta \chi =a_0/2$ in $\chi$-direction and by the width $\Delta \xi =2a_0$ in $\xi$-direction. Here, for example, the matrix elements of the Tight-Binding Hamiltonian can be formed according to the following relations assuming the next nearest neighbor approximation:

$$\begin{aligned} \langle l|{\hat{H}}|k\rangle =\left\{ \begin{array}{ll} \epsilon _{\chi ,\xi }, &{} l=k \\ \gamma _{\chi ,\xi }, &{} l=k\pm 1 \\ 0, &{} \mathrm {otherwise\,.} \end{array}\right. \end{aligned}$$

(14)

These relations can be extended along with the density operator $\hat{\rho }$, implying that the Hamiltonian operator will have elements significantly different from zero between atoms which are second- or third-nearest neighbors [1]. For a selected point ($\chi _0, \xi _0$) the transport equations are set up exemplarily based on (14):

$$\begin{aligned} \begin{aligned} i\hbar \frac{\partial }{\partial t}{\hat{C}}_{\chi _0,\xi _0}&= \gamma _{\chi _0-\frac{1}{2},\xi _0+1}{\hat{C}}_{\chi _0-\frac{1}{2},\xi _0+1} +\gamma _{\chi _0-\frac{1}{2},\xi _0-1}{\hat{C}}_{\chi _0-\frac{1}{2},\xi _0-1}\\&- \gamma _{\chi _0+\frac{1}{2},\xi _0+1}{\hat{C}}_{\chi _0+\frac{1}{2},\xi _0+1} -\gamma _{\chi _0+\frac{1}{2},\xi _0-1} {\hat{C}}_{\chi _0+\frac{1}{2},\xi _0-1}\\&-{\mathcal {E}}_{\chi _0,\xi _0}\\\ \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} \begin{aligned} i\hbar \frac{\partial }{\partial t}{\hat{C}}_{\chi ^\textrm{mid}_0,\xi ^\textrm{mid}_0}&= \gamma _{\chi _0,\xi _0}{\hat{C}}_{\chi _0,\xi _0}+\gamma _{\chi _0,\xi _0-2}{\hat{C}}_{\chi _0,\xi _0-2}\\&- \gamma _{\chi _0+1,\xi _0}{\hat{C}}_{\chi _0+1,\xi _0}-\gamma _{\chi _0+1,\xi _0-2}{\hat{C}}_{\chi _0+1,\xi _0-2} \\&-{\mathcal {E}}_{\chi ^\textrm{mid}_0,\xi ^\textrm{mid}_0}\\ \end{aligned} \end{aligned}$$

(16)

It should be noticed that the index "mid" refers to the grid points of the sub-grid g which lie halfway between the points of grid f indicated by Fig. 2. Applying (15) and (16) to all points of the density operator, this results in a matrix vector expression with the matrices ${\varvec{D}}_f$ and $\varvec{D}_g$ containing the hopping terms $\gamma$ and vectors containing ${\hat{C}}_{\chi _0,\xi _0}$ and ${\hat{C}}_{\chi ^\textrm{mid}_0,\xi ^\textrm{mid}_0}$ which are shown below.

$$\begin{aligned} {\varvec{D}}_f = \begin{pmatrix} -\gamma &{} \gamma &{} &{}0 \\ &{} -\gamma &{} \gamma \\ &{} &{} \ddots \\ 0 &{} &{} -\gamma &{} \gamma \\ \end{pmatrix} \end{aligned}$$

(17)

$$\begin{aligned} {\varvec{D}}_g = \begin{pmatrix} \gamma &{} &{} &{}0\\ -\gamma &{} \gamma &{} \\ &{} &{} \ddots \\ &{} &{} -\gamma &{} \gamma \\ 0 &{} &{} &{} -\gamma \\ \end{pmatrix} \end{aligned}$$

(18)

The positions (indices) of the hopping terms are left out since all the terms have the same value. The matrix ${\varvec{V}}_f$ containing the potential for one of the grids is shown as an example.

$$\begin{aligned} {\varvec{V}}_{f} = \begin{pmatrix} {\mathcal {E}}_{\chi _0,\xi _0} &{} &{} 0 \\ &{} {\mathcal {E}}_{\chi _1,\xi _1} &{} \\ &{} \hspace{5.0pt}\hspace{5.0pt}\hspace{5.0pt}\ddots &{} \\ 0&{} &{} {\mathcal {E}}_{\chi _n,\xi _n} \\ \end{pmatrix} \end{aligned}$$

(19)

Analogously, the matrix ${\varvec{V}}_g$ can be constructed similarly with its potential values on the main diagonal. Finally, the two general matrix–vector equations result:

$$\begin{aligned} i\hbar \frac{\partial }{\partial t}\hat{{\varvec{C}}}_{\chi ,\xi } = {\varvec{D}}_f\cdot \hat{{\varvec{C}}}_{\chi ,\xi } -{\varvec{V}}_f \cdot \hat{{\varvec{C}}}_{\chi _\textrm{mid},\xi _\textrm{mid}} \end{aligned}$$

(20)

$$\begin{aligned} i\hbar \frac{\partial }{\partial t}\hat{\varvec{C}}_{\chi _\textrm{mid},\xi _\textrm{mid}} = {\varvec{D}}_g\cdot \hat{\varvec{C}}_{\chi _\textrm{mid},\xi _\textrm{mid}}-{\varvec{V}}_g\cdot \hat{\varvec{C}}_{\chi ,\xi } \end{aligned}$$

(21)

The matrices, ${\varvec{D}}_f$ and ${\varvec{D}}_g$, which include all the elements of the density matrix related to the hopping between the atoms, are of the size [$N_{\xi }-1\times N_\xi$] and [$N_{\xi }\times N_{\xi }-1$], respectively. The matrix ${\varvec{V}}_f$ has the dimension [$N_{\xi }\times N_\xi$] and ${\varvec{V}}_g$ the dimension [$N_{\xi }-1\times N_{\xi }-1$]. $N_{\xi }$ are the number of elements in $\xi -$direction.

Figure 2 illustrates the transformation into center of mass coordinates.

Fig. 2

Integration of the Tight-Binding Model into the Von Neumann equation leads to a two staggered grid formulation. The resulting distribution functions f and g are defined on different grid points and are coupled together via the potential

The discrete density matrix consists of two sub-grids offset to each other. One sub-grid is located on even grid points; while, the other contains grid points for odd numbers in $\chi$-direction. The density operator $\hat{\rho }$ is now mapped to the corresponding functions $f(\chi ,k)$ and $g(\chi _\textrm{mid},k)$ with the help of a Wigner–Weyl Transformation introducing a plane wave basis $\varvec{\Phi }_f$ and $\varvec{\Phi }_g$. In this respect, the Weyl transform according to

$$\begin{aligned} W(\chi ,k)= \int d\xi \exp (-ik\xi )\quad \langle \chi +\xi /2 | \hat{\rho } |\chi -\xi /2 \rangle \end{aligned}$$

(22)

is applied, in which the density operator $\hat{\rho }$ in center of mass coordinates is defined by

$$\begin{aligned} \hat{\rho }=|\Psi (\chi +\xi /2)\rangle \langle \Psi (\chi -\xi /2)|. \end{aligned}$$

(23)

The Weyl transform is approximated by using the values at discrete locations $\xi _p$, where the density matrix is defined. Hence, we have

$$\begin{aligned} W(\chi ,k)= \sum _p \Delta \xi \exp (-ik\xi _p)\, \langle \chi +\xi _p/2 | \hat{\rho } |\chi -\xi _p/2 \rangle . \end{aligned}$$

(24)

Introducing the expansions

$$\begin{aligned} |\Psi (\chi +\xi /2)\rangle = \sum _p {\hat{c}}_{\chi +\xi _p/2} |n(\chi +\xi _p/2)\rangle \end{aligned}$$

(25)

and

$$\begin{aligned} \langle \Psi (\chi -\xi /2)|= \sum _p {\hat{c}}_{\chi -\xi _p/2}^\dagger \langle n(\chi -\xi _p/2)| \end{aligned}$$

(26)

dependent on the orbital functions $|n\rangle$, the Wigner function result

$$\begin{aligned} W(\chi ,k)= \sum _p \Delta \xi \exp (-ik\xi _p)\hspace{5.0pt}{\hat{c}}_{\chi +\xi _p/2} \hspace{5.0pt}{\hat{c}}_{\chi -\xi _p/2}^{\dagger } \end{aligned}$$

(27)

Accordingly, the inverse transform for both grids can be expressed by the use of different expansion coefficients $f_{\chi ,k}$ and $g_{\chi _\textrm{mid},k}$ as

$$\begin{aligned} {\hat{C}}_{\chi ,\xi } =\frac{1}{2\pi \hbar }\sum _{k_l} \Delta k\exp {(-ik_l\xi )}f_{\chi ,k}. \end{aligned}$$

(28)

and

$$\begin{aligned} {\hat{C}}_{\chi _\textrm{mid},\xi _\textrm{mid}} = \frac{1}{2\pi \hbar }\sum _{k_l}\Delta k \exp {(-ik_l\xi _g) g_{\chi _\textrm{mid},k}} \hspace{5.0pt}, \end{aligned}$$

(29)

where the wave number $k$ is defined by

$$\begin{aligned} k = [-L_k/2...,k_l,...L_k/2]\,\Delta k\,, \end{aligned}$$

(30)

with $L_k$ as the number of $k$-values, the reduced Planck constant $\hbar$ and $\Delta k=\pi /(L_k\Delta x)$. The resulting plane wave basis for $\varvec{\Phi }_f$ is of the size [$N_{\xi }\times N_{L_k}$] and [$N_{\xi -1}\times N_{L_k}$] for $\varvec{\Phi }_g$. In order to arrive at the final Quantum Liouville type equations, the relations (28) and (29) with their basis matrices $\varvec{\Phi }_{f,g}$ and their Hermitian conjugate $\varvec{\Phi }^\dagger _{f,g}$ are applied onto the matrices of Eqs. (15) and (16):

$$\begin{aligned}{} & {} i\hbar \frac{\partial }{\partial t}f_{\chi ,k} = (\varvec{\Phi }_g^\dagger {\varvec{D}}_f \varvec{\Phi }_f)g_{\chi ,k}-(\varvec{\Phi }_f^\dagger \varvec{V}_f \varvec{\Phi }_f)f_{\chi ,k}. \end{aligned}$$

(31)

$$\begin{aligned}{} & {} i\hbar \frac{\partial }{\partial t}g_{\chi ,k} = (\varvec{\Phi }_f^\dagger {\varvec{D}}_g \varvec{\Phi }_g)f_{\chi ,k} -(\varvec{\Phi }_g^\dagger \varvec{V}_g \varvec{\Phi }_g)g_{\chi ,k}. \end{aligned}$$

(32)

In these equations $\varvec{\Phi }_{f,g}$ denote the basis of the plane waves, ${\varvec{D}}_{f,g}$ include the kinetic energy operator and ${\varvec{V}}_{f,g}$ depend on the Hartree–Fock potential for each grid $f$ and $g$, respectively. The resulting transformation matrices are $\varvec{F}=\varvec{\Phi }_g^\dagger {\varvec{D}}_f \varvec{\Phi }_f$ and ${\varvec{G}}=\varvec{\Phi }_f^\dagger {\varvec{D}}_g \varvec{\Phi }_g$ such as $\varvec{V_F}=\varvec{\Phi }_f^\dagger {\varvec{V}}_f \varvec{\Phi }_f$ and $\varvec{V_G}=\varvec{\Phi }_g^\dagger {\varvec{V}}_g \varvec{\Phi }_g$. This scheme is related to a formalism presented by Mains and Haddad [8] which is based on a finite difference discretization of the discrete Schrodinger equation to determine the Wigner functions. Thus, as an alternative, a continuum Hamiltonian can also be discretized using finite differences to produce a Tight-Binding Hamiltonian [12]. The basic idea is that by using two discrete Wigner functions, $f(x_j,k_m)$ and $g(x_{j}^\textrm{mid}, k_m^g)$, which are defined on meshpoints and midway between meshpoints, the inconsistencies between the density operator and the Wigner function as a result of the transformation are resolved. These inconsistencies can be described as a loss of information in the density matrix occurring during the Wigner–Weyl transformation and as an incomplete translation from the conventional Wigner function’s domain into the density matrix domain [7]. According to the statistical ensemble of the density matrix all the information can be contained the way presented here and by Mains and Haddad, what should lead to a more accurate description of the quantum system. However, in contrast to the method used in [8], here the same basis with respect to $k$ is applied for both grids and distribution functions (31) and (32), respectively. The wave vector $k$ with the discretization width $\Delta k$ take the same values for both functions. Another difference to Haddad’s method is that a CAP is used as a supplementary boundary condition in $\xi$-direction; whereas, Haddad’s method uses artificial scattering terms, which is associated with challenges like stability issues when solving time-dependent problems as described in [8]. The occurrence of negative charge carrier densities is the result, which could be successfully prevented in this work.

In Fig. 3 the structure of the complete system matrix with the corresponding matrix blocks is sketched.

Fig. 3

The structure of the system matrix. Each block is a matrix of size [$N_{L_k}\times N_{L_k}$]

All the matrices are of the block size $N_{L_k}\times N_{L_k}$ and span the global matrix of the system, where boundary conditions including the CAP have to be added yet. The structure of the global matrix and the inclusion of the boundary terms will be discussed in the next section.

3.1 Boundary conditions

First, boundary conditions are specified in the $\chi$-domain with regard to the inflow and outflow concept [7]. The approach taken here consists of the implementation of the inflow boundary conditions splitting the wave vector (30) into a positive (incoming waves) and a negative part (outgoing waves). Hence, the distribution functions $f$ and $g$ can be divided according to their propagation properties. The first $N_{L_k}/2$ values of $k$ of $f$ and $g$ are correlated with the forward components $f^+$, $g^+$ and the last $N_{L_k}/2$ values with the backward components $f^-$, $g^-$, so we have

$$\begin{aligned} f(\chi )= \left( \begin{array}{c} f^+(\chi ) \\ f^-(\chi )\end{array}\right) \,,\,g(\chi )= \left( \begin{array}{c} g^+(\chi ) \\ g^-(\chi )\end{array}\right) \end{aligned}$$

(33)

Now the following auxiliary equations are set up for the f-grid and g-grid at the left and right contact:

$$\begin{aligned}{}[IL]\,f^-(\chi _1)=f^L_{BC}\,,\, [IR]\,f^+(\chi _{N_{\chi _f}})=f^R_{BC}. \end{aligned}$$

(34a)

$$\begin{aligned} \,g^-(\chi _{1.5})=g^L_{BC}\,,\, [IR]\,g^+(\chi _{N_{\chi _g}})=g^R_{BC}. \end{aligned}$$

(34b)

The auxiliary Eq. (34) are now embedded as Dirichlet boundary conditions within the system matrix. By introducing and embedding the unity matrices $[IL]$ and $[IR]$ of dimension [$N_{L_k} \times N_{L_k}$] the system matrix then results as indicated in Fig. 3. The block matrix $[IL]$ is composed of $[IL] = [[Id], [0]]$ at the left edge for the electron transport. The unit matrix $[Id]$ and the zero valued matrix $[0]$ form a dimension of [$N_{L_k}/2 \times N_{L_k}/2$] each. Analogously, the block matrix [IR] indicates the electron transport at the right edge $[IR]=[[0], [Id]]$. The inflow of electrons is determined by the Fermi–Dirac statistics at the contacts. For one-dimensional transport problems, the two-dimensional Fermi gas $f^{FD}_{2D}(E_c(k)-\mu _c)$ is defined according to

$$\begin{aligned} f^{FD}_{2D}(E_c(k)-\mu _c) = \frac{mk_BT}{2\pi \hbar ^2}\cdot \log \bigg (1+\exp {\bigg (\frac{E_c(k)-\mu _c}{k_BT}}\bigg )\bigg ) \end{aligned}$$

(35)

with energy $E_c(k)$ in the system at temperature $T$ and the chemical potential $\mu _c$. The Boltzmann constant $k_B$, the effective mass $m$ and the reduced Planck constant $\hbar$ are part of the equation as well. Furthermore, the boundary conditions are supplemented by a CAP in $\xi$-direction to ensure that outgoing wave functions decay exponentially, preventing reflections at the boundaries of the $\xi$-domain. The basic concept behind a CAP is to add a complex-valued potential to the system’s Hamiltonian before the basis transformation is carried out. Consequently, the matrices related to the Hartree potential are extended by the CAP:

$$\begin{aligned}{} & {} V_f(\chi ,\xi ) = V_f(\chi ,\xi )-i{\mathcal {C}}_f(\xi ). \end{aligned}$$

(36a)

$$\begin{aligned}{} & {} V_g(\chi ,\xi ) = V_g(\chi ,\xi )-i{\mathcal {C}}_g(\xi ). \end{aligned}$$

(36b)

This complex potential causes the statistical density matrix within the layers to decay, reducing reflections at the computational domain’s edges considerably. There are many different types of CAPs that have been developed over the years, each with its own strengths and weaknesses [13]. Choosing the right CAP for a particular application will require careful consideration [14]. The complex absorbing potential can be efficiently constructed within the proposed formalism by a $\xi$-dependent monomial basis of the form:

$$\begin{aligned} {\mathcal {C}}(\xi ):= {\left\{ \begin{array}{ll} \beta \cdot (|\xi |-(\frac{L_\xi }{2}-\epsilon ))^n,&{} \text {if } \frac{L_\xi }{2}-\epsilon< |\xi |<\frac{L_\xi }{2}\\ 0, &{} \text {elsewhere} \end{array}\right. } \end{aligned}$$

(37)

The width of the area containing the CAP is given by $\epsilon$ and the coefficient $\beta$ factorizes the amplitude of the complex potential. The exponent $n$ is the third adjustable parameter and defines the monomial order of the CAP.

Finally, the global system matrix can be set up. Putting the block matrices together and adding the boundary conditions, the structure is given by

$$\begin{aligned} \begin{pmatrix} f_{BC}^L \\ g_{BC}^L \\ 0\\ 0 \\ \vdots \\ 0 \\ 0 \\ g_{BC}^R \\ f_{BC}^R \end{pmatrix} = \begin{pmatrix} [IL] &{} [IL] \\ [F] &{} [V_F] &{} [F]\\ &{} [G] &{} [V_G] &{} [G] \\ &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} [F] &{} [V_F] &{} [F]\\ &{} &{} &{} [IR] &{} [IR]\\ \end{pmatrix} \begin{pmatrix} f(\chi _1) \\ g(\chi _{1.5}) \\ f(\chi _2) \\ g(\chi _{2.5}) \\ \vdots \\ g(\chi _{N_{\chi g}})\\ f(\chi _{N_{\chi f}}) \end{pmatrix} \end{aligned}$$

(38)

The system matrix has a quadratic dimension and adding the inflow boundary conditions yields an unambiguous solution. This completes the formulation of the transport equations and the density matrix from the Von Neumann equation is expressed in terms of the staggered phase space distribution functions f and g. The next section contains the evaluation and the validation of this method by applying it on a resonant tunneling diode (RTD). The RTD is a simple quantum device often used as a standard model to evaluate methods for electron transport, both steady-state and transient. Here, it is used to validate the derived model.

4 Numerical evaluation

A RTD is investigated in the stationary and dynamic regime to evaluate the suggested approach. The findings are validated by comparing them to those obtained using the Quantum Transmitting Boundary Method (QTBM) [15]. The atomic description of the system is defined based on the lattice constant of the material used. The self-consistent Hartree potential is calculated by combining the transport and Poisson equations. To determine the carrier densities and the numerical current, the continuity equations are employed and extended to this methodology. Specifically, the carrier densities for electrons are expressed using (23)

$$\begin{aligned} n_f(\chi )&=\frac{\Delta k}{2\pi }\sum _j f(\chi ,k_j). \end{aligned}$$

(39a)

$$\begin{aligned} n_g(\chi _\textrm{mid})&=\frac{\Delta k}{2\pi }\sum _j g(\chi _\textrm{mid},k_j). \end{aligned}$$

(39b)

Similarly, the current densities are calculated using (24):

$$\begin{aligned} j_f(\chi )&=\frac{-q\Delta k}{2\pi } \frac{\hbar }{m(\chi )}\sum _j k_j f(\chi ,k_j). \end{aligned}$$

(40a)

$$\begin{aligned} j_g(\chi _\textrm{mid})&=\frac{-q\Delta k}{2\pi } \frac{\hbar }{m(\chi _\textrm{mid})}\sum _j k_j g(\chi _\textrm{mid},k_j). \end{aligned}$$

(40b)

Here, $q$ is the elementary charge, $\hbar$ the reduced Planck’s constant, and $k$ represents the wave vector. A homogeneous effective mass is considered. The formulation of the numerical current density requires the explicit consideration of the two-staggered grid formalism. To calculate the total current, the average of both partial currents, $j_f$ and $j_g$, is formed:

$$\begin{aligned} j_{tot}=\frac{j_f+j_g}{2}. \end{aligned}$$

(41)

This relationship is due to the fact that the time derivative of the density matrix at the location between $\chi '$ and $\chi _\textrm{mid}'$ has to be determined. Hence, the derivative of the density matrix is approximated through difference approximation at the locations $\chi '=\chi + \delta$ and $\chi _\textrm{mid}'=\chi - \delta$.

4.1 AlGaAs resonant tunneling diode

A RTD serves as a test device. Figure 4 sketches the schematic structure with all relevant areas and dimensions. A length $L_\chi =150~\textrm{nm}$ in the $\chi$-direction is assumed first for the numerical study. The associated interval is split into $N_{\chi f}=271$ cells for grid f and $N_{\chi g}=270$ cells for grid g. The $\xi$-direction is split into $N_{\xi f}=161$ cells and $N_{\xi g}=160$ cells. The parameters chosen in dependency to the lattice constant $a_0$, $\Delta \chi =a_0/2$ and $\Delta \xi = 2a_0$, result from the center of mass transformation. Here, one aspect around the Tight-Binding formalism set up is briefly mentioned. Both transport Eqs. (31) and (32) converge to the conventional Wigner equation if the distance between the sub-grids converges to zero. This could be shown in previous work by performing a Taylor expansion exemplarily at a grid point and taking the limits $\Delta \chi \rightarrow 0$ and $\Delta \xi \rightarrow 0$ [16]. The diode under investigation is made up of seven different layers in the material system $\textrm{Al}_{0.3}\textrm{Ga}_{0.7}\mathrm {As/}\textrm{GaAs}$. At the edges there are two n-doped GaAs contact layers (60 nm) followed by a buffer region made of undoped GaAs (10 nm). The doping concentration amounts to $N_D=2\cdot 10^{24}\,m^{-3}$. The two barriers and the quantum well complete the structure, which can be seen in Fig. 4.

Fig. 4

Schematic representation of a resonant tunneling diode with double barrier structure and spatially constant effective mass

4.2 Flat band calculation

At first, the carrier concentration is calculated for the flat band case to validate the model. For this purpose, the carrier density for the thermal equilibrium case is shown followed by a simulation with an applied external bias of $U=0.1~\textrm{V}$. The conventional Wigner Transport Equation (WTE) serves as a reference method to compare the obtained results.

Fig. 5

Calculated carrier densities $n$ in dependency to the $\chi$-direction. The black dots indicate the values of the reference solution obtained from the WTE

As it can be seen from Fig. 5, there is a good agreement for both cases, assuming thermal equilibrium. However, there is a notable deviation compared to the solution from the WTE when a voltage of 0.1 V is applied. This deviation occurs as small oscillations at the left side of the barrier as well as within the barrier itself. The carrier density for the TB-QLTE is slightly higher. The conditions are adjusted to more realistic potential profiles to see if this deviation still occurs. For this reason, the self-consistent solution is considered.

4.3 Self-consistent calculation

In general, self-consistent calculations take into account the interaction between the charge distribution and the potential profile and therefore are considered more accurate. In both instances (WTE and TB-QLTE), a standard Newton–Raphson method is used to account for the corresponding nonlinearity when coupling the transport equations with the Poisson equation. The i-th iteration’s stop criterion is specified as

$$\begin{aligned} \frac{||V_H^i-V_H^{i-1}||}{N_{\chi }} < 1\cdot 10^{-3}, \end{aligned}$$

(42)

where the vector $V_H^i$ includes the $N_{\chi }$ discretized Hartree potential values at the i-th iteration. The simulations for calculating the carrier densities were performed with the externally applied voltages $0.2\,\text {V}$ and $0.4\,\text {V}$.

From Fig. 5c and d, it can be concluded that, once again, the results from the proposed method agree very well with the results obtained from the WTE. In the next step, the I-V characteristic is adopted as an important characteristic parameter of an RTD. Therefore the steady-state I-V curve is computed for the proposed method and the WTE by using (41). Furthermore, the Quantum Transmitting Boundary Method is consulted as an approved reference method to identify differences or similarities between the conventional Wigner method and the TB-QLTE. As the solution of the Quantum Transmitting Boundary Method is closely linked to the solution of the Schrödinger equation, the abbreviation "SE" will be used instead of "QTBM" to avoid any confusion between the methods, particularly in the legend of Fig. 6.

The contact area at both ends of the device is shortened by 20 nm (so 40 nm in total) to test the method also under more critical conditions. The results are shown in Fig. 6.

Fig. 6

Steady state I-V curves are shown for the proposed approach (TB-QLTE) and the reference methods. The current density is shown for two differently dimensioned test devices. The absolute error $|\epsilon |$ compared to the Quantum Transmitting Boundary Method (SE) is also displayed

The range of the applied voltage is varied from 0 V up to 0.5 V. The steady-state I-V characteristics curve obtained from the proposed method shows an excellent agreement with the results obtained from the Quantum Transmitting Boundary Method. However, differences occur between the proposed method and the classical Wigner method. The absolute error $|\epsilon |$ between the staggered grid formalism and the Quantum Transmitting Boundary Method is negligible; while, there are notable deviations between the classical Wigner method and the SE. Therefore, the staggered grid formalism based on the TB-QLTE could provide more accurate results with respect to the calculated I-V-characteristics and carrier densities compared to the conventional Wigner Equation approach as indicated in Fig. 6.

5 Complex absorbing potential

5.1 Eigenvalue spectrum

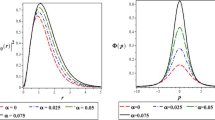
The dynamic behavior of the system is of particular interest, as it allows for the analysis of switching behavior and nonlinear effects. To investigate the transient solution, the TB-QLTE approach was employed using the fourth-order Runge–Kutta (RK4) method [17]. The stability was evaluated by analyzing the eigenvalues of the time-dependent system matrix. To ensure the stability of the system, a complex absorbing potential was used to enforce decay of the distribution functions at the edges of the computational domain. This results in an eigenvalue spectrum consisting of purely negative real parts as depicted in Fig. 7.

Fig. 7

Eigenvalues $(\lambda )$ on the energy complex plane derived from the system matrix of 81 cells in $\chi$- and 21 cells in $\xi$-direction

Fig. 8

Spatially time-dependent carrier density $n_f$. The time step is chosen to $dt=10^{-18}\textrm{s}.$

For demonstration purposes and to illustrate the impact of the CAP on the system stability with respect to the eigenvalue spectrum a relative small system matrix is considered with 3220 Eigenvalues. The matrix result from 81 cells in $\chi$-direction as well as 21 cells in $\xi$-direction. As it can be seen in Fig. 7, an appropriate CAP ensures that the eigenvalues are shifted to the left half plane. Depending on the selected CAP parameters, the eigenvalues can be shifted further and thus contribute to the system stability. Because a detailed analysis would require more space for discussion, the topics are discussed here only in a conceptual framework. For a more comprehensive treatment please refer to [9].

5.2 Transient calculation

Once the system stability is ensured, a transient simulation is carried out beginning with the system in thermal equilibrium $t=0\,\textrm{fs}$. As an external bias of $0.1~\textrm{V}$ is applied, the system evolves toward a steady state, and the statistical density matrix is reached under these conditions. The external bias is introduced through a time-dependent step function with an amplitude of $0.1~\textrm{V}$. This evolution can be observed through the time-dependent behavior of the carrier density $n_f$, as demonstrated in Fig. 8. The carrier density is obtained using Eq. (39a) at each time step.

6 Conclusion and outlook

In summary, this paper addresses a novel approach for the analysis of Quantum Devices based on the Tight-Binding Method within Quantum Liouville type equations. The proposed method delivers adequate results with sufficiently small errors when compared to conventional algorithms for solving Quantum transport equations such as the classical Wigner Transport Equation and the Quantum Transmitting Boundary Method, which is used here as a reference method. It was shown that the new formalism achieves higher accuracy compared to the conventional Wigner method and is suitable for explicit transient calculations. Furthermore, the importance of a CAP is emphasized with respect to the system stability and the method is validated under both steady-state and dynamic conditions. Various approximations exist within the Tight-Binding model to capture realistic band structures. By modifying the Tight-Binding Hamiltonian (2), this approach can be extended to encompass 2D and 3D systems. Additionally, employing more sophisticated atomic models for individual atoms, incorporating additional orbitals and bands, or addressing spin effects enables the modeling of spintronic devices, realistic channel/oxide interfaces, heterojunctions, and heterostructures, among others [1]. The methodology presented in this study serves as a useful framework for conducting such atomistic device simulations.