Rapid time-domain simulation of fractional capacitors with SPICE

Abstract

Fractional capacitors, commonly called constant-phase elements or CPEs, are used in modeling and control applications, for example, for rechargeable batteries. Unfortunately, they are not natively supported in the well-used circuit simulator SPICE. This manuscript presents and demonstrates a modeling approach that allows users to incorporate these elements in circuits and model the response in the time domain. The novelty is that we implement for the first time a particular configuration of RC elements in parallel in a Foster-type network with SPICE in order to simulate a constant-phase element across a defined frequency range. We demonstrate that the circuit produces the required impedance spectrum in the frequency domain, and shows a power-law voltage response to a step change in current in the time domain, consistent with theory, and is able to reproduce the experimental voltage response to a complicated current profile in the time domain. The error depends on the chosen frequency limits and the number of RC branches, in addition to very small SPICE numerical errors. We are able to define an optimum circuit description that minimizes error while maintaining a short computation time. The scientific value is that the work permits rapid and accurate evaluation of the response of CPEs in the time domain, faster than other methods, using open source tools.

1 Introduction

Constant-phase elements (CPEs) play an important role in many electrical situations—examples include rechargeable batteries [1,2,3,4,5], impedance of biological tissue [6,7,8,9,10], and control theory [11,12,13,14,15]. A CPE exhibits a constant phase between voltage and current, independent of frequency, and, for a capacitive element, a power scaling of impedance with exponent between 0 and 1. Specifically, the impedance Z of a CPE is given by

$$\begin{aligned} Z(\omega ) = \frac{1}{C_f(j \omega )^{\alpha }} \end{aligned}$$

(1)

where $\omega$ is the angular frequency ($=2\pi f$ where f is the frequency), $j^2 = -1$, $\alpha$ is the order of the CPE ($0< \alpha < 1$) and $C_f$ is the fractional capacitance. In the limit of $\alpha \rightarrow 0$ the CPE becomes a resistor; in the limit of $\alpha \rightarrow 1$ the CPE becomes a capacitor. A CPE with $\alpha =0.5$ is a Warburg element, common in electrochemical modeling such as the well-used Randles circuit [16]. There are many ways of approaching the modeling of CPEs, as summarized in [17], such as via Fourier theory [18], Laplace transforms [11, 19], transfer functions and control theory  [20,21,22], circuits [23,24,25,26,27], in addition to more generalized approaches [25]. There have also been efforts to construct CPEs of defined specifications with hardware, for example [12, 13, 23].

Despite the common use of CPEs in modeling of physical and electronic systems, and the use of the popular open source SPICE family of circuit simulators to model fractional systems such as fractional order filters [14, 15], SPICE still does not include CPEs as native elements. Realizing a CPE as a native element is desirable because it would allow SPICE to be used to model electronic elements known to have fractional behavior, for example, rechargeable batteries [3, 4], using a standard tool in electronic modeling. The lack of a CPE native SPICE element is partly because the fractional derivative is non-local in time and so current and voltage are not instantaneously related, which is required for the matrix operations performed by SPICE to simulate a time domain response. Ray et al. [11] have recently implemented a Laplace transform approach to modeling a CPE within SPICE, but this method relies on numerical Fourier transforms and becomes impractically slow and memory intensive for long time series. An alternative method, using a capacitor with time-varying capacitance [26] results in unreasonable parameter values for long time simulations. A way around this lack of capability is to create a CPE using a network of resistors and capacitors. For example, Morrison [27] identifies several schemes by which a CPE can be decomposed into an array of such elements. Morrison demonstrated a circuit practically for $\alpha =0.5$. The approach was formalized notably by Oustaloup et al. [28] putting such approaches to creating fractional elements on a secure mathematical footing. In this present work, we have taken the approach of using an existing network definition using resistors and capacitors [27, 29], implementing it efficiently within SPICE, and analyzing its performance.

There have been several hardware and software realizations of a CPE using R and C elements, including Cauer-type and Foster-type networks [25]. Hardware implementations are often problematic because choices of component values are practically limited and truncation of the network is required to keep the complexity reasonable. However, software implementations are less limited. Oldham & Zoski [30] used a Foster-type chain of parallel RC elements to produce a CPE which was then implemented in an oscillator circuit. Recently, López-Villanueva et al. used the same configuration to simulate a CPE using Matlab [31]; the authors provided code to export the required parameters to SPICE and demonstrated success with reproducing frequency and time-domain data. Additionally, Adihikary et al. have analyzed Foster-type chains in some detail, including SPICE simulation in the frequency domain but not the time domain, with the intention of producing a practical hardware realization of a CPE within user-defined specifications [23]. Other hardware approaches to fractional order elements are summarized in [32]. However, the review of Li et al. of numerical approaches to simulating fractional elements overlooked the possibility of using circuit simulators such as SPICE [17].

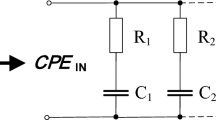
A less considered Foster-type scheme, but one analyzed by Morrison in some detail, uses an array of RC elements in parallel, as shown in Fig. 1 [27, 33]. The essential concept is that the characteristic frequencies of the branches form a geometric progression. Conceptually, the network is infinite in extent at both high and low frequencies, but in practice it requires termination. There have been different approaches to termination in the literature, including different combinations of terminating resistors and capacitors. In this work we describe an implementation of Morrison’s RC-elements-in-parallel with SPICE, and demonstrate that it reproduces the expected impedance-frequency relationship across a wide frequency range and time-domain responses to current input. The network enables use of CPE elements in equivalent circuit models such as [3, 4].

Fig. 1

A network of parallel R & C elements, as described by Morrison [27], with a terminating R and C as described by [29], that reproduces a CPE of order $\alpha =1/m$. The “home” branch has a resistance and capacitance of $R_0$ and $C_0$ respectively; there are $N_h$ RC branches with higher characteristic frequency (shorter RC time constant, to left) and $N_l$ branches with lower characteristic frequency (higher RC time constant, to right). k is the scaling factor on the R branches, defined in (9) such that the time constants of successive branches scale as $k_f = k^m$. The network is terminated by a resistor at the low characteristic frequency end and by a capacitor at the high characteristic frequency end, as detailed in Sect. 2.4

A major benefit of defining a CPE with SPICE is that it opens the possibility for rapidly simulating such elements in the time domain, using an open source tool in standard use in the electronic engineering field. An extensive summary of the advantages and disadvantages of different methods for computing time-domain responses for fractional elements is given by Valério and Da Costa [34]. A computational toolbox for time-domain computation of Riemann–Liouville-type fractional integrals [35] has been provided by Marinov et al. [36] at https://github.com/SantamariaLab/Fractional-Integration-Toolbox/tree/master/src, though we note that this toolbox has been optimized for ease-of-use rather than computational speed. Time-domain computation of the Riemann–Liouville integrals is computationally expensive and slows when time series are long because of the need to include the history of the signal. An alternative approach based on the Grünwald–Letnikov definition of a fractional integral [35] is provided in the FOMCON toolbox for Matlab [21, 37]. The fractional-order transfer function is approximated using a combination of integer-order transfer functions [38] allowing for stable time-domain evaluation of fractional integrals, for use in for example fractional control systems. However, as with the Riemann–Liouville approach, the computation time grows nonlinearly with the number of data-points in a time-series. Thus the ability to represent a CPE with SPICE not only allows use of a well-used open-access modeling tool but opens the possibility of rapid evaluation of time-domain responses that would be of considerable benefit for time-domain modeling of fractional systems.

In this manuscript, we describe a SPICE model for the Foster-type representation of parallel RC elements used by Morrison [27] (Fig. 1) with terminations of a single R branch and a single C branch in contrast to Adhikary et al. who had terminating RC and C branches [23]. We present for the first time a detailed analysis of the model for frequency and time-domain inputs, including a quantification of the sources of error. Of particular significance is that we provide Matlab and C code that allows a user to construct a network within SPICE to model a CPE of parameters of the user’s choosing to a user-specified accuracy, exploiting SPICE’s ability to calculate circuit responses extremely quickly. Although our focus is on providing an implementation with the SPICE model as opposed to reducing computation time, we demonstrate nonetheless that the approach allows rapid and accurate evaluation of a voltage response in the time domain to a current with rich spectral content defined over an extended time period (12 days).

2 Defining a circuit with SPICE

We require a model that reproduces CPE behavior over a defined, large frequency range, for a wide range of fractional orders $\alpha$. Furthermore, we require the model user to be able to specify the detail of the circuit representation, via the scale factor $k_f$ (a parameter controlling precision of the representation) as used by Morrison [27]. The final computational model is available at https://github.com/Rockscanfly/Fractional_Capacitor_SPICE.

2.1 Inputs to model

We now detail how a circuit can be defined to meet specific requirements. Using [27] and [29] with some elucidation allows development of a program that will create a SPICE subcircuit for a CPE. The parameters that specify a circuit are:

$\alpha$:

The order of the CPE, such that $0<\alpha <1$

$Z_0$:

The magnitude of the impedance of the CPE at $f_0$

$f_0$:

The frequency at which the impedance of the CPE is specified

$f_{\textrm{min}}$:

The minimum required simulation frequency

$f_{\textrm{max}}$:

The maximum required simulation frequency

$k_f$:

The precision parameter according to [27] That defines the density of branches; $k_f > 1$

We define a “home branch” as being a branch with resistance $R_0$ and capacitance $C_0$ which has a characteristic frequency ($1/2 \pi R_0 C_0$) equal to the chosen frequency $f_0$. The R and C values for subsequent branches are found from the home branch as detailed below.

It is also possible to specify $C_f$, the constant of proportionality of the CPE, instead of the more intuitive $Z_0$ and $f_0$ combination, but when this form is given, the $Z_0(f_0)$ form is immediately computed using

$$\begin{aligned} Z_0 = \frac{1}{C_f \times (j 2 \pi f_0)^\alpha } \end{aligned}$$

(2)

where $f_0 = \sqrt{f_{\textrm{min}} \times f_{\textrm{max}} }$ is assigned the geometric mean value of the frequency limits, placing the “home” branch in the middle region on a logarithmic scale.

2.2 Number of RC branches required

The program calculates the number of branches using the precision parameter $k_f$, the ratio of the characteristic frequency between adjacent parallel branches. There may be an unequal number of branches on either side of the “home” branch. From Morrison [27],

$$\begin{aligned} N_h = \left\lfloor \frac{\log (f_{\textrm{max}}/f_0)}{\log (k_f)}\right\rfloor \end{aligned}$$

(3)

and

$$\begin{aligned} N_l = \left\lfloor \frac{\log (f_0/f_{\textrm{min}})}{\log (k_f)}\right\rfloor \end{aligned}$$

(4)

where $N_h$ (‘h’ for ‘high’) and $N_l$ (‘l’ for ‘low’) are the number of branches beyond the home branch in the directions of increasing characteristic frequency (smaller RC time-constant) and decreasing characteristic frequency (increasing RC time-constant), respectively. The final branch in each direction from the center frequency is the last branch whose characteristic (corner) frequency just falls short of the frequency limit.

2.3 Finding R and C branch values

The R and C values of each branch may now be found. We commence by finding the values for the “home” branch, and then use these to construct the values for other branches.

Morrison’s equation (48) in [27] relates the values of R and C of the home branch, $R_0$ and $C_0$ respectively, to an approximate value for the magnitude of the impedance Z of the network:

$$\begin{aligned} |Z(f)| \approx \frac{R_0}{y_\theta (2 \pi R_0 C_0 f)^{\frac{1}{m}} } \end{aligned}$$

(5)

where

$$\begin{aligned} y_\theta = \frac{\pi }{m \ln {(k)}} \sec { \left[ \frac{\pi }{2} \left( 1-\frac{2}{m}\right) \right] } . \end{aligned}$$

(6)

The “home” branch, centered at $f_0$, has by definition

$$\begin{aligned} 2 \pi R_0 C_0 f_0 = 1. \end{aligned}$$

(7)

Equation (5) gives at $f_0$:

$$\begin{aligned} Z_0 \approx \frac{R_0}{y_\theta (2 \pi R_0 C_0 f_0)^{\frac{1}{m}} }, \end{aligned}$$

(8)

and thus using (7) $R_0 = Z_0 y_\theta$. We hence obtain a value for $R_0$, and subsequently substitution in (7) gives $C_0$.

The remaining branches’ values may be obtained as depicted in Fig. 1 by multiplying or dividing the value of the previous branch’s resistor by k and the value of its capacitor by $k^{(m-1)}$, where

$$\begin{aligned} k = k_f^\alpha \end{aligned}$$

(9)

and

$$\begin{aligned} m = \frac{1}{\alpha }. \end{aligned}$$

(10)

Moving higher in characteristic frequency (to the left of Fig. 1), R gets smaller and C gets smaller; moving lower in characteristic frequency (to the right of Fig. 1) R and C both get larger.

2.4 Termination of network

Finally, the network is terminated. This can be achieved by viewing the infinite series of RC elements with characteristic frequencies below $f_{\textrm{min}}$ as being approximated by a single resistor; and the infinite series of RC elements at characteristic frequencies above $f_{\textrm{max}}$ as being approximated by a single capacitor. The values of these terminating components can be obtained from summing a geometric series. The mathematics laid out in [29] corrects Morrison’s incorrect description of the series, but the authors were unclear in whether the termination was added in addition to or replaced the last branch. In this manuscript, we choose to add extra branches for the termination.

For branches with characteristic frequencies $1/2\pi RC$ well below the given frequency $f_0$, the impedance at frequency $f_0$ is simply the resistance of the RC branch, R. To evaluate the effect of the branches below the lowest explicitly modeled branch, we sum their admittances $1/R_i$ where $R_i$ is the resistance of the i-th branch. Explicitly, then:

$$\begin{aligned} Y_l = \sum _{i=1}^{\infty } \frac{1}{k^i R_{\textrm{largest}}} = \frac{1}{R_{\textrm{largest}}} \sum _{i=1}^{\infty } \frac{1}{k^i}, \end{aligned}$$

(11)

where $R_{\textrm{largest}}=R_0 k^{N_l}$ is the largest resistance in an explicitly modeled branch, that is the resistance of the adjacent low-frequency branch. Noting that $k>1$ we can sum the geometric series on the far right-hand-side of Eq. (11) to give $1/(k-1)$, thus giving us an admittance of $Y_l = 1/(k-1) R_{\textrm{largest}}$. Therefore, we obtain an equivalent resistor of size

$$\begin{aligned} R_T = R_{\textrm{largest}} \times (k-1), \end{aligned}$$

(12)

as indicated in Fig. 1.

For branches with characteristic frequencies well above the given frequency $f_0$, the impedance at $f_0$ will be a result of the capacitance of the branch, C. Adding the values of these parallel capacitances gives us:

$$\begin{aligned} C_T = \sum _{i=1}^{\infty } \frac{C_{\textrm{smallest}}}{ (k^{m-1})^i} = C_{\textrm{smallest}} \sum _{i=1}^{\infty } \left( k^{1-m} \right) ^i, \end{aligned}$$

(13)

where $C_{\textrm{smallest}}=C_0/k^{N_h (m-1)}$ is the smallest explicitly-modeled capacitor, found in the adjacent high-frequency RC branch. Noting that $k^{(1-m)} < 1$, we can sum the geometric series to give $1/(k^{m-1}-1)$, and hence the high-frequency termination consists of one capacitor of value

$$\begin{aligned} C_T = \frac{C_{\textrm{smallest}}}{ k^{(m-1)} - 1}. \end{aligned}$$

(14)

Termination becomes significant when one operates close to the frequency boundaries as detailed in Sect. 3.1.

2.5 Outputs of model

The resulting scheme produces values of R and C for the various branches, including terminating branches. We verify that the networks reproduce CPEs correctly by computing the admittance of the network by summing the admittances of each RC branch across a wide frequency range with SPICE.

2.6 Impedance calculation

After construction of the circuit, impedance across a broad frequency range can be calculated with SPICE. For a test case, we have chosen, somewhat arbitrarily, $k_f=1.1$ (being a small multiplier), $f_{\textrm{min}} = 10^{-9}$ Hz, $f_{\textrm{max}} = 10^6$ Hz, being a very wide range of frequencies that span the limit of what is relevant for rechargeable batteries, and specified that the magnitude of the impedance should be $Z_0 = 17.5~\Omega$ at a frequency $f_0 = 10^{-3}$ Hz. The impedance specification implies $C_f = 0.7209$ A s$^{\alpha }$ V$^{-1}$ for $\alpha =0.5$. The resulting network has 362 RC branches, plus a terminating R branch and a terminating C branch. We have then used SPICE to evaluate the magnitude and phase of impedance across a frequency range defined beyond $f_{\textrm{min}}$ and $f_{\textrm{max}}$.

2.7 Time domain simulation

In the time domain, the voltage response of a CPE to a current-step of size $I_0$ at $t=0$ is given by

$$\begin{aligned} V(t) = \frac{ I_0 t^\alpha }{ C_f \Gamma (\alpha +1) }, \end{aligned}$$

(15)

where $\Gamma$ is the gamma function. We have tested the CPE voltage response to a current step for the cases of $\alpha =0.1$, 0.5 and 0.9 with the circuit built to the same specifications as for the impedance modeling described in 2.6.

To analyze the computational speed, we have additionally simulated in the time domain a square current wave of period 1 min, consisting of currents of +1 A for 30 s, followed by −1 A for 30 s and compared the SPICE performance to the fractional integration algorithm of [36].

2.8 Code availability

We have made the C code for writing out the circuit as a SPICE file available at https://github.com/Rockscanfly/Fractional_Capacitor_SPICE.

3 Results and discussion

In this section, we detail results first in the frequency domain, with plots of impedance against frequency, and then in the time domain, showing responses to step changes in current and square-wave inputs. Finally to illustrate the potential of the method for time domain simulation, we show results of the voltage response to a complicated current input.

3.1 Impedance

Figure 2 shows results for a CPE of $\alpha =0.1$ (red), $\alpha =0.5$ (blue), and $\alpha =0.9$ (green), for the parameters defined in 2.6. The figure shows (a) Magnitude and (b) Phase of the impedance, for the cases of (i) Theory (dashed line), that is a pure CPE as defined by Eq. (1), and (ii) The impedance of the constructed Morrison network of Fig. 1 as evaluated using SPICE (solid line).

Fig. 2

a The magnitude and b The phase of the impedance of CPEs of orders 0.1, 0.5, 0.9 against frequency. The dashed lines shows the ideal CPE, that is the impedance that we wish to recreate using a Morrison network and the solid line shows the impedance evaluated with SPICE. The black lines indicate the frequency ranges bounded by $f_{\textrm{min}}$ and $f_{\textrm{max}}$. The blue vertical lines indicate a chosen long and short timescale (equal to 1/f) for guidance (Color figure online)

Figure 3 shows the difference between the theoretical CPE impedance, $Z_{\textrm{CPE}}$, and the impedance of the Morrison network in SPICE, $Z_{\textrm{SPICE}}$, under the same test conditions. In part (a), we show the relative error in magnitude of impedance, $|Z_{\textrm{SPICE}}/Z_{\textrm{CPE}}| -1$. In part (b), we show the phase error. For frequencies one decade above $f_{\textrm{min}}$ and one decade below $f_{\textrm{max}}$, the error in impedance is less than 0.5% and the error in phase is less than 0.6 degrees, for all values of $\alpha$. Under our test conditions, this relates to periods ranging from 0.01 ms to 3 years, large enough to cover a wide range of practical applications. The error in magnitude of impedance continues to drop at a rate of between 1 and 2 decades per decade in frequency from the termination (depending on $\alpha$). Although not shown on the plots for clarity, the drop in error away from the frequency boundaries has been confirmed at a range of values of $\alpha$ ranging from 0.001 to 0.999.

Fig. 3

The error in the a magnitude and b phase of the impedance of CPEs of orders 0.1, 0.5, 0.9 against frequency generated with precision parameter $k_f$ of 1.2. The black lines indicate the frequency ranges bounded by $f_{\textrm{min}}$ and $f_{\textrm{max}}$. The blue vertical lines indicate a chosen long and short timescale (equal to 1/f) for guidance

The accuracy of the representation is determined by the precision parameter $k_f$ so long as the operating frequency is sufficiently far from the frequency bounds $f_{\textrm{min}}$ and $f_{\textrm{max}}$. Values of $k_f$ closer to 1 give a more accurate description of the impedance at the expense of more RC branches and greater computation time. The effect of $k_f$ on impedance is shown in Fig. 4, for $\alpha =0.5$. In part (a) we show the relative difference between the magnitude of the SPICE model impedance, and the target impedance (that of the CPE we aim to fit), $|Z_{\textrm{SPICE}}/Z_{\textrm{CPE}}|-1$, for various values of $k_f$. In part (b) we show the difference in phase between the model impedance and the target impedance for the same values of $k_f$. The limiting loci (the ‘V’ shape on Fig. 4a) are controlled by the frequency bounds and $\alpha$ — further simulation (not shown) implies these loci have gradients of $-(1+\alpha )$ and $+(2-\alpha )$ for lower and higher frequencies respectively. For values of $k_f$ sufficiently close to one, the error in the representation becomes small enough such that the error in modeling is dominated by numerical error in SPICE itself. With lower and upper frequency bounds of $10^{-9}$ Hz and $10^{6}$ Hz respectively, Fig. 4 demonstrates that a $k_f$ of 1.2 (which gives 191 branches including terminations) achieves as good an approximation as possible to the impedance.

Fig. 4

The effect of precision parameter $k_f$ on the accuracy of the model. a The relative difference between the magnitude of the impedance of the modeled fit and the target CPE for various $k_f$ values as shown in the legend, for $\alpha =0.5$. b The difference between the phase of the modeled fit and the target CPE for the $k_f$

In Fig. 5, we plot the maximum relative error in impedance against precision parameter $k_f$ for the region where the error is dominated by $k_f$ rather than the termination—i.e., avoiding the frequency extremes. Plots have been given for frequency bounds $f_{\textrm{min}}$ and $f_{\textrm{max}}$ of $10^{-9}$ and $10^{6}$ Hz (black), $10^{-7}$ and $10^{4}$ Hz (blue) and $10^{-5}$ and $10^{2}$ Hz (red). The plot shows that at low $k_f$, close to 1, there is a point at which reducing $k_f$ does not produce any lower error. This is where we have reached the floor of the valley defined in Fig. 3. The size of $k_f$ when this happens depends on the frequency bounds; the larger the frequency range the smaller we can reduce $k_f$ to reduce the error in approximation, and the smaller the resulting error is. Note that the error for larger $k_f$ simply depends on $k_f$, not the frequency range used.

Fig. 5

A plot of the maximum relative error in impedance against precision parameter $k_f$, in the region where the error due to $k_f$ dominates that of the termination, for different chosen $f_{\textrm{min}}$ to $f_{\textrm{max}}$ frequency ranges: $10^{-9}$  to $10^{6}$ Hz (black), $10^{-7}$ and $10^{4}$ Hz (blue) and $10^{-5}$ and $10^{2}$ Hz (red). The legend gives the number of decades of frequency spanned by $f_{\textrm{min}}$ and $f_{\textrm{max}}$ (Color figure online)

Figures 4 and 5 give valuable insight into optimizing the RC network representation. For example, if relative errors in impedance of $10^{-2}$ are acceptable across a small frequency range (red line of Fig. 5), a value of precision parameter $k_f$ of 7 could be used. The resulting circuit has just 10 branches (including terminating branches) leading to an extremely fast computation of the voltage response to current input. The lower bound $k_f$ (i.e., its optimum value for computation speed given a frequency range) can be approximately generalized to $k_f \approx 1+6/N_d$ where $N_d$ is the number of frequency decades between $f_{\textrm{min}}$ and $f_{\textrm{max}}$. As a further example, a $k_f$ of 2 (51 branches including terminations) leads to an error of order 1 part in $10^6$ or lower from $10^{-6}$ Hz through to $10^{2}$ Hz, allowing rapid and accurate evaluation of equivalent circuit models for rechargeable batteries [4]. We emphasize that while many tens or more branches might be required in a model this does not cause problems for the SPICE solver, and the values of the R and C elements can be generated automatically (Sect. 2.8).

3.2 Time domain

In Fig. 6a, we plot the theoretical response of voltage against time using Eq. (15) and the simulated response with SPICE on linear scales for $\alpha =0.5$; in part (b), we plot the same data as (a) using logarithmic scales to demonstrate the power law voltage response. We have used the same network as for the impedance plots discussed in Sect. 3.1. The current was requested from SPICE at intervals of 0.01 s.

Fig. 6

The voltage response to a step change in current at $t=0$ s from 0 to 1 A, for a CPE of order $\alpha =0.5$ and $C_f=0.7209$ A s$^{\alpha }$ V$^{-1}$. a Voltage response on a linear scale. The thick gray line gives the theoretical response calculated with Eq. (15); the black solid line is the SPICE simulation; the dashed line is the response calculated using the toolbox of Marinov et al. [36]. The inset is a close-up at small times. b The same voltage response data but on logarithmic scales

The SPICE predictions are extremely close to the theoretical response, showing that it has successfully modeled a step response. Indeed, for the first ten data points, they are more accurate than the response calculated using [36]. We emphasize that SPICE optimizes its internal time steps and calculations to ensure accuracy at the chosen time intervals (in our case 0.01 s apart), meaning that it is not simply iterating using 0.01 s steps but making subsidiary calculations too. In contrast, the Marinov et al. method does not make such optimizations and thus gives a small error for a few time steps. The relative error for SPICE is below $3 \times 10^{-3}$ by the first required time $t_{\textrm{step}}$ after a transition, and decreases quickly for further times without addition of more time points. To simulate one hour of voltage response sampled at 10 ms, SPICE takes eight seconds CPU time using one thread of a i7-8700K CPU.

Figure 7 generalizes Fig. 6 by including results for CPEs of $\alpha =0.1$ (red), $\alpha =0.5$ (blue), and $\alpha =0.9$ (green), for the parameters defined in 2.6. Figure 7 shows (a) Magnitude and (b) Phase of the impedance, for the cases of (i) The theoretical case (dashed line), that is a pure CPE as defined in Eq. (15), and (ii) The impedance of the constructed Morrison network of Fig. 1 as evaluated using SPICE (solid line). All cases are extremely close to theory.

Fig. 7

The voltage response to a step change in current at $t=0$ s from 0 to 1 A, for CPEs of orders 0.1, 0.5, 0.9, on a linear and b logarithmic scales. The dashed lines gives the theoretical response calculated with Eq. (15) and the solid lines gives the voltage response evaluated with SPICE (Color figure online)

To illustrate the computational speed of SPICE, both SPICE and the toolbox of Marinov [36] were used to simulate a square wave of period one minute with currents of 1 A for 30 s followed by −1 A for 30 s. The voltage response was calculated every 10 ms. In one minute of CPU time using one thread on a i7-8700K CPU, the Marinov toolbox was able to simulate 490 s of square wave, as shown in Fig. 8, while SPICE was able to simulate $2.7 \times 10^{4}$ s. We emphasize that the Marinov toolbox has been optimized for ease of use, not reduced CPU-time, so a direct comparison of timings is not appropriate. However, of particular significance is that the time for SPICE to complete is proportional to the number of branches and to the number of samples. This is in contrast to explicit evaluation of a fractional integral in the time domain, where, unless approximations are introduced, the required CPU-time is proportional to the square of the simulated time. SPICE also has the advantage of being able to add additional points at transitions to improve accuracy. Under most conditions, this drastically improves the accuracy at a given sampling rate, with little reduction in speed.

Fig. 8

a The current and b The resultant voltage for a square wave applied to a CPE, as calculated with the Marinov toolbox. The results from the SPICE simulation are identical on this scale

As an illustration of the capabilities of the SPICE approach, we have simulated the voltage response of a circuit consisting of two CPEs and a resistor in series [4] under a driving current representing the approximate current profile of a cell in an electric vehicle. The profile was created by digitizing the measured current through a cell in an electric scooter battery, for 12 days, sampled at 10 Hz. The profile, shown in Fig. 9a and the inset of (c), consisted of periods of constant positive current (representing charging of the battery), a period of zero current (vehicle at rest), and then a period consisting of short (seconds to minutes) bursts of high negative and positive currents (representing ‘morning commute’ driving including acceleration and regenerative braking, respectively). A period of a few hours rest followed (parked) and then a second period of activity (‘evening commute’). Similar but not exactly equivalent profiles were obtained for successive days. This profile was given experimentally to an INR 18650 Lithium Cobalt Oxide cell using an Agilent 66332A programmable power supply, and the experimental voltage response measured. The experimental response is shown by the black line in Fig. 9b and on a finer time resolution in (c). We also simulated the response of a circuit consisting of two CPEs in series with a resistor (CPE-CPE-R) with SPICE, where the component parameters (orders of the CPEs, fractional capacitances of the CPEs, resistance of the resistor and starting voltage) were optimized to match the experimental response. Each CPE was modeled with frequency bounds $f_{\textrm{min}}$ and $f_{\textrm{max}}$ of $10^{-9}$ Hz and $10^{6}$ Hz, respectively. The precision parameter $k_f$ for both CPEs was chosen as 1.2, giving 191 branches (including terminating branches) for each CPE. The first CPE was of order $\alpha _1 = 0.90$ and fractional capacitance $C_{f1}=7500$ A s$^{\alpha }$ V$^{-1}$; the second CPE was of order $\alpha _2 = 0.25$ and fractional capacitance $C_{f2} = 50$ A s$^{\alpha }$ V$^{-1}$. The series resistance was $R_s=0.15$ $\Omega$ and the starting voltage $V_0=4.00$ V.

Results of the simulation are shown in Fig. 9b and c by the gray line. The SPICE simulation of 12 days of data sampled at 10 Hz using our network representation of a CPE with 100 branches took approximately 1 h of CPU time on one thread on a i7-8700K CPU. The accuracy of the match of the experimental and modeling results demonstrates the validity of the model. Although the focus of this work has not been on improving computation speed for fractional integrals per se, the speed of computation demonstrates that the approach of simulating a CPE with an RC-network using SPICE is valuable for time-domain applications particularly for long data sets since it scales approximately linearly with the size of the data set. In this specific case, 12 days of data were sampled at 10 Hz, meaning that the time series consisted of approximately $10^7$ datapoints. The length of the data series would challenge many other approaches to calculating CPE responses in the time domain [11, 26, 36, 37], although we expect all computational methods for calculating CPE responses will improve as computational power increases.

Fig. 9

The experimental and simulated response of an INR 18650 lithium cobalt oxide cell to a spectrally-rich current input. a The current against time. b The voltage response measured experimentally (black) and simulated using SPICE with a CPE-CPE-R model (gray). c A section of the voltage response showing finer time resolution. The inset shows the current over the same time period

4 Conclusions

In this work, we have demonstrated for the first time that SPICE can be used in the time domain to model a CPE element accurately and rapidly using the circuit of Morrison [27]. We have shown that the model successfully reproduces the required impedance across a very broad frequency range and have quantified how the error depends on frequency range parameters $f_{\textrm{min}}$ and $f_{\textrm{max}}$ and the precision parameter $k_f$. The model can be optimized according to required speed of calculation and accuracy of the representation. We have illustrated the model in the time domain by correctly simulating a current step response to greater accuracy with greater speed than achieved by a standard numerical approach to evaluating fractional integrals. For example, we can simulate one hour of voltage response to a current step in 8 s with an accuracy of one part in a thousand or lower once the first time step is passed. The approach offers a trade-off between accuracy and speed via the multiplier $k_f$ which controls the number of RC branches. The model will be useful for rapid evaluation of equivalent circuit models, for example for rechargeable batteries and biological tissue. As a demonstration of the specific merit of the approach, we have successfully simulated the voltage response of a lithium cobalt oxide cell to 12 days of current input, using a CPE-CPE-R model, in approximately 1 h of CPU time, a result that would challenge many other methods. Moreover, given that it is a representation of a fractional element, it may have applications in any situation where fractional integrals are used, allow rapid evaluation of a fractional integral across a wide range of contexts by describing the integral in terms of an electrical circuit.