1 Introduction

Graphene, the first ever two-dimensional (2D) material [1], has been identified as promising material with high thermal and electrical conductivity [2], high carrier mobility [3] and quantum Hall effect at room temperature [4]. However, the gapless nature of graphene limits its applications in optoelectronics, because of the resulting large off-current and small on-off ratio [5]. Beyond graphene, a large family of two-dimensional materials, including hexagonal boron nitride (h-BN) [6,7,8], silicene [9, 10], germanene [11, 12], phosphorene [13], transition metal dichalcogenides (TMDCs) [5, 14, 15], have been reported owing to their unusual physical properties. Recently, two-dimensional group IV–VI have been successfully exfoliated from their bulk counterpart [16, 17]. Kamal et al. investigated three different geometrical phases (planar, buckled, and puckered) of group IV–VI compounds [18]. MX (M = Ge, Si, Sn, and X = S, Se) monolayers have been theoretically demonstrated as indirect band semiconductors, which is suitable for photocatalytic water splitting [19,20,21]. The group IV monochalcogenides have shown excellent capability for information storage [22] and piezoelectric performance [23] and exhibit high thermoelectric performance with large figure of merit (ZT) [24].

Parallel to 2D materials, the fabrication of van der Waals (vdW) heterostructure is gaining much attention for tuning the physical properties of 2D materials [25,26,27]. Heterostructures with type-II band alignment are widely reported for photodetection and energy harvesting applications [28, 29]. In type-II band alignment, the conduction band minimum (CBM) and valence band maximum (VBM) are localized in different constituents of heterostructures. This enhances the separation of photogenerated charge carriers which is crucial for solar cell devices. Recently, Li et al. showed that SnX (X = S or Se) bilayers and heterostructures are found to be promising for efficient thermoelectric devices applications [30]. Type-II band alignment and large power factor has been found in TMDC-TMDC [31]. Weiyang et al. [32] studied tunable electronic properties of GeSe/phosphorene vdW heterostructure and demonstrated type-II band alignment for promising solar cell applications.

These unusual physical and chemical properties of group IV–VI monolayers make them promising materials for the fabrication of vdW heterostructures. The lattice mismatch for the given heterostructures, found to be less than 2%, which is excellent for making van der Waals heterostructure. To date the electronic structural properties of GeO/CSe, GeS/SiSe, GeSe/SnS, and GeTe/SnS heterostructures are completely unknown. Hence, a clear physical insight into the electronic properties of these heterostructures is indispensable. In present work, we performed first principles calculations to investigate the structural, electronic, and thermoelectric performance of van der Waals heterostructures of group IV–VI monolayers.

2 Computational details

The present calculation is based on the density functional theory (DFT) which is implemented in quantum espresso code [33] within the framework of pseudopotentials and Grimme (DFT-D2) [34]. For exchange correlation, we employ generalized gradient approximation (GGA) of the Perdew–Burke-Ernzerhof (PBE) [35]. The plane waves with energy cut-off of 450 eV have been used. The artifacts of periodic boundary conditions are avoided by adding a vacuum of 25 Å along z-axis. For energy in SCF cycles, the convergence criteria is chosen to be 106 eV. For structural optimization, the total force on each individual atom is 10–3 eV/Å. For structural relaxation, a 6 × 6 × 1 Γ-centered Monkhorst Pack k-mesh is chosen, whereas a denser 12 × 12 × 1 k-mesh is used for optimized structure.

The transport coefficients including Seebeck coefficient (S), electrical conductivities (\(\sigma )\), thermal conductivities (K), and power factor (PF) are calculated using Boltzmann transport theory as implemented in BoltzTrap code [36]. The Seebeck coefficient (S), electrical conductivity \(\left( \sigma \right)\), and power factor can be mathematically expressed as follows:

$$S = ek_{g} \sigma^{ - 1} \sum k\left( { - \frac{{{\text{d}}f_{0} }}{{{\text{d}}}}} \right)v_{k}^{2} \tau_{k} \frac{{k_{B} - \mu }}{{K_{{\text{B}}} T}}$$
$$\sigma = e^{2} \sum k \left( { - \frac{{{\text{d}}f_{0} }}{{{\text{d}}\varepsilon }}} \right)v_{k}^{2} \tau _{k}$$
$${\text{Power}}\;{\text{factor}} \left( {{\text{PF}}} \right) = S^{2} \sigma$$

where e is the charge of carrier, \(K_{{\text{B}}}\) is the Boltzmann’s constant, \(f_{0}\) is the Fermi distribution function,\(v_{0}\) is the group velocity, \(\tau_{k}\) is the relaxation time, \(\varepsilon\) is the energy, and \(\mu\) denotes the chemical potential.

3 Results and discussion

As group IV–VI monolayers possess planar, buckled, and puckered crystal phases. In present work, we choose the buckled configuration of group IV–VI monolayers including GeO, CSe, GeS, GeSe, GeTe, SnS, SnSe, and SiSe monolayers because of dynamically stability and minimum binding energies which is close to that of puckered configuration. The calculated lattice constant, bond length, binding energies, and band gap of monolayers are presented in Table 1. These findings are in close agreement with the available literature, indicating the reliability our work [18].

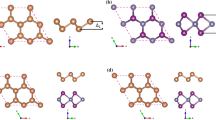
Table 1 Optimized lattice constant (Å), bond length (Å), bond angle, and band gap (eV) of group IV–VI monolayers
Full size table

The small lattice mismatch up to 2% in the understudy heterostructures allows the possible experimental fabrication of the vertical van der Waals (vdW) heterostructure [37, 38]. Owing to the symmetry of the structure, there are six possible stacking configurations of AB/XY (A = Ge, B = O, S, Se, Te, X = C, Sn, Si, Sn, and Y = Se, S) vdW heterostructures as shown in Fig. 1; (a) In AA stacking, the chalcogen atom (B = O, S, Se, Te) coincides with Y atom (Se, S), whereas the A = Ge and X = (C, Sn, Si, Sn) occupied the center of the hexagonal structure, respectively, (b) AB stacking, atom B coincides on Y atom, while the atom A and X take place the central position in hexagonal structure, respectively, (c) BB stacking, A atom lies above X atom, while atom B coincides with Y atom, (d) \(AA^{\prime}\) stacking, the position of atom A lies above atom X, whereas atom B locates at the central position in XY hexagonal structure, similarly X atom takes place the center position in AB stacking, (e)\(AB^{\prime}\) stacking, no atom possesses central position, A atom coincides with X atom, while B atom coincides with Y atom, finally (f) stacking \(A^{\prime}B\), A and X coincide, while the B and Y are located in central position of monolayer XY and AB, respectively.

Fig. 1
figure 1

(Color online) Top and side views of six possible stacking configuration (a) \(AA,\) (b) \(AB\), (c) \(AB\), (d) \(AA\), (e) \(AB\), (f) \(A^{\prime}B\) of AB/XY vdW heterostructures, see text for details

Full size image

To find the energetically favorable stacking, we have calculated the binding energy by the following equation:

$$E_{b} = E_{{{\text{Hetero}}}} - E_{AB} - E_{XY}$$

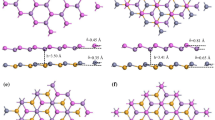
where \(E_{{{\text{Hetero}}}}\) is the total energy of heterostructure, and \(E_{AB}\) and \(E_{XY}\) are the total energies of the isolated AB and XY monolayers. The obtained lattice constant, lattice mismatch, binding energies, interlayer distance, and band gap values are given in Table 2. It is evident from the table that stacking AA with comparatively smaller interlayer distance and more negative binding energy is found energetically more favorable stacking among all understudy heterobilayer systems.

Table 2 Optimized lattice constant (Å), lattice mismatch (%), binding energies (eV), d-spacing (Å) and band gap (eV) of AB/XY heterostructures
Full size table

To further verify the thermal stability of the stacking (AA) of AB/XY (A = Ge, B = O, S, Se, Te, X = C, Sn, Si, Sn, and Y = Se, S) vdW heterostructures, we have used the AIMD simulation. We have chosen a 3 × 3 supercell with top view, as shown in Fig. 2. It is clear from the figure that after heating for 5 ps and 1 fs of the time step at 300 K, the AB/XY (A = Ge, B = O, S, Se, Te, X = C, Sn, Si, Sn, and Y = Se, S) vdW heterostructures shows no broken bonds (remain stable), while the free energy oscillates slightly (see Fig. 2.), which confirm the thermal stability of these systems at 300 K. Therefore, staking (AA) of the AB/XY (A = Ge, B = O, S, Se, Te, X = C, Sn, Si, Sn, and Y = Se, S) vdW heterostructures is the most stable structure configuration.

Fig. 2
figure 2

Geometrical structure before heating and after heating of GeO-CSe vdW heterostructure and thermal stability of (a) GeO-CSe, (b) SnS-GeSe, and (c) GeS-SiSe, (d) GeTe-SnSe vdW heterostructure using AIMD simulation

Full size image

To insight the electronic properties of monolayers and their vdW heterostructures, electronic band structure and partial density of states are investigated which are shown in Figs. 3 and 4, respectively. The calculated band gap of monolayers GeO, CSe, GeSe, SnS, GeS, SiSe, GeTe, and SnSe indicate that indirect band gap semiconducting nature shows good agreement to Ref. [18]. This confirms the accuracy of our calculations. The valence band maxima (VBM) and conduction band minima (CBM) of these monolayers are located at different symmetry points of Brillouin zone (BZ). Similarly, the vdW heterostructures GeO/CSe, GeSe/SnS, GeS/SiSe, and GeTe/SnSe possess narrow indirect band gap nature at high symmetry k-points, i.e., Γ-K-M- Γ in the BZ. The CBM of GeO/CSe is located at M-point, and VBM lies between Γ-K and M-Γ point. For GeSe/SnS, GeS/SiSe, and GeTe/SnSe, the lowest CB is found between Γ-M of Brillouin zone. A decreasing trend in band gap is found by construction of vdW heterostructures, as given in Table 2.

Fig. 3
figure 3

(Color online) Calculated band gap of monolayers (red) and heterostructures (pink), respectively

Full size image
Fig. 4
figure 4

(Color online) Partial density of state (PDOS) of AB/XY vdW heterostructures

Full size image

The partial density of states (PDOS) is crucial to investigate the band alignment of understudy vdW heterostructures, as shown in Fig. 4. In case of GeSe/SnS, the major contribution across the fermi level occurs due to the different monolayers, i.e., from GeSe and SnS. The valence band minimum (VBM) is due to S-px state in SnS, and conduction band maximum (CBM) is attributed by Ge-px state in GeSe monolayer, thus leading to type-II band alignment. For GeS/SiSe, GeTe/SnSe, and GeO/CSe heterobilayers, the VBM is mainly contributed by S-px, Se-px and C-px states in GeS, SnSe, and CSe, whereas CBM is dominated by Se-px, Ge-px, and Ge-px states in SiSe, GeTe, and GeO, indicating type-II band alignment. The localization of VBM and CBM from different layers is obtained without any external electric field, which is due to the intrinsic electric field induces because of bond bending by making vdW heterostructures. This induced field drive photogenerated electrons and holes in different directions. Thus, the photogenerated electrons and holes are spatially separated and indicating the practical realizations of the understudy heterostructures for promising solar cell applications [39].

Furthermore, for charge transfer, we have calculated the charge transfer difference, and the number of electron transfer is calculated by Bader charge analysis. The yellow and cyan areas in Fig. 5 represent electrons accumulation and depletion, respectively. One can easily see that electrons are transferred from GeO to SeC layer at the interface of GeO/CSe vdW heterostructures with total charge transfer of 0.0121 (see Fig. 5). Similarly, electrons are transferred from GeSe to SnS, GeS to SiSe, and GeTe to SnSe with total number of charge transfer of 0.0424, 0.0177, and 0.031, respectively (see Fig. 5).

Fig. 5
figure 5

Charge density difference of (a) GeO-CSe and (b) SiSe-GeS vdW heterostructures. The yellow and cyan areas represent electrons accumulation and depletion, respectively

Full size image

The Seebeck effect is the most fundamental approach to understand thermoelectric performance of a material. Chemical potential (µ) defines the doping level or carrier concentration in a material, which is very important for enhancing the thermoelectric nature of a material for practical realization. For n-type doping, µ has positive value and responsible for shifting up the fermi level, while for p-type doping, µ has negative value and shifts downward the fermi level. Transport parameters including Seebeck coefficient, electrical conductivity and power factor versus chemical potential (µ) are calculated using Boltzmann theory implemented within BoltzTrap code [36].

The Seebeck coefficient as a function of chemical potential at 300 K and 800 K temperatures is shown in Fig. 6. The calculated value of Seebeck coefficient of understudy vdW heterostructures (except GeO/CSe) is higher in n-type region than p-type doping level and further decreases with an increase in temperature from 300 to 800 K. The corresponding peak values of Seebeck coefficient at 300 K are 1620, 1166, and 1031 µV/K and further reduced to 623, 471, and 401 µV/K in n-type region at 800 K for GeSe/SnS, GeS/SiSe, and GeTe/SnSe heterostructures, respectively. However, GeO/CSe has p-type doping with maximum Seebeck values of 783 µV/K (at 300 K) and 289 µV/K (at 800 K). It has been reported that materials with Seebeck values larger than 200 µV/K are excellent for enhanced thermoelectric applications [40]. The corresponding heterostructures have considerable large Seebeck values, realizes their suitability for thermoelectric devices.

Fig. 6
figure 6

(Color online) Seebeck coefficient, electrical conductivity, and power factor of AB/XY vdW heterostructures

Full size image

In materials, the electrical conductivity arose both due to holes and electrons. In metals, the dominant part is due to electrons, whereas in semiconductor, both holes and electrons contribute to the electrical conductivity. To achieve good thermoelectric devices for commercial purposes, a higher electrical conductivity is required. The electronic structures of these materials underpin transport properties which are important to its use as the thermoelectric materials. The electrical conductivity (\(\sigma\)) as a function of chemical potential is investigated for AB/XY, as shown in Fig. 6. Figure 6 shows that at both temperatures 300 K and 800 K, \(\sigma\) is higher in p-type region for GeS/SnS and GeTe/SnSe and in n-type region for GeS/SiSe and GeO/CSe heterobilayers. At 300 K, the peak value of electrical conductivity is \(1.55 \times 10^{20}\) and \(1.81 \times 10^{20} \; 1/\Omega \cdot {\text{m}} \cdot {\text{s}}\) in p-type region for GeS/SnS and GeTe/SnSe, and \(1.06 \times 10^{20} \; {\text{and}}\; 3.05 \times 10^{20} 1/\) Ω·m·s in n-type region for GeS/SiSe and GeO/CSe, respectively. At 800 K, a small decrease in electrical conductivity is found with peak values \(1.5 \times 10^{20}\) and \(1.78 \times 10^{20} 1/\Omega \cdot {\text{m}} \cdot {\text{s}}\) in p-type region for GeS/SnS and GeTe/SnSe and \(1.0 \times 10^{20} \; {\text{and}}\; 2.93 \times 10^{20} 1/\) Ω·m·s in n-type region for GeS/SiSe and GeO/CSe, respectively. Among these heterobilayers, GeO/CSe possesses high electrical conductivity at both 300 K and at 800 K in n-type region, indicating electrons as major carriers.

To measure thermoelectric efficiency of a material, power factor (PF) is one of the key parameter and defined as PF = S2σ, where S and σ represents Seebeck coefficient and electrical conductivity of the material. The calculated values of the power factor for AB/XY heterostructures are given Fig. 6. Figure 6 shows that peak values of PF at both 300 K and 800 K in n-type region are greater than p-type. At 300 K, the power factor with maximum values are \(1.54 \times 10^{11}\), \({3}.{1} \times 10^{11}\), \(2.84 \times 10^{11} ,\) and \(2.91 \times 10^{11}\) W/\(K^{2}\) ms in n-type region, while a considerable increase is found at 800 K in n-type region with peak values \(2.8 \times 10^{11}\), \(6.14 \times 10^{11}\), \(5.25 \times 10^{11}\), and \(7.62 \times 10^{11 }\) W/\(K^{2}\) ms for GeS/SnS, GeS/SiSe, GeTe/SnSe, and GeO/CSe heterostructures, respectively. Further, it can be seen that GeO/CSe has large PF (at 800 K) because of smaller Seebeck coefficient and higher electrical conductivity than GeS/SnS, GeS/SiSe, and GeTe/SnSe, making it promising for thermoelectric applications.

4 Conclusions

In summary, we studied the structural, electronic, and thermoelectric properties of AB/XY van der Waals heterostructures based on group IV–VI monolayers. All GeS/SnS, GeSe/SiSe, GeTe/SnSe, and GeO/CSe heterostructures are energetically stable and exhibit semiconducting behavior with narrow indirect type-II band alignment. The understudy heterostructures have considerably large power factor in n-type doping, making them suitable for efficient thermoelectric applications at higher temperatures. Among these, GeO/CSe heterobilayer has comparatively large power factor at 800 K than 300 K, indicating it highly promising for thermoelectric devices. These results provide theoretical understanding for practical realization of designing van der Waals heterostructures of group IV–VI monolayers for future nanoelectronics and thermoelectric device applications.